Introduction

Scots pine (Pinus sylvestris L.) is one of the main forest tree species in high demand in Turkey and covers 1.4 million ha (6.2% of the total forest area) in Turkey (GDF 2015). Ecologically, Scots pine forests provide important ecological services such as protecting soil and water resources, mitigating, and adapting to the negative effects of climate change, and protecting biological diversity (Fischer et al. 2008; Lebedev 2022). Moreover, due to its valuable, versatile wood, it is in high demand and has high economic value. Last but not least, Scots pine forests that dominate the study region and Anatolian black pine (Pinus nigra Arnold. subsp. pallasiana Lamb.), trembling poplar (Populus tremula L.) and oriental beech (Fagus orientalis Lipsky) support a huge variety of wildlife worthy of consideration in a management strategy for the forest. To create planning and management strategies to protect these forests, reliable and accurate information on the status, growth and development characteristics of these forests is needed.

Tools capable of considering the structures and special attributes of Scots pine stands are required for managing these natural resources in a multifunctional approach. Detailed and accurate predictions of stand development under different management strategies often needed. Diameter classes help to obtain information such as stand structure, age distribution, and stand establishment that is needed to plan important silvicultural interventions. Knowledge on tree diameters, a principal factor in the production phase, is required because the type of machinery need for production and the transportation of the wood must be suitable for the diameters in the stands (Bailey and Dell 1973). Information needed for forest management studies such as estimates of the energy that can be obtained from biomass, carbon, or wood for each diameter class can be easily obtained with the help of diameter distribution models (Borders et al. 2008). Bankston et al. (2021) stated that the diameter distribution of a stand also gives information about the ecological or economic value of this stand. While the diameter distributions of the stands can provide information about stand structures that benefit different wildlife characteristics, estimating future product quantity from the relevant stand and its distribution for different commercial standards (paper production, timber, etc.) is economically important and will inform management design. Actual diameter distributions of the stand are needed to accurately estimate of growth and yield, and design management plans suitable for that forest. Management decisions about the management of forests are shaped by the current and future conditions of the resources. Since the volume and other properties of the tree depend on the diameter of the tree, the diameter distribution can characterize the properties of a stand quite well (Bailey and Dell 1973).

Forest resource managers benefit from knowing how much stand volume is distributed into different size classes at any given time. Diameter distribution models, which employ a probability density function (PDF) to distribute a stand feature over size classes such as diameter at breast height (DBH) or tree height, are of great importance for forest management decisions. Although the PDF is a continuous function defined by a parameter vector that does not have any direct biological significance on its own, it is used in many forestry studies to model the distribution of trees in stands in different diameter or height classes. Since the studies analyzing the diameter distribution numerically in the early 1900s until today, many PDFs have been used in modeling diameters such as lognormal, Weibull, Gamma, normal and Johnson’s SB (Fonseca et al. 2009; Mirzaei et al. 2016; Sun et al. 2019; Ogana et al. 2020; Araújo et al. 2021). Because of the flexibility of Johnson’s SB distribution for the possible shape that a tree diameter distribution can produce, we selected it as the most appropriate for our study. In addition, the ease of integration of the cumulative density function (CDF) (Zhang et al. 2003) is a considerable advantage. Finally, the relative forest literature supports the Johnsons SB distribution use for tree: (1) diameter description (Hafley and Schreuder 1977; Lopes 2001; Kiviste et al. 2003; Parresol 2003; Fonseca 2004; Özçelik et al. 2016; Ogana et al. 2017; Gorgoso-Varela et al. 2020; Vega et al. 2022), (2) height (Hafley and Schreuder 1977), and (3) volume ratio (Newberry and Burk 1985). However, it is a difficult procedure to select the appropriate theoretical distribution that can model the source of randomness appropriately in the study variable. For this reason, we used probability theory to express the likelihood of chance as a source for the difference in end outcome. On the other hand, a distribution’s parameter recovery method has to be carefully selected, so as to produce reliable results. Furthermore, if there are no trees in some diameter classes, then both the sampling error and the sampling distribution of these classes may lead to a violation of regression assumptions. Free of such assumptions and due to its computational efficiency, in order to overcome the above difficulties, the support vector machine (SVM) learning methodology (Vapnik et al. 1997; Basak et al. 2007; García-Nieto et al. 2012; Gu et al. 2016) with the support vector regression (SVR) procedure was used to simulate as accurately as possible the empirical diameter distribution of the ground truth data to predict the structure of a stand. Previous studies highlighted the effectiveness of the support vector machine methodology for solving forest modeling problems. Guo et al. (2005) applied SVMs to predict the distribution of sudden oak death in California, Monnet et al. (2011) showed that the support vector regression models adequately predicted dominant tree height, basal area, mean diameter, and stem density, and Jiao et al. (2012) used SVR methodology to estimate timber volume. SVM approaches were also used by Diamantopoulou et al. (2018) to predict tree bark volume, by Nguyen et al. (2019) to classify tree species, and by Iizuka et al. (2022) to estimate DBH of Japanese cypress.

DBH values for trees are related to basal area, stand density and tree volume determination, and can be used for downscaling from stand-level information to tree level (Newton et al. 2005). However, the available information concerning the diameter distribution of Scots pine species is highly limited, and no such models have been developed for the Türkmen Mountain region. For this purpose, Johnson’s SB distribution was used due to its flexible structure in representing or explaining biological variables. The three-parameter recovery approach, which is based on the percentile moment method suggested by Fonseca et al. (2009), was used to estimate the model’s parameters. Furthermore, the support vector machine for regression methodology was used for the simulation based on the empirical diameter distribution modeling. The use of support vector methodology is a fairly new approach for diameter distribution modeling and has not been used for Scots pine stands.

Materials and methods

Study area

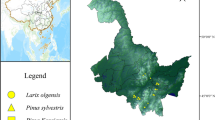
The study region is between 39°16′ and 39°38′ N and 30°06′ and 30°36′ E on Turkmen Mountain (Fig. 1). Rhyolite and dacite are the most common geological parent minerals in the study area; others are also present, e.g., basalt, claystone, and limestone. Grey brown and podsolic grey brown forest soils are the most common soil types (Güner 2006). The mean annual temperature is from 10.6 °C to 11.1 °C, and annual precipitation is between 374 and 562 mm, according to data from meteorological stations in Eskişehir, Kütahya, and Afyonkarahisar. In the Thornthwaite water-balancing system, the climate type of the research region ranges between semihumid and humid (Güner 2006). Scots pine dominates the research area. The other main plant species in the study area are Anatolian black pine, trembling poplar, and oriental beech.

Fig. 1
figure 1

Location of study area in Turkey

Full size image

In natural stands, sample plots were carefully selected to reflect all the existing variability such as site, stand age and stand density. Plot size varied between 200 and 300 m2, depending on the density of the stands. All trees in the sample plots (total 1219) were numbered, then the diameters of all trees at 1.30 m height were measured. The height of some trees was measured with an accuracy of 0.1 m using Blume-Leiss ALTimeter (Carl Leiss Berlin, Berlin, Germany) to estimate stand height. In addition, for each plot, variables such as average diameter (\(\overline{d }\)), quadratic mean diameter (\({d}_{g}\)), number of trees per hectare (\(N\)), basal area per hectare (\(G\)), minimum diameter (\({d}_{min}\)), maximum diameter (\({d}_{max}\)), and median diameter (\({d}_{0.50}\)) were calculated. Descriptive statistics (mean, maximum, and minimum values and SD) of the main stand variables are given in Table 1.

Table 1 Descriptive statistics for stand variables used to develop diameter distribution models (1219 trees from 55 plots)
Full size table

The SB distribution and localization of the empirical distributions

Due to the moment statistics ability to provide sufficient information to construct a frequency distribution function, the third standardized moment (skewness, β1) and the fourth standardized moment (kurtosis, β2) were used to estimate and evaluate the asymmetry (left or right skewed distribution) and kurtosis (heavy- or light-tailed distribution) of our ground-truth data, respectively. To obtain the estimator \(\left(\sqrt{{b}_{1}}\right)\) of the coefficient of skewness, the centered third-order moment was divided by the sample standard deviation raised to the third power. The estimated skewness \(\left(\sqrt{{b}_{1}}\right)\) values ranged from − 1.47 to 1.20. The estimator \(\left({b}_{2}\right)\) of kurtosis was obtained by dividing the centered fourth-order moment by the sample standard deviation raised to the fourth power. The estimated kurtosis values ranged from − 1.50 to 4.36. Figure 2 shows these estimates in the (\({\beta }_{1}, {\beta }_{2}\)) space with two reference lines. \({\beta }_{1}\) represents the square of the standardized measure of skewness and \({\beta }_{2}\) is the standardized measure of kurtosis. Some combinations of \({\beta }_{1}\) and \({\beta }_{2}\) are mathematically impossible and occur above the \({\beta }_{1}-{\beta }_{2}-1=0\) line. In Fig. 2, 54 empirical distributions are in the \({\mathrm{S}}_{\mathrm{B}}\) region (some of which are quite close to the \({\mathrm{S}}_{\mathrm{L}}\) region) and the remaining one is in the \({S}_{\mathrm{U}}\) region. Figure 2 shows that the diameter distribution for approximately 1.8% of the sample areas used in the study can be better represented by another distribution instead of Johnson’s SB distribution.

Fig. 2
figure 2

Representation of the observations in the (\({\beta }_{1}, {\beta }_{2}\)) space of skewness squared and kurtosis

Full size image

Johnson’s SB probability density function is one of the components of Johnson’s distribution function family, which was first introduced by Johnson (1949). This distribution system consists of SU, SL and SB distributions which are for unbounded variates, variates bounded at one end, and bounded from below to above, respectively. The PDF for a variable X which follows an SB PDF can be expressed as:

$$f\left( x \right) = \frac{\delta \lambda }{{\sqrt {2\pi } \left( {x - \xi } \right)\left( {\xi + \lambda - x} \right)}}\exp \left( { - \frac{1}{2}\left[ {\gamma + \delta \ln \left( {\frac{x - \xi }{{\xi + \lambda - x}}} \right)} \right]^{2} } \right),\;x \in \left( {\xi ,\xi + \lambda } \right),$$
(1)

where, \(f\left(x\right)\) is the probability density associated with diameter \(x\); λ, δ > 0, − ∞ < ξ < ∞, − ∞ < γ < ∞. The parameter λ gives the range parameter, ξ is the location parameter and represents lower bond, δ and γ are shape parameters, and γ = 0 indicates symmetry.

The SB PDF can represent variables that have natural or physical constraints on their range thanks to the lower (ξ) and upper (ξ + λ) bounds. Moreover, a remarkable amount of flexibility to fit a wide range of distribution can be achieved by two parameters (δ and γ) which control the shape. These attributes of the Johnson’s SB PDF make this distribution system suitable for representing the biological variables (Fonseca et al. 2009).

The approaches commonly used to estimate Johnson’s SB distribution parameters are the linear and nonlinear regression, maximum likelihood, percentile and the moment methods. However, for most of these techniques, knowledge of the distribution boundaries is essential. The use of Johnson’s SB distribution for diameter distribution in growth and yield models and the use of parameter prediction or parameter recovery methods for parameter estimation have been tested, albeit in limited numbers (Özçelik et al. 2016). However, the parameter prediction method has some important disadvantages such as not being able to provide a match between the estimated stand value and the stand value obtained from the distribution, along with the possibility that a very small part of the variation in the parameters will be explained by the stand variables. For example, the shape parameter of the function shows a very weak relationship with age. Better results will be obtained with the parameter recovery-based approach (Scolforo et al. 2003; Fonseca 2004).

Three-parameter recovery method (3-PRM)

Extreme diameter values in the sample data set were used to estimate the location and range parameters of the Johnson’s SB PDF distribution, which has been converted from a four-parameter to a three-parameter distribution. The remaining parameters of the distribution model can be estimated using a percentile or moment method. Scolforo et al. (2003) defined a moment method to estimate the shape parameters. Parresol (2003) developed a percent-moment method for simultaneous solution of range and shape parameters. Alternatively, it can be used to directly estimate average stand properties using parameter recovery models and then to estimate the base diameter distribution. The parameter recovery method provides compatibility between the stand characteristics estimated from the regression and created from the distribution function. For applying the parameter recovery method, the equation system should include certain tree characteristics, and SB parameters should be developed (Fonseca et al. 2009).

Parresol (2003) introduced a new estimation approach for the recovery of three parameters. In the method, a parameter recovery method has been developed for the range and shape parameters by using the median, first and second noncentral moments of the diameter distribution in general. In this approach, the location parameter is also estimated. Parresol (2003) estimated the location parameter ξ using a regression technique to extrapolate the random variable breast height diameter (d) to the lower bound. Using this estimated location parameter and the transformation given by Johnson and Kotz (1970), the two shape and range parameters can be solved. Although there is no closed form expression for the SB probability density function (PDF), if the random variable is X ~ SB (δ, λ, γ, δ), where \(X\) is the diameter (Parresol 2003; Fonseca et al. 2009), then

$$z = \gamma + \delta {\text{ln}}\left[ {\frac{{\left( {x - \xi } \right)}}{{\left( {\xi + \lambda - x} \right)}}} \right]\sim N \left( {0, 1} \right)$$
(2)

Given a new variable,

$$y = \frac{{\left( {x - \xi } \right)}}{\lambda },$$
(3)

It follows from Eq. 2 that

$$z = \gamma + \delta {\text{ln}}\left[ {\frac{y}{{\left( {1 - y} \right)}}} \right] \sim N \left( {0, 1} \right).$$
(4)

The new random variable \(Y\) will follow a distribution with the same shape parameters as \(X\) (Johnson and Kotz 1970). Using the \(Y\) random variable, the SB PDF Eq. (1) becomes (Parresol 2003; Fonseca et al. 2009):

$$f\left( y \right) = \frac{\delta }{{y\left( {1 - y} \right)\sqrt {2\pi } }}{\text{exp}}\left( { - \frac{1}{2}\left[ {\gamma + \delta ln\left( {\frac{y}{1 - y}} \right)} \right]^{2} } \right), 0 < y < 1.$$
(5)

Setting z in Eq. (4) equal to 0 and rearranging in terms of parameter γ gives

$$\gamma = \delta {\text{ln}}\left( {\frac{1}{{y_{0.50} }} - 1} \right),$$
(6)

where \(y_{0.50}\) is the median of \(Y\).

Following the expected value of \(X^{p}\) in terms of the \(Y\) variable, then

$$\overline{d} = \xi + \lambda \mu_{1}^{^{\prime}} \left( Y \right)$$
(7)
$$dg^{2} = {\text{E}}\left( {\xi + \lambda Y} \right)^{2} = \xi^{2} + 2\xi \lambda \mu_{1}^{^{\prime}} \left( Y \right) + \lambda^{2} \mu_{2}^{^{\prime}} \left( Y \right)$$
(8)

where \({\mu }_{1}^{^{\prime}}\left(Y\right)\) and \({\mu }_{2}^{^{\prime}}(Y)\) are first and second noncentral moment of distribution of Y, respectively. \(\overline{d }\) is the average tree diameter. Equation 7 denotes average tree diameter (\(\overline{d }\)) as a function the first noncentral moment of Y. It is worth noticing that Eq. 8 is a function of the first two noncentral moments of \(Y\). The quadratic mean diameter (dg) is functionally related to the number of trees per unit area (\(N\)) and basal area per unit area \(\left(G\right):G=kNd{g}^{2}\), \(\mathrm{where }k\) is the conversion factor for the basal area per square meter \(\left(k=\frac{\pi }{40000}\right)\). Hence, Eq. 8 is equivalent to

$$G = kN\left[ {\xi^{2} + 2\xi \lambda \mu_{1}^{^{\prime}} \left( Y \right) + \lambda^{2} \mu_{2}^{^{\prime}} \left( Y \right)} \right].$$
(9)

Because z is a unit normal variance, the rth noncentral moment of Y is

$$\mu_{r}^{^{\prime}} \left( Y \right) = \frac{1}{{\sqrt {2{\uppi }} }}\mathop \smallint \limits_{ - \infty }^{ + \infty } \left[ {1 + {\text{e}}^{{ - \frac{z - \gamma }{\delta }}} } \right]^{ - r} {\text{e}}^{{ - z^{2} /2}} dz$$
(10)

As indicated by Fonseca et al. (2009), the relationship in Eq. 6 is first used to eliminate γ in Eqs. 7 and 9 by substitution in Eq. 10. The solution system of the two equations and the two unknown parameters is nonlinear and must be solved by numerical procedures (see Parresol 2003 for details). Given the estimates of \(G\), \(N\), \(\overline{d }\), median tree diameter (d0.50), and location parameter, and Eqs. 7 and 9, the system of equations for δ and λ must be solved by iteration. The parameter γ is then found from Eq. 6.

As a result, ξ is predetermined, λ and δ are solved by iteration using Eqs. 7 and 9, and then the range parameter γ is solved with the help of Eq. 6. More details on technical solution for the three-parameter recovery approach can be found in Parresol (2003) and Fonseca et al. (2009). Parameters of Johnson’s SB distribution were estimated in SAS 9.2 (SAS Institute, Cary, NC, USA) with the parameter recovery method based on the percent-moment method. This program is implemented with the nonlinear Levenberg–Marquardt (NLPLM) method with the help of the interactive matrix language CAPABILITY subroutine (SAS Institute 2010). Detailed information can be found in Parresol et al. (2010).

Support vector regression models (SVRs)

The support vector regression modeling approach belongs to the type of supervised machine learning algorithms and can be considered as a generalization of the support vector machine (SVM) methodology for regression-type problems (Vapnik 1995, 1998, 1999, 2000; Vapnik et al. 1997). The SVR methodology represents a promising nonparametric learning algorithm with surprising characteristics such as the recognition of all patterns in the available data set. The methodology used in this paper is the SVR with the ε-insensitive loss function based on the determination of the support vectors (SVs) that produced an ε-insensitive tube, supported by the nonlinear kernel functions (Smola and Schölkopf 2004). That is, in order for the learning error to be disclosed for the nonlinear SVR, the input vector x (training sample) with a dimension mapped onto a higher dimensional space (let’s say n-dimensional space) via the fixed nonlinear mapping function \(\varphi (x)\in {R}^{n}\), a linear combination is constructed:

$$f\left( x \right) = \left[ {w,\varphi \left( x \right)} \right] + b,$$
(11)

with \(\left(x\right)\in R\), that due to φ(x) leads to a nonlinear function. By ignoring the errors that are within the ε-insensitive tube, the function is minimized:

$${\text{min}}\frac{1}{2} ||w||^{2} + C\mathop \sum \limits_{i = 1}^{{\text{n}}} \xi_{i} + \xi_{i}^{^{\prime}}$$
(12)
$${\text{with constraints}}:\;\left\{ {\begin{array}{*{20}c} {y_{i} - f\left( x \right) \le \varepsilon + \xi_{i}^{^{\prime}} } \\ {f\left( x \right) - y_{i} - \le \varepsilon + \xi_{i} } \\ {\xi_{i} , \xi_{i}^{^{\prime}} \ge 0, i = 1, \ldots ,n} \\ \end{array} } \right.$$
(13)

where yi is the output value, w denotes the weight parameters, C is the parameter that represents the smoothness of the model, and \({\xi }_{i}\) and \({\xi }_{\iota }^{^{\prime}}\) are slack variables (Fig. 3), that show the deviation of points outside the ε-insensitive zone.

Fig. 3
figure 3

Representation of ε-SVR mapping

Full size image

For the input vector x to be mapped onto a higher dimensional feature space, the Gaussian radial basis function (RBF) kernels was used:

$$k\left( {x,x^{\prime}} \right) = \exp \left( { - \gamma_{{{\text{SVR}}}} x_{i} - x_{j}^{2} } \right),\gamma_{{{\text{SVR}}}} > 0$$
(14)

where \(\gamma_{{{\text{SVR}}}} = \left( {{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {2\sigma^{2} }$}}} \right)\) is the free parameter of the RBF kernels and \(\Vert {x}_{i}-{x}_{j}\Vert\) is the Euclidean distance between the support vectors (SV).

From the above, it is clear that the robustness and the effectiveness of an ε-SVR model depends on three meta-parameters: ε, that determines the width of the ε-insensitive zone; \({\gamma }_{\mathrm{SVR}}\), the parameter that depends on the variance of the training samples (σ2) and thus sets the spread of the kernel; C, the cost parameter, (which can balance the resulting inaccuracy against the desired simplicity of the constructed ε-SVR model.

For the construction of the ε-SVR model, the programming language Python 3.9 (Van Rossum and Drake 2011; Python Software Foundation 2022) and libraries of scikit-learn (Pedregosa et al. 2011) were used. The state-of-the-practice approach utilized for a machine learning model construction (Olson and Delen, 2008), includes the 90% and 10% percentages division for the fitting and testing data sets, respectively. For this purpose, the available data set of the trees of the 55 sample plots was randomly divided into fitting (90% of the total sample plots) and testing (the remaining 10% of the total sample plots) samples to test the predictive ability of the constructed ε-SVR model for new, never-seen data in its construction phase. Furthermore, to prevent overfitting for the best generalization of the constructed ε-SVR model, the k = tenfold cross validation procedure was applied to the fitting data set.

Finally, for a quantitative approach of the concentration of the empirical data around the ε-SVR model fit, the root mean square error (RMSE) function from scikit-learn metrics library was used (Pedregosa et al. 2011) to produce a risk metric that corresponded to the expected values of the root squared (quadratic) error or loss by the ε-SVR model fit.

Evaluation of the simulated distributions using different approaches

For testing the simulated diameter distributions using different approaches, the diameter class width of 5 cm was selected as the most accepted one. The error index (EI) introduced by Reynolds et al. (1988) was calculated related to the basal area of the diameter class as a function of weight as can be calculated as an exact value. Moreover, using the basal area as the weight factor ensures that the different dimensions of the tree bole would be considered in the economic evaluation of the trees (Fonseca et al. 2009; Özçelik et al. 2016). The formula for the error index (EI) is given as:

$${\text{EI}} = \mathop \sum \limits_{j = 1}^{{\text{M}}} \left| {G_{j} - \hat{G}_{j} } \right| = \mathop \sum \limits_{j = 1}^{{\text{M}}} \left| {\mathop \smallint \limits_{{C_{j} }}^{ } \frac{{{\uppi }x^{2} }}{4}\left[ {\hat{f}\left( x \right) - f_{{{\text{emp}}}} \left( x \right)} \right]dx} \right|,$$
(15)

where M is the number of diameter classes, \({G}_{i}\) is the observed basal area of the jth diameter class, \({\widehat{G}}_{j}\) is the predicted basal area of the jth diameter class,\({C}_{j}\) denotes diameter class number j, and \(\widehat{f}\) is the function of the different approaches used for the diameter distribution simulation.

Results

For presenting the values of the parameter estimates obtained from the 55 sample plots using the three-parameter recovery method based on the percent-moment method, the parameter estimations obtained by the simulated Johnson’s SB distribution for the first 10 sample plots are given in Table 2. Similar results were obtained for the rest of the plots. According to the three-parameter solution method introduced by Parresol (2003), two parameters (range and lambda) and both shape parameters (gamma and delta) of the four parameter Johnson’s SB distribution that were estimated for all sample plots, the L1-norm (output variable, which should have a value close to zero) values (Parresol et al. 2010), for almost all sample plots were quite small similar to the results given in Table 2. A delta value less than 0.7 generally indicates a bimodal distribution. More than half of the δ values for the 55 sample areas were less than 0.7. As seen in Fig. 2, Johnson’s SB distribution cover a broad spectrum of shapes, fitting both positively and negatively skewed data. As indicated by Parresol (2003), because the Johnson’s SB distribution is obtained by transformation of a standard normal variate, integration over specific classes can be accomplished by application of the well-tabulated standard normal. Further, the distribution can easily be extended to multivariate forms.

Table 2 Parameter estimates for the first 10 sample plots obtained with Johnson’s SB PDF
Full size table

As for the simulated diameter distribution by the constructed ε-support vector regression (ε-SVR) model using the radial basis function (RBF) kernel, the best combination of the set of ε, the \({\gamma }_{\mathrm{SVR}}\) parameter, and the cost parameter (C) was explored (Fig. 3) by the grid search method (Pedregosa et al. 2011). The grid-search method was used to test and evaluate all possible combinations of the parameters’ values that comprised the grid. Specifically, the tested ε values ranged from 0.00 to 0.45 in steps of 0.01, \({\gamma }_{\mathrm{SVR}}\) from 0.00 to 1.00 in steps of 0.01, while the tested C values ranged from 4 to 30 in steps of 1.

The root mean square error (RMSE; as the square root of the mean of the squares of the deviations between the observed and the predicted by the ε-SVR model diameter values) was used as the statistical evaluation criterion that represented the adaptation of the model to the fitting data set along with its predictive ability to the testing data set, respectively. This measure was used for a quantitative approach of the empirical data concentration around the ε-SVR model fit. Finally, the combination that gave the smallest root mean square errors for both the fitting and the testing data set was ε = 0.01, \({\gamma }_{\mathrm{SVR}}\)= 0.01 and C = 10, with RMSE equal to 1.1152 and 1.1183 for the fitting (training plus validation data sets) and the test data sets, respectively (Fig. 4).

Fig. 4
figure 4

Best combination of ε-SVR parameters as produced by the grid search method

Full size image

Although the behavior of the simulated distributions by both approaches was evaluated for the total available data set of the 1219 trees, it was considered as significant information, and the specific simulation ability of the different approaches according to the small number of trees of each plot separately was also evaluated. The diameter distribution simulation of both approaches for plots 1, 2, and 5–10 plots in Table 2 is shown in Fig. 5. As can be seen, the simulation of both models is more or less acceptable for all plots, with the Johnson’s SΒ distribution outperforming for plots 1, 2 and 5.

Fig. 5
figure 5

Observed and simulated diameter distributions by both methods for sample plots 1, 2 and 5–10

Full size image

The experimental distribution for the sample plot 10 showed a typical right-tie flat distribution while the simulated ε-SVR distribution was a multi-modal distribution. As can be seen, the ε-SVR model showed the ability to capture the diameter distribution pattern of plot 10, except for the case of the 25 cm diameter class (Fig. 5).

For examining the reliability of the simulated distribution using both Johnson’s SB distribution and the constructed SVR model, plots of the experimental distributions and the observed distributions for sample plots 4, 15, and 35, are given in Fig. 6. The motivation behind the usage of these plots was to explore the adaptation of the simulated distributions to the actual slightly skewed distribution. The experimental Johnson’s SB distribution was constructed with δ values less than 0.7 and, according to the 35-sample plot, γ value equal to 0.02. On the other hand, delta, and gamma values for the sample plot 35 showed a left-skewed bimodal distribution with δ = 0.5 and γ = − 0.59 (Fig. 6). As can be seen (Fig. 6) the ε-SVR constructed model gave well-shaped curves that followed the original curve shape. As for the 35-plot, the constructed ε-SVR distribution showed a significant peak of diameter in the 27.5–32.5 cm diameter class. Despite this fact, the distribution simulation by the SVR model can be considered as a successful diameter distribution.

Fig. 6
figure 6

Observed and simulated diameter distributions by the SVR model and Johnson’s SB distribution for sample plots 4, 15, and 35

Full size image

The shape of the 18- and 26-plot distributions are shown in Fig. 7. As can be seen (Fig. 7), the simulated distributions for the 18-plot were sufficient, producing unimodal and uniform distribution patterns for both approaches, while for plot 26, Johnson’s SB simulation produced a bimodal distribution. According to plot 26, for the estimated distribution obtained with the help of Johnson’s SB distribution, the peak values are at 15 cm and 30 cm, while in the observed distribution, the peak value is at 25 cm. As for the SVR approach, the simulated peak was followed the actual distribution’s peak (plot 26). Although for both approaches, partial differences between the observed distribution and the estimated distribution were observed, the diameter distribution was sufficient.

Fig. 7
figure 7

Observed and simulated diameter distributions by both methods for sample plots 18 and 26

Full size image

However, in some sample areas with quite a small number of trees, the estimates with both approaches (Johnson’s SB distribution and SVR model) seem to be quite unsuccessful as for plot 16 (Fig. 8). Quite large differences were observed between the values for estimated distributions and the observed distribution for the sample plot area 16, which includes measured diameters for 15 trees. On the contrary, according to those sample plots that include a relatively large number of trees, for example, plot 3, with measured diameters of 33 trees, the simulated distributions for both approaches were considered as adequate (Fig. 8).

Fig. 8
figure 8

Observed and simulated diameter distributions by both methods for sample plots 3 and 16

Full size image

For evaluating the simulation behavior of the methods applied, the summary statistics of the error index (EI) values for both approaches are given in Table 3.The EI values for 55 sample plots ranged from 2.67 to 28.57 and 4.92 to 13.76 with mean error index values equal to 13.61 and 9.25 and median values equal to 13.88 and 9.27 for the simulation using Johnson’s SB distribution and the ε-SVR model, respectively. Furthermore, the proportion of plots that produced lower values of error index was found equal to 72.73% for the ε-SVR approach, meaning that the diameter distribution simulation by the constructed ε-SVR model was more reliable than the simulation derived by Johnson’s SB distribution for 45 plots, while according to the remaining 15 plots, the Johnson’s SB distribution produced simulation with better accuracy.

Table 3 Summary statistics of the error index (EI) values for the different methods
Full size table

For both methods, the EI values for each sample plot are given in Fig. 9a and the frequency distribution of the EI values in Fig. 9b; the error distribution values for the sample plots can thus be seen to vary. Johnson’s SB distribution gave larger errors for most of the plots than those derived from the simulated distribution using the constructed ε-SVR model (Fig. 9a). In general, as seen from Fig. 9b, a significant part of the EI values for the sample plots are between 4 and 26 m2/ha for Johnson’s SB distribution and between 4 and 14 m2/ha for the ε-SVR model, meaning that the ε-SVR model adequately simulated the diameter distribution for most of the sample plots.

Fig. 9
figure 9

Error index values for each plot (a) and their frequency distribution (b)using the SVR model and Johnson’s SB method

Full size image

Discussion

To explore the use of a machine learning model, such as a support vector regression model, to reliably describe the diameter distribution of a natural Scots pine stand, as an alternative procedure to the known, accepted theoretical distribution method, such as the Johnson’s SB distribution, we used a three-parameter recovery method based on the percentile-moment method to estimate parameters of Johnson’s SB PDF. This distribution was preferred because it allows modeling of different distribution patterns due to its two shape parameters and enables better representation of biological variables (Fonseca et al. 2009; Özçelik et al. 2016). Many studies have shown that Johnson's SB distribution produces remarkably successful results in describing the diameter distributions (Kiviste et al. 2003; Parresol 2003; Lei 2008; Fonseca et al. 2009; Mateus and Tomé 2011; Özçelik et al. 2016).

Further, due to its nonparametric nature and ability to revelal unknown relationships among real world data, the machine learning method support vector regression (SVR) was used (Wang et. al. 2009; Alonso et al. 2013; Diamantopoulou et al. 2018). Specifically, the non-linear ε-SVR algorithm, including the radial basis function (RBF) kernel was used to simulate the distribution of diameter classes of pine trees. Because of the discontinuous nature of the number of trees in each diameter class, the continuous numbers produced by the ε-SVR model were considered equal to the nearest integer.

Data required in this study were obtained from various Scots pine stands in the Türkmen Mountain region. The adaptation of the simulated distributions developed with the Johnson’s SB PDF and the ε-SVR model in this study was evaluated using error index values. For this purpose, diameter classes of 5-cm intervals were created. The basal area is used as a weight function for the error index calculation, since, on one hand, it can be calculated as an exact value and, on the other hand, it considers dimensional differences between trees (Fonseca et al. 2009; Özçelik et al. 2016).

The statistical evaluations revealed that the diameter distribution of the natural Scots pine stands in the Türkmen Mountain region can be modeled successfully with both modeling approaches tested. According to the simulated distributions for the whole pine stand (Fig. 10) examined in this study, it is obvious that both simulated distributions can reliably estimate the basal area of the forest per diameter class and per hectare.

Fig. 10
figure 10

Simulated distributions of basal areas for the whole tree stand using the SVR model and Johnson’s SB method

Full size image

The diameter distribution of some stands was bimodal, others were unimodal, and some were right or left skewed. Due to their features, both the simulated distributions have been found to be successful approaches in describing the ground truth behavior of the tree diameter distribution. Specifically, the most important advantage of estimating the parameters of Johnson’s SB distribution with the parameter recovery method is that it allows estimating the future diameter distributions in growth and yield models, by producing significant information about forecasting the number of trees in a stand by diameter classes. However, the maximum likelihood method cannot be used directly for this purpose. According to the support vector regression approach, it showed great ability for describing the tree diameter distribution, providing a significant alternative to theoretical distribution.

The selection of the appropriate methodology that enables unbiased and accurate diameter distribution simulations requires a multifaceted design that takes into account the nature of the model and its applicability both in the field and in the office. In addition, this decision also requires setting the appropriate priorities for prediction accuracy and convenience. In this context, the two approaches compared in this study make use of the same sample size and data and therefore involve the same field effort. Given the obtained results, the ε-SVR approach enables the adequate capture and simulation of the complex, nonlinear structure of the diameter distributions without the need for first specifying the model form. This is not the case for other nonlinear modeling techniques. As far as office work is concerned, both modeling approaches require extensive knowledge, programming skills, and the corresponding effort to apply the constructed approach. Specifically, given the SVR modeling approach, it is worth noting that the ε-SVR model was constructed using the freely available programming language, (Python). Using Python’s export capabilities, the ε-SVR models can be exported into file(s) and thus very easily loaded and used by a third-party user. Of course, requirements such as proper equipment or skills that are needed for the application of the ε-support vector regression models are not always met in practical forestry. Despite this fact, potential users can gain the experience, knowledge, and accuracy needed for predictions and using advanced models. When convenience is the limiting factor in a survey, loss of prediction accuracy should be seriously taken into account.

Conclusions

For the natural Scots pine forests in the Türkmen Mountain region, which have quite different stand structures due to ongoing destruction over many years, both parametric and nonparametric modeling approaches (Johnson’s SB function and the support vector regression (SVR) procedure, respectively) were tested as accurate and reliable diameter distribution models that can easily fit an empirical diameter frequency distribution. Johnson’s SB probability density function based on the percentile moment approach, due to its flexibility according to the possible shape that a tree diameter distribution, produced a reliable tool to describe the empirical diameter distribution of the pine trees. However, a predetermined function is a requirement for this approach. On the other hand, the data-driven support vector regression modeling, a nonparametric supervised learning algorithm with the ε-insensitive loss function supported by nonlinear kernel functions, provided the desired characteristics (e.g., recognition of all patterns in the available data set) and insignificant ones.

Users can gain the experience, knowledge, and prediction accuracy needed to use advanced models such as the ε-SVR model. In other words, the ε-SVR algorithm has potential to accurately simulate the diameter distribution dynamics and thus can be safely used as a data-driven alternative for the efficient management of a forest ecosystem.