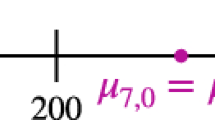Abstract
A model for thermal convection with generalized friction is investigated. It is shown that the linear instability threshold is the same as the global stability one. In addition, decay of the energy in the \(L^2\) norm is shown for the perturbation velocity and temperature fields. However, due to the presence of the generalized friction we establish exponential decay in the \(L^{\beta +1}\) norm for the perturbation temperature, where \(\beta >1\).
Similar content being viewed by others
1 Introduction
In a recent paper [1] have proposed a model for thermal convection in a linearly viscous fluid which is subject to a generalized friction term. [1] study the existence and regularity questions for their model.
The generalized friction consists of a term of form \(-\vert \mathbf{v}\vert ^{\beta -1}v_i\) for a constant \(\beta >1\), where \(v_i\) is the velocity. In porous medium flow such a term is known as a generalized Forchheimer term, cf. [2], chapter 1. The buoyancy effect which drives thermally convective motion is introduced via a Boussinesq approximation, see e.g. [3], pp. 16–21.
The goal of this paper is to study the stability of the steady conduction solution to the model of [1]. We demonstrate an optimum result in that we show the linear instability threshold for the Rayleigh number coincides with the global nonlinear stability one. The energy decay is in \(L^2(V)\) for the velocity perturbation \(u_i\), and the temperature perturbation \(\theta \), where V is a period cell for the solution. However, we here show that the generalized friction term allows one to demonstrate exponential decay of \(\theta \) in the \(L^{\beta +1}(V)\) norm, for \(\beta >1\).
2 Thermal convection equations
The governing equations presented by [1] have form
In these equations \(v_i(\mathbf{x},t),p(\mathbf{x},t)\) and \(T(\mathbf{x},t)\) denote the velocity, pressure and temperature at position \(\mathbf{x}\) and time t. Furthermore, \(\rho _0,\nu ,\omega ,g,{\hat{\alpha }},\beta ,\kappa \) denote the reference density, kinematic viscosity, thermal expansion coefficient, gravity, friction coefficient, friction index, and thermal diffusivity. Throughout this article we employ standard indicial notation in conjunction with the Einstein summation convention, so for example,
where \(\mathbf{v}\equiv (u,v,w)\) and \(\mathbf{x}\equiv (x,y,z)\). For a nonlinear example
The term \(\Delta \) denotes the Laplacian in \({\mathbb R}^3\).
Equation (1) are defined on the horizontal layer \(\{(x,y)\in \mathbb {R}^2\}\times \{z\in (0,d)\}\) for \(t>0\). The boundary conditions are that
\(0<T_U<T_L\), with \(T_L\,,T_U\) constants.
The steady conduction solution to Eqs. (1), (2) in whose stability we are interested has form
where \(\gamma \) is the temperature gradient,
The steady pressure is a quadratic function of z determined from (1)\(_1\) .
To proceed we define perturbation variables \(u_i,\theta ,\pi \) by
These expressions are now substituted into Eq. (1) and are non-dimensionalized with the scalings
and the Rayleigh number Ra is introduced as
In this way we arrive at the non-dimensional perturbation equations, where the *s are dropped,
where (4) hold on \(\mathbb {R}^2\times (0,1)\times \{t>0\}\), with \(w\equiv u_3\). The non-dimensional perturbation boundary conditions are
together with horizontal periodicity of the solution, cf. [4], p. 51. The period cell of the solution is denoted by V.
3 Global nonlinear stability
Before we commence a global nonlinear stability analysis for Eqs. (4), (5), we observe that an analogous problem for the Navier–Stokes equations, i.e. the system
has been analysed by other writers. [5] establish extensive existence, regularity and evolutionary behaviour results for a solution to (6).
For system (4), (5), the linear operator is symmetric and thus the linear instability threshold coincides with the nonlinear stability one, cf. [6, 4], chapter 4. For clarification we multiply Eq. (4)\(_1\) by \(u_i\), we multiply equation (4)\(_3\) by \(\theta \), and integrate each resulting equation over V. Add the resulting equations and after some integration by parts and use of the boundary conditions one may deduce the energy equation.
where the energy function is given by
the dissipation is
and the production term has form
where \((\cdot ,\cdot )\) and \(\Vert \cdot \Vert \) denote the inner product and norm on \(L^2(V)\).
From (7) we discard the \(\Vert \mathbf{u}\Vert ^{\beta +1}_{\beta +1}\) term and then derive
where
H being the space of admissible solutions. One may now show that the Euler-Lagrange equations which arise from (9) have exactly the same form as the linear instability equations which arise from (4). Thus, we obtain the optimal result that the linear instability boundary is the same as the nonlinear stability one, and provided \(R<R_E\) the stability is global. In addition, one shows \(\Vert \mathbf{u}\Vert \) and \(\Vert \theta \Vert \) decay at least exponentially.
This may be improved upon by considering the \(L^{\beta +1}\) norm for \(\theta \). To see this note that from (4)\(_3\), cf. [7],
We next employ Poincaré’s inequality on the second term on the right and employ Young’s inequality on the first term on the right to derive
where a is a constant at our disposal, and \(\lambda _1=\pi ^2\).
Next, form the combination (7)\(+\xi \)(10), for a constant \(\xi >0\) to be selected. We now pick a so that
and then we require
This allows us to define \(\epsilon \) so that
In this manner we derive an energy inequality of form
If now \(R<R_E\) we may employ Poincaré’s inequality on D to show that
where \(c=1-R/R_E>0\). When \(Pr\ge 1\), as it usually is, we let
and then from (12) we may obtain
where
From Eq. (13) we see that when \(R<R_E\), \(\Vert \theta \Vert ^{\beta +1}_{\beta +1}\) also decays exponentially and the stronger decay effect induced by the generalized friction is demonstrated.
Remark
We have chosen here \(Pr\ge 1\). The same proof works when \(Pr<1\), mutatis matuandis.
4 Conclusions
We have addressed the global nonlinear stability problem for thermal convection with generalized friction in a model recently proposed by [1]. It is shown that the linear instability theory correctly captures the onset of thermal convection by showing that the Rayleigh number threshold for global nonlinear stability employing the energy method is exactly the same as the one obtained by a linear analysis. When the Rayleigh number is below the instability threshold it is shown that the solution decays exponentially in time in \(L^2\) norm for the velocity, and in \(L^{\beta +1}\) norm for the temperature, \(\beta >1\).
References
Kim, Y.H., Li, K.O., Kim, C.U.: Uniqueness and regularity for the 3D Boussinesq system with damping. Annali dell Universitá di Ferrara 67, 149–173 (2021)
Straughan, B.: Stability, and Wave Motion in Porous Media. vol. 165. Appl. Math. Sci. Springer, New York (2008)
Straughan,B.: Convection with Local Thermal Non-Equilibrium and Microfluidic Effects. vol. 32. Adv. Mech. Math. Series. Springer, Cham, Switzerland (2015)
Straughan,B.: The Energy Method, Stability, and Nonlinear Convection. vol. 91. Appl. Math. Sci. Springer, New York, second edition (2004)
Hajduk, K.W., Robinson, J.C.: Energy equality for the 3D critical convective Brinkman–Forchheimer equations. J. Differ. Equ. 263, 7141–7161 (2017)
Galdi, G.P., Straughan, B.: Exchange of stabilities, symmetry and nonlinear stability. Arch. Ration. Mech. Anal. 89, 211–228 (1985)
Payne, L.E., Straughan, B.: Unconditional nonlinear stability in temperature-dependent viscosity flow in a porous medium. Stud. Appl. Math. 105, 59–81 (2000)
Acknowledgements
I am indebted to an anonymous referee for finding some misprints in a previous version.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
There are no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Straughan, B. Thermal convection with generalized friction. Ann Univ Ferrara 68, 63–68 (2022). https://doi.org/10.1007/s11565-021-00382-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11565-021-00382-6