Mathematical Modeling of Tumor and Cancer Stem Cells Treated with CAR-T Therapy and Inhibition of TGF-$\beta$

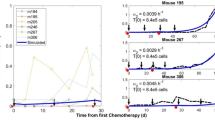
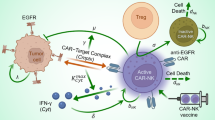
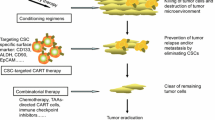
Abstract

The stem cell hypothesis suggests that there is a small group of malignant cells, the cancer stem cells, that initiate the development of tumors, encourage its growth, and may even be the cause of metastases. Traditional treatments, such as chemotherapy and radiation, primarily target the tumor cells leaving the stem cells to potentially cause a recurrence. Chimeric antigen receptor (CAR) T-cell therapy is a form of immunotherapy where the immune cells are genetically modified to fight the tumor cells. Traditionally, the CAR T-cell therapy has been used to treat blood cancers and only recently has shown promising results against solid tumors. We create an ordinary differential equations model which allows for the infusion of trained CAR-T cells to specifically attack the cancer stem cells that are present in the solid tumor microenvironment. Additionally, we incorporate the influence of TGF-$\beta$ which inhibits the CAR-T cells and thus promotes the growth of the tumor. We verify the model by comparing it to available data and then examine combinations of CAR-T cell treatment targeting both non-stem and stem cancer cells and a treatment that reduces the effectiveness of TGF-$\beta$ to determine the scenarios that eliminate the tumor.

Appendix: Stability Analysis

The system of Eq. (1) has four real-valued and biologically sensible equilibrium points, given in Sect. 4. These equilibrium points have been computed using the parameter values by Tang 2020, in Table 1. The Jacobian matrices for each equilibrium point, their eigenvalues and corresponding eigenvectors are given below.

• 1. Equilibrium point $(S^*, T^*, E^*, C^*, B^*, R^*) = (10^7, 9.9\times 10^8, 0, 0, 845.3, 0).$ As stated in Sect. 4, the system has a line of equilibria on $S^*+T^* = K$; meanwhile, we have observed in numerical simulations, a particular equilibrium on this line. Here, we present the eigenvalues and eigenvectors of this system at this particular point.

  The Jacobian matrix at this equilibrium is:

  $$\begin{aligned} \mathfrak {J}_1 =\left[ \begin{array}{cccccc} - 4.9\times 10^{-4}&{}-4.9\times 10^{-4}&{}0&{}-10 &{}0&{}0\\ -4.8\times 10^{-2}&{}-4.8\times 10^{-2}&{}-2.3\times 10^{-1}&{}0&{} 0&{}0\\ 0&{} 0&{} 4.7\times 10^{-1}&{}0&{}0&{}0\\ 0&{}0&{}0&{} 4.8\times 10^{-1}&{}0&{}0 \\ 0&{}{ 2.0\times 10^{-18}}&{}0&{}0&{}-7.0\times 10^{-4}&{}{ 10^{-8}}\\ 0&{}0&{}1.3\times 10^{-1}&{}0&{}0&{}-10^{-5}\end{array} \right] \end{aligned}$$

  The eigenvalues are: $(0, -4.9\times 10^{-2}, -7.0\times 10^{-4}, 4.8 \times 10^{-1}, -1.0 \times 10^{-5}, 4.7\times 10^{-1})$ and the corresponding eigenvectors are:

  $$\begin{aligned} \mathbf {v}_1 = \left[ \begin{array}{c} 7.1 \times 10^{-1}\\ - 7.1 \times 10^{-1}\\ 0\\ 0 \\ 0\\ 0\end{array} \right] , \mathbf {v}_2 = \left[ \begin{array}{c} 1.0 \times 10^{-2}\\ 1.0\\ 0\\ 0 \\ 0\\ 0\end{array} \right] , \mathbf {v}_3 = \left[ \begin{array}{c} 0.0\\ 0.0 \\ 0.0\\ 0.0 \\ - 1.0\\ 0.0\end{array} \right] \\ \mathbf {v}_4 = \left[ \begin{array}{c} - 1.0\\ 9.0\times 10^{-2}\\ 0\\ 4.8\times 10^{-2}\\ 0\\ 0 \end{array} \right] , \mathbf {v}_5 = \left[ \begin{array}{c} 0\\ 0 \\ 0\\ 0 \\ 1.4\times 10^{-5}\\ 1.0 \end{array} \right] , \mathbf {v}_6 = \left[ \begin{array}{c}4.3\times 10^{-4}\\ - 4.1\times 10^{-1}\\ 9.1\times 10^{-1}\\ 0\\ 5.1\times 10^{-10}\\ 2.4\times 10^{-2}\end{array} \right] \end{aligned}$$

• 2. Equilibrium point $(S^*, T^*, E^*, C^*, B^*, R^*) = (0, 0, 0, 0, 0, 0)$

  The trivial solution,

  $$\begin{aligned} (S^*, T^*, E^*, C^*, B^*, R^*) = (0, 0, 0, 0, 0, 0) \end{aligned}$$

  is an unstable equilibrium. The four positive eigenvalues indicate population growth in the directions of the CAR T-cells, the immune cells, tumor and stem cells, all of which are to be expected since the introduction of a few of these cells would instigate growth for that population. The direction of attraction, for the two negative eigenvalues, is the $B-$axis and a line on the $B-R$ plane, meaning the TGF-$\beta$ and Tregs tend to stabilize without the presence of effector cells or the tumor. The Jacobian matrix at this equilibrium is:

  $$\begin{aligned} \mathfrak {J}_2 = \left[ \begin{array}{cccccc} 4.9\times 10^{-2}&{}0&{}0&{}0&{}0&{}0 \\ 0&{} 4.7\times 10^{-1}&{}0&{}0&{}0&{}0 \\ 0&{}0&{}-7.0\times 10^{-4}&{}1.0\times 10^{-8}&{} 0 &{}0\\ 0&{}1.3\times 10^{-2}&{}0&{}-1.0\times 10^{-5}&{}0&{}0 \\ 3.1\times 10^{-1}&{}0&{}0&{}0&{}4.5\times 10^{-2}&{}0\\ 0&{}0&{}0&{}0&{}0&{}4.8\times 10^{-1}\end{array} \right] \end{aligned}$$

  The eigenvalues are: $(4.8\times 10^{-1}, 4.7 \times 10^{-1}, 4.9\times 10^{-2}, 4.54\times 10^{-2}, -7.0\times 10^{-4}, -1\times 10^{-5})$ and the corresponding eigenvectors are:

  $$\begin{aligned} \mathbf {v}_1 = \left[ \begin{array}{c} 0\\ 0 \\ 0\\ 0 \\ 0\\ 1\end{array} \right] , \mathbf {v}_2 = \left[ \begin{array}{c} 0\\ -1.0 \\ -5.6\times 10^{-10}\\ -2.6\times 10^{-2}\\ 2.0\times 10^{-10} \\ 0\end{array} \right] , \mathbf {v}_3 = \left[ \begin{array}{c} -1.2\times 10^{-2}\\ 0 \\ 0\\ 0 \\ -1.0\\ 0 \end{array} \right] , \\ \mathbf {v}_4 = \left[ \begin{array}{c} 0\\ 0 \\ 0\\ 0 \\ -1.0\\ 0 \end{array} \right] , \mathbf {v}_5 = \left[ \begin{array}{c} 0\\ 0 \\ 1\\ 0 \\ 0\\ 0\end{array} \right] , \mathbf {v}_6 = \left[ \begin{array}{c} 0\\ 0 \\ 1.4\times 10^{-5}\\ 1 \\ 0\\ 0\end{array} \right] \end{aligned}$$

• 3. Equilibrium point $(S^*, T^*, E^*, C^*, B^*, R^*) = (0, 0, 37.7, 0, 6.7\times 10^{-1}, 47179)$ This is a tumor and stem cell-free equilibrium. The three positive eigenvalues have eigenvectors that determine the direction of population growth for all cells, which is expected. The two complex eigenvalues with negative real parts provide a spiral sink-type behavior for the immune cells and TGF-$\beta$; without the tumor or the cancer stem cells, the immune system will be in a nonzero equilibrium. The direction for the only attractor is the $B-$axis; without the tumor or Tregs, the TGF-$\beta$ will stabilize at a low level. The Jacobian matrix at this equilibrium is:

  $$\begin{aligned} \mathfrak {J}_2 = \left[ \begin{array}{cccccc}4.9\times 10^{-2}&{}0&{}0&{}0&{}0&{}0 \\ 0&{} 0&{}0&{}-3.8\times 10^{-4}&{}4.2\times 10^{-2}&{}0 \\ 0&{}0&{}-7\times 10^{-4}&{}10^{-8}&{} 0 &{}0\\ 0&{}1.3\times 10^{-2}&{}0&{}-10^{-6}&{}0&{}0 \\ 3.1\times 10^{-1}&{}0&{}0&{}0&{}4.5\times 10^{-2}&{}0 \\ 0&{}0&{}0&{}0&{}0&{}1.2\times 10^{-2}\end{array} \right] \end{aligned}$$

  The eigenvalues are $(4.9\times 10^{-2},4.5\times 10^{-2}, 1.2\times 10^{-2}, -5.0\times 10^{-6}+(2.2\times 10^{-3})i,$

  $-5.0\times 10^{-6}-(2.2\times 10^{-3})i, -7.0\times 10^{-4}).$ The corresponding eigenvectors are:

  $$\begin{aligned} \mathbf {v}_1 = \left[ \begin{array}{c} -8.7\times 10^{-3}\\ -6.4\times 10^{-1}\\ -3.3\times 10^{-8} \\ -1.62\times 10^{-1}\\ -7.5\times 10^{-1} \\ 0\end{array} \right] , \mathbf {v}_2 = \left[ \begin{array}{c} -2.0\times 10^{-9}\\ -6.6\times 10^{-1}\\ -4.0\times 10^{-8} \\ -1.8\times 10^{-1}\\ -7.3\times 10^{-1} \\ 0\end{array} \right] , \mathbf {v}_3 = \left[ \begin{array}{c} 0\\ 0 \\ 0\\ 0 \\ 0\\ 1\end{array} \right] ,\\ \mathbf {v}_4 = \left[ \begin{array}{c}1.8\times 10^{-10}+{ 8.8\times 10^{-11}}\,i\\ 3.9\times 10^{-4}+1.7\times 10^{-1}\,i \\ 1.3\times 10^{-6}-4.1\times 10^{-6}\,i \\ 9.9\times 10^{-1}\\ {4.8 \times 10^{-11}}-4.4\times 10^{-10}\,i\\ 0 \end{array} \right] , \mathbf {v}_5 = \mathbf {v}_4, \mathbf {v}_6 = \left[ \begin{array}{c} -{ 1\times 10^{-13}} \\ -2.0\times 10^{-10}\\ -1 \\ { 7.0\times 10^{-13}} \\ -{9.0\times 10^{-14}} \\ 0\end{array} \right] \end{aligned}$$

• 4. Equilibrium point $(S^*, T^*, E^*, C^*, B^*, R^*) = (0, 10^9, 37.7, 0, 846, 47180)$ The fourth equilibrium is a maximal tumor case where the tumor is at its carrying capacity, which is a saddle. There are two directions of attraction; one of them is the $T-$axis, meaning the tumor population is converging to its carrying capacity, and the other points to a positive tumor, effector cells and TGF-$\beta$ and an opposite behavior for Tregs. The two complex eigenvalues have negative real parts with corresponding eigenvectors that are a complex scalar multiple of $\mathbf {e}_5$ parallel to the $T-$axis. This freedom is due to the equilibrium not being completely defined and rather the equilibrium of $T^*$ and $S^*$ just must satisfy $T^*+S^*=K$. The Jacobian matrix at this equilibrium is:

  $$\begin{aligned} \mathfrak {J}_4 = \left[ \begin{array}{cccccc}9.6\times 10^{-9}&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}-4.7\times 10^{-7}&{}-3.8\times 10^{-4}&{} 2.0\times 10^{-22}&{}0\\ 0&{}0&{}-7\times 10^{-4}&{}10^-8&{}{ 3.0\times 10^{-18}}&{}0\\ 0&{} 1.3\times 10^{-2}&{}0&{}-10^{-5}&{}0&{}0\\ -4.5\times 10^{-2}&{}-2.4\times 10^{-1}&{} 1.1\times 10^{-2}&{}0&{}-4.5\times 10^{-2}&{}0\\ 0&{}0&{}0&{}0&{}0&{}1.2\times 10^{-2}\end{array} \right] \end{aligned}$$

  The eigenvalues are $(-4.5\times 10^{-2}, 1.2\times 10^{-2}, -5.0\times 10^{-6} + (2.1\times 10^{-3})\,i, -5.0\times 10^{-6} - (2.1\times 10^{-3})\,i, -7.0\times 10^{-4}, 9.6\times 10^{-9} ).$ The corresponding eigenvectors are:

  $$\begin{aligned} \mathbf {v}_1 = \left[ \begin{array}{c} 0\\ 0 \\ 0\\ 0 \\ 1\\ 0\end{array} \right] , \mathbf {v}_2 = \left[ \begin{array}{c} 0\\ 0 \\ 0\\ 0 \\ 0\\ 1\end{array} \right] , \mathbf {v}_3 = \left[ \begin{array}{c} 0\\ 2.9\times 10^{-4}- 1.3\times 10^{-1}\,i\\ 9.8\times 10^{-7}+ 3.1\times 10^{-6}\,i\\ 7.4\times 10^{-1} \\ -3.3\times 10^{-2}+6.6\times 10^{-1}\,i \\ 0\end{array} \right] ,\\ \mathbf {v}_4 = \mathbf {v}_3, \mathbf {v}_5 = \left[ \begin{array}{c} 0\\ -6.1\times 10^{-5} \\ -9.7\times 10^{-1}\\ 1.1\times 10^{-3}\\ -2.3\times 10^{-1} \\ 0\end{array} \right] , \mathbf {v}_6 = \left[ \begin{array}{c} -7.1\times 10^{-1}\\ 0 \\ 0\\ 0 \\ 7.\times 10^{-1}\\ 0 \end{array} \right] \end{aligned}$$