1 Introduction

Dengue remains a major public health concern globally, especially in tropics across the world (Gubler and Clark 1995; Otero et al. 2008; WHO 2014). Worldwide, there is an estimated 2.5–3.6 billion individuals who are at risk of dengue infection, with annual estimates of 50–230 million new cases, 500,000 hospitalizations and 25,000 fatal outcomes (Wilder-Smith et al. 2012; WHO 2014). Intervention measures to manage dengue spread and its impact are mainly based on vector control programs (Otero et al. 2008; Wallace et al. 2013; Wilder-Smith et al. 2012).

Dengue is caused by four antigenically distinct virus serotypes, designated as DENv1, DENv2, DENv3 and DENv4 (Carrington and Simmons 2014; Guzman and Kouri 2002). These serotypes can be transmitted from infectious individuals to susceptible individuals through the bites of infectious mosquitoes, mainly the Aedes Aegypti mosquitoes. A second type of mosquito, A. Albopictus, is also a vector for this disease that is becoming increasingly important (Carrington and Simmons 2014; Wilder-Smith et al. 2012). In infected humans, disease symptoms can range from very mild to severe (Gubler and Clark 1995). The mild form (called non-haemorrhagic) can cause fever and headache without the usual respiratory symptoms (Carrington and Simmons 2014). The more severe forms include dengue haemorrhagic fever (DHF) and dengue shock syndrome (DSS), both of which can be life-threatening, and may be related to a secondary infection caused by a dengue serotype that is different from the serotype responsible for the primary infection (Carrington and Simmons 2014). The risk of severe forms of dengue infection is associated with the mechanisms of antibody-dependent enhancement (ADE), by which pre-existing non-neutralizing antibodies form immune complexes with the new serotype-infecting virus that in turn enhance the capacity to infect macrophages and other Fcgamma receptor (FcgammaR)-bearing cells (Cummings et al. 2005; Ferguson et al. 1999a). This phenomenon, although not clinically proven in efforts towards the development of a dengue vaccine, can have important implications for disease outcomes, since the vaccine-induced immunity against a particular serotype may prime an individual to experience a severe form of DHF or DSS upon exposure to a different dengue serotype.

Previous modelling studies have investigated the effect of ADE (as a result of pre-existing cross-protective immunity) in dengue spread and provided important insights into the epidemiological patterns of dengue infection observed in various databases (Coudeville and Garnett 2012; Cummings et al. 2005; Pandey and Medlock 2014; Recker et al. 2009; Reich et al. 2013; Wearing and Rohani 2006). While infection with a particular serotype of dengue provides lifetime protection against reinfection with that serotype (Carrington and Simmons 2014), new infections with other serotypes can occur. However, interactions between dengue serotypes have been shown to confer substantial short-term cross-protection, virtually eliminating the risk of a new infection for a period of 1–4 years after recovery from one serotype of dengue infection (Reich et al. 2013). Once this period has elapsed, ADE may place the individuals at risk of developing DHF or DSS depending on the concentration of non-neutralizing antibodies at the time of a secondary heterologous infection (Cummings et al. 2005; Recker et al. 2009; Reich et al. 2013; Wearing and Rohani 2006). The ADE effect can therefore increase the transmissibility of secondary infections to mosquitoes due to high viral titres (Cummings et al. 2005; Recker et al. 2009; Reich et al. 2013; Wearing and Rohani 2006). The duration of this increased transmissibility is unknown; however, it depends on the decay rate of pre-existing non-neutralizing antibodies. The unknown duration of ADE and its epidemiological impact on transmission dynamics of dengue serotypes remain elusive in understanding the effect of vaccination against dengue serotypes (Guzman et al. 2010). While vaccination is expected to reduce the overall incidence of infection (Coudeville and Garnett 2012; Pandey and Medlock 2014), the effect of vaccine-induced ADE remains both clinically and epidemiologically unaddressed (Guzman et al. 2010).

In this study, we develop a full model of vector–host interactions for the transmission dynamics of dengue to evaluate the potential impact of vaccination and the vaccine-induced ADE on disease prevention. Key parameters in this evaluation include the serotype-specific vaccine-induced protection, duration of ADE, increased transmissibility of secondary infection and reduction in susceptibility to infection as a result of pre-existing partial protection. We simulate the model with parameters estimated in previous literature, present the results and place them in the context of dengue epidemiology and prevention.

2 Model Description

2.1 General Assumptions

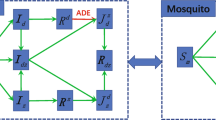
Since dengue serotypes are reported to be pairwise similar in their transmission characteristics (Carrington and Simmons 2014), we considered only two serotypes, referred to as \(\mathcal {S}_1\) and \(\mathcal {S}_2\). Tertiary infections are reported very rarely (Halstead 2003), and therefore most studies assume that individuals are immune to all four serotypes of dengue after two heterologous infections. In line with previous work, we disregard heterologous superinfection. Serotypes \(\mathcal {S}_1\) and \(\mathcal {S}_2\) considered here do not necessarily correspond to the actual DENv1 and DENv2, but rather represent co-circulation of two serotypes that have different transmissibility. Our model incorporates \(\mathcal {S}_1\) and \(\mathcal {S}_2\) with different rates for human-to-mosquito and mosquito-to-human transmission (Carrington and Simmons 2014). While the incubation period and the infectious period of dengue in humans may vary for different serotypes (Carrington and Simmons 2014), we follow previous work and assume that these periods are the same for dengue caused by \(\mathcal {S}_1\) and \(\mathcal {S}_2\). The schematic diagram of the model is presented in Fig. 1.

Fig. 1
figure 1

Schematic model diagram for dengue spread between humans through mosquitoes

Full size image

Like many multi-strain pathogens, dengue has been studied for evidence of immune response and cross-protection after infection with one serotype. Most studies concur that infection with any of the four serotypes induces lifetime immunity to that serotype and confers at least short-term cross-protection against all other serotypes. Several studies (Coudeville and Garnett 2012; Recker et al. 2009; Reich et al. 2013) argue that including the period of cross-protection and increased transmissibility from individuals suffering from DHF or DSS in secondary infections are of particular importance to reproduce the multi-annual patterns observed in surveillance of dengue cases. The work of Reich et al. (2013) provided strong evidence for substantial cross-protection for an average duration of 1.88 years after the primary infection. After this period has elapsed, individuals will enter a period during which the effect of ADE may appear in a secondary infection. This effect is inversely correlated with the concentration of non-neutralizing antibodies and may become inapparent over time due to the decline of antibody concentration to sufficiently low levels. Thus, high antibody concentrations are assumed to be protective, low concentrations are irrelevant in the context of ADE, and medium concentrations are associated with the ADE phenomenon. We assumed that following the period of partial protection associated with the risk of ADE, individuals are fully susceptible to other serotypes. The effect of ADE also appears as increased viral titres in human blood, which in turn influences the likelihood of a mosquito becoming infected after a bloodmeal (Carrington and Simmons 2014). We assumed higher human-to-mosquito transmissibility of the secondary infection during the partial protection period, compared to the primary infection.

To investigate the effect of vaccine on the dynamics of dengue infection, we implemented tetravalent (all serotypes) vaccination in our model for individuals with no prior exposure to dengue serotypes. We consider two scenarios in which vaccination is implemented either for the susceptible population, or for newborns only. We assumed that the vaccine-induced immunity provides some degree of protection to each serotype. Since vaccination primes the individual’s immune response to all serotypes, we assumed that vaccinated individuals are subject to the ADE effect after the period of full protection has elapsed if infection occurs.

2.2 Dengue Dynamics in the Vector Population

We model dengue dynamics with a system of ordinary differential equations, where all variables depend on time t. First, we develop the subsystem for the mosquito population. The total mosquito population is denoted by V. The recruitment (birth) in the mosquito population is given by the function \(\hat{b}(t)\). We elaborate on this birth function and its expression in Eq. (13) when we revisit the subsystem for the mosquito population. Assuming that all mosquitoes are born susceptible and die at the rate \(\hat{\mu }\), the dynamics of dengue in susceptible mosquitoes are governed by

$$\begin{aligned} \dot{S}_V =\hat{b}(t)-\left( F_{V}^{1}+F_{V}^{2}+F_{V}^{A1}+F_{V}^{A2}\right) S_V- \hat{\mu } S_V, \end{aligned}$$
(1)

where \(F_{V}^{1}+F_{V}^{2}+F_{V}^{A1}+F_{V}^{A2}\) is the force of infection for the vector population, describing that a susceptible mosquito can acquire dengue \(\mathcal {S}_1\) or \(\mathcal {S}_2\) from infectious individuals. The term for the force of infection in the mosquito population will be explicitly defined in Sect. 2.3.

Since mosquitoes infected by individuals experiencing DHF or DSS (i.e. the effect of ADE with high viral titres) may become infectious in a significantly shorter incubation period compared to mosquitoes that acquire dengue from infectious individuals with mild form of infection (Carrington and Simmons 2014), we assumed two different extrinsic incubation periods \(1/\hat{\alpha }\) and \(1/\hat{\alpha }_{_A}\). For the exposed classes in the mosquito population, we obtain the system

$$\begin{aligned} \dot{E}_V^{1}= & {} F_{V}^{1} \, S_V-(\hat{\alpha } + \hat{\mu }) E_V^{1}, \quad \dot{E}_V^{A1} = F_{V}^{A1} \, S_V-(\hat{\alpha }_{_A} +\hat{\mu }) E_V^{A1},\nonumber \\ \dot{E}_V^{2}= & {} F_{V}^{2} \, S_V-(\hat{\alpha } + \hat{\mu }) E_V^{2}, \quad \dot{E}_V^{A2} = F_{V}^{A2} \, S_V-(\hat{\alpha }_{_A}+ \hat{\mu }) E_V^{A2}, \end{aligned}$$
(2)

where index A indicates whether infection was acquired from a human with high viral titres that is associated with the ADE phenomenon.

After the extrinsic incubation period has elapsed, infectious mosquitoes are able to transmit the disease and are part of the infection classes that correspond to their exposed compartments. Assuming that such mosquitoes remain infectious for the remaining part of their lifespan, the dynamics of infectious mosquitoes can be expressed by

$$\begin{aligned} \dot{I}_V^{1}= & {} \hat{\alpha } E_V^{1}-\hat{\mu } I_V^{1}, \quad \dot{I}_V^{A1} = \hat{\alpha }_{_A} E_V^{A1}-\hat{\mu } I_V^{A1},\nonumber \\ \dot{I}_V^{2}= & {} \hat{\alpha } E_V^{2}-\hat{\mu } I_V^{2}, \quad \dot{I}_V^{A2} = \hat{\alpha }_{_A} E_V^{A2}-\hat{\mu } I_V^{A2}. \end{aligned}$$
(3)

2.3 Dengue Dynamics in the Human Population

We define the force of infection for \(\mathcal {S}_1\) and \(\mathcal {S}_2\) in the human population by

$$\begin{aligned} F_H^{1}=\lambda _1 \frac{I_V^{1}+I_V^{A1}}{H}, \quad F_H^{2}=\lambda _2 \frac{I_V^{2}+I_V^{A2}}{H}, \end{aligned}$$
(4)

where H is the total human population and \(\lambda _1\) and \(\lambda _2\) are, respectively, the rates at which mosquitoes transmit \(\mathcal {S}_1\) and \(\mathcal {S}_2\) to humans. Denoting susceptible individuals by \(S_H\), the equation

$$\begin{aligned} \dot{S}_H =(1-\phi )B-\big (F_H^{1}+F_H^{2}\big )S_H-\xi S_H- \mu S_H, \end{aligned}$$
(5)

describes the dynamics of infection in humans, where B is the constant birth rate and \(\mu \) is the natural death rate. Susceptible individuals are vaccinated at a rate \(\xi \) and move to the class \(W_H\). The parameter \(\phi \) represents the vaccination coverage of newborns. If \(\phi >0\), a fraction \(\phi \) of newborns are vaccinated and recruited directly to the \(W_H\) class. We assume that vaccinated individuals will be fully protected for a period of time (\(1/\eta \)). After this period has elapsed, they move to the class of individuals with partial protection (\(X_H\)), who are subject to ADE for the rest of their lifetime. The governing equations are

$$\begin{aligned} \dot{W}_H= & {} \phi B+\xi S_H-\eta W_H-\mu \, W_H,\nonumber \\ \dot{X}_H= & {} \eta W_H-\big (p_1 F_H^{1}+p_2 F_H^{2}\big )X_H- \mu \, X_H, \end{aligned}$$
(6)

where the parameters \(0 \le p_1 \le 1\) and \(0 \le p_2 \le 1\) represent, respectively, the reduced probabilities of acquiring infection with \(\mathcal {S}_1\) and \(\mathcal {S}_2\) due to partial protection.

After exposure to a serotype, individuals enter the exposed classes \(E_H^1\) and \(E_H^2\), with average latency periods of \(1/\alpha _1\) and \(1/\alpha _2\) units of time, before becoming infectious. Primary infections with \(\mathcal {S}_1\) (individuals in \(I_H^1\)) and \(\mathcal {S}_2\) (individuals in \(I_H^2\)) will recover at the rates \(\gamma _1\) and \(\gamma _2\), respectively, and move to the corresponding classes \(T_H^1\) and \(T_H^2\) with full protection. The equations describing such dynamics are

$$\begin{aligned} \dot{E}_H^1= & {} F_H^{1} \, S_H-\alpha _1 E_H^1- \mu E_H^1,\nonumber \\ \dot{I}_H^1= & {} \alpha _1 E_H^1- \mu I_H^1-\gamma _1 I_H^1,\nonumber \\ \dot{T}_H^1= & {} \gamma _1 I_H^1-\rho _1 T_H^1- \mu T_H^1, \end{aligned}$$
(7)

and

$$\begin{aligned} \dot{E}_H^2= & {} F_H^{2} \, S_H-\alpha _2 E_H^2- \mu E_H^2,\nonumber \\ \dot{I}_H^2= & {} \alpha _2 E_H^2- \mu I_H^2-\gamma _2 I_H^2,\nonumber \\ \dot{T}_H^2= & {} \gamma _2 I_H^2-\rho _2 T_H^2- \mu T_H^2, \end{aligned}$$
(8)

where \(\rho _1\) and \(\rho _2\) are, respectively, the rates at which individuals in the \(T_H^1\) and \(T_H^2\) classes lose their full protection. We assume that recovery after the primary infection with a particular serotype provides lifelong immunity against that serotype. After the transient period of full protection has elapsed, individuals move to the class \(S_H^{M2}\) (or \(S_H^{M1}\)) and become susceptible to infection with \(\mathcal {S}_2\) (or \(\mathcal {S}_1\)). While this susceptibility is reduced by a factor \(q_2\) (or \(q_1\)) due to partial protection, the secondary infection (if occurs) is subject to ADE. As the partial protection wanes over time, individuals become fully susceptible and the secondary infection may occur without the ADE effect. The infection dynamics are described by the following equations:

$$\begin{aligned} \dot{S}_H^{M2}= & {} \rho _1 T_H^1- q_2 \, F_H^{2} \, S_H^{M2}- (\mu +\theta _2) S_H^{M2},\nonumber \\ \dot{S}_H^{L2}= & {} \theta _2 S_H^{M2}- F_H^{2} \, S_H^{L2}- \mu S_H^{L2},\nonumber \\ \dot{S}_H^{M1}= & {} \rho _2 T_H^2-q_1 \, F_H^{1} \, S_H^{M1}- (\mu +\theta _1) S_H^{M1},\nonumber \\ \dot{S}_H^{L1}= & {} \theta _1 S_H^{M1}-F_H^{1} \, S_H^{L1}- \mu S_H^{L1}. \end{aligned}$$
(9)

where \(\theta _2\) and \(\theta _1\) are the rates at which individuals move from the \(S_H^{M2}\) and \(S_H^{M1}\) classes to \(S_H^{L2}\) and \(S_H^{L1}\) and become fully susceptible to heterologous infections.

Individuals exposed to \(\mathcal {S}_1\) and \(\mathcal {S}_2\) as secondary infection move to the classes \(E_H^{M1}\) and \(E_H^{M2}\) with the ADE effect, or to the classes \(E_H^{L1}\) and \(E_H^{L2}\) without the ADE effect. After the exposed period has elapsed, disease progression with the secondary infection in \(I_H^{M1}\), \(I_H^{L1}\), \(I_H^{M2}\) and \(I_H^{L2}\) is identical to that with the primary infection, and recovery from secondary infection will confer full protection against both serotypes. Since vaccinated individuals have already been primed to all serotypes, infection during partial protection will be considered as secondary infection with the ADE effect. In our model, this means that new infections with \(\mathcal {S}_1\) and \(\mathcal {S}_2\) from the class \(X_H\) move to \(E_H^{M1}\) and \(E_H^{M2}\), respectively. The following equations express such dynamics mathematically as

$$\begin{aligned} \dot{E}_H^{M2}= & {} q_2\, F_H^{2}\, S_H^{M2}+p_2\, F_H^{2}\, X_H -\alpha _2 E_H^{M2}- \mu E_H^{M2},\nonumber \\ \dot{I}_H^{M2}= & {} \alpha _2 E_H^{M2}- \mu I_H^{M2}- \gamma _2 I_H^{M2},\nonumber \\ \dot{E}_H^{M1}= & {} q_1\, F_H^{1}\, S_H^{M1}+p_1 \, F_H^{1}\, X_H -\alpha _1 E_H^{M1}- \mu E_H^{M1},\nonumber \\ \dot{I}_H^{M1}= & {} \alpha _1 E_H^{M1}- \mu I_H^{M1}- \gamma _1 I_H^{M1}, \end{aligned}$$
(10)
$$\begin{aligned} \dot{E}_H^{L2}= & {} F_H^{2} \, S_H^{L2} -\alpha _2 E_H^{L2}- \mu E_H^{L2},\nonumber \\ \dot{I}_H^{L2}= & {} \alpha _2 E_H^{L2}- \mu I_H^{L2}- \gamma _2 I_H^{L2},\nonumber \\ \dot{E}_H^{L1}= & {} F_H^{1} \, S_H^{L1} -\alpha _1 E_H^{L1}- \mu E_H^{L1},\nonumber \\ \dot{I}_H^{L1}= & {} \alpha _1 E_H^{L1}- \mu I_H^{L1}- \gamma _1 I_H^{L1}, \end{aligned}$$
(11)

and

$$\begin{aligned} \dot{R}_H = \gamma _1 \big (I_H^{L1}+I_H^{M1}\big )+\gamma _2 \big (I_H^{L2}+I_H^{M2}\big )-\mu R_H, \end{aligned}$$
(12)

where \(R_H\) is the class of individuals immune against both serotypes.

Now, we revisit our subsystem for dengue dynamics in the mosquito population. Recruitment into the mosquito population is modelled by the non-autonomous (seasonal-dependent) birth term (Wearing and Rohani 2006)

$$\begin{aligned} \hat{b}(t)=k H \hat{\mu } (1-a \cos (2 \pi t)), \end{aligned}$$
(13)

where k is the average number of mosquitoes per person and a is the amplitude of seasonal fluctuation. In the absence of seasonality, recruitment to the vector population is proportional to the total human population. We define the force of infection functions \(F_{V}^{1}\), \(F_{V}^{A1}\), \(F_{V}^{2}\) and \(F_{V}^{A2}\) in the mosquito subsystem as

$$\begin{aligned} F_{V}^{1}= & {} \hat{\delta }_1 \frac{I_H^1+I_H^{L1}}{H}, \quad F_{V}^{A1}=\hat{\delta }_1 \frac{\sigma _1 I_H^{M1}}{H}, \nonumber \\ F_{V}^{2}= & {} \hat{\delta }_2 \frac{I_H^2+I_H^{L2}}{H}, \quad F_{V}^{A2}=\hat{\delta }_2 \frac{\sigma _2 I_H^{M2}}{H}, \end{aligned}$$
(14)

where \(\hat{\delta }_1\) and \(\hat{\delta }_2\) are the transmission rates of \(\mathcal {S}_1\) and \(\mathcal {S}_2\), respectively, from humans to mosquitoes and \(\sigma _1\) and \(\sigma _2\) represent the enhanced transmissibility due to the ADE effect. Summarizing the above, the joint systems (1)–(3) and (5)–(12) with the functions (4) and (14) give a system of differential equations for the dynamics of dengue in the mosquito and human populations. Variables and parameters of the model are listed in Tables 1 and 2.

Table 1 Serotype-specific variables are labelled with indices 1 and 2 that correspond to \(\mathcal {S}_1\) and \(\mathcal {S}_2\)
Full size table
Table 2 Serotype-specific parameters are labelled with indices 1 and 2 that correspond to \(\mathcal {S}_1\) and \(\mathcal {S}_2\)
Full size table

Standard arguments from the theory of ordinary differential equations guarantee that the system for dengue dynamics in the mosquito and human populations admits a unique solution. For the total human population H, there is a globally attracting equilibrium \(\bar{H}=B/ \mu \), that is, \(\lim _{t \rightarrow \infty } H(t)=B/ \mu \). The dynamics of the total mosquito population is given by

$$\begin{aligned} \dot{V}=\hat{b}(t)- \hat{\mu } V. \end{aligned}$$

Considering \(H=\bar{H}\) and the constant recruitment term \(\hat{b}(t)=k \bar{H} \hat{\mu }\) (without seasonal variation) in the vector population, the equation \(\hat{b}(t)- \hat{\mu } {V}=0\) has a unique solution \(\bar{V}=k \bar{H}\), and the total mosquito population converges, that is, \(\lim _{t \rightarrow \infty } V(t)=\bar{V}\).

Non-negative initial conditions give rise to non-negative solutions of the system, and therefore the solutions are bounded and thus exist for all times. When the human population is at the disease-free state (i.e. \(F_{V}^{1}+F_{V}^{2}+F_{V}^{A1}+F_{V}^{A2}=0\)), the subsystem for mosquito dynamics admits a unique equilibrium, at which \(S_V(t) \equiv \bar{V}\) and all other classes are at zero states (i.e. the disease-free equilibrium). When there is no infection in the human population, the unique steady state is globally stable. Similarly, when the mosquito population is at the disease-free state (i.e. \(F_{H}^{1}+F_{H}^{2}=0\)), the subsystem for human population admits a unique equilibrium with

$$\begin{aligned} S_H(t)\equiv & {} \frac{(1-\phi ) B}{\xi +\mu }, \qquad W_H(t) \equiv \frac{\phi B}{\eta +\mu }+\frac{\xi (1-\phi ) B}{(\xi +\mu )(\eta +\mu )},\nonumber \\ X_H(t)\equiv & {} \frac{\eta \phi B}{(\eta +\mu )\mu }+\frac{\eta \xi (1-\phi ) B}{(\xi +\mu )(\eta +\mu )\mu }, \end{aligned}$$

and all other classes are at zero states, which is the disease-free equilibrium. With no infection in the mosquito population, the unique steady state is globally stable.

2.4 The Modified Model

We modify the original model to incorporate the possible difference in the enhanced transmissibility of human to mosquito due to the ADE effect in vaccinated individuals. We include the classes \(Y_H^{1}\) and \(Y_H^{2}\) for vaccinated individuals exposed to \(\mathcal {S}_1\) and \(\mathcal {S}_2\), respectively, and introduce \(Z_H^{1}\) and \(Z_H^{2}\) for the corresponding infection classes. The parameters \(\kappa _1\) and \(\kappa _2\) represent the enhanced transmissibility factors. With these modifications, the system (10) for the dynamics of the human population is expressed by

$$\begin{aligned} \dot{E}_H^{M2}= & {} q_2\, F_H^{2}\, S_H^{M2} -\alpha _2 E_H^{M2}- \mu E_H^{M2},\nonumber \\ \dot{I}_H^{M2}= & {} \alpha _2 E_H^{M2}- \mu I_H^{M2}- \gamma _2 I_H^{M2},\nonumber \\ \dot{E}_H^{M1}= & {} q_1\, F_H^{1}\, S_H^{M1} -\alpha _1 E_H^{M1}- \mu E_H^{M1},\nonumber \\ \dot{I}_H^{M1}= & {} \alpha _1 E_H^{M1}- \mu I_H^{M1}- \gamma _1 I_H^{M1},\nonumber \\ \dot{Y}_{H}^{2}= & {} p_2 \, F_H^{2} \, X_H -\alpha _2 Y_H^{2}- \mu Y_H^{2},\nonumber \\ \dot{Z}_{H}^{2}= & {} \alpha _2 Y_H^{2}- \mu Z_H^{2}- \gamma _2 Z_H^{2},\nonumber \\ \dot{Y}_{H}^{1}= & {} p_1 \, F_H^{1} \, X_H -\alpha _1 Y_H^{1}- \mu Y_H^{1},\nonumber \\ \dot{Z}_{H}^{1}= & {} \alpha _1 Y_H^{1}- \mu Z_H^{1}- \gamma _1 Z_H^{1},\nonumber \\ \end{aligned}$$

and we revise the Eq. (12) to

$$\begin{aligned} \dot{R}_H = \gamma _1 \big (I_H^{L1}+I_H^{M1}+Z_H^{1}\big )+\gamma _2 \big (I_H^{L2}+I_H^{M2}+Z_H^{2}\big )-\mu R_H, \end{aligned}$$

for the class of individuals recovered from both serotypes. The force of infection terms in Eq. (14) for serotypes acquired from infectious humans with the ADE effect is also redefined as

$$\begin{aligned} F_V^{A1}=\hat{\delta }_1 \frac{\sigma _1 I_H^{M1}+\kappa _1\, Z_H^{1}}{H},\quad F_V^{A2}=\hat{\delta }_2 \frac{\sigma _2 I_H^{M2}+\kappa _2\, Z_H^{2}}{H}. \end{aligned}$$

3 Serotype-Specific Reproduction Numbers

In this section, we consider the birth term in the mosquito population without seasonal variation, which guarantees that the full system for dengue dynamics has a unique disease-free equilibrium. We define the reproduction number of serotype \(\mathcal {S}_i\) (\(i=1,2\)) in the absence of vaccination. This number, denoted here by \(\,\mathcal {R}_i\), gives the average number of new infections generated by a single infectious case in a wholly susceptible population. To provide an expression for this quantity, we apply the next-generation method, initially formalized by Diekmann et al. (1990). In this method, the reproduction number arises as the dominant eigenvalue of the next-generation matrix at the disease-free state (Diekmann et al. 1990, 2010).

In the absence of vaccination, the disease-free equilibrium involves only two non-zero components, \(\bar{H}\) and \(\bar{V}\) for the susceptible human and mosquito classes, respectively. Following the procedure described in Diekmann et al. (2010) for obtaining \(\,\mathcal {R}_i\), we identify the infection subsystem as the equations in the compartmental model that describe the generation of new infections and changes in the epidemiological status among infected individuals and mosquitoes. In the case when only one serotype is present, secondary infection in humans is impossible and the infection subsystem for humans consists of only \(E_H^i\) and \(I_H^i\). Without secondary infections, the compartments \(E_V^{Ai}, I_V^{Ai}\) are zero, and we only need to consider the classes \(E_V^{i}, I_V^{i}\) for the dynamics of infected mosquitoes. The infection subsystem is given by the four equations describing \(E_V^{i}\) and \(I_V^{i}\), \(E_H^i\), and \(I_H^i\). During the initial phase of an epidemic, the changes in the susceptible populations are negligible; thus, one can approximate the dynamics in these four classes by linearizing the infection subsystem about the disease-free state. The matrix of the linearized system is decomposed as \(T_i+\varSigma _i\), where \(T_i\) describes the production of new infections (transmission parts in the linear approximation) and \(\varSigma _i\) represents changes in the status, as become infected, recover from infection or die (transition parts in the linear approximation). These matrices are

$$\begin{aligned} T_i = \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad \displaystyle \hat{\delta }_i \frac{\bar{V}}{\bar{H}} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \lambda _i &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{pmatrix},\quad \varSigma _i = \begin{pmatrix} -(\hat{\alpha }+\hat{\mu }) &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \hat{\alpha } &{}\quad -\hat{\mu } &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -(\alpha _i+\mu ) &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \alpha _i &{}\quad -(\gamma _i+\mu ) \end{pmatrix}. \end{aligned}$$

The product of \(T_i\) and \(-\varSigma _i^{-1}\) gives:

$$\begin{aligned} -T_i\,\varSigma _i^{-1}= \begin{pmatrix} 0 &{}\quad 0 &{}\quad \displaystyle \frac{\hat{\delta }_i \alpha _i\bar{V}}{(\alpha _i+\mu )(\gamma _i+\mu )\bar{H}} &{}\quad &{}\quad \displaystyle \frac{\hat{\delta }_i\bar{V}}{(\gamma _i+\mu )\bar{H}}\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad &{}\quad 0\\ \displaystyle \frac{\hat{\alpha } \lambda _i}{(\hat{\alpha }+\hat{\mu })\hat{\mu }} &{}\quad \displaystyle \frac{\lambda _i}{\hat{\mu }} &{}\quad 0 &{}\quad &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad &{}\quad 0 \end{pmatrix}. \end{aligned}$$

Following the description provided in (Diekmann et al. 2010) to derive the next-generation matrix \(K_i\) from \(-T_i\,\varSigma _i^{-1}\), we obtain

$$\begin{aligned} K_i= \begin{pmatrix} 0&{} \displaystyle \frac{\hat{\delta }_i \alpha _i\bar{V}}{(\alpha _i+\mu )(\gamma _i+\mu )\bar{H}} \\ \displaystyle \frac{\hat{\alpha } \lambda _i}{(\hat{\alpha }+\hat{\mu })\hat{\mu }} &{} 0 \end{pmatrix}, \end{aligned}$$
(15)

where \([K_i]_{12}\) is the average number of mosquitoes infected by a single infectious human and \([K_i]_{21}\) is the average number of humans that a single infectious mosquito infects, in a wholly susceptible population. Eigenvalues of \(K_i\) are the solutions of

$$\begin{aligned} x^2-\left( \displaystyle \frac{\hat{\alpha } \lambda _i}{(\hat{\alpha }+\hat{\mu })\hat{\mu }}\right) \left( \displaystyle \frac{\hat{\delta }_i \alpha _i\bar{V}}{(\alpha _i+\mu )(\gamma _i+\mu )\bar{H}}\right) =0. \end{aligned}$$

The dominant eigenvalue of the next-generation matrix is therefore obtained as

$$\begin{aligned} \rho (K_i)=\sqrt{\left( \displaystyle \frac{\hat{\alpha } \lambda _i}{(\hat{\alpha }+\hat{\mu })\hat{\mu }}\right) \left( \displaystyle \frac{\hat{\delta }_i \alpha _i\bar{V}}{(\alpha _i+\mu )(\gamma _i+\mu )\bar{H}}\right) }, \end{aligned}$$

and the disease-free state is locally asymptotically stable (unstable) in the model with only one serotype if \(\rho (K_i)<1\) (\(\rho (K_i)>1\)) (Diekmann et al. 2010).

A different approach to calculating the reproduction number for one serotype can also be taken by tracing an infectious mosquito and an infectious human during their exposed and infectious periods. This method yields \([K_i]_{21}\) and \([K_i]_{12}\), respectively. As humans cannot infect humans, two generations are required to transmit an infection from human to human, the first being from human to mosquito and the second being from mosquito to human. Therefore, the two-generation factor arises as \([K_i]_{21} \cdot [K_i]_{12}\), and the average number of secondary infected mosquitoes that result from a single infectious mosquito is obtained by the same calculations. The average next-generation factor \(\,\mathcal {R}_i\) is therefore the square root of the two-generation factor, given by

$$\begin{aligned} \,\mathcal {R}_i=\sqrt{\left( \displaystyle \frac{\hat{\alpha } \lambda _i}{(\hat{\alpha }+\hat{\mu })\hat{\mu }}\right) \left( \displaystyle \frac{\hat{\delta }_i \alpha _i\bar{V}}{(\alpha _i+\mu )(\gamma _i+\mu )\bar{H}}\right) }. \end{aligned}$$
(16)

In the absence of a different serotype and vaccination, the circulating serotype invades the population of humans if \(\,\mathcal {R}_i>1\) and dies out if \(\,\mathcal {R}_i<1\).

4 Parameterization

Dengue vectors have a life cycle that is influenced by seasonal variation and several climatic factors. To parameterize the model for simulations, we return to the formula (13) and incorporate seasonality into the recruitment of adult mosquitoes. We consider the initial total human population at the steady state \(H_0=5\times 10^5\) and assume that there are two vectors per human (Wearing and Rohani 2006, with the initial total mosquito population of \(V_0=10^6\). With \(a=0.05\), \(\hat{b}(t)\) in (13) becomes

$$\begin{aligned} \hat{b}(t)=10^6 \hat{\mu } (1-0.05 \cos (2 \pi t)). \end{aligned}$$

To calculate the transmission rates \(\hat{\delta }_i\) and \(\lambda _i\), we use the expression (16). Assuming that \(\hat{\delta }_i=\lambda _i\) (Wearing and Rohani 2006), for a given \(\mathcal {R}_i\) and fixed parameters, transmission rates can be calculated from the expression (16) when \(\bar{V}\) and \(\bar{H}\) are the initial number of mosquito and human populations, respectively.

Epidemiological parameters describing the average extrinsic incubation periods (\(1/\hat{\alpha }_{_A}\), \(1/\hat{\alpha }\)), the intrinsic incubation periods (\(1/\alpha _1\), \(1/\alpha _2\)) and the infectious periods in humans (\(1/\gamma _1\), \(1/\gamma _2\)) were derived from the literature (Carrington and Simmons 2014; Coudeville and Garnett 2012; Lourenco and Recker 2013; Wearing and Rohani 2006). Previous work (Carrington and Simmons 2014) indicates that high viral titres during DHF or DSS may shorten the extrinsic incubation period for mosquitoes, and we therefore assumed \(\hat{\alpha }_{_A}>\hat{\alpha }\) (see Table 3 for values and ranges of parameters used in our simulations).

Table 3 Model parameters and their value (range) derived from the published literature (Capeding et al. 2014; Carrington and Simmons 2014; Coudeville and Garnett 2012; Hss et al. 2013; Lourenco and Recker 2013; Reich et al. 2013; Villar et al. 2014; Wearing and Rohani 2006)
Full size table

The duration of cross-protection between serotypes after recovery from the primary infection has been estimated in the range 0.88–4.31 years (95 % confidence interval), with an average of 1.88 years (Reich et al. 2013). We therefore assumed \(1/\rho _1=1/\rho _2=1.88\) years. Following the transient period of cross-protection, pre-existing immunity wanes to levels that can no longer completely neutralize the heterotypic serotypes. Since the susceptibility is reduced, a secondary heterologous infection can occur with a transmission probability that is lower than that for the primary infection. We assumed a duration of 5 years for reduced susceptibility to heterologous serotypes after the period of cross-protection. We simulated the model for different reduction factors in susceptibility when the level of partial protection against the secondary infection is high (\(q_1=q_2=0.25\)) or moderate to low (\(q_1=q_2=0.75\)). Most studies (Coudeville and Garnett 2012; Lourenco and Recker 2013; Reich et al. 2013) consider the strength of ADE (enhanced transmissibility) in the range 1–3, and we therefore assumed \(\sigma _1=\sigma _2=2\).

Clinical trials of a tetravalent vaccine candidate indicate the range 40–50 % of vaccine efficacy for DENv1 and DENv2 and 74–77 % for DENv3 and DENv4 (Villar et al. 2014). Based on these estimates, we consider reduction factors \(p_1=0.55\) and \(p_2=0.25\) for transmission rates following vaccination. Other recent studies (Capeding et al. 2014; Hss et al. 2013) also estimate similar efficacies for the tetravalent vaccine candidate, with a more balanced immune response against all four serotypes after three doses of vaccine in children. Since the effect of vaccine-induced ADE is unknown, we assumed the baseline enhanced transmissibilities \(\kappa _1=\kappa _2=2\) that are the same as enhanced transmissibilities for the secondary infection after the primary infection in unvaccinated individuals. We simulated the effect of vaccination on the dynamics of dengue outbreaks by considering different vaccine coverages for newborns (\(\phi \)) and vaccination rates for the susceptible population (\(\xi \)).

5 Simulations

We simulated the model to explore the dynamics of dengue outbreaks in the presence of two serotypes (\(\mathcal {S}_1\) and \(\mathcal {S}_2\)) with different transmissibilities, reflected in the corresponding reproduction numbers \(\,\mathcal {R}_1=3.5\) and \(\,\mathcal {R}_2=2.5\). These values are within the ranges reported in previous work (Ferguson et al. 1999b; Wearing and Rohani 2006). To evaluate the effect of vaccination, we ran simulations for an extended period of time to bypass the transient behaviour of the system.

Fig. 2
figure 2

Time profiles of infections caused by \(\mathcal {S}_1\) (black curves) and \(\mathcal {S}_2\) (red curves) for different vaccination coverages of newborns (panel A) and vaccination rates of susceptible individuals (panel B). The left and right columns in each panel correspond to the total number of dengue cases and the total number of dengue cases experiencing the ADE effect of both serotypes. Parameter values are \(\hat{\alpha }=365/12\), \(\hat{\alpha }_{_A}=365/8\), \(\mu =1/70\), \(\hat{\mu }=365/15\), \(\alpha _1=365/4\), \(\alpha _2=365/4\), \(\gamma _1=\gamma _2=365/6\), \(\rho _1=\rho _2=\eta =1/1.88\), and \(\theta _1=\theta _2=1/5\) per year, with \(\,\mathcal {R}_1=3.5\), \(\,\mathcal {R}_2=2.5\), \(\sigma _1=\sigma _2=2\), \(\kappa _1=\kappa _2=2\), \(q_1=q_2=0.25\), \(p_1=0.55\), and \(p_2=0.25\) (Color figure online)

Full size image

Using current estimates for vaccine efficacy, Fig. 2 shows that increasing vaccination coverage or vaccination rate reduces the overall burden (i.e. the total number of infections) of both serotypes \(\mathcal {S}_1\) and \(\mathcal {S}_2\). We observed that vaccination interferes with the oscillatory patterns of dengue outbreaks of both serotypes, causing damped oscillations that approach a steady state in shorter time period following vaccination as the vaccine coverage or rate increases. Furthermore, the number of dengue cases with \(\mathcal {S}_2\) who are subject to ADE decreases and stabilizes over several years (Fig. 2; right columns in panels A and B, red curves). However, while the number of dengue cases with \(\mathcal {S}_1\) who are subject to ADE will stabilize over the years (through damped oscillations) for a low vaccine coverage or rate (\(\phi =0.1\), \(\xi =0.1\)), it rises with increase in the vaccination coverage or rate to numbers potentially greater than what is observed in simulations without vaccination (Fig. 2; right columns in panels A and B, black curves). A possible explanation is the difference in transmissibilities of \(\mathcal {S}_1\) and \(\mathcal {S}_2\) at the time for start of vaccination, and the efficacy of vaccine which is higher for serotype \(\mathcal {S}_2\) than for \(\mathcal {S}_1\). We obtained qualitatively similar results when comparing scenarios of \(q_1=q_2=0.25\) versus \(q_1=q_2=0.75\), and \(\kappa _1=\kappa _2=1\) versus \(\kappa _1=\kappa _2=2\). However, regardless of the level of partial protection, we observed an interesting phenomenon that for high values of the vaccination coverage or rate, the scenario without enhanced transmissibility (\(\kappa _1=\kappa _2=1\)) leads to higher numbers of dengue infections with both serotypes \(\mathcal {S}_1\) and \(\mathcal {S}_2\) compared to the scenario with enhanced transmissibility (\(\kappa _1=\kappa _2=2\)) following vaccination. Summarizing these results, we note that with current estimates of the serotype-specific vaccine efficacies, containing dengue outbreaks is infeasible, even when the vaccination coverage of newborns is nearly 100 %. This conclusion holds true even for a high efficacy vaccine if the period of vaccine-induced protection is shorter than the average lifetime of the human population. Figure 3 illustrates these results where we considered 1.88 years for the period of full protection following vaccination, and 95 % protection afterwards. We obtained similar results for longer period of full protection (10–50 years; illustration not included here).

Fig. 3
figure 3

Time profiles of infections caused by \(\mathcal {S}_1\) (black curves) and \(\mathcal {S}_2\) (red curves) for different vaccination coverages of newborns (panel A) and vaccination rates of susceptible individuals (panel B). The left and right columns in each panel correspond to the total number of dengue cases and the total number of dengue cases experiencing the ADE effect of both serotypes. Parameter values are \(\hat{\alpha }=365/12\), \(\hat{\alpha }_{_A}=365/8\), \(\mu =1/70\), \(\hat{\mu }=365/15\), \(\alpha _1=365/4\), \(\alpha _2=365/4\), \(\gamma _1=\gamma _2=365/6\), \(\rho _1=\rho _2=\eta =1/1.88\), and \(\theta _1=\theta _2=1/5\) per year, with \(\,\mathcal {R}_1=3.5\), \(\,\mathcal {R}_2=2.5\), \(\sigma _1=\sigma _2=2\), \(\kappa _1=\kappa _2=2\), \(q_1=q_2=0.25\), and \(p_1=p_2=0.05\) (Color figure online)

Full size image

We simulated the model for a hypothetical scenario in which the vaccine provides lifetime protection to both serotypes (Fig. 4). With baseline values of other parameters given in Table 2, we observed that oscillatory patterns of dengue outbreaks are preserved for a low to moderate vaccine coverage (\(\phi =0.1, 0.4\)). For a high vaccine coverage (\(\phi =0.8\)), inter-outbreak periods are extended compared to a low to moderate vaccine coverage of newborns. For a sufficiently high vaccine coverage (\(\phi =0.95\)), both serotypes disappear from the population within 10 years following the start of vaccination. In contrast to previous scenarios, we do not observe any increase in the number of dengue cases of either serotype subject to ADE with increase in the vaccine coverage. Compared with the results presented in Fig. 3 (panel A) with a high vaccine efficacy (95 % against both serotypes), our simulations suggest that containing dengue outbreaks may be feasible with a high vaccination coverage of newborns only if the vaccine provides lifetime protection against all serotypes (Fig. 4, panel A). The time profiles of infections for the scenarios with vaccination of the susceptible individuals (\(\xi >0\)) are similar to those in the scenarios with vaccination of the newborns. As evident from these simulations, the time profiles of dengue serotypes stabilize in a shorter time period with reduced oscillatory behaviour for the scenarios with vaccination of the susceptible population compared to the scenarios with vaccination of only newborns.

Fig. 4
figure 4

Time profiles of infections caused by \(\mathcal {S}_1\) (black curves) and \(\mathcal {S}_2\) (red curves) for different vaccination coverages of newborns (panel A) and vaccination rates of susceptible individuals (panel B). The left and right columns in each panel correspond to the total number of dengue cases and the total number of dengue cases experiencing the ADE effect of both serotypes. Parameter values are \(\hat{\alpha }=365/12\), \(\hat{\alpha }_{_A}=365/8\), \(\mu =1/70\), \(\hat{\mu }=365/15\), \(\alpha _1=365/4\), \(\alpha _2=365/4\), \(\gamma _1=\gamma _2=365/6\), \(\rho _1=\rho _2=\eta =1/70\), and \(\theta _1=\theta _2=1/5\) per year, with \(\,\mathcal {R}_1=3.5\), \(\,\mathcal {R}_2=2.5\), \(\sigma _1=\sigma _2=2\), \(\kappa _1=\kappa _2=2\), \(q_1=q_2=0.25\), and \(p_1=p_2=0\) (Color figure online)

Full size image

6 Discussion

In this paper, we developed and analysed a full model of vector–host interactions for dengue spread with two serotypes of the virus co-circulating in the mosquito and human populations. Our model incorporates the phenomena of cross-protection (which decreases the risk of heterologous infection) and cross-enhancement (which increases the transmissibility of the virus from human to mosquito). In addition to cross-protection and cross-enhancement, we incorporated seasonality that has been reported to be a key factor in dengue dynamics.

By means of simulations, we have shown several important scenarios for the impact of vaccination on dengue prevention. First and foremost is the fact that dengue eradication is not feasible with the current estimates of vaccine efficacy against different serotypes (Capeding et al. 2014; Villar et al. 2014). Conspicuously, higher vaccine coverages or newborns or vaccination rates of susceptible individuals lead to a lower total number of dengue infections. However, the total number of dengue cases experiencing the ADE effects may increase over time if the vaccine-induced protection is imperfect or the duration of its protection is shorter than the lifetime of the host population. In contrast to previous work that suggests a transient period of higher prevalence following vaccination compared to the pre-vaccination era when the vaccine efficacy is very low or very high (Pandey and Medlock 2014), our model shows a considerable reduction in the overall disease burden, regardless of the vaccine efficacy. Paradoxically, we observed even lower incidence of dengue cases subject to ADE immediately after the introduction of vaccine, and later increase in number of such infections (Figs. 2, 3; right columns in each panel). These observations remain intact with variation in other parameters associated with cross-enhancement and naturally acquired immunity.

Our model is subject to a number of limitations that warrant further investigation. We considered only two serotypes of dengue; however, the inclusion of all four serotypes will provide more realistic scenarios for dengue dynamics. Since studies of the vaccine efficacy involve healthy children (Capeding et al. 2014; Villar et al. 2014), the potential benefits of immunization to different age groups due to indirect effects of herd immunity remain unaddressed. In the absence of vaccination and other pharmaceutical measures, public health interventions are mainly devised and deployed around vector control programs. In order to determine the impact of vaccination, we did not include the effect of vector control programs in our model. These programs have shown to significantly reduce the dengue incidence in several population settings, especially when combined with improved outbreak prediction and detection through coordinated epidemiological and entomological surveillance (WHO 2012). Our model could be expanded to incorporate these measures to reveal potential effects of combined vaccination and vector control programs on the long-term dynamics of dengue infection. Although we have relied on parameter values reported in the previous literature, we acknowledge the possible uncertainty in their estimates. Despite these limitations, the findings of this study have important implications for vaccination strategies, suggesting that other vector control measures may still play a key role in dengue prevention when vaccine becomes available.