An improved version of barodesy for clay

Abstract

Barodesy is a constitutive model based on proportional paths and the asymptotic behaviour of soil. It was originally developed for sand in 2009 by Kolymbas, and a version for clay was introduced in 2012. A shortcoming of former barodetic models was that tensile stresses can occur for certain dilative deformations. In this article, an improved version of barodesy for clay and a simplified calibration procedure are proposed. Basic features are shown, and simulations of element tests are compared with experimental data of several clay types.

1 Introduction

The constitutive model for soil called barodesy, proposed by Kolymbas [9–12], is based on the asymptotic behaviour of granulates expressed by the two rules proposed by Goldscheider [6], which have been experimentally confirmed for sand and clay [3, 6, 26, 27]:  (1) starting at the stress-free state, ${\mathbf { T}}=\mathbf {0}$, proportional strain paths¹ lead to proportional stress paths (see footnote 1); and (2) starting at ${\mathbf { T}}\ne \mathbf {0}$, proportional strain paths lead asymptotically to the corresponding proportional stress paths starting at ${\mathbf { T}}=\mathbf {0}$. This means that proportional stress paths function as attractors.

Barodesy exhibits similarities to hypoplasticity and was introduced by Kolymbas [9] for sand in 2009. In 2012, Medicus et al. [20] modified the sand version [10] and introduced barodesy for clay. A major component of barodesy is the so-called ${\mathbf { R}}$-function, which links proportional strain paths to proportional stress paths and thus acts as a stress-dilatancy relation. Former versions of ${\mathbf { R}}$ in barodesy [4, 9–12, 20] allow proportional stress paths to reach the tensile area. Experiments by Bergholz [1] of saturated reconstituted clay show that, also for highly overconsolidated clay, the stress ratio q/p (in triaxial compression) does not exceed three (i.e., the stress paths stay in the compression regime). The ${\mathbf { R}}$-function according to Medicus et al. [21] explicitly prohibits tensile stresses and is chosen as one of the equations for the improved version of barodesy for clay. However, an article [21] reviews existing experimental evidence on stress-dilatancy relations and discusses it in the framework of barodesy, but does not provide a constitutive model.

The main differences of barodesy for clay [20] and the version presented here are shown in this article. The tensor ${\mathbf { R}}$ and the scalar quantities f and g have been changed, and the calibration procedure is simplified as compared to [20]. The calibration procedure is explained, and simulations of element tests are compared with experimental data.

As in other constitutive models for clay, e.g., the hypoplastic models by Mašín[15, 18] and the Modified Cam Clay model [23], barodesy does not take argotropy (i.e., rate-dependence, relaxation, creep) into account.

2 Notation

We use the symbolic notation for Cauchy stress ${\mathbf { T}}$ and stretching ${\mathbf { D}}$. In some cases, the more familiar symbol $\sigma _i$ instead of $T_i$ is used for the principal stresses. Stress and stretching are defined as negative for compression. Tensors are written in bold capital letters (e.g., ${\mathbf { X}}$). $|{\mathbf { X}}|:=\sqrt{\text{tr}{\mathbf {X}}^2}$ is the Euclidean norm of ${\mathbf { X}}$ and $\text{ tr }\,{\mathbf { X}}$ is the sum of the diagonal components of ${\mathbf { X}}$. The superscript 0 marks a normalized tensor, i.e., ${\mathbf { X}}^0 = {\mathbf { X}}/|{\mathbf { X}}|$. $\mathbf {1}$ denotes the second-order unit tensor. Stresses are considered as effective ones, and the normally used dash is omitted. $\mathring{{\mathbf { T}}}$ is the objective² (co-rotational) stress rate resulting from barodesy, and $\dot{{\mathbf { T}}}$ is the time derivative according to Zaremba/Jaumann, which is obtained by $\dot{{\mathbf { T}}}=\mathring{\mathbf { T}}-{\mathbf { W}}{\mathbf { T}}+{\mathbf { W}}{\mathbf { T}}$, with ${\mathbf { W}}$ being the antimetric part of the velocity gradient. For rectilinear extensions, the objective stress rate $\mathring{{\mathbf { T}}}$ is equal to $\dot{{\mathbf { T}}}$ and will therefore be used in Sect. 4.

The stretching tensor ${\mathbf { D}}$ is the symmetric part of the velocity gradient.³ The mean effective stress is $p:=-\frac{1}{3}\text{tr}\,{\mathbf {T}}$, and $\varepsilon _{\text {vol}}=\text{tr} {\varvec{\varepsilon} }$ is the volumetric strain. In this article, $\delta :=\text{tr }{\mathbf {D}}^0={\dot{\varepsilon}_{\text {vol}}}/{| {\dot{\varvec{\varepsilon} }}}|$ is used as a dilatancy measure. For axisymmetric conditions, e.g., conventional triaxial or oedometric compression, the axial stress is denoted with $\sigma _1$ and the radial stress is denoted with $\sigma _2 (=\sigma _3)$. The associated strains are $\varepsilon _1$ and $\varepsilon _2=\varepsilon _3$. The void ratio e is the ratio of the volume of the voids $V_p$ to the volume of the solids $V_s$. The deviatoric stress is written as $q=-(\sigma _1-\sigma _3)$, and the deviatoric strain reads $\varepsilon _q=2/3\cdot (\varepsilon _1-\varepsilon _3)$. The stress ratio $K=\sigma _2/\sigma _1$ at critical states equals $K_c$, and for oedometric normal compression K is denoted by $K_0$.

Fig. 1

In a, b, $\psi _{\dot{\varepsilon }}$ and $\psi _\sigma$ according to [8] are defined in the Rendulic plane: i refers to isotropic compression; o to oedometric compression; c to isochoric triaxial compression; and $-c$ to isochoric triaxial extension. In c, barodesy for clay [20] (2012) is compared with the version presented here (2016), and $\varphi _c$ is chosen as $22.6^\circ$

3 Barodesy for clay

Barodesy is expressed by an evolution equation of the rate type $\mathring{{\mathbf { T}}}$ $= {\mathbf { h}}({\mathbf { T}}, {\mathbf { D}}, e)$. The general form of the constitutive relation is [9]:

$$\begin{aligned} {\mathring{{\mathbf { T}}}}~=~ h\cdot (f\mathbf {R}^0+g{\mathbf { T}}^0)\cdot |{\mathbf { D}}| \end{aligned}$$

(1)

with

$$\begin{aligned} h=c_3|{\mathbf { T}}|^{c_4}.\end{aligned}$$

(2)

Note that $c_4$ equals 1 for clay, and therefore all material constants are dimensionless⁴. ${\mathbf { R}}^0$ and ${\mathbf { T}}^0$ are the normalized tensors of proportional stress paths ${\mathbf { R}}$ and actual stress, respectively. ${\mathbf { R}}$ is a tensorial argument⁵ of normalized stretching ${\mathbf { D}}^0$ and is chosen according to Medicus et al. [21]:

$$\begin{aligned} {\mathbf { R}} = -\exp (\alpha {\mathbf { D}}^0) \end{aligned}$$

(3)

$$\begin{aligned} \alpha= \dfrac{\ln K}{\sqrt{3/2-\delta ^2/2}} \end{aligned}$$

(4)

$$\begin{aligned} K= 1-\dfrac{1}{1+c_1(m-c_2)^2} ~~ \text{ with }~ m=\dfrac{-3\delta }{\sqrt{6-2\delta ^2}} \end{aligned}$$

(5)

The scalar functions f and g take into account asymptotic states, critical states, the influence of stress level (barotropy) and density (pyknotropy). They are chosen as follows:

$$\begin{aligned} f= c_6\cdot \beta \cdot \delta -\frac{1}{2} \end{aligned}$$

(6)

$$\begin{aligned} g= (1-c_6)\cdot \beta \cdot \delta +\left( \frac{1+e}{1+e_c}\right) ^{c_5}-\frac{1}{2} \end{aligned}$$

(7)

with the critical void ratio $e_c$

$$\begin{aligned} e_c= \exp \left( N-\lambda ^*\ln \frac{2 ~p}{\sigma ^*}\right) -1 \end{aligned}$$

(8)

and the scalar functions $\beta$ and $\varLambda$

$$\begin{aligned} \beta= -\frac{1}{c_3\varLambda }+ \frac{1}{\sqrt{3}}2^{c_5\lambda ^*}- \frac{1}{\sqrt{3}} \end{aligned}$$

(9)

$$\begin{aligned} \varLambda= -\frac{\lambda ^*-\kappa ^*}{2\sqrt{3}}\delta +\frac{\lambda ^*+\kappa ^*}{2}\,. \end{aligned}$$

(10)

where $\sigma ^*$ is the reference pressure 1 kPa; $c_1$ − $c_6$ are material constants which depend on the soil parameters $\varphi _c$, N, $\lambda ^*$ and $\kappa ^*$, cf. Table 1; $\varphi _c$ is the critical friction angle; N is the ordinate intercept of the isotropic normal compression line (NCL) in the $\ln p$ versus $\ln (1+e)$ plot; $\lambda ^*$ is the slope of the NCL; and $\kappa ^*$ is the slope of the unloading line under isotropic compression in the $\ln p$ versus $\ln (1+e)$ plot. A detailed description of the soil parameters is given in Sect. 5.

Table 1 Determination of the constants $c_1$ − $c_6$ on the basis of $\varphi _c$, N, $\lambda ^*$ and $\kappa ^*$

Gudehus and Mašín [8] consider the angles $\psi _{\dot{\varepsilon }}$ and $\psi _\sigma$ according to Fig. 1a, b, for a graphical representation of proportional strain and stress paths. In Fig. 1c a $\psi _{\dot{\varepsilon }}$ - $\psi _\sigma$ plot of barodesy for clay [20] is compared with the improved version presented in this article. The main difference of the models is the choice of the ${\mathbf { R}}$-function. Note that the ${\mathbf { R}}$-function according to (3)–(5) prohibits tensile stresses.⁶ For volume decreasing paths, i.e., $-90^\circ<\psi _{\dot{\varepsilon }}<90^\circ$ the models almost coincide, for certain volume increasing paths⁷. Moreover, the proportional stress paths obtained with the 2012 version [20] lie in the tensile stress region ($\psi _\sigma <-35.3^\circ$ or $\psi _\sigma >54.7^\circ$). The consequences are shown in Fig. 2. Deforming soil with proportional strain paths, and the stress paths approach the corresponding proportional stress paths. Certain stress paths approach proportional stress paths in the tensile region with the old version [20], cf. Fig. 2a. In Fig. 2b, all stress paths stay in the compressive area. Note that, for simulations with barodesy for sand [4, 9–12], qualitatively the same is observed for dense samples. However, this shortage for sand is not as drastic as it is for overconsolidated clay in Fig. 2a.

Fig. 2

Starting from a hydrostatic stress state, a highly overconsolidated Weald clay sample is deformed with proportional strain paths in the range of $-180^\circ<\psi _{\dot{\varepsilon }}<180^\circ$. The stress paths approach the corresponding proportional stress paths. In a, certain stress paths, simulated with barodesy for clay [20], approach proportional stress paths in the tensile region. In b, all stress paths, simulated with the improved version of barodesy for clay according to (1)–(10), stay in the compression regime

4 Calibration

In barodesy, material constants are denoted by $c_i$, unless other symbols are established, such as $\varphi _c$, N, $\lambda ^*$ and $\kappa ^*$ in the case of barodesy for clay. All constants $c_1$ – $c_6$ can be determined on the basis of $\varphi _c$, N, $\lambda ^*$, $\kappa ^*$, see Table 1. In order to calibrate the four parameters $\varphi _c$, N, $\lambda ^*$ and $\kappa ^*$ a consolidated undrained triaxial test (CU) is sufficient. From consolidation, we get the parameters N, $\lambda ^*$ and $\kappa ^*$ and from undrained compression the critical friction angle $\varphi _c$ is obtained. In Sect. 5 the determination of $\varphi _c$, N, $\lambda ^*$ and $\kappa ^*$ is illustrated by element tests. In Table 2, the parameters are shown for several clay types.

Table 2 Critical state soil mechanics parameters used for the calibration of barodesy for clay

Below, the approach for the determination of $c_1$ − $c_6$ is explained.

4.1 Constants $c_1$ and $c_2$

The constants $c_1$ and $c_2$ can be calculated from $\varphi _c$, cf. Table 1. The ${\mathbf { R}}$-function (Eqs. 3–5) includes $c_1$ and $c_2$, captures critical states and Jáky’s relation $K_0=1-\sin \varphi _c$ for oedometric compression and produces similar results to Chu and Lo’s relation [3]. Results are presented in Appendix 1. A detailed explanation and further results are given by Medicus et al. [21].

4.2 Constants $c_4$ and function $\beta$

The NCL

$$\begin{aligned} \ln (1+e)=N-\lambda ^*\ln ({p}/{\sigma ^*}) \end{aligned}$$

(11)

is used for the determination of $c_4$ and $\beta$.⁸ $\sigma ^*$ is a reference pressure equal to 1 kPa. The NCL according to Butterfield [2] as well as the critical state line (CSL) are assumed to be linear in the $\ln (1+e)$ − $\ln p$ plot, cf. Mašín [15, 18].

The constant $c_4$ and the function $\beta$ are chosen in order to ensure that a simulation of hydrostatic normal compression with barodesy starting from $e=\exp N-1$ yields the NCL. A detailed derivation of $c_4$ and $\beta$ is shown in Appendix 2.

4.3 Constant $c_3$

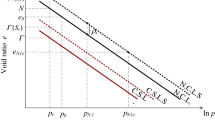
Gudehus and Mašín [8] propose the following graphical representation of admissible states with respect to void ratio and proportional stress paths. Figure 3 shows how proportional stress paths (in terms of $\psi _\sigma$) are assumed to be connected with $p_e/p$. Hvorslev’s equivalent consolidation pressure $p_e$ is the value of mean stress on the NCL, which refers to the current specific volume $(1+e)$, cf. Fig. 3a:

$$\begin{aligned} p_e=\exp \left( \frac{N-\ln (1+e)}{\lambda ^*}\right) \end{aligned}$$

(12)

The distance of a state characterized by e and p from the isotropic normal compression line is therefore indicated by $p_e/p$. For example, for hydrostatic compression it applies $p_e/p=1$ and $\psi _\sigma =0$, and at critical states $p_e/p_c$ is assumed to be equal to 2. Proportional stretching will eventually lead to constant values of $p_e/p$ for compressive stretching, as well as for extensive stretching, so-called asymptotic extension states [7, 8, 16]. Asymptotic extension states correspond to so-called normal extension lines in the $\ln p$ − $\ln (1+e)$ plot [8, 16]. Gudehus and Mašín [8] propose the $p_e/p$−$\psi _\sigma$ plot (Fig. 3b) for the directions of proportional stretching in the range of $-d<\psi _{\dot{\varepsilon }}<d$, according to Fig. 1a. The directions $-d$ and d are theoretical limits of asymptotic behaviour according to Gudehus and Mašín [8]. Discrete element simulations by Mašín [16] demonstrated that asymptotic states could only be obtained in a narrower range of $\psi _{\dot{\varepsilon }}$. However, in barodesy, asymptotic states are obtained for the whole range of $-180^\circ<\psi _{\dot{\varepsilon }}<180^\circ$.

The following procedure for the determination of $c_3$ is proposed: barodesy predicts for sufficiently long proportional compressive stretching $p_e / p =$ const., e.g., for $\psi _{\dot{\varepsilon }}=0^\circ$ the NCL is reached, and $p_e / p_i =1$ (Fig. 3). This also applies for extension paths, which lead to normal extension lines in the $\ln p$ − $\ln (1+e)$ plot. In particular for an isotropic extension path, which is denoted with $-i$ in Fig. 1a, the isotropic normal extension line is reached, see Fig. 3a. It follows that the unloading stiffness in the $\ln p$ − $\ln (1+e)$ plot is characterized by the parameter $\lambda ^*$:

$$\begin{aligned} \frac{\dot{e}}{1+e}=-\lambda ^*\frac{\dot{p}}{p} \end{aligned}$$

(13)

With the general form of the barodetic constitutive relation (1), isotropic compression (i.e. ${\mathbf { T}}= -p\mathbf{1}, {\mathbf { R}}^0={\mathbf { T}}^0=-\frac{1}{\sqrt{3}}{} \mathbf{1}$) is expressed by:

$$\begin{aligned} \dot{p}=c_3|{\mathbf { T}}| \frac{f+g}{\sqrt{3}} |{\mathbf { D}}|. \end{aligned}$$

(14)

For a proportional isotropic extension paths, Eq. 15 follows from Eqs. 13 and 14 (with $\delta =\sqrt{3}$):

$$\begin{aligned} c_3(f+g)=-\sqrt{3}/\lambda ^* \end{aligned}$$

(15)

With f, g and $\beta$ from (6), (7) and (34) and with $(1+e)/(1+e_c)=(2\cdot p_{-i}/p_e)^{\lambda ^*}$, we obtain:⁹

$$\begin{aligned} c_3\left( 2\frac{p_{-i}}{p_e}\right) ^{\lambda ^*c_5}-c_3 + c_3\sqrt{3}\left( -\frac{1}{c_3\kappa ^*}+ \frac{1}{\sqrt{3}}2^{c_5\lambda ^*}- \frac{1}{\sqrt{3}}\right)= -\sqrt{3}/\lambda ^*\end{aligned}$$

Releasing $c_3$, yields:

$$\begin{aligned} c_3=\frac{-\sqrt{3}/\lambda ^*+\sqrt{3}/\kappa ^*}{2^{c_5{\lambda ^*}}+\left( 2\frac{p_{-i}}{p_e}\right) ^{c_5{\lambda ^*}}-2} \end{aligned}$$

(16)

Choosing $p_{-i}/p_e=1/1000$ in (16) yields:

$$\begin{aligned} c_3=\frac{-\sqrt{3}/\lambda ^*+\sqrt{3}/\kappa ^*}{2^{c_5\lambda ^*}+\left( \frac{1}{500}\right) ^{c_5\lambda ^*}-2} \end{aligned}$$

(17)

Fig. 3

a Schematic plot: sufficiently long proportional stretching sweeps out the memory. The distance from the isotropic normal compression line is defined through $p_e/p=\,$const, cf. Gudehus and Mašín [8] and Mašín [16]. b $p_e/p$ − $\psi _\sigma$ plot according to [8]: simulations with barodesy for clay

Note that $p_{-i}/p_e=1/1000$ is arbitrary and cannot be acquired by experiments. However, the overall performance¹⁰ of barodesy for clay is best by choosing $p_{-i}/p_e=1/1000$ and helps to present a calibration procedure which is simple and applicable also for practitioners without performing any least square optimization. Figure 3b shows how $\psi _\sigma$ is related to $p_e/p$ in barodesy.

4.4 Constant $c_5$

The constant $c_5$ has been determined by trial. Setting $c_5=1/K_c$ gives the best fit concerning overall performance. Setting $c_5=1$ would highly overestimate radial stress under oedometric compression.

4.5 Constant $c_6$

It appears reasonable to require that, under isotropic extension, the stress paths follow the shortest way to the origin regardless of its actual stress state, cf. Fig. 4a. From this requirement, we get for isotropic extension:

$$\begin{aligned} \frac{\dot{T_1}}{\dot{T_2}}=\frac{{T_1}}{{T_2}} \end{aligned}$$

(18)

and with ${T_1}/{T_2}={T_1^0}/{T_2^0}$ and (1) we obtain:

$$\begin{aligned} \frac{f R_1^0+g T_1^0}{f R_2^0+g T_2^0}= \frac{{T_1^0}}{{T_2^0}} \end{aligned}$$

(19)

$$\begin{aligned} f \frac{R_1^0}{R_2^0}= f \frac{T_1^0}{T_2^0} \end{aligned}$$

(20)

Equation (20) is valid for a proportional isotropic extension or compression paths or if $f=0$. Setting $f=0$ in (6), we obtain with $\delta =\sqrt{3}$ and $\beta$ from (34):

$$\begin{aligned} c_6= \dfrac{1}{2\left( \dfrac{-\sqrt{3}}{c_3\kappa ^*}+ 2^{c_5\lambda ^*}- {1}\right) } \end{aligned}$$

(21)

In Fig. 4b, simulations of barodesy show that the stress paths for isotropic extension follow the shortest way to the origin. Response envelopes for London clay are added in Fig. 4b.

Fig. 4

Determination of $c_6$: it is required that under isotropic extension (${\mathbf { D}}^0=\mathbf {1}/\sqrt{3}$), the stress paths follow the shortest way to the origin regardless of the actual stress state, cf. schematic plot in a. In b, simulations with barodesy are shown: the stress paths for isotropic extension always follow the shortest way to the origin. Response envelopes for London clay are added

5 Simulations of element tests

In this section, simulations of element tests with and without rotation of principal axes are shown. Element tests in general are an idealization and, as in all experiments inhomogeneities occur. Especially with shearing, localization takes place and the loss of homogeneity is unavoidable. Thus, the comparison of simulations of element tests with experimental data only serves as an approximate reference.

5.1 Rectilinear extensions

Isotropic compression: In Fig. 5, an isotropic compression test and its simulation with barodesy is shown. In Fig. 5b, the calibration of the parameters N, $\lambda ^*$ and $\kappa ^*$ is illustrated with experimental data of Dresden clay [1]. As isotropic normal compression is included in the formulation and calibration of barodesy, normally consolidated isotropic compression test results are therefore in agreement with the simulated NCL, see Fig. 5. The unloading stiffness is described through the parameter $\kappa ^*$. The term $({1+e})/({1 + e_c}) = \text{ const. }$ in (22) indicates a straight line (A-B) in the $\ln p$-$\ln (1+e)$ plot in Fig. 5b, cf. [19]

$$\begin{aligned} \frac{1+e}{1+e_c}=\root c_5 \of {2-2^{c_5\lambda ^*}} \end{aligned}$$

(22)

On this line, the tangential unloading stiffness under isotropic extension is ${\dot{p}}/{\dot{e}}=-{p}/(\kappa ^*(1+e))$ with barodesy. Closer to the NCL, the unloading stiffness is slightly higher, and for lower mean stresses p, the stiffness is lower, cf. Fig. 5b and [19].

Fig. 5

Isotropic compression: experimental results with Dresden clay denoted in [1] with CD 02 and simulations with barodesy. In a a e - p plot is shown. In b, N, $\lambda ^*$ and $\kappa ^*$ are calibrated in the $\ln (1+e)$ versus $\ln p$ plot. $e_0$ refers to the void ratio e at ${p=1 \text{ kPa }}.$

Triaxial compression: The critical friction angle $\varphi _c$ is calibrated with a normally consolidated Weald clay sample and can be obtained from the slope of the critical state line in the p-q plot, cf. Fig. 6a. Test results and numerical simulation with barodesy of a normally consolidated and overconsolidated sample are shown. Note that the simulation of the overconsolidated sample does not allow a higher mobilized friction angle $\varphi _m$ than $\varphi _c$. Barodesy therefore underestimates the peak friction (i.e., the maximum mobilized friction) angle in CU tests, cf. Fig. 6b. The simulations of the normally consolidated and overconsolidated samples in the q/p-$\varepsilon _1$ plot coincide for CU tests, cf. Fig. 6b.

Fig. 6

Undrained triaxial compression of Weald clay (according to Mašín [18], data by Parry [22]) and numerical simulation with barodesy. The initial states of the normally consolidated and overconsolidated samples are $e_0 = 0.622$ and $e_0 = 0.572$. In a, a p−q plot is shown: the slope of the critical state line in the p−q plot is $M=\dfrac{6\sin \varphi _c}{3-\sin \varphi _c}$. Test results and numerical simulation with barodesy of a normally consolidated and an overconsolidated sample are added. The start points are denoted by a circle, and the end points are denoted by a cross. In b, a q/p-$\varepsilon _1$ plot, and $\varphi _m$−$\varepsilon _1$ plot is shown, respectively: The simulations of normally consolidated and overconsolidated samples in the q/p−$\varepsilon _1$ plot coincide for CU tests. Barodesy underestimates the peak friction angle for the overconsolidated sample

In Fig. 7, limit points of normally consolidated samples obtained by true triaxial tests are shown. The data refer to San Francisco Bay Mud from Lade [13] and are compared with predictions by barodesy. Note that the critical state locus of barodesy practically coincides with the locus according to Matsuoka-Nakai, cf. Fellin and Ostermann [5].

Fig. 7

Critical stress points of normally consolidated San Francisco Bay Mud from Lade [13] are compared with critical state predictions by barodesy and Mohr-Coulomb. The calculations refer to $\text{ tr }\,{\mathbf { T}}=-500$ kPa and $\varphi _c=30.6^\circ$. The samples were isotropically consolidated and compressed in conventional and true triaxial tests. The critical stress points are arranged slightly anisotropic, due to the anisotropic orientation of the particles, according to Lade [13]. An isotropic material would leave a rotation in the deviatoric plane by $120^\circ$ undiscovered

In Fig. 8 drained triaxial compression and extension tests of normally consolidated and overconsolidated Weald clay are shown. The simulations with barodesy are realistic. Contractant behaviour for the normally consolidated samples and dilatant behaviour for the overconsolidated clay is observed. Peak strength is well predicted.

Fig. 8

Drained compression and extension of Weald clay (according to Mašín [18], data by Parry [22]) and numerical simulation with barodesy. The consolidation pressures are $\sigma _2=-69.45$ kPa and $\sigma _2=-206.2$ kPa with the initial void ratios $e_\text {ini}=0.572$ and $e_\text {ini}=0.622$. $\varepsilon _1$ versus q plot in a, $\varepsilon _1$ versus $\varepsilon _{\text {vol}}$ plot in b

In Fig. 9, a more general picture of drained triaxial tests simulated with barodesy is shown. Triaxial tests are shown as p–e and p–q plots as well as plots in the normalized stress plane (i.e., $p/p_e$−$q/p_e$). The paths approach the critical state line in the p–e and p–q plots. Highly overconsolidated samples dilate to approach the CSL in the p–e plot, and slightly overconsolidated and normally consolidated samples exhibit contractant behaviour to approach the CSL. Highly overconsolidated samples overshoot the CSL in the p–q plot.

Fig. 9

Barodesy: simulated paths of drained triaxial tests for London clay. The start points are denoted by a circle, and the end points are denoted by a cross

Oedometric compression: In Fig. 10, oedometric compression of London clay is shown. The normal compression behaviour gives reasonable results in the e − p plot, as well as in the $\sigma _1$ − $\sigma _2$ plot.¹¹ For unloading, the radial stress is overestimated.

Fig. 10

Oedometric loading (up to $\sigma _1=-400$ kPa), unloading (up to $\sigma _1=-100$ kPa) and reloading ($\sigma _1=-266$ kPa): experimental results (PhM14) of London Clay (data from Mašín [14]) with $e_\text {ini}=1.476$ and numerical simulation with barodesy. $\ln (1+e)$ versus $\ln p$ plot in a, $\sigma _2$ - $\sigma _1$ plot in b: $\sigma _2$ is overestimated at unloading

5.2 Rotation of principal stress and strain axes

Simple shear test: Figure 11 presents a simulation of a simple shear test with a constant vertical stress of $\sigma _y=-100$ kPa. The evolution of the shear stress $\tau _{xy}$ is plotted over the shear strain $\gamma$ (in radian). The angle $\alpha _\sigma$ denotes the inclination of major principal stress to the horizontal direction x, and $\alpha _D$ is the inclination of major principal stretching, respectively. In Fig. 11, a Weald clay sample with $K_0=1-\sin \varphi _c$ is sheared. The major principal stress direction $\alpha _\sigma$ is $90^\circ$ at zero shear strain and decreases to $\approx$ $45^\circ$ with ongoing shear strain. The difference between the angles $\alpha _D$ and $\alpha _\sigma$, i.e., the angle of non-coaxiality $\alpha _D-\alpha _\sigma$ becomes very small¹², i.e., $\alpha _\sigma \approx \alpha _D\approx 45^\circ$ at the critical state. Similar results with hypoplasticity and an elasto-plastic model are shown in Schranz and Fellin [24]. Experiments on sand according to Roscoe et al. [23] and DEM simulations [25, 29] yield similar results, cf. Yu [28].

Fig. 11

Simple shear test with a constant vertical stress of $\sigma _y=-100$ kPa, the initial radial stress is $\sigma _x=(1-\sin \varphi _c)\cdot \sigma _y=-59.33$ kPa. In b directions of principal stress $\alpha _\sigma$ and principal stretching $\alpha _D$ are shown. Weald Clay with an initial void ratio $e_\text {ini}=0.68$ is simulated with barodesy.

In Fig. 12, the evolution of the angle of non-coaxiality with ongoing shear strain is shown for different initial $K_0$ values. In Fig. 12a, DEM simulations from Thornton and Zhang[25], Zhang [29] show that the angle of non-coaxiality is small for $K_0=1$. For $K_0=2$, the angle of non-coaxiality decreases with ongoing shear strain to $\approx 0^\circ$; and for $K_0=0.5$ it increases to $\approx 0^\circ$. It is stated that non-coaxiality is significant before 10% shear strain [29]. The predictions with barodesy in Fig. 12b are in good agreement with the DEM simulations in Fig. 12a.

The results of the DEM simulations and experiments [23] apply for sand. Therefore, only a qualitative comparison of barodesy for clay (Figs. 11b, 12b) is possible. However, the comparison demonstrates that barodesy is applicable for general deformation, i.e., rotation of principal stress and strain axes.

Fig. 12

Evolution of the angle of non-coaxiality in a simple shear test with different initial $K_0$ values: in a, DEM simulations from Thornton and Zhang [25], Zhang [29] are shown, in b, Weald Clay with $e_\text {ini}=0.68$ is simulated with barodesy

Appendix 3 summarizes all equations of barodesy for clay.

6 Summary and conclusions

Barodesy comprises fundamental characteristics of soil behaviour, such as critical states, asympotic states, barotropy, pyknotropy, and a stress-dilatancy relation. Barodesy can be written symbolically as a single equation of the form ${\mathring{{\mathbf { T}}}}\,=\,{\mathbf { h}}({\mathbf { T}}, {\mathbf { D}}, e)$, i.e., the stress rate is expressed as a function of the stress, stretching and the void ratio. As in basic hypoplastic models, barodesy uses only ${\mathbf { T}}$ and e as memory parameters. This covers many phenomena and is insufficient to capture strong memory effects. Consequently, ratcheting and unrealistic small-strain behaviour are obtained.

In order to calibrate barodesy for clay, four well-known material parameters of soil mechanics, which can be determined from a consolidated undrained compression test, are sufficient. The model provides realistic results, as compared with experimental results of various clay types.

Appendices

Appendix 1: Determination of $c_1$ and $c_2$

The parameters $c_1$ and $c_2$ are determined according to Eqs. 23 and 24 and are included in the ${\mathbf { R}}$-function [21] (Eqs. 3–5).

$$\begin{aligned} c_1= \dfrac{K_c}{c_2^2(1-K_c)}=\dfrac{1-\sin {\varphi _c}}{2\, c_2^2\, \sin \varphi _c} \end{aligned}$$

(23)

$$\begin{aligned} c_2= \dfrac{3\sqrt{K_c({1-K_c}){K_0}({1-K_0})}+3K_c(1-K_0)}{2(K_c-K_0)} \end{aligned}$$

(24)

The stress ratios ${\sigma _2}/{\sigma _1}$ under oedometric compression $K_0$ and at critical states $K_c=\dfrac{1-\sin \varphi _c}{1+\sin \varphi _c}$ are comprised. If we include Jáky’s relation under oedometric compression, i.e., $K_0=1-\sin \varphi _c$, Eq. 24 can be simplified as follows:

$$\begin{aligned} c_2=-\dfrac{3\sqrt{2}+3}{2}\approx -3.6213 \end{aligned}$$

(25)

In Fig. 13, results of the ${\mathbf { R}}$ - function are compared with the relation by Chu and Lo [3].

Fig. 13

Predictions of proportional paths with the ${\mathbf { R}}$ - function [21] in which $c_1$ and $c_2$ are calibrated on the basis $\varphi _c$. The results are in good agreement with the relation by Chu and Lo [3]. $\varphi _c$ is chosen to $25^\circ$ in this plot

Appendix 2: Determination of $c_4$ and $\beta$

Derivation of the NCL (Eq. 11) with respect to time t yields:

$$\begin{aligned} \frac{\dot{e}}{1+e}=-\lambda ^*\frac{\dot{p}}{p} \end{aligned}$$

(26)

With $\frac{\dot{e}}{1+e}=\text{ tr }{\mathbf { D}}=-\sqrt{3}|{\mathbf { D}}|$ and $|{\mathbf { T}}|=\sqrt{3}p$ the NCL reads¹³:

$$\begin{aligned} \dot{p}=|{\mathbf { T}}| ~ \frac{1}{\lambda ^*}~ |{\mathbf { D}}| \end{aligned}$$

(27)

With the general form of the barodetic constitutive relation (1), isotropic compression (i.e. ${\mathbf { T}}= -p\mathbf{1}, {\mathbf { R}}^0={\mathbf { T}}^0=-\frac{1}{\sqrt{3}}{} \mathbf{1}$) is expressed by the following form:

$$\begin{aligned} \dot{p}=c_3|{\mathbf { T}}|^{c_4} \frac{f+g}{\sqrt{3}} |{\mathbf { D}}| \end{aligned}$$

(28)

Comparing (27) and (28) yields:

$$\begin{aligned} c_4=1 \end{aligned}$$

(29)

and

$$\begin{aligned} \dfrac{c_3}{\sqrt{3}}(f+g)=&\dfrac{1}{\lambda ^*} \ . \end{aligned}$$

(30)

Now, we write $f+g$ from (6) and (7) for hydrostatic compression ($\delta =-\sqrt{3}$), use (30), and obtain:

$$\begin{aligned} c_3\left( \left( \frac{1+e}{1+e_c}\right) ^{c_5}-1-\sqrt{3}\beta \right) = \frac{\sqrt{3}}{\lambda ^*} \end{aligned}$$

(31)

Introducing the NCL (Eq. 11) and CSL (Eq. 8) into (31) leads to:

$$\begin{aligned}&\left( \frac{\exp {(N - \lambda ^*\ln {(p/\sigma ^*)}})}{\exp {(N - \lambda ^*\ln \left( 2{p}/\sigma ^*\right) })}\right) ^{c_5}-1-\sqrt{3}\beta = \frac{\sqrt{3}}{c_3\lambda ^*} \end{aligned}$$

(32)

$$\begin{aligned}&\exp \left( {c_5}\lambda ^*\ln 2\right) -1-\sqrt{3}\beta = \frac{\sqrt{3}}{c_3\lambda ^*}\nonumber \\&2^{c_5\lambda ^*} -1-\sqrt{3}\beta = \frac{\sqrt{3}}{c_3\lambda ^*}\nonumber \\&\leadsto \beta =-\frac{1}{c_3\lambda ^*}+ \frac{1}{\sqrt{3}}2^{c_5\lambda ^*}- \frac{1}{\sqrt{3}} \end{aligned}$$

(33)

Setting

$$\begin{aligned} \beta =-\frac{1}{c_3\varLambda }+ \frac{1}{\sqrt{3}}2^{c_5\lambda ^*}- \frac{1}{\sqrt{3}} \end{aligned}$$

(34)

with

$$\begin{aligned} \varLambda :=-\frac{\lambda ^*-\kappa ^*}{2\sqrt{3}}\delta +\frac{\lambda ^*+\kappa ^*}{2} \end{aligned}$$

(35)

yields the following:¹⁴ Equation 30 is satisfied under isotropic compression, i.e., for $\delta =-\sqrt{3}$.

Appendix 3: Equations of barodesy for clay

In this appendix, all equations of barodesy for clay are summarized.

$$\begin{aligned} {\mathring{{\mathbf { T}}}}= c_3|{\mathbf { T}}|^{c_4}\cdot (f\mathbf {R}^0+g{\mathbf { T}}^0)\cdot |{\mathbf { D}}| \end{aligned}$$

(36)

$$\begin{aligned} {\mathbf { R}}= -\exp (\alpha {\mathbf { D}}^0) \text{ with } \alpha =\dfrac{\ln K}{\sqrt{3/2-{\text{tr}\,{\mathbf {D}}^0}^2/2}} \end{aligned}$$

(37)

$$\begin{aligned} K= 1-\dfrac{1}{1+c_1(m-c_2)^2} ~~ \text{ with }~~ m=\dfrac{-3\text{tr}\,{\mathbf {D}}^0}{\sqrt{6-2{\text{tr}\,{\mathbf {D}}^0}^2}} \end{aligned}$$

(38)

$$\begin{aligned} f= c_6\cdot \beta \cdot \text{tr}\,{\mathbf {D}}^0-\frac{1}{2} \end{aligned}$$

(39)

$$\begin{aligned} g= (1-c_6)\cdot \beta \cdot \text{tr}\,{\mathbf {D}}^0+\left( \frac{1+e}{1+e_c}\right) ^{c_5}-\frac{1}{2} \end{aligned}$$

(40)

$$\begin{aligned} e_c= \exp \left( N-\lambda ^*\ln \frac{-2 ~\text{tr}\,{\mathbf {T}}}{\sigma ^*}\right) -1 \end{aligned}$$

(41)

$$\begin{aligned} \beta= -\frac{1}{c_3\varLambda }+ \frac{1}{\sqrt{3}}2^{c_5\lambda ^*}- \frac{1}{\sqrt{3}} \end{aligned}$$

(42)

$$\begin{aligned} \varLambda= -\frac{\lambda ^*-\kappa ^*}{2\sqrt{3}}\text{tr}\,{\mathbf {D}}^0+\frac{\lambda ^*+\kappa ^*}{2} \end{aligned}$$

(43)

In Table 1 the determination of constants $c_1$ - $c_6$ on the basis of $\varphi _c$, N, $\lambda ^*$ and $\kappa ^*$ (Table 2) is shown.