A Comparison of Conventional Gel Stiffness Characterization Techniques with Cavitation Rheology

Abstract

Background

Interest in soft gels has arisen in recent years as they can be applied to many fields such as tissue engineering, food additives, and drug delivery. The importance of these technologies lies in the stiffness of applied materials and hence there is a strong need for determining the stiffness of gels precisely. Cavitation rheology, a novel experimental method, can measure the Young’s modulus in any part of a soft material. However, compared with fully developed conventional techniques, cavitation rheology is not completely exploited and needs more in-depth research conducted.

Objective

In this paper, four experimental approaches have been applied to determine the Young’s modulus of an ultra-soft tri-block copolymer (PMMA-PnBA-PMMA): classic shear rheology, static indentation, cavitation rheology and low-velocity impact. Although there are plenty of examples of soft gel stiffness characterization in the open literature, this is the first time (to the knowledge of the authors), that cavitation rheology and the impact pinch-off experiment have been compared with the more traditional stiffness testing approaches of classic rheology and indentation. Furthermore, the relationship between gel’s stiffness and the von Mises strain rate is investigated in the analysis.

Methods

Benchmark data is obtained from a classic shear rheology experiment. A modification to the previous cavitation rheology analysis is made to improve the accuracy in predicting the Young’s modulus and surface tension. The measurements of static indentation and dynamic low-velocity impact experiments are taken non-invasively by optical visualization. Gel samples with three concentrations are applied to all the experiments to investigate the feasibility of each method.

Results

The comparison between different experiments indicates a slight strain-rate dependence in gel stiffness across various gel concentrations. Cavitation rheology is shown to have a clear correlation with high-strain rate tests, but not quasi-static ones.

Conclusions

This paper has made some significant contributions in regards to broadening the knowledge of cavitation rheology. In addition, we provide an in-depth analysis of pragmatic stiffness measurement techniques and demonstrate their usefulness across various stiffness regimes in a soft polymeric gel with tunable mechanical properties.

Appendix

Cavitation Rheology Derivations

The critical expansion ratio at the instability $\lambda _c$ can be determined by setting the derivative of equation (1) with respect to $\lambda$ equal to zero

$$\begin{aligned} \frac{4}{Er_0}(\frac{-2\gamma \sqrt{\lambda _c^2-1}}{\lambda _c^3}+\frac{\gamma }{\lambda _c \sqrt{\lambda _c^2-1}})+\frac{2}{3}(\frac{1}{\lambda _c^2}+\frac{1}{\lambda _c^5})=0, \end{aligned}$$

(14)

The critical pressure at the instability $P_c$ is calculated by substituting $\lambda _c$ for $\lambda$ in equation (1)

$$\begin{aligned} P_c\cong (\frac{5}{6}-\frac{2}{3\lambda _c}-\frac{1}{6\lambda _c^4})E+(\frac{\sqrt{\lambda _c^2-1}}{\lambda _c^2})(\frac{4\gamma }{r_0}), \end{aligned}$$

(15)

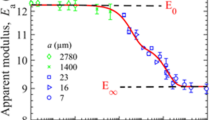
The difference between the critical pressures calculated by equations (1) and (2) is illustrated in Fig. 12. One example of linear regression based on equation (2) is presented in Fig. 13.

Fig. 12

E and $\gamma$ are assumed as $3 \ kPa$ and $0.0269 \ N/m$ for the plot. P is calculated by equation (1), and $P_c^{fit}$ is calculated by equation (2). For a small $r_0$ value (0.005 mm and 0.01 mm), the pressure ratio $P/P_c^{fit}$ reaches a maximum and then decreases with the increase of expansion ratio $\lambda$. For a large $r_0$ value (0.05 mm, 0.10 mm and 0.50 mm), $P/P_c^{fit}$ monotonically increases and asymptotically approaches a certain value. The maximum of $P/P_c^{fit}$ is not equal to 1 for some $r_0$ values, reflecting the difference in maximum pressures (critical pressures) calculated by equations (1) and (2). The black cross (x) on each curve demonstrates the expansion ratio at which the cavity reaches the inner surface of the gel container, assuming the inner radius of the container to be 10 mm

Fig. 13

An example of linear regression performed for our $7.89 \%$ v/v gel using equation (2). E and $\gamma$ are calculated to be $6.6 \ kPa$ and $0.88 \ N/m$ in this case

Von Mises Strain and Strain Rate Calculation for the Static Indentation Experiment

The calculations of von Mises strain and strain rate for the static indentation experiment are as follows: The deformation gradient tensor $\mathbf {F}$ can be expressed as

$$\begin{aligned} \left[ \begin{array}{ccc} \sqrt{\frac{A_{s}}{A_{c}}} &{} 0 &{} 0 \\ 0 &{} \sqrt{\frac{A_{s}}{A_{c}}} &{} 0 \\ 0 &{} 0 &{} \frac{A_{c}}{A_{s}} \end{array}\right] \end{aligned}$$

(16)

where $A_{s}$ and $A_{c}$ are the surface area of the spherical cap which is surrounded by gel and the contact area (projected area), respectively. The ratio between $A_{s}$ and $A_{c}$ can be expressed as

$$\begin{aligned} \frac{A_{s}}{A_{c}}=\frac{2 R h}{\alpha ^{2}} \end{aligned}$$

(17)

where R is the radius of indenter, h is the indentation depth and $\alpha$ is the contact radius. The logarithmic finite Hencky strain tensor $\mathbf {e}$ is

$$\begin{aligned} \mathbf {e}=\ln \sqrt{\mathbf {F}^{\mathrm {T}} \mathbf {F}}=\left[ \begin{array}{ccc} \ln \left( \frac{A_{s}}{A_{c}}\right) &{} 0 &{} 0 \\ 0 &{} \ln \left( \frac{A_{s}}{A_{c}}\right) &{} 0 \\ 0 &{} 0 &{} 2 \ln \left( \frac{A_{c}}{A_{s}}\right) \end{array}\right] \end{aligned}$$

(18)

The von Mises strain $\varepsilon _{\mathrm {vm}}$ can then be calculated with the deviatoric part of the logarithmic finite Hencky strain tensor $\mathbf {e}^{\prime }$

$$\begin{aligned} \varepsilon _{\mathrm {vm}}=\sqrt{\frac{2}{3} \mathbf {e}^{\prime }: \mathbf {e}^{\prime }} = \frac{2 R h}{\alpha ^{2}} \end{aligned}$$

(19)

We take the derivative of equation (18) with respect to time, we can calculate the von Mises strain rate $\dot{\varepsilon }_{\mathrm {vm}}$ is determined

$$\begin{aligned} \dot{\varepsilon }_{\mathrm {vm}}=\sqrt{\frac{2}{3} \dot{\mathbf {e}}^{\prime }: \dot{\mathbf {e}}^{\prime }}=2 \frac{\dot{h}}{h} \end{aligned}$$

(20)

where $\dot{h}$ is the indentation speed, which is estimated by $\sqrt{2gh}$ and h is the indentation depth.

Von Mises Strain and Strain Rate Calculation for the Free-Fall Impact Experiment

The calculations of von Mises strain and strain rate for the free-fall impact experiment are as follows: The deformation gradient tensor $\mathbf {F}$ can be expressed as

$$\begin{aligned} \left[ \begin{array}{ccc} \sqrt{\frac{A_{s}}{A_{c}}} &{} 0 &{} 0 \\ 0 &{} \sqrt{\frac{A_{s}}{A_{c}}} &{} 0 \\ 0 &{} 0 &{} \frac{A_{c}}{A_{s}} \end{array}\right] \end{aligned}$$

(21)

where $A_{s}$ and $A_{c}$ are the estimated surface area of a cylinder created during the penetration process and the contact area (projected area), respectively. $A_{s}$ and $A_{c}$ can be calculated by

$$\begin{aligned} A_{s}=\pi D h_{p}+\frac{\pi D^{2}}{2} \end{aligned}$$

(22)

$$\begin{aligned} A_{c}=\frac{\pi D^{2}}{4} \end{aligned}$$

(23)

The ratio between $A_{s}$ and $A_{c}$ can be expressed as

$$\begin{aligned} \frac{A_{s}}{A_{c}}=2+4 \frac{h_{p}}{D} \end{aligned}$$

(24)

where $h_p$ is the penetration depth, D is the diameter of the projectile. The logarithmic finite Hencky strain tensor $\mathbf {e}$ is

$$\begin{aligned} \mathbf {e}=\ln \sqrt{\mathbf {F}^{\mathrm {T}} \mathbf {F}}=\left[ \begin{array}{ccc} \ln \left( \frac{A_{s}}{A_{c}}\right) &{} 0 &{} 0 \\ 0 &{} \ln \left( \frac{A_{s}}{A_{c}}\right) &{} 0 \\ 0 &{} 0 &{} 2 \ln \left( \frac{A_{c}}{A_{s}}\right) \end{array}\right] \end{aligned}$$

(25)

The von Mises strain $\varepsilon _{\mathrm {vm}}$ can then be calculated with the deviatoric part of the logarithmic finite Hencky strain tensor $\mathbf {e}^{\prime }$

$$\begin{aligned} \varepsilon _{\mathrm {vm}}=\sqrt{\frac{2}{3} \mathbf {e}^{\prime }: \mathbf {e}^{\prime }} = 2 \ln \left( 2+4 \frac{h_{p}}{D}\right) \end{aligned}$$

(26)

We take the derivative of equation (25) with respect to time, we can calculate the von Mises strain rate $\dot{\varepsilon }_{\mathrm {vm}}$ is determined

$$\begin{aligned} \dot{\varepsilon }_{\mathrm {vm}}=\sqrt{\frac{2}{3} \dot{\mathbf {e}}^{\prime }: \dot{\mathbf {e}}^{\prime }}=\frac{4 U_{0}}{2 h_{p}+D} \end{aligned}$$

(27)

where $U_{0}$ is the impact velocity.

Supplementary Plots for Static Indentation Experiment with $4.69 \%$ v/v Gel

See Figs. 14, 15, and 16.

Fig. 14

The load F as a function of C values ($C_1$, $C_2$, and $C_3$) calculated from equations (10) to (12) for the $4.69 \%$ v/v gel sample. The dashed trendlines are also included in the plot

Fig. 15

Non-dimensional plot of the load F-indentation depth h for different indenters of $4.69 \%$ v/v gel sample. Solutions from Hertzian theory (solid diamonds) are compared with the results of Zhang et al. (cross signs) and Sneddon (plus signs)

Fig. 16

Contact pressures calculated for different hollow aluminum indenters in the indentation experiment of $4.69 \%$ v/v gel sample