Novelty Detection with Multivariate Extreme Value Statistics

Abstract

Novelty detection, or one-class classification, aims to determine if data are “normal” with respect to some model of normality constructed using examples of normal system behaviour. If that model is composed of generative probability distributions, the extent of “normality” in the data space can be described using Extreme Value Theory (EVT), a branch of statistics concerned with describing the tails of distributions. This paper demonstrates that existing approaches to the use of EVT for novelty detection are appropriate only for univariate, unimodal problems. We generalise the use of EVT for novelty detection to the analysis of data with multivariate, multimodal distributions, allowing a principled approach to the analysis of high-dimensional data to be taken. Examples are provided using vital-sign data obtained from a large clinical study of patients in a high-dependency hospital ward.

1 Introduction

1.1 Novelty Detection

Novelty detection, alternatively termed one-class classification or anomaly detection, classifies test data as “normal” or “abnormal” with respect to a model of normality. This approach is particularly well suited to problems in which a large quantity of examples of “normal” behaviour exist, such that a model of normality may be constructed, but where examples of “abnormal” behaviour are rare, such that a multi-class approach cannot be taken. For this reason, novelty detection has become popular in the analysis of data from high-integrity systems, such as hospital patients [10, 24, 25], jet engines [4, 11], manufacturing processes [6], or power-generation facilities [27], which spend the majority of their operational life in a “normal” state, and which exhibit few, if any, failure conditions.

Furthermore, the complexity of such systems is usually very high, because they are comprised of large numbers of mutually interacting subsystems, often including very large numbers of components. The number of possible modes of failure in such systems is very large, making explicit modelling of expected failure modes difficult, and the variability in observed behaviour between systems of the same type (such as between jet engines of the same type, or hospital patients of similar ages) can be significant, making it difficult to use fault information obtained from other systems. Thus, the novelty detection approach can be used to best exploit our prior knowledge that the “normal” class is better represented, and more readily defineable, than the large number of ill-defined classes of “abnormality” that may exist.

1.2 Overview

We first consider existing approaches to novelty detection, in Section 2, and describe the disadvantages associated with such approaches. EVT is introduced in Section 3 as being a principled method of avoiding such disadvantages.

A review of existing work in the use of EVT for novelty detection follows in Section 4, which also describes how existing methods are inappropriate for novelty detection in data which have multivariate or multimodal distributions.

Section 5 proposes a numerical solution for using EVT for novelty detection in multivariate, multimodal applications. This is based on the insight that novelty detection in multivariate data is equivalent to performing novelty detection in the probability space of the model of normality.

A closed-form solution is proposed in Section 6 for novelty detection in multivariate, unimodal problems, which avoids the requirement of sampling in the numerical method proposed in Section 5.

An application of the latter proposed technique is given in Section 7, where novelty detection is performed in the monitoring of vital signs obtained from patients in a high-dependency hospital ward.

Conclusions are drawn in Section 8, where potential extensions to the work proposed in this paper are discussed.

2 Existing Work

In much of the existing work on novelty detection, an assumption is made that “normal” data {x ₁ ...x _N } are i.i.d.,¹ and distributed according to some underlying generative distribution f _n (x), which is a probability distribution function² (pdf) over an n-dimensional data space, $\mathcal{D}$; i.e., $\mathbf{x} \in \mathcal{D} = \mathbb{R}^n$, where n is the number of features in the data (or the dimensionality of each feature vector x). Typically, the underlying distribution f _n is multivariate and multimodal; it could be, for example, approximated using a Gaussian mixture model (GMM), a Parzen window estimator, or some other mixture of components [2]. If we define a null hypothesis H ₀ that test data x are generated from f _n , then novelty detection evaluates the hypothesis that H ₀ is true; if H ₀ holds with probability P < κ for some threshold probability κ, then the null hypothesis is rejected, and x is classified “abnormal” w.r.t. f _n . The problem then becomes one of setting the novelty threshold.

In previous work [10, 16, 17, 26], a heuristic novelty threshold has been set on the pdf f _n (x) = κ, such that x is classified “abnormal” if f _n (x) < κ. Such thresholds are set with no principled probabilistic interpretation: f _n (x) is used simply as a novelty score, and the threshold is set such that separation between “normal” and any “abnormal” data is maximised on a validation dataset. Some authors [10, 14] have interpreted f _n probabilistically, by considering the cumulative probability F _n associated with f _n . That is, they find the probability mass obtained by integrating f _n over the region $\mathcal{R}$ where f _n exceeds the novelty threshold; i.e., the region $\mathcal{R}=\{\mathbf{x} \in \mathcal{D} | f_n(\mathbf{x}) \geq \kappa\}$:

$$ F_n(\kappa) = \int_\mathcal{R} f_n(\mathbf{x})\ d\mathbf{x} $$

(1)

An example is shown in Fig. 1, in which the distribution f _n is univariate and multimodal, and which has been approximated using a GMM with two components of equal variance ($\sigma_1^2 = \sigma_2^2 = 1$) and with prior probabilities³ P(μ ₁) = 0.75, P(μ ₂) = 0.25. A novelty threshold is shown at f _n (x) = κ = 0.05 in the figure, where the probability mass P enclosed by that threshold is shaded. The probability mass will fall in the range 0 ≤ P ≤ 1. In this example, the shaded areas from each Gaussian component do not significantly overlap, and it is possible to approximate closely the integration in Eq. 1 in closed form, treating each component distribution independently.

Figure 1

Integrating a bimodal probability distribution p(x) to the contour p(x) = 0.05. The contour is shown as a horizontal dashed line, intercepting the distribution function at the locations shown by the vertical straight lines. The area corresponding to the integration is shown in grey.

For a unimodal pdf, Eq. 1 corresponds to integrating from the mode of f _n to the pdf contour defined by the novelty threshold f _n (x) = κ, which can usually be determined in closed form. However, for a multimodal pdf, the integration may need to be performed using Monte Carlo techniques [17]. Setting the novelty threshold using the above method, and then determining the probability mass F _n enclosed by that f _n (x) = κ contour, allows a probabilistic interpretation: if we were to draw one sample from f _n , we would expect it to lie outside the novelty threshold with probability 1 − F _n . Thus, we could set the novelty threshold f _n (x) = κ such that F _n is some desired probability mass; e.g., F _n (κ) = 0.99. We note in passing that this approach is equivalent to the high-density region (HDR) approach of [14], which has been used for novelty detection [15, 18].

However, setting a novelty threshold using F _n has associated disadvantages for novelty detection. In order to examine these disadvantages, we must first consider a different method for determining the location of novelty thresholds: that of EVT.

3 Classical Extreme Value Theory

EVT is a branch of statistics concerned with modelling the distribution of very large or very small values (extrema) w.r.t. a generative distribution f _n . Here, we consider “classical” EVT as previously used in novelty detection [19, 20, 23, 28], in contrast to a method commonly used in estimating financial risks, often termed the peaks-over-threshold (POT) technique [8].

3.1 Extreme Value Distributions

Consider a set of m i.i.d. data X = {x ₁, x ₂, ..., x _m }, which are univariate (n = 1) for classical EVT, and are distributed according to some pdf f ₁(x), with maximum $x_{\textrm{max}} = \max(\mathbf{X})$. We define the cumulative distribution function (cdf) for $x_{\textrm{max}}$ to be $H^+(x_{\textrm{max}} \leq x)$; i.e., H ⁺ models our belief in where the maximum of m data generated from distribution f ₁ will lie.⁴ This is directly applicable to novelty detection, in which we wish to determine where the boundary of “normality” lies under normal conditions. We here term H ⁺ the extreme value distribution (EVD), because it describes the expected location of the extremum of m data generated from f _n .

According to the Fisher–Tippett theorem [9] upon which classical EVT is based, H ⁺ must belong to one of the following three families of distributions,⁵ no matter what the form of f ₁:

$${\rm Gumbel},\ \ \ H^+_1(y) = \exp(-\exp(-y))\label{eq:Gumbel} $$

(2)

$${\rm Fr}{\acute{\rm e}}{\rm chet},\ \ \ H^+_2(y) = \begin{cases} 0 & {{\rm if}\;\; y \leq 0} \\ \exp(-y^{-\alpha}) & {{\rm if}\;\; y > 0} \end{cases}$$

(3)

$${\rm Weibull},\ \ \ H^+_3(y) = \begin{cases} \exp(-(-y)^\alpha) & {{\rm if}\;\; y \leq 0}\\ 1 & {{\rm if}\;\; y > 0} \end{cases} $$

(4)

for α ∈ ℝ⁺ , and where y is a transformation⁶ of x, y = (x − c _m )/d _m , for location and scale parameters c _m and d _m , respectively. In classical EVT, these parameters for the EVD corresponding to the univariate Gaussian are dependent only on the number of data m drawn from the underlying distribution f ₁ [8]:

$$ c_m = \sqrt{2\ln m}-\frac{\ln\ln m + \ln 4\pi}{2\sqrt{2\ln m}},\ \ \ \ \ \ d_m = \frac{1}{\sqrt{2\ln m}} \label{eq:GumbelParams} $$

(5)

In this paper, we are primarily concerned with mixtures of Gaussian distributions, for which the limiting distribution of maxima is the Gumbel distribution $H^+_1$. We label this limiting cdf $F^e_n = H^+_1$, which has a corresponding pdf $f^e_n$ (the EVD).⁷ Here, the superscript e is used to denote the fact that these are the cdf and pdf of the extremum of our dataset X, where that dataset X has its own cdf F _n and pdf f _n , as described previously.

Note that in the case of m = 1 (i.e., when we observe only one data-point from f _n ), the EVD is the original generative distribution $f^e_n = f_n$; i.e., the original distribution describes where a single sample drawn from f _n will lie, because the extremum of a singleton set {x} is simply x.

In Section 6.2, we are interested in the Weibull-type EVD of minima, or minimal Weibull, for which the attractor is [3]:

$$ {H_3^-}(x,\alpha) = \left\{ \begin{array}{ll} 0, & x<0 \\ 1-\exp(-(x)^{\alpha}), & x\geq0 \end{array} \right.. \\ $$

(6)

3.2 Disadvantages of Using F _n

With a method of describing where we expect the extremum of a set of m samples generated from f _n to occur, we can examine the disadvantages associated with setting a novelty threshold using F _n , as was introduced in Section 2. For the purpose of illustration, suppose that f ₁ = N(0,1), the standard univariate Gaussian distribution.

The upper plot in Fig. 2 shows the generative distribution f ₁, and the EVDs $f^e_1$ for increasing numbers m of observed data x. As more data are observed from f ₁, the expected location of their maximum increases on the x-axis. This matches our intuition: if we generate large numbers of random data, the extremum of those random data is likely to be more extreme than if we generate small numbers of data. Similarly, in the case of novelty detection, if we observe more “normal” data, distributed according to f _n , then we expect their extremum to be more extreme than if smaller numbers of data are observed.

Figure 2

EVDs $f^{e}_{1}(\mathbf{x})$ and probability $1-F^{e}_{1}({\kappa})$ in the upper and lower plots, respectively, for increasing number m of data x.

A novelty threshold has been set at F ₁(κ) = 0.99 in the figure, which occurs at x = x _κ , and which is shown in the upper plot of the figure as a dashed line. We anticipate that this novelty threshold will be exceeded with probability 1 − F ₁(κ) = 1 − 0.99 = 0.01 when generating a single sample (i.e., m = 1) from f ₁. However, when generating multiple samples (m > 1) from f ₁, the probability that the novelty threshold will be exceeded is given instead by the extreme cdf, $1 - F_1^e(\kappa)$, and not by the original distribution f _n . This is a key point in the use of EVT for novelty detection: only EVT provides the correct probability distribution of the boundary of “normality” when more than one data-point has been observed.

The lower plot in Fig. 2 shows the probability that the novelty threshold set at F ₁(κ)  = 0.99 will be exceeded for increasing numbers m of observed data x. After m = 10 observations, the threshold will have been exceeded with probability P = 0.163, and after m = 100, the threshold will have been exceeded with probability P = 0.797. The threshold is exceeded with probability P = 0.99 after m = 248 samples have been generated. That is, if we observe 248 data from f ₁, then the novelty threshold is almost certain to be exceeded (P = 0.99), rather than being exceeded with probability P = 0.01 that we would expect if we were to use the cdf F ₁.

Thus, setting a novelty theshold using F _n only has a valid probabilistic interpretation when m = 1; i.e., for classification tasks in which a single entity is being compared with a model of normality. An example of this is when comparing a single mammogram to a model constructed using “normal” mammogram data [26].

4 EVT for Novelty Detection

Existing work on the use of EVT for novelty detection has been limited to [4, 5, 19, 20, 23, 28]. We here consider the use of EVT for novelty detection with (i) multivariate and (ii) multimodal data, and identify problems with existing approaches in both cases.

4.1 EVT in Multivariate Novelty Detection

Multivariate extrema defined in the EVT literature [3, 8], also termed component-wise extrema, are those n-dimensional data x _n that are maxima or minima in one or more dimensions of n. For novelty detection, we require extremes w.r.t. our multivariate model of normality, rather than considering extrema in each dimension independently. EVT was first used for novelty detection in multivariate data in [19, 20], where models of normality were represented by mixtures of Gaussian distributions. In multivariate space, the Gaussian distribution describes a hyperellipsoid with f _n (x) varying along a radius r according to the univariate Gaussian (scaled by a normalisation factor dependent on dimensionality n). That is, to determine the probability density f _n (x) at any point in the hyperellipsoid, the problem is reduced to a univariate case f ₁(r), in Mahalanobis radius r. Roberts [19, 20] uses this assumption to reduce the problem of determining the EVD for a multivariate Gaussian kernel to a corresponding univariate case. As illustrated in Fig. 3, the EVD for a single Gaussian distribution along a radius r varies according to a univariate Gumbel distribution.

Figure 3

The bivariate Gaussian f ₂ and its EVD $f^{e}_{2}$ (shown in the upper plot), which is a torus with Gumbel cross-section (shown in the lower plot).

Existing work uses classical EVT to estimate the parameters c _m ,d _m of this Gumbel cross-section $f^e_n$ in multivariate n-space, as defined in Eq. 5. Figure 4 shows the estimates of c _m ,d _m given by classical EVT compared to maximum likelihood estimates (MLEs) obtained using the unimodal, univariate method of [3] for increasing dimensionality n of the Gaussian distribution. For the univariate case f ₁, it may be seen from the figure that classical EVT correctly estimates the Gumbel parameters. For n > 2, the location parameter c _m of $f^e_n$ is significantly underestimated, and this error becomes greater with increasing dimensionality n.

Figure 4

Ratio c/d of the MLE parameters for the multivariate Gumbel cross-section as a function of m for increasing dimensionality n = 1...5 (thin lines), compared to c/d estimated by classical EVT (thick line). MLEs were obtained from N = 10⁶ experiments for each value of m and n. Confidence intervals are shown at two standard deviations from the mean.

Figure 5 shows the error between the actual parameters c _m ,d _m of $f^e_n$ and varying estimates $\hat{c_m},\hat{d_m}$ for n = 2 and m = 100, where it may be seen that classical EVT fails to estimate c _m correctly.

Figure 5

Error in estimates of Gumbel parameters c _m ,d _m for $f^{e}_{2}$, for varying c _m and d _m . The MLE is shown by the marker at c _m  = 3.04, d _m  = 0.32; the classical EVT estimates are shown by the marker at c _m  = 2.37, d _m  = 0.33, which is significantly far from the desired MLE values.

Thus, we conclude that for multivariate distributions f _n , we cannot use classical EVT to estimate the EVD, $f^e_n$.

4.2 EVT in Multimodal Novelty Detection

EVT defines an “extreme value” to be that which is either a minimum or maximum of a set of observations x. This is due to the conventional use of EVT [7] for determining events of extremely large or small magnitude, such as extreme financial events, extreme meteorological events, etc. In novelty detection, when considering the extrema of unimodal distributions, as is the focus of most previous work in the field of EVT [5, 23, 28], this existing definition of “extreme value” is sufficient for univariate f ₁. For multivariate data, providing that f _n is unimodal,⁸ the existing definition may be taken to mean the minimum or maximum radius r from the single mode of f _n (reducing the multivariate problem to a univariate problem in r, as we have described in Section 4.1).

However, for multimodal f _n , whether uni- or multivariate, the notion of minimum or maximum value is no longer sufficient, because there is no single mode from which distance may be defined.⁹ The upper plot in Fig. 6 shows a univariate bimodal pdf. While the minimum or maximum should be treated as extrema (e.g., x = 1 or x = 28), values between the two modes (such as x = 10) should similarly be taken to be extreme in terms of probability density f _n (x), because they are just as improbable as the minimum or maximum on the x-axis.

Figure 6

Multimodal distributions require redefinition of the term “extreme value”. The upper plots shows a bimodal distribution f ₁, where extrema could fall between the two modes, and so we must consider more than “minimum” and “maximum” values on the x-axis. The lower plot shows a multimodal Parzen windows model formed from k = 60 components, where extrema could fall in the “horseshoe” between clusters of modes.

This is a key point of departure in our work with EVT for novelty detection, in which we are interested in determining extremely unlikely events, whereas conventional EVT is interested in determining events of extremely large or small magnitude. As illustrated in Fig. 6, while events of extremely large or small magnitude may be events that are extremely unlikely, not all events that are extremely unlikely are events of extremely large or small magnitude.

Similarly, the lower plot of Fig. 6 shows a multivariate, multimodal distribution. For bivariate data x = (x ₁,x ₂), data-points which represent a minimum or maximum in either dimension x ₁ or x ₂ should be considered “extreme”,¹⁰ but it is also desireable that similarly improbable areas of data space, such as the origin x = (0,0) in this example, should be considered “extreme” for the purposes of novelty detection.

Given that the goal of using EVT for novelty detection is to identify improbable events w.r.t. f _n , rather than events of extreme absolute magnitude, we redefine “extreme value” in terms of probability:

Definition 1

For novelty detection, the “most extreme” of a set of m samples $\mathbf{X} = \left\{\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_m\right\}$ distributed according to pdf f _n (x) is that which is most improbable with respect to the distribution; i.e., $\operatornamewithlimits{arg min}_{\mathbf{x}\in\mathbf{X}} \left[f_n(\mathbf{x})\right]$.

The conventional use of “extrema” to mean minimum or maximum values with respect to a unimodal distribution becomes a special case of the above definition: because the pdf f _n typically decreases monotonically with increasing distance from the single mode, selecting the samples furthest from that mode (i.e., the minimum or maximum of a set of samples) is equivalent to selecting the samples for which f _n is minimised.

This selection of extrema based on minimising f _n is equivalent to selecting extrema by maximising F _n using Eq. 1. Our definition satisfies the condition of [14], which states that the probability of observing data inside a novelty boundary should be at least as large as the probability of observing data outside the novelty boundary. That is, the novelty boundary is a lower bound on f _n for “normal” data.

Definition 1 provides us with the mechanism we require to determine the extent of data space that is considered “normal”: if we observe m “normal” data generated from a model of normality f _n , the EVD $f^e_n$ now describes where the least probable of those m normal data will lie. Thus, we can use the EVD to set a novelty threshold, as will be described, and perform novelty detection in a principled manner.

As with multivariate novelty detection, little work exists in using EVT for novelty detection with multimodal f _n [19, 20]. In this work, the multimodal distribution represented by a mixture of Gaussian component distributions was reduced to a single-component problem: to find the value of the EVD $f^e_n$ at some location x, the closest component distribution (determined using Mahalanobis distance) was assumed to dominate $f^e_n$, and thus the EVD is based on the Gumbel distribution corresponding to that closest component (using radius r from that component’s centre, as described in Section 4.1). Here, the contribution of other components to $f^e_n$ is assumed to be negligible, and they are ignored.

4.2.1 Problems Arising due to Differing Component Variances

Figure 7 shows the EVD $f_1^e$, determined using the existing method, corresponding to the univariate, bimodal distribution f ₁ from Fig. 6, which is a mixture of two Gaussian component distributions. Here, the prior probabilities of each component are equal, P(μ ₁) = P(μ ₂) = 0.5, and the kernel variances are $\sigma^2_1 \!=\! 1, \sigma^2_2 \!=\! 4$. Figure 7 also shows the corresponding cdf $F_1^e$, from which it may be seen that each component is responsible for 0.5 of the total probability mass. The EVD modes for component μ ₂ have a maximum value of $f_1^e(x) = 0.15$, half of the maximum value of the modes for component μ ₁, because the modes for μ ₂ are spread out twice as far (σ ₂ = 2σ ₁).

Figure 7

Comparison of EVD determined using the existing method (solid line) and histograms of 10⁶ extrema (circles) drawn from bimodal distribution f ₁(x) (dashed line). The left- and right-hand plots show the pdf $f^{e}_{1}$ and cdf $F^{e}_{1}$, respectively. Extrema are drawn from each component of f ₁(x) independently, according to their prior, P(μ ₁) = P(μ ₂) = 0.5, and so each component generates half of the samples. This closely matches the EVD determined by the existing method, but does not represent the process of drawing m samples from f ₁(x).

In Fig. 7, the circles correspond to a histogram of N = 10⁶ extrema generated from each component distribution independently. That is, component μ ₁ has been responsible for 0.5N extrema and component μ ₂ has been responsible for 0.5N extrema. This is not the same as drawing N extrema directly from the mixture f ₁, which is what we wish to perform.

Figure 8 shows the histogram obtained when N =  10⁶ extrema are generated correctly from the mixture; i.e., where m samples are drawn from the mixture $f_1(x) = \frac{1}{2}\sum_i P(\mu_i)p(x|\mu_i)$, and the most extreme is retained, for each of N  =  10⁶ iterations. The cdf $F_1^e$ in Fig. 8 shows that component μ ₂ is responsible for more than 0.5 of the probability mass (in fact, two-thirds of it).

Figure 8

Comparison of EVD determined using the existing method (solid line), as before, and histograms of 10⁶ extrema (circles) drawn from bimodal distribution f ₁(x) (dashed line). The left- and right-hand plots show the pdf $f^{e}_{1}$ and cdf $F^{e}_{1}$, respectively. Here, the extrema are correctly drawn from the mixture f ₁(x) (i.e., m samples are drawn from f ₁(x) and the most extreme of those m samples is retained). The EVD determined by the existing method does not fit the actual observed extrema.

This example shows that, when samples are generated directly from the model of normality, component μ ₂, having wider variance and thus taking lower f ₁(x) values than component μ ₁, is responsible for more extrema than we would expect from the kernels’ equal prior probabilities. Though in each of N = 10⁶ iterations, we generate, on average, 0.5m samples from each component (in accordance with their equal prior probabilities), we have a greater chance of retaining those samples from μ ₂ because the absolute values of their probability densities f ₁(x) are generally lower, due to the increased variance of that component. This unintuitive phenomenon was observed by [14] when considering conventional integration of mixtures of Gaussian distributions.

Thus, the assumption that only the closest component distribution to x need be considered when determining the EVD $f_n^e(\mathbf{x})$ cannot generally be made. Though the effect of other components on f _n (x) may be negligible, because of their distance from x, their effect on $f_n^e(\mathbf{x})$ may be significant due to the relative differences in variances between kernels, as shown in the example in Fig. 8. This typically occurs with Gaussian mixture models, in which components usually have differing variances.

4.2.2 Problems Arising due to Overlapping Components

The existing method results in a piecewise-hyperspherical EVD, because $f_n^e$ for all x is determined using only a single component (the closest to x). This is illustrated in Fig. 9, in which a mixture of two component distributions with equal variance and significant overlap is shown. The figure shows the actual EVD (shown by the outer solid line) evaluated at $F_2^e(\kappa) \leq 0.999$, evaluated using Monte Carlo methods. The resulting equiprobable contour follows the contours of the underlying distribution f ₂(x). The figure also shows the equivalent contour of the EVD obtained using the existing method (shown by the inner solid line), in which the resultant contour is piecewise-circular. It may be seen that areas of data space that should be considered “normal” (i.e., lying within the outer line, if the contour is used as a novelty threshold) would be incorrectly considered “abnormal” by the existing method.

Figure 9

A mixture of two component distributions with equal variance and significant overlap. The true EVD integrated to $F_{2}^{e}(\mathbf{x}) \leq 0.999$ is shown by the outer solid line. The existing method results in an equiprobable contour $F_{2}^{e}(\mathbf{x}) \leq 0.999$ that is piecewise circular, shown by the inner solid line. Part of the overlapped regions of the components (between the inner and outer solid lines) would incorrectly be classified “abnormal” by the existing method, using this contour as a novelty threshold.

The areas of data space thus misclassified as “abnormal” by the existing method will increase with increasing overlap between components. For models of normality comprising large numbers of components, such as those constructed using Parzen windows estimation, the misclassified areas of data space could be large due to the typically considerable overlap between components and the typically large numbers of components used in such models.

We note that with increasing data dimensionality n, the overlapped hypervolume of data space between neighbouring components (as a proportion of the total probability mass) decreases. Thus, for high-dimensional models with smaller regions of overlapped data space, we expect that these problems will be less significant.

5 Understanding the EVD

We have shown that existing approaches to EVT are unsuitable for novelty detection where the generative data distribution is multivariate or multimodal. This section presents a new method of understanding the EVD, which we require in order to estimate the EVD for multivariate, multimodal f _n .

5.1 The EVD as a Transformation of f _n

The EVD $f^e_n$ for a distribution f _n follows the probability contours of that distribution. This is a consequence of using Definition 1, where extrema are defined in terms of minimising f _n (x) for a set X of m samples (or, equivalently, maximising F _n ).

It is convenient to consider the EVD as a transformation of equiprobable contours on f _n . Figure 10 shows equiprobable contours for a bivariate model of normality f ₂ represented by a mixture of three Gaussian components with full (non-diagonal) covariance matrices. The EVD $f^e_2$ is shown for m = 100. Equiprobable contours of the EVD $f^e_2$ occur at equiprobable contours of f ₂, and thus we may consider the EVD to be a weighting function of the contours of f _n ,

$$ f^e_n(\mathbf{x}) = g\left[f_n(\mathbf{x})\right] $$

(7)

for some weighting function g. With the EVD thus defined in terms of f _n , we have the facility to accurately determine $f^e_n$ for complex, multimodal, multivariate distributions, if we can find the form of g.

Figure 10

Probability contours on f _n for a tri-modal GMM (upper plot) with full (non-diagonal) covariance matrices and corresponding EVD $f^{e}_{n}$ (lower plot).

5.2 The Ψ-Transform

For a standard Gaussian distribution,

$$ f_n(x) = (2\pi)^{-n/2}\exp(-r^2/2) $$

(8)

and so, rearrangement gives

$$ r = \left(-2\ln f_n(x) -n\ln 2\pi\right)^{1/2}. $$

(9)

We define a transform of the extrema x,

$$ \Psi\left[f_n(\mathbf{x})\right] = \begin{cases} \left(-2 \ln f_n(\mathbf{x}) - n\ln 2\pi\right)^{1/2}& \text{if $f_n(\mathbf{x}) < K$}\\ 0& \text{if $f_n(\mathbf{x}) \geq K$} \end{cases} \label{eq:PsiTransform} $$

(10)

where K = (2π)^− n/2. If f _n is a (unimodal) Gaussian distribution $N(\boldsymbol{\mu},\boldsymbol{\Sigma})$, the Ψ-transform would map the f _n (x) values back onto r, the radii of x from $\boldsymbol{\mu}$, which we know are distributed according to the Gumbel distribution (as shown in Section 4.1). The Ψ-transform maps the distribution of f _n (x) values back into a space into which a Gumbel distribution can be fitted, having observed that f _n (x) for extrema are distributed similarly for mixtures of negative exponentials of varying number of kernels, priors, and covariances [4].

The upper plot in Fig. 11 shows a normalised histogram of N = 10⁶ extrema generated from the example mixture of three Gaussian components f ₂ in Fig. 10, for m = 100. The distribution is highly skewed towards f ₂(x) = 0, as is expected for extrema. The lower plot in the figure shows the Ψ-transform of the histogram of extrema, which may be seen to be distributed according to the Gumbel (after normalisation such that its area is unity). The MLE Gumbel distribution fitted in Ψ-space using the univariate, unimodal method of [3] is shown, which is $f^e_2\big(\Psi[f_2(\mathbf{x}]\big)$. Thus, all locations x in the original data space $\mathcal{D} = \mathbb{R}^n$ may be evaluated w.r.t. $f^e_n\big(\Psi[f_n(\mathbf{x})]\big)$, as was shown in Fig. 10, and we have successfully found the multivariate, multimodal EVD which is a transformation of f _n , as required.

Figure 11

Normalised histogram of f ₂(x) values for N = 10⁶ extrema generated from trimodal GMM with m = 100 (upper plot). Histogram of the Ψ-transformed f ₂(x) values shown in grey, with the corresponding MLE Gumbel distribution fitted in Ψ-space, shown in black (lower plot). A novelty threshold at $F^{e}_{2} = 0.99$ is shown as a dashed line.

We may determine the location of a novelty threshold on $f^e_n$ by equating the corresponding cdf $F^e_n$ (which is univariate in Ψ-space) to some probability mass; e.g., $F^e_n[f_n(\textbf{x})] = 0.99$, as shown in Fig. 11. Thus, we have defined a contour in data space $\mathcal{D}$ that describes where the most extreme of m “normal” samples generated from f _n will lie, to some probability (e.g., 0.99).

This is the key insight that allows us to determine the EVD for data of arbitrarily large dimensionality n: we have reduced the problem of analysis in multivariate data space to a simpler, but equivalent, problem in univariate probability space.

Note finally that, though the novelty threshold set using our proposed method occurs at some contour f _n (x) = κ (due to Definition 1), it is not heuristic: the threshold is set such that generating m samples from f _n will exceed the threshold with probability $1 - F^e_n(\kappa) = 1 - 0.99 = 0.01$; that is, the final novelty threshold has a valid probabilistic interpretation provided by EVT.

5.3 Investigating the EVD

The method described in the previous sub-section scales with dimensionality n and the number of components in the mixture f _n . Figure 12 shows the EVD for a trivariate model f ₃ (projected onto four planes for visualisation), which closely matches the EVD observed from experimentally-obtained extrema. Figure 13 also shows the Ψ-transform for a 6-dimensional mixture f ₆ of 15 Gaussian components with full (non-diagonal) covariance, where it may also be seen that the EVD closely matches that of experimentally-obtained extrema.

Figure 12

EVD $f^{e}_{3}$ shown in data space $\mathcal{D}$ estimated using the proposed Ψ-transform method for a trivariate, trimodal f ₃ (upper plot). The EVD determined using the proposed method (lower-right plot) closely matches the histogram of experimentally-obtained extrema (lower-left plot).

Figure 13

Histogram of Ψ-transformed extrema (shown in grey) and MLE Gumbel (shown in black) for a 6-dimensional f ₆ mixture of 15 components. A novelty threshold has been set at $F^{e}_{6} = 0.99$, shown as a dashed line.

We note that this Ψ-transform method is numerical, requiring the sampling of extrema from f _n , and then fitting the MLE Gumbel distribution after application of the Ψ-transformation. Future work aims to find closed-form solutions (or approximations) for multivariate, multimodal distributions f _n . Currently, closed forms have been obtained for multivariate, unimodal distributions, which are presented in the next section.

6 Closed-Form EVT for Multivariate, Unimodal Novelty Detection

In the previous section, we argued the need for a multivariate Extreme Value Theory (mEVT) in machine learning, identified some of the limitations of the existing approach, and proposed a numerical scheme for multimodal, multivariate estimation.

In this section, we offer an analytical approach to mEVT, restricted to single Gaussian distributions; i.e., for dimensionality n ∈ ℕ^*, distributions F _n with probability density functions of the form:

$$ f_n({\mathbf{x}}) = \frac{1}{C_n} {\,\mbox{exp}\left({-\frac{M({\mathbf{x}})^2}{2}}\right)}\\ $$

(11)

where

$$ M({\mathbf{x}}) = \left(({\mathbf{x}} - {\boldsymbol{\mu}})^{\top}{\mathbf{\Sigma}}^{-1}({\mathbf{x}} - {\boldsymbol{\mu}})\right)^{1/2} $$

(12)

is the Mahalanobis distance,

$$ C_n = (2\pi)^{n/2}|{\mathbf{\Sigma}}|^{1/2} $$

(13)

is the normalisation coefficient, ${\boldsymbol{\mu}}$ the centre, and Σ the covariance matrix. We term ${{\cal{D}}} = \mathbb{R}^n$ the data space, and ${{\cal{P}}} = f_n({{\cal{D}}})= \big]0, \frac{1}{C_n}\big]$, the associated probability space. A unimodal approach is of interest because the existing method [19] yields significant errors when estimating EVD parameters, as shown previously, which can be solved directly by the use of analytically-derived estimates. Furthermore, the numerical approach presented in the previous section requires that we generate extrema from a multivariate distribution, which can be time-consuming as the sample size is increased. While a fully analytical mEVT may not be possible, the analytical study presented here paves the way to more elaborate numerical schemes with no need for sampling extrema.

6.1 Probability Distribution of Probability Density Values

6.1.1 Sampling in Data Space is Equivalent to Sampling in Probability Space

Let x ₁,x ₂,...,x _k be samples (vectors of ${{\cal{D}}}$) drawn from the distribution F _n for k ∈ ℕ and f _n (x ₁), f _n (x ₂),..., f _n (x _k ) be the corresponding pdf values of these samples. The probability of obtaining a given value in the probability space by drawing a sample in the data space is strongly related to the form of f _n . Assuming that X is a random variable distributed according to F _n , our aim in this section is to determine the form of the distribution function (df) G _n according to which f _n (X) is distributed on ${{\cal{P}}}$. That is, we wish to determine the probability distribution over probability density values, noting from the previous section that novelty detection in the probability space defined by the model of normality is equivalent to novelty detection in the data space.

6.1.2 Distribution Function Over f _n (X)

We define a distribution over Y = f _n (X) as follows:

$$ \forall y \in {{\cal{P}}},\quad G_n(y) = \int_{f_n^{-1}(]0,y])} f_n({\mathbf{x}}) d{\mathbf{x}} \label{eq:pop1} $$

(14)

where $f_n^{-1}(]0,y])$ is the preimage of ]0, y] under f _n . G _n is the complementary function of that in Definition 1 where κ is now y.

To take advantage of the ellipsoidal symmetry of the problem we rewrite f _n in a Mahalanobis n-dimensional spherical polar coordinate system. Then, $x_v = (r,{\boldsymbol{\theta}})$ such that ${\boldsymbol{\theta}}=(\theta_1, \ldots,$ θ _n − 1) , r = M(x), $\theta_i \in \left[-\frac{\pi}{2},\frac{\pi}{2}\right[$ for i ≤ n − 2 and the base angle θ _n − 1 ranges over [0, 2π].

The Jacobian of the transformation [22] is

$$ |J| = |{\mathbf{\Sigma}}|^{1/2} r^{n-1} \prod\limits_{i=0}^{n-3}(\cos{\theta_i})^{n-i} $$

(15)

Thus, we may now expand Eq. 14, to find the distribution over the pdf f _n ,

$$G_n(y)= \int_{f_n^{-1}(]0,y])} \frac{1}{C_n} {\,\mbox{exp}\left({-\frac{M({\mathbf{x}})^2}{2}}\right)} d{\mathbf{x}}, \label{eq:pop2}\\ $$

(16)

$$ = \int_{f_n^{-1}(]0,y])} \frac{|J|}{C_n} {\,\mbox{exp}\left({-\frac{r^2}{2}}\right)} \mbox{d}r \mbox{d}{\boldsymbol{\theta}}, \label{eq:pop3}\\ $$

(17)

$$ = \Omega \int_{M^{-1}(y)}^{+\infty} \frac{r^{n-1}}{(2\pi)^{n/2}} {\,\mbox{exp}\left({-\frac{r^2}{2}}\right)}\mbox{d}r,\label{eq:pop4}\\ $$

(18)

$$ = \Omega |{\mathbf{\Sigma}}|^{1/2} \int_{0}^{y} \left[-2 {\,\mbox{ln}\left({C_n u}\right)}\right]^{(n-2)/2} \mbox{d}u. \label{eq:pop5} $$

(19)

In the above, $M^{-1}(y) = \sqrt{-2{\,\mbox{ln}\left({C_ny}\right)}}$ is the unique Mahalanobis distance associated with the pdf value y.

Equation 17 is obtained by rewriting Eq. 16 in the spherical polar coordinate system. Integrating out the angles yields Eq. 18, where $\Omega \!=\! \frac{2 \pi^{n/2}}{\Gamma\left(\frac{n}{2}\right)}$ is the total solid angle subtended by the unit n-sphere. Equation 19 is obtained after making the substitution $u \!=\! \frac{1}{C_n}{\,\mbox{exp}\left({\!-\!\frac{r^2}{2}}\right)}$. Note that Eq. 18 and Eq. 19 hold for n = 1, such that they may be applied to univariate distributions as well as multivariate distributions.

The integrand in Eq. 19 is the pdf of G _n , which we aim to find,

$$ g_n(y) = \Omega_n |{\mathbf{\Sigma}}|^{1/2} \left[-2 {\,\mbox{ln}\left({C_n y}\right)}\right]^{n-2/2} \label{eq:pop6} $$

(20)

In the univariate case n = 1, the integration of Eq. 18 yields

$$ G_1(y) ={\,\mbox{erfc}\left({\sqrt{-{\,\mbox{ln}\left({C_1y}\right)}}}\right)} $$

(21)

where ${\,\mbox{erfc}\left({.}\right)}$ is the complementary error function.

For the multivariate case n ≥ 2, the integration of Eq. 19 is possible using a recursive integration by parts, which yields two cases:

$$ G_{2p}(y) = y \sum\limits_{k=0}^{p-1} A_{2p}^k\left(-2{\,\mbox{ln}\left({C_{2p}y}\right)}\right)^{(p-k-1)} \\ $$

(22)

$$ \begin{array}{lll} G_{2p+1}(y) &=& y\sum\limits_{k=0}^{p-1}A_{2p+1}^{k}\left(-2{\,\mbox{ln}\left({C_{2p+1} y}\right)}\right)^{p-k-1/2}\\ &&+ {\,\mbox{erfc}\left({\sqrt{-{\,\mbox{ln}\left({C_{2p+1}y}\right)}}}\right)}\end{array} $$

(23)

for all p ∈ ${\mathbb{N}}$ ^*, where

$$ A_{2p}^{k} = \Omega_{2p}|{\mathbf{\Sigma}}|^{1/2}\frac{2^k(p-1)!}{(p-1-k)!} $$

(24)

and

$$ A_{2p+1}^{k} = \Omega_{2p+1}|{\mathbf{\Sigma}}|^{1/2}\frac{(2p-1)! (p-k)!}{2^{k-1} (p-1)! (2p-2k)!}. $$

(25)

G _n and g _n are plotted for n = 1 to 5 in Fig. 14, together with simulated data. Perhaps counter-intuitively, we observe that, relative to the right endpoint of G _n , the probability mass shifts towards 0 as the dimensionality n increases, which indicates that the probability mass in the data space moves away from the centre of the distribution, as is noted by Bishop in [1] (example 1.4, page 29).

Figure 14

Analytical and simulated G _n and g _n for various values of n. The x-axis is scaled so that all distributions have the same right endpoint. Crosses are the result of drawing 10⁶ samples in the data space and computing the cumulative histograms of their probabilities. F _n is the multivariate standard normal distribution.

This is the key reason that classical EVT cannot accurately estimate the EVD parameters for multivariate data, as was discussed in Section 4.1; as dimensionality of the data increases, the probability mass tends towards regions of low probability density, whereas classical EVT can only estimate the case for n = 1, in which the probability mass is clustered around the mode of f ₁, as shown in Fig. 14.

6.2 Finding the EVD for Probability Density Values

Our approach is based on the idea that pdf values of the EVD in the data space must be equal on a level set of F; i.e., the EVD is obtained by applying a weighting function to the level sets of F, as was shown in Section 5. Consequently, determining the EVD in the data space can be performed by determining the EVD of G in the probability space. We therefore reduce an n-dimensional problem (finding an EVD in $\mathcal{D}$) to a simpler one-dimensional case (finding an EVD in $\mathcal{P}$).

In this section, our aim is to determine the extreme value distribution of minima for G _n and estimate its parameters, using classical EVT.

6.2.1 Maximum Domain of Attraction of the Weibull Distribution

The Fisher–Tippett theorem effectively defines a three-class (Gumbel, Fréchet, and Weibull) equivalence relation on the set of non-degenerate univariate distributions. Embrechts et al. [8] gives the characterizations for each class.

Theorem 3.3.12 in [8] characterizes the maximum domain of attraction (MDA) of the maximal Weibull distribution. We adapt it to the MDA of the minimal Weibull distribution, ${H_3^-}$:

Theorem 1

(Maximum domain of attraction of ${H_3^-}$) The df F belongs to the maximum domain of attraction of the minimal Weibull distribution (α > 0), if and only if x _F  > − ∞ and $F(x_F{\kern-1pt} +{\kern-1pt} x^{-1}) {\kern-1pt}={\kern-1pt} x^{-\alpha} L(x)$ for some slowly varying function L. If $F\in \mbox{MDA}({H_3^-})$ , then $c_m^{-1}(E_m \!-\! x_F) {\stackrel{d}{\rightarrow} } H_3^-$ , where the norming constants c _m ,d _m can be chosen to be $c_m = x_F + F^{\leftarrow}( m^{-1})$ and d _m  = x _F , and where E _m is the extremum of m data.

In the above, x _F is the left endpoint of the df F, F ^←(p) is the p-quantile of F, and L is a slowly varying function at ∞; i.e., a positive function that obeys

$$\forall t > 0 , \lim\limits_{x\rightarrow \infty} \frac{L(tx)}{L(x)} = 1. $$

(26)

From Eq. 26, it may be seen that $y\!\mapsto\! \!-\!{\,\mbox{ln}\left({1/y}\right)}, y\!>\!1$ is slowly varying, as is $y\mapsto -{\,\mbox{ln}\left({1/y}\right)}^\beta$, y > 1, for all β ∈ ℝ. Therefore $y\,G_{2p}\left(1/y\right)$ is a sum of slowly varying functions, which is itself slowly varying. Theorem 1 can therefore be applied to G _2p . A similar process can be followed to show that G _2p + 1 is in the MDA of ${H_3^-}$. Consequently, G _n is in the MDA of ${H_3^-}$ for all values of n.

6.3 Parameter Estimation

If G _n is in the MDA of ${H_3^-}$, Theorem 1 gives the minimal Weibull parameters:

$$ {d_m} = 0, \quad \alpha_m = 1,\\ $$

(27)

$$ {c_m } = G_n^{\leftarrow}\left(\displaystyle\frac{1}{m}\right). \label{eq:scaleparam} $$

(28)

The scale parameter can be easily estimated numerically from Eq. 28 to arbitrary accuracy, as G _n is a strictly increasing function over finite support.

Figure 15 shows that Eq. 28 is a very close approximation to the values of the scale parameter d _m obtained via maximum likelihood estimation. However, the value of the shape parameter α _m , although theoretically guaranteed to converge to 1 in the limit m → ∞ seems to decrease significantly as the dimensionality of the data space increases, and it is overestimated even for large values of m.

Figure 15

Comparison between results of maximum likelihood estimation of the scale parameter c _m (top) and the shape parameter α _m (bottom) parameter, and values obtained using formulae 29 and 28 for increasing m. F _n is again the multivariate standard normal distribution. The dots are obtained by taking the means of 10 MLEs, each with 10⁴ simulated extrema. Error bars are too small to be visible at this scale.

To address this issue, we note that the class of equivalence of ${H_3^-}$ contains all the distributions with a power law behaviour at the finite left endpoint [8]. Therefore the tail of G _n is, in the limit y→0, equivalent to a power law; i.e., $G_n(y) \sim Ky^s$. Here, s can be estimated locally by noting that, in this case, $g_n(y)~\sim~sKy^{s-1}$; i.e., $s = y\frac{G_n(y)}{g_n(y)}$.

We therefore propose the following formula for the shape parameter,

$$\alpha_m = {c_m }\displaystyle\frac{g_n({c_m })}{G_n({c_m })}\label{eq:shapeparam} $$

(29)

Figure 15 shows that Eq. 29, although still inaccurate for very small values of m, gives values closer to the MLE estimates as m and n increase.

Finally, the EVD of G _n is:

$$ G_n^e(y) = 1- {\,\mbox{exp}\left({- \left(y/{c_m }\right)^{\alpha_m}}\right)}, $$

(30)

where c _m and α _m are given by Eqs. 28 and 29, respectively.

6.4 Novelty Scores

In novelty detection, extrema are regarded as potentially abnormal data. Assuming a distribution for the normal data, if we observe m samples for which the extremum has pdf value y _m , the probability of drawing an extremum of lower probability is given by $G_n^e(y_m)$. Therefore, the probability of drawing an extremum of higher probability is $1-G_n^e(y_m)$ and our extremum is abnormal with probability $1-G_n^e(y_m)$.

We define a novelty score in the data space as being the probability of obtaining an extemum closer to the centre of the distribution (in the Mahalanobis sense):

$$F_n^e({\mathbf{x}}) = 1-G_n^e(f_n({\mathbf{x}})),\\ $$

(31)

$$= {\,\mbox{exp}\left({-\left(\frac{1}{C_n {c_m }} \mbox{e}^{-\frac{M({\mathbf{x}})^2}{2}}\right)^{\alpha_m}}\right)}.\label{eq:dataevd} $$

(32)

In the limit m→ ∞, $F_n^e({\mathbf{x}})$ can be interpreted as a Mahalanobis-radial cdf of extrema.

7 Application to a Vital-Sign Monitoring Problem

7.1 Introduction to Patient Monitoring

In this section, we present an application of our proposed mEVT method to a vital-sign monitoring problem. Continuous real-time patient monitoring in hospital is usually based on single vital-sign channel alarms, which yield an unusably large number of false alarms. Recently, efforts have been made to take advantage of the correlation between vital-sign channels. In [10, 25], the authors adopt a novelty detection approach, whereby the model of normality is a 4-dimensional pdf constructed using data from a high-risk adult population. The authors then test for abnormal data by comparing the probability densities f(x) of new measurements obtained in real-time to a predefined threshold.

Here, we introduce the use of mEVT to address the same problem, limited to the use of two vital-sign channels, heart rate (HR) and breathing rate (BR). The data set was collected during the first phase of a trial conducted at the University of Pittsburgh Medical Center [10, 12, 13], which is composed of the recordings of 332 high-risk adult patients, totalling over 32,000 hours of data. Vital-sign measurements are available every second for all patients. Recordings are labeled with “crisis events”; i.e., events that should have caused an emergency call to clinical staff to be made on the patient’s behalf, as they are indicative of potentially adverse events. The cause of each event (high/low HR, high/low BR, etc.) is given with its start-time and end-time. 46 of 113 events are caused by an abnormally high or low heart rate or breathing rate (approximately 19 hours of data).

7.2 Method

We split patients into three groups: a test group, composed of the 28 patients who suffered at least one cardio-respiratory crisis over the course of their stay (approximately 1000 hours of data), a training group, and a control group, these latter two each composed of 154 randomly-assigned patients who did not suffer a cardio-respiratory crisis (approximately 15,500 hours of data each).

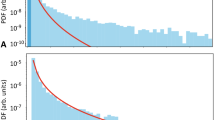
Figure 16 shows histograms of the training data. A bivariate Gaussian distribution F ₂ is fitted to the data of the control group. To ease their graphical interpretation, we define novelty scores to be:

$$ Z_1({\mathbf{x}}_M) = - {\,\mbox{ln}\left({1- F_2^e({\mathbf{x}}_m)}c\right)}. $$

(33)

where x is the extremum of m samples and $F_2^e$ is defined by Eq. 32. Note that Z ₁(x) takes low values if x is close to the centre of the distribution and increases as x becomes more and more “abnormal”. Novelty scores are subsequently assigned to the entire recordings of the patients in all groups. At time t, the highest novelty score of the last m HR and BR measurements is returned. The value of the parameter m is empirically chosen to be 30 for illustration.

Figure 16

Normalised histograms of the heart rate and breathing rate values for all patients in the training group. The means and standard deviations are, 84.41 and 18.45 bpm for the heart rate, and 16.39 and 4.60 rpm for the breathing rate. The covariance is 14.75.

We compare the mEVT-based approach with the classical thresholding approach described in Section 2; i.e., setting a threshold in the probability space to which each measurement is individually compared.

To make the comparison with the mEVT-based method easier, we deduce from Eq. 17 that

$$ P\left(f_2({\mathbf{x}})\geq f_2({\mathbf{x}}_0)\right) = 1 - {\,\mbox{exp}\left({-\frac{M({\mathbf{x}}_0)^2}{2}}\right)} $$

(34)

and therefore define the novelty score for the classical thresholding approach to be:

$$ Z_2({\mathbf{x}}_0) = -{\,\mbox{ln}\left({1-f_2({\mathbf{x}}_0)}\right)} = \frac{M({\mathbf{x}}_0)^2}{2}. $$

(35)

For a sample x, Z ₂ answers the question: “What was the probability of drawing a sample of smaller magnitude?”. Z ₁ answers the question: “Considering x and the m-1 samples observed before it, what was the probability of drawing m samples with a more probable extremum?”

7.3 Results

For both approaches, we define τ _training(q), τ _control(q), τ _test(q) and τ _crisis(q) to be the fraction of the total recording time that novelty scores are higher than the threshold q for the training group, the control group, the test group in the absence of a crisis, and the test group during crises, respectively.

Figure 17 shows the evolution of these fractions as q is increased for the mEVT-based method and the thresholding method. The heterogeneity of the measurements in the crisis windows means that we cannot expect a τ _crisis = 100%. However, it is important to detect as much of the crisis data as possible to avoid false negatives (where the novelty score is below the threshold during a crisis). If we allow τ _crisis to be 90%, then τ _training, τ _control, τ _test equal 1.02%, 1.92%, 5.70% for the mEVT method, respectively, and 4.29%, 4.67%, and 10.25% for the thresholding method.

Figure 17

τ _training, τ _control, τ _test and τ _crisis for the thresholding method (upper plot) and the mEVT-based method (lower plot). A warning system should aim to trigger an alarm only during crises; i.e., we must set the threshold so that for an acceptable value of τ _crisis, τ _control is minimal.

This is a 58.1% reduction of false-positive alert time (where the novelty score is above the threshold in the absence of a crisis) for the control group. This reduction becomes 56.1%, 59.3%, and 50.4% for τ _crisis = 85%, 80% and 70%, respectively.

Therefore, the mEVT-based method consistently brings a significant improvement to the false-positive time while yielding the same true-positive detection rate.

8 Conclusion

8.1 Discussion

Novelty detection can benefit from a comprehensive multivariate Extreme Value Theory. We have motivated the use of EVT for novelty detection, showing that novelty thresholds set on the generative cdf F _n have a valid probabilistic interpretation only for single-point classifications; i.e., m = 1. We must use EVT to describe where the most extreme of m > 1 samples will lie.

We have described existing methods for the estimation of multivariate and multimodal EVDs $f^e_n$ w.r.t. some mixture distribution f _n , and have shown that the estimation of $f^e_n$ is inaccurate for both multivariate and multimodal cases.

We have proposed a numerical method of accurately determining the EVD of a multivariate, multimodal distribution f _n , which is a transformation of the probability density contours of the generative distribution, and have termed this the Ψ-transform. This allows EVDs for mixture models of arbitrary complexity to be estimated by finding the MLE Gumbel distribution $f^e_n$ in the transformed Ψ-space. A novelty threshold may be set on the corresponding univariate cdf $F^e_n$ in the transformed Ψ-space, which describes where the most extreme of m samples generated from f _n will lie.

Furthermore, we have proposed a solution for multivariate, unimodal models of normality. Here, by giving an alternate definition of extrema and closed-form solutions for the distribution function over pdf values, we show that we can obtain accurate estimates of the EVDs of multivariate Gaussian kernels.

We applied our formulae to actual patient vital-sign data and showed that the use of EVD is a significant improvement over the conventional thresholding method.

Obtaining these formulae relies on our ability to proceed from Eq. 16 to Eq. 19; i.e., our ability to parameterise the level sets of the generative probability distribution and integrate the resulting parameterisation. While this is relatively easy for multivariate Gaussian distributions, it is not possible for arbitrarily complex, non-symmetrical distributions and fully-analytical closed-form extreme value distributions are not to be expected. However, depending on our ability to estimate the distribution function over the pdf values, accurate estimates of its minimal EVD can be obtained without any sampling of extrema, which would be a great improvement over the existing numerical approach presented in Section 5.

8.2 Future Work

While we have proposed solutions in closed form for multivariate, unimodal models of normality, it should be possible to determine either closed-form solutions, or good approximations to those solutions, for fully multivariate, multimodal distributions. This paper also proposed a numerical solution to estimating the EVDs from such distributions, which was shown to agree closely with experimentally-obtained extrema from such models, but a more light-weight version (that avoids the sampling requirement of the proposed method) would be beneficial for applications in which model training is performed on-line, and where processing resources are constrained.

EVT considers the distribution of the extremum of a set of observed data, motivated by the fact that we wish to consider the extent of “normality” w.r.t. some normal model. However, by considering the additional information contained in the distributions of other order statistics, not just the distributions of the extrema, we may increase our capacity to perform novelty detection.