Gambling with Death

Abstract

Orthodox expected utility theory imposes too stringent restrictions on what attitudes to risk one can rationally hold. Focusing on a life-and-death gamble, I identify as the main culprit the theory’s Linearity property, according to which the utility of a particular change in the risk of a bad outcome is independent of the original level of risk. Finally, I argue that a recent non-standard Bayesian decision theory, that does not have this property, handles risky gambles better than the orthodox theory.

1 A Russian Roulette

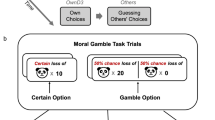
Consider the following scenario. Death holds a gun to your head. There is no way to escape. He informs you that you are about to play Russian roulette with two out of six chambers loaded. Assuming for now that you judge that money will be of no value to you if you are dead,¹ how much would you be willing to pay to have both bullets removed? Now consider the following slightly different scenario. Again, Death holds a gun to your head, but this time he informs you that four out of six chambers are loaded. Still assuming that you don’t care how much money you have when you are dead, how much would you be willing to pay to have one bullet removed?²

Fortunately, I do not know anyone who has had to play Russian roulette with Death. But most people seem to have the intuition that they would pay more in the first scenario than in the second. And more importantly for the present purposes, many people feel that doing so would be perfectly rational. After all, in the first scenario they are offered to purchase a higher absolute increase in the chance of survival than in the second scenario (2/6 compared to 1/6), and, perhaps more importantly, doing so offers them the certainty of surviving the game. Remarkably, however, orthodox expected utility theory—the theory that is meant to formalize what rationality dictates in scenarios like those imagined—requires us to pay the same amount in both scenarios. The reason why the theory has this implication is explained, first informally and then formally, in Sect. 2.

It might seem that our intuitions about the above example are confused by the fact that in both scenarios, most of us would be willing to pay any amount we can (i.e., give up all our wealth) for such a big reduction in the risk of death. But we can avoid monetary amounts entirely, and make the example even more dramatic, by considering the torture one would be willing to endure, in the event that one survives the roulette, in exchange for removing the bullets in the two scenarios. For any type of torture, there will be some length of time t, such that anyone who prefers to live to die should be willing to endure that type of torture lasting t in order to have both bullets removed in the first scenarios.³ Expected utility theory then entails that the person should be willing to endure the torture for the same length of time to remove one bullet out of four in the second scenario (assuming that one cannot be tortured after one’s death). But again, that seems counterintuitive, since the trade in the first scenario both offers a larger absolute reduction in the risk of death than the trade in the second scenario and ensures one’s survival.

The Linearity property of expected utility theory is the reason why the theory has counterintuitive implications in the above examples. This property means that the utility of a particular change in the risk of a bad outcome is independent of the original level of risk. For instance, the utility of removing one bullet from the gun is independent of how many bullets were in the gun before. (However, expected utility theory does not require that the monetary amount one accept to pay for the removal of a bullet is independent of how many bullets were in the gun, as we shall see in Sect. 2.)

To take a more mundane example,⁴ imagine that you have bought a ticket to the theater, believing that the play will almost certainly not be canceled, but then learn that the chance that the play will be canceled is 0.2. I suspect that you would find this outrageous. Now consider a situation where you buy the ticket thinking that there is a 0.3 chance the play will be canceled, but then learn that the chances are actually about 0.5. Although you have in the latter case also learned something undesirable, I think that most people would find the news more undesirable in the first case than in the second, since in the latter case you already knew that you were taking a chance.⁵ Linearity however requires that since the absolute increase in the risk of not seeing the show is the same in both cases (0.2), what is learned in the two cases is equally undesirable.

The theater example shows that the Linearity property of expected utility theory leads to trouble in mundane and everyday circumstances, just as it does in life-and-death gambles.⁶ The aim of this paper is to, first, argue that Linearity is not a general requirement of rationality, and, in particular, that rationality does not require us to pay the same amount when playing the two versions of Russian roulette. But I will not argue that it is irrational to pay the same amount in both scenarios. Rather, my claim is that depending on one’s attitude to risk, one can rationally pay more in one scenario than the other or pay the same amount in both scenarios. Secondly, I will show that a recent non-standard (normative) Bayesian decision theory (Stefánsson and Bradley 2015, ta) offers a principled way to arrive at this conclusion.⁷ It does so by including propositions about chance distributions in the domain of the utility function, and by representing different attitudes to how chances are distributed by different forms of this function. As a result, it makes room for the possibility that one can rationally value a particular change in the risk of a bad outcome differently depending on the original level of risk; i.e., it allows for rational attitudes that violate Linearity. Moreover, unlike both orthodox expected utility theory and the more recent risk-weighted expected utility theory (Buchak 2013), the new theory allows for the possibility that one can rationally take different attitudes to risks and chances depending on what is at stake.⁸ For instance, it allows for the possibility that one can rationally satisfy Linearity in the casino, say, while violating it when it comes to life-and-death gambles.

2 Implications of Expected Utility Theory

Before showing formally that expected utility theory has the above counterintuitive implication in the Russian roulette example, let me try to give an intuitive explanation of why the theory delivers this result. Recall that we are assuming that the value of your wealth (to you) is dependent on you being alive.⁹ Now if you do not pay Death to increase your chances of survival, then the risk of your death in the second scenario is twice the risk in the first scenario. Therefore, in the first scenario (before any payment), the expected utility of your wealth (to you) is twice the expected utility of your wealth (to you) in the second scenario (before any payment). For the chance that you will live to enjoy the wealth, rather than die and let it go to waste, is in the first scenario two times the chance in the second scenario, and the expected utility of your wealth is the utility of your wealth times the chance that you will live to enjoy it. Correspondingly, the expected utility of each dollar in the first scenario is twice the expected utility of each dollar in the second scenario. Moreover, recall that according to the Linearity property of expected utility theory, the utility (but not necessarily monetary value) of removing one bullet from the gun is independent of how many bullets are in the gun. Therefore, you should be willing to pay the same to remove two bullets in the first scenario as you would be willing to pay to remove one bullet in the second scenario. For then the expected utility of what you give up in the second scenario will be half of the expected utility of what you give up in the first scenario.

To arrive at this result more formally, let R denote the outcome where you are alive and ‘rich’; i.e., alive without having paid Death to improve your chances.¹⁰ Let D denote the outcome where you are dead. Since we are assuming, for now, that you don’t care about having money when you are dead, we don’t have to distinguish between being dead and rich and being dead and poor. Let X stand for the sum of money such that you would be indifferent between, on one hand, handing it over to Death in return for the increased chances on offer in scenario one, and on the other hand taking your chances by playing roulette with the greater risk of death, i.e., without paying anything. And let Y stand for the sum of money such that you would be indifferent between, on one hand, handing it over to Death in return for the increased chances on offer in scenario two, and on the other hand taking your chances by playing roulette with the greater risk of death.¹¹ Finally, let $P_X$ denote the outcome where you pay X and as a result survive but are poorer, or worse off, than in outcome R; and let $P_Y$ denote the outcome where you pay Y and as a result survive but are poorer, or worse off, than in outcome R (assuming that you are willing to give up something valuable to increase your chances of survival).¹²

To show that expected utility theory requires you to pay the same amount in both scenarios, it suffices to show that the theory entails that you should be indifferent between outcomes $P_X$ and $P_Y$. For these outcomes only differ in how much you paid to increase your chances of survival. So if you should be indifferent between these outcomes, then, assuming that you are not indifferent between having more and less money,¹³X and Y should be the same amount. Since we are assuming that you would rather be alive than dead, we can stipulate that $u(R)=1$ and $u(D)=0$, that is, that the utility of being alive and rich is 1 according to you, but the utility of being dead is 0. But nothing hangs on the choice of these particular numbers.

Now, according to classical (and orthodox) expected utility theory, developed for instance by John von Neumann and Oskar Morgenstern (1944), the expected utility of an alternative equals the chance-weighted sum of the utilities of the alternative’s possible outcomes. Moreover, it assumes that rational preferences and expectations of utility go together, such that, for instance, a rational person prefers one ‘lottery’ (or gamble)¹⁴ to another just in case the one has a higher expectation of utility (according to her) than the other. More formally, if $\precsim$ is a weak preference relation (meaning ‘... is not preferred to ...’), and $O_{ij}$ an outcome that results from lottery $L_i$ with probability $p_j$, then orthodox expected utility theory holds that for any rational person and any lotteries $L_i$ and $L_k$:

$$\begin{aligned} L_i\precsim L_k\Leftrightarrow \sum _j u(O_{ij})\cdot p_j\le \sum _j u(O_{kj})\cdot p_j \end{aligned}$$

(1)

Thus the fact that you are indifferent between giving up X and taking your chances in the first scenario (with two bullets) entails that:

$$\begin{aligned} u(P_X)=\frac{2}{3}u(R)+\frac{1}{3}u(D)=\frac{2}{3} \end{aligned}$$

(2)

Your indifference between giving up Y and taking your chances in the second scenario (with four bullets) however entails that:

$$\begin{aligned} \frac{1}{2}u(D)+\frac{1}{2}u(P_Y)=\frac{1}{3}u(R)+\frac{2}{3}u(D) \end{aligned}$$

(3)

Hence, $u(P_Y)=\frac{2}{3}=u(P_X)$. So you should be indifferent between X and Y. But recall that these are the maximum amounts of money, or good, that you are willing to give up to reduce the risk of death in the two scenarios. Hence, you should pay the same amount, or give up equally valuable goods, in the two scenarios.

We can arrive at the same conclusion differently, namely, by examining what the axioms of expected utility theory require in the two scenarios. The three axioms we need are Transitivity of indifference, Independence and Reduction. All three axioms are entailed by the theory. That is, according to expected utility theory, a preference cannot be rational if it fails to satisfy one of these axioms.

Transitivity of Indifference requires that if you are indifferent between two alternatives or outcomes A and B, and also between B and C, then you are indifferent between A and C. Some additional notation is needed to state Independence. Let $\{pX;\quad(1-p)Z\}$ denote a lottery that has chance p of resulting in X and chance $(1-p)$ of resulting in Z, where both X and Z could themselves be either lotteries or ‘ultimate’ (i.e., risk-free) outcomes, such as monetary amounts or hours in great pain. Then Independence requires that $\{pX;\quad (1-p)Z\}\precsim \{pY;\quad (1-p)Z\}\Leftrightarrow X\precsim Y$. In other words, comparisons of lotteries should be independent of what they have in common. Finally, Reduction entails that we can simplify a compound lottery by calculating the total probability that it offers for each of its possible ultimate outcomes, and that if it turns out that one compound lottery offers the exact same probabilities for such outcomes as some other (simple or compound) lottery, then one should be indifferent between the two lotteries.

Fig. 1

The four gambles with death

The four trees in Fig.  1 represent the two alternatives on offer in the two scenarios; i.e., to pay ($L_1$ in the first scenario and $L_3$ in the second) or not to pay ($L_2$ in the first scenario and $L_4$ in the second). By Independence, since $L_3\sim L_4$, replacing the outcome $P_Y$ in $L_3$ with $P_X$ should result in a strict preference just in case the agent has a strict preference between $P_X$ and $P_Y$. For instance, since most people prefer $P_Y$ to $P_X$ (i.e., they would pay a greater amount in the first scenario than in the second), replacing the outcome $P_Y$ in $L_3$ with $P_X$ should result in them preferring $L_4$ to (the changed) $L_3$. But since $L_2\sim P_X$,¹⁵ we should, by Independence, get the same result by replacing $P_Y$ in $L_3$ with $L_2$. This replacement results in the new lottery $L_3^*$ in Fig.  2.

Fig. 2

$L_3$ transformed using independence

Now by Reduction, we can simplify $L_3^*$ by calculating the total probability of each ultimate outcome. But when we do so, $L_3^*$ becomes identical to $L_4$, since the former gives a 2/3 chance of Dead (1/2 $\cdot$ 1/3 + 1/2) and 1/3 chance of Rich (1/2 $\cdot$ 2/3). So $L_3^*\sim L_4$. Hence, by Transitivity of indifference, $L_3^*\sim L_3$, which by Independence means that $L_2\sim P_Y$, and so again by Transitivity of indifference, $P_Y\sim P_X$. In other words, we arrive at the same conclusion as before, namely, that according to expected utility theory, you should be willing to pay the same amount—or, more generally, give up something of equal value—in the two scenarios.

3 Defending the Orthodoxy?

In the introduction I claimed that the Linearity property of expected utility theory is the reason why the theory delivers counterintuitive results in the Russian roulette example. The next section contains the main argument for this claim. I will present a new (normative) Bayesian decision theory that does not have this Linearity property, and show that a person for whom money has no value after she is dead can maximize expected value as defined by the new theory by paying more to have both bullets removed in the first scenario than to have one bullet removed in the second scenario.

It is of course open to an expected utility theorist to argue that such violations of Linearity are simply irrational. Recall that in the Russian roulette example, Linearity entails that the removal of a bullet should always be equally valuable (in ‘utility terms’), independently of how many chambers are loaded. So, for instance, removing the last bullet and thereby ensuring one’s survival, or removing one bullet out of six and thereby acquiring some chance of surviving rather than facing certain death, is no more valuable than removing one bullet out of four and thereby securing a fifty–fifty chance of survival. In contrast, I will argue that one can perfectly well value the removal of these bullets differentially. The new theory I present makes room for such values, by allowing that chances, just like e.g. money, can have decreasing marginal utility in some ranges but increasing marginal utility in others.

Could an expected utility theorist plausibly argue that such values are simply irrational? I think that such an argument would go against the (Humean) philosophy that expected utility theory is meant to formalize.¹⁶ The core of this philosophy is the assumption that one can rationally value, and desire, anything, as long as one’s attitudes are internally consistent and one acts in accordance with them. What does it mean for one’s attitudes to be internally consistent? The standard answer given by expected utility theorists is that one’s attitudes are internally consistent just in case one’s preferences can be represented as maximizing expected benefit to oneself (or expected utility, as it is typically called). For if the latter holds, then and only then is there no inconsistency in the set containing the following triple: the agent’s instrumental desires, her non-instrumental desires and her beliefs. Moreover, one’s choices can be seen as the taking of suitable means to one’s ends, the thought goes, if and only if they are based on expected utility maximizing preferences.

So if it were impossible to make the common preference in the Russian roulette example consistent with the maximization of any measure of expected benefit (to the person), then an expected utility theorist could justifiably claim that the attitude in question is inconsistent, and therefore irrational. First, that would suggest that there were some internal inconsistency in the agent’s values or attitudes; second, that would mean that by acting on such a preference one could not be taking suitable means to one’s ends. But it is not impossible to make the preference in question consistent with expected benefit maximization. For as already mentioned, I will present a new theory according to which someone who pays more in the first roulette than the second can be represented as maximizing expected utility; and thus can be understood as taking suitable means to her ends. So if rationality only requires that one’s attitudes be internally consistent and that one takes suitable means given one’s ends, it follows that it need not be irrational to pay more in the first roulette than in the second.¹⁷

Another potential attempt to save orthodox expected utility theory from objections based on the Russian roulette, would be to argue that people’s intuitions that they would pay more in the first scenario than the second stem from the fact that they actually do care about whether or not they have money after they are dead, since the money might benefit their family or friends. The idea would be that on close inspection, there might not be any clash between people’s intuitions and the implications of expected utility theory. For when people try to imagine themselves in the two scenarios, they are simply not able to abstract away from the fact that they actually care about whether they are rich or poor after they are dead, and are thus not answering the questions that they are being asked to answer.

To see if the above defense can be sustained, let’s relax the assumption that you don’t care about whether you have money after you are dead. To do so, we need to refine the outcomes considered in last section. Now let $D_Y$ be the outcome where you are dead after having paid Y to remove one bullet in the second scenario, but let D be the outcome of dying without having paid anything to Death. Note that we don’t need to worry about the outcome $D_X$, since you are sure to survive if you pay X in the first scenario.

Now let’s see what expected utility theory entails given these refined outcomes. The outcomes in the first scenario have not changed, so it is still the case that $u(P_X)=\frac{2}{3}$. However, your indifference between handing over Y and taking your chances in the second scenario now means that:

$$\begin{aligned} \frac{1}{2}u(D_Y)+\frac{1}{2}u(P_Y)=\frac{1}{3}u(R)+\frac{2}{3}u(D) \end{aligned}$$

(4)

Hence, $u(P_Y)=u(P_X)-u(D_Y)$. Now we are assuming that $u(D_Y)$ is negative, i.e., dying after having paid Y is worse than simply dying, which we assigned a utility value of zero. Thus, $u(P_X)<u(P_Y)$ and $Y\prec X$. So for those who care about what happens to their wealth after they are dead, it can be rational, according to orthodox expected utility theory, to pay more in the first scenario than the second.

Does that get the orthodox theory off the hook? Not quite. First, it seems that even if most people actually want to be rich rather than poor after they die, we can easily imagine a person for whom this is not the case. And for the reasons given above, it is hard to see how we could justify the claim that this person cannot rationally place a special value on securing her survival and therefore pay more in the first of the two scenarios. Second, unless we assume that the value of a person’s wealth, to that person, is completely independent of whether she is dead or alive, expected utility theory entails that if we change the first scenario such that there is only one bullet in the gun, then one should be willing to pay more to have one out of four bullets removed in the second scenario than to have the single bullet removed in this new scenario. After all, each dollar is still worth more in the first scenario than the second, and expected utility theory holds that the removal of each bullet is equally valuable (in utility terms). But, for similar reasons that have been discussed above, that seems counterintuitive, and, I contend, is not rationally required.

Third, even if we assume that the value of a person’s wealth, to that person, is completely independent of whether she is dead or alive, expected utility theory still makes implausible demands of her. Recall that I claimed above that one can rationally find the value of removing one bullet when that is the only bullet in the gun to be greater than the value of removing one bullet when there are multiple bullets. This is a very natural thought—whether or not one cares about what happens to one’s wealth after one is dead. That is, it would seem that since one can rationally value securing (or almost securing) one’s survival, over and above the increase in expected value as determined only by the value of one’s life, it can be perfectly rational to pay more to remove the only bullet from the gun than to remove one bullet out of four. But that is not rational according to orthodox expected utility theory, even if, say, the value of a person’s wealth to her is completely determined by the extent to which it provides for her family (even after she is death). The expected value increase from removing one bullet, according to expected utility theory, is always the same. Hence, if the value of one’s wealth is independent of whether one is dead or alive—and thus independent of one’s risk of death—one should always be willing to give up the same amount of utility to remove one bullet, irrespective of whether it is, say, the only bullet in the gun, or one bullet out of four, or one bullet out of six.

4 A New Solution

The aim of this section is to show that a recent non-standard (normative) Bayesian¹⁸ decision theory fits well with common intuitions about examples like those discussed above. One of the observations that motivate the new theory, is that just as different quantities of goods can have decreasing or increasing marginal utility, so different quantities of chances for goods can have decreasing or increasing marginal utility—contra Linearity.

It is generally accepted, in particular by the proponents of orthodox expected utility theory, that a rational person can take money to have decreasing marginal utility within certain ranges but increasing marginal utility within other ranges. (In fact, utility theory was originally largely motivated by the observation that money has non-constant marginal value; see Bernoulli 1738.) To take an example, a $1000 gain typically benefits someone more when he is completely broke and cannot even afford food than when he has more than enough to live on. However, the same gain might benefit him more when he needs additional $1000 in order to buy a house than when he can only afford to rent anyway (in which case the gain would only mean, say, being able to afford a nice holiday).

My suggestion is that chances for goods can have both decreasing and increasing marginal utility, just like quantities of money. So, a 0.1 increase in the chance of of attaining a good can rationally be valued differently depending on whether the chance before the increase was, say, 0, 0.5 or 0.9. For instance, although it is of course (typically) desirable to increase one’s chances of survival from 0.5 to 0.6, it might be even more desirable to go from being quite likely (0.9 chance) to live to surviving for sure, and also more desirable to go from being certain to die to having a 0.1 chance of surviving. To emphasize, I do not claim that this is how one should value chances, but only that this attitude is rationally permitted. As already indicated, I am assuming a traditional instrumental conception of rationality, which decision theory is meant to formalize, and according to which rationality is silent about what one can rationally value as long as the valuation is consistent.

I hope to have made clear that, intuitively, the attitude that chances can have both decreasing and increasing marginal utility is not inconsistent. In what follows, I first establish more formally the consistency of this attitude by showing that it is compatible with the normative Bayesian decision theory developed in Stefánsson and Bradley (2015). Second, I show that as a result of allowing that chances can have non-constant marginal utility, the theory is consistent with the typical intuition that one can rationally pay more to have both bullets removed in the first scenario discussed at the start of this paper than to have one bullet out of four removed in the second scenario.

Here is an outline of Stefánsson and Bradley’s (2015) framework: Let $\Omega$ be a Boolean algebra of propositions describing risk free outcomes, e.g. the proposition that one dies from the Russian roulette, that one lives at a particular level of wealth, etc., and let $\Delta$ be a Boolean algebra of propositions describing all possible objective probability (or chance) distributions over the propositions in $\Omega$. For instance, for any proposition $A\in \Omega$ and any value $x\in [0,1]$, there will be a proposition $Ch(A)=x\in \Delta$ which is true just in case the chance of A is x. Let $\Gamma =\Delta \times \Omega$, and suppose that a rational person’s preferences over propositions in $\Gamma$ satisfy the Bolker-Jeffrey axioms (Bolker 1966, Jeffrey 1965, Chap. 9). Then for any such person, there will be a subjective probability measure on $\Gamma$, and a utility function (or ‘desirability function’, to use Jeffrey’s term) on the same set except that the contradictory proposition has been removed, relative to which the person’s preferences can be represented as maximizing her subjective expectation of utility.¹⁹

An important difference between, on one hand, the above framework and, on the other hand, the classical expected utility theory of von Neumann and Morgenstern (which was presented in Sect. 2), is that the former framework contains both objective probabilities and subjective ones, whereas the latter contains only objective probabilities.²⁰ Moreover, unlike other frameworks that allow for both subjective and objective probabilities (in particular, Anscombe and Aumann’s 1963), this framework explicitly makes chance distributions part of the content of desire, i.e., it includes objective probability distributions in the domain of the utility function. In a moment we will see that this feature makes the framework very well suited to handle the roulette example.

But first, to prepare the ground for the argument that follows, let’s see precisely how the suggested framework differs from von Neumann and Morgenstern’s classical expected utility theory. As Stefánsson and Bradley (2015) show, orthodox expected utility theory can be expressed within their framework by requiring that agents evaluate chances linearly. More formally, let $\langle Ch(A_{i})=\alpha _{i}\rangle$ denote the conjunction of the propositions $Ch(A_{1})=\alpha _{1}$, $Ch(A_{2})=\alpha _{2}$, ..., $Ch(A_{n})=\alpha _{n}$, where $\{A_{i}\}_{i=1}^{n}$ is an n-fold partition of $\Omega$ and the $\alpha _{i}$ are real numbers in $[0,1]$ such that $\sum \nolimits _{i=1}^{n}\alpha _{i}=1$. In other words, we can think of $\langle Ch(A_{i})=\alpha _{i}\rangle$ as a lottery that results in outcome $A_i$ with chance $\alpha _i$. Then von Neumann and Morgenstern’s expected utility theory requires that:

Linearity::

For any lottery propositions $\langle Ch(A_{i})=\alpha _{i}\rangle$, $\langle Ch(B_{i})=\beta _{i}\rangle$:

$$\begin{aligned} \langle Ch(A_{i})=\alpha _{i}\rangle \precsim \langle Ch(B_{i})=\beta _{i}\rangle \Leftrightarrow \sum _i u(A_{i})\cdot \alpha _i \le \sum _i u(B_{i})\cdot \beta _i \end{aligned}$$

Less formally, Linearity states that the agent’s preference between two lotteries is determined by the lotteries’ expectations of utility, where the expectation is calculated using the objective probabilities that the lotteries confer on their possible outcomes. It turns out that Linearity is entailed by the framework under discussion if the agent is ‘neutral’ about chances (Stefánsson and Bradley 2015: Theorem 1), in the sense that the chance of an outcome is a matter of practical indifference once it has been established whether the outcome was realized or not.²¹ Without that assumption, which Stefánsson and Bradley (2015) criticize, Linearity is an optional addition to their framework. In a moment, we will see that when Linearity is added to this framework, it delivers the same verdict about the roulette example as orthodox expected utility theory.

Now let’s return to the goal of rationalizing common intuition in the example discussed throughout this paper. We can start with the simple task of showing that given this framework, it can be perfectly rational, for someone for whom the value of her wealth is independent of whether she is dead or alive, to pay more to have one bullet removed when that is the only bullet in the gun (thereby ensuring her survival) than to have one bullet removed when there are four bullets in the gun. But let’s also add the assumption that the person is willing to pay more to have a single bullet removed when all six chambers are loaded (i.e., to have some chance to live rather than dying for sure) than to have one bullet out of four removed. The added assumption makes the exercise more interesting since we can no longer assume that chances of survival have increasing marginal utility in all ranges; and it arguably makes the example more realistic, since there does seem to be some value in having some chance to live rather than dying for sure which is not exhausted by the increase in expected value as calculated using the probability and value of survival.

The above natural (and common) attitude can be represented as maximizing expected utility, as defined in the new framework, if we assume that chances of life have decreasing marginal utility when the chances are, say, less than 0.5, but increasing marginal utility when the chances are greater than 0.5. Recall that one observation that motivates the new theory is precisely that the marginal utility of chances can be non-constant, in contradiction with Linearity, which is captured by the framework in question by including chance propositions in the domain of the utility function. This feature of the new theory means that there is an infinite number of utility functions, consistent with the new theory (but inconsistent with expected utility theory), that capture the intuition that it is more valuable to remove a single bullet when it is either the only bullet left in the gun or when all six chambers are loaded, than removing a single bullet when four out of six chambers are loaded. I will consider just one such function.

Recall that what is at issue is the value of purchasing greater chances to live. Let’s now denote the outcome that the agent lives by $\mathcal {L}$. Then the utility function in (5) rationalizes the preference in question, as I show in the next paragraph.²² However, it might be worth emphasizing that I do not claim that this is a typical utility function (nor, of course, that it is rationally required), but only that it is one possible utility function that rationalizes the preference under discussion. The graph of function (5) is pictured in Fig. 3. As the graph illustrates, this utility function is such that for any chance x, the utility gain when the chance of life increases by x is greater when the prior chance was close to either end of the zero-one interval than when the prior chance was around the mid-point of the interval.

$$\begin{aligned} u(Ch(\mathcal {L})=x)= {\left\{ \begin{array}{ll} \frac{(\sqrt{x})/4}{(\sqrt{0}.5)/4+0.5^2}\ \ \ \ \ \ \ \ \text {if } x\le 0.5,\\ \frac{(\sqrt{x})/4+(x-0.5)^2}{(\sqrt{0}.5)/4+0.5^2}\ \ \ \ \ \text {if } x>0.5. \end{array}\right. } \end{aligned}$$

(5)

Fig. 3

Decreasing and increasing marginal utility of chances

Now if only one chamber is loaded, then the roulette offers the agent a 5/6 chance of $\mathcal {L}$, but if two chambers are loaded, then it offers a 4/6 chance of $\mathcal {L}$, and so on. Table 1 summarizes the utilities of all the possible chances that the roulette can offer, given the utility function depicted in Fig. 3. We can see from the table that an agent whose desires are represented by the above utility function, and for whom the value of her wealth is independent of whether she is dead or alive, maximizes expected utility by paying more to have the only bullet in the gun removed than to have one bullet out of four removed. For the difference in utility between a 6/6 chance of $\mathcal {L}$ and a 5/6 of $\mathcal {L}$ is much greater than the difference in utility between a 3/6 chance and a 2/6 chance of $\mathcal {L}$ (0.33 compared to 0.07). Moreover, such an agent will, for the same reason, pay more to have one bullet out of six removed than one bullet out of four. In other words, this agent takes suitable means to her ends by paying differently for an extra 1/6 chance of survival depending on the prior chances, in violation of orthodox expected utility theory.

Table 1 Utility of chances of survival

Now let’s introduce the assumption that the agent does not care about whether she is wealthy or poor when she is dead, to see if we can rationalize paying more in the first scenario, where the person has the option of paying to have two out of two bullets removed, than in the second scenario, where the person has the option of having one bullet out of four removed. Recall that the agent is assumed to be indifferent between paying X and taking her chances in the first scenario with two chambers loaded rather than none, and is also assumed to be indifferent between paying Y and taking her chances in the second scenario with four chambers loaded rather than three. Given the present framework:

$$\begin{aligned}&u(P_X)=u\left[ Ch(D)=\frac{2}{6} \& Ch(R)=\frac{4}{6}\right] \end{aligned}$$

(6)

$$\begin{aligned}&u\left[ Ch(D)=\frac{1}{2} \& Ch(P_Y)=\frac{1}{2}\right] =u\left[ Ch(D)=\frac{4}{6} \& Ch(R)=\frac{2}{6}\right] \end{aligned}$$

(7)

By the normalization of u, we have $u(P_X)=0.48$ (assuming that u is separable in Ch(D) and Ch(R) and by setting $R\equiv \mathcal {L}).$ By the same assumptions, $u\left[ {Ch(P_{Y} ) = \frac{1}{2}} \right] = u\left[ {Ch(R) = \frac{2}{6}} \right]$=0.34 (now also assuming that u is separable in Ch(D) and $Ch(P_Y)$). It seems plausible that the form of u over the values of $Ch(P_Y)$ would be roughly the same as the form it has over Ch(R). In any case, since this is entirely consistent with the present theory, we can stipulate that u has that form over $Ch(P_Y)$. That means that $u\left[ {Ch(P_{Y} ) = 1} \right]> u\left[ {Ch(P_{Y} ) = \frac{1}{2}} \right]\cdot2$. In other words, $u(P_Y)>0.68$. Therefore, $P_X\prec P_Y$, which means that $Y\prec X$. So this agent, who doesn’t care about whether she has any money left when she is dead, maximizes expected utility, as defined in this framework, by paying more to have two of two bullets removed in the first scenario than to have one of four bullets removed in the second scenario. In other words, unlike von Neumann and Morgenstern’s orthodox expected utility theory, this new (unorthodox) Bayesian decision theory is consistent with this natural preference, and rationalizes the preference by showing what attitudes to chances can motivate it.

The above theory is of course also consistent with the preference that orthodox expected utility requires, i.e., it is consistent with wanting to pay the same for removing two bullets in the first scenario as removing one bullet in the second scenario. In fact, this is the preference that maximizes expected utility if one is neutral about chances, in the sense discussed above, and therefore satisfies Linearity. Given the normalization of the utility function (and given the separability assumptions made above), equality (6) is equivalent to $u(P_X)=u\left[{Ch(R)=\frac{4}{6}}\right]$. But by the same assumptions, it follows from equality (7) that $u\left[{Ch(P_Y)=\frac{1}{2}}\right]=u\left[{Ch(R)=\frac{2}{6}}\right]$, which by Linearity entails that $u(P_Y)=u\left[{Ch(P_Y)=1}\right]=u\left[{Ch(R)=\frac{4}{6}}\right]$. So someone who satisfies Linearity should be willing to pay the same amount to reduce the risk in the two scenarios discussed at the start of this paper, just like orthodox expected utility theory requires.

Moreover, the new theory is consistent with an agent satisfying Linearity when it comes to some goods but not to others. Since we introduce chance propositions into the domain of the utility function, and because a proposition specifying the chance of, say, health, is a different proposition from one specifying a chance distribution over monetary amounts, the theory allows that a person’s utility curve over chances for health can be very different from her utility curve over chances of money—just as standard expected utility theory allows that, say, the utility curve over monetary amounts looks different from the curve over years in full health.²³

Let’s now briefly return to the axiomatic argument that one should pay the same in the two scenarios. The reason that this argument is not sound given the present framework is simply that both Independence and Reduction can be violated within it. This is simple to see in the case of Reduction. Recall from Fig.  2 in Sect. 2 that an implication of Reduction is that the lottery $L_{3}^*$, which is a 50:50 gamble between Dead and the lottery $L_2$, which in turn offers a 2/3 chance of Rich but 1/3 chance of Dead, can be simplified by calculating the probabilities it offers for the ultimate outcomes (1/3 for Rich and 2/3 for Dead). But when we did that, $L_{3}^*$ turned out to be identical to $L_4$. This was a crucial step in the axiomatic argument, since then the expected utility theorist only needed to apply Independence and Transitivity to establish that the agent should pay the same amount in the two scenarios. But once we give up on the assumption that the value of a gamble is linear in its chances—i.e., once we reject Linearity—Reduction cannot be assumed. For instance, once we abandon Linearity it becomes possible that $u\left[{Ch(D)=\frac{1}{2}}\right]+u\left[{Ch(D)=\frac{1}{6}}\right]\not =u\left[{Ch(D)=\frac{2}{3}}\right]$. Hence, Reduction is unsound, and the axiomatic argument that one should pay the same amount in the two scenarios is blocked.²⁴

5 Comparison

Before concluding this paper, let’s briefly compare my account with other, similar ones.²⁵ First consider how my solution to the Russian roulette problem differs from Howard Sobel’s (1989), who, before now, seems to be the only person who has tried in print to rationalize (as expected utility maximizing) the preference for paying more in the first scenario than the second. Essentially, Sobel’s rationalization consists in the observation that the value of an outcome where one lives but is poor (i.e, an outcome like $P_X$) may depend on what alternatives were on offer. In particular, living poor as a result of a decision-problem where one could either choose this outcome for sure or a more risky outcome that could have resulted in one’s death but could also have resulted in one being alive and rich (e.g. the first scenario), may be different from the value of that same outcome as a result of a decision-problem where both options had a significant chance of resulting in one’s death (e.g. the second scenario).²⁶

While Sobel’s observation (i.e., that the value of an outcome where one lives but is poor may depend on what alternatives were on offer) may be correct, I do not think that this explains the preference under discussion. I claim that people often have non-linear attitudes to chances;²⁷ and in particular, that many people find it much more valuable to reduce their risk of death from 1/3 to 0 than from 2/3 to 1/2. And that is why they are willing to pay more in the first scenario than the second. But this does not mean that the outcome where one lives as a result of the payment in the first scenario (which, recall, ensures that one lives) is more valuable than the outcome where one lives as a result of the payment in the second scenario (which, recall, does not ensure that one lives). In fact, surviving the second scenario may be more (subjectively) valuable than surviving the first scenario, since in the second scenario one might be especially grateful for being alive! Rather, it is the way in which chances are distributed in the prospects on offer—in particular, the fact that one can purchase living another day for sure in the first scenario but not the second—that explains, I think, why people are willing to pay more to improve their chances in the first scenario than in the second.

The question of which of these explanations, mine or Sobel’s, is more psychologically accurate, is of course a topic for empirical psychology, not philosophy. But even if Sobel’s explanation captures the reason why some people are willing to pay more in the first scenario than the second, I contend that my explanation better fits with the reason why others (e.g. me!) have this preference. So it may be worth pointing out that a theory that simultaneously extends decision theory to chance propositions, as Stefánsson and Bradley (2015) do, and to counterfactual prospects, as Bradley and Stefánsson 2017) do, would be able to model both the type of reasoning that I think explains the preference under discussion and the type of reasoning that Sobel thought explained it (since the latter theory allows for the possibility that the value of an outcome partly depends on what one could have chosen but didn’t).

The decision theory on which my suggested solution to the Russian roulette problem is based bares certain similarities to recent theories that generalize expected utility theory to allow for more risk attitudes; in particular, Lara Buchak’s (2013) risk-weighted expected utility theory (and the theories on which it is based). A distinguishing feature of these recent generalisations is that they contain a third function—a risk function—which, in addition to a utility and a probability function, is used to represent rational preferences as expected utility maximizing. The introduction of such a risk-function, that is independent of the agent’s utility function, suggests that the attitudes that the function is meant to represent—i.e., the risk attitudes—are distinct from the agent’s desires. This is no coincidence, as Buchak (2013, pp. 53–54) explicitly states that she takes an agent’s risk attitudes to be distinct from her desires. In contrast, recall that according to the theory favored in this paper, a risk attitude is simply a special type of desire, namely, a desire about how chances are distributed.

Buchak’s idea that risk attitudes are not desires is criticized at length in Stefánsson and Bradley (2017) and Stefánsson (2014). I will not repeat these arguments here. But the gist of them is that risk attitudes look a lot like desires, in particular, if we take desires to be the attitudes to which we try to fit the world. For instance, a risk averse person will (if instrumentally rational) try what she can to make the world fit this attitude, for instance by not accepting certain bets, and by hedging the risks she exposed to. Similarly, a risk averse person prefers, or wants, outcomes to be spread differently across the possibility space than someone who is risk seeking—the latter person prefers, or wants, the goods to be more concentrated than the latter. In sum, it is hard to deny that risk attitudes behave a lot like desires.

Another difference between the framework favored in this paper and Buchak’s, is that the former can but the latter cannot represent the so-called “Ellsberg preference” (Ellsberg 1961) as maximizing an expected value. In fact, the framework discussed in this paper is the first that can represent the Ellsberg-preference and the Allais preference (Allais 1953) as maximizing the same utility function, and thereby provide a unified solution to two problems that have caused great problems for decision theory for decades. Again, since this is discussed at length in Stefánsson and Bradley (2017), I will not discuss it further here.