Determination of the Effective Permeability of Doubly Porous Materials by a Two-Scale Homogenization Approach

Abstract

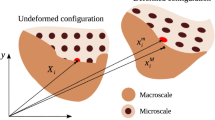
The present work is dedicated to determining the effective permeability of doubly porous materials made of a solid phase comprising a network of interconnected pores at the nanoscale and a network of non-interconnected pores at the microscopic scale. The fluid flow at microscopic scale through the solid phase containing nanopores is described by the Darcy law, while fluid flow in the nano- and microscopic pores is governed by the Stokes equations. A two-scale homogenization approach is proposed to estimate the effective permeability of doubly porous materials in question. In the nanoscopic-to-microscopic upscaling, a micromechanical model based on the generalized self-consistent scheme (GSCS) is elaborated to estimate the microscopic permeability. In the microscopic-to-macroscopic upscaling, the equivalent inclusion method combined with the dilute, Mori–Tanaka, differential schemes is used to obtain different estimates of the macroscopic permeability. In the two-scale homogenization approach elaborated, the pore size and shape effects as well as the solid/fluid interface influence are taken into account. The results given by the proposed two-scale homogenization approach are discussed and compared with the relevant numerical results provided by the finite element method.

Appendices

Appendix 1: Orthogonal Curvilinear Coordinates

Orthogonal curvilinear coordinates, used throughout this paper, are recalled below to rend it self-contained. Consider a surface $\Gamma$ in a three-dimensional Euclidean space. In order to have a mathematical characterization of $\Gamma$, a system of orthogonal curvilinear coordinates $\{y_{1},y_{2},y_{3}\}$ is defined such that the position vector $\mathbf {x}=(x_{1},x_{2},x_{3})$ of any point in space is expressed as

$$\begin{aligned} \mathbf {x}=\mathbf {x} (y_{1},y_{2},y_{3})=[x_{1}(y_{1},y_{2},y_{3}),x_{2}(y_{1},y_{2},y_{3}),x_{3}(y_{1},y_{2},y_{3})]. \end{aligned}$$

(78)

The vector tangent to the $y_{i}$-coordinate curve is calculated and given by

$$\begin{aligned} \mathbf {t}_{i}=\frac{\partial \mathbf {x}}{\partial y_{i}}=h_{i}\mathbf {f}_{i},\quad with \quad h_{i}=\left\| \frac{\partial \mathbf {x}}{\partial y_{i}}\right\| \end{aligned}$$

(79)

where the summation convention does not apply, $h_{i}$ is a metric coefficient and $\mathbf {f}_{i}$ is the unit vector tangent to the $y_{i}$-coordinate curve. Because the curvilinear coordinates $y_{1}$, $y_{2}$ and $y_{3}$ are orthogonal, $\mathbf {f}_{1}$, $\mathbf {f}_{2}$ and $\mathbf {f}_{3}$ are therefore orthonormal so that $\mathbf {f}_{i}\cdot \mathbf {f}_{j}=\delta _{ij}$. The surface $\Gamma$ can be now defined by

$$\begin{aligned} \Gamma =\left\{ \mathbf {x}=\mathbf {x}(y_{1},y_{2},y_{3})\in \mathbf {R}^{3}\mid y_{1}=\gamma _{0}\right\} \end{aligned}$$

(80)

where $\gamma _{0}$ is a constant scalar value.

We denote by $T(\mathbf {y})$ a scalar function and by $\mathbf {T}(\mathbf {y})$ a vector function. The following differential operators for $T(\mathbf {y})$ and $\mathbf {T}(\mathbf {y})$ are given in the orthonormal curvilinear basis $\{\mathbf {f}_{1},\mathbf {f}_{2},\mathbf {f}_{3}\}$ by:

• Gradient of the scalar function $T(\mathbf {y})$

  $$\begin{aligned} \nabla T =\frac{1}{h_{1}}\frac{\partial T }{\partial y_{1}}\mathbf {f}_{1}+\frac{1}{h_{2}}\frac{\partial T}{\partial y_{2}} \mathbf {f}_{2}+\frac{1}{h_{3}}\frac{\partial T}{\partial y_{3}}\mathbf {f}_{3}; \end{aligned}$$

  (81)

• Laplacian of the scalar function $T(\mathbf {y})$

  $$\begin{aligned} \varDelta T =\frac{1}{h_{1}h_{2}h_{3}}\left[ \frac{\partial }{\partial y_{1}}\left( \frac{h_{2}h_{3}}{h_{1}}\frac{\partial T }{\partial y_{1}}\right) + \frac{\partial }{\partial y_{2}}\left( \frac{h_{1}h_{3}}{h_{2}}\frac{ \partial T }{\partial y_{2}}\right) + \frac{\partial }{\partial y_{3}}\left( \frac{h_{1}h_{2}}{h_{3}}\frac{\partial T }{\partial y_{3}}\right) \right] ; \end{aligned}$$

  (82)

• Divergence of the vector function $\mathbf {T}(\mathbf {y})$

  $$\begin{aligned} \nabla \cdot \mathbf {T}=\frac{1}{h_{1}h_{2}h_{3}}\left[ \frac{\partial \left( h_{2}h_{3}T_{1}\right) }{\partial y_{1}}+\frac{\partial \left( h_{1}h_{3}T_{2}\right) }{\partial y_{2}}+\frac{\partial \left( h_{1}h_{2}T_{3}\right) }{\partial y_{3}}\right] ; \end{aligned}$$

  (83)

• Laplacian of the vector function $\mathbf {T}(\mathbf {y})$

  $$\begin{aligned} \varDelta \mathbf {T} = \{\varDelta \mathbf {T}\}_{1}\mathbf {f}_{1}+\{\varDelta \mathbf {T}\}_{2}\mathbf {f}_{2} + \{\varDelta \mathbf {T}\}_{3}\mathbf {f}_{3} \end{aligned}$$

  (84)

  where

  $$\begin{aligned} \{\varDelta \mathbf {T}\}_{1}= & {} \varDelta T_{1} \\+ & {} \frac{2}{h_{1}}\left( \frac{1}{h_1h_2}\frac{\partial h_1}{\partial y_2}\frac{\partial T_{2}}{\partial y_1}+\frac{1}{h_1h_3}\frac{\partial h_1}{\partial y_3}\frac{\partial T_{3}}{\partial y_1} - \frac{1}{h^2_2}\frac{\partial h_2}{\partial y_1}\frac{\partial T_{2}}{\partial y_2}- \frac{1}{h^2_3}\frac{\partial h_3}{\partial y_1}\frac{\partial T_{3}}{\partial y_3}\right) \\- & {} \frac{T_{1}}{h_1^2}\left[ \frac{1}{h_2^2}\left\{ \left( \frac{\partial h_2}{\partial y_1}\right) ^2+\left( \frac{\partial h_1}{\partial y_2}\right) ^2\right\} + \frac{1}{h_3^2}\left\{ \left( \frac{\partial h_3}{\partial y_1}\right) ^2+\left( \frac{\partial h_1}{\partial y_3}\right) ^2\right\} \right] \\+ & {} T_{2}\left[ \frac{1}{h_1h_2}\left\{ \frac{\partial }{\partial y_1}\left( \frac{1}{h_1}\frac{\partial h_1}{\partial y_2} \right) - \frac{\partial }{\partial y_1}\left( \frac{1}{h_2}\frac{\partial h_2}{\partial y_2} \right) \right\} + \frac{h_2}{h_1}\frac{\partial }{\partial y_1}\left( \frac{1}{h_2^2h_3}\frac{\partial h_3}{\partial y_2} \right) \right] \\+ & {} T_{3}\left[ \frac{1}{h_1h_3}\left\{ \frac{\partial }{\partial y_1}\left( \frac{1}{h_1}\frac{\partial h_1}{\partial y_3} \right) - \frac{\partial }{\partial y_1}\left( \frac{1}{h_3}\frac{\partial h_3}{\partial y_3} \right) \right\} + \frac{h_3}{h_1}\frac{\partial }{\partial y_1}\left( \frac{1}{h_3^2h_2}\frac{\partial h_2}{\partial y_3} \right) \right] ; \\ \{\varDelta \mathbf {T}\}_{2}= & {} \varDelta T_{2} \\+ & {} \frac{2}{h_{2}}\left( \frac{1}{h_2h_3}\frac{\partial h_2}{\partial y_3}\frac{\partial T_{3}}{\partial y_2}+\frac{1}{h_2h_1}\frac{\partial h_2}{\partial y_1}\frac{\partial T_{1}}{\partial y_2} - \frac{1}{h^2_3}\frac{\partial h_3}{\partial y_2}\frac{\partial T_{3}}{\partial y_3}- \frac{1}{h^2_1}\frac{\partial h_1}{\partial y_2}\frac{\partial T_{1}}{\partial y_1}\right) \\- & {} \frac{T_{2}}{h_2^2}\left[ \frac{1}{h_3^2}\left\{ \left( \frac{\partial h_3}{\partial y_2}\right) ^2+\left( \frac{\partial h_2}{\partial y_3}\right) ^2\right\} + \frac{1}{h_1^2}\left\{ \left( \frac{\partial h_1}{\partial y_2}\right) ^2+\left( \frac{\partial h_2}{\partial y_1}\right) ^2\right\} \right] \\+ & {} T_{3}\left[ \frac{1}{h_2h_3}\left\{ \frac{\partial }{\partial y_2}\left( \frac{1}{h_2}\frac{\partial h_2}{\partial y_3} \right) - \frac{\partial }{\partial y_2}\left( \frac{1}{h_3}\frac{\partial h_3}{\partial y_3} \right) \right\} + \frac{h_3}{h_2}\frac{\partial }{\partial y_2}\left( \frac{1}{h_3^2h_1}\frac{\partial h_1}{\partial y_3} \right) \right] \\+ & {} T_{1}\left[ \frac{1}{h_2h_1}\left\{ \frac{\partial }{\partial y_2}\left( \frac{1}{h_2}\frac{\partial h_2}{\partial y_1} \right) - \frac{\partial }{\partial y_2}\left( \frac{1}{h_1}\frac{\partial h_1}{\partial y_1} \right) \right\} + \frac{h_1}{h_2}\frac{\partial }{\partial y_2}\left( \frac{1}{h_1^2h_3}\frac{\partial h_3}{\partial y_1} \right) \right] ; \\ \{\varDelta \mathbf {T}\}_{3}= & {} \varDelta T_{3} \\+ & {} \frac{2}{h_{3}}\left( \frac{1}{h_3h_1}\frac{\partial h_3}{\partial y_1}\frac{\partial T_{1}}{\partial y_3}+\frac{1}{h_3h_2}\frac{\partial h_3}{\partial y_2}\frac{\partial T_{2}}{\partial y_3} - \frac{1}{h^2_1}\frac{ \partial h_1}{\partial y_3}\frac{\partial T_{1}}{\partial y_1}- \frac{1}{h^2_2}\frac{\partial h_2}{\partial y_3}\frac{\partial T_{2}}{\partial y_2}\right) \\- & {} \frac{T_{3}}{h_3^2}\left[ \frac{1}{h_1^2}\left\{ \left( \frac{\partial h_1}{\partial y_3}\right) ^2+\left( \frac{\partial h_3}{\partial y_1}\right) ^2\right\} + \frac{1}{h_2^2}\left\{ \left( \frac{\partial h_2}{\partial y_3}\right) ^2+\left( \frac{\partial h_3}{\partial y_2}\right) ^2\right\} \right] \\+ & {} T_{1}\left[ \frac{1}{h_3h_1}\left\{ \frac{\partial }{\partial y_3}\left( \frac{1}{h_3}\frac{\partial h_3}{\partial y_1} \right) - \frac{\partial }{\partial y_3}\left( \frac{1}{h_1}\frac{\partial h_1}{\partial y_1} \right) \right\} + \frac{h_1}{h_3}\frac{\partial }{\partial y_3}\left( \frac{1}{h_1^2h_2}\frac{\partial h_2}{\partial y_1} \right) \right] \\+ & {} T_{2}\left[ \frac{1}{h_3h_2}\left\{ \frac{\partial }{\partial y_3}\left( \frac{1}{h_3}\frac{\partial h_3}{\partial y_2} \right) - \frac{\partial }{\partial y_3}\left( \frac{1}{h_2}\frac{\partial h_2}{\partial y_2} \right) \right\} + \frac{h_2}{h_3}\frac{\partial }{\partial y_3}\left( \frac{1}{h_2^2h_1}\frac{\partial h_1}{\partial y_2} \right) \right] . \end{aligned}$$

Now, we consider the important cases where the surface $\Gamma$ is spherical or spheroidal. The foregoing formulae are now specified in detail.

Spherical coordinate system

First, if the surface $\Gamma$ is spherical, the orthogonal curvilinear coordinate system described above becomes the system of spherical coordinates $(r,\theta ,\phi )$, where $y_{1}\equiv r\in [0,+\infty ]$ is the radial coordinate, $y_{3}\equiv \phi \in [0,2\pi ]$ is the azimuthal angle and $y_{2}\equiv \theta \in [0,\pi ]$ is the elevation angle with

$$\begin{aligned} r=\sqrt{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}},\quad \tan {\theta }=\sqrt{x_{1}^{2}+x_{2}^{2}}/x_{3},\quad \tan {\phi }=x_{2}/x_{1} \end{aligned}$$

(85)

or inversely,

$$\begin{aligned} x_{1}=r\cos \phi \sin \theta ,\quad x_{2}=r\sin \phi \sin \theta ,\quad x_{3}=r\cos \theta . \end{aligned}$$

(86)

This spherical coordinate system $(r,\theta ,\phi )$ is associated with the corresponding spherical orthonormal basis $\{\mathbf {f}_{r},\mathbf {f}_{\theta },\mathbf {f}_{\phi }\}$ given by

$$\begin{aligned} \mathbf {f}_{1}\equiv \mathbf {f}_{r}= & {} \sin \theta (\cos \phi \mathbf {j}_{1}+\sin \phi \mathbf {j}_{2})+\cos \theta \mathbf {j}_{3}, \nonumber \\ \mathbf {f}_{2}\equiv \mathbf {f}_{\theta }= & {} \cos \theta (\cos \phi \mathbf {j}_{1}+\sin \phi \mathbf {j}_{2})-\sin \theta \mathbf {j}_{3},\\ \mathbf {f}_{3}\equiv \mathbf {f}_{\phi }= & {} -\sin \phi \mathbf {j}_{1}+\cos \phi \mathbf {j}_{2}. \nonumber \end{aligned}$$

(87)

The metric coefficients of the spherical coordinate system $(r, \phi , \theta )$ take the simple form

$$\begin{aligned} h_{1}\equiv h_{r}=1,\quad h_{2}\equiv h_{\theta }=r,\quad h_{3}\equiv h_{\phi }=r\sin \theta . \end{aligned}$$

(88)

The differential operators for $T(r,\theta ,\phi )$ and $\mathbf {T}(r,\theta ,\phi )$ take the following forms

• Gradient of the scalar function $T(r,\theta ,\phi )$

  $$\begin{aligned} \nabla T = \frac{\partial T }{\partial r}\mathbf {f}_{r}+\frac{1}{r}\frac{\partial T}{\partial \theta } \mathbf {f}_{\theta }+\frac{1}{r\sin \theta }\frac{\partial T}{\partial \phi }\mathbf {f}_{\phi }; \end{aligned}$$

  (89)

• Laplacian of the scalar function $T(r,\theta ,\phi )$

  $$\begin{aligned} \varDelta T = \frac{\partial ^2 T }{\partial r^2} + \frac{2}{r}\frac{\partial T}{\partial r} + \frac{1}{r^2}\frac{\partial ^2 T}{\partial ^2 \theta } + \frac{1}{r^2\tan \theta }\frac{\partial T}{\partial \theta } + \frac{1}{r^2\sin ^2\theta }\frac{\partial ^2 T}{\partial \phi ^2}; \end{aligned}$$

  (90)

• Divergence of the vector function $\mathbf {T}(r,\theta ,\phi )$

  $$\begin{aligned} \nabla \cdot \mathbf {T} = \frac{\partial T_r}{\partial r} + \frac{2T_r}{r} + \frac{1}{r}\frac{\partial T_{\theta }}{\partial \theta } + \frac{T_{\theta }}{r\tan \theta }+\frac{1}{r\sin \theta }\frac{\partial T_{\phi }}{\partial \phi }; \end{aligned}$$

  (91)

• Laplacian of the vector function $\mathbf {T}(r,\theta ,\phi )$

  $$\begin{aligned} \varDelta \mathbf {T} = \{\varDelta \mathbf {T}\}_{r}\mathbf {f}_{r}+\{\varDelta \mathbf {T}\}_{\theta }\mathbf {f}_{\theta } + \{\varDelta \mathbf {T}\}_{\phi }\mathbf {f}_{\phi } \end{aligned}$$

  (92)

  where

  $$\begin{aligned} \{\varDelta \mathbf {T}\}_{r}= & {} \varDelta T_{r} - \frac{2}{r^2}T_r - \frac{2\cot \theta }{r^2}T_{\theta } - \frac{2}{r^2}\frac{\partial T_{\theta }}{\partial \theta } - \frac{2}{r^2\sin \theta }\frac{\partial T_{\phi }}{\partial \phi };\\ \{\varDelta \mathbf {T}\}_{\theta }= & {} \varDelta T_{\theta } + \frac{2}{r^2}\frac{\partial T_r}{\partial \theta } - \frac{T_{\theta }}{r^2\sin ^2\theta } - \frac{2\cos \theta }{r^2\sin ^2\theta }\frac{\partial T_{\phi }}{\partial \phi }; \\ \{\varDelta \mathbf {T}\}_{\phi }= & {} \varDelta T_{\phi } + \frac{2}{r^2\sin \theta }\frac{\partial T_r}{\partial \phi } - \frac{T_{\phi }}{r^2\sin ^2\theta } + \frac{2\cos \theta }{r^2\sin ^2\theta }\frac{\partial T_{\theta }}{\partial \phi }. \end{aligned}$$

Prolate spheroidal coordinate system

Second, if the surface $\Gamma$ has a prolate spheroidal form, the system of orthogonal curvilinear coordinates described above transforms to the one of prolate spheroidal coordinates $(\alpha ,\beta ,\gamma )$ with $y_{1}\equiv \alpha \in [0,+\infty ]$, $y_{3}\equiv \gamma \in [0,2\pi ]$ and $y_{2}\equiv \beta \in [0,\pi ]$. By defining some additional notations as follows:

$$\begin{aligned} {\rho }=\cos \beta ,\;\bar{{\rho }}=\sqrt{1-{\rho }^{2}}=\sin \beta ,\;\mu =\cosh \alpha ,\;\bar{\mu }=\sqrt{\mu ^{2}-1}=\sinh \alpha \end{aligned}$$

(93)

where b and a ($a>b$, or equivalently $w=a/b>1$) are the equatorial radius and the distance from center to pole along the symmetry axis of the spheroidal surface, respectively. The connection between the prolate spheroidal coordinates $(\alpha ,\beta ,\gamma )$ and the Cartesian coordinates $(x_{1},x_{2},x_{3})$ is expressed by

$$\begin{aligned} x_{1}=c\bar{{\rho }}\bar{\mu }\cos \gamma ,\quad x_{2}=c\bar{{\rho }}\bar{\mu }\sin \gamma ,\quad x_{3}=c{\rho }\mu \end{aligned}$$

(94)

where $c=a/\mu$ denotes the distance from the focal point to the center of spheroidal surface. The prolate spheroidal coordinate system $(\alpha ,\beta ,\gamma )$ is relative to the corresponding prolate spheroidal orthonormal basis $\{\mathbf {f}_{\alpha },\mathbf {f}_{\beta },\mathbf {f}_{\gamma }\}$ by

$$\begin{aligned} \mathbf {f}_{1}\equiv \mathbf {f}_{\alpha }=\frac{1}{\sqrt{\bar{{\rho }}^{2}+\bar{\mu }^{2}}}(\mu \bar{{\rho }}\cos \gamma \mathbf {j}_{1}+\mu \bar{{\rho }}\sin \gamma \mathbf {j}_{2}+\bar{\mu }{\rho }\mathbf {j}_{3}), \nonumber \\ \mathbf {f}_{2}\equiv \mathbf {f}_{\beta }=\frac{1}{\sqrt{\bar{{\rho }}^{2}+\bar{\mu }^{2}}}(\bar{\mu }{\rho }\cos \gamma \mathbf {j}_{1}+\bar{\mu }{\rho }\sin \gamma \mathbf {j}_{2}-\mu \bar{{\rho }}\mathbf {j}_{3}),\\ \mathbf {f}_{3}\equiv \mathbf {f}_{\gamma }=-\sin \gamma \mathbf {j}_{1}+\cos \gamma \mathbf {j}_{2}. \nonumber \end{aligned}$$

(95)

The metric coefficients of the prolate spheroidal coordinate system $(\alpha ,\beta ,\gamma )$ are given by

$$\begin{aligned} h_{1}\equiv h_{\alpha }= & {} c\sqrt{\mu ^{2}-{\rho }^{2}}\equiv 1/h,\quad h_{2}\equiv h_{\beta }=c\sqrt{\mu ^{2}-{\rho }^{2}}\equiv 1/h, \nonumber \\ h_{3}\equiv h_{\gamma }= & {} c\bar{\mu }\bar{{\rho }}\equiv 1/\bar{h}. \end{aligned}$$

(96)

The differential operators for $T(\alpha ,\beta ,\gamma )$ and $\mathbf {T}(\alpha ,\beta ,\gamma )$ are written in the prolate spheroidal coordinate system $(\alpha ,\beta ,\gamma )$ by

• Gradient of the scalar function $T(\alpha ,\beta ,\gamma )$

  $$\begin{aligned} \nabla T =\frac{1}{c}\sqrt{\frac{\mu ^2-1}{\mu ^2 - {\rho }^2}} \frac{\partial T }{\partial \mu }\mathbf {f}_{\alpha } - \frac{1}{c}\sqrt{\frac{1-{\rho }^2}{\mu ^2 - {\rho }^2}} \frac{\partial T }{\partial {\rho }}\mathbf {f}_{\beta }+\frac{1}{c\sqrt{(\mu ^2-1)(1-{\rho }^2)}}\frac{\partial T }{\partial \phi }\mathbf {f}_{\gamma }; \end{aligned}$$

  (97)

• Laplacian of the scalar function $T(\alpha ,\beta ,\gamma )$

  $$\begin{aligned} \varDelta T= & {} \frac{1}{c^2(\mu ^2-{\rho }^2)}\left\{ \frac{\partial }{\partial \mu }\left[ (\mu ^2-1)\frac{\partial T}{\partial \mu }\right] +\frac{\partial }{\partial {\rho }}\left[ (1-{\rho }^2)\frac{\partial T}{\partial {\rho }}\right] \right\} \nonumber \\+ & {} \frac{1}{c^2(\mu ^2-1)(1-{\rho }^2)}\frac{\partial ^2 T }{\partial \gamma ^2}; \end{aligned}$$

  (98)

• Divergence of the vector function $\mathbf {T}(\alpha ,\beta ,\gamma )$

  $$\begin{aligned} \nabla \cdot \mathbf {T}= & {} \frac{1}{c(\mu ^2-{\rho }^2)}\left\{ \frac{\partial }{\partial \mu }\left[ T_{\alpha }\sqrt{(\mu ^2-1)(\mu ^2-{\rho }^2)}\right] \right. \nonumber \\+ & {} \left. \frac{\partial }{\partial {\rho }}\left[ T_{\beta }\sqrt{(1-{\rho }^2)(\mu ^2-{\rho }^2)}\right] \right\} +\frac{1}{c(\mu ^2-1)(1-{\rho }^2)}\frac{\partial T_{\gamma } }{\partial \gamma }; \end{aligned}$$

  (99)

• Laplacian of the vector function $\mathbf {T}(\alpha ,\beta ,\gamma )$

  $$\begin{aligned} \varDelta \mathbf {T} = \{\varDelta \mathbf {T}\}_{\alpha }\mathbf {f}_{\alpha }+\{\varDelta \mathbf {T}\}_{\beta }\mathbf {f}_{\beta } + \{\varDelta \mathbf {T}\}_{\gamma }\mathbf {f}_{\gamma } \end{aligned}$$

  (100)

  where

  $$\begin{aligned} \{\varDelta \mathbf {T}\}_{\alpha }= & {} \varDelta T_{\alpha } - \frac{1}{c^2(\mu ^2-{\rho }^2)}\left[ \frac{2\mu ^2(\mu ^2-1)+(1-{\rho }^2)}{(\mu ^2-1)(\mu ^2-{\rho }^2)}T_{\alpha }\right. \\+ & {} \left. \frac{2{\rho }\sqrt{(\mu ^2-1)(1-{\rho }^2)}}{\mu ^2-{\rho }^2}\frac{\partial T_{\beta }}{\partial \mu }+\frac{2\mu \sqrt{(\mu ^2-1)(1-{\rho }^2)}}{\mu ^2-{\rho }^2}\frac{\partial T_{\beta }}{\partial {\rho }}\right. \\- & {} \left. \frac{2\mu {\rho }}{\mu ^2-{\rho }^2}\sqrt{\frac{\mu ^2-1}{1-{\rho }^2}}T_{\beta }+\frac{2\mu }{\mu ^2-1}\sqrt{\frac{\mu ^2-{\rho }^2}{1-{\rho }^2}}\frac{\partial T_{\gamma }}{\partial \gamma } \right] ; \\ \{\varDelta \mathbf {T}\}_{\beta }= & {} \varDelta T_{\beta } - \frac{1}{c^2(\mu ^2-{\rho }^2)}\left[ \frac{(\mu ^2-1)+2{\rho }^2(1-{\rho }^2)}{(1-{\rho }^2)(\mu ^2-{\rho }^2)}T_{\beta }\right. \\- & {} \left. \frac{2{\rho }\sqrt{(\mu ^2-1)(1-{\rho }^2)}}{\mu ^2-{\rho }^2}\frac{\partial T_{\alpha }}{\partial \alpha }-\frac{2\mu \sqrt{(\mu ^2-1)(1-{\rho }^2)}}{\mu ^2-{\rho }^2}\frac{\partial T_{\alpha }}{\partial {\rho }}\right. \\- & {} \left. \frac{2\mu {\rho }}{\mu ^2-{\rho }^2}\sqrt{\frac{1-{\rho }^2}{\mu ^2-1}}T_{\beta }-\frac{2{\rho }}{1-{\rho }^2}\sqrt{\frac{\mu ^2-{\rho }^2}{\mu ^2-1}}\frac{\partial T_{\gamma }}{\partial \gamma } \right] ;\\ \{\varDelta \mathbf {T}\}_{\gamma }= & {} \varDelta T_{\gamma } - \frac{1}{c^2(\mu ^2-{\rho }^2)}\left[ \frac{\mu ^2-{\rho }^2}{(\mu ^2-1)(1-{\rho }^2)}T_{\gamma }\right. \\- & {} \left. \frac{2\mu }{\mu ^2-1}\sqrt{\frac{\mu ^2-{\rho }^2}{1-{\rho }^2}}\frac{\partial T_{\alpha }}{\partial \gamma }+\frac{2{\rho }}{1-{\rho }^2}\sqrt{\frac{\mu ^2-{\rho }^2}{\mu ^2-1}}\frac{\partial T_{\beta }}{\partial \gamma }\right] . \end{aligned}$$

Appendix 2: Solutions for Two Coupled Stokes–Darcy Problems Used in the First- and Second-Scale Homogenizations

In this appendix, we briefly present the method to determine the expressions of the velocity and pressure fields of the fluid within the solid and fluid domains. For more details, the reader can refer to Tran et al. (2022).

Beginning with the solid domain and starting from the fact that the fluid flow through it is assumed to be incompressible and its velocity–pressure relation obeys to the Darcy’s law, it can be shown that the pressure solution field within the solid domain must satisfy the Laplace equation. This implies that the pressure solution field within the solid domain can be expressed as a scalar harmonic function. By accounting for the fact that the gradient pressure vector $\mathbf {G}^{0}$ at infinity is prescribed, the pressure solution field for the coupled Stokes–Darcy problem of the first- or second-scale homogenization is, respectively, expressed, in the prolate spheroidal coordinate system $(\alpha ,\beta ,\gamma )$, as in Eq. (45) or (63). When the expression of the pressure solution field is obtained, the fluid velocity field can be determined directly by Darcy’s law as provided in Eq. (47) and

$$\begin{aligned} u^{(s)}_{\beta }(\mu ,{\rho },\gamma )= & {} \frac{K}{\sigma }\sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}} \left[ -G_{3}^{0}P_{1}(\mu )P^{\prime }_{1}({\rho }) - (G_{1}^{0}\cos \gamma \right. \nonumber \\+ & {} \left. G_{2}^{0}\sin \gamma )P^{1}_{1}(\mu )P_{1}^{1\prime }({\rho }) + \sum _{n=0}^{\infty }a^{(s)}_{n}Q_{n}(\mu )P^{\prime }_{n}({\rho })\right. \nonumber \\+ & {} \left. \sum _{n=1}^{\infty }(b^{(s)}_{n}\cos \gamma +c^{(s)}_{n}\sin \gamma )Q_{n}^{1}(\mu )P_{n}^{1\prime }({\rho }) \right] , \end{aligned}$$

(101)

$$\begin{aligned} u^{(s)}_{\gamma }(\mu ,{\rho },\gamma )= & {} -\frac{K}{\sigma \sqrt{(\mu ^2-{\rho }^2)(1-{\rho }^2)}}\left[ - (G_{1}^{0}\cos \gamma - G_{2}^{0}\sin \gamma )P^{1}_{1}(\mu )P_{1}^{1}({\rho })\right. \nonumber \\+ & {} \left. \sum _{n=1}^{\infty }(-b^{(s)}_{n}\sin \gamma +c^{(s)}_{n}\cos \gamma )Q_{n}^{1}(\mu )P_{n}^{1}({\rho }) \right] \end{aligned}$$

(102)

for the coupled Stokes–Darcy problem of the first-scale homogenization. Similarly, the fluid velocity field can be expressed as Eq. (65) and

$$\begin{aligned} U^{(s)}_{\beta }(\mu ,{\rho },\gamma )= & {} \frac{K}{\sigma }\sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}} \left[ -G_{3}^{0}P_{1}(\mu )P^{\prime }_{1}({\rho }) - (G_{1}^{0}\cos \gamma \right. \nonumber \\+ & {} \left. G_{2}^{0}\sin \gamma )P^{1}_{1}(\mu )P_{1}^{1\prime }({\rho }) + \sum _{n=0}^{\infty }A^{(s)}_{n}Q_{n}(\mu )P^{\prime }_{n}({\rho })\right. \nonumber \\+ & {} \left. \sum _{n=1}^{\infty }(B^{(s)}_{n}\cos \gamma +C^{(s)}_{n}\sin \gamma )Q_{n}^{1}(\mu )P_{n}^{1\prime }({\rho }) \right] , \end{aligned}$$

(103)

$$\begin{aligned} U^{(s)}_{\gamma }(\mu ,{\rho },\gamma )= & {} -\frac{K}{\sigma \sqrt{(\mu ^2-{\rho }^2)(1-{\rho }^2)}}\left[ - (G_{1}^{0}\cos \gamma - G_{2}^{0}\sin \gamma )P^{1}_{1}(\mu )P_{1}^{1}({\rho })\right. \nonumber \\+ & {} \left. \sum _{n=1}^{\infty }(-B^{(s)}_{n}\sin \gamma +C^{(s)}_{n}\cos \gamma )Q_{n}^{1}(\mu )P_{n}^{1}({\rho }) \right] \end{aligned}$$

(104)

for the coupled Stokes–Darcy problem of the second-scale homogenization.

Concerning the fluid domain, by applying the method based on the Papkovich–Neuber formulation which is proposed initially by Papkovich (1932) and Neuber (1934) for a three-dimensional elasticity problem and then extended to a Stokes flow problem by Tran-Cong and Blake (1982), the fluid pressure and velocity solution fields within the fluid domain can be expressed in terms of both a scalar harmonic function $\chi (\mathbf {x})$ verifying $\varDelta \chi (\mathbf {x}) = 0$ and a harmonic vector $\mathbf {\Psi }(\mathbf {x})$ satisfying $\varDelta \mathbf {\Psi }(\mathbf {x}) = \mathbf {0}$ as follows:

$$\begin{aligned} \mathbf {u}^{(f)}(\mathbf {x})= & {} \nabla (\mathbf {x}\cdot \mathbf {\Psi }+\chi )-2\mathbf {\Psi }, \end{aligned}$$

(105)

$$\begin{aligned} p^{(f)}(\mathbf {x})= & {} 2\sigma \nabla \cdot \mathbf {\Psi }. \end{aligned}$$

(106)

Relative to the prolate spheroidal coordinate system $(\alpha ,\beta ,\gamma )$, the scalar harmonic function $\chi (\mu ,{\rho },\gamma )$ and the harmonic vector $\mathbf {\Psi }(\mu ,{\rho },\gamma )$ can be expressed as follows:

$$\begin{aligned} \chi (\mu ,{\rho },\gamma )= & {} c\sum _{l=0}^{\infty }\sum _{m=0}^{l}\left( D^{(fp)}_{lm}\cos m\gamma + d^{(fp)}_{lm}\sin m\gamma \right) P_{l}^{m}(\mu )P_{l}^{m}({\rho }) \nonumber \\+ & {} c\sum _{l=0}^{\infty }\sum _{m=0}^{l}\left( D^{(fq)}_{lm}\cos m\gamma + d^{(fq)}_{lm}\sin m\gamma \right) Q_{l}^{m}(\mu )P_{l}^{m}({\rho }), \end{aligned}$$

(107)

$$\begin{aligned} \Psi _{\alpha }(\mu ,{\rho },\gamma )= & {} \sum _{l=0}^{\infty }\sum _{m=0}^{l}\left[ \mu \sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}}\cos \gamma \left( A^{(fp)}_{lm}\cos m\gamma + a^{(fp)}_{lm}\sin m\gamma \right) \right. \nonumber \\+ & {} \left. \mu \sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}}\sin \gamma \left( B^{(fp)}_{lm}\cos m\gamma + b^{(fp)}_{lm}\sin m\gamma \right) \right. \nonumber \\+ & {} \left. {\rho }\sqrt{\frac{\mu ^2-1}{\mu ^2-{\rho }^2}}\left( C^{(fp)}_{lm}\cos m\gamma + c^{(fp)}_{lm}\sin m\gamma \right) \right] P_{l}^{m}(\mu )P_{l}^{m}({\rho }) \nonumber \\+ & {} \sum _{l=0}^{\infty }\sum _{m=0}^{l}\left[ \mu \sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}}\cos \gamma \left( A^{(fq)}_{lm}\cos m\gamma + a^{(fq)}_{lm}\sin m\gamma \right) \right. \nonumber \\+ & {} \left. \mu \sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}}\sin \gamma \left( B^{(fq)}_{lm}\cos m\gamma + b^{(fq)}_{lm}\sin m\gamma \right) \right. \nonumber \\+ & {} \left. {\rho }\sqrt{\frac{\mu ^2-1}{\mu ^2-{\rho }^2}}\left( C^{(fq)}_{lm}\cos m\gamma + c^{(fq)}_{lm}\sin m\gamma \right) \right] Q_{l}^{m}(\mu )P_{l}^{m}({\rho }), \end{aligned}$$

(108)

$$\begin{aligned} \Psi _{\beta }(\mu ,{\rho },\gamma )= & {} \sum _{l=0}^{\infty }\sum _{m=0}^{l}\left[ {\rho }\sqrt{\frac{\mu ^2-1}{\mu ^2-{\rho }^2}}\cos \gamma \left( A^{(fp)}_{lm}\cos m\gamma + a^{(fp)}_{lm}\sin m\gamma \right) \right. \nonumber \\+ & {} \left. {\rho }\sqrt{\frac{\mu ^2-1}{\mu ^2-{\rho }^2}}\sin \gamma \left( B^{(fp)}_{lm}\cos m\gamma + b^{(fp)}_{lm}\sin m\gamma \right) \right. \nonumber \\- & {} \left. \mu \sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}}\left( C^{(fp)}_{lm}\cos m\gamma + c^{(fp)}_{lm}\sin m\gamma \right) \right] P_{l}^{m}(\mu )P_{l}^{m}({\rho }) \nonumber \\+ & {} \sum _{l=0}^{\infty }\sum _{m=0}^{l}\left[ {\rho }\sqrt{\frac{\mu ^2-1}{\mu ^2-{\rho }^2}}\cos \gamma \left( A^{(fq)}_{lm}\cos m\gamma + a^{(fq)}_{lm}\sin m\gamma \right) \right. \nonumber \\+ & {} \left. {\rho }\sqrt{\frac{\mu ^2-1}{\mu ^2-{\rho }^2}}\sin \gamma \left( B^{(fq)}_{lm}\cos m\gamma + b^{(fq)}_{lm}\sin m\gamma \right) \right. \nonumber \\- & {} \left. \mu \sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}}\left( C^{(fq)}_{lm}\cos m\gamma + c^{(fq)}_{lm}\sin m\gamma \right) \right] Q_{l}^{m}(\mu )P_{l}^{m}({\rho }), \end{aligned}$$

(109)

$$\begin{aligned} \Psi _{\gamma }(\mu ,{\rho },\gamma )= & {} \sum _{l=0}^{\infty }\sum _{m=0}^{l}\left[ -\sin \gamma \left( A^{(fp)}_{lm}\cos m\gamma + a^{(fp)}_{lm}\sin m\gamma \right) \right. \nonumber \\+ & {} \left. \cos \gamma \left( B^{(fp)}_{lm}\cos m\gamma + b^{(fp)}_{lm}\sin m\gamma \right) \right] P_{l}^{m}(\mu )P_{l}^{m}({\rho }) \nonumber \\+ & {} \sum _{l=0}^{\infty }\sum _{m=0}^{l}\left[ -\sin \gamma \left( A^{(fq)}_{lm}\cos m\gamma + a^{(fq)}_{lm}\sin m\gamma \right) \right. \nonumber \\+ & {} \left. \cos \gamma \left( B^{(fq)}_{lm}\cos m\gamma + b^{(fq)}_{lm}\sin m\gamma \right) \right] P_{l}^{m}(\mu )P_{l}^{m}({\rho }). \end{aligned}$$

(110)

In these equations, $A^{(fp)}_{lm}$, $B^{(fp)}_{lm}$, $C^{(fp)}_{lm}$, $D^{(fp)}_{lm}$, $A^{(fq)}_{lm}$, $B^{(fq)}_{lm}$, $C^{(fq)}_{lm}$, $D^{(fq)}_{lm}$ with $l \ge m \ge 0$ and $a^{(fp)}_{lm}$, $b^{(fp)}_{lm}$, $c^{(fp)}_{lm}$, $d^{(fp)}_{lm}$, $a^{(fq)}_{lm}$, $b^{(fq)}_{lm}$, $c^{(fq)}_{lm}$, $d^{(fq)}_{lm}$ with $l \ge m \ge 1$ are unknown constants to be determined from the interfacial fluid/solid conditions. By introducing Eqs. (107)-(110) into Eqs. (105) and (106) and by accounting for the differential operators specified in Appendix 1 in the prolate spheroidal coordinate system $(\alpha ,\beta ,\gamma )$, we obtain, for the coupled Stokes–Darcy problem of the first-scale homogenization, the expressions for the fluid pressure and velocity fields within the fluid domain as follows:

$$\begin{aligned}&p^{(f)}(\mu ,{\rho },\gamma ) =\frac{2\sigma }{c}\sum _{l=0}^{\infty }\sum _{m=0}^{l}\left\{ \frac{\sqrt{(\mu ^2-1)(1-{\rho }^2)}}{(\mu ^2-{\rho }^2)}\right. \nonumber \\&\times \left. \left[ \mu P_{l}^{m\prime }(\mu )P_{l}^{m}({\rho })-{\rho }P_{l}^{m}(\mu )P_{l}^{m\prime }({\rho })\right] \right. \nonumber \\&\times \left. \left[ \cos \gamma \left( A^{(fp)}_{lm}\cos m\gamma + a^{(fp)}_{lm}\sin m\gamma \right) +\sin \gamma \left( B^{(fp)}_{lm}\cos m\gamma + b^{(fp)}_{lm}\sin m\gamma \right) \right] \right. \nonumber \\&+\left. \frac{1}{\mu ^2-{\rho }^2}\left[ {\rho }(\mu ^2-1)P_{l}^{m\prime }(\mu )P_{l}^{m}({\rho })+\mu (1-{\rho }^2)P_{l}^{m}(\mu )P_{l}^{m\prime }({\rho })\right] \right. \nonumber \\&\times \left. \left( C^{(fp)}_{lm}\cos m\gamma + c^{(fp)}_{lm}\sin m\gamma \right) -\frac{m}{\sqrt{(\mu ^2-1)(1-{\rho }^2)}}P_{l}^{m}(\mu )P_{l}^{m}({\rho })\right. \nonumber \\&\times \left. \left[ \sin \gamma \left( a^{(fp)}_{lm}\cos m\gamma -A^{(fp)}_{lm}\sin m\gamma \right) -\cos \gamma \left( b^{(fp)}_{lm}\cos m\gamma - B^{(fp)}_{lm}\sin m\gamma \right) \right] \right\} , \nonumber \\&+\frac{2\sigma }{c}\sum _{l=0}^{\infty }\sum _{m=0}^{l}\left\{ \frac{\sqrt{(\mu ^2-1)(1-{\rho }^2)}}{(\mu ^2-{\rho }^2)}\left[ \mu Q_{l}^{m\prime }(\mu )P_{l}^{m}({\rho })-{\rho }Q_{l}^{m}(\mu )P_{l}^{m\prime }({\rho })\right] \right. \nonumber \\&\times \left. \left[ \cos \gamma \left( A^{(fq)}_{lm}\cos m\gamma + a^{(fq)}_{lm}\sin m\gamma \right) +\sin \gamma \left( B^{(fq)}_{lm}\cos m\gamma + b^{(fq)}_{lm}\sin m\gamma \right) \right] \right. \nonumber \\&+\left. \frac{1}{\mu ^2-{\rho }^2}\left[ {\rho }(\mu ^2-1)Q_{l}^{m\prime }(\mu )P_{l}^{m}({\rho })+\mu (1-{\rho }^2)Q_{l}^{m}(\mu )P_{l}^{m\prime }({\rho })\right] \right. \nonumber \\&\times \left. \left( C^{(fq)}_{lm}\cos m\gamma + c^{(fq)}_{lm}\sin m\gamma \right) -\frac{m}{\sqrt{(\mu ^2-1)(1-{\rho }^2)}}Q_{l}^{m}(\mu )P_{l}^{m}({\rho })\right. \nonumber \\&\times \left. \left[ \sin \gamma \left( a^{(fq)}_{lm}\cos m\gamma -A^{(fq)}_{lm}\sin m\gamma \right) -\cos \gamma \left( b^{(fq)}_{lm}\cos m\gamma - B^{(fq)}_{lm}\sin m\gamma \right) \right] \right\} \nonumber \\ \end{aligned}$$

(111)

$$\begin{aligned}&u_{\alpha }^{(f)}(\mu ,{\rho },\gamma ) =\sum _{l=0}^{\infty }\sum _{m=0}^{l}\left\{ \sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}}\left[ -\mu {\rho }_{l}^{m}(\mu )+(\mu ^2-1)P_{l}^{m\prime }(\mu )\right] P_{l}^{m}({\rho })\right. \nonumber \\&\times \left. \left[ \cos \gamma \left( A^{(fp)}_{lm}\cos m\gamma + a^{(fp)}_{lm}\sin m\gamma \right) +\sin \gamma \left( B^{(fp)}_{lm}\cos m\gamma + b^{(fp)}_{lm}\sin m\gamma \right) \right] \right. \nonumber \\&+\left. {\rho }\sqrt{\frac{\mu ^2-1}{\mu ^2-{\rho }^2}}\left[ -P_{l}^{m}(\mu )+\mu {\rho }_{l}^{m\prime }(\mu )\right] P_{l}^{m}({\rho })\left( C^{(fp)}_{lm}\cos m\gamma + c^{(fp)}_{lm}\sin m\gamma \right) \right. \nonumber \\&+ \left. \sqrt{\frac{\mu ^2-1}{\mu ^2-{\rho }^2}}P_{l}^{m\prime }(\mu )P_{l}^{m}({\rho })\left( D^{(fp)}_{lm}\cos m\gamma + d^{(fp)}_{lm}\sin m\gamma \right) \right\} \nonumber \\&+\sum _{l=0}^{\infty }\sum _{m=0}^{l}\left\{ \sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}}\left[ -\mu Q_{l}^{m}(\mu )+(\mu ^2-1)Q_{l}^{m\prime }(\mu )\right] P_{l}^{m}({\rho })\right. \nonumber \\&\times \left. \left[ \cos \gamma \left( A^{(fq)}_{lm}\cos m\gamma + a^{(fq)}_{lm}\sin m\gamma \right) +\sin \gamma \left( B^{(fq)}_{lm}\cos m\gamma + b^{(fq)}_{lm}\sin m\gamma \right) \right] \right. \nonumber \\&+\left. {\rho }\sqrt{\frac{\mu ^2-1}{\mu ^2-{\rho }^2}}\left[ -Q_{l}^{m}(\mu )+\mu Q_{l}^{m\prime }(\mu )\right] P_{l}^{m}({\rho })\left( C^{(fq)}_{lm}\cos m\gamma + c^{(fq)}_{lm}\sin m\gamma \right) \right. \nonumber \\&+ \left. \sqrt{\frac{\mu ^2-1}{\mu ^2-{\rho }^2}}Q_{l}^{m\prime }(\mu )P_{l}^{m}({\rho })\left( D^{(fq)}_{lm}\cos m\gamma + d^{(fq)}_{lm}\sin m\gamma \right) \right\} , \end{aligned}$$

(112)

$$\begin{aligned}&u_{\beta }^{(f)}(\mu ,{\rho },\gamma ) = -\sum _{l=0}^{\infty }\sum _{m=0}^{l}\left\{ \sqrt{\frac{\mu ^2-1}{\mu ^2-{\rho }^2}}\left[ {\rho }P_{l}^{m}({\rho })+(1-{\rho }^2)P_{l}^{m\prime }({\rho })\right] P_{l}^{m}(\mu )\right. \nonumber \\&\times \left. \left[ \cos \gamma \left( A^{(fp)}_{lm}\cos m\gamma + a^{(fp)}_{lm}\sin m\gamma \right) +\sin \gamma \left( B^{(fp)}_{lm}\cos m\gamma + b^{(fp)}_{lm}\sin m\gamma \right) \right] \right. \nonumber \\&+\left. \mu \sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}}\left[ -P_{l}^{m}({\rho })+{\rho }P_{l}^{m\prime }({\rho })\right] P_{l}^{m}(\mu )\left( C^{(fp)}_{lm}\cos m\gamma + c^{(fp)}_{lm}\sin m\gamma \right) \right. \nonumber \\&+ \left. \sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}}P_{l}^{m}(\mu )P_{l}^{m\prime }({\rho })\left( D^{(fp)}_{lm}\cos m\gamma + d^{(fp)}_{lm}\sin m\gamma \right) \right\} \nonumber \\&-\sum _{l=0}^{\infty }\sum _{m=0}^{l}\left\{ \sqrt{\frac{\mu ^2-1}{\mu ^2-{\rho }^2}}\left[ {\rho }P_{l}^{m}({\rho })+(1-{\rho }^2)P_{l}^{m\prime }({\rho })\right] Q_{l}^{m}(\mu )\right. \nonumber \\&\times \left. \left[ \cos \gamma \left( A^{(fq)}_{lm}\cos m\gamma + a^{(fq)}_{lm}\sin m\gamma \right) +\sin \gamma \left( B^{(fq)}_{lm}\cos m\gamma + b^{(fq)}_{lm}\sin m\gamma \right) \right] \right. \nonumber \\&+\left. \mu \sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}}\left[ -P_{l}^{m}({\rho })+{\rho }P_{l}^{m\prime }({\rho })\right] Q_{l}^{m}(\mu )\left( C^{(fq)}_{lm}\cos m\gamma + c^{(fq)}_{lm}\sin m\gamma \right) \right. \nonumber \\&+ \left. \sqrt{\frac{1-{\rho }^2}{\mu ^2-{\rho }^2}}Q_{l}^{m}(\mu )P_{l}^{m\prime }({\rho })\left( D^{(fq)}_{lm}\cos m\gamma + d^{(fq)}_{lm}\sin m\gamma \right) \right\} , \end{aligned}$$

(113)

$$\begin{aligned}&u_{\gamma }^{(f)}(\mu ,{\rho },\gamma ) = -\sum _{l=0}^{\infty }\sum _{m=0}^{l}\left\{ \sin \gamma \left( A^{(fp)}_{lm}\cos m\gamma + a^{(fp)}_{lm}\sin m\gamma \right) \right. \nonumber \\&-\left. \cos \gamma \left( B^{(fp)}_{lm}\cos m\gamma + b^{(fp)}_{lm}\sin m\gamma \right) +m\cos \gamma \left( a^{(fp)}_{lm}\cos m\gamma -A^{(fp)}_{lm}\sin m\gamma \right) \right. \nonumber \\&+\left. m\sin \gamma \left( b^{(fp)}_{lm}\cos m\gamma -B^{(fp)}_{lm}\sin m\gamma \right) \right. \nonumber \\&+ \left. \frac{m{\rho }\mu }{\sqrt{(\mu ^2-1)(1-{\rho }^2)}}\left( -C^{(fp)}_{lm}\sin m\gamma + c^{(fp)}_{lm}\cos m\gamma \right) \right. \nonumber \\&+\left. \frac{m}{\sqrt{(\mu ^2-1)(1-{\rho }^2)}}\left( -D^{(fp)}_{lm}\sin m\gamma + d^{(fp)}_{lm}\cos m\gamma \right) \right\} P_{l}^{m}(\mu )P_{l}^{m}({\rho }) \nonumber \\&-\sum _{l=0}^{\infty }\sum _{m=0}^{l}\left\{ \sin \gamma \left( A^{(fq)}_{lm}\cos m\gamma + a^{(fq)}_{lm}\sin m\gamma \right) \right. \nonumber \\&-\left. \cos \gamma \left( B^{(fq)}_{lm}\cos m\gamma + b^{(fq)}_{lm}\sin m\gamma \right) +m\cos \gamma \left( a^{(fq)}_{lm}\cos m\gamma -A^{(fq)}_{lm}\sin m\gamma \right) \right. \nonumber \\&+\left. m\sin \gamma \left( b^{(fq)}_{lm}\cos m\gamma -B^{(fq)}_{lm}\sin m\gamma \right) \right. \nonumber \\&+ \left. \frac{m{\rho }\mu }{\sqrt{(\mu ^2-1)(1-{\rho }^2)}}\left( -C^{(fq)}_{lm}\sin m\gamma + c^{(fq)}_{lm}\cos m\gamma \right) \right. \nonumber \\&+\left. \frac{m}{\sqrt{(\mu ^2-1)(1-{\rho }^2)}}\left( -D^{(fq)}_{lm}\sin m\gamma + d^{(fq)}_{lm}\cos m\gamma \right) \right\} Q_{l}^{m}(\mu )P_{l}^{m}({\rho }). \end{aligned}$$

(114)

In the coupled Stokes–Darcy problem corresponding to the second-scale homogenization, the fluid pressure and velocity fields, $P^{(f)}$ and $\mathbf {U}^{(f)}$, within the fluid domain, take the same expressions as in Eqs. (111)-(114). However, the requirement of the pressure and velocity of the fluid at the center of the spheroidal fluid-filled pore, i.e., $\mu =1$, to be finite implies that $A^{(fq)}_{lm} = B^{(fq)}_{lm} = C^{(fq)}_{lm} = D^{(fq)}_{lm}= a^{(fq)}_{lm}= b^{(fq)}_{lm} = c^{(fq)}_{lm} = d^{(fq)}_{lm} = 0$.

Appendix 3: Expression of the Classical Eshelby Permeability Tensor $\mathbf {S}$ for an Ellipsoidal Inclusion

This appendix is dedicated to specifying the expression of the classical Eshelby permeability tensor $\mathbf {S}$ for an ellipsoidal inclusion, with three axis lengths $2a_{1}$, $2a_{2}$ and $2a_{3}$ such that $0<a_{1}<a_{2}<a_{3}$, embedded in an infinite homogeneous isotropic medium of permeability k. By considering the case where the principal axes of lengths $2a_{1}$, $2a_{2}$ and $2a_{3}$ of the ellipsoidal inclusion are aligned along the directions defined by three orthonormal vectors $\mathbf {n}_{1}$, $\mathbf {n}_{2}$ and $\mathbf {n}_{3}$, the explicit expression of the classical Eshelby tensor is given by (see, e.g., Duan et al. (2006))

$$\begin{aligned} \mathbf {S}=\sum _{i=1}^{3}S_{ii}\mathbf {n}_{i}\otimes \mathbf {n}_{i} \end{aligned}$$

(115)

where

$$\begin{aligned}&S_{11}=\frac{1}{1-\lambda _{1}^{2}}-\frac{\lambda _{1}}{(1-\lambda _{1}^{2})\sqrt{1-\lambda _{1}^{2}\lambda _{2}^{2}}}E(\nu ,\kappa ), \nonumber \\&S_{33}=\frac{\lambda _{1}\lambda _{2}^{2}}{(1-\lambda _{1}^{2})\sqrt{1-\lambda _{1}^{2}\lambda _{2}^{2}}}[F(\nu ,\kappa )-(E(\nu ,\kappa )], \nonumber \\&S_{22}=1-S_{11}^{\mathcal {E}\omega }-S_{33}^{\mathcal {E}\omega }. \end{aligned}$$

(116)

In Eq. (116), $\lambda _{1}=a_{1}/a_{2}$ and $\lambda _{2}=a_{2}/a_{3}$; $F(\nu ,\kappa )$ and $E(\nu ,\kappa )$ are elliptic integrals of the first and second kinds defined by

$$\begin{aligned} F(\nu ,\kappa )=\int _{0}^{\nu }(1-\kappa ^{2}\sin ^{2}t)^{-1/2}\text {d}t,\quad E(\nu ,\kappa )=\int _{0}^{\nu }(1-\kappa ^{2}\sin ^{2}t)^{1/2}\text {d}t \end{aligned}$$

(117)

with

$$\begin{aligned} \nu =\arcsin \sqrt{1-\lambda _{1}^{2}\lambda _{2}^{2}},\quad \kappa =\sqrt{1-\lambda _{2}^{2}}\sqrt{1-\lambda _{1}^{2}\lambda _{2}^{2}}. \end{aligned}$$

(118)

In particular case of spheroidal inclusion with $w=a_{3}/a_{1}=a_{3}/a_{2}$, the expressions of $S_{11}^{\mathcal {E}}$, $S_{22}^{\mathcal {E}}$ and $S_{33}^{\mathcal {E}}$ reduce to

$$\begin{aligned} S_{11}=S_{22}=\frac{L(w)}{2},\quad S_{33}=1-L(w), \end{aligned}$$

(119)

where L(w) is defined by

$$\begin{aligned} L(w)=\left\{ \begin{array}{ll} \frac{w[\cos ^{-1}(w)-w\sqrt{1-w^{2}}]}{\sqrt{(1-w^{2})^{3}}} &{} \quad \text {for w<1,} \\ \frac{w[w\sqrt{w^{2}-1}-\cosh ^{-1}(w)]}{\sqrt{(w^{2}-1)^{3}}} &{} \quad \text {for w>1.} \end{array} \right. \end{aligned}$$

(120)

We recall that $w<1$ corresponds to an oblate spheroid whereas $w>1$ relative to a prolate spheroid. In particular, the expressions (119) for a spherical inclusion are considerably simplified and reduce to $S_{11}^{\mathcal {S}\omega }=S_{22}^{\mathcal {S}\omega }=S_{33}^{\mathcal {S}\omega }=\frac{1}{3}$.

Appendix 4: Derivation of the Self-consistency Condition (19)

We first consider an effective homogeneous and infinite permeable solid medium $\varOmega$ of external boundary $\partial \varOmega$ and permeability tensor $\mathbf {k}^{\text {micro}}$. Under the boundary condition (18), the velocity vector and pressure fields in $\varOmega$ are given by

$$\begin{aligned} p^{(0)}(\mathbf {x}) = -\mathbf {G}^{0}\cdot \mathbf {x},\quad \mathbf {u}^{(0)}(\mathbf {x}) = \frac{1}{\sigma }\mathbf {k}^{\text {micro}}\cdot \mathbf {G}^{0}. \end{aligned}$$

(121)

Consequently, the viscous dissipation $\mathcal {W}_{0}(\mathbf {G}^{0})$ of $\varOmega$ takes the following simple form

$$\begin{aligned} \mathcal {W}_{0}(\mathbf {G}^{0}) = \frac{1}{2}\int _{\varOmega }u^{(0)}_{i}(-p^{(0)}_{,i})\text {d}\mathbf {x} =\frac{1}{2\sigma }\text {vol}(\varOmega )\mathbf {G}^{0}\cdot \mathbf {k}^{\text {micro}}\cdot \mathbf {G}^{0}. \end{aligned}$$

(122)

After introducing the coated prolate spheroidal inclusion $\text {RVE}^{\text {n}-\mu }$ into $\varOmega$ and imposing the same boundary condition on $\partial \varOmega$ as before, the viscous dissipation $\mathcal {W}(\mathbf {G}^{0})$ is given by

$$\begin{aligned} \mathcal {W}(\mathbf {G}^{0}) = \frac{1}{2}\int _{\varOmega ^{(s)}}u^{(s)}_{i}(-p^{(s)}_{,i})\text {d}\mathbf {x} + \int _{\omega ^{(f)}}\sigma \varepsilon ^{(f)}_{ij}\varepsilon ^{(f)}_{ij}\text {d}\mathbf {x} \end{aligned}$$

(123)

where $\varepsilon ^{(f)}_{ij} = (u^{(f)}_{i,j}+u^{(f)}_{j,i})/2$ denotes the component of the strain-rate tensor of the fluid within $\omega ^{(f)}$.

It follows from Eqs. (122) and (123) that

$$\begin{aligned} 2(\mathcal {W}_{0}(\mathbf {G}^{0})-\mathcal {W}(\mathbf {G}^{0}))= & {} \int _{\varOmega ^{(s)}}(u^{(0)}_{i}+u^{(s)}_{i})(p^{(s)}_{,i}-p^{(0)}_{,i})\text {d}\mathbf {x} + \int _{\varOmega ^{(s)}}(u^{(s)}_{i}p^{(0)}_{,i}-u^{(0)}_{i}p^{(s)}_{,i})\text {d}\mathbf {x}\nonumber \\- & {} \int _{\omega ^{(f)}}2\sigma \varepsilon ^{(f)}_{ij}\varepsilon ^{(f)}_{ij}\text {d}\mathbf {x}-\int _{\omega ^{(f)}\cup \omega ^{(s)}}u^{(0)}_{i}p^{(0)}_{,i}\text {d}\mathbf {x}. \end{aligned}$$

(124)

By applying the divergence theorem and by taking into account that $\nabla \cdot \mathbf {u}^{(s)} = \nabla \cdot \mathbf {u}^{(0)} = 0$, it is immediate that

$$\begin{aligned} 2(\mathcal {W}_{0}(\mathbf {G}^{0})-\mathcal {W}(\mathbf {G}^{0}))= & {} \int _{\varOmega ^{(s)}}(u^{(s)}_{i}p^{(0)}_{,i}-u^{(0)}_{i}p^{(s)}_{,i})\text {d}\mathbf {x}+ \int _{\partial \varOmega }(u^{(0)}_{i}+u^{(s)}_{i})n_i(p^{(s)}-p^{(0)})\text {d}\mathbf {x}\nonumber \\- & {} \int _{\partial \text {RVE}^{\text {n}-\mu }}(u^{(0)}_{i}+u^{(s)}_{i})n_i(p^{(s)}-p^{(0)})\text {d}\mathbf {x}-\int _{\omega ^{(f)}}2\sigma \varepsilon ^{(f)}_{ij}\varepsilon ^{(f)}_{ij}\text {d}\mathbf {x}\nonumber \\- & {} \int _{\omega ^{(f)}\cup \omega ^{(s)}}u^{(0)}_{i}p^{(0)}_{,i}\text {d}\mathbf {x}. \end{aligned}$$

(125)

Accounting for the boundary condition $p^{(0)}(\mathbf {x}) = p^{(s)}(\mathbf {x}) = -\mathbf {G}^{0}\cdot \mathbf {x}$ with $\mathbf {x}\in \partial \varOmega$ and the Darcy’s law $\mathbf {u}^{(s)}(\mathbf {x}) = -\frac{1}{\sigma }\mathbf {k}^{\text {micro}}\cdot \nabla p^{(s)}(\mathbf {x})$ and $\mathbf {u}^{(0)}(\mathbf {x}) = -\frac{1}{\sigma }\mathbf {k}^{\text {micro}}\cdot \nabla p^{(0)}(\mathbf {x})$ with $\mathbf {x}\in \varOmega ^{(s)}$, it is clear that

$$\begin{aligned} \int _{\varOmega ^{(s)}}(u^{(s)}_{i}p^{(0)}_{,i}-u^{(0)}_{i}p^{(s)}_{,i})\text {d}\mathbf {x} = 0\quad \text {and}\quad \int _{\partial \varOmega }(u^{(0)}_{i}+u^{(s)}_{i})n_i(p^{(s)}-p^{(0)})\text {d}\mathbf {x} = 0. \end{aligned}$$

(126)

Once again, it follows from the divergence theorem and the incompressibility condition $\nabla \cdot \mathbf {u}^{(0)} = 0$ that

$$\begin{aligned} \int _{\partial \text {RVE}^{\text {n}-\mu }}u^{(0)}_{i}n_ip^{(0)}\text {d}\mathbf {x}-\int _{\omega ^{(f)}\cup \omega ^{(s)}}u^{(0)}_{i}p^{(0)}_{,i}\text {d}\mathbf {x} = 0. \end{aligned}$$

(127)

Substituting Eqs. (126) and (127) into Eq. (125), we have

$$\begin{aligned} 2(\mathcal {W}_{0}(\mathbf {G}^{0})-\mathcal {W}(\mathbf {G}^{0}))= & {} \int _{\partial \text {RVE}^{\text {n}-\mu }}(u^{(s)}_{i}n_ip^{(0)}-u^{(0)}_{i}n_ip^{(s)})\text {d}\mathbf {x}-\int _{\omega ^{(f)}}2\sigma \varepsilon ^{(f)}_{ij}\varepsilon ^{(f)}_{ij}\text {d}\mathbf {x}\nonumber \\- & {} \int _{\partial \text {RVE}^{\text {n}-\mu }}u^{(s)}_{i}n_ip^{(s)}\text {d}\mathbf {x}. \end{aligned}$$

(128)

On the other hand, we have

$$\begin{aligned} \int _{\omega ^{(f)}}2\sigma \varepsilon ^{(f)}_{ij}\varepsilon ^{(f)}_{ij}\text {d}\mathbf {x}= & {} \frac{\sigma }{2}\int _{\omega ^{(f)}}(u^{(f)}_{i,j}+u^{(f)}_{j,i})(u^{(f)}_{i,j}+u^{(f)}_{j,i})\text {d}\mathbf {x} = \sigma \int _{\omega ^{(f)}}(u^{(f)}_{i,j}u^{(f)}_{i,j}+u^{(f)}_{i,j}u^{(f)}_{j,i})\text {d}\mathbf {x}\nonumber \\= & {} \sigma \int _{\omega ^{(f)}}[(u^{(f)}_{i}u^{(f)}_{i,j})_{,j}-u^{(f)}_{i,jj}u^{(f)}_{i}+(u^{(f)}_{j}u^{(f)}_{i,j})_{,i}-u^{(f)}_{i,ji}u^{(f)}_{j}]\text {d}\mathbf {x}. \end{aligned}$$

(129)

Using the divergence theorem together with $\mathbf {u}^{(f)} = \mathbf {0}$ on $\partial \omega ^{(s)}$, $\sigma \varDelta \mathbf {u}^{(f)} = \nabla p^{(f)}$ and $\nabla \cdot \mathbf {u}^{(f)} = 0$ in $\omega ^{(f)}$, Eq. (129) is reduced to

$$\begin{aligned} \int _{\omega ^{(f)}}2\sigma \varepsilon ^{(f)}_{ij}\varepsilon ^{(f)}_{ij}\text {d}\mathbf {x}= & {} \int _{\partial \text {RVE}^{\text {n}-\mu }}[\sigma (u^{(f)}_{i,j}+u^{(f)}_{j,i})n_ju^{(f)}_{i}-u^{(f)}_{i}n_ip^{(f)}]\text {d}\mathbf {x} . \end{aligned}$$

(130)

By setting $\varvec{\tau }^{(f)} = \sigma [\nabla \mathbf {u}^{(f)}+\nabla ^{T}\mathbf {u}^{(f)}]$ and $\mathbf {t}^{(f)} = \varvec{\tau }^{(f)}\cdot \mathbf {n}$, it follows from Eq. (130) that

$$\begin{aligned} \int _{\omega ^{(f)}}2\sigma \varvec{\varepsilon }^{(f)}:\varvec{\varepsilon }^{(f)}\text {d}\mathbf {x}= & {} \int _{\partial \text {RVE}^{\text {n}-\mu }}(\varvec{\tau }^{(f)}\cdot \mathbf {n}-p^{(f)}\mathbf {n})\cdot \mathbf {u}^{(f)}\text {d}\mathbf {x} \nonumber \\= & {} \int _{\partial \text {RVE}^{\text {n}-\mu }}[\mathbf {n}\otimes \mathbf {n}\cdot \varvec{\tau }^{(f)}\cdot \mathbf {n}-p^{(f)}\mathbf {n}+(\mathbf {I}-\mathbf {n}\otimes \mathbf {n})\cdot \varvec{\tau }^{(f)}\cdot \mathbf {n}]\cdot \mathbf {u}^{(f)}\text {d}\mathbf {x} \nonumber \\= & {} \int _{\partial \text {RVE}^{\text {n}-\mu }}(\mathbf {n}\cdot \varvec{\tau }^{(f)}\cdot \mathbf {n}-p^{(f)})\mathbf {u}^{(f)}\cdot \mathbf {n}\text {d}\mathbf {x}\nonumber \\+ & {} \int _{\partial \text {RVE}^{\text {n}-\mu }}\mathbf {t}^{(f)}\cdot (\mathbf {I}-\mathbf {n}\otimes \mathbf {n})\cdot \mathbf {u}^{(f)}\text {d}\mathbf {x}. \end{aligned}$$

(131)

When the interfacial conditions (20)-(22) are adopted, Eq. (131) can be expressed in the following equivalent form

$$\begin{aligned} \int _{\omega ^{(f)}}2\sigma \varvec{\varepsilon }^{(f)}:\varvec{\varepsilon }^{(f)}\text {d}\mathbf {x}= & {} \int _{\partial \text {RVE}^{\text {n}-\mu }}-p^{(s)}\mathbf {u}^{(s)}\cdot \mathbf {n}\text {d}\mathbf {x}. \end{aligned}$$

(132)

By combining Eq. (128) with Eq. (132), we have

$$\begin{aligned} 2(\mathcal {W}_{0}(\mathbf {G}^{0})-\mathcal {W}(\mathbf {G}^{0})) =\int _{\partial \text {RVE}^{\text {n}-\mu }}(u^{(s)}_{i}n_ip^{(0)}-u^{(0)}_{i}n_ip^{(s)})\text {d}\mathbf {x}. \end{aligned}$$

(133)

Since this last equation, the self-consistency condition $\mathcal {W}_{0}(\mathbf {G}^{0}) = \mathcal {W}(\mathbf {G}^{0})$ can be recast into (19).