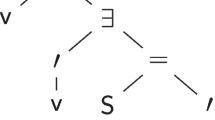Synthetic proofs

Abstract

This is a contribution to the idea that some proofs in first-order logic are synthetic. Syntheticity is understood here in its classical geometrical sense. Starting from Jaakko Hintikka’s original idea and Allen Hazen’s insights, this paper develops a method to define the ‘graphical form’ of formulae in monadic and dyadic fraction of first-order logic. Then a synthetic inferential step in Natural Deduction is defined. A proof is defined as synthetic if it includes at least one synthetic inferential step. Finally, it will be shown that the proposed definition is not sensitive to different ways of driving the same conclusion from the same assumptions.

1 Introduction

Whether logical reasoning is analytic or synthetic is an enduring question. Depending on the theories and techniques available to them at the time, different thinkers have offered a variety of responses. The persistence of the question can be explained by its dual nature, it consisting of both semantic and epistemological aspects. From a semantic point of view—thinking in a model-theoretic way—logical truths are tautologies; that is they are true in every logically possible valuation or scenario.¹ This understanding leads to an immediate and interesting epistemic question about logical truths: do such truths convey any information? Although many such truths seem to carry no new information, some do. Michael Dummett refers to this problem as “the tension between legitimacy and fruitfulness” of logical reasoning.²

If we accept that logical truths are analytic, and that some of these truths convey information, then the problem is how to explain this situation. A reasonable step to tackle this problem is to clarify different meanings of ‘analytic’ and ‘information’. In this paper, we consider three notions of analyticity, the first being tautologous or true in every logically possible scenario, with logic here being understood classically. The second notion takes analyticity as being justified in virtue of meaning. We call the first two notions of analyticity ‘semantic’.³ The third notion of analyticity takes ‘analytic’ as ‘being verified by analytic methods’. This notion is suggested by Hintikka⁴ and we call it ‘methodic analyticity’. The last notion of analyticity will be the main focus of this paper.

Information is an even vaguer concept as there are many understandings of it. A crucial distinction however is between subjective and objective accounts of information. If a given account of information is sensitive to agents, then it is subjective; otherwise it is objective. Bar-Hillel and Carnap (BH &C), for example, provide an objective account of information which they call ‘semantic information’.⁵ They argue that although logical truths could be informative in a subjective sense of the term, they are not semantically informative. So, following BH &C, one possible response to the tension between the legitimacy and fruitfulness of deduction is to claim that analytic truths do not really convey any information in an objective sense of the term, but they can be informative for anyone who is, say, new to logic.

In “Are Logical Truths Analytic”,⁶ Hintikka suggests that although all of the theorems in first-order logic (FOL) are analytic in the first sense, some of them are not in the third sense. He argues that some FOL truths can be verified only via synthetic rather than analytic proofs. His proof method is based on attempting to verify a formula in disjunctive normal form which is formed from assumptions and the negation of the conclusion of any given argument. On other occasions, Hintikka uses the same proof method, combined with a modified version of BH &C’s semantic account of information to argue for the informativity of some FOL truths. However, his proof method did not become vary popular and his account of information is too cumbersome.

In this paper, we primarily aim at reviving and modifying Hintikka’s idea that some logical truths, although analytic in the semantic sense, need to be verified via synthetic methods. A secondary aim for us will be to suggest an account of information which is objective and justifies the informativity of synthetic methods. In section two, we start with reviewing BH &C’s theory of semantic information and analyticity and explain why their account of information is objective and what the properties of such an account of information are. Then we outline how Hintikka’s idea of assigning information to steps of a proof method can have the same property as semantic information and can explain the informativity of some deductions in an objective manner. Section two will provide the philosophical motivation behind the other sections of this paper.

Next, in section three, we pursue Hintikka’s idea of synthetic verification method in the context of natural deduction (ND) systems.⁷ To understand synthetic proofs in the context of ND, we attempt to recreate the idea of synthetic geometric proofs in ND inspired by some of the ideas in the existing literature. In “Logic and Analyticity”,⁸ Allen Hazen explains Hintikka’s idea via a thought experiment of drawing dots and arrows to represent the steps of proving a synthetic argument in ND.⁹ We first expand Hintikka’s notion of degree by using Hazen’s idea to assign a graphical form to the monadic and dyadic fraction of FOL. Hazen represents variables as dots and relations as arrows. We give Hazen’s insights a graph-theoretic flavor by interpreting variables as vertices, monadic predicates as labels of the vertices, and dyadic predicates as labels of the edges connecting up to two vertices.

Then in the fourth section we use these graphical forms to define synthetic proof steps echoing the classical definition of synthetic geometrical proofs. An inference step is synthetic if it increases the number of graphical elements we need to consider in relation to each other. Inferential step is understood to include the sub-derivations with the premises of that step in their roots. We shall see that an increased number of vertices (variables) is not the only way an inference step can be synthetic; as an increased number of edges, the appearance of a different type of edge, or an additional label of a vertex can also make an inference step synthetic. Moreover, we will see that $\exists E$ is not the only inference rule that introduces fresh variables to the content of proofs.

Section five examines some examples of this process, and in the last section before the conclusion, we show that synthetic proof steps are necessary for proving synthetic argument: in other words, we cannot transform a synthetic proof to an analytic one in ND.

2 Semantic information and analyticity

Building on Carnap’s Logical Foundations of Probability, BH &C define the notion of semantic information for any given formal language. Let us consider a language with two monadic predicates $P_{1}$ and $P_{2}$, and a name a. All the possible scenarios in regard to this language are summarized in the following table:

$P_{1}a$	$P_{2}a$
1	1
1	0
0	1
0	0

Each row of the above table summarizes possible states of affairs in each scenario. According to BH &C, $P_{1}a \wedge P_{2}a$ provides us with the maximum information about the state of affairs in the first scenario and $P_{1}a \vee P_{2}a$ gives us the minimum information about that. They call $P_{1}a \vee P_{2}a$ a ‘content-element’. The set of the content elements of this language has three other members which are not difficult to guess. Now, provided that the language does not have any meaning postulates, that is a postulate that establishes logical connections between the elements of the language, given any expression, such as $P_{1}a$, rows in which it is false, it implies the content-elements of that row. The set of such content-elements is called the ‘content’ of $P_{1}a$. That is:¹⁰

$$\begin{aligned} Cont(P_{1}a) = \left\{ \lnot P_{1}a \vee P_{2}a , \lnot P_{1}a \vee \lnot P_{2}a \right\} \end{aligned}$$

As can be seen, each atomic element of the language has the half of content-elements as its content; any tautology of the language has none; and any contradiction of the language has all. BH &C take content as the information conveyed by any statement in question. They also define a quantitative measure for the amount of information conveyed by any statement in the language. They do so by employing a function called m that assigns a positive real number to each possible scenario (each row of the table) such that the sum of all these numbers is equal to 1. Then they define the amount of information conveyed by a statement like $P_{1}a$ as follows:¹¹

$$\begin{aligned} cont(P_{1}a) = m(\lnot P_{1}a) \end{aligned}$$

To summarize BH &C’s theory of semantic information informally, the amount of information conveyed by an expression, is the number assigned to the scenarios assuming its truth excludes from the possible states of affairs. In this setting, tautologies carry zero information. This is so because they are always true, and assuming their truth, does not exclude any scenario. On the other hand, contradictions are fully informative. Between these two extremes, there are what BH &C call ‘factual statements’. These statements are about things that could be otherwise without breaking laws of classical logic or contradicting the meaning postulates of the theory at hand.¹²

BH &C’s semantic account of information is objective, meaning that it is not agent-sensitive. This is so because it is built on a certain—in this case semantic—interpretation of the syntax. And syntax is something that everyone has equal access to. It also sits well with at least some of the ordinary uses of the term ‘information’. However, it denies any objective informativity for logical truths and this does not fit well with the ordinary use of information. For sure, arithmetic theorems are informative and they are built on a formal language very similar to the one used by BH &C. Of course their theory leaves room for what they call psychological information. But ‘psychological’ usually means ‘subjective’. Even if this is not the case, ‘psychological’ certainly does not capture the objectivity of arithmetical truths either. And it is hard to think the information we gain from arithmetical truth is subjective.¹³

Inspired by Kant’s ideas on arithmetic, on a number of occasions Hintikka points at the distinction between semantic analyticity and methodic analyticity.¹⁴ According to his reading of Kant, if we are forced to consider new elements in the course of a reasoning, that reasoning is synthetic. Classical examples of synthetic reasoning comprise some proofs in geometry in which we need to add extra geometrical elements such as lines, points, or circles to the original figure that we want to prove something about.¹⁵ Hintikka extends this notion to logical proofs; accordingly a logical truth is synthetic, if in the process of proving it, we are required to consider new individuals, that is individuals that are not explicit in the logical truth in question.

To define synthetic proofs,¹⁶ Hintikka first defines ‘the degree’ of a formula as the sum of the maximum number of nested quantifiers (the maximum depth of quantification), plus the number of free variables in that formula.¹⁷ Next, without being clear about which proof method he is using, he defines an inference step as synthetic when it increases the degree of a formula at hand by introducing a new variable or a nested quantifier to it, in the process of proving.¹⁸ Adding a first-order variable (bound or free) in a proof process is analogous to constructing a new element such as a line or a point in the process of proving a geometrical theorem.

The proof method that Hintikka most likely had in mind, was disproving the conjunction of assumptions and the negation of the conclusion expressed in Distributive Normal Form. The synthetic inferential steps that he considers are steps within this proof method.¹⁹ However, he argues that the above mentioned phenomenon is demonstrable in Natural Deduction (ND) systems too.²⁰ According to Hintikka, a version of the Existential Instantiation rule, with the more common name ‘existential elimination’ ($\exists E$), is responsible for introducing new variables to ND proofs.²¹ He also argues that to count the number of variables involved in an instance of the $\exists E$ inference step, we have to “count not only the free individual symbols which occur in the premises of this particular step but also all the ones that occur at earlier stages of the proof.”²²

Hintikka’s proof method did not become a popular method of theorem proving among logicians due to its complicated nature.²³ As a result, his definition of synthetic proofs has not attracted much attention. Also there have been doubts about whether his definition of synthetic proofs is demonstrable in other proof-theoretic systems.²⁴ To overcome these shortcomings, this paper pursues Hintikka’s idea in ND, a popular proof method.

Hintikka also attempted to explain how synthetic proofs are informative by adjusting Carnap and Bar Hillel’s semantic account of information and by using a notoriously complicated probabilistic theory of surface and depth information.²⁵ By pointing at the distinction between semantic and methodic analyticity, on one hand and attempting to modify BH &C’s account of semantic information on the other, Hintikka seems to pursue the goal of showing the objectivity of the information gained in the process of verifying some logical truths in two separate lines. However, in none of the works referred to in this paper, has he shown that the methodically synthetic proofs are the ones that increase our information about the objects the theorems are about. Bridging between methodically synthetic proofs and informative proofs is another ambition of this paper.

If we accept that the objectivity of BH &C’s account of information is due to its ties with syntax, and not the semantic nature of this tie, then an alternative strategy to show the informativity of some first-order theorems is to develop a syntactic definition of methodic analyticity first, and then develop a theory of information that explains the informativity of theorems verified using non-analytic (synthetic) methods. This is the strategy we shall follow in the coming sections. Our plan is to find an interpretation of ND derivations, following Hintikka’s insights about synthetic geometrical proofs and Hazen’s contributions to the discussion, that most resembles the synthetic proofs in geometry. After establishing such an interpretation, we propose an account of information based on this interpretation in the final section. In this way, we aim to meet the second ambition of this piece of work.

3 Graphical forms of first-order formulae

At the first step we set some intuitive rules for assigning graphical forms to formulae. These graphical forms are not intended to capture the full logical structure of a formula in the sense that Peirce’s existential graphs or recent works on combinatorial proofs do. They just provide us with what the formula is ‘about’ in a more structured manner than Hintikka’s notion of degree.²⁶ Charles Sanders Peirce invented a graphical presentation of FOL which is called the Beta system. There are different readings of Peirce’s notation and it has been shown that the Beta system is isomorphic to FOL.²⁷

Recent works on combinatorial proof-theory, starting from Girard’s proof nets,²⁸ represent proofs with graphs. Each vertex represents an application of an inference rule and edges of the graph represent formulae.²⁹ Even more recent works in this field, under the title of ‘proofs without syntax’ assign graphs to logical formulae.³⁰ In the case of propositional logic, atomic formulae and their negations label vertices, and the edges connect the vertices that their atomic formulae are conjoined. The conditional in the formulae is translated to the disjunction in the process of drawing the corresponding graph of a formula. In case of FOL, variables, predicates, and their negation label vertices. The edges connect the vertices labeled by existentially bound variables to all the vertices labeled by the variables, predicates, and their negation in the scope of that existentially bound variable. Edges also connect vertices labeled by conjoined predicates and the conditional is translated as mentioned before.

Investigating the insights combinatorial proofs can offer in philosophical studies is a very interesting topic for further research.³¹ However in what follows, we are about to suggest yet another graphical representation of first-order formulae. The new representation attempts to capture only non-logical parts of the first-order formulae; that is the parts which are not logical constants. This is, to some extent, what Hintikka attempted to do. Hintikka’s definition of the degree of a formula attempts to capture some non-logical aspects of formulae; namely, the number of variables. The other such aspects are the number of properties and the relations among variables. These can be read off the formulae, by paying attention to the parts which are not logical constants.

On different occasions, Hintikka defines the degree of a formula as the sum of the maximum number of nested quantifiers, plus the number of free variables.³² He explains that the degree of a formula defines what the formula is about.³³ Variables represent individuals, so the degree of a formula tells us the number of individuals the formula is about. However, more than this can be extracted from the non-logical vocabulary of a formula. Since our initial motivation is to find an account of information that explains the informativity of deduction, it serves our purpose better to extract more than ‘the number of individuals’ from non-logical vocabulary. In particular, there are predicate symbols in a formula as well as variables. These predicate symbols give us the number of properties and relations among individuals.³⁴

Explaining Hintikka’s point on synthetic methods of verification, Allen Hazen considers a visual thought experiment in the process of proving a first-order theorem, in which individual variables are nodes and relations—dyadic predicates— are arrows or directed edges.³⁵ Hazen’s thought experiment shows a way to extract more than just the number of individuals form formulae. If we add monadic predicates to this picture, then we have all we want. To sum up, in our interpretation of first-order formulae, which aims at resembling geometry, variables are going to be represented by vertices, one-place predicates by labels of vertices, and two-place predicates by labels of edges that connect up to two vertices. The following definitions will set the interpretation by defining the graphical form of a formula. They are intended to be applied to the monadic and dyadic fragment of FOL in prenex normal form.

Definition 3.1

Any variable, free or bound, represents a vertex.

Definition 3.2

Any monadic predicate represents a label of a vertex.

Definition 3.3

Any dyadic predicate represents a label of an edge connecting up to two vertices.

Definition 3.4

The directions of edges are determined by the order of appearance of variables in each predicate.

Bearing in mind that we are working with first-order formulae in prenex normal form, the graphical form of a formula is just an expansion of Hintikka’s definition of the degree of a formula.³⁶ Some examples would clarify these definitions: Fx represents a vertex x that has the label or property F;³⁷ both Rxy and $\forall x \forall y Rxy$ represent vertices x and y, with an edge directed from the first to the second.³⁸Rxx represents a vertex x; with an edge from x to itself. Different formulae may share the same graphical form. For instance $\forall x(Px \rightarrow Qx)$, $\exists x(Px \wedge Qx)$, and $Px \wedge Qx$ have the same graphical form as they all represent one vertex and two same labels of that vertex.

As can be seen, different variables represent different vertices, the same variables the same vertices and similarly for predicates. An edge from x to y is different from an edge from y to x, however they are the same ‘type’ of edge, namely edges with distinct source and target. This type of edge is different from the type with the same source and target.

In this interpretation, each formula in monadic and dyadic fraction of FOL is about some vertices, their properties, and the connections among those vertices. For example, formula (1) is about three vertices and three edges of the same type that connect these vertices, as shown in a graph next to it. This is what we are going to call the ‘graphical form’ of a formula.

Now that we have established a graphical interpretation for formulae in prenex normal form, we will proceed to provide a graphical interpretation of proofs in FOL.

4 Synthetic proofs, from geometry to ND

According to Hintikka, a proof in geometry is synthetic if new elements are constructed in the existing figure in the process of constructing it. However, when he discusses synthetic proofs in FOL, Hintikka is only concerned with the number of variables we need to consider in relation to each other in a proof. Most likely, his way of interpreting FOL vocabulary in this context was to understand variables as representing geometrical entities. Therefore to consider n variables means considering n geometrical entities. And if, after defining ‘considering variables in relation to each other’ in a proof system, we consider n variables in an argument while considering $n+1$ variables in the proof of that reasoning, then the proof is synthetic.

This interpretation offers a very straightforward connection between FOL and geometrical reasoning, but misses some more fine-grained aspects of reasoning in FOL which are important from an information point of view. Even before further elaboration about how to understand considering individuals in relation to each other, and looking only at Hintikka’s definition of the degree of formulae, we can find some examples. If one finds the reasoning from $\forall x \forall y Rxy$ to $\forall x Rxx$ informative, then one should not find Hintikka’s definition of synthetic proofs a good candidate for explaining informativity of FOL reasoning. In Hintikka’s interpretation the assumption of the argument is about two geometrical elements, but in the process of proving the conclusion we only need to consider one geometrical element (a FV). This makes the proof an analytic one. Thus Hintikka’s notion of methodic analyticity does not capture the sort of informativity the above-mentioned example instantiates.

With the proposed graphical form for formulae we will be able to achieve a more fine-grained picture of the information in FOL and its changes. This point will become clearer as we go. First we need to define how to calculate the number of elements we are considering ‘in relation to each other’ and what counts as a ‘new’ element in the context of our proof system of choice, namely ND. In the previous section we defined the graphical form of a formulae, now we need to expand our definitions to cover the graphical forms we are dealing with in an ND derivation. ND derivations have assumptions, open or discharged. We refer to the set of open assumptions and the final conclusion of a derivation as the ‘argument’ that the derivation is proof of. Formulae immediately above an inference line are its ‘premises’ and the formula immediately below it is the ‘root’ or the conclusion of that step.

The graphical form of each assumption provides us with the number and kind of graphical elements that that assumption is about. It can be said that the graphical form of each assumption defines the number of graphical elements that we are considering in relation to each other in that assumption. However, we need to define what does it mean to consider elements of different assumptions in relation to each other. Let us assume that $\forall x (Fx \rightarrow Gx)$ and $\forall x (Gx \rightarrow Hx)$ are assumptions of a derivation. We know that each is about a given individual and its properties, in our adopted interpretation, about a vertex and its labels. Nevertheless, we cannot say that we are considering these two assumptions in relation to each other because we do not know if they are about the same individual, or vertex in our interpretation. FVs help us to consider assumptions together.

Hintikka’s suggestion, that the number of variables we are considering in relation to each other in an instance of $\exists E$ in ND is equal to the number of FVs occurring free in the undischarged assumptions for the deduction of the minor premise of that inference step, is an attempt to address the above point. But it is not general enough. What if we replace all the existential quantifiers with the negation of universal negation? FVs do not need to be assumed only in $\exists E$ instances, they can be just assumed via an assumption.³⁹ Let us define assuming a variable in a general manner:

Definition 4.1

Variable x is ‘assumed’ in derivation $\mathcal {D}$

if it appears free in any $B \in \Gamma$.

Note that x can be assumed in some sub-derivations of $\mathcal {D}$ while not being assumed in $\mathcal {D}$ itself. We can define a scope for an assumed variable to single out inferences that rely on it as an open assumption.

Definition 4.2

The scope of an assumed variable x in derivation $\mathcal {D}$ is the set of all the sub-derivations of $\mathcal {D}$.

Note that the scope of an assumed variable x may include sub-derivations in which x is not assumed. In the following derivation schema the right hand side sub-derivation is a member of the scope of x while x is not assumed in it:

Now we have enough vocabulary to define considering variables in relation to each other:

Definition 4.3

In a derivation $\mathcal {D}$, variable y is ‘considered in relation’ to variable x if it is assumed in the scope of x.

For instance, y is assumed in the scope of x in the following derivation schema. Both sub-derivations with roots B and C are in the scope of x, The derivation with root C is the one in which y is considered in relation to x because it appears free in the assumption of that derivation.

The next step is to define how formulae are considered in relation to each other. It is fair to say that once we are considering two variables in relation to each other, every atomic formulae in their common scope with either of those variables appearing in them are considered in relation to each other:

Definition 4.4

In a scope $\mathcal {S}$ of x in derivation $\mathcal {D}$ in which variables x and y are considered in relation to each other, any atomic formulae with either x or y in them are considered ‘in relation to each other’.

For example, in the following derivation schema the sub-formula of $\chi$ with x in it is considered together with the sub-formula of $\omega$ with y in it.

In the next section, when we clarify our inference rules,⁴⁰ we shall see examples to illustrate what these definitions attempt to capture.

After defining how formulae are considered in relation to each other, let us define what a ‘new’ element is in a ND proof. From Hintikka’s comments on EI being responsible for introducing new variables, it is clear that he takes ‘fresh’ variables as new. Since EI is existential elimination, it can be argued that a fresh variable is substituted for an existentially bound variable in an assumption of a derivation and therefore has already been expected in that derivation, by anyone who knows the side conditions of $\exists E$. The same goes for $\forall I$ when the universal quantifier appears in the final conclusion of a derivation. Thus, fresh variables, either introduced by an instance of the $\exists E$ rule or eliminated by an instance of the $\forall I$ rule, are not new in the sense of being surprising or being unexpected. It seems that in Hintikka’s proof method, EI actually does add new variables to proofs, but it is not the case for ND proofs.

Having that said, there is an interesting phenomenon to observe in reasoning in ND systems: some FVs get introduced to derivations by quantifier elimination rules, but do not get eliminated by quantifier introduction rules. For instance, FVs introduced by EI rules happen to not being substituted by bound variables in proofs of arguments (14)-(16) of the next section. And some FVs get introduced to derivations by rules other than quantifier elimination rules while getting eliminated by quantifier introduction rules. For example, a FV may be introduced to a proof by an instance of negation introduction and then be substituted by a universally bound variable as exemplified in proof (11) of the next section.

We use the word ‘new’ for the later FVs with the following justification: we usually have a practical reason for applying rules in any particular derivation from certain assumptions to a certain conclusion. For instance, we apply quantifier elimination rules to introduce FVs to the context of derivation, or we apply $\vee I$ to introduce a formula to the context of deduction, possibly by adding a new formula as one of the disjuncts. There is no harm in speaking loosely about these practical reasons as the justification for applying a rule. Now some of these justifications are explicitly about FVs, like quantification rules, while some are not. It can be said that a FV is new to the context of a derivation if the justification of the rule which is applied to introduce the formula it occurs in, is not explicitly about FVs. Hence we only take a fresh FV as new if it is introduced to the context of a derivation by rules other than quantifier eliminations.

After discussing new FVs—or vertices in our adopted interpretation—it is time to define new predicates—or new labels for vertices and edges in our adopted interpretation. A monadic or dyadic predicate is new to the context of a derivation if it does not appear in the assumptions of that derivation. The same goes for an a edge type; it is new to the context of a derivation if that type of edge does not appear in the assumptions of that derivation. It needs to be kept in mind that as the formulae inferred from the assumptions of a derivation change, the graphical form assigned to those formulae might change as well. For instance, assume that formula (1) from the previous section is an assumption of a derivation and formula (5) is inferred from it in the process of reasoning. As shown below, (5) is about two vertices, not three; also the three edges are not the same type anymore. In the graphical form of (5), there is an edge of the type with same source and target:

We shall see that neither every proof with new elements in it is synthetic, nor does every synthetic proof contain new elements.

By knowing how to assign a graph to a formula, and how to consider formulae in relation to each other in a given derivation, at this stage we are in a position to define a synthetic inferential step inspired by synthetic proofs in geometry. When we consider the assumptions and the conclusion of a derivation (its argument), the formula with the maximum elements in its graphical form defines the maximum number of elements we are considering when we consider the argument that the derivation proves or verifies. Graphs from different assumptions can’t be added together. This is because, as explained before, with bound variables appearing in those assumptions and in the conclusion, we do not know whether they are about the same entities. Then in the process of constructing the derivation, once the bound variables are substituted with FVs, by following the definitions 4.1–4.4, we are able to determine the set of formulae being considered in relation to each other in each inferential step and assign a graph to it. The following definition gives us what we need:

Definition 4.5

The set $\mathcal {G}$ of graphical elements being considered in relation to each other in an inference step $\mathcal {I}$ of derivation $\mathcal {D}$ is the graphical form assigned to the set of formulae being considered in relation to each other in sub-derivations of $\mathcal {D}$ with the premises of $\mathcal {I}$ as their conclusions.

If the number of graphical elements that we consider in relation to each other in an inference step of a derivation happens to be more than the maximum number of elements we consider in relation to each other in the argument of that derivation, or there are new types of elements involved in that inference, then the situation in that inference step is very similar to that of synthetic geometrical proofs. And this is how we are going to define a synthetic inferential step in a derivation:

Definition 4.6

An inference step $\mathcal {I}$ in derivation $\mathcal {D}$ of argument $\mathcal {A}$ is synthetic if and only if the number of graphical elements ‘considered in relation to each other’ in $\mathcal {I}$ is greater than the number of graphical elements in the formula with the maximum number of elements in $\mathcal {A}$, or there are elements of a new type in the graphical elements considered in relation to each other in $\mathcal {I}$.

An inference step is analytic otherwise. As an example, in the derivation schema number (6) if the number of elements in $\chi x$,$\sigma y$, and $\theta xy$ all together is bigger than either of the open assumptions $\psi x$, $\omega y$, and $\forall z \forall w\phi zw$ and the conclusion E, then the last inference step is synthetic. Because then the first three formulae, considered in relation to each other, make us consider more geometrical elements than we did in considering each of the assumptions or the conclusion.

After defining a synthetic inference step, we can define a synthetic proof as follows:

Definition 4.7

A derivation $\mathcal {D}$ is synthetic if it includes at least one synthetic inferential step.

A derivation is analytic if all steps of it are analytic. A synthetic argument is defined as:

Definition 4.8

An argument $\mathcal {A}$ is synthetic if it has only synthetic derivations.

According to (Def.4.8), a synthetic inferential step needs to be essential for proving an argument in order to count that argument as synthetic. It is reasonable to take normal derivations in ND as the most straightforward way of proving an argument. Normal derivations avoid unnecessary inferential moves. So in the rest of this paper we will focus only on normal derivations.⁴¹ At the same time, it is known that cut-free derivations, the sequent calculus version of normal derivations in ND, can be very long and it is much more practical to shorten them using cut.⁴² Whether synthetic normal derivations turn into analytic non-normal ones is a crucial topic which will be addressed in section six.

5 Examples of synthetic proofs in ND

In this section, after a brief review of normal derivations and introducing our inference rules, we shall present some examples of synthetic arguments and explain why they are synthetic. All the derivations that we will discuss are normal. The idea of normal derivations goes back to Gerhard Gentzen who believed a good proof should not have detours.⁴³ That is every formula which appears in proof steps, either has already appeared as part of the assumptions or should appear in the conclusion of the argument.

The result of applying this idea is that, in a ND derivation, if we apply elimination rules prior to introduction rules every formula that appears in that derivation is the subformula of either the assumptions or conclusion of the argument. It is not difficult to see why. When we apply elimination rules we are just breaking formulae, in the assumptions, into their parts, and when we start using introduction rules we are just making more complex formulae, so whatever appears in the proof steps either has been part of assumptions or will appear in the conclusion since the last applied rules are all introduction rules. What has been said, suggests that the rules of ND can be used in a certain way to form direct and detour-free proofs.⁴⁴ This kind of proof is called normal in the literature. Here we take the definition given by Von Plato and Negri:⁴⁵

Definition 5.1

A derivation $\mathcal {D}$ in ND with general elimination rules is in normal form if all major premises of elimination rules are assumptions.⁴⁶

After clarifying what normal derivations are, it remains to clarify our inferential rules. Here are our quantification rules:⁴⁷

There are restrictions on universal introduction and existential elimination schemas; y must not occur free in any assumption $A(y \backslash x)$ relies on, neither in $\forall x Ax$, $\exists x Ax$, C, nor any other possible side assumption. And here are our rules for negation:

The rest of the rules are as usual. Now let us start with defining the number of variables that we are considering in relation to each other in a derivation. Recall, we are considering two variables in relation to each other if one is assumed in the scope of another. For instance, a and b are not considered in relation to each other in (9) because b is not assumed in the scope of a. That is b does not appear free in any assumption in the scope of a. The scope of a includes the whole right hand side branch. Also note that the fresh FV b is added to the context of the proof by an instance of disjunction introduction and is considered ‘new’.

And they are considered in relation to each other in (10), because b is assumed in the scope of a. The scope of a includes the entire derivation as Pa is one of the open assumptions of the derivation. Even the other open assumption of the derivation is in the scope of a although a does not appear free in it. This is so because this assumption is a sub-derivation of the whole derivation. The scope of b includes the top three inferences on the right hand side.

If we consider the derivation of an argument classically equivalent to that of the derivation (10) we will see some interesting phenomena. In derivation (11) we have an instance of what we call ‘new’ individual. the fresh FV b is introduced to the context of our derivation with an assumption that is discharged in an instance of negation introduction. That is we have a fresh FV introduced to our reasoning via a rule other than quantifier elimination.

Let us move to examples of synthetic proofs. Derivation (12) is a very simple—to the point of triviality—example of a synthetic proof. Inferring Sa relies on considering only one FV (individual) a which appears in the assumption Pa together with two other formulae with a appearing in them, namely $Pa \rightarrow Qa$, $Qa \rightarrow Sa$. Note that the FV in $Pa \rightarrow Qa$ and $Qa \rightarrow Sa$ is not considered in relation to the FV in Pa. What makes this proof synthetic is that the FV is identical in all of the mentioned expressions. We are considering an individual and three of its properties in inferring Sa which is more than any single open assumption of the derivation, or its conclusion. The graphical representation of the assumptions and the conclusion are shown on the left hand side and that of the inference step with Sa in its root in the right:

Derivation (13) is more complicated in terms of considering individuals togather. In the first five steps of the derivation from the top right, we are considering three individuals in relation to each other. Each of them has a different property. In inferring Sc we rely on these three individuals and their distinct properties. This is still the case till inferring $\exists y(Pa \rightarrow Sy)$ for the first time. The inferences between these two inference steps are synthetic as they rely on more individuals and properties than we consider in every open assumption of the derivation, or its conclusion individually. The graphical representation of the assumptions and the conclusion are shown on the left hand side and that of the inference step with Sc in its root in the right:

There are more interesting examples to consider. This one is introduced by Hazen:⁴⁸

The normal proof of this argument is too long to fit here,⁴⁹ but it can be seen that we are invited to consider four variables in relation to each other by assuming the first assumption once, that in turn makes us assume the second assumption three times, the third one nine times, and the fourth one 27 times. In this process we are considering 28 variables in relation to each other. And the graphical form of the inference that gives us the quantifier-free version of the conclusion includes 27 vertices with label F, one edge with label R, three edges with label S, nine edges with label T, and 27 edges with label U. This number of elements is obviously larger than the maximum of elements that we consider in relation to each other in the assumptions, or the conclusion which is four vertices and four edges.

The next example has a much shorter proof, but long enough to do not fit here. However, we still are able to present the graphical forms. The graphical representation of the assumptions—from top to bottom, the conclusion, and that of the inference step with Raa in its root are shown from left to right respectively:⁵⁰

In the normal proof of this argument there is a conditional elimination rule with Raa as the conclusion in which we consider Rab, $Rab \rightarrow Rba$, and $(Rab \wedge Rba) \rightarrow Raa$ in relation to each other. This inferential step is synthetic because in it, Raa has a new graphical form. If we replace the existential quantifier in the first assumption of this argument with negation of universal negation, the same inferential step will still appear in the proof of the argument.

Our last example is as follows, the graphical representation of the assumptions—from top to bottom, the conclusion, and that of the inference step with Rba in its root are shown from left to right respectively:⁵¹

In the normal proof of this argument there is a conditional elimination rule with Rba as the conclusion in which we consider $Rab \wedge Rac$, $(Rab \wedge Rac) \rightarrow Rcb$, and $(Rac \rightarrow Rcb)\rightarrow Rba$ in relation to each other. This step is synthetic because in it we consider four edges among three vertices and this is more than the maximum of elements we consider in the argument which comprises three edges among three vertices.

6 Non-triviality of the analytic/synthetic distinction

In Logic and Analyticity⁵², Allen Hazen notes that we can reduce the number of variables we need to consider in relation to each other in a proof of (14) by proving intermediate steps such as $\forall x \forall y ((Txy \wedge Fx) \rightarrow Fy)$ from $\forall x \forall y ((Uxy \wedge Fx) \rightarrow Fy)$ and $\forall x \forall y (Txy \rightarrow \exists z \exists w (Uxz \wedge Uzw \wedge Uwy))$. The idea is to break the proof into smaller sections, by reintroducing quantifiers in the proof procedure. In those smaller sections we consider fewer variables in relation to each other. In other words, we consider fewer vertices in relation to each other at the same time if we divide the whole proof into smaller subproofs. However, the whole proof is no longer normal because we need to eliminate quantifiers just after introducing them.

Hazen mentions that the above suggestion will only reduce the severity of the problem of variables inflating, not solve it completely. By the end of this section we shall show that Hazen’s suggested subproofs are synthetic too, but the suggested idea raises a possible problem for our account of synthetic proofs: whether a synthetic proof, that is a normal proof with the number of graphical elements greater than that of its argument, can be turned into an analytic non-normal proof, that is one with the number of graphical elements no more than its argument? If the answer to this question turns out to be positive, then the analytic/synthetic distinction is built on a shaky ground as the syntheticity of an argument is only due to a choice of the way of combining proofs together in order to prove that argument.

To answer the question above requires us to consider all the possible ways of building a non-normal proof from an existing normal one and check if any of them is analytic. This is a really tough task. Fortunately there is an easier way to answer a question equivalent to the above question. We can check if it is possible that a non-normal but analytic proof turns into a normal but synthetic proof. This task is easier as there are well-known procedures of normalization in ND and all we need to do is check them.

Since we are starting with an analytic proof, we need to watch for any possible increase in the number of graphical elements considered in relation to each other in the process of normalization. According to Def.4.4 in the scope of variables x and y any atomic formulae with either of x or y in it are considered in relation to each other. Therefore we need to check if any of the normalization processes either lead to an increase in the number of FVs appearing in the scope of another FV or add to the number of formulae appearing in a derivation. We are going to prove that the answer to this question is ‘No’ for a disjunction-free fragment of FOL and show that it is not guaranteed for full FOL.

Theorem 6.1

The number of FVs assumed in the scope of another FV does not increase in the process of normalizing a derivation in the disjunction-free fragment of FOL.

Proof

We prove this theorem by induction on normalization, also known as reduction, process on each pair of introduction and elimination rules. In normalizing a proof, we remove any inference step in which the conclusion of an introduction rule for a logical constant is the major premise of an elimination rule of the same word. Let us start with the conjunction. Here is the reduction process for the conjunction where the left hand side derivation reduces to the one on the right hand side: $\square$

The number of FVs assumed in the scope of one another does not increase from the left hand side derivation to the right hand one. According to Def.4.1 a variable is assumed in a derivation if it appears free in any open assumption of that derivation. Consequently, if there is any FV in either of $\Gamma _{1}$ or $\Gamma _{2}$, the number of FVs assumed in relation to each other may even decrease from left to right. This is so because $A_{i}$ in the left hand side derivation relies on both $\Gamma _{1}$ and $\Gamma _{2}$, while it relies on either $\Gamma _{1}$ or $\Gamma _{2}$ in the right hand side derivation.

The same applies to the reduction of conditional and negation. Considering the reduction processes in (18) and (19), the number of assumed FVs in the scope of one another may decrease from left to right, if anything. Because B and $\bot$ in the derivations (18) and (19) respectively are inferred on the left hand side, for the first time, relying on both $\Gamma$ and A and on the right hand side derivations only on $\Gamma$.

Next let us consider the reduction processes for universal quantification. The process goes as follows:

We need to check if the number of FVs assumed in the scope of one another has increased. What has changed from left to right is that the derivation from $\Gamma$ to $A(y\backslash x)$ has been replaced by a derivation from $\Gamma$ to $A(y\backslash t)$.⁵³ That is we have a proof in which all appearances of y have been replaced by t. From the restrictions of universal introduction, we know that y does not appear free in $\Gamma$. This means that the term t should be selected such that it appears free in $\Gamma$. Consequently, the number of FVs assumed in the scope of one another is not going to change in the first subproof. The second and third subproofs will remain untouched from left to right.

And here is the reduction process for existential rules:

Again, the derivation on the left hand side is assumed to be analytic and we want to see if the one on the right hand side is analytic too. In order to do so we need to check if the number of FVs assumed in the scope of another FV is increased in the right hand side derivation. What has changed from left to right is the subproof from $A(x\backslash y)$ to C which has been substituted by a subproof from $A(t\backslash y)$ to C. That is all occurrences of y in the subproof proof from $A(x\backslash y)$ to C have been replaced by t. From the restrictions on existential elimination, we know that y should not appear free in any assumption that $A(x\backslash y)$ relies on (that is $\Gamma$), neither in C. Therefore, t is not going to appear free in the first and the third subproofs. This means that no new variable is going to be assumed in the first and third subproofs on the right. Here the proof of Theorem 6.1 ends.

Disjunction has been set aside from the above theorem for a good reason. The reduction process in the presence of disjunction reduces the complexity of a formula, but it does so at the expense of a more complex proof. Here is the elimination rule for disjunction:

Now assume that the formula C has been inferred by an introduction rule, say for the logical constant $\bullet$, in one of the subproofs of the disjunction elimination rule and then formula C in the conclusion of the disjunction elimination rule has been the major premise of $\bullet$ elimination rule in a derivation. In other words, $\bullet$ has been introduced in one of the subproofs of disjunction elimination and almost immediately eliminated. The process of reducing such a derivation includes pulling the $\bullet$ elimination up inside the subproofs of the disjunction elimination as shown below:

The formula D in the left hand side derivation is inferred relying on $\Gamma$ and $\Delta$. However the first inference of D in the right hand side derivation relies on either of A and B as well as $\Gamma$ and $\Delta$. Thus, if the left derivation is analytic, the analiticity of the right derivation is not guaranteed because the number of assumptions an inference relies on increases from left to right and this may lead to an increase in the number of FVs assumed in the scope of one another.

So far we have proved that the number of assumed FVs nested in another assumed FV does not increase in a reduction process. However, this is only one way an analytic derivation can turn into a synthetic one. We still need to check for one more possibility, namely an increase in the number of atomic formulae that are considered in relation to each other. Since it is assumed that the considered non-normal derivations are already analytic, we need to check if the number of formulae that the inferences rely on increases in the process of normalization.

Theorem 6.2

The number of formulae inferences rely on does not increase in the process of normalizing a derivation in the disjunction-free fragment of FOL.

Proof

The proof method, the same as Theorem 6.1, is induction on the process of normalization for each logical vocabulary. As a matter of fact, what has been said in the case of each of the previous proofs suffices to prove theorem 6.2 as well. In the reduction process for conjunction, demonstrated schematically in (17), the only inference step that changes is the one with $A_{i}$ as its conclusion. And in that case $A_{i}$ is inferred relying only on either of $\Gamma _{1}$ or $\Gamma _{2}$. Hence the number of formulae that inference relies on has not been increased. In reduction processes for conditional and negation, as shown in (18) and (19), the only changes happen to inferences with B and $\bot$ as the conclusion respectively. They are concluded from only $\Gamma$ after reduction. As a result, the number of formulae that those inferences rely on has not been increased either. And the reduction process for quantifiers does not change the scope of the FVs in formulae. Thus there is no need to check them. What has been said about the effect of the reduction process on assumed FVs nested in the scope of one another in the presence of disjunction applies to formulae inferences rely on too.

We have just shown that an analytic and non-normal proof will not turn into a synthetic normal proof. Consequently, if a normal proof is synthetic, it will not turn into a non-normal analytic one. Because in that case, by normalizing an analytic proof, we reach a synthetic one. And this was something we just proved cannot happen. This means that the analytic/synthetic distinction in the sense introduced in this paper is not simply a matter of the way proofs are combined together. $\square$

Let us finish this section by examining Hazen’s suggested subproofs. The first subproof makes the following argument:

The maximum number of elements we consider in the argument is eight; four vertices, one edge labeled T, and three edges U. To proof this argument we need to assume the second assumption three times in order to show that if the first FV has the property F, so does the rest. This means three vertices having property F will be added to the other eight above mentioned elements in the last instance of the conditional elimination in the normal derivation of the above argument. Thus, the subproof is synthetic. This is the case in relation to the other sub-arguments of (14) too. So none of the subproofs of (14) are analytic, but in each subproof, we consider significantly fewer number of FVs in relation to each other. However, we need to bear in mind that there are three of such sub-arguments to prove, therefore it does not change what it takes to prove the original argument in terms of FVs occurring in the whole process.

7 Conclusion

We started with two notions of analyticity, semantic and methodic. Then we studied proofs in FOL paying special attention to the second idea of analyticity using ND as proof system. We showed that Hintikka’s hypothesis about syntheticity being independent of one specific proof method is correct at least so far as ND is concerned. The provided account of synthetic proofs sheds some light at least in two areas of research. One area is the informativity of deduction. The account tells us how sometimes confirming the conclusion is not so obvious from a mere understanding of each of the assumptions and the conclusion. Moreover, the graphical form of the formulae provides us with some vocabulary to investigate the type of information we gain in the process of reasoning. And this may lead to a theory of information different from the existing ones in the literature.

Here is an outline of such a theory: we can think of the information about the number of individuals, abstract or concrete, the properties they have, and the relations holding among them as ‘intuitive information’. The adjective ‘intuitive’ is inspired by the Kantian idea that our understanding of objects, their properties, and the relations among them is intuitive. If we adopt this point of view, then the graphic form of the formulae in an argument can be seen as different pieces of intuitive information we have when thinking about that argument. In the process of proving that argument, when we put those pieces of information together, if we get a more complicated graph, that is one with more elements or richer in terms of the variety of elements, then it means that we gained more intuitive information in that process compared to when we were just entertaining with the formulae in the argument. This process still could be called ‘psychological’ by whoever thinks it is so, but it is also objective as it has strong enough ties with the syntax of FOL.

The proposed theory provides an answer to Dummett’s tension between the legitimacy and fruitfulness of deduction—in a fraction of FOL—by explaining how legitimate deductions are fruitful. It also improves Hintikka’s original position on the informativity of deduction by arguing that the methodically synthetic proofs are the informative ones. Hintikka did not create such a connection, although he may believed there is such a connection. Moreover, Hintikka’s theory of information was accused of taking only the polyadic fraction of FOL as informative.⁵⁴ Although there are doubts about the accuracy of this accusation⁵⁵ the suggested account of information makes certain arguments in monadic predicate logic informative, because as we saw, there are synthetic proofs with only monadic predicates in their arguments.