Not so distinctively mathematical explanations: topology and dynamical systems

Abstract

So-called ‘distinctively mathematical explanations’ (DMEs) are said to explain physical phenomena, not in terms of contingent causal laws, but rather in terms of mathematical necessities that constrain the physical system in question. Lange argues that the existence of four or more equilibrium positions of any double pendulum has a DME. Here we refute both Lange’s claim itself and a strengthened and extended version of the claim that would pertain to any n-tuple pendulum system on the ground that such explanations are actually causal explanations in disguise and their associated modal conditionals are not general enough to explain the said features of such dynamical systems. We argue and show that if circumscribing the antecedent for a necessarily true conditional in such explanations involves making a causal analysis of the problem, then the resulting explanation is not distinctively mathematical or non-causal. Our argument generalises to other dynamical systems that may have purported DMEs analogous to the one proposed by Lange, and even to some other counterfactual accounts of non-causal explanation given by Reutlinger and Rice.

There is currently a major debate in the philosophy of science as regards whether genuine mathematical explanations of physical phenomena are possible. Proponents of their existence point to various putative real-world examples, including, notably, discrete mathematical explanations of the lengths of cicada life-cycles (Baker, 2009), graph-theoretic explanations as to why it isn’t possible to cross each of Königsberg’s bridges exactly once on a walk through the town (Pincock, 2007), topological explanations of dynamical systems such as why double pendulums have at least four equilibria (Lange, 2016), and geometric explanations of soap films and soap bubbles (Pincock, 2015). Sceptics of mathematical explanations of physical phenomena provide rebuttals of these alleged real-world examples; they argue against such abstract mathematical necessities and instead point to the pragmatic virtues of these mathematical explanations, such as their cognitive value (Knowles & Saatsi, 2019) or their role in indexing and representing physical constraints (Melia, 2000; Daly & Langford, 2009; Saatsi, 2011; Skow, 2013)¹ or suggest a metaphysically lighter reading of these mathematical explanations (Baron, 2016).²$^,$³

Lange (2016) proposes a modal conception of mathematical explanations⁴ that he calls ‘distinctively mathematical explanations’ (DMEs). The explanatory power of a DME is said to derive not from its describing the causal nexus of a target system, involving the particular forces acting on it, but rather from its identifying ‘modally exalted’ mathematical constraints on the system which have an associated degree of necessity surpassing that of any causal law. This paper focuses on Lange’s account of DMEs, and in particular on his claim that a topological DME can be given for why any double pendulum has at least four equilibrium points (2016, pp. 27–31).

We choose to focus on Lange’s pendulum example because the question as to whether the properties of dynamical systems can be explained topologically is of far-reaching importance, in view of just how pervasive dynamical systems are in science, and has gained a lot of traction in the scientific literature as well (Aoki & Hiraide, 1994; Katok & Climenhaga, 2008; Palis Jr & de Melo, 1982; Pettini, 2007). Lange’s pendulum example is notable in being one of only a very small number of attempts in the philosophical literature to explain the property of a dynamical system in wholly mathematical terms (see Colyvan, 2001; Lange, 2016; Pincock, 2015; Skow, 2013; Saatsi, 2018 for a brief survey of such examples). This makes it a very tempting target. Our claim will be that Lange is unsuccessful in his attempt to provide a DME where the double pendulum is concerned. He is unsuccessful, we contend, because the explanation he provides isn’t really a DME at all. Rather than being a purely mathematical explanation, it is—so we argue—a causal explanation in disguise, because it depends on hidden assumptions about the particular forces acting on the double pendulum that Lange illicitly smuggles in through the back door. This becomes evident (a) when his explanation is generalised, as we demonstrate in this paper, and (b) when his explanation collapses when the particular forces acting on the system are varied using a perturbations-based approach. Even as we focus on Lange’s modal account of DMEs, we will briefly show how our arguments affect other philosophical views, such as that of Reutlinger (2018) and Rice (2021), who have advanced a general philosophical account to accommodate a variety of both causal and non-causal explanations, including mathematical explanations such as DMEs.

As per Morrison (2018), explanations concerning dynamical systems seek to:

$\ldots$describe the typical behaviour of trajectories for many different types of systems as time (rather than space) tends to infinity, and to understand how this behaviour changes under perturbations. What we want to know is the extent to which the system is stable; whether it is possible to deform a perturbed system in a way such that we can recover the original one. In that sense the goal is to answer general questions about, for example, whether there is any relation between the long-term behaviour and initial conditions, rather than trying to find precise solutions to the equations defining the system itself, something that is often not possible. (pp. 222–223)

A simple explanation of a dynamical system can sometimes be given in terms of transformation of the system’s parameters on a topological space by using either its configuration space, such as in Lange (2016, p. 31), or its phase space.⁵ These transformations allow the prediction of the trajectories of the dynamical system under varied initial conditions. These transformations can also reveal certain global constraints on the system or hidden symmetries that may not be evident in detailed (and often cumbersome) causal explanations of the system. If the explanation concerning the dynamical system is a DME, then these symmetries and constraints are preserved even after the parameters of the system are perturbed.

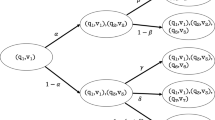
Lange proposes one such explanation concerning the equilibrium positions of a double pendulum. He argues that any double pendulum system, whether simple or complex, must have four or more equilibrium positions, and that this fact is modally constrained by certain distinctively mathematical facts which pertain mainly to the configuration space of the system (a torus) irrespective of the contingent laws governing these systems (2016, p. 31). Lange’s argument relies on some fundamental results in differential topology, such as the Morse theory, which studies the critical point behaviour of a differentiable function when mapped onto the configuration space of a dynamical system. He argues that no amount of causal reasoning can give such a precise constraint on the number of equilibrium positions because any causal strategy has to be deployed on a case-to-case basis taking into account the nature of the forces acting on the system. Since his account of DMEs bypasses such causal reasoning, he calls them non-causal ‘[scientific] explanations by constraint’ because the explained fact about the target system, i.e., the number of equilibrium positions, would remain invariant even if the contingent laws of nature were to be different. Thus, the modal strength of his topological explanation comes from its unifying nature and the necessarily true conditional that remains invariant under a range of contextually relevant antecedents.

This paper refutes his modal claim not only for a double pendulum or a class of double pendulums, but also for much stronger DMEs that could be proposed for explaining the number of equilibrium positions of any n-tuple pendulum system. (We expand the pool of candidate DMEs of pendulum systems to illustrate this point.)

In order to understand our argument, it will be helpful, first of all, to introduce the notion of a “conditionalised explanation”, by which we mean an explanation fitting the following form:

If a physical system satisfies the condition C, then it will have the property P, for the reason R.

Such an explanation has two parts, an explanandum (that which is to be explained) and an explanans (that which does the explaining). The explanans is R. The explanandum is the conditional statement that if a physical system satisfies the condition C, then it will have the property P. Since the explanandum is a conditional statement, it has two parts in its turn, its antecedent and its consequent. The antecedent specifies the condition that a physical system must meet in order for the explanation to be applicable to it, namely, C. The consequent specifies the property of the system that is explained when the explanation is applicable, namely, P.

We give the name, “E1", to Lange’s explanation as to why double pendulums have at least four equilibrium positions. E1 can be framed in the following conditionalized form:

(E1) If a physical system is a double pendulum, then it has four or more equilibrium positions, for the reason that when the potential energy function of such a pendulum is mapped to its configuration space the result is a distorted torus with no fewer than four stationary points.

We will explain E1 in detail below, along with Lange’s reasons for holding it to be a DME.

Having described E1, we then go on to describe two other possible (and greatly improved) explanations as to why pendulums have as many equilibrium positions as they do, these being the extension of E1 and E2:

(Extension E1) If a physical system is an n-tuple pendulum, then it has at least $2^n$ equilibrium positions, for the reason that when the potential energy function of such a pendulum is mapped from its configuration space the result is a distorted n-torus, having an invariant Euler characteristic and satisfying the Morse inequalities, with no fewer than $2^n$ stationary points.

(E2) If a physical system is an n-tuple pendulum, then it has at least $2^n$ equilibrium positions, for the reason that the lower bound on how many equilibrium positions it has is given by the sum of the associated Betti numbers⁶ of the distorted n-torus (as in E1), and these sum to $2^n$.

Notice that the extension of E1 and E2 both appear superior to E1 in the respect of being more general: their antecedents are such that they apply not just to all double pendulums, but to all n-tuple pendulums. We go on to show, however, that, initial appearances to the contrary notwithstanding, neither E1’s extension nor E2 meet the conditions for being a DME that Lange lays down. In relation to E1 and its extension we show that they both, in effect, sneak in causal reasoning through the back door; and in relation to E1, its extension and E2 we show that all of them are only satisfied for certain kinds of arrangements of particular forces (that give out a Morse potential energy function).

We then develop a criticism of Lange’s account by introducing perturbations to the pendulum systems that allows us to vary the antecedents of the conditionals E1, E1’s extension and E2 to test their modal strength. We show that introducing perturbations to the pendulum systems falsifies these conditionals by generating various exceptions in a way that leaves no unobjectionable way to circumscribe them in a necessarily true conditional by a suitable change in the antecedents, including the initial conditions. This is because, as we show, any such circumscription will inevitably involve a detailed consideration of the particular causal forces acting on the system. And if circumscribing the antecedent for a necessarily true conditional involves making a causal analysis of the problem, then we argue that the resulting explanation is not distinctively mathematical. (Such an explanation involves bracketing various causal assumptions which are revealed in cases where the explanation breaks down upon introducing perturbations.) We believe that our perturbation-based approach is important because it may be generalised to other dynamical systems, such as the ones with periodic orbits and n degrees of freedom that have topological explanations analogous to the one proposed by Lange.

The plan for the paper is as follows. In Sect. 1, we discuss E1, which is Lange’s explanation of the double pendulum based on configuration spaces. In Sect. 2, we extend E1 to n-tuple pendulums after introducing Morse theory and show how both E1 and its extension sneak in causal reasoning through the backdoor. In Sect. 3, we introduce E2, which improves on both E1 and extended E1, and show why, prima facie, this is a superior strategy for avoiding direct causal reasoning with the particular forces. In Sects. 4.1 and 4.2, we show how all the candidate DMEs fail to explain the number of equilibrium positions arising in various cases involving perturbations in the length of the pendulum rods, which has to do with the particular forces acting on the pendulum system. In Sect. 4.3, we discuss potential workarounds and show why they fail as general solutions to the problems, raised by us, concerning these candidate DMEs.⁷ In Sect. 5, we summarise the findings of this paper, respond to potential objections concerning a narrowing down of the conditional in cases where the explanation collapses and highlight how our account is relevant to other counterfactual accounts of mathematical explanation. Finally, we conclude that there are no DMEs for any n-tuple pendulum systems and that analogous DMEs pertaining to other dynamical systems are also flawed in general. This reveals a causal upshot of the problem—that many non-causal mathematical explanations conceal various underlying causal mechanisms on which they crucially depend—and reinforces our thesis that that if circumscribing the antecedent for a necessarily true conditional involves making a causal analysis of the problem, then the resulting explanation is not distinctively mathematical or non-causal.

1 Lange’s account

1.1 Causal explanation

Before critiquing Lange’s arguments, we first briefly sketch the causal and non-causal versions of the explanation of the number of equilibrium positions of the double pendulum given by Lange (2016). In the next section we show that the strategy employed in E1, the non-causal version of the explanation, of using topological invariants of the configuration space can be potentially extended to n-tuple pendulum systems, and not merely to double pendulums. Extending Lange’s account allows us to showcase how causal reasoning sneaks through the backdoor and also refute not only his strategy but also a more general and greatly improved strategy that concerns n-tuple pendulum systems.⁸

Fig. 1

A double pendulum with stiff rods and its four equilibrium positions

To begin with the causal explanation, the potential energy (PE) function for the double pendulum, shown in Fig. 1, can be written as:⁹

$$\begin{aligned} U(\alpha , \beta ) = -mgy_m - Mgy_M, \end{aligned}$$

(1)

where m is the mass of the bob of the pendulum freely attached at the origin, and whose arm of length L makes the angle $\alpha$ with the downward direction in which y is taken to be positive. The second pendulum, whose arm of length K makes the angle $\beta$ with the vertical, has a bob of mass M. With this notation, the y-position of the two bobs is given by:

$$\begin{aligned} y_m=L\cos \alpha \quad \text {and} \quad y_M=L\cos \alpha + K\cos \beta , \end{aligned}$$

(2)

which yields

$$\begin{aligned} U(\alpha , \beta ) = -mgL\cos \alpha - Mg(L\cos \alpha + K\cos \beta ) \end{aligned}$$

(3)

One way to find the number of equilibrium positions of the pendulum is to find positions where the partial derivatives of $U(\alpha , \beta )$ with respect to the angles are zero because the partial derivatives show how the potential energy of each bob varies with a change in the angle of inclination of the bobs. The positions where these partial derivatives are individually zero are critical points (equilibrium points) for a given bob, and the positions where these partial derivatives are simultaneously zero are critical points for both the bobs, i.e. for the double pendulum. Since these derivatives are

$$\begin{aligned} \frac{\partial U}{\partial \alpha }= -m g L \sin \alpha - M g L \sin \alpha , \end{aligned}$$

(4)

and

$$\begin{aligned} \frac{\partial U}{\partial \beta }= -M g K\sin \beta , \end{aligned}$$

(5)

the four equilibrium positions are those where $\sin \alpha$ and $\sin \beta$ are simultaneously zero, namely $(\alpha , \beta ) = (0,0), (0, \pi ), (\pi , 0)$ and $(\pi , \pi )$. More such equilibrium positions are at $(\alpha +2n\pi , \beta +2n\pi )$, where $n\in Z$, since they represent the same configuration of the pendulum. Lange (2016) calls this a causal explanation since the explanation crucially relies on tracking the causal features of the system involving a change in the PE function owing to the particular forces acting on the system.

1.2 E1: The first DME

According to Lange, another way to find out these equilibrium positions involves non-causal reasoning about the configuration space of the double pendulum which retains certain topological invariants despite physical alterations to the pendulum system or a change in the contingent force laws acting on the system. These invariants can then be used to reason about the number of equilibrium positions of a pendulum system under any contingent set of forces. We first briefly discuss configuration spaces and topological invariants to set the context for the discussion of potential non-causal DMEs, E1, its extension and E2, which use configuration-space-based reasoning.

A configuration space represents all possible points that a physical system may realise given its geometrical constraints (Lyon & Colyvan, 2008, pp. 231–233). (Only a subset of these points may be realised based on contingent laws and initial/boundary conditions.) For instance, the configuration space of a freely hinged simple pendulum that can move in two dimensions is a full circle, whereas that of a pendulum free to move in three dimensions is a sphere or $S^2$.

In algebraic topology, such surfaces can be assigned a topological invariant termed the genus (g), which, loosely speaking, can be defined as the number of holes in a surface.¹⁰ The genus of a surface is a topological invariant because the value of g does not change under homeomorphic transformations—that is, under bending and stretching of the surface.¹¹ The genus of a surface can be related to another topological invariant, the Euler characteristic, $\chi$. For a smooth, compact, and orientable surface, this relationship is $\chi = 2-2g$. For instance, the number of holes in a $S^2$ sphere is 0, and so $g=0$ and $\chi =2$. Importantly, one can study the qualitative aspects of these surfaces, such as their critical points, by defining certain kinds of differentiable functions over them. (We will say more about what we mean by ‘certain’ functions, in some detail, in the next section.) For instance, the number of critical points of these differentiable functions defined over such surfaces can be related to the Euler characteristic of the surface as: $\chi = N_{max} - N_{saddle} + N_{minima} = 2-2g$, where N refers to the number of critical points of the differentiable function defined over the surface M. (We extend the treatment of a surface to a more general notion of manifold in the next section.) This is sufficient background to discuss Lange’s non-causal explanation¹² of the number of equilibrium positions of the double pendulum.

Fig. 2

Torus configuration space of a double pendulum

The explanation given by Lange (2016, pp. 27–28) goes as follows. The configuration space of the double pendulum is a torus of genus or $g=1$ (see Fig. 2). If we assume that the PE function $U(\alpha , \beta )$ remains finite and continuous, then $U(\alpha , \beta )$ can be “represented by distorting the torus so that each point $(\alpha ,\beta )$’s height equals $U(\alpha , \beta )$. Any such distortion remains a surface of genus $g = 1$ (i.e., topologically equivalent to a torus, which is a sphere with $g=1$ holes in it).” If $U(\alpha , \beta )$ is also a Morse function (a constraint that Lange does not mention but is critical for the explanation to work), then the number of critical points of $U(\alpha , \beta )$ will follow the invariance: $N_{max} - N_{saddle} + N_{min} = 2- 2g$. Given that Morse functions are defined over smooth, orientable and compact spaces, one can reason as follows. For such a surface, there must be at least one minima and one maxima (by compactness) and if $g=1$, then there must be at least two saddle points for the invariance to hold. This implies a total of four or more critical points for $U(\alpha , \beta )$. Lange maps this back to the double pendulum claiming that the double pendulum must also have at least four critical or equilibrium points, and that this provides us with a non-causal explanation or “explanation by constraint” because it only appeals to the topological properties of the distorted configuration space of the double pendulum. That is, we do not even need to get into the phase space of the pendulum which will appeal to causal details such as the Lagrangian of the double pendulum. Nor do we need to know anything about the potential energy function except that it is finite, continuous and smooth. Here is how Lange makes a case for the DME:

This [his DME] is a non-causal explanation because it does not work by describing some aspect of the world’s network of causal relations. No aspect of the particular forces operating on or within the system (which would make a difference to $U(\alpha ,\beta )$) matters to this explanation. Rather, the explanation exploits merely the fact that by virtue of the system’s being a double pendulum, its configuration space is the surface of a torus–that is, that U is a function of $\alpha$ and $\beta$. (2016, p. 27)

Since the configuration space of any double pendulum is a torus, the same explanation applies to any double pendulum, not just to a simple one. For example, the same explanation applies to a compound square double pendulum$\ldots$It also applies to a double pendulum where the two suspended extended masses are not uniformly dense and to a complex double pendulum under the influence of various springs forcing its oscillation. Each of these has at least four equilibrium configurations, though the particular configurations (and their precise number) differ for different types of double pendulums. (2016, p. 28)

Thus, he claims that this DME works for any kind of double pendulum – with stiff rods, non-stiff rods, spring suspension systems and so on, irrespective of the particular forces acting on the system, as long as Newton’s second law (which he claims to be a modally exalted framework law) is not violated.¹³ Moreover, the two quotations above suggest that his DME, in so far as it is deemed a legitimate non-causal explanation, unifies the explanation of the number of equilibria for any double pendulum because all that one requires to prove the existence of at least four equilibria of such systems, with a higher order of necessity, is the knowledge of a certain mathematical abstraction of the system—its configuration space. (Of course, the knowledge of some causal principles such as Newton’s second law and the potential energy are also warranted but they are subsumed under Lange’s account of the varying degrees of necessity of such causal principles.) The existence of a common configuration space for all such systems therefore makes the existence of at least four equilibrium points inevitable (in a stronger sense than causal considerations could), as he argues.

Before critiquing Lange’s arguments, in particular his non-trivial assumptions about the potential energy function and the configuration space of the pendulum systems, we must provide a detailed mathematical backdrop to his strategy since not only the special case of double pendulums discussed by him can be refuted but also a generalised explanation concerning n-tuple pendulums, and certain other dynamical systems with periodic orbits and n degrees of freedom, can also be refuted. This sets the stage for introducing numerous complications that are oversimplified in Lange’s account and which will allow us to demonstrate how causal reasoning sneaks in through the backdoor in Lange’s explanation and why the topological framework on which Lange bases his arguments does not support a modal interpretation. Folllowing this, we will be able to demonstrate a broader philosophical problem with Lange’s arguments (and some other counterfactual accounts of non-causal explanation), which relates to the circumscription of antecedents for a non-causal or necessarily true conditional.

2 Morse theory

We begin with a discussion of Morse theory—the core mathematical framework on which Lange’s arguments rest. Morse theory was developed in 1926 by Marston Morse, an American mathematician, as a branch of differential topology, and he spent most of his career working on this theory. Morse theory allows one to study the topological properties of a manifold (a generalisation of a surface to higher dimensions) by defining differentiable functions on the manifold as a map. The primary interest of the theory is to understand how the shape of the manifold constrains the distribution of the critical points of these differentiable functions (Matsumoto, 2001). We discuss some properties of critical points before we state Morse theory formally because these properties are central to our discussion ahead.¹⁴

Fig. 3

Degenerate critical point bifurcating into two non-degenerate critical points in one-dimensional space upon bending or twisting

2.1 Index of critical points

Critical points are classified by their index, which is defined, loosely speaking, as the total number of downward directions (or dimensions) allowable starting from the critical point. As an illustration, consider Fig. 3, which represents a potential energy function, where the points A, B and C are the local minima, inflection point and maxima respectively. Point A is a stable equilibrium position because a ball rolled towards A will likely remain at A unless disturbed by other external forces. No downward directions are available from A, so its index is 0. Point C is an unstable equilibrium since a ball moved even slightly to the left or right of C will move away from C in a downward direction and not return to it unless an external force acts on it. Downward movement is possible in one direction (dimension) from C, so its index is 1. In a two-dimensional topological projection (which pertains to a three-dimensional ${\mathbb {R}}^3$ space), one will be able to move in two directions from point C (think of the highest point of an inverted cup shape), given that it remains as a maxima, and its index will be equal to 2; point A will still have the index 0 since movement in any downward direction is not permissible (think of the lowest point of an upright cup shape). Point B is stable in one direction (when moving to the left of B) and unstable in another (when moving to the right of B), and thus the index of B is undefined. In the language of differential functions, the index of B is undefined because the rate of change of the gradient of the PE function is 0 at B, or in other words, the double derivative of the PE function of B (with respect to the height of B) is 0. For A, the double derivative of the PE function with respect to its height yields a positive value and for C it returns a negative value indicating that they are stable and unstable directions respectively. We call A and C non-degenerate points, and B a degenerate point. (This distinction forms the fulcrum for the discussion ahead.)

If a surface is bent or twisted, it may still be classified as the same topological surface but it may not have the same total number of critical points (and their corresponding indices) after being bent or twisted. Degenerate points are crucial for our discussion ahead because, under certain kinds of bending or twisting, various non-degenerate points may collapse into only one degenerate point. In other words, it may be the case that upon introducing a certain perturbation in a function, defined over the surface, some non-degenerate critical points vanish and are replaced by fewer degenerate critical points. This is shown in Fig. 3, for a curve, where the non-degenerate critical points $B_1$ and $B_2$ are replaced by the degenerate point B resulting in fewer critical points in the top portion of the figure. (Section 4 shows the relevance of this result to the total number of equilibrium positions of pendulum systems in which the PE function was perturbed to introduce degenerate points.)

In higher dimensions, the index of a critical point is defined using the Hessian of the differentiable function (such as the potential energy function) defined over the manifold. If p is a critical point of a function $f: M\rightarrow {\mathbb {R}}$, then the Hessian (H) of f at p for an m-dimensional manifold is defined as:

$$\begin{aligned} H_f(p) = \begin{vmatrix} {\frac{\partial ^2 f (p)}{\partial x_1^2}}&{...}&{\frac{\partial ^2 f (p)}{\partial x_1 \partial x_m}} \\ \vdots&\vdots&\vdots \\ {\frac{\partial ^2 f(p)}{\partial x_m \partial x_1}}&{...}&{\frac{\partial ^2 f (p)}{\partial x_m^2}} \\ \end{vmatrix} \end{aligned}$$

(6)

The index of the differentiable function is equal to the total number of negative eigenvalues of $H_f(p)$. If a critical point is non-degenerate, then $D_{H_f(p)} \ne 0$, where $D_{H_f(p)}$ is the determinant of $H_f(p)$. For degenerate points, $D_{H_f(p)}=0$.

We are now equipped to define Morse functions, state the Morse lemma, and then discuss the Morse inequalities, fundamental results of the Morse theory which relate the index and number of critical points of the differentiable function to the shape of the manifold. This general result is what allows us to extend our findings from a double pendulum to n-tuple pendulums and to other dynamical systems with period orbits and n degrees of freedom.

2.2 Morse functions and the Morse lemma

If M is a smooth manifold, then a Morse function is any function $f: M \rightarrow {\mathbb {R}}$ if every critical point p of f satisfies these two criteria: (a) p is isolated (i.e., it is the only critical point in its immediate neighbourhood), and (b) p is a non-degenerate point, meaning that $D_{H_f(p)}\ne 0$. For instance, in the case of a single-variable function, a Morse function should pass the second-order derivatives test, which is to say that it should not be the case that $f'(p)=f''(p)=0$. For instance, $f_1=x^2$ is a Morse function since at the critical point $x=0$, $f''(0) = 2 \ne 0$. Another function $f_2=x^3$ is a non-Morse function since at the critical point $x=0$, $f''(0) = 6x = 0$.

The Morse lemma states that every Morse function near a non-degenerate critical point can be expressed in a quadratic form. This is because near each such non-degenerate critical point a Morse function behaves as a quadratic function (see Fig. 4), and therefore, its index can be readily ascertained. For a degenerate point, this behaviour is much more complicated, depending on the degree of degeneracy of the point, and, thus, its index cannot be calculated in a straightforward way as suggested in Sect. 2.1 for the non-degenerate cases. (We will have more to say about degenerate critical points in Sect. 4.)

Fig. 4

Local behaviour of an isolated non-degenerate critical point

For Morse functions, the index of a non-degenerate point can be ascertained. The following inequality associates the topology of the manifold to the index and number of the critical points of the differentiable function mapped to the manifold:

$$\begin{aligned} \chi (M) \le \sum _{k=0}^{k=m} (-1)^k {N_k}, \end{aligned}$$

(7)

where $\chi (M)$ is the Euler characteristic of the manifold M, m is the dimension of M and $N_k$ is the number of critical points with the index k. This inequality becomes an equality for $k=n$. We will discuss other more general variants of this inequality, called the Strong and Weak Morse inequalities, in the next section when we introduce the requisite mathematical formalism, and also examine how Morse theory can be extended to handle degenerate critical points.

2.3 Extension to n-tuple pendulums

Lange’s account can now be extended to n-tuple pendulums. We first show the applicability of Eq. (7) to simple pendulums. The configuration space of a simple pendulum is a circle with $m=1$ and $g=1$. Equation (7) yields: $(-1)^0 N_0 + (-1)^1 N_1 = 2 - 2 \times 1$ which is equal to $N_0 - N_1 = 0$ or $N_{min} - N_{max} = 0$. Since a circle (or even a distorted circle which may represent the PE function) has at least one minima and one maxima, it satisfies this equality. Similarly, for a spherical pendulum, the configuration space is an even dimensional sphere $S^2$ with $m=2$ and $g=0$. A sphere has at least one critical point with an index equal to 0 ($N_0=1$), which is a minima, and at least one maxima with index equal to 2 ($N_2=1$) because we can move downward along two directions. There are no saddle points in an undistorted¹⁵ sphere so there are no critical points with an index equal to 1 ($N_1=0$). (From a two-dimensional saddle point, one can move downward along one direction, but the other direction is an upward direction, so the index is 1). Equation (7), therefore, yields: $N_0 + N_2 = 2=\chi$ (since $N_1=0$) and satisfies the equality. For double pendulums, $m=2$, Eq. (7) reduces to the familiar $N_0 - N_1 + N_2 = 0$ or $N_{maxima} - N_{saddle} + N_{minima} = \chi = 2-2g$ = 0. For triple and higher order n-tuple pendulums, the configuration space is an n-dimensional torus with $\chi =0$ and thus Eq. (7) can be extended to n-tuple pendulums in the form

$$\begin{aligned} \sum _{k=0}^{k=m} (-1)^k {N_k} \ge 0, \end{aligned}$$

(8)

which becomes an equality for $k=n$.

While we have formally extended Lange’s account to n-tuple pendulums, there is a major worry that prevents this account from being useful for higher dimensional pendulums. (We set the concerns arising from degeneracy aside for now.) Our worry is that such explanations sneak in causal reasoning via the backdoor.¹⁶ Unlike the homology of a circle, a sphere or a torus, we cannot find out (by plain geometric reasoning) the number and the index of associated saddle points that occur in a distorted n-torus, even as we can reason about the indices of the local minima and maxima using the dimension of the manifold. (A global minima will have an index equal to 0 and a global maxima will have an index equal to the dimension of the manifold.) One therefore needs to use the Hessian to find out the index of the critical points which defeats the very purpose of using purely topological reasoning—for two reasons. Firstly, using the Hessian already involves all the groundwork (causal reasoning) that is needed to find the number of critical points of the system—a subsequent topological embedding (non-causal reasoning) then seems much less useful or enlightening. That is, the information on the number of critical points will already be revealed after analysing the Hessian in the first place (with some more back-of-the-envelope calculations)! Secondly, the Hessian employs not merely causal reasoning with ordinary empirical facts (such as the length of the rods or their shape, which constitute the task at hand or form its background conditions), it rather involves causal reasoning with the particular forces at work, a strategy that Lange may want to avoid:

Any causal explanation in terms of forces must go beyond Newton’s second law to exploit the particular forces at work – if not specifying them fully, then at least appealing to their relevant features (such as their proportionality to the inverse-square of the distance). This is not done by the distinctively mathematical double-pendulum explanation (which is why it can apply to double pendulums that differ in the particular forces at work). (2016, p. 30)

Contrary to Lange’s claim above, reasoning with partial derivatives of the PE function to evaluate the index of the topological mapping needs to be done on a case-to-case basis using the Hessian, which involves an appeal to the causal considerations of the particular forces at work—this is not permitted in an explanation which claims to be a DME. The reason why we did not face similar difficulties with the torus case in E1 is because the indices of all the critical points were intuitively evident after glancing at the torus—an approach that is not suitable for higher dimensions. Nonetheless, causal reasoning was involved even in the case of the two-dimensional torus since the index needs to be determined formally via the Hessian. An intuitive glance at the torus seemed to bypass causal reasoning, yet it did not, because we had prior information about the indices of the critical points of the torus, and thus causal reasoning snuck in via the backdoor.

A reader may object here that Lange’s account does not preclude the possibility of embedding certain physical or empirical facts in a DME.¹⁷ But including an analysis of the Hessian is not any ordinary physical fact about the system—it is all the causal reasoning that one needs to engage in to make the explanation work, whether causal or non-causal. Saatsi (2018) also raises an objection about Lange’s consideration of the equilibrium information derived using the Newton’s second law with his DME, without requiring an analysis of the specific forces, as a non-causal explanation. Saatsi argues: “....I am not sure why an explanation should thus involve any more specific features of the forces at work (or their effect on motion) in order to be causal. Admittedly, the causal information provided by (the pared-down version of) Newton’s second law is rather abstract, but arguably this is all the causal information that is relevant for the (relatively abstract) explanandum at stake” (2018, p. 267). Our argument is more modest than Saatsi’s in that even if the more abstract form of Newton’s second law is embedded in the arguably non-causal explanation, it should not include a detailed analysis of the particular forces that provide us with all the information (about the changes in potential energy caused by the particular forces when embedded in the Hessian) we need about the system’s equilibrium positions, because if that is so, then the explanation violates the very premises that Lange sets for them to be considered as a DME. Thus, even as the number of critical points of any n-tuple pendulum may be allegedly constrained by Eq. (8), as set out by the extension of E1, one cannot use this as a legitimate DME because it needs to appeal to the particular forces at work via the Hessian. (Note that this causal implication was not directly evident in the case of the torus, but one can now appreciate how a large amount of causal information concerning particular forces can get buried under a deceptively simple ‘non-causal’ explanation.) Is there a way to shell out a potential DME which can avoid these problems? In the next section, we discuss a more general approach to finding the equilibrium positions of pendulum systems, which not only removes the problems (with the associated causal reasoning) of ascertaining the index and number of critical points for n-tuple pendulums but also provides more information on the nature of the critical points of such pendulum systems. But after sketching the improved account in Sect. 3 below, we show in Sect. 4 why both the original account, that Lange provides, and the extended account fail as modal interpretations.

3 E2: Improved strategy: Betti numbers

The strategy sketched in the previous section relies on the index of critical points and the associated Euler characteristic. In this section, we sketch an alternative and improved strategy of using Betti numbers, which are epistemically more conducive for reasoning with higher dimensional configuration spaces including n-tuple pendulums. The strategy is an improvement both over Lange’s and its extension in that it gives a more precise lower bound on the number of equilibrium positions including both stable and unstable positions. Even though we refute this improved account (along with Lange’s original account and the extension) as a modal explanation in the later sections, we sketch it here to be able to show later how even the most precise and widely applicable topological explanations cannot count as modal explanations for any n-tuple pendulums.

Table 1 k-th Betti number for a circle, sphere and torus

We first introduce Betti numbers. Betti numbers are topological invariants for smooth and compact topological surfaces that are Morse functions (See Table 1). The k-th Betti number shows the number of k-dimensional holes on a topological surface. (For any k-dimensional surface, the n-th Betti number is always zero for any $n>k$.) This result can be connected with the number of stable positions obtained in a pendulum system (after its PE function has been mapped to its configuration space). For any n, the k-th Betti number (where $k<n$) of the n-dimensional torus can be shown to be equal to the lower bound on the number of equilibria of the n-tuple pendulum with k stable directions where each stable direction implies a pendulum rod pointing downward.

This is because the number of k-stable directions for an n-tuple pendulum is $n \atopwithdelims ()k$, which is equal to the k-th Betti number of the n-torus. The reason why $n \atopwithdelims ()k$ describes the k-th Betti number of the n-torus is because of the total number of dimensions, n, one can choose k number of ways to travel from a given point, and if one reaches the same point after travelling then such a direction can be designated as a k-dimensional hole.

As an illustration, consider this. The configuration space of a double pendulum is a torus. As shown in Table 1, for a torus, $\beta _0 =1$ shows the number of connected surfaces, and $\beta _1 =2$ and $\beta _2 =1$ correspond to the number of k-th dimensional holes (i.e. 1D and 2D) in the torus. A double pendulum can have $2 \atopwithdelims ()1$ or 2 stable directions when only one rod is pointing down, which is equal to $\beta _1=2$ , or $2 \atopwithdelims ()2$ or 1 stable direction when both rods are pointing down which is equal to $\beta _2=1$ , and also $2 \atopwithdelims ()0$ or 1 stable direction, which is equal to $\beta _0=1$ when no rods are pointing down. The same can be illustrated for a simple pendulum, a spherical pendulum or for any higher order n-tuple pendulum.

We now state E2 again:

(E2) If a physical system is an n-tuple pendulum, then it has at least $2^n$ equilibrium positions, for the reason that the lower bound on how many equilibrium positions it has is given by the sum of the associated Betti numbers of the distorted n-torus (as in E1), and these sum to $2^n$.

The strategy used in E2 is backed by the Morse theory, in particular the Morse inequalities. There are two versions of the Morse inequalities:

Strong Morse inequalities:

$$\begin{aligned} \sum _{k=0}^{k=r} (-1)^k {N_k} \ge \sum _{k=0}^{k=r} (-1)^k {\beta _k}, \end{aligned}$$

(9)

where $\beta _k$ is the k-th Betti number; r is a positive number less than m, which is the dimension of the manifold M; and $N_k$ is the number of critical points with the index k. This inequality becomes an equality for $r=m$.

Weak Morse inequalities:

$$\begin{aligned} N_k \ge B_k. \end{aligned}$$

(10)

Also, the Euler characteristic of a manifold is an alternating sum of Betti numbers as shown below:

$$\begin{aligned} \chi (M) = \sum _{k=0}^{k=m} (-1)^k {\beta _k}. \end{aligned}$$

(11)

The equations above reveal how Betti numbers determine the nature of the critical points of differentiable functions defined on M.

Not only does this strategy give the lower bound on the number of stable positions for every k-th Betti number, but it also gives us the lower bound on the total number of equilibrium positions (both stable and unstable). If we add all the possible Betti numbers associated with the stable positions of the pendulum system (or all Betti numbers of the configuration space), using induction and Pascal’s identity for binomials, we obtain

$$\begin{aligned} \sum _{k=0}^{k=n} {n \atopwithdelims ()k} = {n \atopwithdelims ()0} + {n \atopwithdelims ()1} + {n \atopwithdelims ()2} + \cdots + {n \atopwithdelims ()n} = 2^n. \end{aligned}$$

(12)

The summation of all the Betti numbers gives $2^n$ as the total number of such positions. (This can also be obtained purely by binomial induction observing the positions of a pendulum system. Each rod can be either up or down, and thus for n rods there are $2^n$ ways of doing this.) The difference between this strategy and the extended strategy (discussed in Sect. 2.3) thus lies mainly in using Betti numbers in a way that obviates the need to calculate the index of the critical points, even as Betti numbers are related to the index of the critical points via the Morse inequalities.

We have shown how E2, using Betti numbers, provides a more appealing way to explain the number of critical points of a pendulum system as compared to the extended E1. We are now equipped to show why these explanations, despite their wide applicability and striking precision, fail as modal explanations or DMEs.

4 Failure of E1 and E2

Let us reiterate the modal argument first. Lange argues that the DME for a double pendulum applies to all kinds of double pendulums, whether those with stiff or non-stiff rods, or even pendulums with spring rods (2016, p. 31). This is because all double pendulums share the same configuration space, a non-causal mathematical abstraction of the system, and mapping the differentiable PE function of the pendulum system onto its configuration space results in a distorted torus which preserves the homology of the configuration space despite a change in various causal details related to the system. (A change in causal details implies a change in the antecedents of Lange’s necessarily true conditional. A change in the antecedents may include a change in the type of rod of the pendulum system, such as spring rods or compound wide-bodied rods, or even a change in the particular forces acting on the system.) Because the homology related to the PE function is preserved under a wide range of forces, it allows us to reason about the number of critical points of the PE function using the Morse inequalities as a constraint which Lange argues to hold with a greater degree of necessity than the related causal laws. (In the previous sections, we extended this argument to potentially cover all n-tuple pendulums.) This unifying strategy (encompassing a varied range of forces and all kinds of double pendulums) is what gives a strong modal flavour to Lange’s explanation since no other causal explanation (such as using partial derivatives of the PE function that analyse forces on a case-to-case basis) reveals why every double pendulum has four or more equilibrium positions. However, we suggest that Lange’s DME fails as a modal explanation (apart from the problems associated with causal reasoning sneaking in via the backdoor) because the various causal details related to the particular forces acting on the system do matter to the explanation—we show how the causal upshot of his DMEs, and their extensions and improvements on them, is further revealed when we vary the antecedents of his conditional by introducing perturbations in the pendulum system. We will also show how the candidate DMEs may fail to predict the number of equilibrium positions in a range of cases and why we cannot account for their failure by narrowing down the antecedent of the conditional.

It will be useful to briefly discuss what we mean by ‘perturbations’¹⁸ and why introducing perturbations lead to a failure of Lange’s account. Perturbations here mean an intervention (in the sense of Woodward, 2003) or a small change in one of the parameters or variables of the system in the sense of being an active causal intervention on the system in relation to changes in the particular forces acting on the system. Another sense in which perturbations can be understood here is as a consideration of what-if-things-had-been-different questions without necessarily engaging in an actual intervention in the system.¹⁹ Consider a system S with the variables x and y, which define a state of the system, and suppose we introduce a small change to the variables x or y by replacing x with $x+\epsilon x_1$ or y with $y+\epsilon y_1$, where $\epsilon$ is small. In the case of pendulum systems these variables are the length of the rods, the inclination of these rods with respect to the horizon and any forces acting on the system, all of which help define the potential energy of the pendulum system and thereby its equilibrium positions. While a perturbation in these variables will alter the potential energy of the pendulum system, this change will leave the configuration space of the system unaffected. This is because the configuration space simply depends only on the degrees of freedom of the pendulum rods—if each of the n rods can move around in a path space of $2\pi$ radians, then the configuration space of the system will be an n-torus. Lange’s argument is that the number of equilibria is constrained (with a higher order of necessity than involving the particular causal forces) due to the system’s configuration space being what it is. And thus, an intervention in the length of the rods should leave the number of equilibria unchanged in so far as the non-causal explanation is deemed correct. Notice that an intervention of the kind that will alter the configuration space of the system, such as physically constraining the movement of the rod, is ruled out here since it is a change in the empirical facts (and related antecedents) that set up the case. (The antecedent takes the configuration space of any double pendulum, where each of the rods is free to move in a path space of $2\pi$ radians, to be a torus, and if the pendulum is prevented from moving freely around the hinge, the configuration space of the restricted pendulum will not be a torus.) We aim to show that even if the contextually relevant antecedents remain largely invariant, preserving the empirical facts of the case, a perturbation introduced in the pendulum system may still lead to the failure of the conditional in two ways:

• (a) It will invalidate the truth expressed by the conditionals E1, its extension and E2, such as by showing that it is not necessary for every double pendulum to have at least four or more equilibria despite their configuration space being a torus, which reveals that causal details related to the particular forces are relevant to the conditionals, and

• (b) The applicability of the modal conditional itself depends on the causal details of the system, i.e., the conditional fails to be a generalised mathematical ‘explanation’ in cases where non-Morse potential energy functions are involved.

Both the arguments rob the modal status of Lange’s conditional by showing that the strong form of necessity that Lange accords to mathematical explanations is incorrect. Further below, we consider a potential objection to our arguments where one may attempt to narrow down the conditional to preserve its modal strength by packaging the exceptions (such as the non-Morse PE functions) out of the conditional by using a suitable change in the antecedents or initial conditions. We defuse the objection by arguing in Sect. 5.2 that any such packaging will inevitably involve a detailed consideration (causal analysis) of the particular forces acting on the system. If a suitable change in the antecedent of a necessarily true conditional is arrived on a case-to-case basis based on a causal analysis of the system (considering whether the potential energy function is a Morse function or not), this makes it evident that the seemingly non-causal explanation involves bracketing various causal assumptions which reveal themselves where the non-causal explanation breaks down.

A major presumption in using the configuration space to predict the number of equilibrium positions of the pendulum system is that the PE function of such a complex dynamical system is always a Morse function. This by no means is a trivial presumption and we show how both E1 and E2 may break down if the PE function is a non-Morse function, which is not uncommon to find across complex dynamical systems.²⁰ In such a case, the Morse inequalities (or its extensions, as discussed in Sect. 4.3) do not explain why the pendulum system has such and such number of equilibrium positions. Our argument is based on exposing the inapplicability of the topological framework when perturbations are included in the PE function in such a way that:

• (a) one or more critical points of the PE function become degenerate, which makes it difficult or impossible to calculate the index of these degenerate critical points, because they are undefined, making Morse inequalities inapplicable, and/or

• (b) the PE function may no longer be mappable to a smooth or compact manifold, and thus Morse inequalities fail to be applicable.

We also discuss some extensions of Morse theory that deal with a sub-set of the cases as outlined in (a) and (b) above, but we show why these are not overarching solutions and how a gap remains in addressing (a) and (b) more generally in differential topology unifying the topological explanation of the number of critical points for both Morse and non-Morse functions. We then conclude this section by noting that, at best, E1, its extension and E2 can be seen as important and restricted applications of algebraic topology for the study of pendulum systems, but they by no means constitute DMEs.

4.1 Case (a): Degeneracy due to perturbations

If all pendulum rods are stiff, and if they obey the restrictions on length suggested in the previous subsection, then it would appear that Lange’s explanation and our improved versions thereof should work well. After all, in this case the PE function is a Morse function, its critical points are non-degenerate points with a well-defined index, and the distorted manifold obeys the Morse inequalities. However, when the pendulum rods are non-stiff, the PE function may become degenerate at one or all of its critical points. Morse inequalities fail to be applicable in such cases and fail to explain why the pendulum system has as many equilibrium positions as it does. (We deal with extensions of Morse inequalities to special cases of degeneracy in Sect. 4.3.)

To introduce non-stiffness in the pendulum rods, we make use of non-linear perturbations in the length of the pendulum rods which will affect the PE function in a non-trivial way. To begin with, we look into length perturbations in the rod of a simple pendulum, and then extend this treatment to any n-tuple pendulum.

For a simple pendulum, the PE function $U(\alpha ) = L \cos \alpha$ is a distorted circle in the case that the rod remains stiff, the length remains unperturbed and the angle of inclination made by the rod with respect to the downward direction is $\alpha$. In this subsection, we perturb the length of the rod L is such a way that the distorted configuration space of the simple pendulum remains smooth and compact (a restriction we relax in the next subsection), and its PE function thus remains definable over the configuration space. In order to do so, we impose the following constraints on the perturbation $g(\alpha )$. If

$$\begin{aligned} U_{pert}(\alpha ) = (L + g(\alpha )) \cos \alpha , \end{aligned}$$

(13)

then

$$\begin{aligned}&U_{pert}(\alpha ) = U_{pert}(\alpha - 2\pi ), \end{aligned}$$

(14)

$$\begin{aligned}&U'_{pert}(\alpha ) = U'_{pert}(\alpha - 2\pi ), \end{aligned}$$

(15)

and

$$\begin{aligned} U''_{pert}(\alpha ) = U''_{pert}(\alpha - 2\pi ), \end{aligned}$$

(16)

where $U_{pert}(\alpha )$ is the perturbed PE function, $U'_{pert}(\alpha )$ is the first partial derivative of $U_{pert}(\alpha )$ with respect to $\alpha$, and $U''_{pert}(\alpha )$ is the second such partial derivative. Equation (14) ensures that the PE function remains mappable to the topological circle which may be definable on $(\alpha , \alpha - 2\pi )$ for any $\alpha$. Equation (15) ensures that the perturbed PE function is differentiable on the circle as defined on $(\alpha , \alpha - 2\pi )$. (If the PE function is not differentiable, then it implies that the force cannot be defined at that point, which is physically impermissible as per Newtonian mechanics.) Equation (16) ensures that the second partial derivative is definable because if this condition is not met, then the index of the critical point becomes indeterminate (as shown previously in Sect. 2.1).

Based on the aforementioned conditions, and assuming $mg=1$ for the sake of simplicity, we introduce the perturbations,²¹ as in the following Eqs. (17) and (18) for the values of $L=1$ and $L=2$ respectively. We plot their degeneracy at certain critical points in Fig. 5. (We have now assumed the potential energy to be positive rather than negative, as is conventionally assumed—this gives us better-looking graphs.)

$$\begin{aligned}&U_{pert_1}(\alpha ) = (1 + \sin \alpha ) \cos \alpha \end{aligned}$$

(17)

$$\begin{aligned}&U_{pert_2}(\alpha ) = (2 + \sin ^2 \alpha ) \cos \alpha \end{aligned}$$

(18)

Fig. 5

Degeneracy in the perturbed PE functions: both $U_{pert_1}(\alpha )$ and $U_{pert_2}(\alpha )$ are degenerate at the inflection points $(2n\pi - \frac{\pi }{2})$ and $n\pi$, respectively, for $n \in {\mathbb {Z}}$, where the first-order partial derivative meets the second-order partial derivative

For functions dependent on only one variable, degeneracy occurs where the first-order partial derivative meets the second-order partial derivative at the horizontal axis. (A Hessian matrix is used for multi-variable functions, as shown in Sect. 2.1.) As shown in Fig. 5, degeneracy is introduced in some of the critical points of $U_{pert_1}(\alpha )$, such as at $(2n\pi - \frac{\pi }{2})$, whereas in $U_{pert_2}(\alpha )$, all critical points are degenerate at $n\pi$, where $n \in {\mathbb {Z}}$. Also, the degree of degeneracy is higher in $U_{pert_2}(\alpha )$ since the second-order partial derivative is flat where it meets the first-order partial derivative. One may verify that even the third-order partial derivative gives a flat slope at $n\pi$ in the case of $U_{pert_2}(\alpha )$ implying that all the critical points of $U_{pert_2}(\alpha )$ are badly degenerate. One cannot use Morse theory for these functions (save some of the extensions, which we discuss in Sect. 4.3), especially in the case of $U_{pert_2}(\alpha )$ since ascertaining the index of such badly degenerate critical points is not possible (Popescu, 2004, p. 47). Morse inequalities fail to apply here, and the force of the modal explanation is broken.

The argument can be easily extended for perturbations introduced to the rods of any n-tuple pendulum. Let us extend this to double pendulums first and then by induction one can see how it extends to higher-order pendulums. The Hessian matrix (H) of the partial derivatives of the PE function concerning a double pendulum can be written as:

$$\begin{aligned} H_{U(\alpha , \beta )}(p) = \begin{vmatrix} {\frac{\partial ^2 U(\alpha , \beta )}{\partial \alpha ^2}}&{\frac{\partial ^2 U(\alpha , \beta )}{\partial \alpha \partial \beta }} \\ {\frac{\partial ^2 U(\alpha , \beta )}{\partial \beta \partial \alpha }}&{\frac{\partial ^2 U(\alpha , \beta )}{\partial \beta ^2}}, \\ \end{vmatrix} \end{aligned}$$

(19)

where $U(\alpha , \beta )$ is the PE function of the double pendulum, $\alpha$ and $\beta$ are the angles of inclination of the rods with respect to the horizon, and p is a critical point of the PE function. If we assume that mg and Mg equal to 1 for the sake of simplicity, then $U(\alpha , \beta ) = (L + g(\alpha )) \cos \alpha + (L + K + g(\beta )) \cos \beta$, where L and K are the lengths of the top and bottom rods respectively. For the perturbations $g(\alpha ) = \sin \alpha$ and $g(\beta ) = \sin \beta$, introduced independently to each of the rods respectively, the Hessian becomes:

$$\begin{aligned} H_{U(\alpha , \beta )}(p) = \begin{vmatrix} {\frac{\partial ^2 U(\alpha , \beta )}{\partial \alpha ^2}}&0 \\ 0&{\frac{\partial ^2 U(\alpha , \beta )}{\partial \beta ^2}} \\ \end{vmatrix} \end{aligned}$$

(20)

because functions containing $\alpha$ as the only variable get cancelled out when taking a partial derivative with respect to $\beta$ and vice versa, and thus, ${\frac{\partial ^2 U(\alpha , \beta )}{\partial \alpha \partial \beta }}$ and ${\frac{\partial ^2 U(\alpha , \beta )}{\partial \beta \partial \alpha }}$ become zero. The test of degeneracy is that $H_{U(\alpha , \beta )}(p)$ should be invertible, that is,

$$\begin{aligned} D^2(H_{U(\alpha , \beta )}(p)) = {\frac{\partial ^2 U(\alpha , \beta )}{\partial \alpha ^2}} \times {\frac{\partial ^2 U(\alpha , \beta )}{\partial \beta ^2}}=0. \end{aligned}$$

(21)

If $D^2(H_{U(\alpha , \beta )}(p))=0$, then either ${\frac{\partial ^2 U(\alpha , \beta )}{\partial \alpha ^2}}$ or ${\frac{\partial ^2 U(\alpha , \beta )}{\partial \beta ^2}}$, or both must be equal to 0. Simultaneously, $\frac{\partial U(\alpha , \beta )}{\partial \alpha }$ and $\frac{\partial U( \alpha ,\beta }{\partial \beta }$ must also be equal to 0 at p because p is a critical point of the PE function. The PE function of the perturbed double pendulum is:

$$\begin{aligned} U(\alpha , \beta ) = (L + \sin \alpha ) \cos \alpha + ((L + \sin \alpha )\cos \alpha + (K + \sin \beta )\cos \beta ). \end{aligned}$$

(22)

The resulting partial derivatives are:

$$\begin{aligned}&\frac{\partial U(\alpha , \beta )}{\partial \alpha } = \frac{\partial (2 (L + \sin \alpha ) \cos \alpha )}{\partial \alpha }, \end{aligned}$$

(23)

$$\begin{aligned}&\frac{\partial U(\alpha , \beta )}{\partial \beta } = \frac{\partial ((K + \sin \beta ) \cos \beta )}{\partial \beta }. \end{aligned}$$

(24)

However, $\frac{\partial U(\alpha , \beta )}{\partial \alpha }$ and $\frac{\partial U(\alpha , \beta )}{\partial \beta }$ are essentially the same equations, only with a replaced symbol and an additional constant, which is 2 here. These are also the same prototypical equations that we encountered in the case of the simple pendulum when considering Eq. (17). Since the first partial derivative is the same function, the second partial derivative will also be the same function (with an additional constant). Thus, the degeneracy conditions of the PE function of a double pendulum reduce to just this:

$$\begin{aligned} \frac{\partial ^2 U(\alpha , \beta )}{\partial \alpha ^2} = \frac{\partial U(\alpha , \beta )}{\partial \alpha }= 0, \quad \text {or} \quad {\frac{\partial ^2 U(\alpha , \beta )}{\partial \beta ^2}}= \frac{\partial U(\alpha , \beta )}{\partial \beta } =0. \end{aligned}$$

(25)

These are essentially the same conditions (just replace the constants) that make the PE function of the simple pendulum a non-Morse function. Thus, for independent perturbations in each rod for any n-tuple pendulum, the degeneracy conditions will only be:

$$\begin{aligned}&\frac{\partial ^2 U(\alpha _1, \alpha _2, ...)}{\partial \alpha ^2} = \frac{\partial U(\alpha _1, \alpha _2, ...)}{\partial \alpha }= 0, \quad \text {or} \quad \nonumber \\&{\frac{\partial ^2 U(\alpha _1, \alpha _2, ...)}{\partial \alpha _{r}^2}}= \frac{\partial U(\alpha _1, \alpha _2, ...)}{\partial \alpha _r} =0, \end{aligned}$$

(26)

where $\alpha _1$, $\alpha _2$ and so on are the angles of inclination of the rod with the horizon for any $r \le n$ such that . Hence, the same family of solutions that make a simple pendulum’s PE function degenerate may be applicable to n-tuple pendulums if the perturbations in each rod are independent of each other.²² Therefore, we have shown that perturbations may generally make the PE function of any n-tuple pendulum a non-Morse function. Since Morse inequalities are inapplicable to such functions (save for some special cases, which we discuss shortly in Sect. 4.3), as the information about the number and index of the critical points cannot always be ascertained, the ‘modal’ strength of the topological explanation collapses for such perturbations. The explanation does not collapse because pendulums with degenerate critical points will always have a lower or higher number of critical points compared to cases where all critical points are non-degenerate. In fact, it may still be the case that most double pendulums with a smooth, compact and orientable configuration space, even those with degenerate critical points in the distorted configuration space, have four or more equilibrium positions.²³ (Those with a non-smooth distorted configuration space do not necessarily have four or more critical points as shown in the next subsection.) The explanation, and its modal reading, rather collapses because the causal upshot concerning the dependence of the explanation on particular forces is revealed: Morse inequalities fail to ‘explain’ the existence of so and so number of equilibrium positions if one or more such points are degenerate, where such degeneracy was introduced by perturbations, which may correspond to a change in the particular forces acting on the pendulum system. The theoretical framework of the Morse inequalities is not general enough to explain or accommodate these cases when such particular forces are involved.

The reader may recall that Lange’s account, as discussed in Sect. 1.2, leads to a unified explanation of the number of equilibria of double pendulums in that all such pendulums have at least four or more equilibria because they share the same configuration space, and the details of the particular forces acting on them do not matter. However, we have just shown that the details of the particular forces do matter and the broad conditional encompassing all double pendulums is not necessarily true. At this point, can Lange adopt a narrower conditional by accepting the relevant restrictions raised in this section and save his account by adopting a narrower version of E1, its extension or E2? That is, while there are DMEs for double pendulums where the PE function is a Morse function, this claim does not extend to systems with non-Morse PE functions?²⁴ We respond to these claims in Sect. 5.2 in detail by showing that there is no unobjectionable way to narrow down the conditional in a way that preserves its modal strength as a non-causal explanation.

4.2 Case (b): Mapping and perturbations

In the previous subsection we considered only such perturbations that ensured the smoothness and compactness of the distorted configuration space of the pendulum system. In this subsection we consider perturbations that break the compactness or smoothness of the distorted configuration space. In such a case the differentiable PE function fails to be definable over a smooth and compact manifold (the configuration space of the pendulum), and thus the strategy of studying Morse differentiable functions on smooth, compact and orientable manifolds fails as well. This leads to a further collapse of the modal argument because (i) it is not necessary that the distorted configuration space of all n-tuple pendulums, including double pendulums, are compact manifolds and (ii) not all pendulums necessarily have smooth configuration spaces.

To illustrate case (i) for non-compact manifolds, we no longer need to restrict ourselves to the constraints specified in Eqs. (14), (15) and (16) that pertained to the compactness of the manifold over which the PE function was defined. (The PE function still needs to be differentiable, but not necessarily ‘over’ a closed or bounded manifold; it can be differentiable over an open manifold.) Consider the following perturbations that lead to a continuous increase in the length of the rod of a simple pendulum (see Fig. 6 where one such case is demonstrated):

$$\begin{aligned}&U_{pert_3}(\alpha ) = (2 + \alpha ^2) \cos \alpha , \end{aligned}$$

(27)

$$\begin{aligned}&U_{pert_4}(\alpha ) = \left( 2 + \frac{\alpha ^2}{1+\alpha ^2} \right) \cos \alpha . \end{aligned}$$

(28)

Fig. 6

Non-compact manifolds have only one critical point for a simple pendulum and there is additional degeneracy at $\alpha =0$

In the case of (27), the rods spiral outwards at a rapid rate. If such a PE function is mapped onto the configuration space of the simple pendulum, the distortion will result in an unbounded (non-compact) manifold. In (28), the rods converge to a total perturbation of $\lim _{\alpha \rightarrow \infty } {\frac{\alpha ^2}{1+\alpha ^2}} = 1$ over a long duration of time, but, nonetheless, result in a distortion that gives an unbounded manifold. In other words, the PE functions $U_{pert_3}(\alpha )$ and $U_{pert_4}(\alpha )$ cannot be defined over a bounded circle (manifold) which is the configuration space of the simple pendulum. One way to verify this is to check whether the partial derivatives of $U_{pert_3}(\alpha )$ and $U_{pert_4}(\alpha )$ are defined over the configuration space of the original bounded circle. One may verify that $U_{pert_3}(\alpha ) \ne U_{pert_3}(\alpha - 2\pi )$ and $U'_{pert_3}(\alpha ) \ne U'_{pert_3}(\alpha - 2\pi )$; the same is true for $U_{pert_4}(\alpha )$. These PE functions are also degenerate at $\alpha =0$. Also, there is only one equilibrium position in $(-\pi , \pi )$ (the complete path space of the pendulum) for the perturbed simple pendulum (see Fig. 6), which implies that for a double pendulum, with this perturbation, there can be only two equilibrium positions within this path space, and for an n-tuple pendulum, there can be only n such equilibrium positions. Thus, it is not necessary that every double pendulum has four or more equilibrium positions and that every n-tuple pendulum has at least $2^n$ equilibrium positions because such non-compact manifolds are a physical possibility, which are not covered within the theoretical framework of the Morse inequalities. The reason why these systems have less than four equilibrium positions can be explained by the external or internal forces that caused these perturbations. If these perturbations are caused by a variable force, then the net force on the pendulum bobs may not be zero at many (or even none) of the positions which were equilibrium positions earlier. Thus, depending on the force conditions, an n-tuple pendulum system may have anywhere between 0 and $2^n$ equilibrium positions. This makes the causal upshot of Lange’s DME explicit in that the details of the particular forces matter to the system and the purported non-causal explanation must bracket several causal assumptions in order to work.

Fig. 7

(left) Spherical pendulum suspended in a frame which rotates about a vertical axis and the resulting $(\varphi , \vartheta )$ configuration spaces (middle and bottom) for two different values of the moment of inertia or rotational inertia of the frame. (The one on the right is non-smooth when the rotational inertia limits to zero.) Adapted from Richter et al. (1996, pp. 19125–19132)

We now illustrate (ii) concerning non-smooth configuration spaces with the help of an example of spherical pendulums. Consider the case shown in Fig. 7 from Richter et al. (1996), where the angle $\varphi$ describes the position of the frame to which the (massless) $\vartheta$-axis is attached. Ordinarily, a spherical pendulum comprises a mass point suspended with the help of a rod that is free to move on a sphere $S^2$. The configuration space of such an idealised spherical pendulum is also $S^2$. The setup imagined here is idealised, in a non-trivial way, because Richter et al. (1996) note that:

In a physical implementation of [the spherical pendulum], a device must be chosen to hold the mass point on the sphere. It is practically impossible to do this without changing the dynamics in an essential way....[such that] the enlarged total system [which contains these modifications, such as a frame] almost inevitably has a configuration space different from [that of the sphere] $S^2$. This poses the interesting problem as to how the pure spherical pendulum may be recovered in a physical limit of some kind. (p. 19124)

When a frame is introduced, to implement a possible setup of spherical pendulums, as in Fig. 7, the configuration space of the spherical pendulum changes from that of a sphere $S^2$ to a torus or $T^2$ (the torus in the middle of Fig. 7). One might reason that when the frame gradually vanishes, such that its moment of inertia or rotational inertia $\theta$ limits to zero, $S^2$ might be recovered as a limiting case from $T^2$ as the configuration space of the spherical pendulum. But Richter et al. (1996, p. 19125) show that the $T^2$ instead dynamically decomposes into two spheres $S^2$ of opposite spins (bottom of Fig. 7). This is because, they argue, from the point of view of the suspended mass m alone, the positions ($\varphi$, $\vartheta$) and ($\varphi + \pi$, $2\pi - \vartheta$) are the same, but from the point of view of the frame, these are different positions distinguished by the position of the frame and value of the spin variable. (The spin is defined by the sign of $(\pi - \vartheta )$, which is $+1$ when $0< \vartheta < \pi$, and $-1$ when $\pi< \vartheta < 2\pi$.) The dynamics of the pendulum allow a change in the spin values in the presence of the frame but in the limit of a vanishing $\theta$, the spin becomes a conserved quantity resulting into this non-smooth bifurcation.²⁵

Thus, the Morse inequalities cannot apply to such cases because the manifold resulting in the limiting case when the spherical pendulum is recovered (with a vanishing frame) is non-smooth.²⁶ Moreover, ascertaining whether the configuration space of a spherical pendulum is smooth or non-smooth is non-trivial because it may depend on the physical implementation of the pendulum system, as noted above. (The configuration space may be a torus or two bifurcated spheres, depending on the value of $\theta$.) Thus, before applying the Morse inequalities to a particular spherical pendulum, one may not even know whether such a pendulum system has a smooth configuration space or not, and whether Morse inequalities even apply to such systems.

It is interesting that Lange does not even seem to consider that such physical possibilities may arise in pendulum systems or that topological reasoning about the number of equilibrium positions may fail in such cases. In all such cases, the strategies outlined in E1, its extension and E2 all fail to work because the configuration space of the pendulum system, which may be non-smooth or non-compact or both, cannot be mapped to Morse functions. The argument concerning the modal failure of his argument extends to n-tuple pendulums mutatis mutandis on grounds analogous to those introduced in the previous subsection. It may be noted, importantly, that the causal explanation, including the partial derivatives of the PE function, works in every single case irrespective of whether the PE function is a Morse or a non-Morse function, or whether the configuration space of the pendulum system is a non-smooth and/or a non-compact manifold. We have also shown previously that they fail for degenerate cases for smooth and compact manifolds.

4.3 Degeneracy workarounds

Are there ways in which the degeneracy or the non-compactness of the distorted configuration space may be worked around so that Morse inequalities are still applicable? We answer in the affirmative, but only concerning special cases. (This does not hurt our argument since modal force can still be denied provided the workarounds are not generally applicable to all cases involving degeneracy or non-compactness—we defend this argument in Sect. 5.2.) Morse theory has been extended to establish degenerate Morse inequalities (Bartsch et al., 2008; Bismut, 1986; Castrigiano & Hayes, 2019; Popescu, 2004; Witten, 1982) in restricted cases. We briefly discuss these accounts one by one and show why these extensions are inadequate as a general explanation of the behaviour of critical points for pendulum systems.

Bartsch et al. (2008) show that degenerate Morse inequalities may be proved for differentiable functions defined over a Hilbert manifold²⁷ with the critical assumption that these manifolds must be $2\pi$ periodic (or periodic in general as periods other than $2\pi$ may be re-scaled to a $2\pi$ period). But this assumption is non-trivial because it is not necessary that the distorted configuration space of a pendulum system has a constant period that may be re-scaled within ($-2\pi , 2\pi )$. Damped-driven pendulums and the perturbation equations sketched in (27) and (28) are some such examples (see Fig. 6 for a demonstration). So, his account does not tackle cases of degeneracy in cases where such distorted manifolds show quasi-periodic or non-periodic behaviour.

Popescu (2004), on the other hand, sketches an elaborate account in which degenerate Morse inequalities are proved by using heat flow vectors defined over a manifold. However, his account proves degenerate Morse inequalities for a non-compact manifold only as as a limiting case, and not strictly for compact manifolds (pp. 47–53). His account is not an extension of degenerate Morse inequalities to non-compact manifolds, it rather uses non-compact manifolds as a reasonable heuristic to prove degenerate Morse inequalities over compact manifolds. To see why Morse inequalities cannot be extended to all non-compact manifolds, consider the following. If a system is constrained to move within a compact, smooth and orientable manifold, a minima and a maxima are guaranteed by compactness. For example, if one moves around a smooth and closed circular surface (the configuration space of a simple pendulum), starting from a minima and returning to the same minima, one must encounter a maxima somewhere on the path, giving a total of at least two critical points. But this is not necessarily the case when either the path or the configuration space is non-smooth, non-compact or non-orientable. Non-compact manifolds, which are not closed, will not admit, in general, a non-trivial bound on the number of critical points because a minima on such manifolds may not necessarily be followed by a maxima (within a $2\pi$ period), which is crucial for Morse inequalities to constrain the number of critical points over such manifolds. However, if the motion is quasi-periodic, such as in Fig. 6, then a minima may follow a maxima, but this does not need to happen within one full rotation of the pendulum system (indeed, in Fig. 6 it doesn’t). This means that the number of critical points in such cases will be fewer compared to the cases when the motion is unperturbed and periodic, and therefore, a simple pendulum may have fewer than two critical points or a double pendulum may have fewer than four critical points within one full rotation. In addition to the problems concerning non-compactness, badly degenerate points, even in compact manifolds, cannot be handled using his account because the index of such points cannot be assessed generally, especially in higher dimensions. [We consider this case shortly when discussing Castrigiano and Hayes (2019) in Sect. 4.3.1.]

The account sketched by Bismut (1986) improves on that of Witten (1982). Bismut proves degenerate Morse inequalities for Morse–Bott functions which are generalisations of Morse functions. In Morse functions, the critical points are required to be non-degenerate in all directions, but in Morse–Bott functions, the critical point is required to be non-degenerate only in a direction normal to the tangent space of the manifold at the critical point, and not necessarily in every direction. However, this extended account also cannot handle degenerate cases, in general, since the normal to the tangent space may not necessarily be non-degenerate at a critical point, as is the case with badly degenerate points (for instance, Eq. (18) or its demonstration at the bottom of Fig. 5, which shows critical points that are degenerate in all directions). Thus, such functions cannot be classified as Morse–Bott functions, and the generalization to Morse–Bott functions does not necessarily hold for badly degenerate points. It, therefore, also fails to be a unifying framework accommodating all kinds of perturbations.

Having discussed all accounts except that of Castrigiano and Hayes (2019), we now turn to theirs and introduce the requisite mathematical framework as well. (We spend some time discussing this framework because it is the most general among the aforementioned, and perhaps also the most illuminating with regards to the topology of perturbed functions concerning our case.)

4.3.1 Catastrophe theory and degeneracy

Castrigiano and Hayes (2019) illustrate the Catastrophe theory, which is an extension of Morse theory dealing with a general classification of degenerate critical points. Catastrophe theory is built primarily on two theorems given by René Thom, a French mathematician. The theorems focus on the change in the number of critical points of a degenerate point (which is naturally unstable) when perturbed. For instance, $f=x^3$ has only one critical point at $x=0$, which is also degenerate. But upon introducing a perturbation ux, for small values of u, $f_{pert} = x^3 + ux$ now has three critical points for $u<0$, which are all non-degenerate, and only one non-degenerate critical point for $u>0$ (see Fig. 8). We can now state the theorems informally, which suffices for our purposes here.

Fig. 8

Three cases of perturbation and the unfolding of the function $x^3 + ux$

The first theorem of Thom states that it is possible to capture all possible unfoldings of a large family of functions by what he calls the seven elementary catastrophes. (These are called catastrophes because the behaviour of the function changes suddenly when the perturbation changes, causing a major shift in the topology of the manifold—see Fig. 8 as an example.) The critical points of the functions $x^3$, $x^4$, $x^5$, $x^6$, $x^3+y^3$, $x^3 - xy^2$ and $x^2y + y^4$ are called the seven elementary catastrophes. If one could reduce a function g(x) (such as by using Taylor expansion) to any of these elementary functions, then perturbations introduced in g(x) will behave in a similar fashion to these elementary catastrophes and one will be able to calculate the index of degenerate critical points of g(x). The second theorem of Thom states that this classification remains stable under small perturbations. The idea behind classifying the functions is that each elementary catastrophe behaves in predictable ways: one can assess the number of non-degenerate points that emerge after perturbing degenerate points (which, as shown before, are hard to deal with because of the lack of information about their index). From these non-degenerate points, one can then assess the index of the critical points of the function and then use Morse inequalities to reason about the number of critical points of even some non-Morse PE functions.

We now discuss why these two theorems, despite their immense usefulness in classifying degenerate critical points, do not deal with all the cases of degeneracy. Firstly, these classifications are only possible for functions in which the total number of variables or parameters does not exceed 4 or, in some exceptional cases, does not exceed 5 (Castrigiano & Hayes, 2019, p. 145). For triple pendulums and higher-order n-tuple pendulums, where a large number of interdependent parameters (such as interdependent perturbations of the rods which may be functions of the angles of more than one rod) are involved, these theorems fail to be applicable. Secondly, the classifications suggested by these theorems are not suitable for large perturbations, such as in Eq. (27) or Fig. 6. Thirdly, one needs to classify a particular function within one of the seven elementary catastrophes manually—the classification is not obvious from merely glancing at the function. For instance, it is not obvious that the function $h=\sin \beta (\alpha - \sin \alpha )$ can be classified as an $x^3$ catastrophe (Castrigiano & Hayes, 2019, pp. 204–205) . This is derived manually by using Taylor’s expansion, and unless one knows the prior association of a PE function to some elementary catastrophe, one is unlikely to be able to comment on the classification of the function. As the classification of the function is crucial for finding the general qualitative behaviour of the non-degenerate points obtained from perturbing degenerate points, there is always the worry that some PE function will not be classifiable into these elementary catastrophes. Even if such a PE function can be classified, accordingly, the index of the non-degenerate points of the functions obtained after perturbing the degenerate points needs to be assessed manually using the Hessian of the function, which creates the familiar difficulties discussed in Sect. 2.3 of this paper; this was the major difficulty which motivated the introduction of Betti numbers so that a manual calculation of the index using the Hessian matrix (a causal strategy) can be avoided. To sum up, the Catastrophe theory is inapplicable to a number of real-world pendulum systems, and it brings familiar problems of manually calculating the index of the critical points of the PE function (using causal reasoning), which defeats the very point of using a non-causal explanation. Therefore, this account, as well, does not generally explain the behaviour of critical points in perturbed pendulum systems and is thus insufficient as a supporting framework to allow a modal interpretation of E1, its extension or E2.

5 Summary, potential objections and generalisation of the findings

We first summarise the key findings of this paper, discuss our responses to potential objections to our arguments, and then make a brief remark on why these results hold importance more generally for other dynamical systems and some other views on mathematical explanations such as that of Reutlinger (2018) and Rice (2021).

5.1 Summary

• 1. Lange’s account (E1) can be extended to n-tuple pendulums and a greatly improved strategy (E2), using Betti numbers, to find a potential constraint on the number of equilibrium positions of n-tuple pendulums.

• 2. E1 and its extension sneak in causal reasoning through the backdoor. E2 bypasses this problem, but we show that E1, its extension and E2 are not modal conditionals since they apply only to cases where the PE function defined over the configuration space of the pendulum is a Morse function. This is revealed by the use of perturbations introduced to the length of the non-stiff pendulum rods (which may be caused due to a variation in the particular forces acting on the system). This shows that the explanations do depend on the particular forces acting on the system.

• 3. Workarounds concerning degeneracy or non-compactness fail to generally explain the behaviour of the critical points of n-tuple pendulum systems (including double pendulums). Even for the cases where the workarounds seem to provide reasonable explanations, it is not obvious by merely glancing at the pendulum system as to what technique or theoretical framework best explains the behaviour of critical points in that particular pendulum system. This needs to be figured out on a case-to-case basis employing an analysis of the particular causal forces, which defeats the very purpose of using a purported ‘unifying’ modal strategy.

• 4. It is not necessary that a double pendulum will always have four or more equilibrium positions (or that an n-tuple pendulum will always have $2^n$ or more equilibrium positions), and even for the cases where it has four or more such positions, this fact is not explained by any general topological framework such as Morse inequalities or its extensions that can handle degenerate or non-compact cases.

• 5. The failure of the conditionals E1, its extension and E2 due to a suitable change in the antecedents (such as perturbations caused by a set of particular forces) highlights a causal upshot of the problem, which was conveniently buried under the purported non-causal explanation.

• 6. Thus, Lange’s explanation of the constraint on the number of equilibria of pendulum systems and the more general and improved accounts cannot be held as DMEs because either (a) they sneak in causal reasoning via the backdoor, and/or (b) the associated conditionals either fail to be true under a suitable change in the antecedents or cannot be obtained without appealing to the particular forces at work. (The second point, a general philosophical point concerning DMEs, is elaborated in some more detail below when discussing the potential objections to our account.)

5.2 Potential objections

An objection to our arguments may be that the three candidate DMEs—E1, its extensions, and E2—still work for all pendulums with stiff rods and many pendulums with non-stiff rods. This being so—the objection continues—all we have shown is that these candidate DMEs apply with rather more restricted antecedents than Lange claims.²⁸ To this we reply that no change in the antecedent will let us frame a necessarily true conditional without admitting causal factors into consideration and thereby undermining the explanation’s purported distinctively mathematical and non-causal status. To help see why this is true, let us look at some examples. One way of restricting the antecedent to obtain a necessarily true conditional is as follows:

(E3): If a physical system is an n-tuple pendulum with a PE function that is a Morse function, then it has at least $2^n$ equilibria because of the mathematical constraints imposed by its configuration space, which is an n-torus.

Here the threat posed to Lange’s purported DME by non-Morse PE functions is avoide d by simply tightening the antecedent to exclude such problematic PE functions from the scope of the conditional. The problem with this way of proceeding is that in order to ascertain whether the antecedent of the conditional is true in the case of a given pendulum, it is now necessary to know whether the pendulum’s potential energy function is a Morse function, or not. Unfortunately for Lange, in order to know this, it is necessary, in turn, to conduct an analysis of the particular forces acting on the system—these forces being what determine the system’s potential energy. This being so, E3 is a causal explanation after all, initial appearances to the contrary notwithstanding. Instead of explaining why the pendulum has as many equilibria as it does based on purely mathematical considerations regarding the topology of the pendulum’s abstract configuration space, it requires that all the forces that are operative within the pendulum system be taken into consideration. It is these forces that are doing the explanatory weightlifting, not the mathematical abstraction.

Of course, E3 isn’t the only possibility. Another option is E4:

(E4): If a physical system is an n-tuple pendulum with completely stiff rods, then it has at least $2^n$ equilibria, because of the mathematical constraints imposed by its configuration space, which is an n-torus.

This conditional is necessarily true because the PE function associated with a pendulum system with stiff rods will invariably be a Morse function (since each rod will move in a predictable circular orbit, giving rise to an associated minimum and maximum in the pendulum’s potential energy function). But is E4 a DME? No, for two reasons. Firstly, in order to know whether a pendulum has stiff rods (or whether the rods will remain stiff during the course of the oscillations of the pendulum) we need to know about the particular forces acting on the system and the physical constitution of the pendulum rod. A large amount of causal reasoning about the particular forces and whether they may end up perturbing the length of the rod needs to be engaged in to ascertain whether the antecedent is even satisfied. (Also, are there any pendulums with perfectly stiff rods?) Secondly, if E4 is held to be a DME, then it gives rise to the following dilemma concerning the limited success of the original broader conditionals, namely E1, its extension and E2. It calls for a justification of how E1, its extension or E2 were even applicable as mathematical explanations for many double pendulums with non-stiff rods (perturbed or unperturbed): one can either accept this as an explanation by “coincidence” or an explanation by “constraint” (which is how DMEs are supposed to explain physical phenomena in Lange’s account). If one accepts this as an explanation by coincidence (for instance, that E1 was still applicable as a matter of coincidence to a bunch of pendulums with non-stiff rods), then it goes against the modal thesis. This is because the same mathematical explanation cannot be a coincidental explanation for a system with one set of initial conditions (for pendulums with perturbed non-stiff rods) and be an explanation by constraint for the same system with another set of initial conditions (for pendulums with stiff rods or unperturbed non-stiff rods). Since Lange claims that his DMEs are explanations by constraint, and, in fact, devotes a major part of his book arguing for the thesis that the necessity imposed by DMEs is not coincidental, one clearly cannot accept that the broader original conditionals, such as E1, worked as an explanation by coincidence for many of these double pendulums with non-stiff rods. Is it then an explanation by constraint? It is not, because we have shown earlier that many pendulums with non-stiff rods cannot be explained under this framework. The only way out of this dilemma is, therefore, to accept that E1 is not a DME and, mutatis mutandis, its extension and E2 are also not DMEs. The narrowed down conditional E4, which is essentially a restriction of the extension of E1 based on a certain set of initial conditions, thus faces the same dilemma and cannot be held as a DME either. So, a strategy based on narrowing down of the conditional based on a suitable change in the antecedents fails since it either involves an explicit analysis of the particular forces (as in E3) or it raises a dilemma concerning the applicability of the conditional in cases where it has had a limited success (as in E4).

Our aim in this paper was to analyse in detail how some mathematical explanations of rich and complex dynamical systems have a causal upshot, despite their promises to the contrary, and our largely mathematical approach is a fresh departure from most accounts in the literature that aim at a general philosophical critique of the problem without necessarily critiquing the scientific foundations of the problem. Therefore, another objection to our arguments may be that, given the sheer technicality that the reader must go through in the paper, the conclusion ends up being fairly narrow in scope: that is, it seems limited merely to Lange’s modal account of mathematical explanations and only discusses one putative example among many.²⁹ But the findings of this paper do generalise to other dynamical systems for which purported mathematical explanations may be given, especially those with periodic orbits and n degrees of freedom (we sketch this out briefly below in Sect. 5.2.1). We also show in Sect. 5.2.2 how our account is a critique of not only the modal account of mathematical explanations, which is Lange’s account of DMEs, but also some other general counterfactual accounts of mathematical explanations.

5.2.1 Extension to some other dynamical systems

Every dynamical system that moves in periodic orbits and has n degrees of freedom can be modelled topologically using configuration spaces and the distortion of its PE function upon mapping it on the configuration space. The degrees of freedom of the system correspond to the dimensions of its configuration space and the presence of periodic orbits allows a mapping of the system’s PE function onto a closed and bounded manifold of its configuration space. (The modelling then follows a framework similar to that of n-tuple pendulums as suggested in the previous sections.) The results of the previous sections concerning the degeneracy of PE functions of periodic systems (such as pendulums) then hold wider importance since they place certain general restrictions on the applicability of topological explanations (purported DMEs) that rely on the configuration spaces of such dynamical systems. This is because, to the best of our knowledge, Morse theory is the most suitable device in differential topology that connects differentiable functions related to the dynamics of a physical system to the topology of its configuration space, and it is simply not the case that the parameters of a physical system (such as its potential energy or any other energy function) must realise Morse functions. There is no general topological framework that can explain the behaviour of the critical points of both Morse and non-Morse functions that are mappable (or not mappable) to the configuration space of the physical system, and thus DMEs that exploit the configuration space in such a way are not tenable. The burden of finding whether such topological frameworks even exist rests on the proponent of such DMEs. Moreover, causal reasoning may sneak in via the backdoor, as we have shown in this paper. Thus, any purported DME that aims to accommodate the behaviour of such dynamical systems faces the challenges raised in this paper. Given the complexity of dynamical systems it is hard to see how we can have a non-causal explanation for certain aspects of their behaviour when no general topological framework explains their dynamics.

5.2.2 Applicability to some counterfactual accounts of explanation

We now briefly discuss two counterfactual accounts³⁰ of mathematical explanations that present a general theoretical framework for (most) non-causal explanations. We choose to focus on Reutlinger (2018) and Rice (2021) because their accounts claim to be general enough to account for various non-causal (and causal) explanations, and also because their counterfactual accounts fit well with the approach of this paper, namely looking into causally relevant antecedents for allegedly mathematical conditionals or explanations of some dynamical systems. Rather than attempting an in-depth examination of these accounts,³¹ we only aim to indicate the relevance of our arguments to the non-causal aspect of their counterfactual accounts in that (a) in order to support non-causal counterfactual conditionals we need to be able to circumscribe the antecedents in a non-causal way, failing which (b) it becomes evident that the counterfactual statements that, prima facie, seem non-causal actually have causal presuppositions.

Reutlinger (2018) argues that his monist account of counterfactual explanation (CTE) can accommodate both causal and non-causal explanations. The CTE consists of nomic generalisations, statements about the initial conditions and some further auxiliary assumptions, concerning an explanandum E, that, when assumed to be true or approximately true, allow us to deductively infer E or infer a conditional probability on E. The counterfactual dependency in E is revealed by a change in the initial conditions because if the initial conditions had been different, then E or its conditional probability would have been different as well. Rice (2021) points out that Reutlinger’s account of CTE does not include information about the factors that are irrelevant to E, which is crucial to understand why a non-causal explanation should be deemed a non-causal explanation. Rice thus introduces an additional layer in his account of the CTE by adding the desideratum that a CTE should be able to account for not only those factors that are relevant to understanding why E occurred, but also those that are irrelevant to its occurrence. He argues: “.....understanding that the initial conditions and trajectory of the system are counterfactually irrelevant to the occurrence of the explanandum is a crucial part of the [non-causal] explanation” (2021, p. 128). He also argues that a wide range of causal and non-causal explanations can be unified by looking at the counterfactual dependence and independence relations that hold between the explanans and the explanandum E. The central motivation for introducing irrelevant factors in his account is to provide a better understanding of why some factors that are irrelevant to E help constitute a universality class of the phenomena in question, which then helps us understand why the explanations of some phenomena are immune to changes in the initial conditions or their micro-physics. (His account is not necessarily an interventionist account, in the sense of the account of counterfactual explanations given by Woodward (2003)—it rather captures what-if-things-had-been-different questions aiming to capture a broader range of counterfactual information about non-causal explanations.)³²

However, their accounts face the same problem that Lange’s modal conditional does, because Lange’s conditional also includes information on why some factors are relevant or irrelevant to the occurrence of E. In this view, the shape of the pendulum or of rods or even the forces acting on the pendulum system are irrelevant to the occurrence of at least four equilibria of the system. The only major factor that is relevant to E is the torus shape of the configuration space, which allegedly preserves its homology upon being bent or twisted by a subsequent mapping of the PE function of the pendulum system on it. E1, its extension and E2 are all counterfactual conditionals of the form that, given certain initial conditions (a double pendulum subjected to an array of forces) and some auxiliary assumptions (such as a finite and continuous PE function), the nomic generalisation of the occurrence of at least four equilibria in a double pendulum, E, is explained by its dependency on the shape of the configuration space of the system. Even if the initial conditions were different, E would still occur in most cases; concerning the initial conditions where E fails to occur, one may resort to a narrower conditional of the form E3 or E4 to save the counterfactual account. However, as we have noted in the previous section, the occurrence of E, after all, is affected by a change in those initial conditions or such factors which were earlier considered as irrelevant to its occurrence. Although this is not so much of a problem for the CTE overall, because a different counterfactual with different initial conditions can still be correctly stated, it is a serious problem for a non-causal account of such a counterfactual explanation. As we have shown in the previous sections, narrowing down a counterfactual conditional to a form akin to E3 or E4 involves an analysis of those very causal factors (particular forces) that were considered to be irrelevant in the counterfactual explanation. If E is affected by factors that were seemingly irrelevant and if there is no unobjectionable way to circumscribe the antecedents of a counterfactual conditional (in a non-causal way that does not involve explicit causal reasoning with the particular forces), then one must admit that the seemingly non-casual counterfactual is not non-causal after all. The counterfactual conditional may claim to appeal primarily to non-causal mathematical factors, but, as we have shown, it is not actually a non-causal mathematical explanation—the counterfactual conditional involved has causal information in its antecedent.

6 Conclusion

The upshot of our paper is that non-causal mathematical explanations may conceal various underlying causal mechanisms (on which they crucially depend), which can be revealed by examining a general form of the explanation or by testing the associated conditionals using a perturbations-based approach. We have also shown that if circumscribing the antecedent for a necessarily true conditional involves making a causal analysis of the problem, then the resulting explanation is not distinctively mathematical or non-causal. Based on the arguments outlined in this paper, we cannot claim that DMEs of the physical properties of a dynamical system are flatly impossible. But we do claim that any such explanations that are based on configuration spaces—analogous to Lange’s purported topological DME of the number of equilibrium points of a double pendulum—will be flawed in general.