Criteria for naturalness in conceptual spaces

Abstract

Conceptual spaces are a frequently applied framework for representing concepts. One of its central aims is to find criteria for what makes a concept natural. A prominent demand is that natural concepts cover convex regions in conceptual spaces. The first aim of this paper is to analyse the convexity thesis and the arguments that have been advanced in its favour or against it. Based on this, I argue that most supporting arguments focus on single-domain concepts (e.g., colours, smells, shapes). Unfortunately, these concepts are not the primary examples of natural concepts. Building on this observation, the second aim of the paper is to develop criteria for natural multi-domain concepts. The representation of such concepts has two main aspects: features that are associated with the concept and the probabilistic correlation pattern which the concept captures. Conceptual spaces, together with probabilistic considerations, provide a helpful framework to approach these aspects. With respect to feature representation, the existence of characteristic features (i.e., that apples have a specific taste) is essential. Moreover, natural concepts capture peaks of a probabilistic distribution over complex spaces. They carve up nature at its joints, that is, at areas with no or low probabilistic density. This last aspect is shown to be closely related to the convexity demand.

1 Introduction

Humans and many other animals categorise things and events. They consider different entities as members of one category, that is, as instances of the same concept. The concepts that are involved in this cognitive process are not arbitrary but follow certain guidelines. Rosch (1978) starts her seminal overview of the prototype theory (‘Principles of categorisation’) by citing Borges’s fictional Chinese encyclopedia of animals, which consists of categories such as ‘those that tremble as if they were mad’ or ‘those that resemble flies from a distance’. She notes that such ‘types of categorisation [...] are never found in the practical or linguistic classes of organisms’ (Rosch 1978, p. 28). They are unnatural. The same quote from Borges is also found in one of Peter Gärdenfors’s first papers on conceptual spaces (Gärdenfors 1990, p. 90), where he proposed a geometric framework of natural concepts.

Although it is difficult and probably even impossible to define the naturalness of a concept, several characteristics are intuitively associated with such concepts. They are often found in the core lexicon of natural languages—meaning that many languages have words that (roughly) corresponds to such concepts—and are acquired without much instruction during language acquisition. Moreover, a large part of the knowledge about one instance of a natural concept is transferable to other yet unobserved instances of it. Prime examples of natural concepts are animal species: rabbit, horse, mole etc.¹ They occur in most folk taxonomies. We can generalise our knowledge about a species member to other members and children learn animal concepts quite easily. Other natural concepts only satisfy some conditions. For example, theoretical concepts such as electron are hard to learn without instruction but knowledge about instances is applicable in many contexts, including future observations. Note that the naturalness of the concept does not mean that the instances are natural rather than cultural objects. For example, car is a natural concept even though it refers to artefacts. In general, most concepts that play a role in our cognition are (more or less) natural concepts. A potential exception are ad-hoc concepts such as things to carry out of a burning house (Barsalou 1983). These can be arguably cognitively useful in a specific context but they are not natural concepts in the above sense. Also note that conceptual naturalness comes in degrees. According to Rosch (1978), basic level concepts such as dog are more natural than subordinated ones (e.g., Dachshund) or superordinated ones (e.g., animal).² Nevertheless, the latter concepts are still natural, especially in comparison to clearly unnatural concepts such as animals that resemble flies from a distance.

The philosophical debate about naturalness in concepts was very much influenced by Goodman (1955) and his example of the unnatural colour concepts grue and bleen. Things are called ‘grue’ if they are green when observed before a future time point t and blue afterwards. Bleen things, on the other hand, are blue before t and green afterwards. Until t, the statement ‘Grass is grue’ is as true and justified as ‘Grass is green’, but only the latter is a reasonable law on which one is willing to base predictions about the future. As Goodman states, green is projectible while grue is not. On the symbolic level, it is difficult to distinguish natural concepts. Goodman has famously shown that we cannot justify why to favour ‘green’ and ‘blue’ over ‘grue’ and ‘bleen’ without ending in a circular argument:

True enough, if we start with ‘blue’ and ‘green’, then ‘grue’ and ‘bleen’ will be explained in terms of ‘blue’ and ‘green’ and a temporal term. But equally truly, if we start with ‘grue’ and ‘bleen’, then ‘blue’ and ‘green’ will be explained in terms of ‘grue’ and ‘bleen’ and a temporal term. (Goodman 1955, p. 79)

Another example of a problematic concept mentioned in Goodman (1955) is non-raven, known from Hempel’s raven paradox (Hempel 1945).³ Again, logical reconstruction provides little help. The statements ‘Ravens are black’ and ‘Non-black things are non-ravens’ are logically equivalent and there is no logical criterion why to favour the first sentence. In response to the debate about arbitrary concepts, Quine (1977) introduced the notion of natural kinds as categories that ‘carve nature at its joints’. However, he did not give a final answer on how this carving is actually achieved.

The observation that not all important aspects of concepts are explainable on a symbolic level is a main motivation for using conceptual spaces. Taking a geometric viewpoint illuminates semantic aspects that remain concealed from a purely symbolic perspective and that are important for judging conceptual naturalness. Gärdenfors (1990, 2000, 2004) suggests capturing the naturalness of concepts by geometric and topological criteria, especially the famous criterion of convexity. In its most general form, the criterion of convexity states that natural concepts cover convex regions in conceptual spaces (Gärdenfors 2004). However, this criterion is more difficult to grasp than it appears at first sight. There are several non-equivalent formulations of the criterion and, in addition, different ways to interpret them. The first aim of the paper is thus to analyse this criterion and to note its advantages as well as its limitations. This will be done in Sect. 2. The result of this analysis is that most evidence in favour of convexity assumptions comes from the study of simple domains, such as the colour space. A large class of natural concepts, among them most noun concepts (e.g., raven, dog), however, are more complex. They are representable in many domains. For these concepts, the question becomes how convexity and other criteria contribute to their naturalness. The second and central aim of this paper is to find criteria for naturalness of multi-domain concepts and to relate them to the convexity assumption. Sect. 3 thus consists of an in-depth discussion of conceptual spaces as applied to multi-domain concepts.

2 Conceptual spaces and convexity

2.1 Conceptual spaces

Before delving deeper into the discussion of topological criteria for naturalness, I will provide an outline of the theory of conceptual spaces and their application in this paper. The most influential proponent of this theory is Peter Gärdenfors (1990, 2000, 2014). However, an earlier version of conceptual spaces (so-called attribute spaces) is already found in the work of Carnap (1971, 1980), who developed them as a background theory of an inductive epistemology.⁴ Moreover, the theory of conceptual spaces draws on psychological models of categorisation, such as Shepard (1987) or Nosofsky (1986).

The definition of a conceptual space, given by Gärdenfors (2000), is as follows:

A conceptual space consists of a class $D_1, \ldots , D_n$ of quality dimensions. A point in the space is represented by a vector $v=\langle d_1,\ldots , d_n\rangle$, with one index for each dimension. Each dimension is endowed with a certain geometrical or topological structure. (Gärdenfors 2000, p. 67)

Typical examples of quality dimensions are YEAR OF BIRTH and AGE, which can be measured quantitatively (on interval or ratio scales, respectively). In principle, however, non-quantitative dimensions are not excluded. An example of a comparative dimension is GENERATION (daughter, granddaughter, great-granddaughter etc.). Even dimensions with merely classificatory values such as GENDER or SEX are not excluded, though their topological structure is quite poor.

If several dimensions belong together, such as HUE, SATURATION and BRIGHTNESS, they are called integral. Intuitively, this means that it is psychologically impossible to assign a value on one dimension but not on the other one. For example, one cannot perceive the HUE of a shade of red without also perceiving its SATURATION. Another example of integral dimensions are PITCH and LOUDNESS. Dimensions that are not integral in this sense are separable. A complete set of integral dimensions forms a domain. For example, HUE, SATURATION and BRIGHTNESS form the COLOUR domain, in which specific colours are represented as regions, that is, as subsets of the colour space. Domains can consist of only one dimension that is separable from all other dimensions. For example, AGE is a one-dimensional domain and as such a primitive conceptual space. Most research, however, is focused on conceptual spaces that consist of several dimensions. Then the question becomes how the distance between points in the whole space relates to their distance on the single dimensions that form the space. Integral dimensions are usually associated with a Euclidean distance:⁵

$$\begin{aligned} d\left( x,y\right) =\sqrt{\sum \nolimits _{i=1}^nw_i(x_i-y_i)^2}. \end{aligned}$$

If the conceptual spaces connects non-integral, that is, separable dimensions, one uses the Manhattan distance:

$$\begin{aligned} d\left( x,y\right) =\sum _{i=1}^nw_i\left| x_i-y_i\right| . \end{aligned}$$

Both are special cases of the more general Minkowski distance:

$$\begin{aligned} d\left( x,y\right) =\left( \sum _{i=1}^nw_i\left| x_i-y_i\right| ^p\right) ^{1/p}, \end{aligned}$$

where the Manhattan distance corresponds to $p=1$ and the Euclidean distance to $p=2$.

The distance represents perceived dissimilarity. In a space with Manhattan distance, the dissimilarities on the dimensions are additive. That means that the overall dissimilarity is the sum of the dissimilarities in the single dimensions. In integral dimensions, dissimilarity does not add up in this way. For example, in a Euclidean but not in a Manhattan space, two points that have a medium distance in several dimensions are perceived as closer to each other than two points that are very close in one dimension but have a larger distance on the other (see also Fig. 1 on p. 7).

Conceptual spaces are mostly used to represent similarity judgements about stimuli. The aim is to translate degrees of dissimilarities into geometric distance. The number, meaning, and relation between the resulting dimensions are a matter of empirical research. The most commonly used method is multi-dimensional scaling by which one optimises the model fit in as few dimensions as possible. Ideally, the resulting dimensions are interpretable. That means, they should correspond to a certain aspect (attribute) of the concept, such as the dimension of BRIGHTNESS does in the colour space. When constructing spaces in this way, it is also empirically tested whether the dimensions are integral, that is, whether the Euclidean metric is appropriate (see e.g., Johannesson 2001).

Within the literature on conceptual spaces, one also often encounters spaces that are not drawn from similarity data but composed from pre-defined dimensions. For instance, Bechberger and Kühnberger (2019) treat a combination of AGE and HEIGHT as a conceptual space (see Fig. 4 on p. 14). Gärdenfors (1990) uses a space that combines a colour disk with the time dimension (Fig. 5 on p. 22) in order to illustrate the unnaturalness of the concept grue. Such product spaces are obviously not based on similarity data. I nevertheless view product spaces of intrinsically plausible dimensions or domains as conceptual spaces, even if they are not based on similarity data. It makes sense to demand that conceptual spaces are combinable into complex conceptual spaces. Indeed, combined spaces are already used extensively. For example, they play a role in the representation of part-whole relationships (Fiorini et al. 2014) or models of compositionality (Lewis and Lawry 2016; Bolt et al. 2017). To emphasise the difference to conceptual spaces that are directly drawn from similarity data, I will call them ‘combined conceptual spaces’ or ‘complex conceptual spaces’.

The general ambition of conceptual spaces is to represent concepts geometrically. The approach has some compelling advantages. Being a mathematical theory, it can be fruitfully implemented in artificial intelligence and machine learning. Moreover, it is also a psychologically adequate and empirically informed theory of cognition because it captures the important role of similarity for categorisation. However, there are also some philosophical caveats. During the last century, an intense debate revolved around the question what concepts are and whether they can be equated with definitions, theories or prototypes.⁶ Some philosophers, most famously Jerry Fodor, have argued against the idea that concepts should be equated with such kind of cognitive content. This reservations also concern conceptual spaces representations. For example, Fodor and Lepore (2002) explicitly criticised similarity-based models, including geometric ones.⁷

There are many roles that can be associated with concepts, such as referring, forming propositions, categorising, or drawing inferences. I readily concede that geometric representations cannot explain all these phenomena equally well. This article does not argue that concepts should be equated with geometric representations. I also do not aim to define concepts in terms of geometric structures. Rather I use these representations to explicate conceptual naturalness. For this goal, it is not necessary to assume that concepts are identical to regions in conceptual spaces. The more modest assumption to which I commit myself is that important aspects of concepts can be represented in conceptual spaces and that these representations are particularly helpful to understand why some concepts are more natural than others. This possibility to distinguish natural concepts opens a great philosophical potential of conceptual spaces.

2.2 Versions of convexity

The criterion of convexity is a core subject of conceptual spaces theory. Gärdenfors (1990, p. 88) first proposed it, stating ‘a property, that is, a region of a conceptual space, is natural only if the region is convex’.⁸ The criterion has been repeated in many of his other works, often in slightly different variations.

The notion of convexity relies on a ternary betweenness relation Babc, which states that b is between a and c. Note that the definition of the betweenness relation does not require a metric space, but merely quality dimensions at an ordinal level of measurement. From Babc, one can define convexity as follows: A region R in a conceptual space CS is convex if and only if for any points x, y, and z of the space, it holds that x is in the region if x is between two points y and z that are both in the region; more formally: $\forall x y z ((y,z\in R \wedge Byxz) \rightarrow x \in R)$. Convexity is thus closure under betweenness. There are no gaps at any line one can draw in the region. In one-dimensional spaces the convexity criterion collapses into the quite weak restriction that regions should be connected. In higher dimensional spaces, convexity is obviously stronger: e.g., a doughnut-like region is connected but not convex. An intermediate restriction between convexity and connectedness is star-shapedness, which demands that there is at least one point in the region such that all points between this central point and another point of the region are part of the region; formally $\exists y (y\in R \wedge \forall x z ((z \in R \wedge Byxz)\rightarrow x \in R))$.

The particular form of the betweenness relation, and thus convexity, depends heavily on the underlying metric of the space. Figures 1a, b give a graphical depiction of connectedness and star-shapedness as well as several forms of convexity in a two-dimensional space. The important observation is that convexity depends on the structure of the space. For example, the polar convex shape in Fig. 1b is not convex in a Euclidean space. In addition, Euclidean convex shapes are often not convex in a Manhattan metric.

Fig. 1

Geometric criteria for conceptual spaces: a displays unconnected, connected, star-shaped and convex regions in a Euclidean space. As demonstrated by b, the shape of convex regions also depends on the underlying betweenness relation

Convexity plays a major role in conceptual spaces research. However, the specific formulations and interpretations of this criterion vary considerably. Therefore, the criterion raises many questions: What kind of concepts are representable by convex regions? In which kind of spaces does the convexity criterion hold? Is it also found in complex spaces? Why does convexity hold (if it holds)? How is it justified? Is it an analytic truth or an empirical thesis?

In Gärdenfors (2000, p. 71), convexity appears in criterion P: ‘A natural property is a convex region of a domain in a conceptual space’. This restricts the demand to a specific kind of concepts, namely property concepts in domains. Natural concepts in general—most notably, noun concepts—are not directly restricted by criterion P. Rather with his criterion C, Gärdenfors claims that they consist of ‘a set of regions in a number of domains together with an assignment of salience weights in the domains and information about how the regions in different domains are correlated’ (Gärdenfors 2000, p. 105). Convexity is not mentioned in this criterion. Note, however, that several later formulations of criterion C explicitly include a convexity requirement (e.g., Osta-Vélez and Gärdenfors 2020, p. 5). Moreover, there are also very general formulations of the convexity requirement. In Gärdenfors (2004, p. 18), criterion P is stated as follows: ‘A natural concept is a convex region of a conceptual space’.

The most elaborated versions of the convexity principle are found in Gärdenfors (2014), where the semantics of different word classes are investigated. In this book, one finds a basic distinction between object categories, which largely coincide with the semantics of nouns, and all other kinds of concepts. For the latter, Gärdenfors proposes the so-called single-domain thesis: ‘Words in all content word classes, except for nouns, refer to a single domain’ (Gärdenfors 2014, p. 239). For all of these single-domain concepts, convexity criteria are proposed. The position in Gärdenfors (2014) can thus be summarised as follows: Natural concepts, except for object categories, are represented in one domain, namely by a convex region. An exception are object categories, which are determined by:

• (i) a set of relevant domains (may be expanded over time)

• (ii) a set of convex regions in these domains (in some cases, the region may be the entire domain)

• (iii) prominence weights of the domains (dependent on context)

• (iv) information about how the regions in different domains are correlated

• (v) information about meronomic (part-whole) relations. Gärdenfors (2014, p. 124)

This definition of object categories resembles the one for natural concepts in Gärdenfors (2000, p. 105) but explicitly includes the demand that the contributing regions have to be convex.

In view of its many versions, it seems quite misleading to discuss the convexity thesis. There are many non-equivalent formulations of it. I suggest distinguishing the following claims about natural concepts:⁹

• 1. Property convexity: Property concepts are represented as convex regions in a domain.

• 2. Domain specific convexity: Concepts, except for object categories, are

  • (a) domain-specific, and

  • (b) represented by a convex region in their domain.

• 3. Feature convexity: Object categories are represented by sets of convex regions in several domains.

• 4. General convexity: Concepts are represented by convex regions in conceptual spaces.

• 5. Complex spaces convexity: Object categories refer to convex regions in complex conceptual spaces.

Thesis 1 is the criterion P from Gärdenfors (2000). Thesis 2, which also includes the proposal of domain specificity, generalises this assumption for other concepts. Gärdenfors (2014) has argued for this thesis at length. The thesis of feature convexity (3) is proposed there as well. The assumption of general convexity (4), found in Gärdenfors (2004, p. 18), is perhaps the most general and famous formulation of the criterion.¹⁰

I am not aware of any explicit formulation of thesis 5, which thus needs some further explanation. It states that multi-domain concepts can be represented in a complex space, i.e., a product space of the salient contributing domains, and that they cover a convex region therein.¹¹ If the convexity thesis is generally true for all kinds of concepts, as suggested by thesis 4, then thesis 5 follows straightforwardly. It can even be argued that the complex spaces convexity criterion of thesis 5 is an immediate consequence of thesis 3. If $C_1$ and $C_2$ are convex regions in two domains $CS_1$ and $CS_2$, then the Cartesian product $C_1\times C_2$ is a convex region in the complex space $CS_1\times CS_2$. However, using such an argument presupposes that a complex concept is nothing more than the product of its features. Neither Gärdenfors nor other proponents of conceptual spaces theory endorse this view. Quite to the contrary, Gärdenfors (2014, p. 28) explicitly claims ‘that convex regions in product spaces are not just the products of convex regions of the underlying dimensions’.

It is difficult to single out one particular assumption as the convexity thesis. This obviously has implications for arguments in favour of or against convexity assumptions because they might only be relevant for one particular formulation while being irrelevant for another. Nevertheless, in the research on conceptual spaces, little attention has been paid to these possible differentiations and most arguments were interpreted in a general way. However, the interesting question is not so much whether convexity holds but rather which formulation of convexity should be accepted.

To complicate matters further, there are different ways to access and justify the convexity theses. Many analytic arguments have been advanced in favour of convexity. This suggests that it is a formal theorem. However, convexity can also be understood as psychological law that needs to be confirmed on empirical grounds (Gärdenfors 2019). Finally, many applications of conceptual spaces presuppose convexity in some form because it is a useful assumption for many purposes. The following subsections present and discuss the different forms of justifying convexity: analytic, empirical and the last, which I call programmatic.

2.3 Analytical support of convexity

Convexity theses can and have been supported on analytic grounds. In particular, two related arguments have been provided in favour of convexity. First, convexity follows from a Voronoi tessellation of a Euclidean space. Second, evolutionary models of language predict that the space will be carved into convex regions.

The argument based on Voronoi tessellation rests on accepting a version of prototype theory according to which there are salient cognitive prototypes (e.g., typical colours, shapes) that guide categorisation in terms of similarity (Rosch 1973). Translated to a conceptual spaces approach, this means that the space has some prototypical points and each point in the space is matched to its closest prototype.¹² The resulting regions (polygons) in a Euclidean space are convex (Okabe et al. 2000). Based on this observation, Gärdenfors (2000, p. 88) argues that convexity follows from prototype theory, at least for conceptual spaces with integral dimensions. As explicitly noted in Gärdenfors (2000, p. 91), the same argument does not hold in Manhattan spaces. Voronoi tessellations in such spaces yield star-shaped regions, but not necessarily convex ones. Fig. 2 shows the difference between a Voronoi tessellation in a Euclidean and a Manhattan space.

Fig. 2

Voronoi tessellations with a Euclidean and a Manhattan distance. Modified version of graphics from Jahobr’s Voronoi gallery (https://commons.wikimedia.org/wiki/User:Jahobr/Voronoi)

The relation between convexity and Voronoi tessellation is one important reason to distinguish between the convexity assumption for concepts that are represented in one domain (usually a Euclidean space) and concepts in non-domains (usually Manhattan spaces). The argument from Voronoi tessellation only supports domain convexity and, at least tendentiously, undermines it in other spaces. Additionally, the argument rests on the assumption that categorisations are driven by prototypes and similarity to them. However, the evidence for prior prototypes is largely limited to a few perceptual domains, especially colour (see Berlin and Kay 1969; Rosch 1973).

A powerful and parsimonious way to justify that human cognition favours a Voronoi tessellation, even without the existence of primary prototypes, comes from evolutionary game theory, which is used by Jäger (2007) and Jäger and van Rooij (2006). The linguists apply signaling game models to show that convexity is an expected consequence of language evolution. Signaling games first appeared in Lewis (1969) who developed them to solve the mystery of agreeing on semantics without any available language that could be used to define or explain the first symbols. Meanwhile such games have been further developed into an evolutionary model of language development (Skyrms 2010).

The idea of a signaling game is simple. One assumes a matter of fact is known to one player (the sender). Another player (the receiver), who is ignorant of this fact, has to choose between several actions. The utility of the actions depends on the matter of facts. If the receiver chooses the right action, both players will be rewarded. Depending on the state of the world, the sender uses a signal, that is, some arbitrary behaviour that can be perceived by the receiver. If the receiver associates the right kind of action with the signal, both players will benefit. Assuming that the players replicate their behaviour depending on their previous success, they will develop a meaningful communication. This is an example: Two persons go hunting together and share the prey. One person climbs up a tree and looks for animals. The other, who has a more limited vision field, does the active hunting. Nature decides whether a prey or a dangerous predator appears. The sender makes some noise (‘flee’ or ‘hunt’, for example) and the receiver acts accordingly. Successful communication will be rewarded (because both player end up with food) and finally stabilise. Unsuccessful interactions are unlikely to be repeated.

Signaling games are highly parsimonious with respect to cognitive assumptions about the players. The players can be human agents who intentionally enter a signaling game but this is not a necessary assumption of the model. The only critical assumption is that the reproduction of behavioural patterns depends on prior success. As Brian Skyrms puts it, ‘monkeys, birds, bees, and even bacteria have signaling systems’ (Skyrms 2010, p. 6).

The argument for convexity, which Jäger (2007) has elaborated, relies on the assumption that there are more states the sender perceives than available signals. For example, there are more perceivable colours, tastes or emotions than one could possibly name. The second assumption is that success in communication comes in degrees and that it depends on the similarity of the receiver’s interpretation and the state the sender perceived. The receiver associates a signal with particular points in the similarity space, for example, ‘red’ (primarily) with a highly saturated shade of red with medium brightness and ‘black’ with a very dark shade. Since both, sender and receiver, are rewarded if the receiver’s interpretation is similar to what the sender perceives, the sender should use a signal that is close to the particular point that the receiver (primarily) associates with the signal. For example, a slightly dark shade of red is usually better signalled by ‘red’ than ‘black’. A very dark shade of red, however, might be closer to the point that is associated with ‘black’.¹³ In any case, the sender optimises outcomes if she uses terms that are close to the receivers interpretation. Jäger (2007) shows that, in the long run, the receiver and sender will end up with a Voronoi tessellation of the conceptual space. In a Euclidean space, this means that the space is carved up into convex regions. The argument makes no assumptions about the cognitive abilities of the sender and the receiver; no prototype is needed. The centroid of the tessellation arises from the receiver’s interpretation of the signals. The matching of points to the closest centroid occurs because it is the most rewarding response of the sender.

Compelling as this argument is, it primarily supports Voronoi tessellation. It provides no support for convexity independently of Voronoi tessellation, for example, in Manhattan spaces (see also Hernández-Conde 2016). Since the Euclidean metric is usually associated with domains, the analytic arguments support first and foremost the thesis of domain convexity.

2.4 Empirical support of convexity

The above arguments, which are based on quite formal considerations, suggest that convexity must be viewed as an analytic property of natural concepts. However, according to Gärdenfors (2019), convexity is an empirical prediction of the conceptual spaces framework. This suggests that it has to be confirmed by the empirical study of concepts.

Currently, such empirical support is mostly found in the colour space. Jäger (2010) has investigated the colour terms in the languages of the world and confirmed that they are, with only negligible deviations, convex. This provides strong empirical confirmation of the convexity assumption in the field of colour semantics. However, it is still slim evidence in favour of convexity for all natural property concepts, let alone for other concepts.

Fig. 3

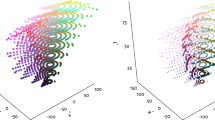
The vessel shape study in Douven (2016): Similarity judgements of the items shown in a are modelled in a three-dimensional Manhattan space in b. The region in front (green) represent bowl shapes while purple region represents the shape of vases. Graphics directly taken from Douven (2016, p. 85, 89). Copyright: Wiley, reprinted with permission from the author and Wiley

Additional empirical support comes from Douven (2016), who constructed a conceptual space of vessel shapes. His stimuli, shown in Fig. 3a, were inspired from Labov (1973). Douven constructed a shape space (see Fig. 3b) and gathered classification judgements. High and narrow vessels were typically viewed as vases, while low and wide shapes were categorised as bowls. He tested whether these classifications accorded with the convexity assumption by checking whether the smallest convex regions of objects that were classified as bowls (or vases, depending) also contained objects that were not classified as such. With only few exceptions, the individual classifications of every participant were consistent with the convexity assumption. Moreover, the majority vote satisfied it: the smallest convex region of objects that were classified as bowls (or vases) by the majority of participants did not contain stimuli that were not rated as such by most participants. His empirical data are thus consistent with the convexity assumption. This finding is particularly important because the shape space of Douven (2016) is not about property concepts but about object categories. In particular, Douven provides some support for the assumption that features of object categories (here: the shape of vessels) correspond to convex regions (Thesis 3 on p. 8).

Some support for convexity can also be derived from Dautriche and Chemla (2016). They show that words are typically perceived as homophones (i.e., different concepts that are labelled by the same form of symbol) when there are gaps between exemplars. They call this the ‘convexity constraint’. However, they do not consider the alternative criteria of connectedness and star-shapedness. While their experimental data indicate a decisive role of topological criteria, it is thus not so clear whether they really support convexity or a considerably weaker constraint, such as connectedness.

Though empirical evidence in favour of several versions of the convexity thesis has been found—especially the evidence from colour studies is overwhelming—current research findings are still insufficient to confirm all versions of the convexity assumption. In view of the diversity of human concepts, it is difficult to say how much positive evidence would be needed for this. However, in critical rationalist terms, convexity assumptions gain plausibility from the fact that they are easily falsifiable but not (yet) falsified. Accordingly, Gärdenfors (2014, 269) concludes his semantic theory by saying ‘following the Popperian methodology, I find it more rewarding to be fruitfully wrong than to be boringly correct’. This leads to a final way to justify convexity assumptions, namely in terms of their fruitfulness for research.

2.5 Programmatic justifications

Convexity can be viewed as a useful research assumption. Convex geometry is a highly developed field of mathematics with many established results. Against this background, it is reasonable to assume convexity—unless it is proven to be inappropriate—and make use of the rich repertoire of tools this assumption offers.

A particularly important notion is that of a convex hull. In many cases, we lack information about conceptual regions; we only have knowledge about some points that belong to a conceptual region. By creating the convex hull, one generates a unique subspace, namely the smallest convex region that includes all these points. Derrac and Schockaert (2015), for example, used convex hulls to define different genres of films in their conceptual space of movies. Creating convex hulls makes it prima facie difficult to empirically test convexity, because one presupposes its validity. However, if one also has data about points that are not perceived as part of the region, it is possible to check whether the convex hull includes such non-members. This is exactly how Douven (2016) has confirmed that the conceptual regions of vases and bowls are consistent with the convexity thesis.

To summarise, convexity assumptions can be justified on analytic grounds and on empirical ones. Furthermore, convex regions are well understood mathematical objects. This makes the assumption that concepts correspond to convex regions a fruitful default research hypothesis. Nevertheless, convexity criteria have been criticised. The next subsection addresses arguments against convexity.

2.6 Critics of convexity

The most explicit and extensive critique of convexity assumptions is found in Hernández-Conde (2016). The central point of his argument is that the analytic argument from above, namely the linkage between convexity and Voronoi tessellation, only holds for spaces with integral dimensions. This fact was already noted by Gärdenfors (2000, p. 91), but Hernández-Conde (2016) used it for a general attack against convexity. In a reply, Gärdenfors (2019) claims that convexity was never intended to be an analytic truth about concepts. He accepts that it might be false. Contrary to Hernández-Conde (2016), he claims that a lack of analytical support is not a problem. Rather, the convexity assumptions gain empirical content from being falsifiable.

Hernández-Conde (2016) also explicitly denies that the features of object categories are represented by convex regions (Thesis 3 on p. 8). He uses the example of swans, whose colour could be either black or white. Note that his example not only speaks against convexity but even against the weak constraint of connectedness. Gärdenfors (2019) answers that the concept of swan is not represented by the attribute COLOUR but rather by SHAPE. However, there are currently no criteria for what it means that a multi-domain concept is represented in a particular domain. This question will become the central issue in Sect. 3.3.

A critical position towards convexity is also found in the work of Bechberger and Kühnberger (2017, 2019). They note that a geometric representation of correlations in conceptual spaces becomes possible only if the convexity requirement is given up. As an example, they consider a representation of child in a product space of AGE and HEIGHT with a Manhattan metric. The choice of this metric is justified by the intuitive assumption that these dimensions are perceived separately and are thus not integral. Furthermore, Bechberger and Kühnberger (2019) emphasise that only cuboids are convex in Manhattan spaces. As a consequence, the correlation between younger age and smaller size is not captured in a convex representation. According to Bechberger and Kühnberger (2019), one should give up convexity requirements in favour of representing this correlation. They prefer the non-convex representation in Fig. 4b to the convex one in Fig. 4a.

Fig. 4

Representation a is convex but does not represent the correlation of age and height in children. The non-convex representation in b indicates a relation between the dimensions

An objection that could be raised against the representation in Fig. 4b is that it misrepresents the concept of child. For example, an extraordinarily tall 13-year-old kid is still a child. Many other important features of children, cognitive ones as well as physical ones, are ignored. Nevertheless, even if Fig. 4b is not a good representation of child, Bechberger and Kühnberger (2019) certainly raise an important point. They show that a critical aspect of concepts, namely correlation, might come into conflict with convexity. Many researchers, including Gärdenfors himself, emphasise the importance of correlations in natural concepts. The tension between representing correlations and convexity is thus worrying. An extensive discussion of this problem and its solution will follow in Sect. 3.4. For now let us note that the tension between representing correlation and convexity undermines the thesis that multi-domain concepts occupy convex regions in complex spaces, that is, thesis 5 on p. 8.

2.7 Beyond convexity

Some criticism against convexity assumptions does not concern their validity but their salience in a theory of concepts. Within conceptual spaces theory, they take a very central place. But is this justified? Are there different and perhaps even more salient principles of natural concepts?

Gärdenfors (1990) himself notes an important limitation: even if convexity is a necessary condition of conceptual naturalness, it is not a sufficient one. For example, it says nothing about the preferred level of specificity: non-black and non-white are as convex as red or blue, but the former concepts are extremely broad and thus uninformative in many contexts. As Rosch et al. (1976) have convincingly argued, the right level of informativeness is central to how easily a concept is learned and how cognitively salient it is.

Another limitation concerns the role of the convexity thesis. In the analytic arguments outlined above, convexity was justified by its relation to Voronoi tessellation as a basic mechanism of conceptual learning. In the argument, convexity is not an intrinsically plausible cognitive principle, but rather a derived criterion that is based on more basic rules of classification. This does not mean that convexity is uninteresting. The point is rather that the convexity theses, if true, are not an explanation but rather call for one, such as, for example, the evolutionary argument offered by Jäger (2007).

Recent work by Douven and Gärdenfors (2020) acknowledges the fact that convexity is insufficient for a characterisation of natural concepts. Instead of convexity or other topological criteria, they suggest that natural concepts occupy optimally designed partitions of a conceptual space. Their arguments proceed from a number of criteria that have intrinsic cognitive plausibility:

• PARSIMONY: The conceptual structure should not overload the system’s memory.

• INFORMATIVENESS: The concepts should be informative, meaning that they should jointly offer good and roughly equal coverage of the domain of classification cases.

• REPRESENTATION: The conceptual structure should be such that it allows the system to choose for each concept a prototype that is a good representative of all items falling under the concept.

• CONTRAST: The conceptual structure should be such that prototypes of different concepts can be so chosen that they are easy to tell apart.

• LEARNABILITY: The conceptual structure should be learnable, ideally from a small number of instances. (Douven and Gärdenfors 2020, p. 318)

Note that parsimony and informativeness pull the conceptual system in different directions. On the one hand, we need as many and as informative concepts as possible. On the other hand, a system with few concepts is more parsimonious.

As a general criterion of naturalness, Douven and Gärdenfors (2020) suggest well-formedness: A concept is well-formed if and only if its instances are as similar to each other as possible while being dissimilar to instances of other concepts. Naturalness is thus a property of a whole conceptual system in which internal similarity and external dissimilarity are optimised. The criterion of well-formedness is reminiscent of the above-mentioned basic level categories (Rosch et al. 1976; Rosch 1978). Superordinated concepts, such as entity or animal, refer to entities with a low internal similarity. Instances of subordinated concepts such as dachshund and collie, on the other hand, have little external dissimilarity, or their dissimilarities are unimportant for many contexts. A basic level concept such as dog does reasonably well on both criteria.

The criterion of optimising external dissimilarity and internal similarity has several advantages over convexity. It is cognitively intrinsically plausible, more restrictive than convexity, and related to findings about the basic level of categorisation. Douven and Gärdenfors (2020) discuss their criterion mainly by referring to the colour space, specifically the CIELAB space. This is already the best understood domain in human perception. By using the colour example, Douven and Gärdenfors (2020) can rely on this existing research. However, conceptual spaces aim to be a universal framework of concept formation. Research that explicitly focuses on the colour space tendentiously undermines the ambition of providing a more general theory of concepts. Douven and Gärdenfors (2020) explicitly mention this restriction and note that research for different types of conceptual spaces is needed.

2.8 Convexity: advantages and limitations

Let me conclude this section with an interim conclusion. Convexity is the most prominent geometric constraint of natural concepts. The criterion is well supported in spaces with integral dimensions. However, it should not be seen as a separate cognitive principle; rather it must be understood in relation to basic cognitive or evolutionary constraints such as prototype-based categorisation or the optimisation of internal similarity and external dissimilarity. In the simple perceptual domains and in particular in colour concepts, convexity is expected to arise from such simple cognitive and evolutionary constraints. Difficulties with convexity arise if one considers concepts that cover different domains. For these multi-domain concepts, correlations between dimensions become more salient. However, as noted by Bechberger and Kühnberger (2019), the representation of correlations can prima facie conflict with convexity requirements.

For a general theory of conceptual naturalness, this result is unsatisfying because the multi-domain concepts, for which convexity criteria are less plausible, are prime examples of natural concepts. Admittedly, among possible colour concepts, some are more natural than others. For example, red is more natural than the concept blue-or-yellow. However, compared to object category concepts such as car and dog, colour properties and other simple perceptual properties are not the prime examples of natural concepts. They are not the first concepts that are acquired in childhood. The seemingly more complex noun concepts are learned much faster (Werning 2010; Poth and Brössel 2019). Such multi-domain concepts have an advantage in learnability. Moreover, they are more informative; compare ‘It is white’ and ‘It is snow’. The latter sentence is clearly the more informative one as it includes information about temperature, material, texture, and colour. If a concept is restricted to one domain, then it is almost trivially the case that it is not very informative. To conclude, a property concept such as red is natural within the colour domain, but it still lacks features of naturalness we typically associate with multi-domain concepts, that is, most noun concepts. This makes the study of such concepts particularly important for understanding the naturalness of concepts. Within the rest of this paper, I investigate how conceptual spaces can be used to determine criteria for naturalness of these multi-domain concepts.

3 Multi-domain concepts

3.1 The boundaries of domain-specific concepts

According to Gärdenfors, ‘words in all content word classes, except for nouns, refer to a single domain’ (Gärdenfors 2014, p. 239). Generally, we lack words that characterise things as solid and cold or as red and sweet. However, there are exceptions if properties are related, as shown in the concepts frozen or ripe. These two property concepts are informative in several domains. Domain-specificness can be violated, even by property concepts, if there are correlations between domains.¹⁴ My notion of a multi-domain concept is thus not limited to noun concepts but they are without doubt the best examples of multi-domain concepts.

The central thesis of the paper is that natural multi-domain concepts capture correlations, that is, probabilistic dependencies in the world we perceive. For example, if we see an animal with a dog-shape, then it is likely that we will perceive the specific sound pattern of barking rather than chirping or meowing. The category of dog consists of entities that (mostly) share the correlated properties. This literally captures the correlation because it no longer persists in a separate consideration of instances and non-instances. For example, redness and sweetness of strawberries are correlated: redder fruits are sweeter. But if you consider only ripe fruits, then this correlation (almost) vanishes because of a lack of variation in these respects. Likewise, within the category of dogs, there is no strong correlation between dog-shape and barking. A concept thus captures correlations if and only if its instances have common features that distinguish them from non-instances. These features are often sufficient to identify an instance of the concept (you identify the dog by its shape) and many further properties (the behaviour of the dog) can be inferred with a reasonable degree of certainty.

The view of concepts as means to capture correlation and to facilitate inferences is very influential. It is not only advocated by psychologists such as Rosch (1978) but spread to other disciplines. For example, the computer scientist John Holland, philosopher Paul Thagard and the psychologists Keith Holyoak and Richard Nisbett jointly developed a theory of cognition that is based on the ability to learn and apply rules: ‘categories are best defined as clusters of interrelated rules’ (Holland et al. 1986, 179). They also rightfully point out the analogy between the way philosophers understand natural kinds (Quine 1977) and the way proponents of prototype theory, especially Rosch (1978), characterise basic-level concepts. While Gärdenfors (2000) refers to Holland et al. (1986) and largely agrees with them, conceptual spaces theory has not been used to explicitly flesh out the role of correlations as a foundation of concepts.

The remainder of Sect. 3 has three parts. It starts with a broader philosophical discussion of why multi-domain concepts are of primary importance when focusing on conceptual naturalness in Sect. 3.2. After that, the topology of conceptual spaces together with probabilistic considerations will be used to characterise naturalness in multi-domain concept. In Sect. 3.3, I consider how to model features, that is, properties that are closely associated with multi-domain concepts. The second important aspect is the representation of correlations in complex spaces. This is the focus of Sect. 3.4. Finally, Sect. 3.5 discusses how the shape of the probability distribution over conceptual spaces influences the development of natural concepts.

3.2 The naturalness of multi-domain concepts

Two philosophically important aspects distinguish natural multi-domain concepts from domain-specific concepts. First they relate different features that are strongly associated. Therefore, they have the potential of carving nature at its joints and are thus candidates for natural kinds in the sense of Quine (1977). Second, multi-domain concepts are ostensively learnable without depending on a specific kind of perceptual input. While the domain-specific concept red is not (directly) learnable by a person who lacks the ability to view colours, concepts such as car or cat are usually more open with respect to the sensory input that is needed to acquire them (e.g., by vision or hearing). They are learnable by perception but independent of a specific perceptual content. These two aspects are at the core of the following pages. I first consider the relation to natural kinds, followed by a discussion of ostensive learnability.

3.2.1 Natural kinds, realism and correlations

Natural multi-domain concepts capture highly stable correlations within the world. The shape of apples, their taste, and specific nutritious profile occur together, namely in the instances of the concept apple. What seems to be natural about such object categories is that they capture something beyond our human cognition: a mind-independent reality. In contrast, conceptual spaces theory emphasises that concepts are a cognitive achievement of humans (or, in principle, other animals). For example, the criteria for naturalness presented in Douven and Gärdenfors (2020)—parsimony, informativeness, learnability, etc.—appeal to our cognition, that is, to our cognitive nature rather than a mind-independent nature.

The question of what makes categories natural, our categorisation or a mind-independent structure of the world, is reminiscent of the philosophical debate about natural kinds (for an overview, see Bird and Tobin 2018). Natural kinds are said to carve nature at its joints. This metaphor is as old as the whole question of how to categorise things. It is first found in Plato’s Phaedrus 265d-e, where Socrates discusses two principles, ‘that of perceiving and bringing together in one idea the scattered particulars’ and ‘that of dividing things again by classes, where the natural joints are’ (Platon 1914, pp. 533–35, transl. by Fowler). In the 20^th century, the natural kind debate focused on distinguishing categories that allow inductive inferences from concepts such as non-raven or grue things (Quine 1977). The theory of conceptual spaces and its convexity criteria address the same problem and can be viewed as contribution to the natural kinds debate.

A central question in the discussion of natural kind concepts is a metaphysical one. Do these natural concepts refer to an ontic distinction, independent of our own cognitive needs? While the conventionalist position denies this, realists claim that the categories to which many of our concepts refer, especially those that allow for inductive inference, represent metaphysically real groups. Among the realist positions, there is a large spectrum from weak to strong versions.

In its strong version, realism has a tendency to externalise categories from the human mind to the mind-independent reality. That is, the categorisation of natural kinds is not due to us but fixed by the nature of the things to which we refer. As such, metaphysical realism on natural kinds has a tendency of rejecting cognitivism, that is, the thesis that concepts are (primarily) determined by cognitive content. The position is known via Putnam (1975), who famously claimed that ‘meanings ain’t in the head’. For instance, not our cognition about water but its chemical details are crucial for what the word ‘water’ means. Conceptual spaces are obviously a cognitivist theory of meaning and it is hardly surprising that Gärdenfors explicitly rejects an externalist semantics that is based on natural kind realism as ‘putting the cart before the horse’ (Gärdenfors 2000, p. 201).¹⁵

There are indeed good reasons to reject a theory that replaces conceptual content by an appeal to natural kinds, especially from the viewpoint of cognitive science. First, the realist position comes with a strong ontological commitment. If it is not the human mind that builds categories, then they must exist independently of our cognition. Some philosophers find this intuitively plausible while others reject it. In any case, it would be problematic if cognitive science committed itself to a controversial metaphysical position. A cognitivist theory of natural concepts, on the other hand, allows one to postulate psychological principles of natural categorisation that can be empirically tested. The only criterion an externalist position has to offer is a deference to the metaphysical reality of natural kinds. In addition, externalism is hardly compatible with the existence of conceptual change in natural languages as well as in scientific theories.¹⁶ Finally, we often form categories that do not refer to something external. Intentionally (hobbit) or unintentionally (phlogiston), human minds create concepts that cannot be accounted for by externalist semantics. Even if natural kind realism is true and offers a semantic background for some concepts, we would still need a cognitivist theory for non-referring concepts. In this sense, externalist positions entail a strong ontological commitment, yet have limited explanatory power regarding our categorisation.

In opposition to strong realism and externalism, there are also positions that view natural kinds as real while accepting a decisive role of cognition. A pluralistic version of realism is found in Dupré (1993), who calls his position ‘promiscuous realism’. He claims that categorisation is driven by several aspects (cognition, pragmatics etc.) rather than being pre-defined by the nature or essence of individuals that belong to the kind (cf. Dupré 1993, p. 57). Nevertheless, there is a real natural aspect about them. The clusterings and discontinuities that are captured by natural concepts, even if they are not sharp and lack essential properties, are real, and this allows us to say that they correspond to natural kinds. Though Dupré (1993) is mostly concerned with the scientific taxonomies in biology, his view can be applied to folk taxonomies and concepts in natural languages, as well.

In contrast to externalist realist views, a pluralist account of natural kinds leaves room for cognitive agents to shape the boundaries of categories according to their needs. Moreover, weak realism provides a very attractive background position in which cognitive principles of categorisation can be investigated. Concepts and categorisations develop in the context of an external world. It is hard to explain how categorisations evolved and promoted the survival of their cognitive hosts if they are not themselves adapted to the external world. This becomes apparent when we look at food sources. A folk taxonomy that distinguishes plants and mushrooms solely by similar appearance but is uninformative about toxicity has a tendency to harm its cognitive hosts and is thus unlikely to spread. It is important for categories to fix the right correlations between appearance, toxicity and, ideally, taste.¹⁷ Even if semantic externalism is rejected (for good reasons), the naturalness of some categorisations does depend on external facts, namely on covariances in the world. This is especially true for the multi-domain concepts of folk taxonomies.

To summarise, weak realist positions are attractive for cognitive science. They leave the categorisation task to the human mind but assume a natural structure that makes categorisation worthwhile. There are important covariances in our world, but it is up to us to carve nature at its joints. There are certainly some merely cognitive requirements of how this should be done but also extrinsic limitations of what a natural characterisation can be and especially of what it cannot be.

What does this mean for the theory of conceptual spaces? Weak realism fits the cognitivist approach of conceptual spaces theory. However, in many cases, a purely topological characterisation will not suffice. One has to consider the structure of the outside world from which perceptual input comes. In particular, because dimensions are correlated, some regions in conceptual spaces are more inhabited than others. Zenker (2014) suggests including knowledge about such correlations in terms of population patterns: ‘To mimic this in conceptual spaces, [...] one may speak of sub-regions of a conceptual space being empty (or comparatively unpopulated)’ (Zenker 2014, p. 82f). For example, certain combinations of colour and flavour are very common in berries: red and dark colours indicate sweetness. In a combined colour-taste space, the corresponding regions are more inhabited while others (sweet, green berries) are almost empty. The question of how inhabitation patterns contribute to conceptual naturalness will be the main topic of Sect. 3.4. For now it suffices to note that such consideration of inhabitation patterns fits to a weakly realist position on natural kinds: nature provides us with a pattern of correlations but the carving is up to our cognition.

3.2.2 Ostensive learnability and the multitude of domains

A second aspect of naturalness that is only found for multi-domain concepts is a relatively low dependence on specific sensory input. Many people (at least in western societies) associate typical situations of conceptual learning with visual experiences. For example, the concept dog can be taught by a caregiver who directs a child’s gaze to a dog and says ‘This is a dog’ or even by showing a representative picture of a dog. In a similar way, one can present monochrome red cards and give the information: ‘This is red’. These are idealised examples of ostensive learning. However, there is an important difference between the two concepts involved. The concept red can only be learned by vision. The acquisition of an object category concept such as dog, however, does not depend on any particular visual experience. A blind person may learn the concept (perceptually) without having any visual experience of dogs at all.

The ostensive learnability of concepts plays an important role in philosophical debates. For example, Schurz (2015) suggests it as a criterion of theory-independence. According to him, there is an empirical way to distinguish theory-neutral observation concepts. One introduces an artificial word X for a concept and presents a subject with instances. After that, it is possible to test whether the person has learned the concept by asking her whether some novel stimuli is X or is not X. A concept is theory-neutral if and only if it is teachable in such a way. Schurz (2015, p. 152) assumes that concepts such as red, square, or bird are teachable ostensively, while typical theoretical concepts such as atom, electric force, or oxidation are not learnable ostensively because they require an understanding of related background theories. He notes that the ostensive learnability experiments should include persons of very different cultural background but emphasises normal observation conditions such as that ‘the person does not have any empirically detectable deficiencies of the sensory organs or the nervous system’ (Schurz 2015, p. 151). For many multi-domain concepts, this condition can be relaxed. They are not only independent of theories, but they do also not depend on a specific perception. A person with hearing impairment and a blind person may both learn the concept bird without sharing the same perceptual experiences. Colour concepts, on the other hand, are more like theoretical concepts for people with impaired colour vision. They can learn the colour concept by acquiring background knowledge but not by perception.

The last pages argued that some aspects of conceptual naturalness are specifically found in multi-domain concepts. The following subsections delve deeper into the issue of how these aspects can be explicated as criteria for naturalness in conceptual spaces.

3.3 Features of multi-domain concepts

With his Criterion C, Gärdenfors proposes representing natural concepts, in particular object categories, by their features:

A natural concept is represented as a set of regions in a number of domains together with an assignment of salience weights to the domains and information about how the regions in different domains are correlated. (Gärdenfors 2000, p. 105)

As noted above, newer literature (Gärdenfors 2014; Osta-Vélez and Gärdenfors 2020) extends this criterion with a convexity assumption, stating that the concept is determined by convex regions in domains. According to this extension, features of multi-domain concepts must be natural properties as defined by Criterion P. This demand seems prima facie reasonable. The colour of emeralds should rather be described by natural property concepts, that is, by green rather than by grue. While this is of course correct, I argue for a different view on features of object categories by emphasising their differences from property concepts.

Within the next pages I develop and justify an altered version of criterion C:

A natural multi-domain concept is represented as a set of non-locational and characteristic regions in several independent conceptual spaces.

The demand of non-locationality excludes grue-like properties as well as features that lack stability, such as date of birth for the concept newborn. The characteristicness criterion is about the specificness and reliability of the feature: How strongly is a certain region in the conceptual space associated with a specific concept (e.g., a region of the taste space to salt)? I now explore these two points in more detail.

3.3.1 Non-locational features and problems of projectability

An essential motivation of working with conceptual spaces is to avoid problems of non-projectability as they arise with such concepts as bleen and grue. As Gärdenfors (1990) has shown, the convexity criterion can solve this problem. In order to illustrate this, he combines a colour disk with a time dimension (see Fig. 5): the concept grue picks out a non-convex region. Note, however, that a distinction between green and grue does not depend on convexity. The simple fact that the representation of grue, contrary to blue and green, is only possible by taking into account the time dimension distinguishes these kinds of concepts.

Fig. 5

The colour cylinder from Gärdenfors (1990, p. 89), demonstrating the non-convexity of grue. Copyright: University of Chicago Press, reprinted with permission from the author and University of Chicago Press

As laid out in the introduction, Goodman (1955) argued that the green-blue distinction is not more basic than the grue-bleen distinction because both can be defined in terms of each other. On the symbolic level, this is correct. On the level of conceptual spaces, however, it is very clear that only the latter distinction requires the addition of the time dimension.

Carnap (1971, 1980) already discussed the potential problem of temporal and spatial attributes when he introduced attribute spaces. He notes that there are requirements of permissibility for attributes. In particular, he distinguishes locational and descriptional attributes (Carnap 1971, 70–76). The main purpose of locational attributes is to indicate the position of some entity in space-time. Descriptional attributes, on the contrary, can be used to describe entities. Locational attributes depend on temporal or spatial dimensions. However, Carnap accepts some temporal dimensions as admissible for descriptions. Durations of events, for example, are temporal but admissible because they are not absolute but relative, and this makes them non-locational. By the criterion of non-locationality, Carnap (1971, p. 73) explicitly excludes grue, which combines a locational dimension (time point of observation) and a non-locational one. Gärdenfors (1990) acknowledges that Carnap’s solution can handle the problem of grue. Nevertheless, he prefers the convexity criterion because it also excludes concepts like red-or-green, which are non-locational and definable in a normal colour space (just like green) but still intuitively unnatural.

Even though the convexity requirement solves the grue-problem, Carnap’s solution, which emphasises the role of temporal and spatial dimensions, is still worth considering as an approach to projectability. Convexity is a plausible restriction of property concepts but not necessary for ensuring projectability. It is not only a stronger assumption than one would need for this purpose but also more controversial. Gärdenfors (2019) emphasises that convexity is an empirical law. A concept like grue, on the other hand, is unnatural on analytic grounds. In this sense, a Carnapian criterion of non-locational features remains useful when convexity turns out to be too strong.

A reason to be sceptical about the thesis that features of multi-domain concepts are convex is that they are not necessarily like natural properties in domains. What we associate with multi-domain concepts is different from what is associated with a property concept. For example, there is some intuitive appeal to the idea that we partly represent the concept blossom (of a plant) by colour, where they cover light tones and highly saturated areas of the colour space, excluding shades of green. Conceived as a property of being colourful, this concept is quite unnatural. However, conceived as a feature of flowers, this does not seem problematic. In particular, there is no problem of projectability in a statement such as ‘Blossoms are colourful’. This is a reasonable regularity that distinguishes the blossom from the rest of the plant. Natural property concepts, as they are expressed by many adjectives, need to be informative and useful independent of the context. Features of multi-domain concepts, on the other hand, are restricted by a specific context, namely an object category. Hence, it should not be surprising if features differ from natural properties. However, projectability is always an issue.

How can non-locational features be identified in a conceptual space? The representation of a concept’s features in a certain conceptual space should be independent of any kind of locational dimension. This non-locationality can be defined as follows:

Let CS be a conceptual space, consisting of n quality dimensions $X_1, X_2,\ldots , X_n$ and let L be an absolute locational dimension (e.g., time or place of observation) such that $CS\times L$ is the combined conceptual space. A region $C\subseteq CS\times L$ is independent from L if and only if, for all $l, l' \in L$ and all $x_1\in X_1, \ldots , x_n\in X_n$ it holds that $\langle x_1,\ldots , x_n, l' \rangle \in C$ iff $\langle x_1,\ldots , x_n, l\rangle \in C$.

A concept has a non-locational feature C in the space CS if and only if, for each locational dimension L, its representation $C \subseteq CS\times L$ is independent from L.

Like Carnap, I do not exclude all temporal or spatial attributes. However, in contrast to his general distinction of relative and absolute locational dimensions, my criterion of non-locationality is focused on the context of the multi-domain concept. For example, historical entities such as languages, cultures and species can be described in terms of when and where they occurred. There is nothing problematic about the statement ‘The Spanish flu lasted from 1918 to 1920’ or ‘Penguins live in the southern hemisphere’. Even though the statements include an absolute temporal or locational attribute, they are independent from the point of utterance, evaluation or observation. On contrast, AGE-related features are commonly found for concepts that refer to developmental stages. For example, even though the concept one-year-old human changes its extension from year to year, general and inductively successful statements have been made about one-year-old humans in developmental psychology. Whether a conceptual region is non-locational in the required way thus depends on the concept. AGE contributes to the concept of children but not to the concept of generations, such as millennials or baby boomers. This is illustrated in Fig. 6. In order to characterise millennials non-locationally, one has to consider YEAR OF BIRTH instead of AGE.

Fig. 6

The age of children and adults (in a) is representable in a time-independent way and thus non-locational. For generations (in b), on the other hand, AGE is locational (i.e., depending on the time of observation)

3.3.2 Characteristic features

Non-locationality is a minimal requirement for features of multi-domain concepts, but it is not a very strong one and barely sufficient. Natural multi-domain concepts need to be recognisable in terms of their features. There should be several domains (or combination of them) along which category members are easily detected. For example, the colour of a ripe strawberry is a certain shade of red, but this is not very specific to these fruits. The shape of the fruit, however, is sufficient to recognise a strawberry. It is to be expected that a conceptual space of shapes has a region such that almost all strawberries will be represented in this region and that (almost) the whole region is associated with strawberries and nothing else than strawberries. This is what I call a characteristic feature.

This notion of characteristicness resembles the idea of typicality. Schurz (2012) proposes to define a typical property (in the wide sense) as a property P that is probable for a category member of C. The probability of P given C, Pr(P|C), has to be high. The diagnosticity, also called cue validity, of a property P is the reverse conditional probability Pr(C|P). A property is typical in the narrow sense if C indicates P and P indicates C. In other words, the probability of the exclusive disjunction of category and property (i.e., C or P but not both) $Pr(C\veebar P)$ is small.

These probabilistic considerations can be related to conceptual spaces if one introduces a probabilistic conceptual space, that is, an n-dimensional conceptual space with an n-variate probability distribution over it. These distributions are either probability masses ($p_{X1,\ldots , Xn}$) in the discrete case or densities ($f_{X1,\ldots , Xn}$) in the continuous one. The probabilities of C and P follow by additivity from $p_{X1,\ldots , Xn}$ for discrete distributions. In the continuous case, C and P are regions the probability of which is determined by the integral of $f_{X1,\ldots , Xn}$ over these regions. Here we need to assume that C and P are measurable subsets of the space. This is an extremely mild constraint, even weaker than connectedness. The question of how probabilistic densities influence the development of concepts is further addressed in Sects. 3.4 and 3.5. For now, I just use probabilistic conceptual spaces to translate the probability-based view of typicality into the topology-based approach of conceptual spaces.

The probabilistic demand that $Pr(C\veebar P)$ must be small is related to the demand that the symmetric difference between the regions C and P, $(C\cup P)\setminus (C\cap P)$ (short: $C\triangle P$), is small. If the probability distribution over the space is uniform, then the relation between $\mu (C\triangle P)$ (i.e., the size of $C\triangle P$), and $Pr(C\veebar P)$ is clear: $Pr(C\veebar P)=\frac{\mu (C\triangle P)}{\mu (CS)}$.¹⁸ If the probability distribution is not uniform, then the connection is less straight forward. Nevertheless, the following holds: If $C'\triangle P' \subseteq C\triangle P$, then $P(C'\veebar P')\le P(C\veebar P)$. In other words, the probability of the exclusive disjunction increases only if the size of the symmetric difference increases as well.

Conceptual spaces improve the ability to represent typical features considerably. In feature lists (Rosch and Mervis 1975) or frames (Minsky 1975; Barsalou 1983) one has to use symbols to describe typical features. For example, ‘having a beak’ or ‘being feathered’ are used to describe features associated with bird. This approach works reasonably well in this and many other examples. However, we often lack words to describe typical features. Conceptual spaces overcome the limitations that are set by our language. For example, it is almost impossible to accurately describe the typical shape of birds in few words (without just calling it ‘bird shape’). In comparison, a representation in terms of a subregion in a shape space (e.g., Bechberger and Scheibel 2020) is impressively accurate and nevertheless parsimonious. While it is often hard to name characteristic features, the ability to represent them in conceptual spaces is not affected by this limitation.

To give another example, there is a specific odour of coffee. Most people, I assume, are able to represent and imagine this sensation. It is a characteristic feature of coffee to produce this sensation. Of course, the sentence ‘Coffee typically smells like coffee’ is trivial and uninformative. In particular, one would not use it to teach the concept coffee. However, a representation in a conceptual space is not a word or a sentence but can be viewed as a representation of a perception one might experience even without having acquired the concept.

What about geometric constraints on features? I do not postulate convexity for characteristic features (e.g., thesis 3 above). Many general arguments in favour of convexity rely on the fact that convexity is expected to arise if one aims to partition a space in an efficient way. However, as noted above, representations of features like the taste of a strawberry or the colour of a chestnut are not like property concepts (sweet or brown), even if they are represented in the same spaces. One reason to think of features as (natural) property concepts is that, on a symbolic level, they are usually expressed in terms of property concepts, but conceptual spaces provide ways to represent characteristic features without needing to rely on other concepts. Moreover, its seems that violations of convexity are a widespread phenomenon. For example, most animal species have a distinct female and a male subtype. If there is a strong sexual dimorphism, these might lead to representations (e.g., in the shape space) that are not even connected, let alone convex. Nevertheless, this unconnected subspace seems to represent a characteristic feature of species members.

By that, I do not deny that topological constraints of features are important. In order to be cognitively processed as a characteristic feature, the regions in the space must be restricted in some way. Otherwise, any arbitrary collection of points that correspond to category members would count as characteristic feature. A minimal requirement is that only few disconnected subregions may be involved and that these subregions need to be convex or at least star-shaped. Also note that such disconnected regions are probably processed as alternative features rather than as one characteristic feature (e.g., female shape and male shape of animal X rather than as the shape of animal X). Moreover, a multi-domain concept with an unconnected feature is only acceptable if it also has many connected (and even convex) characteristic features in other conceptual spaces. I will not postulate a specific constraint, but leave their specification as an open question for future research.¹⁹

Let me illustrate the criterion of characteristicness by referring to the example of apple, as discussed by Gärdenfors (2000). Table 1 displays his suggestion for how to represent the concept and a contrasting representation in terms of characteristic features. Gärdenfors (2000) suggests representing the concept, inter alia, along the attributes COLOUR, SHAPE, TEXTURE, and TASTE. Apples have a red, yellow or green colour; a cycloid shape; smooth texture; and so on. In my approach, the central question becomes whether a certain conceptual space has a characteristic region associated with apples. The colour domain is obviously unspecific. It is impossible to characterise an object as an apple only by knowing its colour. For this reason, the concept apple has no characteristic feature in the colour domain. In contrast, the shape of apples is quite characteristic. This association is so strong that we would, at least metaphorically, apply the term ‘apple’ to all apple-shaped things, such as golden apples. Texture is not distinctive. Another specific representation can be expected in the taste space. Especially if the domain does not merely include taste in the narrow sense (sweet, sour, bitter, saline, umami) but flavour, it is likely that there exists a characteristic apple taste.

Table 1 Comparison: representation of apple from Gärdenfors (2000, p. 103) (excerpt) and in terms of characteristic features

My discussion of characteristic features focussed on perceptual attributes. These are indeed particularly interesting because they provide the basic bridge from perception to concepts (see also Brössel 2017). Note, however, that the notion of characteristic features is not limited to perceptual spaces. They can also be based on attributes that only become known through scientific inquiry, such as MOLECULAR GEOMETRY, MASS, or GENETIC CODE. For example, the particular nutritious profile of apples or the phylogenetic diagram of apple trees are likely to represent characteristic features of apples, as well.

The specification of multi-domain concepts in terms of characteristic features leaves aside some properties that are connected to the concept. In the left column of Table 1, for instance, the attributes COLOUR and TEXTURE drop out. Apples have varied colours and many other things have similar colours as apples have. The texture of apples is close to that of other fruits and vegetables. In Gärdenfors’s depiction such regions are part of a natural concept. He claims that ‘in some cases, the region may be the entire domain’ (Gärdenfors 2014, p. 124). Such features are obviously not characteristic. Nevertheless, the inclusion of such regions informs one that a concept is related to the domain. For example, each car has a colour but there is no restriction on which colour this is. As a consequence, it is hardly possible to represent car by COLOUR. Nevertheless, we know that cars—contrary to viruses, music, and thoughts—have colours. In order to do justice to the fact that such attributes are largely unable to contribute to categorisation but are applicable to the concept, I suggest to say that they are related to the concept. In this sense, the regions of red, yellow, and green in the colour space are related to the concept of apple, even if they are not characteristic.

Combining all of this, I conclude with the following revision of Criterion C:²⁰

The central demand of this criterion, namely that a concept has several characteristic features, implies a strong correlation between these features. Apple shapes are correlated with apple taste. This brings me to the next aspect discussed in this paper: correlations and multi-domain concepts.

3.4 Correlations in combined conceptual spaces

When discussing how concepts capture correlation, a combination of probabilistic arguments and conceptual spaces is needed. Such a connection was already alluded to in Sect. 3.3.2, when linking probabilistic typicality and characteristic features. Quite early in their development, geometric models of concepts were linked to probabilities. Carnap (1971, 1980) originally introduced his attribute spaces as a background of inductive logic (see Sznajder 2016). He used them to formulate a principle of indifference according to which all possible hypotheses should be treated as equally probable as long as no evidence supports one of it.²¹ Moreover, he applied attribute spaces to account for similarity effects. An observation of a black raven, for instance, arguably raises not only the expectation of seeing another black raven. It also makes it more likely to find grey ravens than yellow ones. Carnap (1980) called this the $\eta$-rule.

After inductive epistemology and geometric representation of concepts developed separately for a long time, more recent research is devoted to the connection between probability and conceptual spaces. For example, Brössel (2017) combines probability theory and conceptual spaces in order to provide a link between perceptual experience (perceiving X as green) and credences (believing that X is green). Decock et al. (2016) extended Carnap’s principle of indifference for properties with vague boundaries such as colour terms. The $\eta$-rule was further elaborated by Sznajder (2017), whose work I turn to in Sect. 3.5. First, I will use probabilistic approaches to address correlations between values of different dimensions. Note that, contrary to the mentioned approaches, probabilities do not represent credences but perceived frequencies, that is, inhabitation patterns (see p. 20).

As noted in Sect. 2.6, Bechberger and Kühnberger (2017, 2019) explicitly suggest using conceptual spaces to represent correlations geometrically. Their motivating example was already illustrated in Fig. 4 (see p. 14). Let us now consider their argumentation more closely. The dimensions HEIGHT and AGE covary within the category of children. Bechberger and Kühnberger (2019) convincingly argue that only a non-convex representation of the concept child can capture this correlation. Moreover, they also claim that the non-convex representation is closer to an intuitive understanding of child.

Fig. 7

a Represents the correlation of age and height in children. In the fine-grained representation in b, concepts capture the correlations

The reason behind the apparent intuitiveness of a non-convex representation is that it excludes uninstantiated or at least very unlikely combinations such as persons who are one year old and 1.40 m high. Surely, a one-year-old is a child and most 1.40 m tall people are also children. However, this particular combination of properties is unlikely. The preferred representation of Bechberger and Kühnberger (2019) avoids the inclusion of empty or barely inhabited regions of the conceptual space. While they do not explicitly refer to population patterns, the criterion behind their preference for the non-convex representation is eventually concerned with them. A natural concept in a multi-domain space should not cover uninhabited or barely inhabited regions. In probabilistic terms, a narrow concept is preferred over a wide one if the latter does not include additional populated regions and is thus not more likely:

As the example of Bechberger and Kühnberger (2019) illustrates, there is a tension between this principle and topological restrictions such as convexity. For example, S could be a non-convex region, and P its convex hull. According to the topological criterion, P is the preferable choice, but the principle of inhabitedness demands that non-inhabited parts of P should not belong to the conceptual representation.

The conflict between inhabitedness and convexity can be resolved if additional concepts are introduced that capture the correlation. For example, the concepts infant or toddler capture a correlation between very young age, small body size and many other physical and mental attributes. As is seen in Fig. 7b, the finer distinction within minors allows for the reconciliation of the principle that only inhabited areas are included in the conceptual region and the principle of convexity. Indeed, natural language has a much richer vocabulary to distinguish minors: ‘infants’, ‘toddlers’, ‘teenagers’, etc. In comparison, we have few concepts to distinguish adults with respect to their age.

Fig. 8

Sznajder’s presentation of how a probabilistic density is derived from several observation. Directly taken from Sznajder (2017, p. 88), reprinted with permission of the author

The finer graduations lead to a capturing of correlations by the concepts. The representations of the more specific concepts are both convex and do not cover largely empty regions. However, the resulting partitioning is unbalanced with respect to category size. It has been hypothesised that finer graduations, that is, more concepts in a region of a conceptual space, are expected to be found in densely populated regions of the space (Sznajder 2021). However, this is not exactly what happens here. The concept of minors occupies only a comparatively small fraction of the space and is barely more densely populated than the adult’s region. The finer categories of younger persons arises from correlations. These finer subcategories allow us to have concepts with convex and narrow representations in conceptual spaces. This characterises concepts that capture a correlation.

3.5 The topology of probabilistic densities

Having a probabilistic conceptual space allows one to specify the naturalness of concepts not only in terms of the topology of conceptual regions, but also in terms of the form the probability distribution takes. At this point, I focus explicitly on the shape of probability densities $f_{X_1, \ldots , X_n}$ over n-dimensional conceptual spaces. As I said above, these probabilities represent perceived frequencies, that is, observations. How do we come from such observations, which are inherently discrete, to continuous probability densities? A detailed account of this process is presented by Sznajder (2017, 2021). Her work builds up on Carnap’s account of analogical reasoning according to which an observation not only influences one predicate but also semantically similar predicates. She extends his work in two aspects. First, her confirmation function works on the points of the space and is thus independent from pre-existing predicates. Second, she accounts for the role of multiple observed entities. As a result, Sznajder (2017, ch.4) presents a model of how observations shape a probabilistic density (see Fig. 8).

While Sznajder’s work is concerned with inductive reasoning and thus with credences of a rational agent, it is quite plausible that perceived frequencies of human agents follow the same pattern. Neither our perception nor our memory are precise enough to represent the multitude of our observations in a discrete way, that is, as points in a conceptual space. Sznajder (2017) also suggests that the formation of concepts is influenced by the resulting probability: ‘Only later on [...] can the space be divided into predicates, following the shape of the posterior’ (Sznajder 2017, p. 113). This leads me to a final constraint. How does the shape of a probability density influence the development of (natural) concepts?

A well-known formal constraint of univariate (i.e., one-dimensional) probability distributions, also part of Sznajder’s (2017) framework, is unimodality.²² A unimodal probability distribution has only one local maximum, that is, one peak. Examples are the normal distribution, the uniform distribution, as well as many of the distributions that are used in statistical testing (e.g., chi-quared and student’s t distribution)

Human cognition is biased towards unimodality. Fried and Holyoak (1984) showed that agents can easily learn categories by developing a representation of the distribution of exemplars in a space if it follows a normal distribution. Flannagan et al. (1986) compared the results with those of a U-shaped distribution, where mean values are unlikely and extreme values are more likely. This distribution is not unimodal: there are two distinct peaks in the probability distribution. Subjects had difficulties in learning such a category. Moreover, even if they learned the category, their answers indicated that they misrepresented the probability distribution. They categorised instances with mediate values as members and were more sceptical about the extreme values, while the U-distribution actually indicates that the extreme values are more likely to come from category members than the mean values. Based on these findings, Holland et al. (1986, p. 196) argued that the assumption of unimodality is a strong bias of human category learning.

Assumptions of unimodality also had a profound influence in science. The famous historical example to mention here is that of Karl Pearson who proposed a method to detect subpopulations from biometric data. Pearson’s friend Walter Weldon and his wife had measured shore crabs and found that the frequency curve of their front width was not unimodal but ‘double-humped’. This made Weldon suspect that there were two different subpopulations underlying this pattern of data. He consulted Pearson about this (see Magnello 2001, p. 262). Pearson (1894) used the data to develop his method of analysing probability distributions as mixtures of underlying normal distributions. The deviation from the normal distribution was interpreted as result of a mixture of several distributions rather than as a counterexample to the normal distribution. This is a historic example of how formal constraints of naturalness guide category development.

The generalisation of unimodality from one-dimensional to n-dimensional spaces (i.e., multivariate distributions) is highly researched within mathematical literature (cf. Dharmadhikari and Joag-Dev 1988; Bertin et al. 1997). One basic generalisation of unimodality is quasi-concavity. This is the demand that points with a probability density above any threshold t form convex regions. That is, for each $t>0$, $\{\langle x_1,\ldots , x_n\rangle |f_{X1,\ldots , Xn}(x_1,\ldots , x_n)\ge t\}$ is convex. In addition to being related to unimodality, quasi-concavity has also been discussed as a generalisation of convexity to fuzzy concepts (Tull 2021): for any two objects that are members of a category to some degree, there is no object between them that is member to a lesser degree.

Quasi-concavity mathematically relates convexity and unimodality. This relation is indeed very intuitive from a cognitive viewpoint. For the same reason humans perceive a point that lies between two points of a category as belonging to the same category (the convexity criterion), they judge that the point between two points with a certain probability is at least as probable (the principle of unimodality). Hence, the principle of unimodality from Holland et al. (1986) and the convexity criterion by Gärdenfors seem to refer to one and the same cognitive bias.

If we assume an n-dimensional conceptual space CS and $f_{X1,\ldots ,Xn}$, a probability density over CS that represents perceived inhabitation patterns, then we are cognitively biased to partition the space into concepts that are represented by regions over which $f_{X1,\ldots ,Xn}$ is quasi-concave. In other words, if less inhabited regions of the concept are eliminated, the conceptual regions will still be convex. Building on quasi-concavity as a generalisation of unimodality, I propose the following criterion of conceptual naturalness in probabilistic conceptual spaces.

The criterion formally captures the metaphor that natural concepts carve nature at its joints if we interpret joints as areas with low probability density. On the other hand, it builds upon the convexity assumption from conceptual spaces. It thus connects different traditions of thinking about natural concepts, namely the convexity criterion of conceptual spaces and the idea that concepts capture peaks of natural covariation, known from prototype theory as well as from the natural kinds debate.

4 Conclusion

This paper discussed the notion of natural concepts. Symbolic representations are usually unable to formulate criteria for whether a symbol refers to a natural concept. This main motivation for the development of geometric representations is already found in Carnap (1971, 1980) and was further elaborated by Gärdenfors (1990, 2000, 2014). The most prominent criterion of naturalness is convexity. The discussion in Sect. 2 analysed different versions of it and outlined its main supporting arguments. The criterion is extremely plausible for single-domain concepts such as colour terms. There it can be derived from principles of optimal design (Douven and Gärdenfors 2020) or the evolution of signaling systems (Jäger 2007).

Serious objections against convexity are raised in regard to complex spaces, correlations between domains, and multi-domain concepts. However, central concepts in human cognition are multi-domain concepts, which capture a correlational structure between different domains. This is why the second part of this paper examined these multi-domain concepts. I proposed three criteria for naturalness: 1) the existence of characteristic representations in several independent conceptual spaces (Revised Criterion C), 2) a narrow representation in a complex space that avoids the inclusion of unpopulated regions (Principle of Inhabitedness), and 3) a quasi-concave probability density over natural concepts in a probabilistic conceptual space (Criterion of quasi-concavity). These three criteria should be viewed as complementary. The first criterion states how the features of a complex concept are represented. It implies that there are correlations between features. These correlations can be represented by probability distributions over complex conceptual spaces (product spaces of the domains). The second criterion demands that natural multi-domain concepts cover the populated regions of such complex conceptual spaces while the third gives a more specific constraint on how the probability distribution influences concept development. While none of these criteria explicitly demands convexity, it is implicitly assumed in the criterion of quasi-concavity that generalises the bias for unimodal probability densities from univariate distributions to n-dimensional spaces.

This paper began with the question of what makes concepts natural. Some notable examples of non-natural concepts were grue and bleen. As argued in Sect. 3.3.1, the weirdness of these colour concepts can be explicated as a lack of convexity (Gärdenfors 1990). Their usage as features of complex concepts is also excluded by the criterion of non-locationality dating back to Carnap (1971). Another example of a non-natural concept was non-raven, as used in the sentence ‘Non-black things are non-ravens’. The classical argument from conceptual spaces is that the concept fails to be representable as a convex region. However, the discussion in the last section gave further reasons why we do not rely on such a concept. As argued in the second part of the paper, natural multi-domain concepts should have characteristic regions. The features of non-raven are arguably too unspecific, and they overlap with many other concepts. Moreover, in a complex probabilistic conceptual space, the concept includes many empty regions and does not occupy a region with a quasi-concave probability distribution. The restrictions developed throughout this paper give the intuitively expected results about non-natural concepts. The fact that humans, especially in philosophical debates or in arts, are able to develop, understand, and use strange concepts such as grue, non-raven or animals that tremble as if they were mad demonstrates the considerable flexibility of human cognition in violating its own conceptual biases.