An analysis of Existential Graphs–part 2: Beta

Abstract

This paper provides an analysis of the notational difference between Beta Existential Graphs, the graphical notation for quantificational logic invented by Charles S. Peirce at the end of the 19th century, and the ordinary notation of first-order logic. Peirce thought his graphs to be “more diagrammatic” than equivalently expressive languages (including his own algebras) for quantificational logic. The reason of this, he claimed, is that less room is afforded in Existential Graphs than in equivalently expressive languages for different ways of representing the same fact. The reason of this, in turn, is that Existential Graphs are a non-linear, occurrence-referential notation. As a non-linear notation, each graph corresponds to a class of logically equivalent but syntactically distinct sentences of the ordinary notation of first-order logic that are obtained by permuting those elements (sentential variables, predicate expressions, and quantifiers) that in the graphs lie in the same area. As an occurrence-referential notation, each Beta graph corresponds to a class of logically equivalent but syntactically distinct sentences of the ordinary notation of first-order logic in which the identity of reference of two or more variables is asserted. In brief, Peirce’s graphs are more diagrammatic than the linear, type-referential notation of first-order logic because the function that translates the latter to the graphs does not define isomorphism between the two notations.

1 Introduction

According to Michael Dummett (1973), Frege’s discovery of quantifiers and variables to express generality was the most important discovery in logical theory since Aristotle. Frege solved a problem that had blocked progress in logic for centuries: the problem of how to treat multiply quantified sentences such as “everything loves something”. Frege’s discovery consisted in regarding a sentence in which multiple quantifiers occur as constructed in stages each corresponding to the quantifiers that occur in it. Thus the sentence “everything loves something”, in which the quantifier “something” occurs within the scope of the quantifier “everything”, is not obtained by attaching the two quantifiers to the dyadic relational expression “x loves y”; it is obtained in two stages: first by combining “x loves y” with “something”, obtaining “x loves something”, and then by combining this with “everything”, obtaining the complete sentence. Only under this mode of analysis, Dummett explained, can the truth-conditions of a multiply quantified sentence be satisfactorily determined.

That the discovery of generality and the treatment of multiply quantified sentences was necessary for contemporary logical theories to have evolved is of course no news. Worthy of notice is, however, that this discovery is independent of the specifics of the notation that Frege had devised. A symptom of the neglect of this independence is that Dummett feels no need to present Frege’s Begriffsschrift in order to expound Frege’s discovery. Frege’s insight that sentences are constructed in stages might equally well be represented in notations other than the Begriffsschrift. The point has become part and parcel of modern quantificational logic in the ordinary form of the Peano-Russell notation, where the stages at which quantifiers are introduced in the constructional history of a well-formed formula are represented by the linear concatenation of the quantifiers. This is exactly how quantifier dependencies are expressed in the ordinary notation of first-order logic: “$(\forall x) (\exists y) (Lxy)$” represents “everything loves something”, while “$(\exists y) (\forall x) (Lxy)$” represents “something is loved by everything”.

By 1882, on the other side of the ocean, Charles S. Peirce had made the same discovery. The very first complete notational system for quantificational logic that he published was the “general algebra of logic” (Peirce 1885). In the general algebra the universal and the existential quantifiers are symbolized by “” and “”, respectively, and their linear concatenation indicates their dependencies. Thus, if “$l_{xy}$” represents the dyadic relational expression “x loves y”, then “” represents “everything loves something”, while “” represents “something is loved by everything”, very much like in the later Peano-Russell notation. In fact, the general algebra of logic was a pioneering presentation of first-order logic.

Unlike Frege, however, Peirce did not stick to any one formalism. His writings of the 1880s and 1890s are characterized by continuous experimentations with alternative notations for the theory of quantification. The outcome of these notational experiments was the system of Existential Graphs (EGs), which Peirce invented in 1896 and one part of which he termed “Beta graphs”, equivalent in its expressive power to (fragments of) first-order logic (Pietarinen 2015b; Roberts 1973). Presentations of EGs appeared in print in 1901 in the Dictionary of Philosophy and Psychology edited by J. M. Baldwin (Vol. 1, entry “Symbolic Logic”), in the Syllabus for the Lowell Lectures of 1903, and in the 1906 Monist article “Prolegomena to an Apology for Pragmaticism” (Peirce 1906). Most of his work on the matter remained unpublished, however, and the ideas did not spread (Pietarinen 2015a; LF 1–3). On Christmas Day of 1909 he wrote to William James that these graphs “ought to be the logic of the future” (RL 224).

Why did not Peirce stick to his first successful formalism, like Frege did? Why did he move from the general algebra to EGs, if the former was already substantially capable of capturing what we now reckon as first-order logic? In what sense are EGs “different” from the general algebra of logic and the ordinary notation of first-order logic? The primary purpose of the present paper is to provide a philosophical analysis of the difference between Beta graphs and the ordinary notation of first-order logic. A fortiori, this account will also provide an explanation of Peirce’s own shift from the general algebra of logic of 1885 to the graphs. The present paper focuses on the relation between EGs and the ordinary notation of first-order logic for simplicity’s sake; one can however bear in mind that this latter is a typographical variant of Peirce’s own general algebra.¹

Some current accounts of EGs have failed adequately to explain the difference between this system and the ordinary notation of first-order logic. One common explanation of the nature of EGs makes appeal to the distinction between “diagrammatic” and “non-diagrammatic” (or “symbolic”) notations (Shin 2002; Dipert 2006; Legg 2008; Moktefi and Shin 2012). On this account, EGs would be diagrammatic while the general algebra and the ordinary notation of first-order logic would be non-diagrammatic, and the movement from the latter to the former would be explainable as a search for a diagrammatic version of first-order logic. Yet, this explanation neglects a distinction which is necessary if we are to understand Peirce’s doctrine of diagrammatic reasoning. It is the distinction between what Stjernfelt (2014) calls the “operational” and the “optimal” notion of “iconicity”. Peirce never explicitly distinguishes the two notions from one another, but Stjernfelt shows that the distinction is not only implicit in what Peirce says, but constitutes the only interpretation that will make sense of his doctrine of diagrammatic reasoning. According to the “operational” notion, all deductive reasoning is diagrammatic, independently of the notation in which it is performed (CP 1.54, 2.778, 3.429, 5.148, 5.162). This idea emerged while Peirce was working on the algebraical versions of quantificational logic (1882–1885) and thus appeared well before the invention of the logical graphs in 1896. Algebraical notations too are “diagrammatic” (CP 3.363, 3.456), and in many places Peirce wrote that diagrams are either algebraical or geometrical: “there are two general classes of diagrams which are used to assist the mind in deduction; and there is no logical reason why either of these should not be sufficient. There are algebraical and geometrical diagrams” (RS 97, pp. 208–209; cf. also R 17, c. 1896; CP 2.778, 1901; CP 4.233, 4.246, 1902). In light of this, the claim that EGs differ from other equivalently expressive notations such as the general algebra of 1885 because they are diagrammatic, explains very little.

Peirce never says that his EGs differ from the general algebra because the former are diagrammatic. What he does say is that EGs provide a more diagrammatic system of logical representation and analysis than the algebraical versions. This idea corresponds to Stjernfelt’s notion of “optimal” iconicity, namely the idea that among systems of logical representation that are equivalent under the “operational” notion, some may still be “more diagrammatic” than others. In the very first paper that he wrote on EGs he makes the following claim: “The more diagrammatically perfect a system of representation, the less room it affords for different ways of expressing the same fact” (R 482 = LF 1, p. 229). We take this claim to provide a criterion for diagrammatic perfection: a system is more diagrammatic (equivalently, more diagrammatically perfect) than another if the former affords less room for different ways of expressing the same fact than is afforded by the latter.²

As far as we know, Peirce nowhere does explicitly say that this is his, or his only, criterion for diagrammatic perfection. Yet not only manuscript R 482 (1896) but also his continually evolving solutions with respect to the notation for quantificational logic from 1885 onwards unmistakably show that he had some such criterion in mind all along. In the sequel we refer to this criterion as “Peirce’s criterion”, with the understanding that it is our interpretation both that the claim in R 482 provides such criterion and that this criterion propelled, and thus explains, his notational experiments.

It is important to clarify what is meant by “different ways of expressing the same fact”. In the Short Logic of 1895 Peirce writes: “For logical purposes two judgments which assert the same fact are precisely equivalent. Whatever can be inferred from the one can equally be inferred from the other, and when one can be concluded, so can the other. They are necessarily true and false together” (R 595 = LF 1, p. 195). In the Logical Tracts. No. 2 of 1903 we read: “Two propositions are said to represent the same fact or truths, if, and only if, in each supposable state of the universe either both are true or both false” (R 492 = LF 2.2, p. 216). What in the Short Logic was called a “judgment” and in the Logical Tracts a “proposition” is better understood as what is usually called a “sentence”. Moreover, Peirce’s talking of “facts” is better construed in terms of “truth-conditions”. The two passages thus say that sentences represent the same fact if and only if they have the same truth-conditions.³

When do distinct sentences have the same truth-conditions then? Two sentences with different primitives may have the same truth-conditions, such as “$\sim \!(\mathrm{P}\ \& \sim \mathrm{Q})$” and “$\mathrm{P} \supset \mathrm{Q}$” in the standard language of sentential logic. Now one way to understand Peirce’s criterion is by reference to the vocabulary, or set of primitive constants, of the language. Consider a language ${\mathscr {L}}_{1}$ with the negation and conjunction operators as its logical vocabulary $({\mathscr {L}}_{1}\,{=}\,\{\sim ; \& \})$ and another language ${\mathscr {L}}_{2}$ with the negation, conjunction, and implication operators as its logical vocabulary $({\mathscr {L}}_{2} = \{\sim ; \& ;\supset \})$. The two languages are equivalently expressive, as both express sentential logic. Yet, ${\mathscr {L}}_{2}$, given its richer vocabulary, affords more room for different ways of expressing one and the same fact than is afforded by ${\mathscr {L}}_{1}$. For example, in ${\mathscr {L}}_{2}$ the fact expressed by the sentence “$\sim \!(\mathrm{P}\ \& \ \sim \!\mathrm{Q})$” is also expressed by the sentence “$\mathrm{P} \supset \mathrm{Q}$”, while this is not the case with ${\mathscr {L}}_{1}$. Or consider a sentential language with the negation operator among its primitives: in such a language there will be infinite ways of expressing one and the same fact: “$\mathrm{P}$”, “$\sim \sim \mathrm{P}$”, “$\sim \sim \sim \sim \!\mathrm{P}$”, “$\sim \sim \sim \sim \sim \sim \!\mathrm{P}$”, etc. express one and the same fact (i.e., have the same truth-conditions).⁴

In many of his papers on the algebra of logic, Peirce was clear that a language with a greater amount of primitive operators is less “economic”, or as he said, less “analytical”, than a language with a lesser amount thereof, because in the richer (less economic, less analytical) language there will always be more room for different ways of expressing the same fact than there are in the poorer (more economic, more analytical) language. Yet, this cannot explain Peirce’s shift from the general algebra of logic to EGs. For if the greater diagrammaticity of EGs over the general algebra were simply due to a difference in their vocabularies, then a version of the general algebra that uses the same primitive operators and quantifiers as EGs would be as diagrammatic as EGs are. As we shall see, this is not the case: there are further differences between EGs and the general algebra that cannot be explained only in terms of logical vocabulary.⁵

Peirce’s criterion of diagrammaticity therefore needs to be qualified in the following manner: of two equivalently expressive systems with the same or corresponding primitive constants, a system is more diagrammatic than another if the former affords less room for different ways of expressing the same fact than is afforded by the latter. How two systems with the same or corresponding primitive constants may be said to differ is what the present paper explains by reference to Peirce’s logical graphs. It is argued that the notational difference between EGs and the ordinary notation of first-order logic is that, ceteris paribus (i.e., given the equivalence of primitive constants), the translation from the latter to the former is a non-injective, surjective function: it is surjective because any sentence of the ordinary notation of first-order logic has a corresponding graph; it is non-injective because every graph corresponds to several, syntactically distinct sentences of the ordinary notation of first-order logic. In other words, every graph type corresponds to a class of logically equivalent sentence types of a language with equivalent primitive constants.

EGs divide into three departments: Alpha, corresponding to sentential calculus (Ma and Pietarinen 2020); Beta, corresponding to quantificational logic with identity (Pietarinen 2015b); and Gamma, consisting of elements of modal logics, higher-order logics, abstraction, and logics for non-declarative assertions (Roberts 1973; Pietarinen 2015a). Since Beta builds upon Alpha and inherits from it a fundamental syntactical convention, it will be necessary to explain what this convention is. Even more fundamentally, a conceptual distinction between the notions of “type”, “token”, and “occurrence” has to be first introduced, because it is necessary to explain the specific notational features of EGs.

2 Types, tokens, and occurrences

The distinction between type and token expressions is well known in linguistic theory. Consider the following sentence:

$$\begin{aligned} \mathrm {war}\ \mathrm {is}\ \mathrm {war} \end{aligned}$$

(1)

Sentence (1) may be said to contain either two or three words. In one sense, (1) contains three word tokens (“war”, “is”, and “war”). In another sense, it contains two word types (“war” and “is”). A type is a general, abstract, and unique kind of entity; a token a concrete and individual one. When an editor asks an author to write a paper of 8.000 words, what she means is 8.000 word tokens. When a corpus linguist says that Dante’s Divina Commedia contains 12.831 words, what she means is 12.831 word types. Peirce was the first to draw this distinction and to provide the current terminology (cf. Wetzel 2014).

However useful Peirce’s distinction may have proven to be, it is insufficient for the purposes of even some basic linguistic analyses. An example of its insufficiency, adapted from Wetzel (1993), is the following. Let us assume that the type/token distinction is exhaustive, namely that a simple or composite expression is either an expression type or an expression token. Let us further assume that (1) is a sentence type. The sentence consists of three words. Are these three word types or three word tokens? The sentence cannot consist of three word tokens, because we have assumed it to be a sentence type and thus an abstract entity, while tokens are concrete entities. Nor can (1) consist of three word types, because there are only two word types of which it can consist.

The problem is solved by recognizing a third level of linguistic analysis, the occurrence of an expression in some linguistic context. Assuming (1) to be a sentence type, we may say that the word type “war” occurs twice in (1), and is instantiated or betokened twice in every token of that sentence. The two occurrences of the word type “war” in (1) can be differentiated by saying that one of them is the “the first occurrence of ‘war’ in (1)”, the other the “second occurrence of ‘war’ in (1)”. A parallel differentiation can be made for the two occurrences of the word token “war” in every token of (1). The notion of occurrence thus solves the problem exemplified in the preceding paragraph quite well: as a sentence type, (1) contains one type of the word “war” (and not two of them), and two occurrences of it (and not two tokens of it).

This tripartite distinction between type expressions, token expressions, and occurrences of expressions is necessary to explain how EGs differ from the ordinary notation of first-order logic.

3 Alpha graphs

Alpha graphs are written on a two-dimensional sheet, called the “sheet of assertion”. Any such graph written on the sheet is asserted, and any number of graphs juxtaposed on the sheet are asserted independently of one another, that is, their conjunction is asserted. The graph in Fig. 1a means “it is true that P”, or “P”; the graph in Fig. 1b means “P and Q”, and the graph in Fig. 1c means “P and Q and R”. In order to negate a graph, a lightly drawn oval or “cut” is placed around it. The Alpha graph in Fig. 2a means “it is not true that P”, that is, “not P”; the Alpha graph in Fig. 2b means “it is true that P and it is not true that Q”, that is, “P and not Q”; the Alpha graph in Fig. 2c means “it is not true that (P and not (Q and R))”, that is, “If P, then Q and R”.

Fig. 1

Alpha graphs

Fig. 2

Alpha graphs

Topologically, the sheet of assertion represents an isotropic space, unordered and without direction. A partial ordering is introduced in the sheet by the cuts. This feature—the sheet of assertion being partially ordered by the cuts—is possible because the cuts are both signs of negation and collectional signs, namely signs that indicate the order of application of the operations.⁶ In linear notations this is typically achieved by parentheses. Being collectional signs, cuts divide the sheet of assertion into “areas”. In Fig. 2c the sheet is divided into three areas: the area outside the outer cut, the area inside the outer cut and outside the inner cut, and the area inside the inner cut. EGs are thus not interpreted linearly from left to right or from right to left, but “endoporeutically”: “the interpretation of existential graphs is endoporeutic, that is proceeds inwardly; so that a nest sucks the meaning from without inwards unto its center, as a sponge absorbs water” (R 650, 1910). The endoporeutic interpretation prescribes that we consider the outermost area first, systematically proceeding inward into any area enclosed in whatever cut is placed on the first area, and so on. Thus any enclosed area depends, or is in the scope of, the area on which the enclosing cut lies. Graphs in the same area are endoporeutically neutral. In order words, the sheet is partially ordered by the cuts.

Since the sheet and any area in it are projections of isotropic spaces, no continuous transformation that preserves the topological property of “lying within the same area” can produce syntactically distinct graphs; such transformations only produce graphs tokens of one and the same graph type.⁷ Only the juxtaposition of graphs on the same area counts as a syntactically relevant fact. Their position and orientation within an area is syntactically irrelevant. Thus, each of the Alpha graphs in Fig. 3a–c, since they all depict the two sentential variables “P” and “Q” as lying on the same area (the sheet of assertion), is a distinct token of the same graph type.

Fig. 3

Alpha graphs

By contrast, (2a) and (2b) are not distinct sentence tokens of the same sentence type but distinct sentence types (syntactically distinct sentences), which in classical sentential logic are logically equivalent.

$$ \begin{aligned}&{\mathrm{P}}\ \& \ {\mathrm{Q}} \end{aligned}$$

(2a)

$$ \begin{aligned}&{\mathrm{Q}}\ \& \ {\mathrm{P}} \end{aligned}$$

(2b)

The reason for this divergence is that the notation in which (2a) and (2b) are written is linear, and thus any permutation of elements in a string results in a syntactically distinct string (whether logically equivalent to the permuted string or not), while Alpha graphs are non-linear, and thus any mutation of the position and orientation of graphs lying on the same area (since each area is an isotropic space) results in distinct graph tokens of the same graph type. The Alpha graphs in Fig. 3 differ not in the manner in which (2a) and (2b) differ, but in the manner in which, say, “P & Q” and “P & Q” may be taken to differ.⁸

Let us assume that (2a) and (2b) are sentences from ${{\mathscr {L}}}$, where ${{\mathscr {L}}}$ is a linear sentential language with negation and conjunction $({{\mathscr {L}}} = \{\sim ; \& \})$. Alpha graphs and ${{\mathscr {L}}}$ are expressively equivalent, since they both can capture sentential logic, and have the same primitive constants (negation and conjunction). Yet, while in ${{\mathscr {L}}}$ the equivalence of (2a) and (2b) is a logical equivalence (that is, two distinct sentence types can be said in the metalanguage to have the same truth-conditions), in the system of Alpha graphs the equivalence of Fig. 3a and b is a syntactical equivalence (that is, two distinct graphs tokens can be said in the metalanguage to be tokens of the same graph type).⁹ In ${{\mathscr {L}}}$ there are two distinct ways, namely (2a) and (2b), of expressing the “fact” (i.e., the truth-conditions) expressed in Alpha graphs by the graph type of which Fig. 3a–c are graph tokens. Given Peirce’s criterion of diagrammaticity, Alpha graphs are therefore more diagrammatic than ${{\mathscr {L}}}$, because in Alpha graphs there is only one graph type expressing those facts that in ${{\mathscr {L}}}$ are expressed by multiple sentence types that merely differ in the linear ordering of those elements that in the corresponding Alpha graph type lie on the same area. Another way of stating this is that the translation of formulas from ${{\mathscr {L}}}$ to Alpha graphs is non-injective and surjective: every Alpha graph type corresponds to a class of logically equivalent ${{\mathscr {L}}}$ sentence types.

4 Beta graphs

Let us now move to the Beta part. In any notation for quantificational logic, two phenomena are typically to be represented: the co-reference of variables bound to certain quantifiers, and the logical scope of the quantifiers that bind the variables.¹⁰

$$ \begin{aligned}&(\forall x) (Fx \, \& \, Gx) \end{aligned}$$

(3)

$$\begin{aligned}&(\forall x) (\exists y) (Lxy) \end{aligned}$$

(4)

In (3) the fact that the bound variable in “Fx” refers to the same individual as that in “Gx” is expressed by the fact that the variable is the same in the two cases (“x”). One the other hand, in (4) the fact that the individuals referred to by the two bound variables in “Lxy” may (though they need not) be distinct is expressed by the fact that the variables are distinct (“x” and “y”).

With the distinction between type and occurrence we can be more specific about the sense of such “sameness” and “distinctness”. The co-reference of the variables in (3) is expressed by the sameness of the variable type: when the sentence gets interpreted, all occurrences of the variable type “x” occurring within the scope of a quantifier refer to the same individual. In the same fashion, in (4) the possibility that the individuals referred to by the variables are distinct is expressed by the difference of the variable types “x” and “y”: when the sentence gets interpreted, all occurrences of the same variable type refer to the same individual, while occurrences of distinct variable types may (though they need not) refer to distinct individuals.

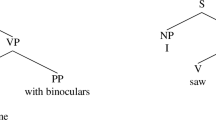
All this appears somewhat trivial only if we neglect the fact that there are different means for expressing the co-reference of variables not based on the sameness or the distinctness of variable types. Take the sentence “No man has seen every city”. In the notation of Quine’s Mathematical Logic (1940), such a sentence would be represented as in (5):

$$\begin{aligned} (x)(x\ \mathrm {is\ a\ man}\ .\supset \ \sim \ (y)\ (y\ \mathrm {is\ a\ city}\ .\supset .\ x\ \mathrm {has\ seen}\ y)). \end{aligned}$$

(5)

But since, as Quine observes, the variables “serve merely to indicate cross-references to various positions of quantification”, another notation that captures the same meaning may represent such cross-references by “curved lines or bonds” (1940, p. 70). Thus, as an equivalent representation for (5), Quine produces the “quantificational diagram” of Fig. 4.

Fig. 4

Quine’s quantificational diagram

That Quine dismisses quantificational diagrams immediately after having introduced them by merely stating that they are too “cumbersome” and “unpractical”, need not concern us here. What is important is that such a notation is a possible one. In Quine’s quantificational diagrams, the co-reference of variables bound by the same quantifiers is expressed by the sameness of bonds, each bond representing a variable. But bonds being all alike, they can only be distinguished as occurrences of one and the same bond type, just like the three “xs” in (3) are occurrences of one and the same variable type. In Quine’s quantificational diagrams, the co-reference of the variables bound by the same quantifiers is expressed by the sameness of bond occurrences: each “position of quantification” connected by the same bond denotes the same individual, distinct occurrences of the bond may (though they need not) denote distinct individuals.

Following a suggestion by John Etchemendy to Keith Stenning,¹¹ we call “type-referential” a language in which sameness of variable type determines sameness of reference, while distinctness of variable type may (though it need not) determine distinctness of reference. We call “occurrence-referential” a language in which sameness of variable occurrence determines sameness of reference, while distinctness of variable occurrence may (though it need not) determine distinctness of reference. (In the definition of “type-referential” languages, “sameness of variable type” is relative to the occurrences of a variable type that are in the scope of the same quantifier, and “distinctness of variable type” is relative to occurrences of variable types that have overlapping scope, where the scope of a variable is the scope of the quantifier that binds it.) Quine’s “quantificational diagrams” are occurrence-referential; the ordinary notation of first-order logic is type-referential. Peirce’s Beta graphs, as we shall now see, are an occurrence-referential language.¹²

Beta adds two elements to the syntax of Alpha: the “spots” and the “lines of identity”. Spots correspond to predicates and relational expressions; they have to be regarded as having a specific number of “hooks” at their periphery, or places at which lines of identity may be attached. A spot with n hooks corresponds to a predicate or relational expression with n variable arguments. The “adicity” of a spot is the number of its hooks. Since the sheet of assertion is an isotropic space, the hooks at the periphery of a spot need to be numbered or otherwise distinguished. Spots are not “graphs”, that is, they do not express complete propositions but correspond to open formulas. A line of identity is a graph that expresses the identity of that which is denoted by its endpoints. When a line of identity is attached to the hook of a spot, this attachment represents the existential quantification that relates specifically to that hook of the spot. The line of identity is therefore a sign of both identity (“$=$”) and existential quantification (“$\exists$”). No hook can be occupied by more than one end of a line of identity.

In the Syllabus of 1903 (R 478) Peirce wrote: “The line of identity is a Graph any replica of which, also called a line of identity, is a heavy line with two ends and without other topical singularity (such as a point of branching or a node), not in contact with any other sign except at its extremities. Otherwise, its shape and length are matters of indifference. All lines of identity are replicas of the same graph” (LF 2.2, p. 368). This passage is important for two reasons. First, it makes it clear that in the system of Beta graphs there is only one line type, which may multiply occur in a Beta graph. Since there is only one such line type, it is the occurrence of the line type that determines sameness and possible distinctness of reference: Beta graphs are occurrence-referential. In the second place, the only syntactically relevant feature of any occurrence of a line of identity is its running continuously between its two extremities without crossing the boundaries of an area, while shape, orientation, and length are syntactically not significant.

Fig. 5

Beta graphs

In Fig. 5, the letter “G” is a spot that expresses the triadic relational expression “x gives y to z”. Fig. 5a is the “unsaturated” spot with its hooks (the empty circles at its periphery), without lines attached to them; it corresponds to the open formula which may be expressed in ordinary notation as “Gxyz”. No unsaturated spot can be written on the sheet of assertion, i.e. no spot is a well-formed graph. In Fig. 5b to each of the three hooks of the spot three distinct occurrences of the line of identity are attached. Since attaching a line to a hook means quantifying existentially with respect to that hook, Fig. 5b expresses what in ordinary notation is expressed by “$(\exists x) (\exists y) (\exists z) (Gxyz)$”. As mentioned, since the sheet of assertion is an isotropic space, the hooks at the periphery of a spot are to be distinguished from one another by some other means than linear ordering. In his very first papers on the logical graphs (R 482 = LF 1, pp. 211–261; R 483 = LF 1, pp. 292–303) Peirce suggests that the hooks of a spot have a definite order of interpretation beginning at a designated hook and continuing clockwise. One can place a numerical index (or any other distinguishing mark) next to a line to indicate the starting of the clockwise interpretation of lines and the corresponding hooks. So, if Fig. 5b expresses what in ordinary notation is expressed by “$(\exists x) (\exists y) (\exists z) (Gxyz)$”, Fig. 5c expresses what in ordinary notation is expressed by “$(\exists x) (\exists y) (\exists z) (Gyzx)$”, and Fig. 5d expresses what in ordinary notation is expressed by “$(\exists x) (\exists y) (\exists z) (Gzxy)$”. The numerical index can also be omitted in what Peirce suggests to consider as the default case, i.e. the case in which the clockwise counting begins from the left hand side of the spot. Thus, Fig. 5b would retain its meaning even if the numerical index were omitted, while in Fig. 5c and d the numerical index is necessary. If, moreover, any special ordering of the variables is required, additional numerical indices can be used to the purpose. The question of the ordering of the quantifiers, discussed in the next section, is a quite different problem and demands a different solution.

Fig. 6

Beta graphs

Let us consider some more examples. The Beta graph in Fig. 6a is obtained by attaching an occurrence of the line of identity to the single hook of the monadic spot “M”, thus existentially quantifying in that position, “$(\exists x) (Mx)$” in ordinary notation. The Beta graph in Fig. 6b is obtained by attaching two occurrences of the line of identity to the two hooks of the dyadic spot “L”, thus existentially quantifying in both those positions. If there is no numerical index, the interpretation is the default one, i.e. the first hook is the one on the left, “$(\exists x) (\exists y) (Lxy)$” in ordinary notation. The Beta graph in Fig. 6c is obtained by joining the two occurrences of the line of identity of Fig. 6b, thus obtaining a graph in which there is only one occurrence of the line, “$(\exists x) (Lxx)$” in ordinary notation. The Beta graph in Fig. 6d is obtained by combining the Beta graph in Fig. 6a with that in Fig. 6b, thus obtaining a graph that in ordinary notation is written as “$(\exists x) (\exists y) (Lxy \& My)$”.

We saw above that in order to explain certain features of Alpha graphs we need a distinction between a graph type and a graph token. In order to explain Beta graphs, both the notions of a token and of an occurrence are needed. The only syntactically relevant feature of any occurrence of a line of identity is its running continuously between its two extremities, while shape and length are syntactically not significant. This means that no continuous transformation of an occurrence of a line of identity that preserves the topological property of connecting its two extremities within an area produces a distinct Beta graph type. It can only produce a distinct Beta graph token of the same type, just as in Alpha graphs no movement that maintains the topological property of lying in the same area produces a distinct Alpha graph type but only a distinct Alpha graph token of the same type. Consider the Beta graphs in Fig. 7. The Beta graph in Fig. 7a is the same type as that in Fig. 7b, each being a distinct Beta graph token of the same type. Each of these tokens contains two occurrences of the line of identity. The notion of a token is needed to explain in what sense Fig. 7a and b are “the same”; the notion of an occurrence is needed to explain in what sense the individuals denoted by the two lines in either Fig. 7a or b are distinct.

Fig. 7

Beta graphs

Fig. 8

Beta graphs

We are now in the position to evaluate Beta graphs based on Peirce’s criterion of diagrammaticity (as defined above). Since the sheet of assertion is isotropic, the lines of identity can be subjected to any continuous transformation that preserves their connectedness within an area. Thus, just like any of (a–c) in Fig. 3 is a distinct Alpha graph token that instantiates one and the same Alpha graph type, so any of (a–d) in Fig. 8 is a distinct Beta graph token that instantiates one and the same Beta graph type. In the ordinary notation of first-order logic, there are infinitely many syntactically distinct sentences types for this unique Beta graph type, of which the following are some of the representative samples:

$$ \begin{aligned}&(\exists x) (Fx\ \& \ Gx) \end{aligned}$$

(6a)

$$ \begin{aligned}&(\exists x) (Gx\ \& \ Fx) \end{aligned}$$

(6b)

$$ \begin{aligned}&(\exists y) (Gy\ \& \ Fy) \end{aligned}$$

(7a)

$$ \begin{aligned}&(\exists z) (Gz\ \& \ Fz) \end{aligned}$$

(7b)

Sentences (6a) and (6b) are in the ordinary notation of first-order logic distinct (because this notation is linear) but logically equivalent. They differ as  (2a) and (2b) above differ: they are different ways of expressing the same fact.

Sentences (7a) and (7b) are distinct in another sense: they are the same but use distinct variables types. This difference cannot be expressed in Beta graphs, because in Beta graphs there is only one variable type, the line of identity, which determines sameness and distinctness of reference by means of the sameness and distinctness of its occurrences. The same point could be made with reference to Fig. 6a, which is equivalent to infinitely many first-order sentences, e.g. to “$(\exists x) (Mx)$”, “$(\exists y) (My)$”, “$(\exists z) (Mz)$”, “$(\exists t) (Mt)$”, etc. The fact that Beta graphs are an occurrence-referential notation thus determines that to one and the same Beta graph type, e.g. that in Fig. 8, of which (a–d) are tokens, there correspond infinitely many syntactically distinct sentences, i.e. sentence types, in the ordinary notation of first-order logic. The impossibility of expressing in Beta graphs the difference between (6a) and (6b) follows from the non-linearity of the graphs; the impossibility of expressing in Beta graphs the difference between (7a) and (7b), as well as the difference between the infinitely many distinct sentences that may be constructed with as many distinct variables, follows from the occurrence-referentiality of the graphs.

This is not all. It was mentioned that in Beta graphs a line of identity represents both quantification and identity; it is a single notational device that does what in first-order logic with identity is done by the combined performance of the symbol of the quantifier (“$\exists$”) and the symbol of the relation of identity (“$=$”). That Beta graphs should combine quantification and identity is a consequence of its being an occurrence-referential notation: two disconnected occurrences of the line of identity on the sheet of assertion mean that there may be two distinct individuals (Fig. 9a); if we then wish to identify them, the only way to do so without destroying occurrence-referentiality is to join the two occurrences, thus changing them into one single occurrence of the line of identity (Fig. 9b). Any other means of expressing the identification would leave the two occurrences of Fig. 9a disconnected, which in the language of Beta graphs means that the two individuals referred to may be distinct.

Fig. 9

Beta graphs

Occurrence-referentiality therefore offers a third explanation of the diagrammaticity (as defined above) of Beta graphs. Consider the following two sentences:

$$ \begin{aligned}&(\exists x) (\exists y) (Fx \, \& \, Gx \, \& \, x = y) \end{aligned}$$

(8a)

$$ \begin{aligned}&(\exists x) (Fx \, \& \, Gx) \end{aligned}$$

(8b)

Sentences (8a) and (8b) are logically equivalent in first-order logic with identity. They are distinct sentences with equivalent truth-conditions, that is (as Peirce put it), “different ways of expressing the same fact”. In Beta graphs there is no means of expressing (8a) without thereby expressing (8b), and there is only one Beta graph type that can correspond to (8a) and (8b), namely the graph type of which those in Figs. 8a–d are graph tokens.

Any occurrence of the line of identity non-attached to a spot, like that in Fig. 9b, is itself a well-formed graph, i.e. is a complete assertion. It expresses what in the notation of first-order logic with identity is expressed, for example, by (9a–b), and by infinitely many other sentences that can be constructed with as many distinct variables such as (9c–d), plus their permutations of (9e–f).¹³

$$\begin{aligned}&(\exists x) (x=x) \end{aligned}$$

(9a)

$$\begin{aligned}&(\exists x) (\exists y) (x=y) \end{aligned}$$

(9b)

$$\begin{aligned}&(\exists y) (y=y) \end{aligned}$$

(9c)

$$\begin{aligned}&(\exists y) (\exists z) (y=z) \end{aligned}$$

(9d)

$$\begin{aligned}&(\exists x) (\exists y) (y=x) \end{aligned}$$

(9e)

$$\begin{aligned}&(\exists y) (\exists z) (z=y) \end{aligned}$$

(9f)

Let us assume that (9a) and (9b) are sentences from ${{\mathscr {L}}}$, where ${{\mathscr {L}}}$ is the ordinary linear language of first-order logic with identity, with negation, conjunction, the existential quantifier, and the identity sign $({{\mathscr {L}}} = \{\sim ; \& ; \exists ; =\})$. Beta graphs and ${{\mathscr {L}}}$ are expressively equivalent, since they both can capture first-order logic with identity and have the same primitive constants. Yet, while in ${{\mathscr {L}}}$ the equivalence of, e.g., (9a) and (9b) is a logical equivalence, that is, two distinct sentence types are said in the metalanguage to have the same truth-conditions, in the system of Beta graphs no such syntactical distinctness is representable at all. In ${{\mathscr {L}}}$ there are infinitely many distinct ways of expressing the “fact” (i.e. the truth-conditions) which is expressed in Beta graphs by Fig. 9b. Given Peirce’s criterion of diagrammaticity, Beta graphs are therefore more diagrammatic than ${{\mathscr {L}}}$, because in Beta graphs there is only one Beta graph type expressing facts that in ${{\mathscr {L}}}$ are expressed by infinitely many sentences. Another way of stating this is that the translation of formulas from ${{\mathscr {L}}}$ to Beta graphs is non-injective and surjective: every Beta graph type corresponds to a class of logically equivalent ${{\mathscr {L}}}$ sentence types.

5 Dependent quantification

Let us now return to Dummett’s claim mentioned in the introduction, namely that the single most important aspect of Frege’s discovery of quantification was his regarding any sentence in which signs of generality occur as having been constructed in stages corresponding to the signs of generality occurring in it. Not only is this perfectly true of Peirce’s Beta graphs, but also the graphs provide a more diagrammatic analysis (in the specified sense) of the relations of dependence between quantifiers than what Frege’s or the ordinary notation of first-order logic do.

In order to appreciate this point we briefly mention another notation that Peirce proposed before the Beta graphs of 1896. In parallel to the general algebra of logic of 1885, which is type-referential, Peirce invented a system of logical graphs that is occurrence-referential. Let us call these the “proto-graphs” of 1882 (W 4, pp. 391–399).¹⁴ Two kinds of bonds are used in the proto-graphs: plain lines that stand for existentially quantified variables and crossed lines that stand for universally quantified variables. Thus, the proto-graph in Fig. 10a expresses what in the ordinary notation of first-order logic is expressed by (10a). But since the sheet of assertion is unordered, there is no syntactical reason why the proto-graph in Fig. 10a should be taken as representing (10a) and not the logically distinct (10b), which differs from (10a) only in the order of the quantifiers.

This problem is not the same as the problem of representing the order of the hooks of a spot (the order of the free variables of a predicate or relational expression). It was seen above that the problem of representing the order of the hooks can be solved, and at some point Peirce proposed to solve it, by placing a numerical index (or any other distinguishing mark) next to a line to indicate that the clockwise interpretation of lines and the corresponding hooks has to start from there. So, if Fig. 10a represents (10a) (where the left hand side line is interpreted by default as the first in the clockwise counting of the hooks), Fig. 10b may be taken to express (10c), which differs from (10a) only in the order of the hooks. Yet, we are still unable to express distinct (and logically distinct) orderings of quantifiers: Fig. 10a would represent both (10a) and (10b), while Fig. 10b would represent both (10c) and (10d). This is a main problem for Peirce’s 1882 proto-graphs: having abandoned linearity, Peirce must find other means to express the relations of dependence between the quantifiers, for otherwise his proto-graphs would fall short of adequately expressing what his own general algebra and first-order logic can express.

$$\begin{aligned}&(\forall x) (\exists y) (Lxy) \end{aligned}$$

(10a)

$$\begin{aligned}&(\exists y) (\forall x) (Lxy) \end{aligned}$$

(10b)

$$\begin{aligned}&(\forall x) (\exists y) (Lyx) \end{aligned}$$

(10c)

$$\begin{aligned}&(\exists y) (\forall x) (Lyx) \end{aligned}$$

(10d)

Fig. 10

The proto-graphs of 1882

Peirce had two solutions, both unsatisfactory. One solution was to express quantifier dependence by means of an additional layer of numerical indices, where a higher number means wider scope (W 4, p. 393). For example, the graph in Fig. 11a would now express (10a), in which the universal quantifier (the crossed line numbered 2) has wider scope than the existential quantifier (the plain line numbered 1), and the graph in Fig. 11b would express (10b), in which the universal quantifier (the crossed line numbered 1) has narrower scope than the existential quantifier (the plain line numbered 2). Likewise, the graph in Fig. 11c would now express (10c), in which the universal quantifier (the crossed line numbered 2) has wider scope than the existential quantifier (the plain line numbered 2), and the graph in Fig. 11d would express (10d), in which the universal quantifier (the crossed line numbered 1) has narrower scope than the existential quantifier (the plain line numbered 2).

Fig. 11

The proto-graphs of 1882 with quantifier dependence expressed by numerical indices

But this won’t work. In the ordinary notation of first-order logic it is the linear concatenation that allows us to express both the sequences of the variables and the sequences of (and thus the dependencies among) quantifiers. The ordering provided by linear concatenation can be re-introduced by the use of numerical indices, but it has to indicate either the ordering of the variables or the ordering of the quantifiers; it cannot indicate both. For given the isotropic nature of the sheet, there is no way to distinguish the numerical index that indicates the ordering of the hooks and the numerical index that indicates the ordering of the quantifiers. If the numerical indexing has to be used for ordering the hooks, it cannot also be used for ordering the quantifiers, on pain of syntactical ambiguity.

Another solution was to express quantifiers dependence by means of the length of the corresponding lines, where a longer line has wider scope (W 4, p. 396). For example, the graph in Fig. 12a would now express (10a), in which the universal quantifier (the longer crossed line) has wider scope than the existential quantifier (the shorter plain line), and the graph in Fig. 12b would express (10b), in which the universal quantifier (the shorter crossed line) has narrower scope than the existential quantifier (the longer plain line). Likewise, the graph in Fig. 12c would now express (10c), in which the universal quantifier (the longer crossed line) has wider scope than the existential quantifier (the shorter plain line), and the graph in Fig. 12d would express (10d), in which the universal quantifier (the shorter crossed line) has narrower scope than the existential quantifier (the longer plain line).

Fig. 12

The proto-graphs of 1882 with quantifier dependence expressed by line length

This is also unsatisfactory. For it is one of the essential features of the logical graphs, in both the 1885 and the 1896 versions, that sameness and distinctness of reference is determined by sameness and distinctness of line occurrences independently of any other feature that each token of the line may possess which does not affect the topological property of connectedness within an area. This means, as noticed, that length, orientation and shape of the line are not syntactically relevant facts in this notation. If therefore the length of a line occurrence is to express the wider scope of the quantifier associated to that occurrence with respect to any shorter occurrence, this constitutes a plain violation of the syntax of the logical graphs. Peirce was unsatisfied with both these devices for expressing quantifiers dependence in a non-linear language. The device based on the length of the lines is immediately abandoned, while the device based on numerical indices is retained in his later graphical experiments only to express the ordering of the hooks.

Although Peirce continued working on both the sentential calculus and quantificational logic, it was only fourteen years after the invention of the general algebra and of the proto-graphs that he could finally solve the problem of properly representing dependent quantification. Recall that one of the essential features of Alpha graphs is that the cut is both a sign of negation and a collectional sign, namely a sign whose office is to indicate the order of application of the operations. In Beta graphs, the endoporeutic structure created by the cuts corresponds to the stages at which the quantifiers—here the occurrences of the line of identity—are introduced. Thus a line occurrence has wider scope than another (i.e., the other depends on it) if its outermost part is less enclosed within cuts than the outermost part of the other. Verbatim: “bonds whose outermost parts are less enclosed being taken before those whose outermost parts are more enclosed” (R 480, 1896); “Individuals represented by less enclosed lines are to be selected before individuals represented by more enclosed lines” (R 430–431, 1902); “The interpretation of the Entire Graph is to proceed endoporeutically. That is to say, it is the less enclosed parts which must determine to what the more enclosed parts are to be understood as referring, and not the reverse” (R 292, 1906).

In this manner, no ad hoc sign regarding scope is needed: the nesting of an already existing sign, the cut, suffices to determine the recursive structure of the graphs and thus the stages at which the quantifiers are introduced. The relations of dependency between line occurrences are fully determined by their topological relations to the endoporeutic structure determined by the cuts. The cuts impose a partial ordering over the isotropic sheet of assertion, but within each area determined by the cuts no ordering is imposed on the graphs.

Fig. 13

Beta graphs

In the ordinary notation of first-order logic the difference between logically non-equivalent pairs of sentences such as those in (10a) and (10b) is represented by the linear ordering of quantifier strings. The same difference is represented in Beta graphs by the endoporeutic structure. In the Beta graph of Fig. 13a, the line occurrence to the left of the spot “L” is less enclosed than the one to the right of it. Hence its corresponding quantifier has wider scope. In Fig. 13b, the dependence relation is reversed, because the line occurrence to the right of the spot “L” is less enclosed than that to the left of it, and thus its quantifier has wider scope. By means of the endoporeutic structure, which Peirce is now able to express by the nesting of the cuts, Beta graphs determine how sentences are constructed in stages corresponding to the quantifiers occurring in them, precisely as Dummett had underscored.

Now let us consider the following sentences:

$$\begin{aligned}&(\exists x) (\exists y) (Lxy) \end{aligned}$$

(11a)

$$\begin{aligned}&(\exists y) (\exists x) (Lxy) \end{aligned}$$

(11b)

$$\begin{aligned}&(\forall x) (\forall y) (Lxy) \end{aligned}$$

(11c)

$$\begin{aligned}&(\forall y) (\forall x) (Lxy) \end{aligned}$$

(11d)

A theorem of quantificational logic says that (11a) and (11b) are logically equivalent, as indeed are (11c) and (11d): when immediate consecutive quantifiers are of the same kind, their relative ordering is logically irrelevant. The order of the quantifiers becomes logically relevant only when they are of a different kind. In this sense, in (11a) the occurrence of “$\exists x$” before “$\exists y$” mark a stage in the constructional history of the formula only in a peculiar sense, because the fact that “$\exists x$” occurs before “$\exists y$” is logically irrelevant; in (11a) the quantifier “$\exists x$” has logically speaking no wider scope than the quantifier “$\exists y$”. It is the linearity of the notation that forces us to put them in a certain order, and thus to create two syntactically distinct sentences with no difference in truth-conditions.¹⁵

In Beta graphs no two syntactically distinct but logically equivalent sentences, such as (11a–b) and (11c–d), can be written. Consider Fig. 14. In the Beta graph in Fig. 14a the two line occurrences are in the same area (the sheet of assertion), and thus neither occurs before the other. This graph corresponds to the two syntactically distinct but logically equivalent sentences (11a) and (11b), which are in fact syntactically distinct only because they are written in a language that forces quantifiers to stand in a linear order. In the Beta graph in Fig. 14b the two line occurrences are in the same area (the area of the outer cut), which means that neither occurs before the other. This graph corresponds to the two syntactically distinct but logically equivalent sentences (11c) and (11d).

Fig. 14

Beta graphs

One could put the matter as follows: in the ordinary linear notation of first-order logic, no distinction is made between (i) stages at which quantifiers are introduced which have logical relevance, shown by the fact that switching the quantifier introduced at some stage with that introduced at some subsequent stage yields a logically distinct sentence; and (ii) stages at which quantifiers are introduced which have no logical relevance, shown by the fact that switching the quantifier introduced at some stage with that introduced at some subsequent stage does not yield a logically distinct sentence. Linear languages, in forcing everything into a linear order, are insensitive to the fact that not all stages are alike. Beta graphs are more finely-grained in distinguishing between (i) those stages that have logical relevance and (ii) those that have no logical relevance, and only provide an explicit representation of the former (by means of the endoporeutic structure expressed by the nesting of cuts), while leaving the latter unrepresented.

Another way of stating this is the following: only those essential syntactical differences which need to be represented (because they correspond to logical differences) are representable in Beta graphs, while those inessential syntactical differences that need not be represented (because they mark no logical difference, but only “different ways of representing the same fact”) are not representable. In particular, in the endoporeutic, nested structure projected by the cuts, only those stages are represented at which a quantifier is introduced that has wider scope than another one has. Beta graphs totally dispense with the representation of inessential syntactical differences in scope, namely differences (ii) which do not bring out logical differences.

6 Conclusion

Peirce considered all deductive reasoning, independently of the notation in which it is expressed, to be diagrammatic. He also thought that “the more diagrammatically perfect a system of representation, the less room it affords for different ways of expressing the same fact” (R 482). In this paper it was explained why Existential Graphs, and especially the Beta department which corresponds to (fragments of) first-order quantificational logic, are more diagrammatically perfect than the ordinary notation of first-order logic, and in what sense less room is afforded in Beta graphs than in ordinary notation for different ways of representing the same fact. The reason for the graphs’ superior diagrammatic power (so defined) is that they are a non-linear, occurrence-referential notation. As a non-linear notation, each Beta graph corresponds to a class of logically equivalent but syntactically distinct sentences of the ordinary notation of first-order logic that are obtained by permuting those elements (sentential variables, predicate expressions, and quantifiers) that in Beta graphs lie in the same area. As an occurrence-referential notation, each Beta graph corresponds to a class of logically equivalent but syntactically distinct sentences of the ordinary notation of first-order logic in which the identity of reference of two or more variables is asserted. In brief, Beta graphs are more diagrammatic than the linear, type-referential notation of first-order logic because the function that translates the latter to the graphs does not define isomorphism between the two notations: every Beta graph type corresponds to a class of logically equivalent sentence types of the ordinary notation of first-order logic.