Skip to main content
SpringerLink
Log in

Information-devoid routes for scale-free neurodynamics

  • Published:
Synthese Aims and scope Submit manuscript

Abstract

Neuroscientists are able to detect physical changes in information entropy in the available neurodata. However, the information paradigm is inadequate to describe fully nervous dynamics and mental activities such as perception. This paper suggests explanations to neural dynamics that provide an alternative to thermodynamic and information accounts. We recall the Banach–Tarski paradox (BTP), which informally states that when pieces of a ball are moved and rotated without changing their shape, a synergy between two balls of the same volume is achieved instead of the original one. We show how and why BTP might display this physical and biological synergy meaningfully, making it possible to model nervous activities. The anatomical and functional structure of the central nervous system’s nodes and edges makes it possible to perform a sequence of moves inside the connectome that doubles the amount of available cortical oscillations. In particular, a BTP-based mechanism permits scale-invariant nervous oscillations to amplify and propagate towards widely separated brain areas. Paraphrasing the BTP’s definition, we could state that: when a few components of a self-similar nervous oscillation are moved and rotated throughout the cortical connectome, two self-similar oscillations are achieved instead of the original one. Furthermore, based on topological structures, we illustrate how, counterintuitively, the amplification of scale-free oscillations does not require information transfer.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

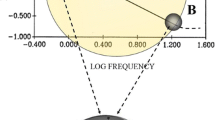
Modified from: Allen and Triantaphillidou (2009)

Fig. 2
Fig. 3
Fig. 4
Fig. 5

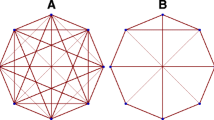
Modified from: https://wiki.biac.duke.edu/biac:analysis:resting_pipeline

Similar content being viewed by others

References

  • Alexandroff, P. (1932, 1961). Elementary concepts of topology. New York: Dover Pubs Inc. ISBN 0-486-60747-X.

  • Ali, A., Rafique, H., Arshad, T., Alqarni, M. A., Chauhdary, S. H., & Bashir, A. K. (2019). A fractal-based authentication technique using Sierpinski triangles in smart devices. Sensors (Basel). https://doi.org/10.3390/s19030678

    Article  Google Scholar 

  • Allen, E., & Triantaphillidou, S. (2009). The Manual of Photography (10th ed.). Abdingdon, Oxon: Taylor and Francis Group.

    Google Scholar 

  • Atmanspacher, H. (2016). On macrostates in complex multi-scale systems. Entropy, 18(12), 426. https://doi.org/10.3390/e18120426

    Article  Google Scholar 

  • Attwell, D., & Laughlin, S. B. (2001). An energy budget for signaling in the grey matter of the brain. Journal of Cerebral Blood Flow and Metabolism, 21(10), 1133–1145. https://doi.org/10.1097/00004647-200110000-00001

    Article  Google Scholar 

  • Banach, S., & Tarski, A. (1924). Sur la décomposition des ensembles de points en parties respectivement congruentes. Fundamenta Mathematicae, 6, 244–277.

    Article  Google Scholar 

  • Bekenstein, J. D. (2003). Black holes and information theory. arXiv:quant-ph/0311049.

  • Bromiley, P. A., Thacker, N. A., & Bouhova-Thacker, E. (2010). Shannon entropy, Renyi entropy, and information. Tina 2004-004, Statistic and Inf Series, Imaging Sci. and Biomed. Eng., Univ. of Manchester, UK

  • Aliprantis, C. D., & Border, K. C. (2006). Odds and Ends. Berlin: Springer. ((ISBN-10 3-540-29586-0)).

    Google Scholar 

  • Cafaro, C., Ali, S. A., & Giffin, A. (2016). Thermodynamic aspects of information transfer in complex dynamical systems. Physical Review E, 2016(93), 022114.

    Article  Google Scholar 

  • Churkin, V. A. (2010). A continuous version of the Hausdorff–Banach–Tarski paradox. Algebra and Logic, 49(1), 81–89. https://doi.org/10.1007/s10469-010-9080-y

    Article  Google Scholar 

  • de Arcangelis, L., & Herrmann, H. J. (2010). Learning as a phenomenon occurring in a critical state. Proceedings of the National Academy of Sciences, 107, 3977–3981.

    Article  Google Scholar 

  • Don, A. P., Peters, J. F., Ramanna, S., & Tozzi, A. (2020). Topological view of flows inside the BOLD spontaneous activity of the human brain. Frontiers in Computational Neuroscience. https://doi.org/10.3389/fncom.2020.00034

    Article  Google Scholar 

  • Fox, M. D., & Raichle, M. E. (2007). Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nature reviews. Neuroscience, 8, 700–711.

    Google Scholar 

  • Friston, K. (2010). The free-energy principle: A unified brain theory? Nature Reviews Neuroscience, 11(2), 127–138. https://doi.org/10.1038/nrn2787

    Article  Google Scholar 

  • Furstenberg, H. (1967). Disjointness in ergodic theory, minimal sets, and a problem in diophantine approximation. Mathematical Systems Theory, 1, 1–49.

    Article  Google Scholar 

  • Glasner, E., & Weiss, B. (2018). On the disjointness property of groups and a conjecture of Furstenberg. arXiv:quant-ph/0311049.

  • Glasner, E., Tsankov, T., Weiss, B., & Zucker, A. (2019) Bernoulli disjointness. arXiv:quant-ph/0311049.

  • Jaynes, E. T. (1957). Information theory and statistical mechanics. Physical Review, 106, 620.

    Article  Google Scholar 

  • Kantor, F. W. (1977). Information Mechanics. Hoboken: Wiley.

    Google Scholar 

  • Kawe, T. N. J., Shadli, S. M., & McNaughton, N. (2019). Higuchi’s fractal dimension, but not frontal or posterior alpha asymmetry, predicts PID-5 anxiousness more than depressivity. Scientific Reports, 9(1), 19666. https://doi.org/10.1038/s41598-019-56229-w

    Article  Google Scholar 

  • Lloyd, S. (2000). Ultimate physical limits to computation. Nature, 406, 1047–1054. https://doi.org/10.1038/35023282

    Article  Google Scholar 

  • Lübeck, S. (2004). Universal scaling behavior of non-equilibrium phase transitions. International Journal of Modern Physics B, 18, 3977–4118.

    Article  Google Scholar 

  • Mandelbrot, B. (1967). How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science, 56(3775), 636–638.

    Article  Google Scholar 

  • Marzuoli, A., & Rasetti, M. (2005). Computing spin networks. Annals of Physics, 318, 345–407.

    Article  Google Scholar 

  • Milstein, J., Mormann, F., Fried, I., & Koch, C. (2009). Neuronal shot noise and Brownian 1/f2 behavior in the local field potential. PLoS ONE, 4(2), e4338. https://doi.org/10.1371/journal.pone.0004338

    Article  Google Scholar 

  • Ỏzgủr, N., Taş, N., & Peters, J. F. (2020). New complex-valued activation functions. An International Journal of Optimization and Control Theories & Applications, 10(1), 66–72. https://doi.org/10.11121/ijocta.01.2020.00756

    Article  Google Scholar 

  • Özgür, N., & Taş, N. (2019). Pata Zamfirescu type fixed-disc results with a proximal application. arXiv:quant-ph/0311049.

  • Papo, D. (2014). Functional significance of complex fluctuations in brain activity: From resting state to cognitive neuroscience. Frontiers in Systems Neuroscience, 8, 112.

    Article  Google Scholar 

  • Peron, S., Pancholi, R., Voelcker, B., Wittenbach, J. D., Ólafsdóttir, H. F., et al. (2020). Recurrent interactions in local cortical circuits. Nature, 579(7798), 256–259. https://doi.org/10.1038/s41586-020-2062-x ((Epub 2020 Mar 4)).

    Article  Google Scholar 

  • Peters, J. F. (2018). Proximal vortex cycles and vortex nerves. Non-concentric, nesting, possibly overlapping homology cell complexes. Journal of Mathematical Sciences and Modelling, 1(2), 80–85.

    Article  Google Scholar 

  • Peters, J. F. (2019). Vortex nerves and their proximities. Nerve Betti numbers and descriptive proximity. Bulletin of The Allahabad Mathematical Society, 34(2), 263–276.

    Google Scholar 

  • Peters, J. F. (2020). Computational geometry, topology and physics of digital images with applications. Shape complexes, optical vortex nerves and proximities. Cham: Springer.

    Book  Google Scholar 

  • Pritchard, W. S. (1992). The brain in fractal time: 1/f-like power spectrum scaling of the human electroencephalogram. The International Journal of Neuroscience, 66, 119–129.

    Article  Google Scholar 

  • Reese, T. M., Brzoska, A., Yott, D. T., & Kelleher, D. J. (2012). Analyzing self-similar and fractal properties of the C. elegans neural network. PLoS ONE, 7(10), e40483. https://doi.org/10.1371/journal.pone.0040483

    Article  Google Scholar 

  • Sengupta, B., & Stemmler, M. B. (2014). Power consumption during neuronal computation. Proceedings of the IEEE, 102, 738–750.

    Article  Google Scholar 

  • Shannon, C. E. (1948). A mathematical theory of information. The Bell System Technical Journal, 27, 379–423.

    Article  Google Scholar 

  • Sporns, O. (2006). Small-world connectivity, motif composition, and complexity of fractal neuronal connections. Biosystems, 85(1), 55–64. https://doi.org/10.1016/j.biosystems.2006.02.008

    Article  Google Scholar 

  • Tinker, J., & Velazquez, J. L. (2014). Power law scaling in synchronization of brain signals depends on cognitive load. Frontiers in Systems Neuroscience, 8, 73. https://doi.org/10.3389/fnsys.2014.00073

    Article  Google Scholar 

  • Tozzi, A., & Peters, J. F. (2016). A topological approach unveils system invariances and broken symmetries in the brain. Journal of Neuroscience Research, 94(5), 351–365. https://doi.org/10.1002/jnr.23720

    Article  Google Scholar 

  • Tozzi, A., & Peters, J. F. (2017). From abstract topology to real thermodynamic brain activity. Cognitive Neurodynamics, 11(3), 283–292. https://doi.org/10.1007/s11571-017-9431-7

    Article  Google Scholar 

  • Tozzi, A., Peters, J. F., & Cankaya, M. N. (2018). The informational entropy endowed in cortical oscillations. Cognitive Neurodynamics, 12(5), 501–507. https://doi.org/10.1007/s11571-018-9491-3

    Article  Google Scholar 

  • Tozzi, A., & Papo, D. (2020). Projective mechanisms subtending real world phenomena wipe away cause effect relationships. Progress in Biophysics and Molecular Biology, 151, 1–13. https://doi.org/10.1016/j.pbiomolbio.2019.12.002

    Article  Google Scholar 

  • Tozzi, A., & Peters, J. F. (2020). A topological approach to infinity in physics and biophysics. Foundations of Science. https://doi.org/10.1007/s10699-020-09674-0

    Article  Google Scholar 

  • Van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organization of the human connectome. Journal of Neuroscience, 31, 15775–15786. https://doi.org/10.1523/JNEUROSCI.3539-11.2011

    Article  Google Scholar 

  • Wheeler, J. A. (1990). Information, physics, quantum: The search for links. In W. H. Zurek (Ed.), Complexity, Entropy, and the Physics of Information. Redwood City: Addison-Wesley.

    Google Scholar 

  • Watanabe, T., Hirose, S., Wada, H., Imai, Y., Machida, T., et al. (2013). A pairwise maximum entropy model accurately describes resting-state human brain networks. Nature Communications, 4, 1370. https://doi.org/10.1038/ncomms2388

    Article  Google Scholar 

  • Watanabe, T., Kan, S., Koike, T., Misaki, M., Konishi, S., et al. (2014). Network-dependent modulation of brain activity during sleep. NeuroImage, 98, 1–10. https://doi.org/10.1016/j.neuroimage.2014.04.079

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Center for Nonlinear Science, University of North Texas, 1155 Union Circle, #311427, Denton, TX, 76203-5017, USA

    Arturo Tozzi

  2. Department of Electrical and Computer Engineering, University of Manitoba, 75A Chancellor’s Circle, Winnipeg, MB, R3T 5V6, Canada

    James F. Peters

  3. Department of Mathematics, Adıyaman University, 02040, Adıyaman, Turkey

    James F. Peters

  4. Department of Mathematics, Faculty of Arts and Sciences, Adıyaman University, 02040, Adıyaman, Turkey

    James F. Peters

  5. Computational Intelligence Laboratory, University of Manitoba, Winnipeg, MB, R3T 5V6, Canada

    James F. Peters

Authors
  1. Arturo Tozzi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. James F. Peters
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Arturo Tozzi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tozzi, A., Peters, J.F. Information-devoid routes for scale-free neurodynamics. Synthese 199, 2491–2504 (2021). https://doi.org/10.1007/s11229-020-02895-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11229-020-02895-7

Keywords

Search

Navigation