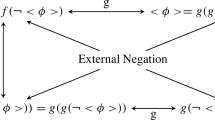
Abstract
Most paradoxes of self-reference have a dual or ‘hypodox’. The Liar paradox (Lr = ‘Lr is false’) has the Truth-Teller (Tt = ‘Tt is true’). Russell’s paradox, which involves the set of sets that are not self-membered, has a dual involving the set of sets which are self-membered, etc. It is widely believed that these duals are not paradoxical or at least not as paradoxical as the paradoxes of which they are duals. In this paper, I argue that some paradox’s duals or hypodoxes are as paradoxical as the paradoxes of which they are duals, and that they raise neglected and interestingly different problems. I first focus on Richard’s paradox (arguably the simplest case of a paradoxical dual), showing both that its dual is as paradoxical as Richard’s paradox itself, and that the classical, Richard-Poincaré solution to the latter does not generalize to the former in any obvious way. I then argue that my argument applies mutatis mutandis to other paradoxes of self-reference as well, the dual of the Liar (the Truth-Teller) proving paradoxical.
Similar content being viewed by others
Notes
I use the phrase ‘paradoxes of self-reference’ to fix the reference to paradoxes that are of the same kind as the Liar paradox, whether or not they actually involve self-reference.
For general presentations of the duals of classical paradoxes, see Mackie (1973), Eldridge-Smith (2008) and Armour-Garb and Woodbridge (2012). It is sometimes said that the Gödel sentence, on which Gödel’s Incompleteness theorems hinge expresses its own unprovability, and can be considered as a ‘provability version’ of the Liar [see e.g. Gaifman (2006) on this analogy]. The Henkin sentence, which can be described as expressing its own provability [see Halbach et al. (2014)] is likewise a provability version of the Gödel sentence and might be taken to be the dual of the Gödel sentence.
It is, to my knowledge, Herzberger (1970, pp. 148–149), who coined the term “pathological” to characterize the Truth-Teller. He called the classical paradoxes “negative pathologies”, their duals “positive pathologies” and claimed that only the former give rise to paradoxes. Mackie (1973) investigated many duals, calling them “truth-teller variants of the paradoxes”, and claimed that they involve undecidability without contradiction, while the paradoxes involve undecidability and contradiction. Woodbridge (2004) and Woodbridge and Armour-Garb (2005) claim that semantic paradoxes involve “apparent inconsistency” while their duals involve “apparent indeterminacy”. Eldridge-Smith (2008) argues that duals involve underdetermination while paradoxes involve overdetermination. As emphasized by an anonymous referee for this journal, these claims are close but they are really different. Undecidability without contradiction, for example, is not the same as underdetermination (the former does not imply the latter). Nor is it exactly the same as as apparent indetermination (something might be indeterminate on first appareances but prove decidable). Importantly, these claims also differ in scope. To my knowledge, Eldridge-Smith’s claim has the widest scope: he has conjectured that the duality between hypodoxes and paradoxes concerns all the paradoxes of self-reference, he has shown that it concerns most of them [including some non-classical ones that he himself discovered, see Eldridge-Smith (2015)] and he has convincingly argued that it even generalizes to time-travel paradoxes (Eldridge-Smith 2007).
Drawing on Kripke (1975)’s semantics, Kremer (1988) argues that one can ascribe truth, falsity or “neither true or false” to the truth-teller and that the latter accordingly refutes the supervenience of the semantic. Gupta and Belnap (1993)’s develop a revision theory of truth that allows restoring the supervenience claim by attributing to the truth-teller a definite semantic characterization in terms of revision rules. Yaqub (1993) has argued on more general grounds that the supervenience of semantics does not hold (see pp. 39–42) and he has developped an interpretation of the revision-theoretic formalism in which the supervenience of the semantics fails.
In order to do that, moreover, I will not rely on the claim that the supervenience of semantic facts is nearly as plausible as the principles on which we rely to derive a contradiction from the Liar. I will rely, instead, on the logic of definitions.
In fact, the only researchers I know who disagree are Austin (1950), who claims that “a statement to the effect that it is itself true is every bit as absurd as one to the effect that it is itself false (p. 122, fn. 22)”, and Priest and Mortensen (1981), who grant that the Truth-Teller is genuinely paradoxical. Both Austin (1950) and Priest and Mortensen (1981) only consider the Liar’s dual, though, and the reasons they invoke are quite different from those presented here. The former claims that “a statement to the effect that it is itself true is every bit as absurd as one to the effect that it is itself false (p. 122, fn. 22)”, and that “It takes two to make a truth. (...) Hence (...) a statement cannot without absurdity refer to itself (p. 118, fn. 13)”. Priest and Mortensen (1981), argue that even though we have reasons to believe that the Truth-Teller is neither true nor false, (for there is no proof that the Truth-Teller is true, and no proof that it is false) there is a proof that it is either true or false. Finally, Beall (2009, pp. 14–5) recently suggested that the Truth-Teller is both true and false, admitting that this claim is “ultimately defeasible”.
The defined term is often omitted when it is specified by the context. The definition symbol ‘\(=_{def}\)’ should never be confused with the mere identity symbol‘\(=\)’. Just like the defined term corresponds to a defined object the definiendum corresponds to an ‘identifying object’ and the definiens to ‘defining object’.
Notice that even if the two definitions above were stipulative, this would not be the case of the one below. X has already been introduced (and defined) above, so the definition of X below cannot be a stipulative definition. It is a so-called descriptive or explanatory definition: it specifies the object or the meaning of the term that has already been defined.
A referee for this journal alerted me of an interesting caveat. Suppose a is defined by
$$\begin{aligned} a: a=_{def} b \end{aligned}$$Replacing the definiendum ‘a’ by the definiens ‘b’ in this very definition, we would get that \(a: \quad b=_{def} b\), but a is certainly not defined like that. Wagner (2017, §6) puts forward other counter-examples involving quotations. Suppose the number one is defined by the fact that it is the least (strictly) positive interger. ‘One’ is three letters long. It does not follow that ‘the least (strictly) positive integer’ is three letters long. Interestingly, however, none of these counter-examples threaten our practice of unfolding embedded definitions (this practice does not require replacing occurrences of a definiendum in the very definiendum of a definition, and we can deal with the occurrences of a definiendum within quotation marks by separating its contribution to the morphology and the meaning of the resulting, quoted expression). In what follows, I will only use a very restricted Definiendum-Elimination rule, to the effect that in the definiens of a given definition, we can replace occurrences of a definiendum by its definiens when they are not under quotation marks. We shall see later that some researchers expressed important reservations about Definiendum-Elimination, even in this restricted form, precisely because some definitions are problematic and seem to generate paradoxes (p. 28). It should be noticed, finally, that everything I have said about Definiendum-Elimination applies mutatis mutandis to the dual rule of Definiendum-Introduction to the effect that we can substitute a definiendum to its definiens.
This last supposition can be be derived from Definiendum-Elimination and from its converse (and equally plausible) principle, namely Definiendum-Introduction. Together, these principles allow one to derive D’ from D and D from D’.
There is a close connection between the two disjuncts of this definition. Consider the claim that if \(X\in D\)
$$\begin{aligned} X : X=_{df} ---\quad \forall \; x \in D,\, \Phi (x)---- \end{aligned}$$then
$$\begin{aligned} X : X=_{df} ---\Phi (X) \wedge \quad \forall \; x \in D,\, \Phi (X)---- \end{aligned}$$Provided that this plausible claim is accepted, a definition whose definiens generalizes over a totality containing the defined object will yield one whose definiens contains the defined term.
To my knowledge, there is no canonical way to define circular definitions. A definition which is circular in my sense is circular, intuitively, in that we seem to run into circles when we try to use the definition to find out what it refers to. It might however be reducible to a definition that is not circular, and need not, in that sense, be essentially circular [see Gupta (2015, §2–7)].
The definition of a function (or predicate) on natural integers is typically called ‘recursive’ when it contains (i) an initialization clause, defining its initial value, (ii) and an inductive clause, specifying the relationship between the functions’s value on n and on \(n+1\) for an arbitrary n. Inductive definitions are, more broadly, definitions appealing to an initialization clause and an inductive clause. Impredicative definitions have a definiens generalising over a totality to which the defined object belongs. It should be emphasized however that many authors use inductive and recursive interchangeably, and that the concept of impredicativity have been used to refer to different (if related) phenomena [cf. Feferman (2005)]
Circular definitions seem essential to ordinary arithmetics (cf. e.g. the definition of natural numbers), classical analysis (cf. e.g. the least upper bound principle) and set theory (cf. e.g. the axiom of separation). They are also integral to the practice of defining objects as the fixed points of certain functions. Feferman has conjectured that the part of mathematics that is indipensable to the natural sciences might dispense with predicative definitions provided that it already accepts arithmetics [see Feferman (2005) and the works cited there].
The problem here is somewhat analogous to that confronting the prospects of banning self-reference on the ground that it has been accused of generating paradoxes. Self-reference often seems benign, and even if we could ban direct self-reference, there seems to be no way to be safe from indirect, empirical self-reference [see Kripke (1975, pp. 690–693)’s classical remarks]. It should also be emphasized that even if definitions in so called ‘normal form’ [see Gupta (2015)] are guaranteed to be non-circular, such definitions are much too restrictive. They not only forbid circular definitions (which, as we have seen seem essential to mathematics and to our ordinary practice of defining objects and terms) they also forbid so called implicit definitions such as the implicit definition of a set by the axioms of set theory.
As noticed by Simmons (1993, p. 27), Richard explicitly constructs a surjective/onto enumeration h, but he wrongly assumes that the enumeration he has constructed is bijective. Although it is not the one Richard picked out, there is in fact a bijective enumeration of E. To explicitly construct a bijective enumeration, one can list all the finite definitions of numbers in lexicographic order and take h to be the function defined recusrively as follows: (i) it associates to the first definition in the list, the number in E defined by this definition, (ii) and it associates to the nth definition the smallest number in E that is not in the image of \(\{1,\ldots ,n-1\}\) by h. Even though, I think we can obtain Richard’s paradox (and its dual) without relying on the fact that h is injective , relying on this fact makes things slightly simpler.
The ring of integers modulo 10 (\(\mathbb {Z}/10\mathbb {Z}\)) is the ten first numbers \(0,1,\ldots 9\) endowed with the addition and multiplication operations, and where (to put it rather roughly) it is assumed that for all number x, \(x=x+10\).
I follow Jules Richard in construing the eponymous paradox as a paradox of definability rather than denotation. Under that denotation construal, the paradox relies on the denotation schema, to the effect that ‘a’ refers (if at all) to a, and on the principles governing definite descriptions [see Priest (2006b) for the denotation construal]. On the definability construal, it relies on the logic of definitions, and in particular on the claim that the definiens of a definition defines (if anything at all) the definiendum of that definition. We shall see that it also relies on Definiendum-Elimination.
To get a definiens that is identical to the defined term below, we could also introduce the function \(h^{-1}\) (defined by the fact that for all x, \(h(h^{-1})(x)=h^{-1}(h(x))=x\)). We would then have \(n_\alpha : n_\alpha =_{def} h^{-1}(\alpha )\).
A fixed point of a function f in a domain D is a member x of D such that \(x=f(x)\).
Quite generally, if the logic is classical, in order not to violate this ‘Constraint of Non-Creativity’ and to be benign, the definition of a name must satisfy both Existence (i.e. pick at least one object) and Uniqueness (i.e. pick at most one object). If it did not satisfy Existence, the defined term would not refer (which would contradict, for example, the classical rule of Existence-Generalization). If it violated Uniqueness, the defined term would refer to more than one object (which would entail a contradiction to the effect that that these two different objects are identical). See the related remarks in Gupta (2015§2-4)’s discussion of definitions in ‘normal form’.
Interestingly, however, it seems that circularity as such is to blame for the definition’s vicious character. It can indeed be checked that if \(g=g_{BR}\) (‘BR’ stands for Benign Richard) is a function that has only one fixed point in \(\mathbb {Z}/10\mathbb {Z}\) (say \(g_{BR}(x)=2x+1 \,(\text {mod}\, 10)\), which has 9 for unique fixed point), the definition of \(\alpha \) will still be circular, but \(\alpha _{n_\alpha }\) will pick a unique and definite number (the fixed point of \(g_{BR}\)) and the same will arguably be true of \(\alpha \) (arguably, that is, if, as is commonly assumed in discussions of Richard’s paradox, the other decimals of \(\alpha \) are not problematic).
Assuming that paradoxes of the same kind must admit a solution of the same kind (this is what Priest (1994) calls the “principle of a uniform solution”), this implies, moreover, either that the classical solution to Richard’s paradox is not a good solution, or that Richard’s paradox and its dual, depsite their resemblance and their striking symmetry, are not of the same kind. Given that it shows that Richard’s dual is paradoxical too and arises from very similar principles as Richard’s paradox itself, the present article provides some reasons to favour the first option. Even if I won’t come back to it, similar remarks could apply to the Liar and its Truth-Teller dual, with which I deal below.
One could have derived this conclusion more simply by appealing to the fact that both lines of the definiton (\(7_{def}\)) are independant of each other (because the morphological part does not depend on Ptr, as opposed to the sequence of marks M(‘Ptr’)), which seems to entail that:

and hence, if P is functionally defined, that \(V(Ptr): V(Ptr)=_{def} g_\mathcal {P} (V(Ptr))\) and that \(g_\mathcal {P}\) has a unique fixed point. However, in order to properly justify the transition from (\(7_{def}\)) to (\(10_{def}\)) we would have had to demonstrate a lemma relating the definition of a vector to that of its parameters when one of them is independent of the others.
This are natural language versions of the Liar and the Truth-Teller in which the Liar and Truth-Teller sentences are defined in a stipulative and explicitly circular way. It is well-known that there are versions of the Liar and the Truth-Teller that do not rely on such definitions. Consider this demonstrative version:
$$\begin{aligned} DPtr: Dtr=_{def}\text {`this very sentence is}\,P\hbox {'} \end{aligned}$$Or this ‘Quinean’ version using a ‘syntactic function’ and meant to avoid explictly circular definitions (Quine 1953, pp. 133–134):
$$\begin{aligned} QPtr: QPtr =_{def}\,\text {``yields a sentence that is P when applied to itself' yields a sentence that is P'} \end{aligned}$$[See also Gaifman (2004) who neatly relates this version to Gödel’s diagonalization lemma, and claims that it does not really avoid circularity.] These two versions can however be treated like Ptr. The reason why, roughly, is that even though they are not explcitly circular, the definitions of DPtr and QPtr are still implicit circular. Consider DPtr. Just like we derived (\(9_{def}\)), we can derive

Now, the semantic value of the demonstrative expression ‘this very sentence’ is arguably defined by the fact that it is the same as that of the sentence in which it occurs:
$$\begin{aligned} V(\text {`this very sentence is P'}): V(\text {`this very sentence is P'})=_{def} V(\text {`DPtr is P'}) \end{aligned}$$From this we get that:

Deriving a contradiction from that is exactlty the same as deriving a contradiction from (\(9_{def}\)) (just replace ‘Ptr’ by ‘DPtr’ in the main text’s derivation). The case QPtr is not different, provided that we grant that \(V(``\text {yields a sentence that is } P \text { when applied to itself' yields a sentence that is } P \hbox {'}): V(``\text {yields a sentence that is } P \text { when applied to itself' yields a sentence that is } P\hbox {'})=_{def} V(`\text {QPtr is a sentence that is } P\hbox {'})\).
See especially Yaqub (1993, pp. 27–36), where he distinguishes this thesis from neighbouring ones and attributes them to important historical figures.
Another classical objection against views such as (TS) that define truth in terms of the Truth-Schema [an objection which can be traced back at least to Lewy (1947)] claims that the former entail that instances (\(T_{=}\)) are necessary and analytic but (roughly) that they cannot be either because a given sentence ‘s’ could mean something different from what it happens to mean and thus be true while it is not the case that s. This objection might be thought to generalize to instances of (\(T_{def}\)) as the latter entail that instances of (\(T_{=}\)) are indeed analytic and necessary. However, as noticed by many [see, for instance, the very clear exposition of Raatikainen (2003)] the classical argument to the effect that instances of (\(T_{=}\)) are not analytic or necessary rests on the assumption that the sentences under scrutiny are uninterpreted sentences. But the sentences we have considered so far are all interpreted sentences.
The most developed contemporary versions of such a trivalent approach stem from the works of Kripke (1975) who showed that it could countenance a strong enough version of the Truth-Schema. Some have however voiced dissatisfaction with Kripke’s framework, most notably with its the expressive power, its difficulties to meet so-called revenge problems or with the weakness of its underlying logic. In response, many sophistications of Kripke’s approach have been put forward [see, among many others Burge (1979), Priest (2006a), McGee (1991), Soames (1999), Horsten (2011), Ripley (2013) and Cobreros et al. (2013)]. Although it can be considered as a trivalent approach, in which the valuation function attributes \(\frac{1}{2}\) to sentences that are both true and false, Priest (2006a)’s dialetheist solution is more naturally considered as a ‘plurivalent’ approach, in which the valuation function is replaced by a non-functional relation that can relate a sentence to true (1), false (0) or to both truth-values at the same time [see Priest (2006a, p. 288, 2014)].
This criticism applies to Kripke (1975)’s approach. According to the latter, equally acceptable interpretations of the truth predicate classify the Liar as true, false and neither true nor false. Now, either we pick one interpretation as the correct interpretation or we insist that there no such thing as the correct interpretation [the latter is Kripke’s preferred option, see Kremer (2009, fn. 8)]. In both cases however, \(g_{true}\) will have at least two semantic statuses as fixed points—true, false—whereas it should have only one.
One must watch out, by the way, not to confuse the fixed points of Kripke’s construction with the ones I have been referring to throughout this article. They are all fixed points all right, but of very different functions, and they have little in common.
Notice that this is not the same as claiming that our definition of the Truth-Teller picks just one interpreted sentence, with one complex semantic value, say a couple of truth values or a function from contexts to truth-values. The latter claim will not, it seems, help us solve the Truth-Teller because it just consists in expanding the set of semantic values. It will thus run into a problem which is similar to the one posed by the trivalent approach. Indeed, when ‘P’ is substituted with truth, \(g_\mathcal {P}=g_{\text {true}}\) will still arguably have more than one fixed point in this extended set of semantic values, whereas it should have at most one. If, for example, the semantic values are functions from contexts to truth-values, it seems that we will be bound to acknowledge that if a sentence q is true (res. false) in all contexts, so is the sentence asserting that q is true. Yet, this implies that all true acontextual sentences are a fixed point of \(g_\mathcal {P}=g_{\text {true}}\), a function which has accordingly more than one fixed-point.
The word ‘pluralism’ has been used by Read (2008b) to designate a solution to the Liar that is quite different from what I call ‘pluralism’ here. What Priest (2014) calls a ‘plurivalent’ semantic (that is the claim that sentences can be associated with no, or with many semantic-values) is, on the other hand, a view that fits both cassationist solutions to the Liar and what we have called ‘pluralist’ solutions to the Truth-Teller.
See Gupta (1997, 439ff). for some caveats concerning so-called revenge problems and their significance.
A referee for this journal has put forward the following definition of a natural number:
$$\begin{aligned} a:(x=a) \quad =_{def} (x=1)\vee (x=2) \end{aligned}$$which picks two objects (1 and 2) for a and accordingly allows to derive the absurd claim that 1 \(=\) 2. He or she has also suggested that (a) there is some \(\mathcal {D}\) constraint that this definition does not meet (b) that our definitions of \(\alpha \) and Ptr do not meet \(\mathcal {D}\) either, and (c) that this allows one to discount the paradoxical character of our hypodoxes. Finally, he or she also has added that \(\mathcal {D}\) might be a constraint of homogeneity, which imposes the defined term to be of the same logical category as the definiendum (and the definiens).
However, heterogeneous definitions seem ubiquitous and generally unproblematic, and they are sometimes indispensable [see for example Gupta (2015) on implicit definitions]. Morover, we only use heterogeneous for clarificatory purposes, on p. 14, rehearsing an argument that originally relied on homogeneous definitions with heterogeneous, sentential, definitions of numbers instead. More deeply, as we have seen above, if there is a constraint on definitions whose infringement is directly responsible for the paradoxical hypodoxes it is the the constraint of picking exactly one object. But if \(\mathcal {D}\) was taken to be the constraint of picking exactly one object (c) would not hold (ie. one could not discount the paradox) because, again and as stated by (1), we have an argument to the effect that this constraint is in fact satisfied, and this precisely is where the paradox comes from.
The only obvious exception I see is what is sometimes called ‘Routley’s paradox’ [see Routley (1980)]. The following definition of Ro leads to a paradox, at least if we assume a very liberal form of the Naïve Comprehension Schema which guarantees that this definition picks at least one set.
$$\begin{aligned} Ro:Ro=_{def} \, \{x: x\not \in Ro\} \end{aligned}$$The related hypodox, which hinges on \(DRo:DRo=_{def} \, \{x: x\in DRo\}\) will not be paradoxical however, because neither Extensionality, nor any plausible axiom of Naïve Set Theory give us reason to believe that this definition should pick at most one set.
I have already put forward arguments for the paradoxical character of the Truth-Teller elsewhere (Billon 2011, 2013). The present argument supersedes these. I am grateful to Peter Eldridge-Smith, Graham Priest, Lucas Rosenblatt and four referees of this journal for their useful comments on earlier drafts of this paper. Primitive versions of this paper have been presented at the Logic CNRAP Networkshop in Princeton in 2013, at the IEC/MCMP Paris-Munich Networkshop in Munich in 2013 and at the University of Lille in 2016. I have benefited from founds of the program New Ideas in Mathematical Philosophy from the ENS “département d’études cognitives”.
References
Armour-Garb, B., & Woodbridge, J. A. (2012). Liars, truthtellers and naysayers: A broader view of semantic pathology i. Language and Communication, 32(4), 293–311.
Austin, J. L. (1950). Truth. Aristotelian Society Supplements, 24(1), 111–29.
Beall, J. (2009). Spandrels of truth. Oxford: Oxford University Press.
Belnap, N. (1993). On rigorous definitions. Philosophical Studies, 72(2), 115–146.
Billon, A. (2011). My own truth, relative truth and the semantic pathologies of self-reference. In S. Rahman & G. Primiero (Eds.), Antirealism: The realism/antirealism debate in the age of alternative logics,., Logic, epistemology, and the unity of science Dordrecht: Springer.
Billon, A. (2013). The truth-tellers paradox. Logique Et Analyse, 224, 371–389.
Burge, T. (1979). Semantical paradox. Journal of Philosophy, 76, 169–198.
Cobreros, P., Égré, P., Ripley, D., & Van Rooij, R. (2013). Reaching transparent truth. Mind, 122(488), 841–866.
Eldridge-Smith, P. (2007). Paradoxes and hypodoxes of time travel. In J. L. Jones, P. Campbell, & P. Wylie (Eds.), Art and time (pp. 172–189). Melbourne: Australian Scholarly Publishing.
Eldridge-Smith, P. (2008). The liar paradox and its relatives. Melbourne: The Australian National University.
Eldridge-Smith, P. (2012). A hypodox! a hypodox! a disingeneous hypodox!. The Reasoner, 6(7), 8–10.
Eldridge-Smith, P. (2015). Two paradoxes of satisfaction. Mind, 124(493), 85–119.
Feferman, S. (2005). Predicativity. In S. Shapiro (Ed.), The Oxford handbook of philosophy of mathematics and logic (pp. 590–624).
Gaifman, H. (2004). The easy way to gödel’s proof and related matters. http://www.columbia.edu/~hg17/Diagonal-Cantor-Goedel-05.pdf.
Gaifman, H. (2006). Naming and diagonalization, from cantor to gödel to kleene. Logic Journal of IGPL, 14(5), 709–728.
Goldstein, L. (2000). A unified solution to some paradoxes. In Proceedings of the Aristotelian Society, New Series. The Aristotelian Society, Blackwell Publishing.
Goldstein, L. (2006). Fibonacci, yablo, and the cassationist approach to paradox. Mind, 115(460), 867–890.
Gupta, A. (1993). Minimalism. Philosophical Perspectives, 7, 359–369.
Gupta, A. (1997). Definition and revision: A response to McGee and Martin. Philosophical Issues, 8, 419–443.
Gupta, A. (2015). Definitions. In Zalta, E. N. (Eds.), The stanford encyclopedia of philosophy, Summer 2015 edn.
Gupta, A., & Belnap, N. (1993). The revision theory of truth. Cambridge: MIT Press.
Halbach, V., & Visser, A. (2014). The henkin sentence. In E. Alonso., M. Manzano & I. Sain (Eds.), The life and work of Leon Henkin (pp. 249–263). Springer.
Herzberger, H. G. (1970). Paradoxes of grounding in semantics. The Journal of philosophy, 67(6), 145–167.
Horsten, L. (2011). The Tarskian turn: Deflationism and axiomatic truth. Cambridge: MIT Press.
Kremer, M. (1988). Kripke and the logic of truth. Journal of Philosophical Logic, 17(3), 225–278.
Kremer, P. (2009). The revision theory of truth. In Zalta, E. N. (Eds.), The stanford encyclopedia of philosophy, Spring 2009 edn.
Kripke, S. (1975). Outline of a theory of truth. Journal of Philosophy, 72(19), 690–716.
Lewy, C. (1947). Truth and significance. Analysis, 8(2), 24–27.
Mackie, J. L. (1973). Truth, probability and paradox: Studies in philosophical logic. Oxford: Oxford University Press.
McGee, V. (1991). Truth. Hackett: Vagueness and Paradox.
Poincaré, H. (1906). Les mathématiques et la logique. Revue de métaphysique et de Morale, 14(3), 294–317.
Priest, G. (1994). The structure of the paradoxes of self-reference. Mind, 103(409), 25–34.
Priest, G. (2006a). In contradiction (2nd ed.). New York: Oxford University Press.
Priest, G. (2006b). The paradoxes of denotation. In T. Bolander, V. F. Hendricks, & S. A. Pedersen (Eds.), Self-reference (pp. 137–150). Stanford: CSLI Publications.
Priest, G. (2014). Plurivalent logics. The Australasian Journal of Logic, 11(1). https://ojs.victoria.ac.nz/ajl/article/view/1830.
Priest, G., & Mortensen, C. (1981). The truth-teller paradox. Logique et Analyse, 24, 381–388.
Quine, W. V. O. (1953). Notes on the theory of reference. In From a logical point of view (pp. 130–138). Harper & Row.
Raatikainen, P. (2003). More on Putnam and Tarski. Synthese, 135(1), 37–47.
Read, S. (2008a). Further thoughts on Tarski’s T-scheme and the liar. In S. Rahman, T. Tulenheimo, & E. Genot (Eds.), Unity, truth and the liar (Vol. 8, pp. 205–225)., Logic, epistemology, and the unity of science Dordrecht: Springer.
Read, S. (2008b). The truth schema and the liar. In S. Rahman, T. Tulenheimo, & E. Genot (Eds.), Unity, truth and the liar, logic, epistemology, and the unity of science (Vol. 8, pp. 3–18). Dordrecht: Springer.
Richard, J. (1905). Les principes des mathématiques et le problème des ensembles. Revue générale des Sciences Pures et Appliquées, 16(541), 142–144.
Ripley, D. (2013). Paradoxes and failures of cut. Australasian Journal of Philosophy, 91(1), 139–164.
Routley, R. (1980). Exploring meinong’s jungle and beyond. Camberra: Australian National University.
Russell, B. (1906). Les paradoxes de la logique. Revue de métaphysique et de morale, 14(5), 627–650.
Sainsbury, R. M. (1995). Paradoxes. Cambridge: Cambridge University Press.
Scharp, K. (2013). Replacing truth. Oxford: OUP Oxford.
Simmons, K. (1993). Universality and the liar: an essay on truth and the diagonal argument. Cambridge: Cambridge University Press.
Smith, J. W. (1984). A simple solution to Mortensen and Priest’s truth teller paradox. Logique et Analyse, 27, 217–220.
Soames, S. (1999). Understanding truth. Oxford: Oxford University Press.
Sorensen, R. (2001). Vagueness and contradiction. Oxford: Oxford University Press.
Suppes, P. (1957). Introduction to logic. New York: Dover Publications.
Tarski, A. (1943). The semantic conception of truth: And the foundations of semantics. Philosophy and Phenomenological Research, 4(3), 341–376.
Wagner, P. (2017). Definition. In Kristanek, M. (Eds.), L’encyclopédie Philosophique.
Woodbridge, J. A. (2004). A neglected dimension of semantic pathology. In Logica yearbook (pp. 277–292). Prague. Filosofia: Institute of Philosophy, Academy of Sciences of the Czech Republic.
Woodbridge, J., & Armour-Garb, B. (2005). Semantic pathology and the open pair. Philosophy and Phenomenological Research, 71(3), 695–703.
Yablo, S. (1993). Hop, skip, and jump: The agnostic conception of truth (Corrections in Philosophical Perspectives, 9, 509–506). Philosophical Perspectives, 7, 371–393.
Yaqub, A. M. (1993). The liar speaks the truth: A defense of the revision theory of truth. Oxford: Oxford University Press.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Billon, A. Paradoxical hypodoxes. Synthese 196, 5205–5229 (2019). https://doi.org/10.1007/s11229-018-1711-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-018-1711-1