1 Introduction

A probability forecast (for binary or “yes vs no” events) is called calibrated (or reliable) if the probability of the event, conditionally on the forecast taking a specific value, is equal to that same value; this should hold for any value the forecast may assume. Similar definitions of calibration exist for other types for forecasts, for instance conditional mean or conditional quantile forecasts.

In the context of an operational forecasting system for real world variables (e.g. environmental or economic), calibration can only be assessed in a statistical sense. That is, provided with an archive of verification–forecast pairs, we may formulate calibration as a statistical hypothesis and perform statistical tests for that hypothesis. Typically though, calibration is a hypothesis not about a finite dimensional parameter but about an entire functional relationship, a long noted difficulty when assessing the calibration of forecasting systems. Tests for calibration based on estimating deviations from that functional relationship at specific values of the forecast meet with the problem of a very general alternative hypothesis. A possible remedy is to consider weaker forms of calibration instead, for instance that the average of the forecast agrees with the average of the verification. This unconditional calibration is but a necessary consequence of full calibration, and forecasting systems exhibiting merely unconditional calibration are generally inadequate for decision support. Regression based tests (e.g. Mincer–Zarnowitz regression, see Mincer and Zarnowitz 1969; Diebold and Lopez 1996; Engle and Manganelli 2004; Gaglianone et al. 2011, and references therein) provide a viable alternative, but they operate within a specific parametric model class (typically linear), effectively testing the hypothesis that the optimal recalibration function from that model class is the identity. Although such tests will provide good power in situations where this hypothesis is violated, there generally exist uncalibrated forecasting systems which nonetheless satisfy this null hypothesis, and regression based tests will fail to identify these.

The aim of the present paper is to discuss tests that use an estimate of the supremum of all cumulative deviations from calibration. The tests are thereby able to take the functional character of the calibration hypothesis fully into account. The asymptotic distribution of the test statistic is established and turns out to be universal, that is, independent of the specifics of the underlying data source, the only structural assumption being that forecasts always verify at the next time step in the future. The main analytical fact employed in the present work is that under the hypothesis of calibration, the estimated cumulative deviations can (asymptotically) be expressed through a Wiener process. More precisely, the cumulative deviations converge in distribution, for the topology of uniform convergence, to a Wiener process but with nonuniform time rescaling. The asymptotic distribution of the test statistic is given by that of an appropriate functional of the Wiener process (basically the supremum norm). To the best of our knowledge, no other testing methodology has been rigorously shown to develop power against alternatives of comparable generality (i.e. to be consistent in the sense of Bierens 1990) in the current context (but see Sec. 3.4 for a brief discussion of the work of Bierens 1990; De Jong 1996). In addition to the quantitative tests, plots of the estimated cumulative deviations (which we will refer to as “Random Walk Plots”) may serve as a qualitative tool to identify specific forecast values for which calibration is particularly poor.

Relevant concepts and notation will be introduced and made precise in Sect. 2. In particular, the concept of calibration for probability forecasts (of binary events), and in fact also for more general types of forecasts will be discussed. Conditional mean forecasts, and conditional quantile forecastswill serve as further examples. Sect. 3 introduces uniform calibration tests, with detailed instructions as to how to perform them as well as their asymptotic properties, in particular regarding size and power. The mathematical analysis is deferred to the Supplement for the interested reader. The section furthermore contains a brief review of relevant existing literature. In Sect. 4, Monte–Carlo experiments using artificial data are discussed, confirming that the uniform calibration tests exhibit the correct size. We also confirm numerically that uniform calibration tests develop power against a wide class of alternatives, and compare these tests with established regression based tests. Section 5 applies uniform calibration tests to forecasts from an operational weather forecasting centre. The main purpose of these experiments is to demonstrate the feasibility of the methodology, and to illustrate further practical aspects. Section 6 concludes and discusses further avenues of research, for instance regarding forecasts with larger lead times.

2 Calibration of probability, mean, and quantile forecasts

To introduce calibration formally, let \(\{Y_k, k = 1, 2, \ldots \}\) be a series of verifications (i.e. observations), which in the present paper we assume to be random variables on some probability space \((\Omega , {\mathcal {F}}, {\mathbb {P}})\) having values either in the real numbers or just in the binary set \(\{0, 1\}\). These two cases will be referred to as the continuous and the binary case, respectively. We consider corresponding forecasts \(\{f_k, k = 1, 2, \ldots \}\) which are radom variables with values in the real numbers in both cases. Our tests will be based on the joint data \(\{(Y_k, f_k), k = 1, 2, \ldots \}\) to which we refer as the verification–forecast pairs. The index k is a temporal index or time step, and the forecast \(f_k\) corresponds to the verification \(Y_k\) which obtains at some point \(t_k\) in actual time. Typically, the forecast \(f_k\) is issued at some point prior to \(t_k\), and the lag \(L_k\) between the time when \(f_k\) is issued and the time it verifies (i.e. \(t_k\)) is often referred to as the lead time. Although the lead time is often independent of k, there are examples where this is not the case, for instance in seasonal forecasting systems that focus on specific periods of the year; we will however assume the lead time to be constant and drop the subscript on L for notational simplification.

A fundamental assumption of this paper is that the lead time L is never larger than \(t_k - t_{k-1}\), or if measured in time steps rather than absolute time, the lead time is equal to (or smaller than) one. (This is the “small lead time” condition alluded to in the title of this paper.) We can therefore assume that when issuing the forecast \(f_k\), the forecaster has access not only to all previous forecasts but also to all previous verifications, that is, she knows \((Y_1, \ldots , Y_{k-1})\). Therefore, this information can in principle factor into the forecast.

The concept of calibration (or reliability) refers, strictly speaking, to different things depending on the type of forecasts. We start with the binary case. Here, a common interpretation of calibration is that for each k, the forecast \(f_k\) is equal to the probability of the event \(Y_k = 1\), conditional on the forecast \(f_k\) itself. We might express this as

$$\begin{aligned} {\mathbb {P}}(Y_k = 1 | f_k) = f_k \qquad \text {for all} \; k = 1, 2, \ldots . \end{aligned}$$
(1)

This definition of calibration though makes no reference to (temporally) previous forecasts and verifications. To develop tests, however, and to rigorously establish their statistical properties, the temporal dependencies of the verification–forecast pairs have to be taken into account. Rather than introducing specific assumptions concerning these dependencies ad hoc (or worse still, tacitly), the approach of the present paper is to obtain all necessary information regarding these temporal dependencies from the calibration assumption itself, potentially at the expense of using a stronger but nonetheless well motivated calibration hypothesis.

As noted previously, the forecaster has access to all previous forecasts and verifications when issuing the forecast \(f_k\), and in an ideal world, the forecaster would take this information into account in an optimal way. Therefore, we would expect that for each k the forecast \(f_k\) is equal to the probability of the event \(Y_k = 1\), conditional on the current forecasts as well as all previous forecasts and observations. We might write this as

$$\begin{aligned} {\mathbb {P}}(Y_k = 1 | f_{1:k}, Y_{1:k-1}) = f_k \qquad \hbox {for all} \; k = 1, 2, \ldots \end{aligned}$$
(2)

where here (and in the following) we use the shorthand \(Y_{k:l} := (Y_k, \ldots , Y_l)\) for any \(k \le l\). Condition (2), which implies condition (1), will constitute our null hypothesis, and the main aim of the present paper is to develop statistical tests for this hypothesis. We need to emphasise however that even though the null hypothesis (2) is assumed throughout our analysis for binary forecasts, the tests are expected to develop power only against alternatives to what we will call the restricted hypothesis (1). This is due to the great generality of the alternative to the hypothesis expressed in Eq. (2).

To formulate a calibration hypothesis for other types of forecasting problems we use the concept of identification functions (for a general discussionof identification functions in connection with the elicitability or identifiability problem see e.g. Gneiting 2011; Steinwart et al. 2014). In the context of the present paper, a verification function is simply a measurable function \(\Phi :V \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) (where V is either the real line or the set \(\{0, 1\}\), depending on the type of verifications considered).

We say that the forecasts \(\{f_k, k = 1, 2, \ldots \}\) are calibrated (for the verification \(\{Y_k, k = 1, 2, \ldots \}\)) if \(\phi _k := \Phi (Y_k, f_k)\) is integrable for all \(k = 1, 2, \ldots \) and furthermore

$$\begin{aligned} {\mathbb {E}}(\phi _k | f_{1:k}, Y_{1:k-1}) = 0 \qquad \text {for all} \; k = 1, 2, \ldots . \end{aligned}$$
(3)

We will focus on mean forecasts and quantile forecasts as further examples. In the first case, we require

$$\begin{aligned} {\mathbb {E}}(Y_k| f_{1:k}, Y_{1:k-1}) = f_k \qquad \hbox { for all}\; k = 1, 2, \ldots , \end{aligned}$$
(4)

which can be written as in Eq. (3) with \(\Phi (Y, f) = Y - f\). In the case of conditional quantiles (of a fixed level \(\alpha \)), we require that

$$\begin{aligned} {\mathbb {P}}(Y_k \le f_k| f_{1:k}, Y_{1:k-1}) = \alpha \qquad \hbox {for all}\; k = 1, 2, \ldots , \end{aligned}$$
(5)

which can be written as in Eq. (3) with \(\Phi (Y, f) = \mathbbm {1}_{\{Y \le f\}} - \alpha \). Regarding power, a remark similar to the one made for the binary case applies to our calibration tests for general identification functions: even though hypothesis (3) is imposed, power can only be demonstrated against equivalent forms of the restricted hypothesis (1), namely against

$$\begin{aligned} {\mathbb {E}}(\phi _k | f_k) = 0 \qquad \hbox {for all} \; k = 1, 2, \ldots . \end{aligned}$$
(6)

(This form of calibration is referred to as T–calibration in Gneiting and Resin 2021 ).

3 Methodology and main results

In this section, we will introduce and motivate the test statistics and present the main results regarding the properties of the tests. (The proofs can be found in the Supplement for the interested reader.) The Random Walk Plots as a qualitative way to assess (departure from) calibration will also be discussed.

3.1 Assumptions

From now on, we make the following assumptions (these are made precise in Assumptions 1 in the Supplement and augmented by several integrability conditions, which are always satisfied in the cases of probability and quantile forecasts):

  1. (1)

    the calibration hypothesis (2) (or (3), (4), (5) for general identification functions, the conditional mean, or the conditional quantile case, respectively) is in force;

  2. (2)

    the verification–forecast pairs \(\{(Y_k, f_k), k = 1, 2, \ldots \}\) form a strictly stationary and ergodic process;

  3. (3)

    the distribution of the forecast \(f_k\) conditionally on \((Y_l, f_l)\) for \(l = 1, \ldots , k-2\) is continuous (see Supplement for precise statements).

With regards to the interpretation of condition 3, note that \(f_k\) is not measurable with respect to \((Y_l, f_l)\) for \(l = 1, \ldots , k-2\); the information necessary to compile the forecast \(f_k\) will only be complete in the next step. The condition therefore means that provided with this incomplete information, the distribution of the forecast has no atoms; no single forecast value carries nontrivial probability.

3.2 Forecasts for binary verifications

One of the most popular tools to assess the calibration (or reliability) of binary forecasts is the reliability diagram. If we write hypothesis (1) as

$$\begin{aligned} {\mathbb {P}}(Y_k = 1 | f_k = p) = p \qquad \text {for all} \; k = 1, 2, \ldots ; p \in [0, 1],\nonumber \\ \end{aligned}$$
(7)

estimate the left hand side for several values of p and plot those estimates versus p, we obtain what has been called a reliability diagram (see for instance Wilks 1995; Atger 2004; Bröcker and Smith 2007; Bröcker 2012). It should exhibit a graph close to the diagonal, up to “random fluctuations”, provided the forecasting system is calibrated. This however requires dividing the range of \(f_k\) into several bins in a somewhat arbitrary fashion. An original motivation to develop the presented methodology was to remove this requirement and construct a test that assesses calibration uniformly across the entire unit interval. An alternative methodology to circumvent the problem of binning (as well as other problems) has been developed in Dimitriadis et al. (2021, 2022) using isotone regression. The methodology provides a robust way of reconstructing reliability diagrams as well as score decompositions but no statistical tests.

To motivate our test statistic, we integrate Eq. (7) over \(p \in [0, \zeta ]\) against the distribution function F of \(f_k\). (Note that by stationarity, F does not depend on k.) We obtain

$$\begin{aligned} {\mathbb {P}}(Y_k = 1, f_k \le \zeta ) = \int _0^{\zeta } p \;\textrm{d}F(p). \end{aligned}$$
(8)

The hypotheses (7) and (8) are entirely equivalent. Estimating the difference between both sides of hypothesis (8) by empirical averages gives

$$\begin{aligned} \frac{1}{\sqrt{n}}{\textbf{U}}_{n}(\zeta ) := \frac{1}{n} \sum _{k = 1}^{n} (Y_{k} - {f}_{k}) {\mathbbm {1}}_{\{{f_{k}} \le \zeta \}}. \end{aligned}$$
(9)

(By \(\mathbbm {1}_{\{A\}}\) we denote the indicator function of the event A; to include the factor \(\frac{1}{\sqrt{n}}\) in the definition of \({\textbf{U}}_n\) in Eq. (9) will turn out to be convenient.) We would then expect that for every \(\zeta \in [0, 1]\) the random quantity \({\textbf{U}}_n(\zeta )/\sqrt{n}\) should be small for large n. If in addition a central limit theorem holds, \({\textbf{U}}_n(\zeta )\) would be normally distributed with mean zero and a certain variance. The variance of this quantity can be calculated from its definition using hypothesis (2), but essentially the same calculations give the following more general result: Defining the function \(G(\zeta ) := \int _0^{\zeta } p(1-p) \;\textrm{d}F(p)\) we find

$$\begin{aligned} {\mathbb {E}}\big ( {\textbf{U}}_n(\xi ) {\textbf{U}}_n(\eta ) \big ) = G(\xi \wedge \eta ), \end{aligned}$$
(10)

where \(a \wedge b\) denotes the minimum of a and b. For each \(n \in {\mathbb {N}}\), we might thus regard \({\textbf{U}}_n\) as a stochastic process in the continuous parameter \(\zeta \in [0, 1]\); this process has mean zero and covariance function given by Eq. (10). Note that the covariance function is independent of n.

A Wald–type test statistic could be constructed by first evaluating \({\textbf{U}}_n\) at several points \(\zeta _1, \ldots , \zeta _K\), then forming a K–dimensional row vector \({\textbf{u}}_n := ({\textbf{U}}_n(\zeta _1), \ldots , {\textbf{U}}_n(\zeta _K))\) and finally using \({\textbf{u}}_n\Gamma _n^{-1}{\textbf{u}}^t_n\) as a test statistic, where \(\Gamma _n\) is a consistent estimator of the covariance of \({\textbf{u}}_n\).

In this approach, the indicators \(f \rightarrow \mathbbm {1}_{\{f \le \zeta _k\}}\) for \(k = 1, \ldots , K\) would serve as test functions or instruments in the sense of Nolde and Ziegel (2017), see also Bröcker (2021).

Our test will generalise this idea, based on the following fact:

Uniform Central Limit Theorem (See Thm. 1 in the Supplement for precise statement) If Assumption 1 in the Supplement holds, then \({\textbf{U}}_n\) converges in distribution to the process \({\textbf{U}}:= W \circ G\) with respect to the topology of uniform convergence on the unit interval. Here W is the Wiener process (aka standard Brownian motion).

It is easy to see that the limit in distribution of \({\textbf{U}}_n(\zeta )\) as \(n \rightarrow \infty \) is given by \({\textbf{U}}(\zeta )\) pointwise for every \(\zeta \in [0, 1]\).

Since the Wiener process \(\{W(t); t \in [0, 1]\}\) is a Gaussian process with mean zero and covariance function given by \({\mathbb {E}}W(t) W(s) = t \wedge s\), we find that \(\{W(G(\zeta )), \zeta \in [0, 1]\}\) is a Gaussian process with mean zero and covariance function

$$\begin{aligned} {\mathbb {E}}\left[ W(G(\xi )) W(G(\eta )) \right] = G(\xi ) \wedge G(\eta ) = G(\xi \wedge \eta ), \end{aligned}$$
(11)

the last equality being true because G is monotonically increasing. Comparing with Eq. (10) we find that \({\textbf{U}}\) and \(W \circ G\) have the same mean and covariance function. As they are Gaussian processes, it follows that they have the same distribution.

As a (preliminary) candidate for a test statistic, we consider

$$\begin{aligned} \tau _n := \sup _{\zeta \in [0, 1]} |{\textbf{V}}_n(\zeta )|, \qquad \text {with} \qquad {\textbf{V}}_n(\zeta ) := \sqrt{\frac{1}{G(1)}} {\textbf{U}}_n(\zeta ).\nonumber \\ \end{aligned}$$
(12)

Due to the central limit theorem being uniform, we can conclude that for \(n \rightarrow \infty \) we get

$$\begin{aligned} \begin{aligned} \tau _n&{\mathop {\rightarrow }\limits ^{{\mathcal {D}}}} \sup _{\zeta \in [0, 1]} \frac{1}{\sqrt{G(1)}} |{\textbf{U}}(\zeta )| \\&= \sup _{\zeta \in [0, 1]} \frac{1}{\sqrt{G(1)}} |W \circ G(\zeta )|\\&= \sup _{\zeta \in [0, G(1)]} \frac{1}{\sqrt{G(1)}} |W(\zeta )| \\&{\mathop {=}\limits ^{{\mathcal {D}}}} \sup _{\zeta \in [0, G(1)]} |W\left( \frac{\zeta }{G(1)}\right) | \\ {}&\qquad \text {(by time rescaling of Wiener process)}\\&= \sup _{\zeta \in [0, 1]} |W(\zeta )|. \end{aligned} \end{aligned}$$
(13)

Here \({\mathop {\rightarrow }\limits ^{{\mathcal {D}}}}\) means convergence in distribution, and the second to last equality \({\mathop {=}\limits ^{{\mathcal {D}}}}\) is an equality in distribution only. We stress that by taking the supremum, we are able to remove the dependence on the function G (up to the scaling factor G(1)).

The distribution of the supremum of the Wiener process is well known, see Erdös and Kac (1946); in the following, the symbol \({\mathcal {K}}\) will denote the corresponding cumulative distribution function. Strictly speaking, \(\tau _n\) as in Eq. (12) is not a test statistic as it contains the unknown factor \(G(1) = {\mathbb {E}}f_k (1 - f_k)\). This factor or nuisance parameter has to be replaced with a consistent estimator, for instance an empirical average; the uniform central limit theorem will still hold with a consistent estimator replacing G(1), see Corollary 1 in the supplement. A python package containing code for all uniform calibration tests discussed in the present paper is available online (Bröcker 2020).

3.3 General identification functions; conditional mean and quantile forecasts

In the case of general identification functions, similar considerations apply and we will refrain from a detailed calculation. Starting from the general calibration condition (3) and taking the same steps as for probability forecasts for binary verifications, we are led to the statistic \(\tau _n\) as in Eq. (13) but with

$$\begin{aligned} {\textbf{V}}_n(\zeta ) := \frac{1}{\sqrt{n \gamma _n}} \sum _{k = 1}^n \phi _k \mathbbm {1}_{\{f_k \le \zeta \}}, \end{aligned}$$
(14)

with \(\gamma _n := \frac{1}{n} \sum _{k = 1}^{n} \phi ^2_k\) as an estimator for \({\mathbb {E}}(\phi _k^2)\).

For mean forecasts, this gives

$$\begin{aligned} {\textbf{V}}_n(\zeta ) := \frac{1}{\sqrt{n \gamma _n}} \sum _{k = 1}^n (Y_k - f_k) \mathbbm {1}_{\{f_k \le \zeta \}}, \end{aligned}$$
(15)

with \(\gamma _n := \frac{1}{n} \sum _{k = 1}^{n} (Y_k - f_k)^2\) as an estimator for \({\mathbb {E}}((Y_k - f_k)^2)\). In the case of conditional quantile forecasts, we have

$$\begin{aligned} {\textbf{V}}_n(\zeta ) = \frac{1}{\sqrt{\alpha (1 - \alpha ) n}} \sum _{k = 1}^n (\mathbbm {1}_{\{Y_k \le f_k\}} - \alpha ) \mathbbm {1}_{\{f_k \le \zeta \}}. \end{aligned}$$
(16)

Since Assumption 1 and Corollary 1 in the Supplement apply to general identification functions and random functions of the form (14), we can argue as before and conclude that for \(n \rightarrow \infty \) we get \( \tau _n {\mathop {\rightarrow }\limits ^{{\mathcal {D}}}} \sup _{\xi \in [0, 1]} |W(\xi )|\). Remarkably, in case of conditional quantile forecasts, the test statistic does not contain any additional nuisance parameter that needs estimating. Note also that in Eqs. (14, 15, 16) we have \(\zeta \in {\mathbb {R}}\) because now our forecasts range over the whole real line. Still the distribution of the supremum is given by that of the supremum of a standard Wiener process over the unit interval.

3.4 Power considerations

As said previously, the uniform calibration tests are only guaranteed to develop power against violations of the relation (1) (or relation (6) in the case of general identification functions). We will demonstrate this here from a theoretical perspective and carry out a few numerical experiments in Sect. 4.3, where we will furthermore compare the uniform calibration tests with established tests discussed in Sect. 3.4.

Our theoretical analysis will focus on the binary case as the considerations for general identification functions are very similar.

Proposition

(Power of Uniform Calibration Tests) Suppose that Assumptions (2,3) in Sect. 3 are satisfied, but that for eack \(k \in {\mathbb {N}}\), Eq. (1) fails to be true on a set \(\Omega _k \subset \Omega \) with positive probability.

Then \(\tau _n \rightarrow \infty \) almost surely and the hypothesis is rejected with probability converging to one as \(n \rightarrow \infty \).

Note that although the set \(\Omega _k \subset \Omega \) on which Eq. (1) fails to be true depends on k, the probability of \(\Omega _k\) does not due to stationarity.

We will write \(\{g_k, k = 1, 2, \ldots \}\) for a potentially uncalibrated set of forecasts corresponding to the verifications \(\{Y_k, k = 1, 2, \ldots \}\).

For the proof, we observe that

$$\begin{aligned} {\mathbb {P}}(Y_k = 1 | g_k) = {g_k} + \psi (g_k) \qquad \quad \text{ for } k = 1, 2, \ldots \end{aligned}$$
(17)

for some function \(\psi \), simply because \({\mathbb {P}}(Y_k = 1 | g_k)\) is always a function of \(g_k\). The hypothesis (1), if in force, would imply that \(\psi = 0\) almost surely with respect to the distribution of \(g_k\); this distribution does not depend on k due to stationarity. Now we assume this to be no longer the case. More specifically, we assume that there is some \(\epsilon > 0\) and a set \(A \subset [0, 1] \) which contains forecasts with positive probability such that either \(\psi (x) \ge \epsilon \) for all \(x \in A\), or \(\psi (x) \le -\epsilon \) for all \(x \in A\).

This is equivalent to saying that there exists a \(\zeta _* \in [0, 1]\) such that

$$\begin{aligned} {\mathbb {E}}(\psi (g_k) \mathbbm {1}_{\{g_k \le \zeta _*\}}) = \eta \ne 0. \end{aligned}$$
(18)

This expectation value does not depend on k if we assume stationarity. The random function \({\textbf{U}}_n\) now reads as

$$\begin{aligned} \begin{aligned} {\textbf{U}}_n(\zeta )&= \frac{1}{\sqrt{n}} \sum _{k = 1}^n (Y_k - g_k) \mathbbm {1}_{\{g_k \le \zeta \}}\\&= \frac{1}{\sqrt{n}} \sum _{k = 1}^n (Y_k - (g_k + \psi (g_k)) \mathbbm {1}_{\{g_k \le \zeta \}}\\&\quad + \frac{1}{\sqrt{n}} \sum _{k = 1}^n \psi (g_k) \mathbbm {1}_{\{g_k \le \zeta \}}, \end{aligned} \end{aligned}$$
(19)

which we write as \({\textbf{U}}^{(1)}_n(\zeta ) + {\textbf{U}}^{(2)}_n(\zeta )\).

For \({\textbf{U}}^{(1)}_n\), we can again apply the uniform central limit theorem, and in particular, the conclusion of Eq. (13) still holds, essentially because \(f_k := g_k + \psi (g_k)\) is now a calibrated forecast. For the second contribution however we have

$$\begin{aligned} \frac{1}{\sqrt{n}}{\textbf{U}}^{(2)}_{n}(\zeta ) \rightarrow {\mathbb {E}}(\psi ({g_{k}}) {\mathbbm {1}}_{\{g_{k} \le \zeta \}}) \end{aligned}$$
(20)

by the law of large numbers, and in view of Eq. (18), we see that \({\textbf{U}}^{(2)}_n(\zeta _*)\) behaves like \(\sqrt{n} \eta \), which diverges to either \(+\infty \) or \(-\infty \), depending on the sign of \(\eta \). As a result, the test statistic \(\tau _n\) will diverge to \(\infty \) and the hypothesis will be rejected with probability converging to one as \(n \rightarrow \infty \). This demonstrates that the test will exhibit asymptotically unit power against any alternative of the form (17) (unless \(\psi \) is zero with probability one), that is, the test is consistent.

3.5 Existing methods for testing forecast calibration

De Jong (1996) presents a test for the correct specification of time series models, based on the work of Bierens (1990).

The test is similar to those presented here in that a functional central limit theorem is applied to a family of instruments indexed by a continuous parameter. There are a number of differences however, both in terms of the setup as well as the potential performance, and therefore a direct comparison would require an extensive discussion (including of the associated caveats) which was deemed to be beyond the scope of the present paper. The de Jong test assesses a stronger hypothesis, more akin to (2) and including regression parameters. The test is thus likely to have less power against the alternatives discussed here.

For essentially the same reasons, the results pertaining to the asymptotic distribution of the test statistic make stronger assumptions (including for instance a mixing condition).

The calibration of binary, mean, or quantile forecasting systems can also be tested by regressing the forecast errors on a vector of instruments or test functions, which in the notation of the present paper are random variables which are measurable with respect to \(\{f_{1:k}, Y_{1:k-1}\}\) for each \(k \in {\mathbb {N}}\) (recall the discussion in Sec. 3.1). For the case of conditional mean forecasts or binary probability forecasts, square loss is used (Mincer and Zarnowitz 1969; Gaglianone et al. 2011), while quantile loss (i.e. skewed absolute loss, Engle and Manganelli 2004) is a proper loss function for the quantile case. If the forecasting system is calibrated, the optimal regression coefficient is zero, and this is the hypothesis assessed by regression based tests (we refer to the Supplement, Sec. 1 for details of the tests).

We stress that this regression hypothesis is weaker than (i.e. implied by) Eq. (4) (or (5) in the quantile case), since the former merely requires that the regression residuals are orthogonal to some specific test functions, while the latter is equivalent to this being true for any test function. In case that the test function is taken as a function of \(f_k\), the hypothesis is even implied by the restricted hypothesis (6), since the latter still requires that the residuals are orthogonal to any function of \(f_k\). According to Gaglianone et al. (2011), empirical studies indicated that simply taking \(f_k\) as a test function appeared to be a good choice in the context of assessing models for forecasting Value at Risk (essentially quantile forecasts for financial portfolio values). Therefore, in our numerical experiments in Sect. 4.3, we will compare the uniform calibration tests proposed in the present work with regression tests using \(f_k\) as test function.

3.6 Larger lead times

We will finish this section with a discussion as to how the conditions for calibration need to be modified for larger lead times, and why in that case a rigorous testing methodology is harder to develop. As discussed above, the lead time is, roughly speaking, the lag between the time when the forecast is issued and when the verification obtains. This means that if the forecast \(f_k\) has a lead time L (where L might be larger than one), then at the time the forecast is issued, only the verifications \(Y_1, \ldots , Y_{k - L}\) are available to the forecaster while the verifications \(Y_{k - L + 1}, \ldots , Y_k\) are still in the future. Therefore in the conditioning in hypotheses (2,4,5), we merely have to replace the verifications \(Y_{1:k}\) with \(Y_{1:k-L}\). Hypothesis (1) for instance will now read as

$$\begin{aligned} {\mathbb {P}}(Y_k = 1| f_{1:k}, Y_{1:k-L}) = f_k \qquad \text {for all}\;k = 1, 2, \ldots . \end{aligned}$$
(21)

As discussed, a difficulty lies in the fact that the verification–forecast pairs are dependent random variables, with the only a priori information about the nature of the dependencies being the calibration hypothesis itself. In that regard, the hypothesis (2) for the case of lead time \(L=1\) provides a lot more information than the corresponding hypothesis (21) for larger lead times. As a consequence, the statistical properties of the test can be derived in the case of lead time \(L=1\) under minimal additional assumptions, while we expect that further assumptions will be required for the case of higher lead times. This is entirely analogous to the difficulties one faces when testing calibration of ensemble forecasting systems (see Bröcker and Ben Bouallègue 2020). Having said this, a key result for our methodology (Thm 1 in the Supplement) remains true even in the case of larger lead times, provided a mixing condition is imposed. Thus there does exist an avenue for extending the presented methodology to larger lead times.

A straightforward alternative is based on the observation that in the case of lead time \(L > 1\), the original time series \({\mathcal {V}}:= \{(Y_k, f_k), k \in {\mathbb {N}}\}\) of verification–forecast pairs can be split into the L time series \({\mathcal {V}}_l := \{(y^{(l)}_{k}, f^{(l)}_{k}), k \in {\mathbb {N}}\}\), where \(y^{(l)}_{k} := Y_{L(k-1) + l}\) and \(f^{(l)}_{k} = f_{L(k-1) + l}\) for \(l = 1, \ldots , L\) and \(k \in {\mathbb {N}}\). Each of the L time series \({\mathcal {V}}_l\) will now have unit lead time (because L steps in the original time series \({\mathcal {V}}\) now correspond to a single time step in the new time series \({\mathcal {V}}_l\)). Therefore the presented tests can be applied to the new time series \({\mathcal {V}}_l\) individually for each \(l = 1, \ldots , L\). These tests are not independent though and multiple testing has to be accounted for, for instance by a Bonferroni correction. As is usually the case when accounting for multiple testing with this approach, the resulting tests are conservative even asymptotically.

4 Monte–Carlo experiments with synthetic data

In this section, we will present Monte–Carlo experiments using artificial data . In Sects. 4.1 and 4.2, the null hypothesis will be assumed valid in order to confirm whether the uniform calibration tests exhibit the correct size. In Sect. 4.3 we study the power of uniform calibration tests in comparison with that of regression based tests. All experiments were done using the mentioned python package franz (Bröcker 2020).

The artificial data for our experiments is generated with an autoregressive process of order one. We define the process \(\{X_n, n = 1, 2, \ldots \}\) recursively trough

$$\begin{aligned} X_{n+1} = a X_n + R_{n+1} \qquad \hbox {for} \; n = 0, 1, \ldots \end{aligned}$$
(22)

where \(X_0, R_1, R_2, \ldots \) are independent and normally distributed with mean zero and variances \({\mathbb {E}}(X_0^2) = \frac{1}{1 - a^2}\) and \({\mathbb {E}}(R^2_k) = 1\) for all \(k = 1, 2, \ldots \). Further, \(a = 0.8\) for most experiments except for a few experiments with the conditional mean forecasts (where still \(0<a<1\), see below). These choices render the AR process \(\{X_n, n = 1, 2, \ldots \}\) stationary and ergodic.

Table 1 Rejection frequencies (in percent) for uniform calibration tests in 5000 independent Monte–Carlo runs. Nominal size is \(5\%\), and the expected fluctuation is approximately \(0.3\%\)
Full size table

4.1 Binary forecasts

As binary verification we consider \(Y_k = \mathbbm {1}_{\{X_k \ge \theta \}} \cdot Z_k + \mathbbm {1}_{\{X_k < \theta \}} \cdot (1 - Z_k)\), where \(\theta \) is a fixed threshold and \(\{Z_k, k = 1, 2, \ldots \}\) are independent and identically distributed Bernoulli variables (also independent from the \(\{X_k\}\)) with success probability \(p_s = 0.95\). The additional Bernoulli variables \(\{Z_k\}\) represent a form of observational noise or confusion of the observables.

As forecasts we use \(f_k = {\mathbb {P}}(Y_k = 1 | X_{k-1})\), which can be calculated explicitly through

$$\begin{aligned} f_k = p_s (1 - {\mathcal {N}}(\theta - a X_{k-1}) + (1 - p_s) {\mathcal {N}}(\theta - a X_{k-1}), \end{aligned}$$
(23)

for \(k = 1, 2, \ldots \), where \({\mathcal {N}}(.)\) denotes the standard normal cumulative distribution function. The verification-forecast pairs satisfy the calibration hypothesis (2) because the AR process is Markov. Furthermore, the distribution of \(X_k\) is continuous (in fact it is normal); it then follows from Eq. (23) that the forecasts \(\{f_k, k = 1, 2, \ldots \}\) are stationary and ergodic and have a continuous distribution. Hence the conditions stated at the beginning of Sect. 3 are satisfied and hence our test should exhibit the stated asymptotic behaviour.

To verify that the tests have the correct size, we ran Monte–Carlo experiments. Each experiment comprised 5000 runs; in each run, the test was applied to a set of \(N\) verification-forecast pairs, where \(N\) varied between 91 and 728 (i.e. between roughly three months and two years of daily forecasts). Then the test statistic and finally the p–value was computed. The runs constituted identical and statistically independent experiments. The relative proportion of runs rejecting the hypothesis at the \(5\%\) significance level (empirical rejection rates) are recorded in Table 1 and should be equal to or smaller than the nominal size of \(5\%\).

Sub–table 1(a) applies to binary forecasts and shows empirical rejection rates for different values of \(N\) and threshold values \(\theta \) (as the standard deviation of \(X_k\) is 15/9, these threshold values correspond to 0, 1/3, 2/3, 1 times the standard deviation). The conclusion from the results is that the uniform calibration test is conservative for N small (as it should be) and appears to approach the nominal size for larger N.

Random Walk plots are shown in Fig. 2, panel (a), which exhibits five typical realisations of the process \({\textbf{V}}_n\). The fluctuations of the process are readily apparent, but the magnitude of the increments is not necessarily homogenous for different values of \(\zeta \), as the limiting process is a Wiener process with (nonuniform) re-scaling of time, rather than a pure Wiener process. The dashed lines indicate quantiles for the supremum of \({\textbf{V}}\) for the levels 0.1, 0.05, 0.01 and 0.005. That is, the path of \({\textbf{V}}\) exceeds the innermost pair of dashed lines with probability 0.1, the pair of lines next further out is exceeded with probability 0.05 and so on, while \({\textbf{V}}\) exceeds the outermost pair with probability 0.005. Plotting these lines gives a direct visual indication as to whether a given path of \({\textbf{V}}\) would be typical under the null hypothesis.

4.2 Conditional mean and quantile forecasts

A similar experiment was applied to conditional mean forecasts. As verification we consider \(Y_k = X_k\), that is the current state of the AR process; forecasts were based on the previous state \(X_{k-1}\). More specifically, we use \(f_k := {\mathbb {E}}(Y_k| X_{k-1}) = a X_{k-1}\). The verification-forecast pairs satisfy the calibration hypothesis (2), again because the AR process is Markov. It follows as before that the forecasts \(\{f_k, k = 1, 2, \ldots \}\) are stationary and ergodic and have a continuous distribution. Hence the conditions stated at the beginning of Sect. 3 are satisfied and hence our test should exhibit the stated asymptotic behaviour.

Again, Monte–Carlo experiments were run using the same setup as for the binary case, with the exception that we now vary the AR coefficient a. Thereby, we explore different levels of predictability in the AR process. Sub–table (b) of Table 1 applies to mean forecasts and shows empirical rejection rates for different values of \(N\), and for different values of the AR coefficient. The conclusion is again that the uniform calibration test is conservative for N small and appears to approach the nominal size for larger N. The rejection rates tend to get larger for larger predictablity; they even exceed \(5\%\) for \(N = 728\) and an AR coefficient of 0.8 but note that the difference from the nominal size is not statistically significant.

Finally, similar experiments were conducted for conditional quantile forecasts. As verification we consider again the current state of the AR process \(Y_k = X_k\), while as forecasts we use quantiles of \(X_k\) conditionally on \(X_{k-1}\). These can be computed directly using the quantile function of the normal distribution since the noise in our AR process is normal. As once more the conditions stated at the beginning of Sect. 3 are satisfied, the uniform calibration test should exhibit the stated asymptotic behaviour. Empirical rejection rates are shown in sub–table 1(c) for different values of \(N\), and for different quantile levels. Once again, we find that the uniform calibration test is conservative for N small and appears to approach the nominal size for larger N.

Fig. 1
figure 1

Power function of uniform calibration tests (solid lines) and of regression based tests (dashed lines), applied to forecasts of binary events (panel a) and mean forecasts (panel b). Different plot symbols correspond to different sizes of the verification–forecast archive

Full size image

As a final remark, we note that according to the theoretical results, the uniform calibration tests should not only show the right rejection rates at typical sizes but the entire distribution of the p–values should be uniform (at least asymptotically for large n). We carried out further experiments for binary, mean, and quantile forecasts, varying both the number of Monte–Carlo runs as well as size of the verification–forecast archive. We will not provide detailed results here but the general message seems to be that at a size \(N = 728\) of the verification–forecast archive, the p–values for the binary and quantile forecasts are indistinguishable from uniformity, while for the mean forecasts a uniform distribution of p–values gets rejected by a Kolmogorov-Smirnov test (p–value of 0.002), although this does not seem to affect the size of the test. This finding however is strongly dependent on the specific setup. In particular, it emerges from the proof of the uniform central limit theorem that the decay of correlations in the forecast time series plays a role, as do large outliers in the sum \({\textbf{U}}_n\) (see Eq. 9). Outliers cannot happen in the binary case and the quantile case (as the entries in the sum are bounded) but they can in the conditional mean case. We have therefore repeated the experiment with an AR process featuring bounded and uniformly distributed noise, thus removing the possibility of outliers. The p–values of all uniform calibration tests (at \(N = 728\)) now show no indication of deviation from uniformity, according to a Kolmogorov-Smirnov test (p–value of 0.468), consistent with the above discussion.

4.3 Monte–Carlo experiments regarding power

We will now discuss a few numerical experiments, largely in order to compare the power of uniform calibration tests with that of regression based tests. In all regression tests, the test function (or instrument) will be the forecast itself (see discussion at the end of Sec. 3.4). As in Sect. 4, data will be generated through an AR process. The verifications will be as before for binary, mean, and quantile forecasts. Consider a forecast \({\tilde{f}}_k\) given by

$$\begin{aligned} {\tilde{f}}_k := f_k + \epsilon \phi (f_k) \qquad \hbox {for}\; k \in {\mathbb {N}}\end{aligned}$$
(24)

where \(f_k\) are the calibrated forecasts considered in Sect. 4, \(\phi \) is a distortion we will select below, while \(\epsilon \) serves as a parameter controlling the amount of distortion or deviation from calibration. As will be discussed in detail below, a further transformation is going to be applied to the forecasts \({\tilde{f}}_k\) for each \(k = 1, \ldots , N\), depending on the type of forecast used, resulting in forecasts \(g_k\); these are the definite (uncalibrated) forecasts for our experiment. As a measure of deviation from calibration, we will use the relative mean square deviation between \(g_k\) and \(f_k\), namely

$$\begin{aligned} \rho := \frac{\sqrt{{\mathbb {E}}(g_k - f_k)^2}}{\sqrt{{\mathbb {E}}(f_k - {\mathbb {E}}f_k)^2} }, \end{aligned}$$
(25)

which due to stationarity does not depend on k. We estimate this quantity through empirical averages.

We start with forecasts for binary events. As a distortion we use \( \phi (x) = \sin (2 \pi x)\). With this choice, it is guaranteed that \(x + \epsilon \phi (x) \in [0, 1]\) if \(x \in [0, 1]\), provided \(\epsilon \) is small enough which we will ensure. We apply another transformation to the forecast; namely we use

$$\begin{aligned} g_k := \frac{{\tilde{f}}_k \lambda }{1 + {\tilde{f}}_k (\lambda - 1)} \qquad \hbox {for all} \; k = 1, 2, \ldots , \end{aligned}$$
(26)

as our definitive forecast, where \(\lambda \) is chosen so that \({\mathbb {E}}(g_k) = {\mathbb {E}}(Y_k)\). By this transformation, we ensure that \(g_k\) is at least unconditionally calibrated.

Figure 1, panel (a) shows the power of the uniform calibration tests as a function of the bias \(\rho \) (see Eq. 25) as solid lines. Experiments for \(N = 91, 182, 364\) and 728 we carried out but only results for \(N = 182\) and 728 are shown to avoid clutter (marked with \(\blacktriangle \) and \(\blacklozenge \), resp). The other experiments do not alter the qualitative conclusions. The power of the regression test is also shown as dashed lines. It is clear that in this situation the regression based test has more power especially for smaller distortions and smaller N. This is probably not surprising, since a simple linear regression will achieve a lot in terms of recalibrating these forecasts (save the problem that the recalibrated forecasts will not necessarily be in the unit interval anymore). This finding however is entirely specific to the distortion chosen in this particular example, as we will see for the other types of forecasts.

Fig. 2
figure 2

Random Walk plots with five typical realisations of the process \({\textbf{V}}_n\). The dashed lines indicate nested regions that the path of \({\textbf{V}}\) leaves with probability 0.1 (innermost), 0.05, 0.01 and 0.005 (outermost) under the null hypothesis. Panel (a) shows Random Walk plots for synthetic data satisfying the null hypothesis (see Sec. 4.1). Panel (b) shows five realisations of the process \({\textbf{V}}_n\) with a the deviation from calibration of \(\rho \cong 0.2\) (see text for details)

Full size image

For the mean forecasts, we use a distortion of the form

$$\begin{aligned} \phi (x) = x \exp (-\frac{3}{10} x^2). \end{aligned}$$
(27)

The exponential factor merely ensures that if \(f_k\) is large, then \(f_k \cong g_k\), or in other words forecasts with large magnitude remain calibrated. Thereby, we avoid a situation where the test power against this alternative is due to very few instances with forecasts exhibiting a large magnitude. Further, we apply a linear transformation to the forecasts, that is we use

$$\begin{aligned} g_k := \beta _0 + \beta _1 {\tilde{f}}_k \qquad \text {for all} \; k = 1, 2, \ldots , \end{aligned}$$
(28)

as our definite forecasts. The parameters \(\beta _0, \beta _1\) were determined by linear regression in an offline experiment with 5000 data points. Since the verification is now (nearly) optimally regressed on the forecasts, we expect the regression based tests to have close to no power, despite the \(g_k\) still showing substantial deviation from calibration, as we will see soon.

Figure 1, panel (b), shows the results of the Monte–Carlo experiment for \(N = 91, 364\) and 720, marked with \(\bullet , \blacktriangle \) and \(\blacklozenge \), resp. (The experiment for \(N = 182\) is in line with the conclusions.) The power of the uniform calibration tests and the regression tests are shown as solid and dashed lines, respectively. As expected, the regression based test develops close to no power despite substantial deviations from calibration; the uniform calibration test however develops good power for increasing deviation from calibration and for increasing N. Five Random Walk Plots are shown in Fig. 2, panel (b). If the Null were true, the paths should look like that of a Wiener process, but this is evidently not the case for forecast values around \(\zeta = 0\). This illustrates the usefulnes of Random Walk Plots as a qualitative tool to investigate at which forecast values the deviation from calibration is particularly pronounced. Regression based tests in contrast do not have this feature.

Fig. 3
figure 3

Power function of uniform calibration tests (solid lines) and of regression based tests (dashed lines), applied to quantile forecasts of level 0.7 (panel a) and 0.9 (panel b). Different plot symbols correspond to different sizes of the verification–forecast archive

Full size image

The setup for conditional quantile forecast is essentially the same, except that as distortion we use

$$\begin{aligned} \phi (x-q) = (x-q) \exp (-\frac{3}{10} (x - q)^2), \end{aligned}$$
(29)

which is similar to Eq. (27) but for a recentering at q which is the unconditional quantile of the verification \(Y_k\). Further, we apply a linear recalibration to the forecasts as in Eq. (28), but now with the parameters determined through quantile regression. Again, despite substantial deviation from calibration, we expect the regression based tests to have close to no power.

Figure 3 shows the results of the Monte–Carlo experiment, where panels (a) and (b) are for quantile forecasts of level 0.7 and 0.9, respectively. The power of the uniform calibration tests and the regression tests are shown as solid and dashed lines, respectively, marked with \(\blacktriangle \) for \(N = 182\) and with \(\blacklozenge \) for \(N = 728\). (The experiments for other N and quantile levels support the conclusions.) For level 0.7, the regression based test develops close to no power while the uniform calibration test however develops good power for increasing deviation from calibration and increasing N. For level 0.9, the power of all tests is generally smaller with only the uniform calibration test for \(N = 728\) developing appreciable power. We also observe that for this level, the regression based test shows increasing (albeit small) power for fewer data but this appears to be a size problem (potentially due to the somewhat unsophisticated way in which we chose the regression parameters).

5 Application to temperature forecasts

The proposed methodology was applied to operational weather forecasts. The verifications comprise temperature measurements from several weather stations in Germany, taken daily at 12UTC. The forecasts are based on the medium range ensemble prediction system of the European Centre for Medium Range Weather Forecasts (ECMWF, see Appendix A for information regarding data availability). The system produces ensemble forecasts for the global atmosphere and gets initialised four times a day. It comprises 50 ensemble members, where each ensemble member represents a possible future evolution of the global atmosphere out to a lead time of 10 days. For our study however, we will only use the forecasts initialised at 12UTC and with a lead time of 24 hours, or if measured in observation time steps rather than absolute time, the lead time is equal to 1 as per the standing assumption in this paper.

Below we present results for two weather stations (Bremen and Nuremberg, German Weather Service (DWD) Station ID’s 691 and 3668, respectively). We stress that the results are not to be understood as a comprehensive or representative calibration study of the ECMWF ensemble forecasting system, either in its entirety or of parts of it. The aim of the experiments is merely to demonstrate the feasibility of applying the methodology to operational forecast data, and to confirm that quantitatively the results are plausible.

The verification–forecast pairs cover a period between 1st of December 2014 to 30st of September 2020 (resulting in about 2130 values). The verifications and ensembles were converted to anomalies by subtracting a climate normal of the form

$$\begin{aligned}{} & {} \qquad \quad c(k) = c_1 + c_2 \cos (\omega k) + c_3 \sin (\omega k)\nonumber \\{} & {} \text {~~where~~} \omega = \frac{2 \pi }{365.2425}. \end{aligned}$$
(30)

The coefficients \(c_1, c_2, c_3\) were found by a least squares fit onto the entire set of temperature measurements from the station under concern. In the actual experiments to follow, only the first 1000 measurements (of the 2130 available) were used, as in practice this size is not uncommon for forecast–verification archives. The fact that the climate normal has already been fitted to and subtracted from these values strictly speaking constitutes an in–sample calibration of the data. This was deemed not to be a problem here though given that the climate normal comprises a low-complexity model and that the experiment is for illustrative purposes only.

The ensemble forecasts were used to generate mean forecasts, (binary) probability forecasts, and quantile forecasts as follows. We write \({\textbf{X}}_n\) for the entire ensemble at time n; this ensemble comprises 50 ensemble members, and the k’th ensemble member is written as \(X_n^{(k)}\) so that \({\textbf{X}}_n = (X_n^{(1)}, \ldots , X_n^{(K)})\) with \(K = 50\) in our case. The assumption underlying the way we generate mean, probability, and quantile forecasts is basically that the ensemble members at time n are randomly drawn from the forecast distribution (Talagrand et al. 1997), that is the conditional distribution of the verification \(Y_n\), given the information available to the forecaster (which, as discussed, includes all forecasts and verifications up to and including time \(n-1\)). In particular, the ensemble members are completely exchangeable (see Bröcker and Kantz 2011, for a discussion of this point). As the ensemble members are real valued in our case, we may assume that they are sorted in ascending order, that is \(X_n^{(1)} \le \ldots \le X_n^{(K)}\) for each \(n = 1, 2, \ldots \) (this will simplify subsequent notation).

We consider probability forecasts for the binary event \(Y_n > 0\), that is whether the measured temperature exceeds the climate normal. The forecast is constructed by a (regularised) frequency estimator, that is we count the relative number of ensemble members exhibiting the same event

$$\begin{aligned} f_n := \frac{N_n + 1/2}{51} \qquad \qquad \text{ for }\; n = 1, 2, \ldots , \end{aligned}$$
(31)

where \(N_n\) is the number of ensemble members \(X_n^{(k)}\) such that \(X_n^{(k)} > 0\). (Our regularisation of \(f_n\) amounts to assuming that there is an additional fictitious ensemble member “split in half”, one half always exhibiting the event while the other one never does.) It needs to be mentioned that the forecasts only assume a discrete set of 51 values, while our conditions require that the range of forecasts be continuous. This also causes the paths in Panels (a) and (b) in Fig. S1 to look somewhat different from the other panels, as the forecast values do not range continuously over the abscissa. We have not fully analysed this problem but it seems plausible that it is immaterial, in the sense that the stated mathematical results about the limiting distribution of \(\tau _n\) still hold in the limit of an infinitely large ensemble.

Mean forecasts are generated by simply taking the ensemble mean

$$\begin{aligned} {f_n} := \frac{1}{K} \sum _{k = 1}^K X_n^{(k)} \qquad \text{ for }\; n = 1, 2, \ldots . \end{aligned}$$
(32)

Finally, regarding quantile forecasts, we note that the conditional probability of finding the verification \(Y_n\) to be equal to or larger than the k’th ensemble member \(X_n^{(k)}\) is given by \(k / (K+1)\) (see for instance Bröcker and Ben Bouallègue 2020, for a proof). We will use \(k = 25\) and \(k = 38\) here, that is we take \({f_n} := X_n^{(k)}\) with \(k=25\) resp. with \(k = 38\) for \(n = 1, 2, \ldots \) as quantile forecasts with levels \(\alpha = \frac{25}{51} \cong \frac{1}{2}\) resp. \(\alpha = \frac{38}{51} \cong \frac{3}{4}\). Except for the climate normal, no attempt was made to recalibrate these forecasts to improve calibration or to increase the performance in any way, and the following results should be considered with this in mind.

Table 2 contains the p–values, with the four rows and the two columns corresponding to the four types of forecasts and the two stations, respectively. Figure S1 in the Supplement shows all corresponding random walk plots, with the arrangement of the plot panels being the same as in Table 2.

Table 2 The p–values for probability, mean, and quantile forecasts (rows) and two stations (Nuremberg and Bremen; columns).Probability and mean forecasts for Bremen (2nd column, rows 1, 2) show no evidence for deviations from calibration while others do
Full size table
Fig. 4
figure 4

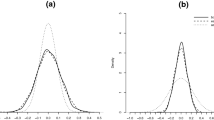
A random walk plot as well as a classical reliability diagram with nine equidistant bins and consistency bars (left and right panels, respectively). The forecasts are probability forecasts for Nuremberg (corresponding to the first row and first column of Table 2)

Full size image

Figure 4 shows a random walk plot as well as a classical reliability diagram with nine equidistant bins and consistency region (left and right panels, respectively, see Bröcker and Smith 2007). The forecasts are probability forecasts for Nuremberg (corresponding to the first row and first column of Table 2). From the table and the figures we obtain a mixed picture, with some experiments showing no evidence for deviations from calibration while others do. Quantile forecasts turn out to be unreliable throughout, while probability and mean forecasts are unreliable for Nuremberg but reliable for Bremen (the quantile forecast of level 3/4 for Bremen and the probability forecasts for Nuremberg give \(p \cong 5\%\) and might be considered on the verge). The results in Fig. 4 provide further indication as to which forecast values exhibit deviations from reliability.

The random walk plot as well as the reliability diagram suggest that low probability forecasts predict too many events.

There seems to be less of a coherent message for higher probability forecasts.

The consistency region of the reliability diagram must be interpreted with care though as the underlying methodology does not take temporal correlations into account.

Although the results must not be interpreted as a representative calibration analysis of this forecasting system, they demonstrate the advantage of testing calibration uniformly over all values of the forecast, rather than using unconditional tests. An unconditional test corresponds to taking the value of the function \({\textbf{V}}_n\) at the end point \(\zeta _{\infty }\) as a test statistic (where \(\zeta _{\infty } = 1\) for probability forecasts and \(\zeta _{\infty } = \infty \) for mean forecasts and quantile forecasts). It turns out that the blue lines in Fig. S1 delineate regions for this statistic with probability approximately 0.05, 0.025, 0.005,  and 0.0025. Considering \(\frac{1}{2}\)-quantile forecasts for Nuremberg or \(\frac{3}{4}\)-quantile forecasts for Bremen for instance (Fig. S1, panels e and h), a test for unconditional calibration based on \({\textbf{V}}_n(\zeta _{\infty })\) would provide p–values of at least 0.05 resp. about 1 judging from the plot (in fact about 0.2 and 0.95), and the hypothesis would not be rejected, while the conditional test based on the entire path gives p-value of about 0.001 resp. 0.047 (see Tab. 2), thus rejecting the null hypothesis. In both cases, we see from Fig. S1, panels (e,h) that the event \(\{Y_k < f_k\}\) happens too frequently as long as \(f_k < 0\), but too rarely if \(f_k > 0\). These effects however cancel out on average over all forecasts, meaning that the overall frequency of the event \(\{Y_k < f_k\}\) is about 1/2 which it is expected to be under unconditional calibration. Therefore, the lack of calibration goes undetected by an unconditional test.

6 Future work

It is clear that the restriction to unit lead time is a severe one, and an extension to larger lead times is needed. The main difficulties have been mentioned at the end of Sect. 2 already, along with possible avenues for solution. The uniform central limit theorem (Thm 1 in the Supplement) holds in case of larger lead times as well, provided several technical assumptions are imposed. (The proof will be presented elsewhere as it requires a number of modifications and is substantially longer.) Unfortunately, the limiting process, although Gaussian, will not have the simple representation in terms of a Wiener process as we have encountered here for unit lead time. The correlation structure of that process will be more complicated and depends on the correlation structure of the time series of verification–forecast pairs. As already discussed at the end of Sect. 2, the calibration hypothesis provides a lot more information on that correlation structure in the case of lead time \(L=1\) than for larger lead times. This means that for larger lead times, more information regarding this correlation structure will have to be estimated from the data itself and factored into the test statistics, most likely requiring further assumptions.

Regarding higher dimensional forecasts, for instance conditional mean forecasts for multi–dimensional verifications, again more work is needed to extend the presented methodology to that situation. The same is true for extensions to higher order identification functions in the sense of Fissler and Ziegel (2016) (such as the pair of mean and variance).

The difficulties are broadly similar to those one would encounter for higher lead times, although they seem to be easier to resolve in the case of higher dimensional forecasts but for unit lead time. The uniform central limit theorem (Theorem 1 in the Supplement) also holds in case of higher dimensional forecasts, although again the proof will require some modifications. The limiting process has a relatively simple correlation structure and we conjecture that it can be represented in terms of a multi–parameter Wiener process or Brownian sheet. But again some information regarding this correlation structure will have to be estimated from the data itself, although probably not as much as in the case of larger lead times.