Estimation of all parameters in the fractional Ornstein–Uhlenbeck model under discrete observations

Abstract

Let the Ornstein–Uhlenbeck process $(X_t)_{t\ge 0}$ driven by a fractional Brownian motion $B^{H }$ described by $dX_t = -\theta X_t dt + \sigma dB_t^{H }$ be observed at discrete time instants $t_k=kh$, $k=0, 1, 2, \ldots , 2n+2$. We propose an ergodic type statistical estimator ${\hat{\theta }}_n$, ${\hat{H}}_n$ and ${\hat{\sigma }}_n$ to estimate all the parameters $\theta$, H and $\sigma$ in the above Ornstein–Uhlenbeck model simultaneously. We prove the strong consistence and the rate of convergence of the estimator. The step size h can be arbitrarily fixed and will not be forced to go zero, which is usually a reality. The tools to use are the generalized moment approach (via ergodic theorem) and the Malliavin calculus.

Appendices

Appendix A: Detailed computations

First, we need the following lemma.

Lemma A.1

Let $X_t$ be the Ornstein–Uhlenbeck process defined by (1.1). Then

$$\begin{aligned} |{\mathbb {E}}(X_tX_s)|\le C(1\wedge |t-s|^{2H-2}) \le (1+ |t-s| )^{2H-2} \, . \end{aligned}$$

(A.1)

The above inequality also holds true for $Y_t$.

Proof

From Cheridito et al. (2003, Theorem 2.3), we have that

$$\begin{aligned} {\mathbb {E}}(Y_sY_t) \le C_{H, \theta } |t-s|^{2H-2} \quad \hbox {for }|t-s| \hbox {sufficiently large}. \end{aligned}$$

(A.2)

But $X_t=Y_t -e^{-\theta t} Y_0$. This combined with (A.2) proves (A.1). $\square$

Lemma A.2

Let $X_t$ be defined by (1.1) and let a, b, c, d be integers. When $H \in (0,\frac{1}{2})\cup (\frac{1}{2},\frac{3}{4})$ we have

$$\begin{aligned}&\lim _{n\rightarrow \infty } \frac{1}{n} \sum _{k,k'=1}^n {\mathbb {E}}\left( X_{kh+ah}X_{k'h+bh} \right) {\mathbb {E}}\left( X_{kh+ch}X_{k'h+dh} \right) \nonumber \\&\qquad = {\mathbb {E}}\left( Y_0 Y_{|b-a|}\right) {\mathbb {E}}\left( Y_0 Y_{|d-c|}\right) + \sum _{m=1}^\infty {\mathbb {E}}\left( Y_0 Y_{|m+b-a|}\right) {\mathbb {E}}\left( Y_0 Y_{|m+d-c|}\right) \nonumber \\&\qquad +\sum _{m=1}^\infty {\mathbb {E}}\left( Y_0 Y_{|m+a-b|}\right) {\mathbb {E}}\left( Y_0 Y_{|m+c-d|}\right) . \end{aligned}$$

(A.3)

Proof

To simplify notations we shall use $X_k$, $Y_k$ to represent $X_{kh}$, $Y_{kh}$ etc. From the relation (3.3) it is easy to see that

$$\begin{aligned} {\mathbb {E}}(X_{k+a}X_{k'+b})= & {} {\mathbb {E}}(Y_{k+a}Y_{k'+b}) - e^{-\theta (k'+b) h} {\mathbb {E}}(Y_0 Y_{k+a} ) \nonumber \\&\qquad -e^{-\theta (k+a)h} {\mathbb {E}}(Y_0 Y_{k'+b} )+ e^{-\theta (k+k'+a+b)h} {\mathbb {E}}( Y_0^2 )\nonumber \\=: & {} \sum _{i=1}^4 I_{i, k,k'} , \end{aligned}$$

(A.4)

where $I_{i, k, k'}=I_{i,a, b, k, k'}$, $i=1, \ldots , 4$, denote the above i-th term.

Let us consider $\frac{1}{n} \sum _{k,k'=1}^n I_{i, k,k'}^2$ for $i=2, 3, 4$. First, we consider $i=2$. By Cheridito et al. (2003, Theorem 2.3), we know that ${\mathbb {E}}(Y_0Y_{k})$ converges to 0 when $k\rightarrow \infty$. Thus by the Toeplitz theorem, we have

$$\begin{aligned} \frac{1}{n}\sum _{k,k'=1}^n I_{2, k, k'}^2= & {} \frac{1}{n} \sum _{k,k'=1}^n e^{-2\theta (k'+b) h}\left[ {\mathbb {E}}(Y_0 Y_ {k+a} )\right] ^2 \nonumber \\\le & {} C\frac{1}{n} \sum _{k }^n \left[ {\mathbb {E}}(Y_0 Y_{k+a})\right] ^2 \rightarrow 0. \end{aligned}$$

(A.5)

Exactly in the same way we have

$$\begin{aligned} \frac{1}{n}\sum _{k,k'=1}^n I_{3, k, k'}^2 \rightarrow 0. \end{aligned}$$

(A.6)

When $i=4$, we have easily

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{n}\sum _{k,k'=1}^n I_{4, k, k'}^2 = \frac{1}{n}\sum _{k,k'=1}^n e^{-2{\theta }(k+k'+a+b)h} \left[ {\mathbb {E}}(Y_0^2)\right] ^2 \rightarrow 0. \end{aligned}$$

(A.7)

Now we have

$$\begin{aligned}&\frac{1}{n} \sum _{k,k'=1}^n {\mathbb {E}}\left( X_{kh+ah}X_{k'h+bh} \right) {\mathbb {E}}\left( X_{kh+ch}X_{k'h+dh} \right) \\&\qquad =\frac{1}{n} \sum _{i,j=1}^4\sum _{k,k'=1}^n I_{i,a,b, k,k'}I_{j, c,d, k, k'}\\&\qquad = \frac{1}{n} \sum _{k,k'=1}^n I_{1,a,b, k,k'}I_{1,c,d, k,k'} +\frac{1}{n} \sum _{i\not =1,\mathrm{or} j\not =1}\sum _{k,k'=1}^n I_{i,a,b,k,k'}I_{j, c,d,k, k'}\\&\qquad ={\mathcal {I}}_{1,1, n} +\sum _{i\not =1,\mathrm{or} j\not =1} {\mathcal {I}}_{i,j, n} . \end{aligned}$$

First, let us consider ${\mathcal {I}}_{1,1,n}$. By the stationarity of $Y_n$, we have

$$\begin{aligned} {\mathcal {I}}_{1,1,n}= & {} \frac{1}{n}\sum _{k,k'=1}^n {\mathbb {E}}(Y_{k+a} Y_{k'+b}) {\mathbb {E}}(Y_{k+c} Y_{k'+d}) \nonumber \\= & {} \frac{1}{n}\sum _{k,k'=1}^n {\mathbb {E}}(Y_0Y_{|k'-k+b-a|}) {\mathbb {E}}(Y_0Y_{|k'-k+d-c|}) \nonumber \\= & {} {\mathbb {E}}(Y_0Y_{| b-a|}) {\mathbb {E}}(Y_0Y_{| d-c|}) + \frac{1}{n}\sum _{m=1}^{n-1} (n-m) {\mathbb {E}}(Y_0Y_{| m+b-a|}) {\mathbb {E}}(Y_0Y_{|m+ d-c|}) \nonumber \\&+ \frac{1}{n}\sum _{m=1}^{n-1} (n-m) {\mathbb {E}}(Y_0Y_{| -m+b-a|}) {\mathbb {E}}(Y_0Y_{|-m+d-c|})\nonumber \\= & {} {\mathbb {E}}(Y_0Y_{| b-a|}) {\mathbb {E}}(Y_0Y_{| d-c|}) + \sum _{m=1}^{n-1} {\mathbb {E}}(Y_0Y_{| m+b-a|}) {\mathbb {E}}(Y_0Y_{|m+ d-c|}) \nonumber \\&+ \sum _{m=1}^{n-1} {\mathbb {E}}(Y_0Y_{| m+a-b|}) {\mathbb {E}}(Y_0Y_{|m+ a-b|}) + \frac{1}{n}\sum _{m=1}^{n-1} m {\mathbb {E}}(Y_0Y_{| m+b-a|}) {\mathbb {E}}(Y_0Y_{|m+ d-c|}) \nonumber \\&+ \frac{1}{n}\sum _{m=1}^{n-1} m {\mathbb {E}}(Y_0Y_{| m+a-b|}) {\mathbb {E}}(Y_0Y_{|m+ c-d|}) . \end{aligned}$$

(A.8)

By Lemma A.1 for $Y_t$ or an expression of ${\mathbb {E}}(Y_0Y_m)$ given in Cheridito et al. (2003, Theorem 2.3):

$$\begin{aligned} {\mathbb {E}}(Y_0Y_m) = \frac{1}{2} \sigma ^2 \sum _{n=1}^{N} \theta ^{-2n}(\Pi _{k=0}^{2n-1} (2H-k)) m^{2H-2n} + O(m^{2H-2N-2}). \end{aligned}$$

This means ${\mathbb {E}}(Y_0Y_m) = O(m^{2H-2})$ as $m\rightarrow \infty$, which in turn means that $\left| {\mathbb {E}}(Y_0Y_{|m+\rho _1|} ){\mathbb {E}} (Y_0Y_{|m+\rho _2|})\right| = O(m^{4H-4})$ for any arbitrarily given integers $\rho _1$ and $\rho _2$. Hence, when $H<\frac{3}{4}$, $\sum _{m=0}^{n-1} {\mathbb {E}}(Y_{0}Y_{|m+\rho _1| } ) {\mathbb {E}}(Y_{0}Y_{|m+\rho _2| })$ converges as n tends to infinity. This shows that the second and third terms in (A.8) are convergent.

Notice that for $H <\frac{3}{4}$, $m {\mathbb {E}}(Y_0Y_m)^2 =O(m^{4H-3})\rightarrow 0$ as $m\rightarrow \infty$. By Toeplitz theorem we have

$$\begin{aligned} \frac{1}{n} \sum _{m=0}^{n-1} m \left| {\mathbb {E}}(Y_0Y_{|m+\rho _1|} ){\mathbb {E}}(Y_0Y_{|m+\rho _2|})\right| \rightarrow 0\quad \hbox {as } n\rightarrow \infty . \end{aligned}$$

Thus, the fourth and fifth terms in (A.8) converges to 0. This implies that ${\mathcal {I}}_{1.1.n}$ converges to the right hand side of (A.3).

When one of the i or j is not equal to 1, we have by the Hölder inequality

$$\begin{aligned} {\mathcal {I}}_{i,j,n}\le & {} \left( \frac{1}{n} \sum _{k,k'=1}^n I_{i,a,b,k,k'}^2\right) ^{1/2} \left( \frac{1}{n} \sum _{k,k'=1}^n I_{j, c,d,k, k'}^2\right) ^{1/2} \end{aligned}$$

which will go to 0 since $\frac{1}{n} \sum _{k,k'=1}^n I_{i,a,b,k,k'}^2, n=1, 2, \ldots$ is bounded when $i=1$ and converges to zero when $i\not =1$ by (A.5)–(A.7). $\square$

Let $G_n$ be defined by (4.2) in Sect. 4. Its Malliavin derivative is given by

$$\begin{aligned} DG_n= & {} \frac{1}{\sqrt{n}} 2\alpha \sum _{k=1}^n X_{k}DX_{k} + \frac{1}{\sqrt{n}} \beta \sum _{k=1}^n ( X_{k} DX_{k+1} + X_{k+1}DX_{k} )\nonumber \\&+ \frac{1}{\sqrt{n}} \sum _{k=1}^n \gamma ( X_{k } DX_{ k +2 }+ X_{ k +2 }DX_{k } ). \end{aligned}$$

(A.9)

Lemma A.3

Define the sequence of random variables $J_n :=\langle DG_n,DG_n\rangle _{\mathcal {H}}$. Then

$$\begin{aligned} \lim _{n\rightarrow \infty } {\mathbb {E}}\left[ J_n-{\mathbb {E}}(J_n)\right] ^2= 0. \end{aligned}$$

(A.10)

Proof

It is easy to see that $J_n$ is a linear combination of terms of the following forms (with the coefficients being a quadratic forms of ${\alpha }, {\beta }, {\gamma }$):

$$\begin{aligned} {\tilde{J}}_n&:=\frac{1}{n} \sum _{k',k=1}^{n} \langle DX_{k_1 },DX_{k_1' }\rangle _{\mathcal {H}} X_{k_2 }X_{k_2' }\nonumber \\&=\frac{1}{n} \sum _{k',k=1}^{n} {\mathbb {E}}(X_{k_1 }X_{k_1' }) X_{k_2 }X_{k_2' }, \end{aligned}$$

(A.11)

where $k_1, k_2$ may take $k, k+1, k+2$, and $k_1', k_2'$ may take $k', k'+1, k'+2$. For example, one term is to take $k_1= k_2=k$ and $k_1'=k'+1$, $k_2'=k'$ which corresponds to the product:

$$\begin{aligned}&\left\langle \frac{1}{\sqrt{n}} 2\alpha \sum _{k=1}^n X_{k}DX_{k}, \frac{1}{\sqrt{n}} \beta \sum _{k=1}^n ( X_{k} DX_{k+1}) \right\rangle \nonumber \\&\quad =\frac{2{\alpha }{\beta }}{n} \sum _{k',k=1}^{n}{\mathbb {E}}(X_k X_{k'+1})X_kX_{k'}=:2{\alpha }{\beta }{\tilde{J}}_{0, n}. \end{aligned}$$

(A.12)

We will first give a detail argument to explain why

$$\begin{aligned} {\mathbb {E}}\left[ {\tilde{J}}_{0, n}-{\mathbb {E}}( {\tilde{J}}_{0, n})\right] ^2\rightarrow 0 \end{aligned}$$

and then we outline the procedure that similar claims hold true for any terms in (A.11). Note that ${\mathbb {E}}( {\tilde{J}}_{0, n})$ will not converge to 0.

From the Proposition 4.2 it follows

$$\begin{aligned} {\mathbb {E}}\left[ {\tilde{J}}_{0, n}-{\mathbb {E}}( {\tilde{J}}_{0, n})\right] ^2&= \frac{1}{n^2 } \sum _{k,k', j, j'=1}^{n}{\mathbb {E}}(X_k X_{k'+1}) {\mathbb {E}}(X_j X_{j'+1}){\mathbb {E}}( X_kX_{j}){\mathbb {E}}(X_{k'}X_{j'})\nonumber \\&\quad + \frac{1}{n^2 } \sum _{k,k', j, j'=1}^{n}{\mathbb {E}}(X_k X_{k'+1}) {\mathbb {E}}(X_j X_{j'+1}){\mathbb {E}}( X_kX_{j'}){\mathbb {E}}(X_{k'}X_{j})\nonumber \\&=: I_{1, n}+I_{2,n}. \end{aligned}$$

Using (A.1) we have

$$\begin{aligned} I_{1, n}\le & {} \frac{1}{n^2 } \sum _{k,k', j, j'=1}^{n} (1+ |k'-k|)^{2H-2} (1+ |j'-j|)^{2H-2} \\&(1+ |j-k|)^{2H-2} (1+ |k'-j'|)^{2H-2}\,; \\ I_{2, n}\le & {} \frac{1}{n^2 } \sum _{k,k', j, j'=1}^{n} (1+ |k'-k|)^{2H-2} (1+ |j'-j|)^{2H-2} \\&(1+ |j'-k|)^{2H-2} (1+ |k'-j |)^{2H-2}. \end{aligned}$$

Now it is elementary to see that $I_{1, n}\rightarrow 0$ and $I_{2, n}\rightarrow 0$ when $n \rightarrow \infty$.

Now we deal with the general term

$$\begin{aligned} {\tilde{J}}_{1, n}:=\frac{1}{n} \sum _{k',k=1}^{n} {\mathbb {E}}(X_{k_1 }X_{k_1' }) X_{k_2 }X_{k_2' } \end{aligned}$$

in (A.11), where $k_1, k_2$ may take $k, k+1, k+2$, and $k_1', k_2'$ may take $k', k'+1, k'+2$. We use Proposition 4.2 to obtain

$$\begin{aligned} {\mathbb {E}}\left[ {\tilde{J}}_{1, n}-{\mathbb {E}}( {\tilde{J}}_{1, n})\right] ^2&= \frac{1}{n^2 } \sum _{k,k', j, j'=1}^{n}{\mathbb {E}}(X_{k_1 }X_{k_1' }) {\mathbb {E}}(X_{j_1 }X_{j_1' }) {\mathbb {E}}( X_{k_2 }X_{j_2 }) {\mathbb {E}}( X_{k_2' }X_{j_2' }) \nonumber \\&\quad +\frac{1}{n^2 } \sum _{k,k', j, j'=1}^{n}{\mathbb {E}}(X_{k_1 }X_{k_1' }) {\mathbb {E}}(X_{j_1 }X_{j_1' }) {\mathbb {E}}( X_{k_2 }X_{j_2' }) {\mathbb {E}}( X_{k_2' }X_{j_2 }) \nonumber \\&=: {\tilde{I}}_{1, n}+{\tilde{I}}_{2,n}, \end{aligned}$$

where $k_1, k_2$ may take $k, k+1, k+2$, and $k_1', k_2'$ may take $k', k'+1, k'+2$, $j_1, j_2$ may take $j, j+1, j+2$, and $j_1', j_2'$ may take $j', j'+1, j'+2$. Using (A.1) we have

$$\begin{aligned} {\tilde{I}}_{1, n}\le & {} \frac{1}{n^2 } \sum _{k,k', j, j'=1}^{n} (1+ |k'-k|)^{2H-2} (1+ |j'-j|)^{2H-2} \\&\quad (1+ |j-k|)^{2H-2} (1+ |k'-j'|)^{2H-2} \,; \\ {\tilde{I}}_{2, n}\le & {} \frac{1}{n^2 } \sum _{k,k', j, j'=1}^{n} (1+ |k'-k|)^{2H-2} (1+ |j'-j|)^{2H-2} \\&\quad (1+ |j'-k|)^{2H-2} (1+ |k'-j |)^{2H-2}. \end{aligned}$$

Now it is elementary to see that $I_{1, n}\rightarrow 0$ and $I_{2, n}\rightarrow 0$ when $n \rightarrow \infty$. $\square$

Appendix B: Determinant of the Jacobian of f

The goal of this section is to compute the determinant of the Jacobian of

$$\begin{aligned} f(\theta , H, \sigma ) = \left\{ \begin{array}{ll} \frac{1}{\pi } \sigma ^2 \Gamma (2H+1)\sin (\pi H)\int _0^{\infty } \frac{x^{1-2H}}{\theta ^2 + x^2} dx\,; \\ \frac{1}{\pi }\sigma ^2 \Gamma (2H+1)\sin (\pi H) \int _0^{\infty } \cos (hx)\frac{x^{1-2H}}{\theta ^2 + x^2}dx\,; \\ \frac{1}{\pi }\sigma ^2 \Gamma (2H+1)\sin (\pi H) \int _0^{\infty } \cos (2hx)\frac{x^{1-2H}}{\theta ^2 + x^2}dx , \end{array} \right. \end{aligned}$$

(B.1)

(we use the integral form of the first component of f to simplify the computation of the determinant).

The Jacobian matrix of f is equivalent (their determinants are up to a sign) to $J = (C_1, C_2, C_3)$, where the column vectors are given by

$$\begin{aligned} C_1= & {} \left( \begin{array}{ll} 2 \sigma \Gamma (2H+1)\sin (\pi H)\int _0^{\infty } \frac{x^{1-2H}}{\theta ^2 + x^2}dx \\ 2\sigma \Gamma (2H+1)\sin (\pi H) \int _0^{\infty } \cos (hx)\frac{x^{1-2H}}{\theta ^2 + x^2}dx \\ 2\sigma \Gamma (2H+1)\sin (\pi H) \int _0^{\infty } \cos (2hx)\frac{x^{1-2H}}{\theta ^2 + x^2} dx \end{array} \right) \,; \\ C_2= & {} \left( \begin{array}{ll} -2\theta \sigma ^2 \Gamma (2H+1)\sin (\pi H)\int _0^{\infty } \frac{x^{1-2H}}{(\theta ^2 + x^2)^2}dx\\ -2\theta \sigma ^2 \Gamma (2H+1)\sin (\pi H)\int _0^{\infty } \cos (hx)\frac{x^{1-2H}}{(\theta ^2 + x^2)^2}dx \\ -2\theta \sigma ^2 \Gamma (2H+1)\sin (\pi H)\int _0^{\infty } \cos (2hx)\frac{x^{1-2H}}{(\theta ^2 + x^2)^2}dx \end{array} \right) \,; \end{aligned}$$

and $C_3 = C_{3,1} + C_{3,2} + C_{3,3}$, where

$$\begin{aligned} C_{3,1}= & {} \left( \begin{array}{ll} \sigma ^2 \Gamma (2H+1)\sin (\pi H) \int _0^{\infty } -2\log (x)\frac{x^{1-2H}}{\theta ^2 + x^2}dx\\ \sigma ^2 \Gamma (2H+1)\sin (\pi H) \int _0^{\infty } -2\log (x)\cos (hx)\frac{x^{1-2H}}{\theta ^2 + x^2}dx \\ \sigma ^2 \Gamma (2H+1)\sin (\pi H) \int _0^{\infty } -2\log (x)\cos (2hx)\frac{x^{1-2H}}{\theta ^2 + x^2}dx \end{array} \right) \,; \\ C_{3,2}= & {} \left( \begin{array}{ll} \sigma ^2 \pi \Gamma (2H+1)\cos (\pi H) \int _0^{\infty }\frac{x^{1-2H}}{\theta ^2 + x^2}dx\\ \sigma ^2 \pi \Gamma (2H+1)\cos (\pi H) \int _0^{\infty } \cos (hx)\frac{x^{1-2H}}{\theta ^2 + x^2}dx \\ \sigma ^2 \pi \Gamma (2H+1)\cos (\pi H) \int _0^{\infty } \cos (2hx)\frac{x^{1-2H}}{\theta ^2 + x^2}dx \end{array} \right) \,; \end{aligned}$$

and

Fig. 2

Determinant of M for $H\in (0,1)$ and $\theta \in (2, 10)$

$$\begin{aligned} C_{3,3}= & {} \left( \begin{array}{ll} \sigma ^2 \partial _H\Gamma (2H+1)\sin (\pi H) \int _0^{\infty }\frac{x^{1-2H}}{\theta ^2 + x^2}dx\\ \sigma ^2 \partial _H\Gamma (2H+1)\sin (\pi H) \int _0^{\infty } \cos (hx)\frac{x^{1-2H}}{\theta ^2 + x^2}dx \\ \sigma ^2 \partial _H\Gamma (2H+1)\sin (\pi H) \int _0^{\infty } \cos (2hx)\frac{x^{1-2H}}{\theta ^2 + x^2}dx \end{array} \right) . \end{aligned}$$

By the linearity of the determinant, we have

$$\begin{aligned} \det (J) = \det (C_1,C_2,C_{3,1}) +\det (C_1,C_2,C_{3,2}) +\det (C_1,C_2,C_{3,3}) \end{aligned}$$

It is easy to see that $\det (C_1,C_2,C_{3,2}) = \det (C_1,C_2,C_{3,3}) =0$ ($C_1$ is a proportional to $C_{3,2}$ and to $C_{3,3}$). Therefore

$$\begin{aligned} \det (J) = \det (C_1,C_2,C_{3,1}). \end{aligned}$$

(B.2)

Notice that

$$\begin{aligned} \det (C_1,C_2,C_{3,1}) = -4\theta \sigma ^5 \Gamma ^3(2H+1) \sin ^3(\pi H) \det (M), \end{aligned}$$

(B.3)

where

$$\begin{aligned} M = \left( \begin{array}{ccc} \int _0^{\infty } \frac{x^{1-2H}}{(\theta ^2 + x^2)}dx &{} \int _0^{\infty } \frac{x^{1-2H}}{(\theta ^2 + x^2)^2} dx &{} \int _0^{\infty } -2\log (x)\frac{x^{1-2H}}{\theta ^2 + x^2} dx \\ \int _0^{\infty } \cos (hx)\frac{x^{1-2H}}{(\theta ^2 + x^2)}dx &{} \int _0^{\infty } \cos (hx)\frac{x^{1-2H}}{(\theta ^2 + x^2)^2}dx &{} \int _0^{\infty } -2\log (x)\cos (hx)\frac{x^{1-2H}}{\theta ^2 + x^2} dx\\ \int _0^{\infty } \cos (2hx)\frac{x^{1-2H}}{(\theta ^2 + x^2)}dx &{} \int _0^{\infty } \cos (2hx)\frac{x^{1-2H}}{(\theta ^2 + x^2)^2} dx&{} \int _0^{\infty } -2\log (x)\cos (2hx)\frac{x^{1-2H}}{\theta ^2 + x^2}dx \end{array}\right) \end{aligned}$$

Since $\theta >0$, $\sigma >0$, $\sin ( \pi H) > 0$ and $\Gamma (2H+1) >0$ (for $H \in (0,1)$), $\det (J)=0$ if and only if $\det (M)=0$.

The determinant $\det (J)$ or the determinant $\det (M)$ depends also on h. To remove this dependence, we write $M=(M_{ij})_{1\le i, j\le 3}$, where

$$\begin{aligned} M_{11}= & {} \int _0^{\infty } h^{2H}\frac{x^{1-2H}}{(h^2\theta ^2 + x^2)}dx, \qquad M_{12}=\int _0^{\infty } h^{2H+2}\frac{x^{1-2H}}{(h^2\theta ^2 + x^2)^2} dx \\ M_{13}= & {} \int _0^{\infty } -2h^{2H}\log (\frac{x}{h})\frac{x^{1-2H}}{h^2\theta ^2 + x^2} dx, \qquad M_{21}=\int _0^{\infty } h^{2H}\cos (x)\frac{x^{1-2H}}{(h^2\theta ^2 + x^2)}dx \\ M_{22}= & {} \int _0^{\infty } h^{2H+2}\cos (x)\frac{x^{1-2H}}{(h^2\theta ^2 + x^2)^2}dx ,\quad \\ M_{23}= & {} \int _0^{\infty } -2h^{2H}\log (\frac{x}{h})\cos (x)\frac{x^{1-2H}}{h^2\theta ^2 + x^2} dx\\ M_{31}= & {} \int _0^{\infty } h^{2H}\cos (2x)\frac{x^{1-2H}}{(h^2\theta ^2 + x^2)}dx , \qquad \\ M_{32}= & {} \int _0^{\infty } h^{2H+2}\cos (2hx)\frac{x^{1-2H}}{(h^2\theta ^2 + x^2)^2} dx\\ M_{33}= & {} \int _0^{\infty } -2h^{2H}\log (\frac{x}{h})\cos (2x)\frac{x^{1-2H}}{h^2\theta ^2 + x^2}dx \end{aligned}$$

Since $\log (\frac{x}{h}) = \log (x) - \log (h)$, the determinant of M is equal to $h^{6H+2}$ multiply the determinant of the following matrix:

$$\begin{aligned} N = \left( \begin{array}{ccc} \int _0^{\infty } \frac{x^{1-2H}}{(h^2\theta ^2 + x^2)}dx &{} \int _0^{\infty } \frac{x^{1-2H}}{(h^2\theta ^2 + x^2)^2} dx &{} \int _0^{\infty } -2\log (x)\frac{x^{1-2H}}{h^2\theta ^2 + x^2} dx \\ \int _0^{\infty } \cos (x)\frac{x^{1-2H}}{(h^2\theta ^2 + x^2)}dx &{} \int _0^{\infty } \cos ( x)\frac{x^{1-2H}}{(h^2\theta ^2 + x^2)^2}dx &{} \int _0^{\infty } -2\log (x)\cos (x)\frac{x^{1-2H}}{h^2\theta ^2 + x^2} dx\\ \int _0^{\infty } \cos (2x)\frac{x^{1-2H}}{(h^2\theta ^2 + x^2)}dx &{} \int _0^{\infty } \cos (2 x)\frac{x^{1-2H}}{(h^2\theta ^2 + x^2)^2} dx&{} \int _0^{\infty } -2\log (x)\cos (2x)\frac{x^{1-2H}}{h^2\theta ^2 + x^2}dx \end{array}\right) \end{aligned}$$

Namely, the determinant $\det (J)$ is a negative number multiplied by the determinant $\det (N)$. Denote $\theta '=h \theta$. The determinant of N a function of two variables only: $\theta '$ and H. The plot in Fig. 2 shows that $\det (N)$ is positive for $H \in (0.03,1)$ and $\theta ' \in (2 , 10 )$. Combining this with (B.2) and (B.3), we see that on

$$\begin{aligned} {\mathbb {D}}_h=\left\{ H>0.03, 2<\theta h<10, \sigma >0\right\} \end{aligned}$$

(B.4)

$\det (J)$ is strictly negative hence is not singular.

Appendix C: Numerical results

For all the experiments, we take $h=1$.

1.1 C.1. Strong consistency of the estimators

In this subsection, we illustrate the almost-sure convergence by plotting different trajectories of the estimators. We observe that when $\log _2(n) \ge 14$, the estimators become very close to the true parameter.

However, since our estimators are random (they depend on the sample $\{X_{kh}\}_{k=1}^n$), what’s important to see in these figures is the deviations from the true parameter we are estimating. Even if three trajectories are not enough to make statements about the variance, the figures predict that the variance of $\tilde{\theta }_n$ is very high compared to the other estimators (see Figs. 3, 4) and that, for H close to 0 (see Fig. 5), the deviations of $\tilde{H}_n$ increase.

Fig. 3

Convergence of $\widetilde{H_n}$ for $H =0.7$ and $H =0.4$ ($\theta =6, \sigma =2$)

Fig. 4

Convergence of $\widetilde{\theta _n}$ for $\theta =6, H=0.7,\sigma =2$

Fig. 5

Convergence of $\widetilde{\sigma _n}$ for $\theta =6, H=0.7,\sigma =2$

1.2 C.2. Mean and standard deviation/Asymptotic behavior of the estimators

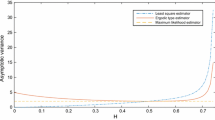
It is important to check the mean and deviation of our estimators. For example, a large variance implies a large deviation and therefore a “weak” estimator. That is why we plotted the mean and variance of our estimators for $n=2^{12}$ over 100 samples.

As we observe, the standard deviation (s.d) of $\tilde{\theta }_n$ is larger than the s.d of $\tilde{\sigma }_n$ which is larger than the s.d of $\tilde{H}_n$ (see Tables 1, 2). Notice also that the s.d of $\tilde{H}_n$ increases as H decreases.

In Hu and Song (2013), the variance of the $\theta$ estimator is proportional to $\theta ^2$. In our case, it is difficult to compute the variances of our estimators (they depend on the matrix $\Sigma$ (see Theorem 4.3) and the Jacobian of the function f (see Eq. (3.9)), however we should probably expect something similar which could explain the gap in the variances since the values of $\theta$ are usually bigger that the values taken by $\sigma$ or H.

Having access to 100 estimates of each parameter, we are also able to plot the distributions of our estimators to show that they effectively have a Gaussian nature (4.5) (Figs. 6, 7, 8).

Remark C.1

In practice, one may already know the value of one parameter, $\sigma$ for example. In this case, it is important to point out that the estimators perform a lot better. For example, in Fig. 9, we plot the density of $\theta _n$ and $H_n$ for $\sigma =1, H=0.6, \theta =6$ and for $\log _2(n)$. Observe how the variance of the estimators is a lot smaller and the shape of the density is smoother.

Table 1 $H =0.7$,$\theta =6$ and $\sigma =2$

Table 2 $H =0.4$,$\theta =6$ and $\sigma =2$

Fig. 6

Distribution of $\widetilde{H_n}$ for $H =0.7$ and $H=0.4$ while $\theta =6,\sigma =2$

Fig. 7

Distribution of $\widetilde{\theta _n}$ for $\theta =6, H=0.7,\sigma =2$

Fig. 8

Distribution of $\widetilde{\sigma _n}$ for $\theta =6, H=0.7,\sigma =2$

Fig. 9

Density plots of $\theta _n$ and $H_n$ when $\sigma$ is known ($=1$)