1 Introduction

The value of a statistical life (VSL) is the monetary valuation of a reduction in the risk of death that would prevent one ‘statistical’ death. Two approaches are available to estimate the VSL. On the one hand, revealed preferences methods seek to identify the trade-off between wealth and mortality risk from the decisions that people make in actual markets. Within this approach, most research has focused on the labour market (Viscusi and Aldy 2003; Viscusi 2018b). On the other hand, the approach based on stated preferences aims to elicit the trade-offs between money and the risk of death from individuals’ responses to surveys where hypothetical markets are recreated. This second approach has been used mostly in the context of health risks (about 50% of all the studies that followed these methodologies), as well as in road safety (30%) and environmental risks (20%) contexts (Viscusi and Masterman 2017). In this paper, we focus on the estimation of the VSL to be used in the context of the design and evaluation of road safety policies. We use the CV/SG chained method proposed by Carthy et al. (1999), which combines both health risks and road safety contexts. In addition, the weaknesses and strengths of this method will be examined by a series of consistency tests.

Contingent valuation (CV) has been the traditional approach to estimate the VSL. Using surveys, CV elicits subjects’ willingness to pay (WTP) to reduce the risk of death or their willingness to accept compensation (WTA) for an increase in the risk of death in a road accident. According to the theory (Jones-Lee 1974), the Marginal Rate of Substitution (MRS) between wealth and the risk of death (\({m}_{d}\)) can be estimated from WTP and WTA valuations. One of the main problems of this method is that it asks subjects to value very small risk reductions since this is the real risk of death that people face of dying in a car accident. Nevertheless, there is plenty of evidence that CV methods entail problems of scope insensitivity (Beattie et al. 1998; Hammitt and Graham 1999). Specifically, while the theory (Jones-Lee 1974) predicts that individuals’ WTPs should be proportional to the size of risk reduction (if risk is marginal or very small), the usual finding is that WTP is much less than proportional to small reductions in the risk of death (Andersson et al. 2016; Søgaard et al. 2012). Thus, VSL estimates change with the size of risk reduction (Dubourg et al. 1997; Jones-Lee et al. 1995).

To overcome those problems Carthy et al. (1999) developed a new method that they called the contingent valuation/standard gamble (CV/SG) chained approach. It is “chained” because the VSL is estimated by combining (i.e., chaining) the responses to two types of questions. Very briefly (the method is explained more in depth in Sect. 2), this approach requires the interviewee to respond to the following questions: (1) WTP for the certainty of a quick and complete cure for a given non-fatal road injury i; (2) WTA for the certainty of sustaining the same injury; and (3) a “modified” Standard Gamble (MSG) question where two lotteries are compared: one with Normal Health and Death as outcomes and the other one with injury i and Death as outcomes. As a consistency check, they incorporated another set of WTP/WTA and MSG questions with another injury j less severe than i. The MSG involved a choice between one lottery with injury i and Normal Health as potential outcomes, and a second lottery with injury i and injury j as outcomes.

From questions 1 and 2, the authors estimated the MRS between wealth and the risk of injury i (\({m}_{i}\)). The important point here is that those questions did not involve the use of small probabilities, as was the case of the traditional CV approach. From question 3, they estimated the so-called “relative utility loss” (RUL) which was the ratio \({m}_{d}/{m}_{i}\). So VSL can be obtained as the product of \({m}_{i}\), calculated from WTP and WTA questions, and the RUL (\({m}_{d}={m}_{i}\times {m}_{d}/{m}_{i}\)). This is the “direct chaining”. From questions involving the milder injury j, they estimated \({m}_{j}\) and the RUL between i and j (\({m}_{i}/{m}_{j}\)). So \({m}_{d}\) could be estimated as \({m}_{j}\times {m}_{i}/{m}_{j}\times {m}_{d}/{m}_{i}\). This is the “indirect chaining”, and consistency would require that both methods lead to the same \({m}_{d}.\)

Their results were encouraging in various aspects. First, they did not have problems of subjects not willing to pay anything or subjects willing to pay the same for the reduction in the risk of injuries of different severity, that is, WTP and WTA responses did not suffer from insensitivity to scope. Second, responses to MSG also showed face validity since subjects were willing to accept higher risks to recover from more severe injuries. For these reasons, some researchers consider this approach to be the best method available to estimate VSL (Nellthorp et al. 2001; Spackman et al. 2011) and it has been used to estimate the official VSL for the UK (DETR 1998; Jones-Lee and Spackman 2013).

However, the method is not without its problems. The main limitation of the CV/SG approach is that the direct and indirect chaining procedures result in different VSL estimates. The indirect method gives extremely large and implausible values for a small (around 10%) group of subjects, producing means that were around 15–30 times larger than those obtained with the direct method. Even excluding those subjects, VSL estimates were clearly higher using indirect chaining. Based on this, Thomas and Vaughan (2015) questioned the internal consistency of the CV/SG, raising a debate on its validity (Chilton et al. 2015; Jones-Lee and Loomes 2015; Olofsson et al. 2019; Balmford et al. 2019).

In this paper we apply the CV/SG method in a large survey (n = 2020), conducted with a random stratified sample representative of the Spanish adult population in 2009, to estimate the official VSL in Spain. The study was commissioned by the Spanish Department of Transport (Dirección General de Tráfico). Besides obtaining a VSL based on the CV/SG method, a basic objective of this paper is to provide more evidence about the consistency of the method. Several consistency tests were conducted by splitting our sample into several groups. In two groups (n3 = 243, n7 = 233) we followed, as closely as possible, the methods used by Carthy et al. (1999) (n = 167). We tried to replicate their results, including their problems of internal consistency. In the other groups: (a) we introduced some changes in an attempt to overcome some of their problems by applying an alternative indirect chaining procedure; and (b) we included new consistency checks, for which we use two different health states (i.e. non-fatal injuries) to elicit WTP and WTA estimates, and we also use two different ways of framing risks (n in 1000 vs. 10n in 10,000).

A range from €1.3 million to €1.7 million for the VSL in the context of road safety in Spain is obtained based on the ‘direct’ CV/SG approach. Regarding consistency checks, we conclude that the disparity between the direct and indirect methods can be reduced by using an alternative indirect chaining procedure, although differences between results from the two approaches persist, thus questioning the consistency of the CV/SG method. We also find that VSL estimates depend on the non-fatal injury used in the direct method, in the sense that more severe health states yield lower VSL estimates. Likewise, we observe that risk framing affects VSL estimates, which could be explained, at least in part, by the so-called ‘ratio-bias’ effect.

In the following section we explain the CV/SG method and describe what we consider to be its main problems according to the literature. In Sect. 3, we detail how we tried to avoid these problems, and the new consistency checks. The empirical study is described in Sect. 4. The main results are reported in Sect. 5. The Discussion closes the paper.

2 The contingent valuation/standard gamble (CV/SG) chained approach and its limitations

As has been said, the CV/SG chained method splits the valuation of risk reductions into three steps:

  1. 1.

    The MRS between wealth and the risk of a non-fatal injury i (denoted by \({m}_{i}\)) is inferred from WTP and WTA estimates by assuming a specific functional form of the utility function.

  2. 2.

    A modified standard gamble (MSG) question is used to estimate what Carthy et al. (1999) call the ‘Relative Utility Loss’ (RUL) or \({m}_{d}]\left/{m}_{i}\right.\), where \({m}_{d}\) is the MRS between wealth and the risk of death. This MSG is a lottery equivalent (McCord & de Neufville 1986) question, which is called ‘modified’ because, contrary to the traditional standard gamble (SG) method, it does not involve comparing between one lottery and one certain option, but between two non-degenerated lotteries. The SG has been shown to be influenced by the ‘certainty effect’ (Kahneman et al. 1979). For example, Jones-Lee et al. (1995) observed this effect, since a large percentage of subjects (more than 50% in some injuries) were not willing to accept any risk of death using the traditional SG. The MSG is intended to avoid this effect (Abellán Perpiñán et al. 2012). More specifically, Carthy et al. (1999) asked subjects to establish indifference between two binary lotteries X and Y. Assume that X = \((q, Death;\, Injury\, i)\) and Y = \(\left(p, Death;\, Normal\, health\right)\), where q and p are the probabilities of death in X and Y respectively. Assume that q is fixed at a predetermined value (1 in 1000 in Carthy et al.). Subjects have to state the value of p that leaves them indifferent between X and Y. The important contribution of Carthy et al. (1999) was to show that if subjects are Expected Utility maximizers,

    $$\frac{{m_{d} }}{{m_{i} }} = \frac{1 - q}{{p - q}}$$
    (1)
  3. 3.

    Finally, since we know \({m}_{i}\) from WTP/WTA questions and \(\frac{1-q}{p-q}\) from MSG, the theoretical result in (1) makes it possible to infer \({m}_{d}\):

    $$m_{d} = \frac{{1 - q_{i} }}{{p_{i} - q_{i} }} \times m_{i}$$
    (2)

Note that the relevant advantage of this method is that we can estimate \({m}_{d}\) without asking subjects WTP questions about very small risk reductions (e.g., 0.00001). This is, we believe, a huge advantage of the CV/SG method.

The main internal problem that was observed in the study by Carthy et al. (1999) was the large discrepancy between VSL values obtained through what they called the ‘direct’ and the ‘indirect’ chaining procedures. Direct chaining is the procedure explained above. The indirect chaining method adds another step, namely, it estimates two RULs, one between two non-fatal road injuries (i and j) and one between i and death. The authors also estimate two MRS between wealth and the risk of the two (i and j) non-fatal injuries. They implemented the indirect method as follows:

  1. 1.

    They chose a health state (j) that was milder than the health state they used for the direct format and estimated \({m}_{j}\) by combining WTP and WTA responses. As j is milder than i, we would expect \({m}_{j}<{m}_{i}\). This is a first consistency check.

  2. 2.

    They asked a second MSG question, where injury i becomes the worst outcome in both lotteries: (\({\theta }_{j}, Injury\, i;\, Injury\, j)\) vs (\({\Pi }_{j}, Injury\, i;\, Normal\, health\)). From this, we have that

    $$m_{i} = \frac{{1 - \theta_{j} }}{{{\Pi }_{j} - \theta_{j} }} \times m_{j}$$
    (3)
  3. 3.

    Consistency requires that

    $$m_{d}^{ind} = \frac{{1 - q_{i} }}{{p_{i} - q_{i} }} \times \frac{{1 - \theta_{j} }}{{{\Pi }_{j} - \theta_{j} }} \times m_{j}$$
    (4)

where \({m}_{d}^{ind}\) is the MRS between wealth and the risk of death calculated using the indirect chaining approach. The theory predicts that \({m}_{d}\)=\({m}_{d}^{ind}\), but they found that \({m}_{d}^{ind}>{m}_{d}\) by a large margin. They explained this difference in terms of “compounding of errors” in the indirect chaining.

The second problem that Carthy et al. (1999) observed was that about 10% of subjects did not want to accept any risk to cure injury i. It seems that MSG could not totally avoid the certainty effect, although it was significantly reduced in relation to Jones-Lee et al. (1995) where they used SG. These were excluded from the analysis along with two outliers who gave extremely large values for VSL. In the case of indirect chaining, they had to exclude about 20% of subjects. These new exclusions were mainly justified in terms of the implausibly large values of VSL that the indirect method yielded. This is worrying since the survey was administered by members of the research team, who were able to explain it carefully and to answer queries.

3 Objectives and hypotheses

We explain here the objectives of our study and the hypotheses to be tested.

The first objective is simply to replicate the original study, which will allow us to derive a VSL for Spain that may be recommended for use in the evaluation of road safety policies. This may have some interest in itself, since one of the main problems in studies using experimental and survey data is that sometimes results are not replicated (Anderson and Kichkha 2017; Berry et al. 2017; Maniadis et al. 2017; Mueller-Langer et al. 2019). In our case, the surveys were conducted by professional interviewers and not by members of the research team. Interviews were face-to-face using computers and physical visual aids. We hypothesized that we would reproduce the main results of (Carthy et al. 1999):

  • MSG and \({m}_{i}\) would show scope effects.

  • The indirect chaining method would produce larger VSL than the direct method.

These hypotheses will be tested between-subjects and not within-subjects because our survey did not include only the CV/SG questions. We also included questions on the standard method and asked subjects their WTP to reduce marginally the risk of death in a road traffic accident. Due to the larger number of questions, we only asked each subject one WTP and one WTA question.

The second objective was to try to overcome one of the limitations observed in Carthy et al. (1999), namely, the disparity between direct and indirect methods. We explain how we tried to do this. Carthy et al. (1999) found that \({m}_{d}^{ind}>{m}_{d}\), which implies:

$$\frac{{m_{i} }}{{m_{j} }} < \frac{{1 - \theta_{j} }}{{{\Pi }_{j} - \theta_{j} }}$$
(5)

There are two possible reasons for this result: (a) a lack of sensitivity in the CV part of the CV/SG method (\(\frac{{m}_{i}}{{m}_{j}}\) is too low); (b) RUL between i and j derived from MSG response is too large.

Carthy et al. (1999) do not provide a very detailed analysis of the reasons behind this disparity. Our hypothesis is that the large VSL estimates resulting from double chaining were related to RULs (i.e., with MSG answers) rather than to the CV component. This was based on their result that 10% of their sample did not want to accept any risk and that the median risk in the lottery where death was the worst outcome was very small (about 1%). Since RUL is a ratio, if the denominators (\({p}_{i}-{q}_{i})\) or (\({\Pi }_{j}-{\theta }_{j}\)) are very small, the product \(\frac{1-{q}_{i}}{{p}_{i}-{q}_{i}} \times \frac{1-{\theta }_{j}}{{\Pi }_{j}-{\theta }_{j}}\) can be extremely large. For this reason, one of our groups was designed to: (a) minimize the disparity between direct and indirect methods, (b) isolate the effect of MSG in the comparison between direct and indirect chaining if the disparity persisted.

Our indirect chaining method works as follows:

  1. a.

    We first ask subjects to establish indifference between lotteries \(({p}_{k}, Death;\, Normal\, health)\) and \(({q}_{k}, Death;\, Injury\, k)\). From this we get

    $$m_{d} = \frac{{1 - q_{k} }}{{{\text{p}}_{k} - q_{k} }} \times m_{k}$$
    (6)

    where k is a health state worse than the health state we used in direct chaining (\(k\prec i\)).

  2. b.

    We ask subjects to establish indifference between lotteries \(({\Phi }_{i}, Injury\, k;\, Injury\, i)\) and \(({\Pi }_{i}, Injury\, k;\, Normal\, health)\). From this we get

    $$m_{k} = \frac{{1 - {\Phi }_{i} }}{{{\Pi }_{i} - {\Phi }_{i} }} \times m_{i}$$
    (7)

and from (6) and (7)

$$m_{d}^{ind} = \frac{{1 - q_{k} }}{{{\text{p}}_{k} - q_{k} }} \times m_{k} = \frac{{1 - q_{k} }}{{{\text{p}}_{k} - q_{k} }} \times \frac{{1 - {\Phi }_{i} }}{{{\Pi }_{i} - {\Phi }_{i} }} \times m_{i}$$
(8)

There are two features of our indirect chaining method that are important for this paper. One is that, unlike Carthy et al. (1999), the health state (k) used in indirect chaining is more severe than the health state i used in direct chaining. We hypothesized that we would have fewer subjects accepting very small risks of death or no risks at all using a more severe health state. This might reduce the number of subjects producing a very small denominator in (6). Smaller RULs would make \({m}_{d}^{ind}\) and \({m}_{d}\) more similar. The second feature is that, if we compare (2) and (8), we can see that any potential discrepancy between \({m}_{d}^{ind}\) and \({m}_{d}\) can only be due to the MSG part of the CV/SG method. In summary, our hypothesis is that the use of this alternative double chaining will reduce the discrepancy between the direct and indirect approaches.

The third objective of our study was to conduct two additional consistency tests. One was the internal consistency of the direct method and the second was the susceptibility of the method to framing effects.

  1. 1.

    Consistency of the direct method. The question we address in our study is to what extent the VSL remains constant when we use the direct method with two different health states. The null hypothesis is that there are no differences between the two VSL calculated with the direct method.

  2. 2.

    Framing effects. Carthy et al. (1999) used a value of q = 0.001 in the status quo lottery, which was framed as 1 in 1000. Subjects had to provide values for p larger than 0.001, framed as a risk of “n in 1000”. In our case, we also use q = 0.001 but, in some groups, we frame it as “10n in 10,000” and subjects have to provide values of p framed as “n in 10,000”. The main reason that led us to study this framing effects is that we have some experience with the phenomenon known as ‘ratio bias’ (Pinto-Prades et al. 2006). According to this bias, when probabilities are presented as a ratio, respondents tend to focus more on the numerator than on the denominator of the ratio. If subjects are influenced by this framing effect, they tend to regard a good outcome with probability specified as 10n in 10,000 as preferable to the same good outcome with probability specified as n in 1000 and regard a bad outcome with probability specified as 10n in 10,000 as worse than the same bad outcome with probability specified as n in 1000. As a result, the risk of treatment failure that respondents will be willing to accept in a standard gamble will tend to be smaller if risks are framed as 10n in 10,000 rather than n in 1000, which will result in increasing RULs and VSLs. We wanted to see to what extent this effect could influence the VSL calculated using the CV/SG method. The null hypothesis is that there will be no framing effects.

4 The valuation study

4.1 Participants

A random multi-phase sampling stratified by autonomous communities (Spanish regions), population size, age groups and gender was carried out, with the aim of obtaining a sample that was representative of the Spanish adult population. The participants (n = 2020) were randomly assigned to one of eight subsamples. The survey was administered face to face through computer assisted personal interviews (CAPI) by GFK Emer, S.A. in 2009. Average time per interview was about 40 min.

4.2 The questionnaire

The questionnaire consisted of 42 questions grouped in five sections. Sections 1 and 5 were identical for all the subsamples, while Sects. 2, 3 and 4 were different. The structure of the questionnaire for each of the groups is summarized in Table 1.

Table 1 Structure of the questionnaire and experimental design
Full size table

Although the sample is split into eight groups, we will combine groups 1 and 2 (group 1&2 from now on) and groups 4 and 5 (group 4&5 from now on) since they share the same tasks in Sect. 3, which is the section devoted to the CV/SG chained method. They are different in some of the tasks conducted in Sect. 2 and will be analyzed elsewhere.

Section 1 informs subjects about the risk of road accidents in Spain using a risk ladder in logarithmic scale (Corso et al. 2001). We also collected data about car use, attitudes toward road safety and subjective risk perceptions.

In Sect. 2, the survey showed four cards (Fig. 1) describing four hypothetical road accident injuries or ‘health states’, anonymously labeled as X, W, R and V, at random, to the respondents. The health states were almost literal translations of the cards used by Carthy et al. (1999) and Jones-Lee et al. (1995). Next, participants had to score the states on a 0–100 Visual Analogue Scale (VAS): first they rank the health states according to their preferences and then place them on the scale such that the intervals between states reflect the differences in preference (Drummond et al. 2015). This was followed by WTP questions for small risk reductions for fatal and non-fatal road injuries (depicted by states X or V, depending on the group). These questions aimed to estimate the VSL through the “standard” CV method.

Fig. 1
figure 1

Description of the Health States (non-fatal injuries) used throughout the questionnaire

Full size image

Sections 3 and 4 asked the questions related to the CV/SG chained approach. In Sect. 3 we asked the maximum WTP to avoid non-fatal road injury (X, V or W, see Table 1) under certainty. Participants were also asked for their minimum monetary compensation (WTA) that would produce a utility gain equivalent to the utility loss of the same non-fatal road injury as before under certainty. A set of payment cards was used to ask WTP and WTA questions. Each card represented a number of euro from the following quantities: 10, 30, 50, 100, 150, 300, 600, 1000, 3000, 6000, 10,000, 30,000, 100,000 and 300,000. The two questions (WTP and WTA) were displayed in a random order. The framing of WTP questions, was as follows: A payment card showing a certain amount of money randomly appeared in the top left corner of the screen, and respondents had to place the card into one of the following categories: (a) “I would pay this amount for sure”; (b) “I would not pay this amount for sure”; and (c) “I am not sure whether I would pay or not”. This method produced an interval defined by the highest amount that they would pay for sure and the lowest amount that they would not pay for sure. An open-ended question asked about the amount they would pay within the range. This open response is the WTP that we use in the analysis. A similar procedure was used to derive WTA values.

The values obtained from WTP and WTA questions were used to infer the MRS between wealth and the risk of non-fatal road accident i (\({m}_{i}\)) on the assumption of a homogeneous underlying utility of wealth function (see Sect. 5.2.2. for a discussion on the choice of the utility function). We obtained three \({m}_{i}\) for three different health states: X (groups 1&2, 3 and 8), V (groups 4&5 and 6) and W (group 7). Estimates of \({m}_{X}\) from groups 1&2 and 3, and \({m}_{V}\) from groups 4&5 and 6, were used to obtain VSL estimates with the direct CV/SG chained approach. Estimates for \({m}_{X}\) and \({m}_{W}\) from groups 7 and 8, respectively, were used to derive VSL estimates with the indirect chained procedure.

Section 4 includes the modified standard gamble (MSG) questions. Respondents were asked to imagine that they had suffered a road accident that would have fatal consequences if they were not treated. In this situation, two treatments were available. Both might be successful, with a certain probability, or they might fail. Outcomes and probabilities in case of success and failure of the were as follows:

  1. (a)

    Groups 1&2 and 3—Subjects had to choose between treatment A and B. If treatment A was successful, it would result in non-fatal health outcome X with probability 0.999. It could fail with probability of 0.001 and this would result in the death of the subject. Treatment B, if successful, would lead a complete recovery in 3–4 days with probability (1 − \({q}_{X}\)) but it could also fail, and this would result in the death of the subject with probability \({q}_{X}\). The elicitation procedure asked the subject about the risk of death in Treatment B (\({p}_{X}\)> 0.001) that would make them indifferent between the two treatments.

    A choice-based matching (CBM) procedure (Pinto et al. 2018) was used to find this probability. This procedure estimates \({p}_{X}\) using a convergent sequence of choices between Treatments A and B using the ‘bisection’ method at first, followed by a ‘ping-pong’ procedure until an interval containing \({p}_{X}\) is produced. Afterwards, respondents were asked to establish the exact value of \({p}_{X}\) within the interval in an open question. The same CBM procedure was used in the remaining groups of the sample.

    In group 1&2, probabilities (\({p}_{i}\), \({q}_{i}\)) were framed as “10n in 10,000”, while in group 3 they were framed as “n in 1000”. VSL was estimated according to Eq. (1) as follows:

    $$m_{d} = \frac{{1~ - ~0.001}}{{p_{X} ~ - ~0.001}}~ \times m_{X}$$
    (10)
  2. (b)

    Groups 4&5 and 6—Everything was the same (risk framing of “10n in 10,000” for group 4&5 and of “n in 1000” for group 6) as in group 1&2 except that the non-fatal health state was V instead of X. The VSL was estimated according to Eq. (1) as follows:

    $$m_{d} = \frac{1 - 0.001}{{p_{V} - 0.001}} \times m_{V}$$
    (10)
  3. (c)

    In group 7 we reproduced the double chaining procedure used by Carthy et al. (1999). The first MSG question was exactly the same as in group 3, namely, to estimate \({p}_{X}\) such that subjects were indifferent between treatment A (with \({q}_{X}\)=0.001) and treatment B (\({p}_{X}\)> 0.001). Probabilities were framed as “n in 1000”. One additional MSG question was asked between treatments C and D. Treatment C, if successful, led to a non-fatal outcome W but failure led to condition X, which the vast majority of subjects evaluated as more severe than W (96,5% in the ranking task, 94% in VAS scoring and 100% in WTP questions). Treatment D, if successful led to a rapid recovery, but failure led to X. The probability of failure for Treatment C (\({\theta }_{W}\)) was set at 1 in 100 and subjects had to provide the probability of failure for treatment D \(({\Pi }_{W}\)) that made them indifferent between C and D. Given that in Group 7 we also obtained \({m}_{W}\), we estimated VSL using Eq. (3) as follows:

    $${m}_{d}^{ind}=\frac{1 - 0.001}{{p}_{X} - 0.001}\times \frac{1-0.01}{{\Pi }_{W}-0.01}\times {m}_{W}$$
    (11)
  4. (d)

    In group 8 we used a different double chaining. The first MSG question was between treatments A and B. If treatment A was successful, it would result in non-fatal health outcome R with probability 0.999. It could fail with probability of 0.001 and this would result in the death of the subject. Treatment B could result in death with probability \({p}_{R}\) and a quick recovery with probability (1 − \({p}_{R}\)). The value of \({p}_{R}\) was changed until indifference was reached between treatment A and treatment B. Probabilities were framed as “n in 1000”. The second MSG question was between treatments C and D. Treatment C was a lottery that resulted in injury R with probability 1 in 100 and in a milder injury X with probability 0.99. Treatment D led to Death with probability \({\Pi }_{X}\) or to a quick and full recovery with probability (1-\({\Pi }_{X}\)). Probabilities were framed as “n in 100”. Since respondents in group 8 were also asked about their WTP and WTP for injury X, we estimated VSL using Eq. (7) as follows:

    $${m}_{d}^{ind}=\frac{1-0.001}{{p}_{R}-0.001}\times \frac{1-0.01}{{\Pi }_{X}-0.01}\times {m}_{X}$$
    (12)

The final part of the questionnaire (Sect. 5) collects socio-demographic information: age, sex, educational attainment, income level, employment status, etc.

4.3 Objectives and hypothesis testing

Hypotheses were tested between-subjects. This is different from Carthy et al. (1999), since they observed the disparity between the direct and the indirect methods within the same sample. We could not include more questions in the survey to make the comparison within subjects since ours also included questions of the standard CV method, namely, asking subjects their WTP to reduce marginally the risk of death in a road traffic accident. Due to the larger number of questions, we only asked each subject one WTP and one WTA question using the CV/SG approach. With the results of the above survey, we test our hypotheses as follows. All between-subject comparisons are performed by using parametric (ANOVA and t-test) and non-parametric tests (Kruskal Wallis and Wilcoxon–Mann–Whitney—WMW-tests) over individual data:

  1. 1.

    Objective 1: replicating (Carthy et al. 1999).

    1. a.

      Sensitivity to scope using MSG. This will be tested by comparing \({p}_{R}\), \({p}_{X}\) and \({p}_{V}\). We should find that \({p}_{R}\) (group 8) > \({p}_{V}\) (group 6) > \({p}_{X}\) (group 3).

    2. b.

      Sensitivity to scope in CV. This will be tested by comparing \({WTP}_{X}\) (groups 1–3 and 8), \({WTP}_{V}\) (groups 4–6) and \({WTP}_{W}\) (group 7), as well as \({WTA}_{X}\), \({WTA}_{V}\) and \({WTA}_{W}\) (same group distribution).

    3. c.

      Discrepancy between direct and indirect chaining. This will be tested by comparing VSL of groups 3 and 7. We expect VSL in indirect chaining to be larger (group 7) than VSL using direct chaining (group 3).

  2. 2.

    Objective 2: reconciling the direct and indirect method.

    We will test if our new indirect chaining method avoids the discrepancy between direct and indirect chaining by comparing the RUL and VSL of groups 3 and 8.

  3. 3.

    Objective 3: testing the consistency of the direct method.

    We will compare VSL estimates obtained by using direct chaining through X (groups 1&2 and 3) or V (groups 4&5 and 6).

  4. 4.

    Objective 4: testing the influence of framing effects

To test whether RUL depends on risk framing, we will compare \({\mathrm{p}}_{X}\) framed as “10n in 10,000” (group 1&2) to \({\mathrm{p}}_{X}\) framed as “n in 1000” (groups 3). We will also compare \({p}_{V}\) framed as “10n in 10,000” (groups 4&5) to \({p}_{V}\) framed as “n in 1000” (group 6).

5 Results

5.1 Sample characteristics and homogeneity of subsamples

Socio-demographic and attitudinal characteristics of our sample can be seen in Table 2, which also shows the distribution of adult population with respect to age and gender, according to the Spanish census, and with respect to education, marital status and employment status, according to the labour force survey (LFS). In general, our sample resembles the characteristics of the general population. More information was collected about other characteristics and can be seen in Table 2.

Table 2 Percentage distribution of sample characteristics (n = 2020)
Full size table

Since most of the subsequent analysis will be performed on a between-subject basis, homogeneity of subsamples must be assessed. According to parametric (ANOVA) and non-parametric (Kruskal Wallis) tests, we could only reject the null hypothesis for the variable age, with individuals in groups 4 and 8 being slightly older than the other groups. There are no differences in the rest of the characteristics among groups. Homogeneity in health preferences has been tested using VAS scores. Both ANOVA and Kruskal Wallis tests (p > 0.05) suggest that no statistically significant differences exist between groups regarding valuations of health states through VAS scoring, which are presented in Table 3.

Table 3 Visual Analogue Scale scores for non-fatal injuries and death, by group and on aggregate
Full size table

5.2 Results of contingent valuation (CV) questions

5.2.1 WTP and WTA estimates

Table 4 shows WTP and WTA statistics based on usable data. There are no valid WTP responses for 23 (1.1%) subjects who were willing to pay any amount of money, no matter its magnitude, to avoid the health state (\(WTP\to \infty\)). Likewise, in 22 (1.1%) cases, respondents stated that no amount of money could compensate them for suffering the injury (\(WTA\to \infty\)). Those 55 subjects were excluded from the analysis. On the other hand, 96 respondents refused to pay any amount of money for any treatment (WTP = 0). Those subjects were not excluded from the analysis.

Table 4 Willingness to pay and willingness to accept in euro to avoid/suffer a health state, and marginal rates of substitution between wealth and health (mi)
Full size table

We can see that WTP and WTA values are sensitive to scope. Non-parametric tests (Wilcoxon–Mann–Whitney test) confirm that there are statistically significant (p < 0.05) differences in WTP and WTA values between the three health states (i.e. groups 1&2, 3 and 8 for state X; groups 4&5 and 6 for state V; and group 7 for state W). The results are also confirmed by the t-test, except for the comparison between X and W (p = 0.17 for WTP and p = 0.74 for WTA). The direction of the effect is consistent with the severity of injuries observed in the VAS scores.

In addition, theoretical validity of WTP estimates have been tested by regression analysis (see Appendix in the Electronic Supplementary Material). The results show a positive and significant relationship between individuals’ income and their WTP. The analysis also confirms the sensitivity to scope since a positive relationship between the size of the health gain and the WTP is observed.

5.2.2 Marginal rates of substitution (MRS)

Individual MRS (\({m}_{i}\)) are inferred from WTP and WTA values by applying a homogeneous utility function, one of the four functional forms used by Carthy et al. (1999). Results do not essentially change when other functional forms (i.e., negative exponential, logarithmic and nth root) are assumed. We show the results in detail for only one functional form, for the sake of simplicity, and we choose the homogeneous one because it minimizes the number of observations that we have to discard due to missing values. The MRS based on all the utility functions (and, hence, the corresponding VSL estimates) will be considered later when a recommended VSL for the evaluation of road safety policies in Spain is proposed in Sect. 5.5. Basic statistics for MRS are shown in the bottom part of Table 4. All the binary comparisons between MRS for states X, V and W are significant (p < 0.05, t-test and WMW) and correspond to the ranking of severity of those injuries.

5.3 Results of the MSG part of the CV/SG chained approach

5.3.1 Risk of death accepted to avoid a non-fatal injury

Indifference probabilities elicited in the different groups, as well as the RULs constructed from them are shown in Table 5. The main results are:

  1. 1.

    MSG responses are sensitive to scope. Mean and median values of the risk of death that participants were willing to take to avoid a non-fatal injury (i.e., probabilities \({p}_{i}\), i = X, V, R) change according to the severity of the condition (\({p}_{R}>{p}_{V}>{p}_{X}\)) at 0.05 level (t-test and WMW).

  2. 2.

    The way that probabilities were framed (“n in 1000” vs “10n in 10,000”) had an effect on the risk assumed (\({p}_{i}\)). There are significant differences (p < 0.05, WMW) both for injury X (i.e., group 1&2 vs. groups 3 and 7) and for injury V (i.e., group 4&5 vs. group 6). This conclusion holds when t-test comparisons are performed, but only for state V. Effects are in line with predictions of the ratio bias effect, namely, individuals accept less risk when probabilities are framed as 10 in 10,000 than when they are framed as 1 in 1000.

  3. 3.

    There is a good number of people whose indifference point coincides with the minimum risk they saw on the screen (see row “Take minimum risk” in Table 5). Note that in groups 3 and 6 the minimum risk that participants may state is 2 in 1000 (the lowest value above q = 0.001 when this risk is framed as 1 in 1000). In contrast, in groups 1&2 and 4&5, the minimum level is 11 in 10,000 (remember that in the lottery used as stimulus the risk of death was framed as 10 in 10,000). The percentage of subjects who take the minimum risk is about the same (20%) in groups 1&2 and 4&5 as in groups 3 and 6.

  4. 4.

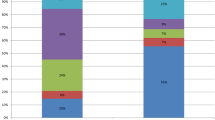
    We show in row “Take ≤ 0.002” the percentage of subjects not willing to take a risk larger than 0.002. Note that in groups 1&2 and 4&5 this percentage is much larger than in groups 3 and 6. We add this information because it confirms the influence of the ratio bias. The reason is that, in practice, the minimum risk subjects could take in groups 3 and 6 was 2 in 1000. This corresponds to 20 in 10,000 in groups 1&2 and 4&5. The change in framing largely increases the percentage of subjects who do not want to accept a risk above 2 in 1000 when it is framed as 20 in 10,000.

Table 5 Modified standard gamble results: probabilities (\({{{p}}}_{{{i}}}\),\({{{\Pi}}}_{{{j}}}\)) and relative utility losses (RULs)
Full size table

5.4 Relative utility losses (RULs)

The main results regarding RULs are:

  1. 1.

    Groups where risk was framed as “10n in 10,000” (groups 1&2 and 4&5) produced much bigger RULs than groups 3 and 6. All differences are statistically significant (p < 0.001; t-test and Wilcoxon–Mann–Whitney test). These results are expected since RULs are a sort of monotonic transformation of the probabilities presented above.

  2. 2.

    Means and medians are very different within each group, especially in groups where risks were framed as “10n in 10,000”. This reflects the fact that some subjects accepted very small increases in the risk of death, producing very large values of RULs.

  3. 3.

    In order to better understand the differences between groups 1&2 and 4&5, on the one hand, and groups 3 and 6, on the other, the RULs of groups 1&2 and 4&5 are capped at 999 (see row “max RUL 999”, Table 5), which is the maximum RUL that a subject could produce in groups 3 and 6 since it corresponds to a risk of 2 in 1000. We can see that, even with capping, the mean RULs in groups 1&2 and 4&5 are still larger than in groups 3 and 6 (p < 0.005).

  4. 4.

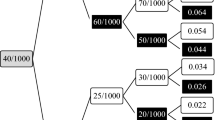
    There is a very large difference between means and medians within groups 7 and 8. This shows the effect of the multiplication of two ratios on these ‘compound’ RULs when some people are willing to take only very small risks in the two MSG: the means are huge. For this reason, we can expect that the mean VSL in these two groups will be much larger than in groups with direct chaining. Take into account that the RUL can reach a value of 99,999 if a subject takes the minimum risk in the two questions. In group 7 there are 22 subjects (9.4%) who take the minimum risk in the two lotteries while in group 8 there are only nine individuals (3.9%). It is not surprising that group 7 is more affected than group 8 by this sort of behavior, since state X is milder than R. The influence of those subjects on the mean is very large.

  5. 5.

    RULs of groups 3 and 8 are different. However, the mean and the median go in the opposite direction. The mean RUL of group 8 is much larger than the mean of group 3, but the median is smaller. Statistical tests are inconclusive. The t-test rejects the hypothesis of equal means (p < 0.05), but the non-parametric test (WMW) cannot reject the null hypothesis (p = 0.188). The reason for this disparity is seen in Fig. 2. The double chaining of group 8 generates very large values in a group of subjects. About 22% of subjects have RUL > 999 in group 8, which is the maximum RUL in group 3. Those subjects generate large RULs, producing a large mean. It is also observed that our indirect chaining produced lower RULs than the direct method in a large proportion of subjects. In spite of that, the multiplication of two ratios generates very large RULs in a (significant) minority of subjects. This result suggests that the mean values for VSL estimated using the CV/SG method will depend on the number of steps (MSG chainings) that we use.

Fig. 2
figure 2

Distribution of relative utility losses (RULs) in groups 3 and 8

Full size image

5.5 Value of statistical life (VSL) estimations based on the SG/CV chained approach

The VSL for groups 1–6 is obtained by combining individuals’ MRS (\({m}_{X}\) or \({m}_{V}\)) with the ratio \({m}_{d}\left/ {m}_{i}\right.\) derived from MSG responses. The VSL estimates for groups 7 and 8 have been calculated by combining \({m}_{W}\) and \({m}_{X}\), respectively, with the corresponding ‘compound’ RUL, at the individual level. The existence of some extreme values led us to discard what we defined as outliers. Carthy et al. (1999) trimmed out values above an ad-hoc threshold of £15 million. We excluded individuals whose VSL values were larger than three standard deviations of the mean. As a result of this trimming procedure, 15 values were discarded, which represents less than 1% of the sample. Table 6 shows trimmed VSL estimates. The main results are:

  1. 1.

    VSL estimated through X (groups 1&2 and 3) is larger than VSL estimated through V (groups 4&5 and 6). The t-test rejects the null hypothesis at the 10% level (p = 0.07). The nonparametric test (WMW) clearly rejects the null hypothesis (p < 0.001), so challenging the consistency of the direct version of the CV/SG method. The results do not change when comparisons are restricted to groups with the same framing (i.e., 1&2 vs. 4&5 and 3 vs. 6).

  2. 2.

    VSL estimated using the indirect chaining method used by (Carthy et al. 1999) (group 7) is much larger than VSL obtained with the direct approach (group 3) (p < 0.05; t-test and Wilcoxon–Mann–Whitney test).

  3. 3.

    In group 8 the results for VSL are similar to those obtained regarding RULs, namely, the t-test rejects the hypothesis of equality of means (p < 0.05), but the non-parametric test (WMW) cannot reject the null hypothesis (p = 0.53). This result implies that using a more severe health state (R) to perform the double chaining does not fully prevent the discrepancy between the indirect and the direct CV/SG estimates of the VSL. However, the discrepancy between the mean VSL estimates obtained in groups 8 and 3 is almost 73% lower than between groups 7 (the indirect chaining used by (Carthy et al. 1999)) and 3 (direct chaining).

Table 6 Value of statistical life (VSL) estimates in euro based on the CV/SG chained “direct” and “indirect” approachesa by groups
Full size table

To obtain the recommended VSL to be used in the economic evaluation of road safety programmes in Spain we consider the results of groups 1–6 jointly, that is, only the VSL estimates obtained on the basis of direct chaining are used for that purpose. Carthy et al. (1999) concluded that the direct approach is less vulnerable to compounding of errors due to its fewer steps, compared to the indirect chaining. Our results confirm this conclusion, since more extreme values are obtained when the indirect or double chaining approach is applied. There being no normative criterion for choosing a specific functional form, we decided to obtain the summary value as the average of the four estimates. Table 7 shows VSL estimates for groups 1–6 considered altogether, based on each of the utility functions. The figures in the table have been obtained after capping RULs from groups 1&2 and 4&5, as explained in Sect. 5.4, and then trimmed by discarding VSL values larger than three standard deviations of the mean.

Table 7 Value of Statistical Life (VSL) estimates in euro based on the CV/SG chained “direct” approacha using alternative wealth utility functions for deriving MRS
Full size table

According to welfare economics, it is the mean values which should be regarded as representative of aggregate preferences. The simple average of mean estimates in Table 7 gives a VSL of 1.7 million euro. Notwithstanding, as Carthy et al. (1999) suggested, at least some weight could be given to the estimates based on median values. Hence, given the large dispersion of the estimates and the notable disparities between mean and median values, a simple arithmetic average of the minimum of the median values (the one derived from the negative exponential function) and the maximum of the mean values (that obtained when the nth root function is used) is calculated, resulting in a VSL of 1.35 million euro. On the other hand, some authors have raised concerns regarding the meaningfulness of WTA values in this context (Viscusi 2018a). Considering this, individual VSL estimates have also been obtained by using only WTP responses to derive the MRS. In that case, no assumption must be made regarding the functional form. A unique VSL estimate is derived for each subject and the mean VSL estimate is 1.6 million euro (median value 0.5 million euro). In view of these results, the recommended VLS for the evaluation of road safety programmes should be in a range from about €1.3 million to €1.7 million.

Finally, theoretical validity of the VSL estimates has been tested by regression analysis (see Appendix in the Electronic Supplementary Material), yielding figures for income elasticity from 0.64 to 0.70, depending on the utility function used to derive MRS from WTP and WTA values. These values are similar to those in a recent meta-analysis of elasticities of studies estimating VSL through stated preferences. Specifically, for middle and high-income countries, a range between 0.55 and 0.85 is reported (Viscusi and Masterman 2017). In any case, the value of the income elasticity is below 1, as is the case in most studies so far (Miller 2000; Viscusi and Aldy 2003).

6 Discussion

A first outcome of the study is the estimation of a VSL for Spain in the context of road accidents. The estimated range from €1.3 to €1.7 million is in line with VSL estimates used in other European countries to evaluate road safety programmes. A recent study including official costs per road traffic fatality in 29 European countries indicates that this range is between 0.7 and 3 million euro (adjusted for PPP and referring to the year 2015) (Wijnen et al. 2019). As it is known, stated preference VSL estimates are usually lower than those implied by revealed preference studies. Our estimate is not an exception to that rule and, in fact, is lower than the market estimates of VSL provided by (Martínez and Méndez 2009) for Spain, which range from €2.8 to €8.3 million. Likewise, our VSL estimate is also lower than estimates based on automobile purchase decisions in the U.S. (O’Brien 2018), from which an inverted-U shape to the age-VSL function that ranges from $1.5 to $19.2 million is obtained. Moreover, since Viscusi and Gentry (2015) find that the current VSL estimate of $9.2 million used by the U.S. Department of Transportation's, based on labor market studies, is appropriate for valuing transport-related fatalities, it can also be stated that our VSL estimated in the specific context of traffic fatalities is much lower than that value. Moreover, the values in the range estimated in this study are lower than those obtained in Spain through revealed preferences in the context of the labour market, which are between €2.8 and €8.3 million (Martinez and Mendez 2009). They are also clearly below the value recently suggested to assess the cost of the current COVID pandemic based on the estimated VSL for the US, using an income elasticity of 1, which is $6.6 million (Viscusi 2020).

Besides this outcome, the main objectives of our study were to understand better the problems observed in Carthy et al. (1999), to overcome some of those problems, and to conduct new consistency checks. Regarding our objectives and hypotheses, we find that:

  1. 1.

    We have reproduced the main results of Carthy et al. (1999). Our survey confirms that CV shows sensitivity to scope. WTP/WTA are larger for more severe conditions. The same happens with MSG, namely, subjects accept higher risks of treatment failure (resulting in death) to avoid more severe injuries.

  2. 2.

    We observe consistency in the relative values of health states using CV and MSG at the aggregate level. Mean WTP (WTA) values for state V (groups 4&5 and 6) are between 2.1 (1.97) and 2.3 (2.1) times the mean values for state X (groups 1&2, and 3). When we assess the relative value V/X implicit in the responses to MSG questions, the results are remarkably similar: ratio of means of RULs for V and X are between 1.8 and 2.8. In summary, the CV/SG method performs much better in terms of scope sensitivity than the standard method of asking WTP questions for very small risk reductions.

  3. 3.

    Regarding objective 2, the attempt to reconcile the direct and the indirect methods, we have managed to reduce the disparity between them. The differences between the means of the direct and indirect methods were smaller using our method (group 8). Statistical tests are not so conclusive about the difference between the direct and indirect approaches. However, we also observe more extreme values in our indirect chaining method than in the direct method, leading to very large means. It seems that the more steps we use in MSG, the more extreme values we will observe. The implication is that the more intermediate steps (chained MSG lotteries) we use to estimate RUL, the larger the mean values of VSL we will find. The problem seems to lie in the skewness of MSG. There is a significant number of subjects who only accept very small increases in risk. This generates very large values of RULs. When these values are combined with the MRS, they may result in very large VSLs. The distribution of MRS is also highly skewed. The combination, at the individual level, of extreme values for \({m}_{i}\) and RUL, generates extremely large values of VSL in a minority of subjects. It looks as if some arbitrary “trimming” will always be necessary.

  4. 4.

    Regarding objective 3, to test the consistency of the direct method when different non-fatal injuries are used, we found that VSL estimates depend on the health state (i.e., injury) used. It looks as if more severe health states produce lower VSLs. This result was also observed by Olofsson et al. (2019). However, their study does not follow as closely as ours does the methods used by Carthy et al. (1999). Also, their VSL figures were based on mean estimates whereas our results are based on individual chaining.

  5. 5.

    Regarding objective 4, the influence of framing effects, we observe an important influence of risk framing in the RUL and, by extension, in the VSL estimates. This impact is particularly strong for the subsamples who value state V. The mean RUL of group 4&5 is about 12 times higher than the corresponding value in group 6. This discrepancy is also large between medians (five times greater) and it cannot be attributed to the influence of a few outliers. One explanation for this finding is the ratio bias effect.

To conclude, responses to WTP, WTA and MSG questions, which are required to apply the CV/SG chained method, are sensitive to scope. Average means and medians are consistent ordinally and cardinally. In this respect, this method is better than the standard CV survey that asks subjects their WTP to reduce very small risks. However, we have observed that the method has two problems. One is that RULs are extremely sensitive to the responses of subjects who accept small risks. For this reason, a simple manipulation such as changing the base of the probabilities generates extremely different responses. This effect is amplified when we use double chaining, since we need to compound two ratios to calculate RUL. The second problem is that the two parameters we need to calculate VSL (\({m}_{i}\) and RUL) tend to have very skewed distributions. When we work with individual data, this may produce very large VSLs. This is one of the reasons why very consistent measures of central tendency for \({m}_{i}\) and RUL can generate problematic VSL values. We conclude that the CV/SG method produces more consistent results than the standard CV method. However, it is very susceptible to changes in the way that it is operationalized.