1 Introduction

Economic theory is traditionally based on deterministic preferencesFootnote 1 leaving little room for probabilistic choice.Footnote 2 Empirical research, however, strongly backs probabilistic choice.Footnote 3 Probabilistic choice may occur for a variety of reasons such as unobserved attributes of choice alternatives (e.g. McFadden 1976), imprecision of preferences (Falmagne 1985; Butler and Loomes 2007, 2011), random errors/noise in decisions (e.g. Fechner 1860; Hey and Orme 1994). Models of probabilistic choice originated in mathematical psychology and include inter alia random utility (also known as random preference or random parameter) approach (e.g., Falmagne 1985; Loomes and Sugden 1995), the Fechner (1860) model of random errors (or strong utility)Footnote 4 and the Luce (1959) choice model (strict utility or multinomial logit).Footnote 5 These models are often used in econometric estimation on microeconomic data.

Yet, psychological models of probabilistic choice may not always suit economic data, which creates a demand for new models of probabilistic choice designed for economic applications. Random utility/preference/parameter approach can rationalize the preference reversal phenomenon in choice under risk (e.g. Loomes 2005, p.310–311) but it cannot account for rare violations of dominance that are occasionally observed in the data (e.g. Loomes and Sugden 1998, p. 585). Fechner (1860) and Luce (1959) models can rationalize some instances of the common ratio effect (e.g. Loomes 2005, p.305) or violations of the betweenness axiom (e.g., Blavatskyy 2006) in risky choice and some instances of the common difference effect (e.g., Blavatskyy 2017, Section 4, pp. 144–145) in intertemporal choice but they generate too many violations of dominance (Loomes and Sugden 1998, p. 593).Footnote 6

Luce (1959) developed a general theory of probabilistic choice from the choice axiom, which is also known as the independence from irrelevant alternatives. Luce (1959) choice model is often used for eliciting risk preferences (e.g., Camerer and Ho 1994; Wu and Gonzalez 1996; Holt and Laury 2002, Eq. (1), p. 1652) and time preferences (e.g., Andersen et al. 2008, p. 599, Eq. 9; Meier and Sprenger 2015, p. 276, Eq. 1). Luce (1959) choice axiom postulates that the ratio of the probability of choosing one alternative to the probability of choosing another alternative is not affected by the presence (or absence) of other “irrelevant” alternatives in the choice set. This axiom is simple and intuitively appealing in choice situations when there are no substitution/complementary effects among choice alternatives.

In Luce (1959) choice model every alternative is chosen with a strictly positive probability. This property may be undesirable in economic applications where clearly inferior alternatives are never chosen. Luce (1959) addressed this problem via a two-stage procedure: first, dominated alternatives are discarded from a choice set; and then a decision maker chooses in a probabilistic manner among the remaining alternatives. Yet, this two-stage procedure creates a discontinuous choice function. This paper proposes a new model of probabilistic choice in which a decision maker may never choose some alternatives (that are sufficiently undesirable compared to other available options).

This paper demonstrates that one can formulate a dual version of Luce (1959) choice axiom that is arguably as intuitively appealing as its classic sibling. The dual choice axiom proposed in this paper postulates that the ratio of the probability of not choosing (i.e. rejecting) one alternative to the probability of not choosing (rejecting) another alternative is not affected by the presence (or absence) of other “irrelevant” alternatives in the choice set. In case of a binary choice, the dual choice axiom simply mirrors Luce (1959) choice axiom. The choice of alternative A over alternative B in a direct binary choice is equivalent to B being rejected in favor of A. Yet, when the choice set contains three or more alternatives, the dual choice axiom has different implications from Luce (1959) choice axiom. This paper derives a new model of probabilistic choice from the above dual choice axiom. In this model, the likelihood that a decision maker does not choose one alternative from some choice set is proportionate to the ratio of the disutility of this alternative to the sum of disutilities of all alternatives in the choice set.

For example, consider a country that is about to leave the European Union and faces three mutually exclusive scenarios: to leave the union without any agreement (“No Deal Exit”), to leave the union with an agreement (“Deal”) and to stay in the union (“No Exit”). According to the classic choice axiom, the relative likelihood that one country leaves the union without any agreement (“No Deal Exit”) rather than stays in the union (“No Exit”) is not affected by the characteristics of any exiting agreement that the country negotiated with the union for an orderly exit (“Deal”). According to the dual choice axiom, the relative likelihood of either “No Deal Exit” or “Deal” rather than either “No Exit” or “Deal” is not affected by the characteristics of the exiting agreement. In other words, the dual choice axiom postulates that the relative chances that the country leaves the union (with or without agreement) rather than does not leave without an agreement are independent from the agreement itself. When choices are hard, a decision maker can formulate the independence from irrelevant alternatives for a probability of rejecting rather than choosing certain options.

This paper is closest to Marley and Louviere (2005) who consider a model of probabilistic choice where a decision maker selects the worst alternative from the choice set.Footnote 7 Their model is similar to Luce (1959) choice model: the higher is the disutility of a choice alternative the more it is likely to be selected as the worst alternative. Marley and Louviere (2005) effectively impose the independence from irrelevant alternatives on the relative probability of selecting the worst choice alternative whereas the dual choice axiom proposed in this paper imposes the independence from irrelevant alternatives on the relative probability of rejecting a choice alternative. In other words, we consider alternatives that are not chosen (rejected) from a choice set, which does not necessarily imply that these alternatives are the worst available alternatives (considered in Marley and Louviere (2005)). In case of a binary choice, when an alternative that is not chosen is automatically the worst available alternative, the model of probabilistic choice derived in this paper from the dual choice axiom coincides with the model of Marley and Louviere (2005) and a binary Luce (1959) choice model.

The remainder of the paper is organized as follows. Section 2 presents mathematical notation, formulates classic Luce (1959) choice axiom and a new dual choice axiom. Section 3 presents a new model of probabilistic choice derived from the dual choice axiom. Section 4 compares the new model with Luce (1959) choice model using an example of ternary choice. Section 5 concludes with a general discussion.

2 Notation, choice axiom and dual choice axiom

Let S be a choice set with n ≥ 2 choice alternatives. A choice alternative A∈S can be a consumption bundle, a risky lottery (a probability distribution), an uncertain act (a random variable), a stream of intertemporal outcomes, a behavioral strategy etc. We denote choice alternatives by capital Latin letters A, B, C etc.

A decision maker can be an individual or a group of individuals. Let P(A|S) ∈ (0,1) denote the probability that a decision maker chooses alternative A∈S from the choice set S. The probability that alternative A∈S is not chosen from the choice set S is given by 1—P(A|S). As Luce (1959), we assume that choice alternatives, which are never chosen, can be deleted from the choice set without any effect on decision making. Thus, without loss of generality, we consider only choice sets that contain alternatives that are chosen with a strictly positive probability. Finally, let P(A,B) ∈ (0,1) denote the probability that a decision maker chooses alternative A over alternative B in a direct binary choice (i.e. B is not chosen from the set {A,B}) and let P(B,A) = 1 — P(A,B) denote the probability that a decision maker chooses alternative B over alternative A in a direct binary choice (i.e. A is not chosen from set {A,B}).

We consider two axioms imposed on choice probabilities. The first axiom is Luce (1959) choice axiom (Eq. 2 below) and the second axiom is a dual choice axiom (Eq. 3 below). To distinguish between these two cases, we use subscript “Luce” to denote choice probabilities that satisfy Luce (1959) choice axiom. For example, PLuce(A,B) denotes the probability that a decision maker chooses alternative A over alternative B in a direct binary choice in Luce choice model.

A decision maker can choose only one choice alternative from the choice set so that

$$ {\sum}_{A\in S}P\left(A|S\right)=1 $$
(1)

Luce (1959) choice axiom postulates that for any A,B∈S, the relative likelihood

$$ \frac{P_{Luce}\left(A|S\right)}{P_{Luce}\left(B|S\right)}=\frac{P_{Luce}\left(A,B\right)}{P_{Luce}\left(B,A\right)} $$
(2)

depends only on the characteristics of choice alternatives A and B (and is independent from the characteristics of other “irrelevant” choice alternatives).Footnote 8 For example, the relative likelihood that an airline purchases a Boeing aircraft rather than an Airbus aircraft depends only on the characteristics of these two aircrafts and is not affected by the characteristics of other aircrafts available on the market.

In his discussion of the independence from irrelevant alternatives, Luce (1959) makes it clear that the choice axiom (2) is only one reasonable version of the independence from irrelevant alternatives in the context of probabilistic choice: “… if one is comparing two alternatives according to some algebraic criterion, say preference, this comparison should be unaffected by the addition of new alternatives or the subtraction of old ones (different from the two under consideration). Exactly what should be taken to be the probabilistic analogue of this idea is not perfectly clear, but one reasonable possibility is the requirement that the ratio of the probability of choosing one alternative to the probability of choosing the other should not depend upon the total set of alternatives available”. In other words, Luce (1959) acknowledged that condition (2) is a choice axiom, not the choice axiom that it became over the last 60 years. This paper formulates a different probabilistic version of the independence from irrelevant alternatives. It is particularly appealing when decision makers face difficult choices so that it may be intuitive to reason in terms of alternatives that are not chosen.

In this paper we formulate a dual choice axiom: the ratio of probability that A∈S is NOT chosen from the set S to probability that B∈S is NOT chosen from the set S depends only on the characteristics of choice alternatives A and B (and is independent from the characteristics of other “irrelevant” choice alternatives). For example, the relative likelihood that a Democratic candidate does not win an election compared to the likelihood that a Republican candidate does not win an election is not affected by the presence of other independent candidates. While the classic choice axiom establishes independence from irrelevant alternatives for the relative probability of choice, the dual choice axiom does the same for the relative probability of not choosing. Arguably, the dual choice axiom has the same intuitive appeal as the classic choice axiom.

Formally, for any two alternatives A,B∈S, our dual choice axiom can be written as

$$ \frac{1-P\left(A|S\right)}{1-P\left(B|S\right)}=\frac{P\left(B,A\right)}{P\left(A,B\right)} $$
(3)

The dual choice axiom (3) constrains binary choice probabilities in the same way as Luce (1959) choice axiom (2). Specifically, if dual choice axiom (3) holds then binary choice probabilities must satisfy the product rule (cf. Eq. (16) in the proof of proposition 1 in the Appendix). Likewise, if Luce (1959) choice axiom (2) holds then binary choice probabilities must satisfy the product rule as well. Thus, the constraints implied by dual choice axiom (3) on binary choice probabilities are the same as the constraints implied by Luce choice axiom (2). For non-binary choice probabilities, the constraints implied by (3) are similar (but not the same) as the constraints implied by Luce choice axiom (2). The main difference is that dual choice axiom (3) restricts probabilities of not choosing (which sum up to n-1, cf. Eq. (7) below) whereas Luce choice axiom (2) restricts probabilities of choosing (which sum up to one, cf. Eq. (1) above).

3 Model of probabilistic choice

First, we show that dual choice axiom (3) implies the same restriction on binary choice probabilities as the classic choice axiom (2) — a binary Luce choice model, which is also known as binary strict utility.

Proposition 1

If n ≥ 3 and dual choice axiom (3) holds then

$$ P\left(A,B\right)=\frac{U(A)}{U(A)+U(B)} $$
(4)

where U : S → ℝ+ is utility function unique up to a multiplication by a positive constant.

The proof is presented in the Appendix.

According to proposition 1, our newly proposed dual choice axiom (3) has the same implication for binary probabilistic choice as the classic choice axiom (2). This result is perhaps not surprising given that only two outcomes are possible in binary choice: either A is chosen, or A is not chosen. In other words, in the context of binary choice, dual choice axiom simply mirrors classic choice axiom. Yet, for choice among n ≥ 3 alternatives, implications of dual choice axiom (3) differ from those of classic choice axiom (2), as demonstrated by the following proposition 2.

Proposition 2

If n ≥ 3 and dual choice axiom (3) holds then

$$ P\left(A|S\right)=1-\frac{n-1}{\sum_{B\in S}\frac{U(A)}{U(B)}} $$
(5)

where U : S → ℝ+ is utility function unique up to a multiplication by a positive constant.

The proof is presented in the Appendix.

Model (5) can be alternatively presented as Eq. (6).

$$ 1-P\left(A|S\right)=\left(n-1\right)\frac{U^{-1}(A)}{\sum_{B\in S}{U}^{-1}(B)} $$
(6)

Equation (6) emphasizes the duality of the new model to classic Luce (1959) choice model. According to formula (6), the probability 1 — P(A|S) of not choosing alternative A from the set S is proportionate to the disutility of this alternative U−1(A). If the choice set contains n alternatives then probabilities of not choosing (rejecting) an alternative should sum up to n-1.

$$ {\sum}_{A\in S}\left[1-P\left(A|S\right)\right]=n-1 $$
(7)

Therefore, disutility U−1(A) in formula (6) is divided by the sum of disutilities of all alternatives and multiplied by n-1.

Model of probabilistic choice (5) has similar properties as Luce (1959) choice model. The higher is utility of alternative A, the higher is the probability that a decision maker chooses A from the choice set S and the lower is the probability that he or she chooses any other alternative B from the choice set S. From a dual perspective, the higher is utility of alternative A, the lower is the probability 1 — P(A|S) that a decision maker does not choose A from the choice set S and the higher is that the probability that he or she does not choose any other alternative B from the choice set S. If alternative A yields a higher utility than alternative B then according to model (5) a decision maker is more likely to choose alternative A rather than alternative B from any choice set containing both A and B. Model (5) satisfies the regularity condition (e.g., Marley 1965): a decision maker is more likely to choose alternative A from a subset of the choice set S than from the set S itself.

In the degenerate case n = 1 Eq. (5) becomes simply P(A|S) = 1, i.e. when the choice set contains only one alternative a decision maker always chooses this alternative. For n = 2 Eq. (5) becomes Eq. (4), i.e. when the choice set contains two choice alternatives a decision maker behaves as in a binary Luce (1959) choice model (strict utility). If all choice alternatives yield the same utility (U(A) = U(B) for all A,B∈S) then Eq. (5) becomes P(A|S) = 1/n, i.e. a decision maker chooses at random among all such alternatives.

In Luce (1959) choice model utility of an alternative is bounded to be a positive number. Yet, it is unbounded in relative terms—utility of alternative A can be much smaller than utilities of other available alternatives and a decision maker still chooses A with a strictly positive probability. This can be viewed as an undesirable feature of Luce (1959) choice model. Arguably, when one alternative is much less desirable than other available alternatives (in terms of utility) a choice decision is simple—a clearly inferior alternative is discarded.

Model of probabilistic choice (5) allows this possibility—an alternative that is much less desirable than other alternatives can be chosen with zero probability. Unlike Luce (1959) choice model, model (5) imposes “smart” relative bounds on the utility of every alternative. For an alternative to be chosen with a positive probability, its utility must be sufficiently high compared to the utilities of other available alternatives.

When utility of alternative A decreases, the probability (5) that a decision maker chooses this alternative decreases as well. Yet, so far, nothing restricts probability (5) to remain strictly positive. In other words, utility of alternative A must remain high enough so that a decision maker chooses alternative A with a strictly positive probability, i.e. the denominator of the fraction on the right-hand-side of Eq. (5) should always exceed the nominator. This imposes a lower bound (8) on the utility of alternative A.

$$ U(A)>\frac{n-2}{\sum_{\begin{array}{c}B\in S\\ {}B\ne A\end{array}}\frac{1}{U(B)}} $$
(8)

When n = 2 inequality (8) becomes simply U(A) > 0, i.e., like in Luce (1959) choice model, utility must be a positive real number. When n > 2 inequality (8) effectively restricts the utility of A not to fall below (n-2)/(n-1) of the harmonic mean of utilities of all other available alternatives.

Second, when utility of alternative A increases, the probabilities, with which a decision maker chooses other alternatives, decrease. Yet, so far, nothing restricts these probabilities to remain strictly positive. Thus, utility of alternative A must remain low enough so that a decision maker chooses other available alternatives with a strictly positive probability. It is sufficient only to check that the alternative that has the lowest utility \( \underset{C\in S}{\min }U(C) \) is chosen with a strictly positive probability (since any alternative that yields a higher utility is chosen with a higher probability). This imposes inequality (9) on utility of alternative A.

$$ \frac{1}{U(A)}>{\sum}_{\begin{array}{c}B\in S\\ {}B\ne A\end{array}}\left[\frac{1}{\underset{C\in S}{\min }U(C)}-\frac{1}{U(B)}\right] $$
(9)

When all available alternatives but A yield the same utility, which is smaller than utility of A, then the right-hand-side of inequality (9) becomes zero, i.e. inequality (9) is satisfied for any positive real valued utility function. This happens, for example, in case of a binary choice when there is only one alternative other than A and this alternative yields a smaller utility than A. If not all available alternatives other than A yield the same utility, the right-hand side of inequality (9) is strictly positive and we can rewrite inequality (9) as an upper bound (10) on utility of alternative A.

$$ U(A)<\frac{1}{\sum_{\begin{array}{c}B\in S\\ {}B\ne A\end{array}}\left[\frac{1}{\underset{C\in S}{\min }U(C)}-\frac{1}{U(B)}\right]} $$
(10)

Inequalities (8) and (10) can be combined in one condition: the least desirable alternative in the choice set must yield utility greater than (n-1)/n of the harmonic mean utility of all available choice alternatives (i.e., \( \underset{C\in S}{\min }U(C)>\left(n-1\right)/{\sum}_{B\in S}\frac{1}{U(B)} \)). In other words, in model (5) the least desirable alternative cannot be significantly inferior compared to other alternatives.

4 Example: Ternary choice

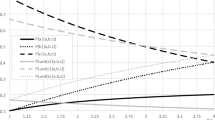
Figure 1 illustrates model of probabilistic choice (5) for ternary choice among three alternatives A, B and C. Utilities of alternatives B and C are fixed at U(B) = 2 and U(C) = 3. Utility of alternative A is shown on the horizontal axis (in this case, the lower bound (8) is U(A) > 1.2 and the upper bound (10) is U(A) < 6). Probabilities P(A|{A,B,C}), P(B|{A,B,C}) and P(C|{A,B,C}) are shown as black, grey and white areas correspondingly. Figure 1 shows that as U(A) increases from 1.25 to 6 probability P(A|{A,B,C}) increases from 0.02 to 0.67; probability P(B|{A,B,C}) decreases from 0.39 to 0 and probability P(C|{A,B,C}) decreases from 0.59 to 0.33. Note that the ratio of probability that B is not chosen to probability that C is not chosen [1—P(B|{A,B,C})]/[1—P(C|{A,B,C})] stays constant at 3/2 for all values U(A)∈[1.25,6], in accordance with the dual choice axiom (3). In contrast, the ratio of probability that B is chosen to probability that C is chosen diminishes from 0.66 to zero, in violation of the classic choice axiom (2).

Fig. 1
figure 1

Model (5) for ternary choice when U(B) = 2, U(C) = 3 and different values of U(A) as shown on the horizontal axis

Full size image

For comparison, Fig. 2 illustrates classic Luce (1959) choice model

$$ {P}_{Luce}\left(A|\left\{A,B,C\right\}\right)=\frac{U(A)}{U(A)+U(B)+U(C)} $$

for the same parameters U(A)∈[1.25,6], U(B) = 2 and U(C) = 3. Figure 2 shows that as U(A) increases from 1.25 to 6 probability PLuce(A|{A,B,C}) in Luce (1959) choice model increases from 0.2 to 0.55; probability PLuce(B|{A,B,C}) in Luce (1959) choice model decreases from 0.32 to 0.18 and probability PLuce(C|{A,B,C}) in Luce (1959) choice model decreases from 0.48 to 0.27. Note that the ratio of probability that B is chosen to probability that C is chosen in Luce (1959) choice model stays constant at 2/3 for all values U(A)∈[1.25,6], in accordance with the classic choice axiom (2). In contrast, the ratio of probability that B is not chosen to probability that C is not chosen in Luce (1959) choice model diminishes from 1.31 to 1.13, in violation of the dual choice axiom (3).

Fig. 2
figure 2

Luce (1959) choice model when U(B) = 2, U(C) = 3 and different values of U(A) as shown on the horizontal axis

Full size image

A comparison of Figs. 1 and 2 shows that model (5) is relatively more sensitive to differences in utility than classic Luce (1959) choice model. For example, as U(A) increases from 1.25 to 2, P(A|{A,B,C}) in model (5) increases from 0.02 to 0.25 and P(B|{A,B,C}) in model (5) decreases from 0.39 to 0.25. In contrast, in Luce (1959) choice model, PLuce(A|{A,B,C}) increases from 0.2 to 0.29 and PLuce (B|{A,B,C}) decreases from 0.32 only to 0.29.

From another perspective, Fig. 3 shows probability P(A|{A,B,C}) in model (5) as a function of utility ratio U(A)/U(B), shown on the horizontal axis, and utility ratio U(A)/U(C), shown on the vertical axis. Note that for a ternary choice bound (8) becomes

$$ \frac{U(A)}{U(B)}+\frac{U(A)}{U(C)}>1 $$
(11)

which is shown as a solid black line on Fig. 3 corresponding to the case P(A|{A,B,C}) = 0. Similarly, for a ternary choice bound (10) becomes

$$ \left|\frac{U(A)}{U(B)}-\frac{U(A)}{U(C)}\right|<1 $$
(12)

which is shown as two parallel dashed black lines on Fig. 3.

Fig. 3
figure 3

Probability P(A|{A,B,C}) in model (5) as a function of utility ratios U(A)/U(B) and U(A)/U(C)

Full size image

For any combination of utility ratios U(A)/U(B) and U(A)/U(C) that are above the solid black line and between two dashed black lines on Fig. 3 there is a well-defined probability P(A|{A,B,C}) in model (5). Figure 3 illustrates the sets of utility ratios U(A)/U(B) and U(A)/U(C) which generate probabilities P(A|{A,B,C}) = p for all p∈{0.1;0.2;…;0.9}.Footnote 9 For comparison, Fig. 4 does the same for Luce (1959) choice model.Footnote 10 Figures 3 and 4 show that both in model (5) and in the classic Luce (1959) choice model a decision maker chooses alternative A with a greater probability when utility ratios U(A)/U(B) and U(A)/U(C) increase. Yet, the same increase in utility ratios has a greater impact on the choice probability in model (5) compared to Luce (1959) choice model. For example, increasing utility ratios U(A)/U(B) and U(A)/U(C) from one to two increases the likelihood of choosing A in model (5) from 1/3 to 0.6 and in Luce (1959) choice model—from 1/3 to 0.5.

Fig. 4
figure 4

Probability PLuce (A|{A,B,C}) in Luce (1959) choice model as a function of utility ratios U(A)/U(B) and U(A)/U(C)

Full size image

If utility ratio U(A)/U(C) is relatively high so that bound (12) is violated (cf. an area above the higher dashed black line on Fig. 3) then alternative C is too inferior (in terms of utility) compared to A and B. In this case C is never chosen with a positive probability and choice becomes binary. The decision maker chooses either A or B. Binary choice probability is given by (4), which depends only on ratio U(A)/U(B). Alternative A is chosen with probability p∈{0.1;0.2;…;0.9} when the ratio U(A)/U(B) equals p/(1-p). Figure 3 illustrates these binary choice probabilities in an area above the higher dashed black line. Similarly, if ratio U(A)/U(B) is relatively high, i.e. bound (12) is violated, then B is too inferior and never chosen with a positive probability. The decision maker chooses either A or C. Binary choice probability now depends only on ratio U(A)/U(C). Alternative A is chosen with probability p∈{0.1;0.2;…;0.9} when the ratio U(A)/U(C) equals p/(1-p). Figure 3 illustrates these binary choice probabilities in an area below the lower dashed black line.

5 Conclusion

Luce (1959) choice model has a comparative advantage over other classic models of probabilistic choice. Specifically, random utility/preference approach (e.g., Falmagne 1985; Loomes and Sugden 1995) violates weak stochastic transitivity akin to the Condorcet (1785) paradox in social choice. Yet, decision makers rarely exhibit such violations (e.g., Rieskamp et al. 2006). Moreover, practical applications of random utility/preference often require restrictive parametric assumptions characterizing utility/preference only with one parameterFootnote 11 to avoid large variance-covariance matrices. Classic Fechner (1860) model of random errors (strong utility) violates dominance.Footnote 12 Yet, decision makers rarely violate transparent dominance (for choice under risk e.g., Carbone and Hey 1995; Loomes and Sugden 1998, Table 2, p. 591; Hey 2001, Table 2, p.14; see however, Birnbaum and Navarrete 1998, p. 61; Birnbaum 2005, p.1356). Moreover, Fechner’s strong utility applies only to binary choice.Footnote 13

Luce (1959) choice model is derived from an intuitively appealing choice axiom. This paper presents a dual choice axiom. A new model of probabilistic choice is derived from this dual choice axiom. For binary choice, the new model coincides with Luce (1959) choice model. For choice among n > 3 alternatives, the new model is qualitatively similar to Luce (1959) choice model (a decision maker is more likely to choose more desirable alternatives) but utility of an alternative is bounded (from above and below) and choice probabilities are relatively more sensitive to differences in utility.

Utility function in the new model of probabilistic choice, as in classic Luce (1959) choice model, maps choice alternatives to positive real numbers. Decision theories often use real valued utility functions (i.e. mapping choice alternatives to zero or negative numbers) that are unique up to a positive affine transformation (e.g., von Neumann and Morgenstern (1947) expected utility function in choice under risk, Samuelson (1937) discounted utility function in intertemporal choice). The newly proposed model of probabilistic choice, like Luce (1959) choice model, can be adapted to such utility functions via transformation U(A) = exp.(V(A)), where V : S → ℝ is utility function that is unique up to a positive affine transformation. With this transformation, our proposed model of probabilistic choice becomes

$$ P\left(A|S\right)=1-\frac{n-1}{\sum_{B\in S}{e}^{b\left[V(A)-V(B)\right]}} $$
(13)

where b > 0 is the scale parameter of utility function V : S → ℝ. This scale parameter can be interpreted as the degree of noise/randomness in probabilistic choice. When b is close to zero, a decision maker chooses every alternative with probability close to 1/n. Model (13) is a special case of a generalized Fechner’s strong utility recently proposed by Blavatskyy (2018): P(A| S) = F(V(A) − V(A2), V(A) − V(A3), …, V(A) − V(An)) where F : ℝn − 1 → [0, 1] denotes a symmetric functionFootnote 14 and A2, …, An ∈ S\{A} denote choice alternatives other than A.

Debreu (1960, p. 188) criticized Luce (1959) choice model with the following example. Let A denote the Debussy quartet, B—the 8th symphony of Beethoven and C—the same symphony with a different conductor. In a direct binary choice a (presumably French) decision maker is indifferent between B and C, so that P(B,C) = 0.5, but he or she has a slight preference for A over B or C, so that P(A,B) = 0.6 and P(A,C) = 0.6. Yet, according to Luce (1959) choice model, in a ternary choice among A, B and C this decision maker chooses A only with probability 3/7, i.e. less than 0.5, revealing now a slight preference for Beethoven. Debreu’s critique also applies to model (5) although in a weaker form. According to model (5), the above decision maker chooses A with probability 0.5, B—with probability ¼ and C—with probability ¼ as well in a ternary choice among A, B and C. The dual choice axiom, as well as the classic choice axiom, are intuitively appealing in choice situations without any significant substitution/complementary effects among available alternatives. Debreu’s example clearly does not fall into this category as the two versions of Beethoven’s symphony are highly substitutable.

McKelvey and Palfrey (1995) developed the concept of logit quantal response equilibrium for solving strategic games based on Luce (1959) choice model. A promising avenue of future research is to develop an analogous equilibrium solution concept when players choose among strategies according to model (5). Compared to Luce (1959) choice model, in model (5) strategies that fall below (greatly exceed) other strategies in terms of expected utility are chosen with probabilities close to zero (one), which can help a decision maker to avoid dominated strategies and to choose dominant strategies more frequently.

Blavatskyy (2009, 2012) presents an algorithm how to extend a model of binary probabilistic choice to choice among n > 2 alternatives: 1) pick at random two out of n > 2 alternatives and choose between them; 2) discard the less preferred alternative back into the choice set; 3) pick at random one out of n-1 alternatives and choose between this alternative and the previously chosen (more preferred) alternative; 4) repeat steps 2–3 ad infinitum. The dual approach proposed in this paper can be also applied to this algorithm. Such dual algorithm extends binary choice probabilities to probabilities of choosing the worst among n > 2 alternatives: 1) pick at random two out of n > 2 alternatives and choose between them; 2) discard the more preferred alternative back into the choice set; 3) pick at random one out of n-1 alternatives and choose between this alternative and the previously retained (less preferred) alternative; 4) repeat steps 2–3 ad infinitum. Asymptotic probability that alternative A∈S is retained as the worst alternative in the choice set S is then given by

$$ Q\left(A|S\right)=\frac{\sum_{G\in \Gamma (S)\left|R(G)=A\right.}{\prod}_{\left\{B,C\right\}\in E(G)}P\left(C,B\right)}{\sum_{G\in \Gamma (S)}{\prod}_{\left\{B,C\right\}\in E(G)}P\left(C,B\right)} $$

where G denotes an arborescence with the vertex set S, Γ(S) is the set of all arborescences with the vertex set S, R(G) denotes the root of arborescence G and E(G) denotes the edge set of arborescence G (probability P(C,B) for any {B,C}∈E(G) is then the probability that a decision maker chooses the terminal vertex (head) C over the initial vertex (tail) B).