Abstract
Repeat-sales indexes are the most widely used type of transaction based property price indexes. However, such indexes are particularly prone to revision. When a new period of transaction data becomes available and is used to update the repeat-sales model, all past index values can potentially be revised. These revisions are especially problematical for commercial real estate (as compared to housing), due to the relative scarcity of transaction data and the heterogeneity of the underlying properties. From a methodological perspective, the magnitude of the revisions is a particularly useful measure of the index quality, as it directly reflects both the precision of the index and its practical usefulness in economic and business applications. This paper focuses on index revisions in thin, commercial property markets, the type of market that is most challenging. We present multiple specifications of the repeat-sales model (both existing and new), seeking to reduce revisions. We are able to reduce overall index revisions by more than 50%, compared to more traditional repeat-sales models.




Similar content being viewed by others
Notes
Both use a slightly different setup than the classical (Bailey et al. 1963) method. The HPI uses a WLS approach to estimate the repeat-sales model as proposed by Case and Shiller (1987). The Moody’s/RCA CPPI uses frequency conversion as proposed by Bokhari and Geltner (2012). Since September 2017 the RCA CPPIs employ a methodology based on the current paper.
Note that βi is specified as a pair fixed effect in this paper, as this the most widely accepted form in both academic literature and in industry. However, it could also be specified as a property fixed effect. So if a property is sold 3 times, we ‘break it up’ into 2 pairs, instead of seeing it as 1 property. See Francke (2010) for the (small) difference in specification.
The metro areas are defined by Real Capital Analytics.
In fact, we also ran some additional indexes as a robustness check in “Robustness”. As such, the total number of indexes we estimate is closer to 5,000.
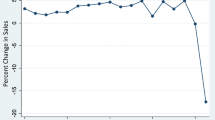
For example, consider Fig. 3. In both markets the crisis is clearly visible. Although the amplitude and the timing for especially the recovery is different. The SFO index started dropping 2 quarters before the LAI index. Subsequently, offices in LAI went down approximately 50%, whereas apartments in SFO ‘only’ decreased 20% in value. However, arguably the biggest difference is that at the end of the sample, the LAI index is still not above its previous peak, whereas the SFO index reached the previous peak already in 2013.
A partial exception is Gatzlaff and Geltner (1998) which estimated repeat-sales indexes of Florida commercial property based on a ridge regression methodology reflecting an a priori assumption of positively correlated ‘true’ returns.
Note that Francke and van de Minne (2017) use a similar setup. Their hierarchical repeat-sales (HRS) model has multiple stochastic log price trends with a hierarchical additive structure: One common trend using information from all sectors and markets, and target market specific trends estimated as deviations from the common trend. In the present approach we simply estimate the aggregate indexes separately and use them as explanatory variables in the granular index estimation. This reduces computing time considerably. Moreover, we found that in some cases of data scarcity, the HRS can result in highly correlated indexes.
We do provide some of the revision statistics for the aggregate indexes in “Robustness”.
In an earlier version we experimented with transaction volume, regional GDP, and unemployment in the state equation, and allowed the variance of the signal and noise component to be time-varying. For the sake of brevity and readability these results have not been included in the paper. Moreover, the results did not improve much, or not at all.
The effective sample size (ESS) is computed as follows; \( \text {ESS} = {n \over 1 + 2 {\sum }_{k = 1}^{\infty } \rho (k)} , \) where n is the number of samples and ρ(k) is the correlation at lag k. One gets a different ESS for every variable. Thus, the difference between the effective sample size and the actual sample size, gives one a measure on how independent the draws are.
The intuition behind the \(\bar {R}\) is that the chains should look alike, if the chains converged. First, the Gelman-Rubin diagnostic is computed, which calculates both the between-chain and the within-chain variance. The \(\hat {R}\) is essentially the fraction between the two, see Gelman and Rubin (1992) and Brooks and Gelman (1998) for more details. A value of 1.1 is usually used as an upper limit.
References
Abraham, J.M., & Schauman, W.S. (1991). New evidence on home prices from Freddie Mac repeat sales. Real Estate Economics, 19(3), 333–352.
Bailey, M.J., Muth, R.F., Nourse, H.O. (1963). A regression method for real estate price index construction. Journal of the American Statistical Association, 58, 933–942.
Barkham, R., & Geltner, D.M. (1995). Price discovery in American and British property markets. Real Estate Economics, 23(1), 21–44.
Betancourt, M., & Girolami, M. (2015). Hamiltonian Monte Carlo for hierarchical models. Current trends in Bayesian methodology with applications, 79, 30.
Bokhari, S., & Geltner, D. (2012). Estimating real estate price movements for high frequency tradable indexes in a scarce data environment. The Journal of Real Estate Finance and Economics, 45(2), 522–543.
Bokhari, S., & Geltner, D.M. (2011). Loss aversion and anchoring in commercial real estate pricing: empirical evidence and price index implications. Real Estate Economics, 39(4), 635–670.
Bourassa, S.C., Cantoni, E., Hoesli, M. (2013). Robust repeat sales indexes. Real Estate Economics, 41(3), 517–541.
Brooks, S.P., & Gelman, A. (1998). General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics, 7(4), 434–455.
Carpenter, B., Gelman, A., Hoffman, M., Lee, D., Goodrich, B., Betancourt, M., Brubaker, M.A., Guo, J., Li, P., Riddell, A. (2017). Stan: a probabilistic programming language. Journal of Statistical Software, 76(1), 1–32.
Case, K.E., & Shiller, R.J. (1987). Prices of single family homes since 1970: new indexes for four cities. New England Economic Review, 45–56.
Case, K.E., & Shiller, R.J. (1989). The efficiency of the market of single-family homes. The American Economic Review, 79, 125–137.
Case, K.E., & Shiller, R.J. (1990). Forecasting prices and excess returns in the housing market. Real Estate Economics, 18(3), 253–273.
Clapham, E., Englund, P., Quigley, J.M., Redfearn, C.L. (2006). Revisiting the past and settling the score: index revision for house price derivatives. Real Estate Economics, 34, 275–302.
Clapp, J.M., & Giaccotto, C. (1999). Revisions in repeat-sales price indexes: here today, gone tomorrow. Real Estate Economics, 27, 79–104.
Clements, M.P., & Galvão, A. B. (2017). Predicting early data revisions to us gdp and the effects of releases on equity markets. Journal of Business & Economic Statistics, 35, 1–18.
De Wit, E.R., Englund, P., Francke, M.K. (2013). Price and transaction volume in the Dutch housing market. Regional Science and Urban Economics, 43(2), 220–241.
Deng, Y., & Quigley, J.M. (2008). Index revision, house price risk, and the market for house price derivatives. The Journal of Real Estate Finance and Economics, 37 (3), 191–209.
Durbin, J., & Koopman, S.J. (2012). Time series analysis by state space methods Vol. 2. Oxford: Oxford Univ Press.
Fisher, J., Gatzlaff, D., Geltner, D.M., Haurin, D. (2003). Controlling for the impact of variable liquidity in commercial real estate price indices. Real Estate Economics, 31(2), 269–303.
Francke, M.K. (2010). Repeat sales index for thin markets: a structural time series approach. Journal of Real Estate Finance and Economics, 41, 24–52.
Francke, M.K. (2017). Repeat sales models, holding periods and index revision. The Hoyt Group; May 2017 50th Anniversary Program Presentations.
Francke, M.K., & De Vos, A.F. (2000). Efficient computation of hierarchical trends. Journal of Business and Economic Statistics, 18, 51–57.
Francke, M.K., & van de Minne, A. (2017). The hierarchical repeat sales model for granular commercial real estate and residential price indices. The Journal of Real Estate Finance and Economics, 55(4), 511–532.
Gatzlaff, D.H., & Geltner, D.M. (1998). A transaction-based index of commercial property and its comparison to the NCREIF index. Real Estate Finance, 15(1), 7–22.
Gelman, A., & Rubin, D.B. (1992). Inference from iterative simulation using multiple sequences. Statistical Science, 7, 457–72.
Geltner, D., & Mei, J. (1995). The present value model with time-varying discount rates: implications for commercial property valuation and investment decisions. The Journal of Real Estate Finance and Economics, 11(2), 119–135.
Geltner, D.M., & de Neufville, R. (2017). Flexibility and real estate valuation under uncertainty. A practical guide for developers. Wiley Blackwell. Available at SSRN: https://ssrn.com/abstract=2998832.
Geltner, D.M., Francke, M.K., Shimizu, C., Fenwick, D., Baran, D. (2017). Commercial property price indicators: sources, methods and issues. Eurostat.
Geltner, D.M., MacGregor, B.D., Schwann, G.M. (2003). Appraisal smoothing and price discovery in real estate markets. Urban Studies, 40(5-6), 1047–1064.
Geltner, D.M., Miller, N.G., Clayton, J., Eichholtz, P.M.A. (2014). Commercial real estate, analysis & investments Vol. 4. Boston: Cengage Learning.
Genesove, D., & Mayer, C. (2001). Loss aversion and seller behavior: evidence from the housing market. The Quarterly Journal of Economics, 116(4), 1233–1260.
Goetzmann, W.N. (1992). The accuracy of real estate indices: repeat sale estimators. Journal of Real Estate Finance and Economics, 5, 5–53.
Guo, X., Zheng, S., Geltner, D.M., Liu, H. (2014). A new approach for constructing home price indices: the pseudo repeat sales model and its application in China. Journal of Housing Economics, 25, 20–38.
Harvey, A. (1989). Forecasting structural time series models and the kalman filter. Cambridge: Cambridge University Press.
Hegde, S.P., & McDermott, J.B. (2003). The liquidity effects of revisions to the S&P 500 index: an empirical analysis. Journal of Financial Markets, 6(3), 413–459.
Hoffman, M.D., & Gelman, A. (2014). The no-U-turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. Journal of Machine Learning Research, 15 (1), 1593–1623.
Koehler, E., Brown, E., Haneuse, S.J.P.A. (2009). On the assessment of Monte Carlo error in simulation-based statistical analyses. The American Statistician, 63(2), 155–162.
Link, W.A., & Eaton, M.J. (2012). On thinning of chains in MCMC. Methods in Ecology and Evolution, 3(1), 112–115.
Lunn, D., Jackson, C., Best, N., Thomas, A., Spiegelhalter, D. (2013). The BUGS Book; A practical introduction to bayesian analysis. Boca Raton: CRC Press.
McMillen, D.P., & Thorsnes, P. (2006). Housing renovations and the quantile repeat-sales price index. Real Estate Economics, 34(4), 567–584.
Plummer, M. (2003). JAGS: a Program for analysis of Bayesian graphical models using Gibbs sampling. In: Proceedings of the 3rd internation workshop on distributed statistical computing, pp. 124.
Quan, D.C., & Quigley, J.M. (1991). Price formation and the appraisal function in real estate markets. The Journal of Real Estate Finance and Economics, 4(2), 127–146.
Schwann, G.M. (1998). A real estate price index for thin markets. Journal of Real Estate Finance and Economics, 16, 269–287.
Shiller, R.J. (1981). Do stock prices move too much to be justified by subsequent changes in dividends? American Economic Review, 71, 421–436.
Shiller, R.J. (1993). Macro Markets, Creating institutions for managing society’s largest economic risks. Oxford: Oxford University Press.
Shrestha, M.L., & Marini, M. (2013). Quarterly GDP revisions in G-20 countries: evidence from the 2008 financial crisis. IMF Working Paper (13/60).
Vehtari, A., Gelman, A., Gabry, J. (2016). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing, 27, 1–20.
Watanabe, S. (2010). Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. Journal of Machine Learning Research, 11(Dec), 3571–3594.
Yu, K., & Moyeed, R.A. (2001). Bayesian quantile regression. Statistics & Probability Letters, 54(4), 437–447.
Acknowledgements
We would like to thank the attendees at the Property Indices session of the 2017 international AREUEA conference in Amsterdam and at the 2016 Hoyt meeting in West Palm Beach. Specifically, we would like to thank Daniel Melser and Martijn Dröes whom both discussed the paper. We also want to thank Real Capital Analytics for providing the data and insights that made this study possible. The comments and observations by Jim Sempere, Elizabeth Szep and Willem Vlaming at Real Capital Analytics were especially appreciated. Finally, we would like to thank the anonymous referee for his comments on this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Revisions in Repeat-Sales Models
A.1 Revisions in the Standard Repeat-Sales Model
The way indexes are revised over time is illustrated by Bailey et al. (1963) and Clapp and Giaccotto (1999). Suppose we have only three periods, t = 0, 1, 2, and we are interested in the revision subsequent to time 1 of an index at time 1, originally estimated from transactions in period 0 and 1. That is, consider the revision of the index history when the transactions for period 2 become available. Let \(\bar {r}_{st}\) be the average log price change between the period of buy s and the period of sell t and let \(\hat {\delta }_{T|\tau }\) be the estimated log index return for period T conditional on all information (transactions) up to time τ, where τ ≥ T. The initial estimate of the log index return for period 1 is simply the average return of the properties in period 1, \( \hat {\delta }_{1|1} = \bar {r}_{01} \) with variance \(2\sigma ^{2}_{\epsilon } / n_{01}\), where nst is the number of transaction pairs with time of buy s and time of sell t. Now the estimated log index return for period 1 conditional on all information up to time 2 is a weighted average of the original estimate \(\hat {\delta }_{1|1}\) and new information with respect to δ1 based on the difference \((\bar {r}_{02} - \bar {r}_{12})\), with variance \(2 \sigma ^{2}_{\epsilon } (1/n_{02} + 1 / n_{12})\),
where the weight w = (n01(n02 + n12)) / (n01(n02 + n12) + n02n12) depends on the variances of \(\bar {r}_{01}\) and \((\bar {r}_{02} - \bar {r}_{12})\). The revision \(\hat {\delta }_{1|2} - \hat {\delta }_{1|1}\) can be expressed as \((1-w)(\bar {r}_{02} - \bar {r}_{12} - \bar {r}_{01})\).
Let us illustrate the revision by a numerical example. Assume that \(\bar {r}_{01}= 0.08, \bar {r}_{02} = 0.15\) and \(\bar {r}_{12}= 0.10\), and n01 = n02 = n12 = 25. The initial estimate \(\hat {\delta }_{1|1} =\bar {r}_{01}= 0.08\). The estimate of δ1 after transactions in period 2 are available, is a weighted average of \(\bar {r}_{01}= 0.08\) and \(\bar {r}_{02} - \bar {r}_{12}= 0.05\), with weight w = 2/3, so \(\hat {\delta }_{1|2} = 0.07\), and the revision is − 0.01.
A.2 Revisions in a Random Walk Repeat-Sales Model
Revisions in structural time series repeat-sales models are different from the standard (Bailey et al. 1963) model described in A.1. In this appendix we provide an algebraic derivation of how indexes are revised over time for a random walk repeat-sales model. For more advanced models the revision expressions become very complicated.
The random walk repeat-sales model for 3 observations \(\bar {r}_{01}, \bar {r}_{02}\) and \(\bar {r}_{12}\) can be expressed as
where δt = Δμt, Var\((\bar {\epsilon }_{st}) = 2\sigma ^{2}_{\epsilon } / n_{st}\), and Var\((\eta _{t}) = \sigma ^{2}_{\eta }\). Rows 1 – 3 are the observation equations, and rows 4 and 5 represent the random walk specification. Define the signal-to-noise ratio q as \(\sigma ^{2}_{\eta } / (2\sigma ^{2}_{\epsilon })\). If only the transactions up to time 1 are available, the model consists only of rows 1 and 4. Note that for the standard Bailey et al. repeat-sales model only rows 1 – 3 are applicable.
The model can be estimated by weighted least squares, giving
the last equation based on on transactions up to time 2. Note that if q →∞, the expressions are identical to the ones in the previous section.
If we assume that the signal-to-noise ratio is equal to q = 0.1, and using the same numbers as in the previous example, then \(\hat {\delta }_{1|1} = 0.057\) (instead of 0.08), and \(\hat {\delta }_{1|2} = 0.063\) (instead of 0.07). The revision is equal to 0.006, and is smaller in absolute magnitude than the revision in the standard repeat sales model (0.006 versus 0.01).
A.3 Calculating Revisions for Different Signal-to-Noise Ratios
In this Section we calculate revisions for different values of the signal-to-noise ratios q in the random walk repeat-sales model as described in A.2. Our purpose here is simply to demonstrate the large role that q plays in revisions. We use typical values for the signal (\(\sigma ^{2}_{\eta }\)) and noise (\(\sigma ^{2}_{\epsilon }\)).
We use the LAI repeat-sales data, see “Data and Descriptive Statistics” to compute the indexes starting from 34 quarters back. We have 338 transaction observation pairs in the final dataset, or about 4.5 per quarter on average. With each new quarter of history, approximately 10 new pairs are added, including second-sales in the new quarter as well as additional pairs earlier in the history. In the calculations we use signal-to-noise ratios q in the range between 0.02 and than 0.6. This range covers the ratios that we do indeed estimate.
Figure 5 provides revision statistics and the volatility and the autocorrelation of the index returns for different values of the signal-to-noise ratio q. In order to conserve space we only look at the absolute mean revisions in levels and returns, for both the total sample and specific for the final period.
It can be seen that lower values of q give less revisions. Note that in an extreme case with q = 0 there would be no revisions; the indexes would be flat. In this case there would also be a first-order autocorrelation of 1, and no volatility. The increase in levels revisions is not linear with an increase in q. For example, with q = 0.1 the average (absolute) revision is 7 bps, whereas with q = 0.5, the average (absolute) revision is ‘just’ 10 bps. However, linearity does seem to hold in the average (absolute) return revisions (Fig. 5d). More interesting is that the final period return revision behaves like a concave function of the assumed signal-to-noise ratio (Fig. 5e). Our results show that at q = 0.16 and q = 0.60 the final period index level revisions are equally large (equal cumulative historical change). For the returns revisions the concavity seems to be mostly absent.
Appendix B: Technical Estimation Details
This appendix contains some technical details on the model estimation. We apply the No-U-Turn-Sampler (NUTS) developed by Hoffman and Gelman (2014). It is a generalization of the Hamiltonian Monte Carlo (HMC) algorithm. The HMC avoids the random walk behaviour and sensitivity to correlated parameters that plague other Markov chain Monte Carlo methods by taking a series of steps informed by first-order gradient information. These features allow it to converge to high-dimensional target distributions much more quickly compared to for example the Metropolis-Hastings algorithm and Gibbs sampling. In addition, the NUTS algorithm avoids setting the parameters for the step size and the desired numbers of steps, which the HMC is so sensitive to. In case of many parameters, the manual setting of step sizes and desired number of steps, becomes intractable. The NUTS algorithm has been introduced in R via the software package called ‘Rstan’ (Carpenter et al. 2017).
The difference in convergence between NUTS and Gibbs sampling is clearly illustrated by the the more elaborate ARAG model. In our applications Gibbs sampling, by using the program JAGS (Plummer 2003), could take hours to converge, while NUTS only needed 10 – 20 seconds.
We apply the ‘Matt trick’ to sample μt by specifying μt = μt− 1 + ηt, where the increments ηt ∼Normal(0, 1) are independent of each other. The effective sample size is increased considerably by doing so, simply because there is less correlation in the index returns compared to index levels.Footnote 10 Intuitively, without the ‘Matt trick’, if an ‘extreme’ value is sampled for price level in period t, this will affect the price level sampled in period t + 1, t + 2, etc. By sampling increments, this relationship is gone. A more technical description is given by Betancourt and Girolami (2015).
We sample 2, 000 times, of which we discard the first 1, 000 when analysing the chains (i.e. the warm-up stage), in parallel over 6 chains (so 6 × 1, 000 = 6, 000 samples in total). We provide different initial values for each variable in each chain and we do not thin the chains (see Link and Eaton 2012, for our reasons to shy away from thinning). We subsequently evaluate whether or not the model converges based on \(\bar {R}\), the potential scale reduction statistic.Footnote 11 We use very strict convergence criteria, i.e. average \(\bar {R} \leq 1.01 \), which is more strict than usual. The fact that the models for our granular indices converge even with such strict criteria, shows the power of the NUTS algorithm. As shown in “Results” and “Results”, the effective and total sample size are almost identical for most models. We also keep track of the Monte Carlo (MC) error (Koehler et al. 2009), but these are not presented in this paper to conserve space. Even with a sample size of only 6,000, the MC error divided by the mean or standard deviation of the posterior, remains very low.
Appendix C: Parameter Estimates and Credible Intervals
Appendix D: Revisions for a Selection of Indexes
Appendix E: Revision Results of our Robustness Section
Rights and permissions
About this article
Cite this article
van de Minne, A., Francke, M., Geltner, D. et al. Using Revisions as a Measure of Price Index Quality in Repeat-Sales Models. J Real Estate Finan Econ 60, 514–553 (2020). https://doi.org/10.1007/s11146-018-9692-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11146-018-9692-x