1 Introduction

Escape from a potential well is a classic problem arising in various fields of natural science and engineering [1,2,3,4,5]. A wide range of physical phenomena from celestial mechanics to the dynamics of molecules has been investigated in the literature, including topics such as energy harvesting [6], transient resonance dynamics of oscillatory systems [7, 8], the physics of Josephson junctions [9] and even the capsize phenomenon of ships and vessels [3, 10]. Another important topic relating to the escape phenomenon is the dynamic pull-in in microelectromechanical systems (MEMS) [11,12,13,14,15,16].

The first investigations of the forced escape phenomenon started in 1940 by Kramers regarding the thermal activation of chemical reactions [17, 18]. Although much research has taken place in the last 80 years, one still encounters important unresolved issues when considering the escape process [19].

For constant forcing, escape may occur because of the slow variation of system parameters and the consequent bifurcations of the steady-state regimes of the response [2, 11, 12].

Paper [3] addressed the escape dynamics of harmonically forced and damped particles in three model potential wells. To give an analytic expression for the escape criterion, the steady-state response of the particle was used, although this criterion is not exact and empirical corrections are performed when necessary.

A common feature of the escape phenomenon is numerically demonstrated in paper [3]. For the investigated potentials, the critical forcing amplitude curve has a sharp minimum value at a frequency value smaller than the frequency of small oscillations in the potential well. Similar escape curves are found in papers investigating the problem of dynamic pull-in in MEMS devices [14, 15].

Further similar patterns were found when investigating the safe basins of attraction for several dynamical systems [20, 21]. The sharp minimum value found in many papers allows the reader to formulate a conjecture about the mentioned property of the curve as a typical characteristic of the escape phenomena. The conjecture was further examined for different model potentials under harmonic forcing in the papers [22, 23].

These papers addressed the escape dynamics of the forced particle in conditions of 1:1 resonance. The transient dynamics of the system can thus be explored in terms of the slow flow on the resonance manifold (RM). Exploration of special trajectories on the RM corresponding to different initial conditions (IC) allows for the identification of two distinct mechanisms of approaching the escape threshold while varying the system parameters. In the first mechanism, the maximum mechanism (MM), the phase trajectory only achieves the boundary of the potential well. In the second mechanism, the saddle mechanism (SM), the special trajectory achieves the saddle point on the RM. Then, the response amplitude drastically grows, and the particle escapes. The combination of these two mechanisms provides an understanding and prediction of the sharp minimum on the frequency-amplitude plane without any empirical corrections. This approach somewhat resembles recent studies of transient phenomena in systems of coupled oscillators in terms of limited phase trajectories (LPT) [24, 25].

In the present paper, a more complex situation is considered. A system of two coupled particles (cf. Fig. 1a) is excited by a sum of two harmonic components. The first one corresponds (in the linear case) to the internal mode of the coupling corresponding to their relative oscillations. The second resonance is close to the 1:1 resonance for the centre of mass of the system. First, after describing the governing equations of the system (Sect. 2), the reduction in the degrees of freedom of the system follows (Sect. 3.1). Then, the arising equations are further simplified using the probability-based convolution to calculate the effective potential (Sect. 3.2). Subsequently, further simplification is achieved by the averaging technique to obtain equations for the slow-flow variables (Sect. 3.3). After giving an explicit solution of the slow-flow equations, the presentation of some numerical results and the discussion of the results follows (Sect. 4). In Sect. 5, the results presented in the paper are summarised.

Fig. 1
figure 1

The basic model of the two particle system

Full size image

2 Description of the model

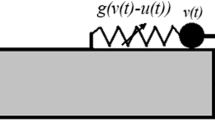
The setting investigated in the paper is depicted in Fig. 1a. Two bodies of mass \(m_1\) and \(m_2\) coupled with a linear spring of stiffness k and a linear damper with the damping coefficient c are located in the corresponding potential wells \(V_1(x)\) and \(V_2(x)\). \(m_1\) is excited by the superposition of two harmonic forces

$$\begin{aligned} A_1(t)+A_2(t)=A_1 \sin (\omega _1 t+ \beta _1)+A_2 \sin (\omega _2 t+ \beta _2), \end{aligned}$$

with the amplitudes \(A_1\), \(A_2\), the excitation frequencies \(\omega _1\), \(\omega _2\) and the phases \(\beta _1\), \(\beta _2\). The potentials act in a way that both bodies have the same linearized eigenfrequency \({\omega _0:=\sqrt{\frac{V'(x=0)}{m}}}\), i.e., \({V_2(x)=\frac{m_2}{m_1} V_1(x)}\).

For example, the truncated parabolic potential well has the following form:

$$\begin{aligned} V_1(x)= & {} {\left\{ \begin{array}{ll} -V_0+\frac{m_1 \omega _0^2}{2} x^2 &{}\quad |x|\le \frac{1}{\omega _0} \sqrt{\frac{2 V_0}{m_1}} \\ 0 &{}\quad \text {else,} \end{array}\right. }\nonumber \\ V_2(x)= & {} {\left\{ \begin{array}{ll} -\frac{m_2}{m_1} V_0+\frac{m_2 \omega _0^2}{2} x^2 &{}\quad |x|\le \frac{1}{\omega _0} \sqrt{\frac{2 V_0}{m_1}} \\ 0 &{}\quad \text {else.} \end{array}\right. } \end{aligned}$$
(1)

The equations of motion are given by

$$\begin{aligned}&\begin{bmatrix} m_1 &{}\quad 0 \\ 0 &{}\quad m_2 \end{bmatrix} \begin{bmatrix} \ddot{x}_1\\ \ddot{x}_2 \end{bmatrix} + \begin{bmatrix} c &{} \quad -c \\ -c &{}\quad c \end{bmatrix} \begin{bmatrix} \dot{x}_1\\ \dot{x}_2 \end{bmatrix} + \begin{bmatrix} k &{}\quad -k \\ -k &{}\quad k \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix}\nonumber \\&\quad +\begin{bmatrix} V_1'(x_1) \\ V_2'(x_2) \end{bmatrix} =\begin{bmatrix} A_1 \sin (\omega _1 t+ \beta _1)+A_2 \sin (\omega _2 t+ \beta _2)\\ 0 \end{bmatrix}, \end{aligned}$$
(2)

where \({V'(x):=\frac{\partial V(x)}{\partial x}}\). Using the following dimensionless values

$$\begin{aligned} \tau= & {} \omega _0 t, \quad \quad \quad \quad \text {d}\tau =\omega _0 \text {d}t, \nonumber \\ \frac{\text {d}}{\text {d}t}= & {} \omega _0 \frac{\text {d}}{\text {d}\tau }, \quad \quad \quad \quad \frac{\text {d}^2}{\text {d}t^2}=\omega _0^2 \frac{\text {d}^2}{\text {d}\tau ^2}, \nonumber \\ q= & {} \omega _0 \sqrt{\frac{m_1}{2 V_0}}x,\quad \quad \quad \frac{\text {d}}{\text {d}x} =\omega _0 \sqrt{\frac{m_1}{2 V_0}} \frac{\text {d}}{\text {d}q},\nonumber \\ \Omega _i= & {} \frac{\omega _i}{\omega _0} \quad i \in \lbrace 1,2 \rbrace ,\quad \quad \quad F_i=\frac{A_i}{\omega _0 \sqrt{2 m_1 V_0}} \quad i \in \lbrace 1,2 \rbrace \end{aligned}$$
(3)

and the dimensionless potential \({U_0(q)}\) (see Eq. 9) with the notation \({\dot{q}=\frac{\text {d}}{\text {d} \tau }q}\) and \({U_0'(q)=\frac{\text {d}}{\text {d} q}U_0}\). Equation (2) can be rewritten in dimensionless form too, although the signs of the masses remain in the equations for clarity:

$$\begin{aligned}&\begin{bmatrix} m_1 &{}\quad 0 \\ 0 &{}\quad m_2 \end{bmatrix} \begin{bmatrix} \ddot{q}_1\\ \ddot{q}_2 \end{bmatrix} + \begin{bmatrix} C &{}\quad -C \\ -C &{}\quad C \end{bmatrix} \begin{bmatrix} \dot{q}_1\\ \dot{q}_2 \end{bmatrix}\nonumber \\&\quad + \begin{bmatrix} K &{}\quad -K \\ -K &{}\quad K \end{bmatrix} \begin{bmatrix} q_1\\ q_2 \end{bmatrix} +\begin{bmatrix} m_1 U_0'(q_1)\\ m_2 U_0'(q_2) \end{bmatrix}\nonumber \\&\quad = \begin{bmatrix} m_1 F_1 \sin (\Omega _1 \tau {+} \beta _1){+}m_1 F_2 \sin (\Omega _2 \tau {+} \beta _2)\\ 0 \end{bmatrix},\nonumber \\ \end{aligned}$$
(4)

where \(C:=\frac{c}{\omega _0} \text { and } K:=\frac{k}{\omega _0^2}\).

To decouple the equations from each other, a new pair of coordinates, \((y_1,y_2)\) is introduced for the position of the centre of gravity and for the relative displacement of the two bodies, respectively:

$$\begin{aligned} y_1:=\frac{m_1 q_1+m_2 q_2}{m_1+m_2}, \qquad \qquad y_2:=q_2-q_1. \end{aligned}$$
(5)

Then,

$$\begin{aligned} \begin{bmatrix} q_1\\ q_2 \end{bmatrix} = \begin{bmatrix} 1 &{} \quad -\frac{m_2}{m_1+m_2}\\ 1 &{}\quad \frac{m_1}{m_1+m_2} \end{bmatrix} \begin{bmatrix} y_1\\ y_2 \end{bmatrix}, \end{aligned}$$
(6)

which substituted back into (4) results in

$$\begin{aligned}&\ddot{y}_1+\mu U_0' \left( y_1-(1-\mu ) y_2 \right) +(1-\mu ) U_0' \left( y_1+\mu y_2 \right) \nonumber \\&\quad = \mu \left( F_1 \sin (\Omega _1 \tau + \beta _1)+ F_2 \sin (\Omega _2 \tau + \beta _2) \right) , \end{aligned}$$
(7)
$$\begin{aligned}&\ddot{y}_2+\frac{C}{m}\dot{y}_2+\frac{K}{m} y_2+\underbrace{ U_0' \left( y_1+\mu y_2 \right) -U_0' \left( y_1 -(1-\mu ) y_2 \right) }_{\text {small coupling term}}\nonumber \\&\quad =-F_1 \sin (\Omega _1 \tau +\beta _1)-F_2 \sin ( \Omega _2 \tau +\beta _2), \end{aligned}$$
(8)

with \(\frac{1}{m}:=\frac{1}{m_1}+\frac{1}{m_2}\) and \(\mu :=\frac{m_1}{m_1+m_2}\).

3 Model reduction

The equations of motion are too complicated in their current form for further analytic investigations. In the following, some assumptions are introduced regarding the properties of the problem. To concentrate on the effects caused by the coupled bodies in contrast to a single body, the truncated, purely quadratic potential (1) is mainly investigated; however, most of the calculations are presented in a general form so that the procedure described below is applicable to arbitrary potentials.

3.1 Reduction in the degrees of freedom

In the following, \({F_2 \gg F_1}\) and \({\Omega _2 \gg \Omega _1}\) will be assumed; furthermore, C is assumed to be not small and \({K \gg 1}\). The approach described in [26, 27] can be applied to simplify the equations. The asymptotic behaviour of the solution can be approximated with a small error by solving Eq. (8), neglecting the small coupling term in Eq. (7).

Since the action of the potential well on \(y_2\) is always present in the coupling term only, the reduction of (8) to a damped, linear ODE of second order is possible for arbitrary potentials.

3.1.1 Example–truncated parabolic potential

In dimensionless form, the truncated parabolic potential takes the following form

$$\begin{aligned} U_0(q)= {\left\{ \begin{array}{ll} -\frac{1}{2}+\frac{q^2}{2} &{}\quad |q|<1\\ 0 &{}\quad \text {else.} \end{array}\right. } \end{aligned}$$
(9)

Neglecting the coupling term and solving the remaining linear ODE for \(y_2\) would be possible here. However, in the above simple case, it turns out to be a slightly more accurate heuristic for the solution of (8), if only the case is considered when both of the particles are inside of the potential well. Then,

$$\begin{aligned}&\ddot{y}_2+\frac{C}{m} \dot{y}_2+ \left( \frac{K}{m}+1 \right) y_2\nonumber \\&\quad =-F_1 \sin (\Omega _1 \tau +\beta _1)-F_2 \sin (\Omega _2 \tau +\beta _2). \end{aligned}$$
(10)

Interesting effects appear when \(\Omega _2\) is chosen close to the resonance frequency of the relative movements of the particles, i.e.,

$$\begin{aligned} \Omega _2\approx \sqrt{\frac{K}{m}+1}. \end{aligned}$$
(11)

Then, the effect of \(F_1\) compared to \(F_2\) is negligible, and the particular solution of equation (8) can be written as

$$\begin{aligned} y_{2,\text {p}}(\tau )=y_0 \sin (\Omega _2 \tau +\gamma _2), \end{aligned}$$
(12)

with the vibration amplitude

$$\begin{aligned} y_0 \approx \frac{F_2}{\sqrt{\Omega _2^4+ \left[ -2 \left( \frac{K}{m}+1 \right) +\frac{C^2}{m^2} \right] \Omega _2^2+ \left( \frac{K}{m}+1 \right) ^2}},\nonumber \\ \end{aligned}$$
(13)

and with the phase shift, \(\gamma _2\) for which the explicit expression is omitted here, because it is not required for further analysis.

Fig. 2
figure 2

Original and effective quantities describing the truncated quadratic potential with \({m_1=m_2=1}\) and \({y_0=0.3}\)

Full size image

Due to the non-small damping, the homogeneous solution \(y_{2,\text {h}}(\tau )\) decays rapidly, so its effect on the behaviour of the solution is also negligible.

$$\begin{aligned} {y_{2}(\tau )= y_{2,\text {h}}(\tau )+ y_{2,\text {p}}(\tau )\approx y_{2,\text {p}}(\tau )}. \end{aligned}$$
(14)

Equation (7) can now be simplified by the elimination of the variable \(y_2(\tau )\).

It should be noted that the method is applied only to the simplest case of truncated quadratic potential here, but according to [26, 27], it is applicable for all kinds of nonlinear potentials as well when the coupling between the particles is much stronger than the effect of the potential on their relative movements.

3.2 Effective potential: PDF Approach

After the approximation, applied above, there are three different dimensionless time scales in equation (7):

  • the very fast time scale includes the fast parametric excitation \(U'_0(y_1(\tau ),\Omega _2 \tau +\beta _2)\) and the fast force excitation \(F_2 \sin (\Omega _2 \tau +\beta _2)\). In the next step, this time scale will be eliminated;

  • in addition, the fast time scale including the motion of the centre of mass of the bodies, \(y_1(\tau )\) and the excitation \(F_1 \sin (\Omega _1 \tau +\beta _1)\) is also present in the dynamics of the system;

  • modulations in the vibration amplitude of the centre of gravity, A (Eq. 32) and its phase difference from the excitation \(F_1 \sin (\Omega _1 \tau +\beta _1)\) can be described by the slowest time scale.

To distinguish the last two time scales from each other, the variable \(t:=\varepsilon \tau \) is altered to denote the slow time, whereas the fast time is denoted by \(\tau \).

To eliminate the fastest time scale, some changes in the modelling approach are helpful. Instead of always considering the the exact position of the bodies, one suggests a statistical approach in which a particle has a probability to be found at an exact position. The movement of the bodies around their common centre of gravity, \(y_1\), is sinusoidal, so the corresponding cumulative distribution function (CDF) is given by the arcsine distribution

$$\begin{aligned} R(x)=\frac{2}{\pi } \arcsin (\sqrt{x})=\frac{\arcsin (2x-1)}{\pi }+\frac{1}{2}, \quad x \in [0,1]. \end{aligned}$$
(15)

The resulting probability density function (PDF) is

$$\begin{aligned} \rho (x)= {\left\{ \begin{array}{ll} \frac{1}{\pi \sqrt{x (1-x)}} &{}\quad \text {if } x \in (0,1)\\ 0 &{}\quad \text {else}. \end{array}\right. } \end{aligned}$$
(16)

After appropriate scaling and normalisation of this PDF, one obtains the density distribution for the bodies depending on \(y_0\) and \(y_1(t)\)

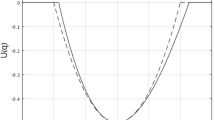
$$\begin{aligned}&M_1:=\frac{m_1}{m_1+m_2}, \qquad M_2:=\frac{m_2}{m_1+m_2},\nonumber \\&\rho _1(x,y_1;y_0)= {\left\{ \begin{array}{ll} M_1 \frac{1}{\pi \sqrt{(x-(y_1-M_2 y_0)) (y_1+M_2 y_0-x)}} &{} \text {if real}\\ 0 &{} \text {else,} \end{array}\right. }\nonumber \\&\rho _2(x,y_1;y_0)={\left\{ \begin{array}{ll} M_2 \frac{1}{\pi \sqrt{(x-(y_1-M_1 y_0)) (y_1+M_1 y_0-x)}} &{} \text {if real}\\ 0 &{} \text {else,} \end{array}\right. }\nonumber \\&\rho (x,y_1;y_0)=\rho _1(y_1,y_0,x)+\rho _2(y_1,y_0,x). \end{aligned}$$
(17)

An example for \(\rho (x,y_1;y_0)\) is depicted in Fig. 1b. The resulting force acting on the center of gravity can now be calculated through the following integration:

$$\begin{aligned} S(y_1)=\tilde{U}_0'(y_1;y_0)=\int _{-\infty }^{\infty } U_0'(x) \rho (x,y_1;y_0) \text {d}x, \end{aligned}$$
(18)

from which the effective potential \(\tilde{U}_0(y_1;y_0)\) is obtained through integration with the condition \(\tilde{U}_0(-\infty ;y_0)\overset{!}{=} 0\).

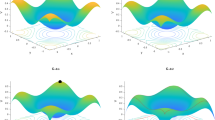
In general (for arbitrary potentials), \(S(y_1)\) cannot be calculated in an analytically closed form. In the following, the calculations are left generic, but for a specific one, the used quantities are determined numerically. (For the truncated quadratic potential, the integrals can be evaluated analytically, but it is quite elaborate and does not provide any significant advantage.) A possible way to handle the problem is piecewise spline fitting on a fine-resolved discrete data set. This step is not particularly complicated when using MATLAB ®Footnote 1. For functions calculated in this way, see Fig. 2.

3.3 Obtaining differential equations for the “slow-flow” variables

One may be interested in the behaviour of the solution if the excitation frequency is close to the natural frequency determined by the potential well. Using the above assumption, Eq. (7) may be rewritten as follows:

$$\begin{aligned}&\ddot{y}_1+y_1=-\underbrace{(S(y_1)-y_1)}_{S^*(y_1):=}+\mu ( F_1 \sin (\Omega _1 \tau +\beta _1)\nonumber \\&\qquad \qquad +F_2 \sin (\Omega _2 \tau +\beta _2)). \end{aligned}$$
(19)

Here, S and \(S^*\) also depend on the parameters \(y_0\), \(m_1\) and \(m_2\). Equation (19) is handled as follows. It is close to a conservative one

$$\begin{aligned} \ddot{y}_1+\tilde{U}_0'(y_1)= & {} \mu F(\tau ),\nonumber \\ F(\tau )= & {} F_1 \sin (\Omega _1 \tau {+}\beta _1){+}F_2 \sin (\Omega _2 \tau +\beta _2),\nonumber \\ \end{aligned}$$
(20)

with \(F_1 = \mathcal {O}(\varepsilon )\) and \(F_2 \ne \mathcal {O}(\varepsilon )\). The unperturbed equation enables the conversion to the variables characterizing the total energy of the system and the corresponding phase:

$$\begin{aligned} E= & {} \frac{1}{2} \dot{y_1}^2+\tilde{U}_0(y_1), \end{aligned}$$
(21)
$$\begin{aligned} \theta= & {} \int _0^{{y}_1}\frac{\text {d}\gamma }{\pm \sqrt{2E-2\tilde{U}_0(\gamma )}}-\tau . \end{aligned}$$
(22)

The choice of the sign in the last equation is determined by the sign of \(\dot{y}_1\).

Although \(F(\tau )\) is not small due to the term \(F_2\), its effect on the energy of the system is small because \({\Omega _2 \gg 1}\). The governing equations of the new variables in the perturbed system are slow:

$$\begin{aligned} \dot{E}= & {} \pm \mu \sqrt{2E-2\tilde{U}_0(y_1)} F(\tau ), \end{aligned}$$
(23)
$$\begin{aligned} \dot{\theta }= & {} -\mu F(\tau ) \int _0^{{y}_1}\frac{\text {d}\gamma }{ 2E-2\tilde{U}_0(\gamma )}. \end{aligned}$$
(24)

These equations are suitable for averaging with respect to the explicit time [28, 29]. The corresponding equations of the first-order approximation can be formally written as follows:

$$\begin{aligned} \dot{E}= & {} \pm \mu \bigg < \sqrt{2E-2\tilde{U}_0} F(\tau ) \bigg >, \end{aligned}$$
(25)
$$\begin{aligned} \dot{\theta }= & {} -\mu \bigg < F(\tau ) \int _0^{{y}_1}\frac{\text {d}\gamma }{ 2E-2\tilde{U}_0(\gamma )} \bigg >, \end{aligned}$$
(26)

where \(\big < \big>\) denotes averaging with respect to explicit time. However, to evaluate these equations, the function \(\tilde{U}_0(y_1)\) has to be expressed explicitly in terms of the new variables \((E,\theta )\). In general, it is impossible. Thus, an approximate heuristic approach is applied for obtaining analytic predictions.

Let us suppose that the solution of (20) can be approximated by almost harmonic oscillations:

$$\begin{aligned} y_1= & {} A(t) \sin (\Omega _1 \tau +\beta _1+\Psi (t)), \end{aligned}$$
(27)
$$\begin{aligned} \dot{y}_1= & {} \hat{v}_1(A(t))\cos (\Omega _1 \tau +\beta _1+\Psi (t)). \end{aligned}$$
(28)

Here, A(t) is the amplitude of the oscillations and \(\Psi (t)\) is the phase shift. Note that these variables depend on the energy of the system, which changes slowly according to (23–24). According to the transformation (21–21), we can replace the total energy with the level of the potential energy at the maximal deflection, i.e. at \(y_1=A\):

$$\begin{aligned} E=\tilde{U}_0(A). \end{aligned}$$
(29)

This means that the time derivative of the energy can be calculated to the first-order approximation through the time derivative of the amplitude:

$$\begin{aligned} \dot{E}=\tilde{U}_0'(A)\dot{A}. \end{aligned}$$
(30)

However, the maximal velocity is achieved as the system passes through the minimum of the potential energy. Hence, the amplitude of the velocity can be calculated as follows:

$$\begin{aligned} \hat{v}_1(A)=\sqrt{2\tilde{U}_0(A)-2\tilde{U}_0(0)}. \end{aligned}$$
(31)

Inserting Eqs. (30) and (31) into (25), the following governing equation for the amplitude is obtained:

$$\begin{aligned} \dot{A}{=}\mu \frac{\sqrt{2\tilde{U}_0(A){-}2\tilde{U}_0(0)}}{\tilde{U}_0'(A)} \bigg < F(\tau ) \cos (\Omega _1 \tau {+}\beta _1{+}\Psi (t)) \bigg >.\nonumber \\ \end{aligned}$$
(32)

Requiring the consistency of the transformation (27) and (28), the following equation for the phase shift is obtained:

$$\begin{aligned} A(\Omega _1+\dot{\Psi })= & {} A \cos ^2(\Omega _1 \tau +\beta _1+\Psi (t))\nonumber \\&\quad +\tilde{U}_0'(A \sin (\Omega _1 \tau +\beta _1+\Psi (t)))\nonumber \\&\quad \times \sin (\Omega _1 \tau +\beta _1+\Psi (t))\nonumber \\&\quad -\mu F(\tau ) \sin (\Omega _1 \tau +\beta _1 \Psi (t)). \end{aligned}$$
(33)

Assuming that the low excitation frequency is close to the eigenfrequency of the system on the bottom of the potential well, a small discrepancy can be introduced:

$$\begin{aligned} \delta =\Omega _1-1= \mathcal {O}(\varepsilon ). \end{aligned}$$
(34)

Then, Eq. (33) can be rewritten as follows:

$$\begin{aligned} A \dot{\Psi }= & {} -\delta A-A \sin ^2(\Omega _1 \tau +\beta _1 +\Psi (t))\nonumber \\&\quad +\tilde{U}_0'(A \sin (\Omega _1 \tau {+}\beta _1{+}\Psi (t)))\sin (\Omega _1 \tau {+}\beta _1 \Psi (t))\nonumber \\&\quad -\mu F(\tau ) \sin (\Omega _1 \tau +\beta _1 \Psi (t)). \end{aligned}$$
(35)

In addition, according to the introduced non-dimensional parameters \(\tilde{U}_0'(y) \vert _{y\rightarrow 0}=y\). Hence, the second and third terms in this equation can be combined:

$$\begin{aligned} A \dot{\Psi }= & {} -\delta A+S^*(A \sin (\Omega _1 \tau +\beta _1 +\Psi (t)))\nonumber \\&\quad \times \sin (\Omega _1 \tau + \beta _1 +\Psi (t))\nonumber \\&\quad -\mu F(\tau ) \sin (\Omega _1 \tau +\beta _1 \Psi (t)),\nonumber \\ S^*(y_1)= & {} S(y_1)-y_1= \tilde{U}_0'(y_1)-y_1. \end{aligned}$$
(36)

In general, the second term in this equation is not small. Hence, averaging of this equation is not completely justified. Nevertheless, we replace Eq. (36) with the averaged one and check the quality of this approximation by comparing its results with the results of the direct numeric simulations of the full system. The averaged Eq. (36) is:

$$\begin{aligned} \dot{\Psi }= - \delta {+}\omega ^*(A){-}\frac{\mu }{A} \bigg < F(\tau ) \sin (\Omega _1 \tau {+}\beta _1+\Psi (t)) \bigg >,\nonumber \\ \end{aligned}$$
(37)

with

$$\begin{aligned} \omega ^*(A):=\omega (A)-1, \end{aligned}$$
(38)

where \(\omega (A)\) is the amplitude-dependent eigenfrequency of the potential. Based on [1], the time period of a particle’s oscillation with mass m and with the given total energy E in a potential well \(\tilde{U}(x)\) without excitation, i.e. having a conservative system, can be calculated as follows:

$$\begin{aligned} T(E)=\sqrt{2m} \int _{x_1(E)}^{x_2(E)} \frac{\text {d}x}{\sqrt{E-U(x)}}. \end{aligned}$$
(39)

Here, \(x_1\) and \(x_2\) are the energy-dependent maximal displacements in the potential with the given total energy of the particle E. Then,

$$\begin{aligned} \omega (A)=\frac{2 \pi }{T(E(A))}. \end{aligned}$$
(40)

The introduced term \(\omega ^*(A)\) describes the effect of nonlinearity on the frequency of free oscillations in the potential well. For several examples of the potential, this function is displayed in Figs. 2d and 7d.

The terms describing the averaged effect of the external excitation can be easily calculated:

$$\begin{aligned} \bigg < F(\tau ) \cos (\Omega _1 \tau +\beta _1 +\Psi (t)) \bigg >= & {} -\frac{\mu }{2}F_1 \sin (\Psi ), \end{aligned}$$
(41)
$$\begin{aligned} \bigg < F(\tau ) \sin (\Omega _1 \tau +\beta _1+\Psi (t)) \bigg >= & {} \frac{\mu }{2} F_1 \cos (\Psi ). \end{aligned}$$
(42)

Inserting (41) into Eqs. (32) and (37), the final form of the first-order approximation is obtained:

$$\begin{aligned} \dot{A}= & {} - \frac{\mu }{2} \frac{\sqrt{2\tilde{U}_0(A)-2\tilde{U}_0(0)}}{\tilde{U}_0'(A)} F_1 \sin (\Psi ), \end{aligned}$$
(43)
$$\begin{aligned} \dot{\Psi }= & {} -\delta +\omega ^*(A)- \frac{\mu }{2} \frac{F_1}{A} \cos (\Psi ), \end{aligned}$$
(44)

with the initial conditions

$$\begin{aligned} A(0)&=A_0,\\ \Psi (0)&=\Psi _0. \end{aligned}$$

The initial values of \(y_\text {1,0}\) and \(\dot{y}_\text {1,0}\) can be converted to find \(\Psi _0\) and \(A_0\). To achieve this, consider the solution of the linearized differential equation of the center of mass neglecting the small right-hand side

$$\begin{aligned} \ddot{y}_1+y_1= & {} 0, \end{aligned}$$
(45)
$$\begin{aligned} y_1(0)= & {} y_{1,0}, \end{aligned}$$
(46)
$$\begin{aligned} \dot{y}_1(0)= & {} \hat{v}_{1,0}. \end{aligned}$$
(47)

Then, the solution is

$$\begin{aligned} y_1(\tau )= & {} A_0\sin (\tau +\gamma _1), \end{aligned}$$
(48)
$$\begin{aligned} \dot{y}_1(\tau )= & {} A_0\cos (\tau +\gamma _1), \end{aligned}$$
(49)

Comparing these equations to (27 –28) and using the initial conditions (46–47) for \(\tau =0\), one obtains

$$\begin{aligned} A_0= & {} \sqrt{y_{1,0}^2+\hat{v}_{1,0}^2}, \end{aligned}$$
(50)
$$\begin{aligned} \Psi _0= & {} \arctan \left( \frac{y_{1,0}}{\hat{v}_{1,0}} \right) -\beta _1. \end{aligned}$$
(51)

Due to the linearization, the conversion is exact only in the case of a purely quadratic potential; still, for smaller deviations from the quadratic potential, it gives a reasonably good approximation of the initial conditions.

Fig. 3
figure 3

Structure of the resonance manifold (RM) [22] for different values of \(F_1\) and \(\Omega _1\) with the parameters \({m_1=m_2=1}\) and \({y_0=0.2}\). The red line represents the limiting phase trajectory (LPT). The unaffected part of the potential \({[-1+\frac{y_0}{2},1-\frac{y_0}{2}]}\) can be observed by the LPT’s straight alignment. The effective potential has, however, a nonlinear force that requires a minimum amount of exciting force to let the escape happen

Full size image

3.4 Solution by integrating factors

It is possible to write the solution to Eqs. (43)–(44) in a closed form with the use of integrating factors. Let us define

$$\begin{aligned} g(A):=\frac{\hat{v}_1(A)}{U'(A)}=\frac{\sqrt{2(U(A)-U(0))}}{U'(A)}. \end{aligned}$$
(52)

Dividing Eq. (44) by Eq. (43) and reorganising the terms, one obtains

$$\begin{aligned} \underbrace{\delta -\omega ^*(A)+\mu \frac{F_1}{2A} \cos \Psi }_{=:p(A,\Psi )} -\underbrace{\mu \frac{F_1}{2} g(A)}_{=:q(A,\Psi )} \frac{\text {d}\Psi }{\text {d}A}=0. \end{aligned}$$
(53)

An appropriate integrating factor \(\mu (A)\) is given by \(\mu (A):=\text {e}^{\int f(A) \text {d}A}\) with

$$\begin{aligned} f(A):=\frac{1}{q} \left( \frac{\partial p}{\partial \Psi }-\frac{\partial q}{\partial A} \right) =\frac{1}{g(A)} \left( \frac{1}{A}-g'(A) \right) .\nonumber \\ \end{aligned}$$
(54)

Then,

$$\begin{aligned} \mu (A)=\frac{\text {e}^{\int \frac{1}{g(A) A} \text {d}A}}{g(A)}. \end{aligned}$$
(55)

Multiplying (53) by \(\mu (A)\), the partial derivatives of the first integral \(C(A,\Psi )\) can be determined

$$\begin{aligned} \frac{\partial C(A,\Psi )}{\partial A}= & {} \left( \delta -\omega ^*(A)+\mu \frac{F_1}{2A} \cos \Psi \right) \mu (A),\nonumber \\ \frac{\partial C(A,\Psi )}{\partial \Psi }= & {} -\mu \frac{F_1}{2} g(A) \mu (A) \sin \Psi . \end{aligned}$$
(56)

The first integral is then

$$\begin{aligned} C(A,\Psi )&=\mu \frac{F_1}{2} \text {e}^{\int \frac{1}{g(A) A} \text {d}A} \cos \Psi \nonumber \\&\quad +\int \left( \delta -\omega ^*(A) \right) \frac{\text {e}^{\int \frac{1}{g(A) A} \text {d}A}}{g(A)}\text {d}A, \end{aligned}$$
(57)

which is due to its complexity being hardly solvable for any given \(U_0\). Although this is an analytic solution in a closed form, its evaluation is even more elaborate than direct numerical integration. Next, we present the numerical results by direct simulation.

Fig. 4
figure 4

\(\Omega _1\)–\(F_{\text {crit}}\)–diagram of the model-based prediction (red line) and the numerically simulated original two-body system (markers) for \({y_0=0.2}\) (by using \(K=799.5, C=0.1, \Omega _2=40, \beta _2=0 \ \mathrm{and}\ F_2=1.6\)), \(m_1=m_2=1\) and \({A_0=0}\). \(\beta _1=0\)–green circles, \(\beta _1=\frac{\pi }{2}\)–blue squares. A shift to the left in the diagram’s right branch can be observed due to the relative motion of the two bodies to each other. \(F_{\text {crit}}\) has been re-scaled to unit mass, i.e., \({F_{\text {crit}}=\frac{F_\text {1,crit}}{m_1+m_2}}\). (Color figure online)

Full size image
Fig. 5
figure 5

\(\Omega _1\)–\(F_{\text {crit}}\)–diagram of the model-based prediction (red line) and the numerically simulated original two-body system (markers) for \({y_0=0.2}\) (by using \(K=799.5, C=0.1, \Omega _2=40, \beta _2=0 \ \mathrm{and}\ F_2=1.6\)), \(m_1=m_2=1\) and \(A_0=0.5\). \(F_{\text {crit}}\) has been re-scaled to unit mass, i.e., \({F_{\text {crit}}=\frac{F_\text {1,crit}}{m_1+m_2}}\). (Color figure online)

Full size image

4 Numerical results and discussion

Equations (43)–(44) are easy to solve numerically. The structure of the resonance manifold is shown in Fig. 3 for the parameter values \(m_1=m_2=1\) and \(y_0=0.2\).

Figures 4 and 5 show the critical force over the excitation frequency diagram for the case of the truncated quadratic potential with a relative amplitude of the bodies of \(y_0=0.2\) for zero initial conditions, which corresponds to the LPT. Given the initial conditions \(q_1\), \(\dot{q}_1\), \(q_2\) and \(\dot{q}_2\) for the particles, one can determine \(y_\text {1,0}\) and \(\dot{y}_\text {1,0}\) and consequently \(A_0\) and \(\Psi _0\) as well. This allows us to investigate the escape scenarios for nonzero initial conditions as well. For nonzero initial conditions, the diagram of the critical force over the excitation frequency changes its shape.

Figure 6 shows a typical scenario when the escape cannot occur, although a single body would escape for any positive excitation force, as the excitation takes place exactly on the natural frequency of the system. However, the nonlinear boundary of the effective potential does not allow such an escape scenario.

Figure 7 shows the graphs of some effective quantities for the reduced system in the case of asymmetrical mass distribution, \(m_1=2m_2=2\) compared to the original graphs derived from the truncated quadratic potential.

Fig. 6
figure 6

Time-amplitude diagram (black line) and direct integration of the two-particle system (red line). (Color figure online)

Full size image

Figure 8 depicts the \(\Omega _1-F_{\text {crit}}\)-diagrams for the system presented in Fig. 7 with two different starting phase difference values, \(\beta _1=0\) and \(\beta _2=\frac{\pi }{2}\).

4.1 Explanation of the stabilizing effect

To explain the stabilizing effect of the high-frequency excited coupled bodies, note that in Eq. (43), the energy transferred to the system is positive and thus increases the amplitude, consequently leading to escape if the phase of the excitation does not differ by more than \(\pm \frac{\pi }{2}\) from the phase of the motion. However, a phase difference larger than \(\pm \frac{\pi }{2}\) means that the system is delivering work to the exciter, and so A decreases.

Fig. 7
figure 7

Original and effective quantities describing the truncated quadratic potential with \({m_1=2}\), \({m_2=1}\) and \({y_0=0.3}\)

Full size image
Fig. 8
figure 8

\(\Omega _1\)–\(F_{\text {crit}}\)–diagram of the model-based prediction (red line) and the numerically simulated original two-body system (markers) for \({y_0=0.3}\) (by using \(K=799.5, C=0.1, \Omega _2=34.645, \beta _2=0 \ \mathrm{and}\ F_2=1.559\)), \(m_1=2\), \(m_2=1\) and \(y_\text {1,0}=-0.1\). \(F_{\text {crit}}\) has been rescaled to unit mass, i.e. \({F_{\text {crit}}=\frac{F_\text {1,crit}}{m_1+m_2}}\). (Color figure online)

Full size image

Due to the progressive or degressive characteristic of the force resulting from the underlying potential, \(\omega (A)\) is either a monotonously increasing or decreasing function. Therefore, for increasing A, the body swings faster or slower, accumulating an increasing phase difference from the phase of the excitation. If this difference reaches \(\frac{\pi }{2}\) or \(-\frac{\pi }{2}\), the energy transferring from the excitation to the energy of the body turns over to the energy transferring from the body to the exciter, and no escape occurs, at least for the moment.

In the case of the truncated quadratic potential, the degressivity of the effective eigenfrequency has a very remarkable explanation. Once one of the bodies gets out of the potential well, a restoring force is no longer acting on it; thus, the restoring force on the center of mass drops to half of the original value (for \(m_1=m_2\)). This results in softening spring characteristics as the bodies spend increasingly more time outside of the potential well for the increasing oscillation amplitude of the center of mass of the bodies, A.

4.2 Some further remarks

It can also be noted that the convolution operator used to determine the effective potential increases the regularity of the effective potential function. The kernel of the integral, the PDF of the arcsin distribution (16), is a Hölder continuous function with the exponent of the Hölder condition \(\alpha =0.5\).

In the limiting case, when \(y_0\rightarrow 0\), the problem reduces itself to a single body problem, which has been investigated by many authors. This agrees with the model, since the integral kernel tends to a Dirac distribution for \(y_0\rightarrow 0\) by having a PDF, whose integral is by definition 1 and whose support’s length tends to 0.

5 Conclusions

The dynamics of a couple of strongly coupled particles in a potential well under biharmonic resonant excitation have been analytically and numerically investigated. Under the assumption of non-small damping, the system’s dynamics have been reduced to one degree of freedom describing movements of the system’s centre of mass in the modified effective potential well, which takes into account the smoothened probabilistic relative vibrations of the particles. The subsequent application of the averaging procedure for the system being close to a conservative one has enabled very accurate prediction of the escape behaviour, especially for small values of the critical excitation force. Both the analytic and numerical results clearly show the stabilizing effect of the high-frequency relative movements of the pair of particles on their escape behaviour. This effect increases with increasing amplitude of the relative vibrations. Although the obtained analytic results demonstrate excellent agreement with the results of direct numerical simulations of the full system, the investigated problem and the applied approach open a whole class of theoretical and practical questions that must be addressed in the future.

Do two bodies with high-frequency excitation always stabilise the escape behaviour? If not, for what kind of potentials does this not occur? What happens to potentials where \(\omega (A)\) is not monotonous? To what extent could the probability-based modelling approach be applied to describe high-frequency excited physical systems? How large is the uncertainty of the solution caused by this approach? Is there a way to synthesize potentials to shape the form of the \(F_{\text {crit}}(\Omega _1)\)-curve?

The authors hope that these open questions can attract the attention of readers to the fascinating problems of escape dynamics for groups of coupled particles and even more complex structures, opening a broad field for analytic investigations and creative applications.