Phase Growth with Heat Diffusion in a Stochastic Lattice Model

Abstract

When a stable phase is adjacent to a metastable phase with a planar interface, the stable phase grows. We propose a stochastic lattice model describing the phase growth accompanying heat diffusion. The model is based on an energy-conserving Potts model with a kinetic energy term defined on a two-dimensional lattice, where each site is sparse-randomly connected in one direction and local in the other direction. For this model, we calculate the stable and metastable phases exactly using statistical mechanics. Performing numerical simulations, we measure the displacement of the interface R(t). We observe the scaling relation $R(t)=L_x \bar{\mathcal {R}} (Dt/L_x^2)$, where D is the thermal diffusion constant and $L_x$ is the system size between the two heat baths. The scaling function $\bar{\mathcal {R}}(z)$ shows $\bar{\mathcal {R}}(z) \simeq z^{0.5}$ for $z \ll z_c$ and $\bar{\mathcal {R}}(z) \simeq z^{\alpha }$ for $z \gg z_c$, where the cross-over value $z_c$ and exponent $\alpha$ depend on the temperatures of the baths, and $0.5\le \alpha \le 1$. We then confirm that a deterministic phase-field model exhibits the same scaling relation. Moreover, numerical simulations of the phase-field model show that the cross-over value $\bar{\mathcal {R}}(z_c)$ approaches zero when the stable phase becomes neutral.

Appendices

Appendix A: Derivation of the Formulas in Sect. 3

In this section, we derive formulas (16), (17), (18), and (22) in Sect. 3.

1.1 A.1 Derivation of (16)

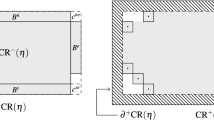
We study a Cayley tree with a root site connected with four sites in the first generation. Each site in the n-th generation $(n \ge 1)$ is connected with three sites in the $n+1$-th generation. See Fig. 13 for the illustration of the Cayley tree.

Fig. 13

Illustration of the Cayley tree

Let Z be the partition function of the Potts model on the lattice. We consider the partition function of a system in which a root site is replaced by the cavity and the state of a site in the first generation is fixed as $\sigma ' \in \{1,\cdots , q\}$, which is denoted by $\tilde{Z}_1(\sigma ')$. Z is then the partition function of the model expressed as

$$\begin{aligned} Z= \sum _{\sigma } \left( \sum _{\sigma '} e^{\beta \delta (\sigma ,\sigma ')} \tilde{Z}_1(\sigma ')\right) ^4. \end{aligned}$$

(A.1)

A graphical representation is displayed in Fig. 14.

Fig. 14

Graphical representation of (A.1)

By setting

$$\begin{aligned} \gamma&\equiv e^\beta -1,\end{aligned}$$

(A.2)

$$\begin{aligned} G_1&\equiv \sum _\sigma \tilde{Z_1}(\sigma ) , \end{aligned}$$

(A.3)

we rewrite (A.1) as

$$\begin{aligned} Z= \sum _{\sigma } \left( \gamma \tilde{Z}_1(\sigma )+G_1 \right) ^4. \end{aligned}$$

(A.4)

Defining $\tilde{Z}_n(\sigma )$ and $G_n$ similarly, we have the iterative equation

$$\begin{aligned} \tilde{Z}_{n}(\sigma )= \left( \gamma \tilde{Z}_{n+1}(\sigma )+G_n \right) ^3, \end{aligned}$$

(A.5)

whose graphical representation is shown in Fig. 15.

Fig. 15

Graphical representation of (A.5)

We define $u_n(\sigma )$ as

$$\begin{aligned} u_n(\sigma )\equiv \frac{\tilde{Z_n}(\sigma )}{G_n}, \end{aligned}$$

(A.6)

which corresponds to the probability of the state $\sigma$ of the cavity-connected site in the n-th generation. By substituting (A.6) into (A.5), we obtain

$$\begin{aligned} G_n u_n(\sigma )&=G_{n+1}^3 \left[ \gamma u_{n+1}(\sigma ) +1\right] ^3. \end{aligned}$$

(A.7)

We also have

$$\begin{aligned} G_n=G_{n+1}^3\sum _\sigma \left[ \gamma u_{n+1}(\sigma )+ 1\right] ^3 \end{aligned}$$

(A.8)

using $\sum _{\sigma } u_n(\sigma )=1$. From (A.7) and (A.8), we derive the iterative equation for $u_n(\sigma )$,

$$\begin{aligned} u_n(\sigma )=\frac{\left[ \gamma u_{n+1}(\sigma )+1\right] ^3}{\sum _\sigma \left[ \gamma u_{n+1}(\sigma )+1\right] ^3 }. \end{aligned}$$

(A.9)

Assuming homogeneity in the equilibrium state, $u_n(\sigma )$ is independent of n in the large-size limit. This provides (16).

1.2 A.2 Derivation of (17)

The order parameter m for the model is calculated by the expectation value of $\delta (\sigma ,1)$ at the root site. That is,

$$\begin{aligned} m=\frac{1}{Z}\sum _{\sigma }\delta (\sigma ,1) \left[ \gamma \tilde{Z}_1(\sigma ) + G_1 \right] ^4. \end{aligned}$$

(A.10)

Using the expression given in (A.4), we have

$$\begin{aligned} m=\frac{[\gamma u_1(1)+1]^4}{\sum _\sigma [\gamma u_1(\sigma )+1]^4}. \end{aligned}$$

(A.11)

By replacing $u_1$ with the solution of the self-consistent equation (16), we obtain (17).

1.3 A.3 Derivation of (18)

To derive the free energy density, we use a tactical method manipulating graphs. We first remove one edge connected to the root site. The partition function of this system with $\sigma$ at the root site and $\sigma '$ at the other site connected by the removed edge is $\tilde{Z}_0(\sigma )\tilde{Z}_1(\sigma ')$. See Fig. 16. We thus express the partition function Z as

$$\begin{aligned} Z&=\sum _{\sigma ,\sigma ^\prime } e^{\beta \delta (\sigma ,\sigma ^\prime )} \tilde{Z_0}(\sigma )\tilde{Z_1}(\sigma ^\prime )\end{aligned}$$

(A.12)

$$\begin{aligned}&=G_0G_1\left[ \gamma \sum _\sigma u_0(\sigma )u_1(\sigma ) +1 \right] , \end{aligned}$$

(A.13)

where $G_0\equiv \sum _{\sigma }\tilde{Z}_0(\sigma )$ and $u_0(\sigma )\equiv \tilde{Z}_0(\sigma )/G_0$. Note that $u_0(\sigma )$ also satisfies (A.9).

Fig. 16

By removing one edge, we get two rooted graphs. $\times$ represents the cavity

Next, we prepare four independent systems. The partition function of the total system is $Z^4$. We remove one edge connected to the root site for each graph. Then, we combine four graphs with the root site by adding one site. See Fig. 17. The partition function of this system, $\check{Z_0}$, is expressed as

$$\begin{aligned} \check{Z_0}=G_0^4\sum _\sigma \left[ \gamma u_0(\sigma )+1 \right] ^4. \end{aligned}$$

(A.14)

Fig. 17

By adding one site, we combine four graphs with the root site

Similarly, another Cayley tree is obtained by combining the other graphs with another added site, and the partition function is written as

$$\begin{aligned} \check{Z_1}=G_1^4\sum _\sigma \left[ \gamma u_1(\sigma )+1 \right] ^4 . \end{aligned}$$

(A.15)

The free energies of the original system and the new system are $-T\log Z^4$ and $-T\log \check{Z_0}\check{Z_1}$, respectively. The difference in free energy is equal to 2f, where f is the free energy density, because the two systems have the same free energy density in the large-size limit and the new system is the original system with two sites added. That is,

$$\begin{aligned} - T\log \check{Z_0}\check{Z_1} + T\log Z^4 = 2f. \end{aligned}$$

(A.16)

This is rewritten as

$$\begin{aligned}&e^{-\beta f}=\left( \frac{\check{Z}_0\check{Z}_1}{Z^4}\right) ^{1/2}\end{aligned}$$

(A.17)

$$\begin{aligned}&=\left( \frac{\sum _{\sigma '}[\gamma u_0(\sigma ')+1]^4 \sum _{\sigma ''}[\gamma u_1(\sigma '')+1]^4}{\left[ \gamma \sum _\sigma u_0(\sigma )u_1(\sigma )+1 \right] ^4} \right) ^{1/2}. \end{aligned}$$

(A.18)

By replacing $u_0$ and $u_1$ with the solution of the self-consistent equation (16), we obtain (18).

1.4 A.4 Derivation of (22)

For later convenience, we set

$$\begin{aligned} \tilde{c} \equiv \frac{1-c}{q-1}. \end{aligned}$$

(A.19)

From the definition of $\tilde{f}$ given in (20), the left-hand side of (22) is calculated as

$$\begin{aligned}&\frac{\partial }{\partial c} e^{-\beta \tilde{f}(\beta ,c)} \nonumber \\&\quad =4\gamma \frac{ (\gamma c+1)^3-(\gamma \tilde{c}+1)^3}{(\gamma c^2+\gamma (q-1)\tilde{c}^2+1)^2} \nonumber \\&\qquad -4\gamma (c-\tilde{c} ) \frac{(\gamma c+1)^4+ (q-1)(\gamma \tilde{c}+1)^4 }{ (\gamma c^2+\gamma (q-1)\tilde{c}^2+1)^3 }. \end{aligned}$$

(A.20)

The self-consistent equation (16) is expressed as

$$\begin{aligned} (\gamma \tilde{c}+1)^3 =\frac{\tilde{c}}{c}(\gamma c+1)^3. \end{aligned}$$

(A.21)

Thus, the right-hand side of (A.20) for the special values of c satisfying (A.21) is calculated as

$$\begin{aligned}&4\gamma \frac{(\gamma c+1)^3 (c-\tilde{c} ) }{c (\gamma c^2+\gamma (q-1)\tilde{c}+1)^2 } \nonumber \\&\quad \times \left( 1-\frac{\gamma c^2+\gamma (q-1)\tilde{c}^2 +c+(q-1)\tilde{c} }{ \gamma c^2+\gamma (q-1)\tilde{c}^2 +1} \right) , \end{aligned}$$

(A.22)

which turns out to be zero from (A.19).

Appendix B: Estimation of $\varDelta$

In this section, we estimate the value of $\varDelta$ defined by (1) for the model we study.

We first calculate the energy density h defined as

$$\begin{aligned} h \equiv \lim _{|\varLambda | \rightarrow \infty } \frac{1}{|\varLambda |} \sum _{\sigma ,p} P_\mathrm{can}(\sigma ,p) H(\sigma ,p), \end{aligned}$$

(B.23)

where $P_\mathrm{can}(\sigma ,p)$ is given in (12). Using the free energy density f calculated in Sect. 3, we express the energy density h as

$$\begin{aligned} h=T+g, \end{aligned}$$

(B.24)

where g is the potential energy density given by

$$\begin{aligned} g(\beta )\equiv \frac{\partial }{\partial \beta } \left( \beta f(\beta ) \right) . \end{aligned}$$

(B.25)

As with the free energy density, $g_0(\beta )$ and $g_*(\beta )$ denote the potential energy densities corresponding to the trivial solution $u_0$ and the nontrivial solution $u_*$ of (16), respectively. In Fig. 18a, $g_0(\beta )$ and $g_*(\beta )$ are displayed. Then, the latent heat per unit volume $T_c\delta s$ at the equilibrium transition temperature is determined by the entropy jump defined as

$$\begin{aligned} \delta s\equiv \beta _c(g_0(\beta _c)-g_*(\beta _c)). \end{aligned}$$

(B.26)

For the model with $q=10$, we obtain $T_c\delta s\simeq 1.07$. Next, we consider the heat capacity per unit volume C expressed as

$$\begin{aligned} C(\beta )\equiv \frac{\partial h}{\partial T} =1+\frac{\partial g}{\partial T}. \end{aligned}$$

(B.27)

Using similar notations, we obtain $C_0(\beta )$ and $C_*(\beta )$ from $g_0(\beta )$ and $g_*(\beta )$. These are shown at the bottom of Fig. 18b. For the cases $q=10$ and $T_L=1.01T_c$, we obtain $C_*(T_L)\simeq 6.95$. Therefore, for the model we numerically study, we have

$$\begin{aligned} \varDelta \simeq 0.05, \end{aligned}$$

(B.28)

which is less than unity. Note that in the stochastic model studied in this paper, C corresponds to $c_p$ in the phase-field model.

Fig. 18

a Potential energy density g as a function of $\beta$. The solid (purple) line represents $g=g_*$ in the range $\beta > \beta _\mathrm{sp}$. The dashed (green) line represents $g=g_0$ in the range $\beta < \beta _\mathrm{un}$. The black line indicates $\beta =\beta _c$. b Heat capacity per unit volume C as a function of $\beta$. The styles (colors) of lines correspond to the graphs in (a) (Color figure online)

Appendix C: Estimation of D

In this section, we estimate the value of the thermal diffusion constant D by measuring the relaxation property of the temperature profile T(x, t), where

$$\begin{aligned} T(x,t)\equiv \frac{1}{L_y}\sum _{y=1}^{L_y} p_{x,y}(t). \end{aligned}$$

(C.29)

For simplicity, we study the case $T_R=T_L=1.2T_c$ with the initial condition

$$\begin{aligned} T(x,0)\equiv 1.2T_c+\sin \left( \frac{\pi (x-1)}{L_x-1}\right) . \end{aligned}$$

(C.30)

To realize the initial condition T(x, 0), $\sigma _i$ is randomly chosen with equal probability and $p_i=T(i_x,0)$ for any i. We then define the spatial average of the local temperature as

$$\begin{aligned} \bar{T}(t)\equiv \left\langle \frac{1}{L_x}\sum _{x=1}^{L_x}T(x,t) \right\rangle , \end{aligned}$$

(C.31)

where $\langle \cdot \rangle$ denotes the average over ten independent samples. Assuming the diffusion equation for T(x, t), we have

$$\begin{aligned} \frac{\bar{T}(t)}{T_c}=1.2+Be^{-D\pi ^2 t/L_x^2}, \end{aligned}$$

(C.32)

where D is the thermal diffusion constant and B is a parameter associated with the initial condition. As shown in Fig. 19, we find that the fitting of (C.31) with (C.32) works well for various system sizes with $B = 1$. From this fitting, we estimate $D = 1.9\times 10^{-2}$.

Fig. 19

$\bar{T}/T_c$ as a function of $\pi ^2t/L_x^2$. The solid line represents the fitting curve (C.32) (Color figure online)