Application of pooled testing in estimating the prevalence of COVID-19

Abstract

Testing at a mass scale has been widely accepted as an effective way to contain the spread of the SARS-CoV-2 Virus. In the initial stages, the shortage of test kits severely restricted mass-scale testing. Pooled testing was offered as a partial solution to this problem. However, it is a relatively lesser-known fact that pooled testing can also result in significant gains, both in terms of cost savings as well as measurement accuracy, in prevalence estimation surveys. We review here the statistical theory of pooled testing for screening as well as for prevalence estimation. We study the impact of the diagnostic errors, and misspecification of the sensitivity and the specificity on the performances of the pooled as well as individual testing procedures. Our investigation clarifies some of the issues hotly debated in the context of COVID-19 and shows the potential gains for the Indian Council for Medical Research (ICMR) in using a pooled sampling for their upcoming COVID-19 prevalence surveys.

1 Introduction

The COVID-19 pandemic, caused by the virus SARS-CoV-2, has been devastating the world now for more than a year. It has created catastrophic social, economic, and health consequences for countries around the world. For an emerging economy like India, it has posed a formidable challenge to the policymakers to contain its spread at a level so that the health care infrastructure is not overwhelmed. While the first COVID-19 case in India was detected on January 30th, 2020, as of 15th December 2020, the number infected has swelled to nearly 10 million, and more than 140,000 deaths have occurred due to COVID-19. India is right now placed second in the world in terms of the total number of cases, right behind the United States, and is battling the rapid rise in the number of cases and resultant unprecedented economic and social consequences. While the government is desperately looking for an exit route to bring the economy back to normalcy, it is facing considerable challenges in the implementation of social distancing, mass testing, contact tracing, and quarantining which are essential to contain the spread of the virus. Given that a large percentage of COVID-19 cases are asymptomatic and are responsible for spreading the virus (Aguilar et al. 2020; Medical Xpress 2020; Yu et al. 2020), it has been advised by the World Health Organization (WHO) that the most effective way to control the spread of the disease is to test as many people as possible. For example, their guidance document on implementing and adjusting public health and social measures suggests testing at least one person per 1000 population per week (WHO 2020a). This was found to be effective in containing the spread of the virus in the initial phases in countries like South Korea, Singapore, and China. However, the high cost and the short supply of testing kits (Alluri and Pathi 2020) are the main impediments for a country like India in conducting mass testing. In order to ramp up the testing efforts, some experts (Bilder et al. 2020; Hanel et al. 2020; Lakdawalla et al. 2020; Pouwels et al. 2020) recommended the use of pooled testing technique, a technique originally proposed by Dorfman (1943) to increase the speed, and reduce the cost, of screening the US army recruits for syphilis during the Second World War. In April 2020, the Indian Council for Medical Research (ICMR) gave its approval (SNS 2020) and issued detailed guidelines (ICMR 2020) for carrying out pooled testing for screening purposes, which was subsequently followed by the Indian states.

In addition to the attempts made towards the containment of the disease, it is also of vital importance to understand the true spread of the disease. To understand the spread of Covid-19 in India, ICMR has conducted two serosurveys (till December 2020), the first during May–June 2020 (Murhekar et al. 2020), and a second one during September–October 2020. A third survey is being planned for the early part of 2021 (Mudur 2020). Such surveys are extremely important to plan for the future requirement of resources to fight the disease effectively. Moreover, as observed by many (Bendavid et al. 2021; Li et al. 2020), the estimation of the prevalence of the SARS-CoV-2 virus is crucial for an accurate estimation of the fatality rate. The initial estimate of the fatality rate given by WHO (2020b) was scandalously high because it was based only on deaths among symptomatic patients. Later, it was revised downward after taking into consideration the fact that a significant percentage of the infected population is asymptomatic, and hence remains undetected. If 80% of the cases are asymptomatic, then the fatality rate computed only from the symptomatic cases would be five times higher than the true fatality rate. Such misinformation may create unnecessary panic in the minds of policymakers, which may lead to wrong decisions. Several serology surveys have been carried out for the estimation of the prevalence of the SARS-CoV-2 virus (Sempos and Tian 2020), and the results suggest that the overestimation of the fatality rate in the population may be between fifty to eighty-five times the original fatality rate. The first serosurvey by ICMR in April–May 2020 in India estimated the true spread of the disease to be 6,468,388 (95% CI: 3,829,029–11,199,423). When compared with the fact that the laboratory-confirmed cumulative number of cases was only around 395,000 even on June 20th, 2020 (Murhekar et al. 2020), it may be said that the findings of the Indian serosurvey were largely in the lines of the findings of Sempos and Tian (2020).

The challenges to be faced by the ICMR in conducting a major survey like this are many. A good estimate requires a large sample size, lack of which may result in a very wide confidence interval, as reported above. Further testing for coronavirus is expensive. As per a recent report (Ghosh and Dasgupta 2020), the cost of the gold standard test for coronavirus, the reverse-transcription polymerase chain reaction test (RT-PCR test), costs the government around Rs. 1 Crore for 10,000 tests, which comes to around Rs. 1000 per test. The ICMR serosurveys used multiple tests to increase their efficacy: the samples were pre-processed using centrifugation, then subjected to commercial ELISA tests, and followed by Euroimmun SARS-CoV-2 ELISA tests for reconfirmation of positive cases (Murhekar et al. 2020). While the cost of the procedure was never reported, a study of the cost for these tests in commercial establishments in India suggests that the per-sample cost would have been close to that of the RT-PCR tests. Hence, controlling the cost, while increasing the sample size, will be vital for the subsequent surveys.

Secondly, as widely reported, although the RT-PCR tests themselves are highly accurate, the sample collection and preservation procedures for the coronavirus tests are not very simple, and introduce significant errors, both false positives, and false negatives, in the RT-PCR test results (Lakdawalla et al. 2020). The sensitivity and specificity of the ELISA assays in laboratory conditions were 92.4 and 97.9 percent, respectively. When we consider that serum was separation was done in local health facilities and transported to the laboratories in the designated ICMR institutes under cold chains, as reported by Murhekar et al. (2020), it is clear that the ELISA tests would also suffer the preservation issues. This also can pose significant challenges in estimating the correct prevalence rates.

It is interesting to observe that most experts recommend the use of pooled testing only for screening purpose. However, the data collected by pooled testing can also be effectively utilized for the estimation of the prevalence of the virus, which is a later development in pooled testing research (Roy and Banerjee 2019). This fact is not as widely known as the use of pooled testing for screening purposes in the general scientific community. We will revisit these results in Sect. 4, and show that pooled testing can be very effective in controlling cost, as well as controlling for estimation errors arising from false positives.

This article mainly serves two purposes. First, we revisit the statistical theory of the pooled testing procedure for screening, and also for the estimation of prevalence using basic probability theory (Feller 1968). Next, we discuss some practical issues arising out of the fact that these tests are imperfect. In other words, the tests may yield false positive and/or false negative results. Naturally, it raises an important practical question: what is the impact of these diagnostic errors on screening as well as on prevalence estimation? What can we do if we do not have an accurate idea about the rate of diagnostic errors? We study these effects using some hypothetical scenarios and discuss their implications in the context of the COVID-19 pandemic.

The rest of the article is divided as follows. In Sect. 2 we present Dorfman’s methodology of pooled testing. In Sect. 3 we discuss the consequences when the test is imperfect. In Sect. 4, we discuss the estimation of prevalence using pooled data and compare it with the estimation procedure with individual data. Finally, we conclude with some remarks in Sect. 5.

2 Dorfman pooled testing technique

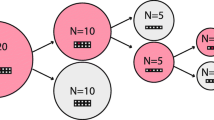
Pooled testing was originally introduced by Dorfman (1943) in infectious disease studies to reduce the cost and increase the speed of data collection. Typically, for an infectious disease, a sample of blood or urine is tested for the presence or absence of the disease. Rarer the disease, the more effective is the pooled testing technique. Dorfman’s technique runs as follows. Suppose n samples of blood are to be tested for the presence or absence of a disease. A sample is either positive (disease present) or negative (disease absent). We attach a dichotomous variable Y to each sample: we assume Y = 1 if the sample is positive, and Y = 0 if it is negative. Instead of testing the samples individually, the samples are pooled into J groups of sizes${n}_{1}, \ldots ,{n}_{J}$. Let ${Y}_{ij}$ denote the Y -value for the ith sample in the jth group. The samples in each group are pooled and tested. Instead of observing${Y}_{ij}$, in the pooled testing set-up, we observe ${Y}_{j}^{*}$=${max}_{i=1, \ldots , {n}_{j}}{Y}_{ij}$, the maximum of ${Y}_{1j}, {Y}_{2j}, \ldots , {Y}_{{n}_{j}j}.$ Notice that this value is 0 if all${ Y}_{ij}$’s in the group equal to 0, and is 1 if even one of them is equal to 1. In other words, ${Y}_{j}^{*}$ = 0 if and only if all samples in the jth group are negative, i.e., ${Y}_{ij}$ = 0, i = 1, $\ldots ,{n}_{j}$ and ${Y}_{j}^{*}$ = 1, if and only if at least one sample in the jth group is positive, i.e., ${Y}_{ij}$ = 1 for at least one i = 1,$\ldots ,{n}_{j}$. If for a group, the test outcome is positive, then the samples in the group are individually tested to detect the positive samples, and hence the diseased individuals. If the result is negative for a group, then no further testing is required. Thus, for a positive test outcome, the number of tests required is one more than the group size, and for a negative test outcome, a single test is enough. If the chance of a positive test outcome for a group is small, in other words, the prevalence of the disease is low, then the average number of tests required would be much smaller in a group testing set-up than individual testing. Thus, it leads to considerable savings in the cost and time of testing. The process diagram is presented in Fig. 1 for a group of size k.

Fig. 1

Process diagram of Dorfman’s algorithm for pooled testing

Now, suppose that the prevalence of a disease is p, and assume without loss of any generality n_j = k, i.e., all groups are of equal size, and consequently n = Jk. Notice that, $P\left({Y}_{j}^{*}=0\right)={\left(1 - p\right)}^{k}$ and $P\left({Y}_{j}^{*}=1\right)$ = 1 − (1 − p)^k. Further, suppose N_j denotes the number of tests for the jth group. Clearly, it is equal to k + 1 if ${Y}_{j}^{*}$ = 1, and 1 if ${Y}_{j}^{*}$ = 0. Thus, the expected number of tests for the jth group, which we henceforth write as E(N_j), is given by

$$E({N}_{j}) = (k + 1) - k{\left(1 - p\right)}^{k}.$$

(1)

If the value of p is small then E(N_j) is close to 1 even for a sufficiently large group size k, and thus leading to a substantial saving in time and cost than individual testing. Notice that the technique is mainly useful when the prevalence is low. In particular, by rearranging (1), we can see that we require $p<1-\frac{1}{{k}^{1/k}}$ for a group size k to be beneficial. A little bit of trial and error shows that no benefit can be achieved if $p\ge 1-\frac{1}{{3}^\frac{1}{3}}=0.3066,$ a fact first noted by Finucan (1964). Note, however, that this limit is valid only for perfect tests. Interesting situations emerge when the tests are less than perfect, which we discuss in the next section.

The simplicity of the idea, and its easy implementation, have led to its wide applicability in different fields, see Roy and Banerjee (2019) and the references therein. Its use in the screening of sexually transmitted diseases like chlamydia, gonorrhea (Lewis et al. 2012), and HIV (Litvak et al. 1994; Wein and Zenios 1996) is worth mentioning. American Red Cross and the European Blood Alliance routinely use it to screen donated blood for infectious diseases, see Aprahamian, Bish, and Bish (2019) and Bilder (2019). Given the huge shortage of test kits around the world, researchers worldwide are recommending the use of pooled testing for COVID-19 (Bilder et al. 2020; Abdalhamid et al. 2020; Lohse et al. 2020; Yelin et al. 2020).

3 Pooled testing for screening when the test is imperfect

Dorfman (1943) proposed the pooled testing technique assuming the test to be perfect, i.e., the chance of a false positive or a false negative test result to be zero. However, in reality, tests are far from perfect. In testing for the SARS-CoV-2 virus, two types of tests are mainly in use. As per Ferran (2020), “the first is a reverse-transcription polymerase chain reaction test or RT-PCR. This is the most common diagnostic test used to identify people currently infected with SARS-CoV-2. It works by detecting viral RNA in a person’s cells – most often collected from their nose. The second test being used is called a serological or antibody test. This test looks at a person’s blood to see if they have produced antibodies for the SARS-CoV-2 virus. If a test finds these antibodies, it means a person was infected and made antibodies in response”. How accurate are these tests? The accuracy of a test is measured by two numbers: sensitivity and specificity attached to it. If a test has a 5% chance of a false negative (positive) outcome, its sensitivity (specificity) is 95%. Although in a laboratory setting it is observed that the RT-PCR test has high sensitivity and specificity, in the real world testing condition the sensitivity and the specificity are usually much lower because of the testing conditions, the method of sample collection and the sample preservation technique are far from perfect. For example, in the real-world testing condition, the sensitivity of the RT-PCR test ranges between 66 and 80% (Ferran 2020). Thus, out of three infected people on average one may test negative. The sensitivity and specificity of the antibody tests are also found to be very high in a laboratory setting, but, then again, in real-world conditions, the accuracy is bound to suffer.

Using the same notations as above, we now find E(N_j) assuming that the sensitivity and specificity of the test are S_e and ${S}_{p}$, respectively. Notice that due to the possible errors in testing, for the jth group, we now observe ${\widehat{Y}}_{j}^{*}$ instead of ${Y}_{j}^{*}$, a surrogate (or proxy) for ${Y}_{j}^{*}$, where ${S}_{e}$ is the conditional probability of the test outcome coming positive for group j when it should, i.e., $P\left({\widehat{Y}}_{j}^{*}= 1|{Y}_{j}^{*}= 1\right)= {S}_{e}$ and P(${\widehat{Y}}_{j}^{*}$ = 0|${Y}_{j}^{*}=0)={S}_{p}$. A simple probability calculation then yields P(${\widehat{Y}}_{j}^{*}$ = 1) = P(${Y}_{j}^{*}$ = 1)S_e + P(${Y}_{j}^{*}$ = 0)(1 − ${S}_{p}$) = S_e + (1 − p)^k(1 − ${S}_{p}$  − S_e), and hence,

$$E\left({N}_{j}\right)=1 + k[{S}_{e}+{(1-p)}^{k}(1 - {S}_{p} - {S}_{e})].$$

(2)

The expected number of tests for n people would then be J × E(N_j), and hence compared to the individual testing, the reduction in the number of tests achieved by using group testing is J × (k − E(N_j)). This reduction is a measure of the efficiency of the pooled testing procedure. Also, notice that for ${S}_{p}$ = S_e = 1, i.e., when the test is perfect, Eq. (2) reduces to (1).

In the previous section, we saw that for a perfect test, i.e., when ${S}_{p}$  = S_e = 1, we need p < 0.3066. However, when the test is less than perfect, this limit can vary drastically. We now provide an illustration. First, we note that, from (2), the maximum value of p for which group testing can be beneficial, satisfies

$${\left(1-p\right)}^{k}>\frac{\frac{1}{k}+{S}_{e}-1}{{S}_{p}+{S}_{e}-1}.$$

Now, this means that when ${S}_{e}<1,$ and ${S}_{p}+{S}_{e}>1,$ the left-hand side of the above inequality can be made negative by choosing a suitably large value of k, and hence for any value of p, there can be a benefit in performing a group test. For illustration, if ${S}_{p}$ = S_e = 0.9, and p = 0.9, we require ${0.9}^{k}>\frac{1.25}{k}-0.125.$ The right-hand side of this inequality is clearly less or equal to zero for $k\ge 10,$ and hence this inequality is achieved for all $k\ge 10.$ (In fact, by trial and error, we can see that this inequality is valid for all positive integers $k\ge 2$.) Hence, for an imperfect test, it may be possible to see a benefit in group testing even when the disease is widely prevalent. It is, of course, true that more significant benefits are achieved when the values of p are relatively lower.

For a perfect test, there is no chance of misclassification of an infected as non-infected or vice versa, and hence the efficiency of the pooled testing procedure is measured only by E(Nj). However, for an imperfect test, E(Nj) is not enough to judge the efficiency of the pooled testing procedure. One also needs to measure the sensitivity and specificity of the pooled testing procedure, and most importantly, the probabilities of the diagnostic errors.

Let T+ and T− respectively denote the events (situations) that an individual is tested positive and negative, respectively, by the pooled testing procedure. Further, let I (${I}^{C}$) denote the events that an individual is infected (uninfected). Then one can easily check that the sensitivity, say, ${S}_{e}^{D},$ and specificity, say, ${S}_{p}^{D}$, of the Dorfman’s pooled testing procedure, are given by

$${S}_{e}^{D}=P\left({T}^{+}|I\right)= {S}_{e}^{2},$$

(3)

and

$${S}_{p}^{D}=P\left({T}^{-}|{I}^{c}\right)= 1-(1-{S}_{p})[{S}_{e}+\left(1-{S}_{p}-{S}_{e}\right){\left(1-p\right)}^{k-1}$$

(4)

respectively. The proofs of (3)–(4) are given in the Appendix.

Notice that ${S}_{e}^{D}$ depends only on S_e while ${S}_{p}^{D}$ depends on all three parameters ${S}_{e}$, ${S}_{p}$ and p. As stated above, ${S}_{e}^{D}$ and ${S}_{p}^{D}$ provide useful information about the performance of the pooled testing procedure. However, the posterior or inverse probabilities $P\left({I}^{c}|{T}^{+}\right)$ and $P\left(I|{T}^{-}\right)$, called the False Positive Predictive Value (FPPV) and the False Negative Predictive Value (FNPV) respectively, are often critical for assessing the performance of the test in a real-life situation. These are measures of diagnostic errors. The FPPV and the FNPV represent the proportion of misclassified individuals among those who are tested positive, and among those who are tested negative, respectively. In the context of testing for sera samples of HIV virus, Litvak et al. (1994) proposed that the five key elements to be used to capture the overall performance of a pooled testing procedure should be: E(N_j), ${S}_{e}^{D},{S}_{p}^{D}$, FPPV and FNPV.

Now, using Bayes’ theorem (Feller 1968), one can easily show that

$$FPPV= \frac{(1-p)(1-{S}_{p}^{D})}{\left(1-p\right)\left(1-{S}_{p}^{D}\right)+p{S}_{e}^{D}}; FNPV=\frac{p(1-{S}_{e}^{D})}{p\left(1-{S}_{e}^{D}\right)+\left(1-p\right){S}_{p}^{D}} .$$

(5)

Notice that for individual testing FPPV and FNPV, denoted henceforth FPPVI and FNPVI respectively, are obtained by substituting ${S}_{e}^{D}$ and ${S}_{p}^{D}$ by Se and ${S}_{p}$ respectively in (5). In Tables 1 and 2, we furnish the values of efficiency, ${S}_{e}^{D}, {S}_{p}^{D},$ FPPV, FNPV, FPPVI, and FNPVI for some appropriately chosen values of the sensitivity (Se), the specificity (${S}_{p}$) and the prevalence (p). The “Eff” (efficiency) column gives the percentage reduction in the expected number of tests achieved by using the pooled testing than the individual testing. For a visual comparison of these factors, we also have plotted efficiency, ${S}_{e}^{D}, {S}_{p}^{D},$ FPPV, FNPV for different values of p in Fig. 2.

Table 1 Optimal group size (k^*), efficiency in terms of reduction in test numbers as percentage of number of individuals tested (Eff), pooled testing sensitivity (${S}_{e}^{D}$) and specificity (${S}_{p}^{D}$) false positive predictive value (FPPV) and false negative predictive value (FNPV) corresponding to different prevalence rates (p), sensitivities (S_e) and specificities (${S}_{p}$) for Dorfman’s algorithm. False positive predictive value (FPPV_I) and false negative predictive value (FNPV_I) for individual tests are given within parentheses to facilitate comparison

Fig. 2

Surface plots representing efficiency, ${S}_{e}^{D}, {S}_{p}^{D},$ FPPV and FNPV for different values of S_e and S_p for p = 0.01, 0.02, 0.05 and 0.10. ${S}_{e}^{D}$ is independent of p and hence only one common surface plot is produced

Evidently, with an increase in p, and decrease in S_e and ${S}_{e}$, the efficiency reduces, as is evident from Fig. 2a. The value of ${S}_{e}^{D} (= {S}_{e}^{2})$ is always less than, or equal to, ${S}_{e}$, as can also be observed in Fig. 2b. However, for a given set of values of p, S_e and ${S}_{p}$, the value of ${S}_{p}^{D}$ is always more than ${S}_{p}$ and for smaller values of ${S}_{p}$, this effect is substantial. Thus, the pooled testing procedure may lead to a significant improvement of the specificity, especially when the specificity of the individual test is low, see Fig. 2c. From Fig. 2d, we can observe that even a slight decrease in ${S}_{p}$ leads to a substantial increase in the value of FPPV for any given values of p and S_e. On the other hand, a change in the value of S_e has a negligible effect on the value of FPPV for any given values of p and S_p. Also, with an increase in p, FPPV decreases for any given values of S_e and S_p. Most importantly, compared to the individual testing, the pooled testing leads to a substantial reduction in the value of FPPV, which is extremely important from the point of view of its application in practice. Still, FPPV can take very high values even for pooled testing for a low prevalence disease with low ${S}_{p}$. While this is undesirable, this compares favorably to individual testing. In contrast, for the range of values considered in Tables 1, 2 and Fig. 2 for p, S_e and ${S}_{p}$, the impact of changes in the values of these parameters has little effect on FNPV, as is obvious from Fig. 2e.

Notice that in case both the sensitivity and the specificity of the test are low, say, for example, S_e = 0.8 and ${S}_{p}$ = 0.7, even with 10% prevalence, 68% (77%) of the pooled (individual) testing results would be falsely positive, which is extremely high. A recent meta-study by Kucirka et al. (2020), a group of medical professionals from the Johns Hopkins University, demonstrated that over different varieties of RT-PCR tests, which are the most commonly used tests for SARS-CoV-2, a best-case scenario is a S_e ≈ 0.8. Another meta-study, by Cohen and Kessel (2020), has looked at thirty-seven different external quality assessment studies of different medical assays and found that in some cases, the specificity was as low as 0.83.

For testing for the SARS-CoV-2 virus, the above observations suggest that at places still at the initial phase of the pandemic, where the prevalence is low, (less than 10%,) pooled testing may lead to a substantially lower rate of false positive cases than individual testing, especially if a low specificity test is used. Admittedly, pooled testing leads to a slightly higher rate of false negative cases compared to individual testing, but as observed from Table 1, that effect is usually negligible.

Finally, it may be noted here that the impacts of the two diagnostic errors are asymmetric. In case of more false positive cases, more people are to be quarantined leading to a lot of economic, social, and emotional turmoil. On the other hand, in case of more false negative results, more infected people will be released into the population causing the disease to spread faster. Where detection and containment of the disease is the goal, the policy planner must make a trade-off. However, these considerations are not relevant when the goal is to the estimation of prevalence.

4 Estimation of prevalence using pooled testing data

In this section, first, we present the theory of estimation of the prevalence of a disease from the test data using basic probability theory (Feller 1968). Next, we study the impact of misspecification of sensitivity and specificity on the estimate of prevalence.

An accurate estimation of the prevalence of SARS-CoV-2-virus, being critical for assessing the lethality of the pandemic, is crucial for the policymakers to make strategic decisions. Recently, Ioannidis (2020), lamented in a highly critical opinion piece on COVID-19: “Three months after the outbreak emerged, most countries, including the U.S., lack the ability to test a large number of people and no countries have reliable data on the prevalence of the virus in a representative random sample of the general population.” Ioannidis argued that in the absence of such data, the estimate of fatality rate is bound to be a substantial overestimate of the true fatality rate if a significant percentage of COVID-19 cases are undetected. It is now well known that a significant percentage of COVID-19 cases are asymptomatic. Raman R Gangakhedkar, chief epidemiologist, ICMR, reported “Of 100 people with infection, 80 do not have symptoms,” (Thacker 2020). A lab in Iceland has suggested that 50% of the infected are asymptomatic, see John (2020). According to a report by Arnold (2020), in a Boston homeless shelter, out of 400 guests staying there, 146 tested positive for COVID-19, but all were reported to be asymptomatic. If, for example, 80% of the cases are asymptomatic, then the estimate of fatality rate would naturally be five times the true fatality rate. While the reported percentage of asymptomatic cases vary from place to place, all agree that it is significant. Considering the possibility of substantial underestimation of infected cases in the absence of test data, Ioannidis has contended that the virus could be less deadly than people think, and destroying the economy in the effort to fight with the virus could be a “once-in-a-century-evidence-fiasco”.

A recent research paper published by Bendavid et al. (2021) lends support to Ioannidis’ contention. By estimating the prevalence of SARS-CoV-2 virus among the residents of Santa Clara County of California using antibody test data of a “properly selected” sample of 3300 residents, it predicted that between 50 and 85 times more residents of the county were actually infected than what appeared in the official tallies, see Regaldo (2020). The authors claimed that “their data helps prove ··· if undetected infections are as widespread as they think, then the death rate in the county may be less than 0.2%, about a fifth to a tenth other estimates.” The publication of this research paper immediately created waves in social media, in the press, and policy circles; if indeed, this number is not far from the truth, then the COVID-19 fatality rate is not very different from common flu. Realizing the findings’ serious policy implications, especially its lending support to the view of lifting the lockdown, some scientists immediately issued a caveat about the accuracy of the estimate. They expressed concerns about the flaws in the sample selection method (through Facebook advertisements), the statistical analysis carried out, and the reliability of the antibody tests (Bajak and Howe 2020; McCormick 2020).

We now discuss the methodology used by Bendavid et al. (2021) for prevalence estimation based on individual serological testing data. Let us denote the probability of a positive test result for an arbitrarily chosen individual by π. Clearly, for a sample of size n, the estimate of π is simply the proportion of people being identified as positive out of the sample. But we know from the previous section that

$$\pi = P(\mathrm{Positive result}) = (1 - p)(1 - {S}_{p}) + p{S}_{p}$$

(6)

Plugging in the proportion of positive test results obtained from the sample, say $\widehat{\pi }$, for π in (6), we obtain.

$$\widehat{p}=\frac{\widehat{\pi }+{S}_{p}-1}{{S}_{e}+{S}_{p}-1}. $$

(7)

However, for estimating prevalence using Dorfman’s algorithm, we simply need to replace S_e and S_p in (6) by ${S}_{e}^{D}$ and ${S}_{p}^{D}$ respectively (cf. Eqs. (3)–(4)). Thus, we have

$$\pi = \left(1 - {S}_{p}\right)\left(1 - {S}_{p}- {S}_{e}\right) {(1-p)}^{k} + \left(1 - {S}_{p}\right){S}_{e}(1 - p) + p{S}_{e}^{2},$$

(8)

or, equivalently,

$$\pi = \left(1 - {S}_{p}- {S}_{e}\right)\left[\left(1 - {S}_{p}\right){(1-p)}^{k} - p{S}_{e}\right]+ \left(1-{S}_{p}\right){S}_{e}.$$

(9)

Now, when Dorfman’s algorithm is used, and the estimate of π is given by ${\widehat{\pi }}^{D}$, the sample proportion of positive results, we can show that ${\widehat{\pi }}^{D}$ is unbiased and consistent for π, and moreover $\sqrt{n}\left({\widehat{\pi }}^{D}-\pi \right)\to N\left(0, C\right),$ where

$$C=\left(\pi -{\pi }^{2}+\frac{k-1}{2}{\left(1-p\right)}^{k+2}{\left(1-{S}_{p}\right)}^{3}+\left(1-{\left(1-p\right)}^{k}\right){S}_{e}{\left({S}_{e}p+\left(1-{S}_{p}\right)\left(1-p\right)\right)}^{2}\right).$$

The details are given in Appendix B.

Now, from (9) we observe that $\frac{d\pi }{dp}=$ $\left({S}_{e}+{S}_{p}-1\right)\left[\left(1 - {S}_{p}\right){(1-p)}^{k-1}+{S}_{e}\right]$, whose sign is the same as that of $\left({S}_{e}+{S}_{p}-1\right);$ as long as ${S}_{e}+{S}_{p}\ne 1$. In practice, S_e and S_p are both high (> 0.5) and so ${S}_{e}+{S}_{p}$ is always positive. Therefore, π is a strictly monotonic function of p, and therefore, if the value of π is known, from (9) we can easily solve for p using a suitable numerical algorithm, e.g., a grid search algorithm. In the current paper, we achieve that using the uniroot function from the statistical software R, which computes the real roots of a polynomial within a given range by implementing an algorithm by Brent (1973) through successive linear interpolations. In Table 2, we report the values of π, the probability of testing positive, for the individual testing as well as for the Dorfman testing procedure, for different values of p, S_e and S_p. We denote by π_I (cf. Equation (6)) and π_D (cf. Equation (8)) the π values corresponding to the individual and Dorfman testing procedure, respectively. Figure 3 and Table 2 compare the values of π_I and π_D for different values of p. It is evident that individual testing leads to a much higher chance of testing positive compared to pooled testing when the test is not perfect.

Table 2 Expected values of the proportion of samples testing positive (π) corresponding to different prevalence rates, sensitivities (S_e) and specificities (${S}_{p}$) for individual testing (π_I) Dorfman’s algorithm (π_D). The π_D values are based on k = 4, the most conservative pooling choice from Tables 1

Fig. 3

Surface plot of π_I and π_D for p = 0.01, 0.02, 0.05 and 0.10

Plugging in ${\widehat{\pi }}^{D},$ the estimate of π obtained from the test data, in (8) or (9) and then solving it numerically for p, we can get an estimate of p, say ${\widehat{p}}^{D}$. This estimate, although biased, is consistent for p, and $\sqrt{n}\left({\widehat{p}}^{D}-p\right)\to N(0, C^{\prime})$, where ${C}^{^{\prime}}=\frac{C}{\left|\frac{d\pi }{dp}\right|},$ $\frac{d\pi }{dp}=\left({S}_{e}+{S}_{p}-1\right)\left(\left(1-{S}_{p}\right)k{\left(1-p\right)}^{k-1}+{S}_{e}\right).$ This allows us to construct confidence intervals for p, for example, an approximate level-α confidence interval for p is given by ${\widehat{p}}^{D}\pm {z}_{\alpha /2}\frac{\widehat{C}^{\prime}}{\sqrt{n}}$, where $\widehat{C}^{\prime}$ is the plug-in estimator of C′, and z_α/2 is the upper α/2th quantile of the standard normal distribution. The details of the derivations are given in Appendix C.

As noted in Sect. 3, both RT-PCR and antibody tests have high sensitivity and specificity in lab settings, but in a real-world situation, these values may be substantially lower than those obtained in lab settings. Suppose ${S}_{e}^{P}$ and ${S}_{p}^{P}$ are respectively the sensitivity and the specificity values as perceived and used by the scientist for estimating the prevalence from Eq. (7) or (8), whereas ${S}_{e}^{T}$ and ${S}_{p}^{T}$ are respectively the true sensitivity and specificity values in the field. In real-life situations, it is often the case that ${S}_{e}^{T} ({S}_{p}^{T})$, is substantially less than ${S}_{e}^{P} ({S}_{p}^{P})$, because the scientist’s perceived values are usually influenced by the values under the lab setting. Thus, given the true value of π, the solution to Eq. (7) or (8) for p is equal to the true prevalence p_T if S_e and S_p are replaced ${S}_{e}^{T}$ and ${S}_{p}^{T}.$ On the other hand, given the true value of π, replacing S_e and S_p respectively by ${S}_{e}^{P}$ and ${S}_{p}^{P}$ in (7) and (8) would yield a solution p_P which is expected to deviate from the true prevalence p_T. We note that for ${\widehat{p}}_{T}$ and ${\widehat{p}}_{P}$, obtained as above, $\left({\widehat{p}}_{T}-{\widehat{p}}_{P}\right)$ is asymptotically consistent for the true bias $\left({p}_{T}-{p}_{P}\right)$, provided the true sensitivity and specificity values are known. In fact, in such a scenario, we can also provide an approximate level-α confidence interval for the bias, which will be of the form $\left({\widehat{p}}_{T}-{\widehat{p}}_{P}\right) \pm {z}_{\alpha /2}\frac{\widehat{C}"}{\sqrt{n}},$ where $\widehat{C}"$ is the plug-in estimator of C”. For detailed derivation and the expression for $C"$, the readers can refer to Appendix D.

We study the effect of the misspecification of sensitivity and specificity values on the estimate of prevalence by evaluating the bias in the estimation of (p_T − p_P). In Table 3, we report the values of the bias (p_T −p_P) resulting from the individual testing as well as Dorfman’s pooled testing, denoted by bias_I and bias_D, respectively, for different values of p, ${S}_{e}^{P}, {S}_{p}^{P}, {S}_{e}^{T}$ and ${S}_{p}^{T}$. The same are also presented in Fig. 4.

Table 3 Bias ${p}_{T}-{p}_{P}$ when perceived sensitivity (${S}_{e}^{P}$) and specificity (${S}_{p}^{P}$) are higher than the true situations. Bias bias_I corresponds to individual tests, while bias_D corresponds to Dorfman tests. The Dorfman values are based on k = 4, the most conservative pooling choice from Tables 1 and 2. A positive bias means the perceived prevalence is lower than the true prevalence, while a negative bias means the opposite

Fig. 4

Surface plots depicting bias_I and bias_D for different values of p, ${S}_{e}^{P}, {S}_{p}^{P}, {S}_{e}^{T}$ and ${S}_{p}^{T}$

The following patterns are visible from Table 3 and Fig. 4:

• (i) With the increase in the prevalence p, the bias is decreasing. Initially, it reduces from positive to zero and then becomes negative. We report the bias for four different values of p: 0.01, 0.02, 0.05 and 0.10.

• (ii) The effect of misspecification of S_e and ${S}_{p}$ are asymmetric in nature. Misspecification of S_e has a little effect on the bias. However, the misspecification of ${S}_{p}$ has a significantly large effect on the bias. Also, more is the deviation from the true values more is the effect on bias.

• (iii) The most interesting observation is, compared to the individual testing, pooled testing reduces the bias due to misspecification of S_e and ${S}_{p}$ substantially. This is extremely important to know given the fact that misspecification of S_e and ${S}_{p}$ are quite common.

In Table 2, we have reported the values of π, the probability of testing positive, for the individual testing as well as for the Dorfman testing procedure, for different values of p, S_e, and S_p. Notice from Table 2 that, like the observation (ii) made above, the value of π is significantly influenced by ${S}_{p}$ but not so by S_e. Also, it is important to note that, for a given value of ${S}_{p}$ (say, 0.9) reduction in S_e (say, from 1 to 0.7) results in a reduction of π, though not a significant reduction. Thus, we may conclude that misspecification of ${S}_{p}$ (S_e) has a large (negligible) effect on the value of π, and consequently, on the estimates of prevalence obtained by solving Eqs. (6) or (8), as the case may be. So, for accurate estimation of prevalence, it is very important to specify the value of ${S}_{p}$ correctly, while misspecification of S_e has little effect.

Finally, we explain a subtle connection between the numbers reported in Table 2 and 3 with a specific example. Consider the case when prevalence p is equal to 0.01, and the true sensitivity (${S}_{e}^{T}$) and specificity (${S}_{p}^{T}$) are both equal to 0.9. From Table 2, we observe that the corresponding value of π (cf. Equation (6)) for individual testing is equal to 0.11. Suppose now the perceived sensitivity (${S}_{e}^{P}$) and specificity (${S}_{p}^{P}$) are equal to 1. To obtain the biased prevalence p corresponding to the perceived sensitivity and specificity, we plug in 0.11 for π on the left-hand side of Eq. (6), and S_e = ${S}_{p}$ = 1 on the right-hand side. The solution can be obtained from Table 2 by observing the value of p corresponding to S_e = ${S}_{p}$ = 1 and π_I = 0.11, which is clearly 0.11. Thus, the resulting bias due to misspecification is 0.11 − 0.01 = 0.10, which is reported in Table 3. By using a similar argument, we can find the bias for pooled testing which is 0.01 using Table 2.

5 Discussions and concluding remarks

In this article, we have revisited the statistical theory behind Dorfman’s pooled testing technique used for screening. We have explained the method of estimation of prevalence from individual testing and pooled testing data. Most importantly, we have provided insights, by looking into the practical issues that are being discussed in the scientific community, arising out of the fact that the tests for the SARS-CoV-2 virus are imperfect. We have illustrated that pooled testing is not only preferable for reducing the time and cost of screening and widening the net of testing, but it also helps in a significant reduction of misclassification among those who are tested positive. We have noted that for prevalence estimation, pooled testing is preferable to individual testing for a wide range of situations, especially when the specificity of the test is low. It helps in reducing the bias of the prevalence estimate significantly. A particularly interesting point that we have made is that for an imperfect test with a sensitivity less than 1, group testing can lead to cost savings even for a widely prevalent disease, which goes against the commonly held perception that group testing is useful only for low values of prevalence It is worth mentioning, however, that the cost-saving benefits are the most pronounced for the lower prevalence rates.

We note that for estimating the prevalence of SARS-CoV-2 of Santa Clara County, California, Bendavid et al. (2021) collected data by conducting individual antibody tests on the 3300 subjects; a similar procedure was followed by ICMR for its serosurveys as well. Instead, had they used pooled testing technique, it would have been possible to collect the test data from a much larger sample for a similar cost and time. Also, as mentioned in the paper, given that the prevalence was quite low (estimated as 2.8%), adopting pooled testing technique would have made all the more sense in the context of their study.

As a final remark, we would like to emphasize that for countries with limited resources like India, pooled testing provides an avenue to achieve more without straining the resources too much and offers a way to follow the WHO guidance of testing enough members of the population (WHO 2020a). For the upcoming ICMR surveys in estimating COVID-19 spread in India, pooled testing can be effectively used, more so in regions where the virus has not spread widely. In some “hot spots,” the prevalence of the disease may be seen to be more than 10% among the exposed population based on the present testing data where the savings would be less compared to areas where prevalence is less. However, when the goal is the estimation of the prevalence of the disease among the wider population, given that India’s number of cases per million population is still among the lowest in the world (Sarkar 2020; The Hindu 2020), the pooled testing methodology can help ICMR in achieving a significant reduction of cost and time, as well as in increasing accuracy and efficiency.

Appendices

Appendix A: Computation of ${{\varvec{S}}}_{{\varvec{e}}}^{{\varvec{D}}}$ and ${{\varvec{S}}}_{{\varvec{p}}}^{{\varvec{D}}}$

In the context of Dorfman’s testing procedure, ${S}_{e}^{D}$, the probability that a positive person can come positive is the probability that both the pooled test as well as the individual test comes correct, which is ${S}_{e}^{2}$.

To compute the misclassification probability that a person is non-diseased and is found to be diseased, we first note that a non-diseased person, say Person j, can either be a part of a pool constituted entirely of non-diseased individuals (Case A) or a pool containing some diseased individuals (Case B). The probability of Case A is ${\left(1-p\right)}^{k}$, and the probability of Case B is ${\left(1-p\right)-\left(1-p\right)}^{k}$.

Now, for Person j to be found to be diseased in Case A, the pooled test, and subsequently, the individual’s test, will both erroneously give a positive result, the probability of which is ${\left(1-{S}_{p}\right)}^{2}$ for the original Dorfman algorithm. On the other hand, in Case B, the pooled test will be positive, but this time correctly, while the individual’s test will still be erroneously positive, the probability of which is ${S}_{e}(1 - {S}_{p}).$ Putting all together, the probability that a non-diseased person is found to be diseased is $[{\left(1-{S}_{p}\right)}^{2}(1-p)k+{S}_{e}(1-{S}_{p})((1-p)-{\left(1-p\right)}^{k}))]/(1-p)=(1-{S}_{p}){S}_{e}+ (1-{S}_{p})(1-{S}_{p}-{S}_{e}){\left(1-p\right)}^{k-1}$. Hence, ${S}_{p}^{D}$ is $1-\left(1-{S}_{p}\right){S}_{e}+(1 - {S}_{p})(1-{S}_{p}-{S}_{e}){\left(1-p\right)}^{k-1}.$

Appendix B: Derivation of the properties of ${\widehat{{\varvec{\pi}}}}^{{\varvec{D}}}$

Let us define ${\widehat{Y}}_{ij}^{*}$=1 if the ith member of the jth pool is positive, and 0 otherwise, i = 1, …, k, j = 1, …, J. Therefore, we have ${\widehat{\pi }}^{D}=\frac{1}{Jk}\sum_{j=1}^{J}\sum_{i=1}^{k}{\widehat{Y}}_{ij}^{*}$, where Jk = n. As π is the probability of a positive result, E(${\widehat{\pi }}^{D}$) = π. This also means that ${\widehat{\pi }}^{D}$ is consistent for π as $J\to \infty ,$ and k remains fixed. Now, noting that observations from different groups are independent,

$$V({\widehat{\pi }}^{D})=V\left(\frac{1}{n}\sum_{j=1}^{J}\sum_{i=1}^{k}{\widehat{Y}}_{ij}^{*}\right)= \frac{1}{{n}^{2}}\sum_{j=1}^{J}V\left(\sum_{i=1}^{k}{\widehat{Y}}_{ij}^{*}\right) = \frac{Jk}{{n}^{2}}V\left({\widehat{Y}}_{ij}^{*}\right)+\frac{Jk(k-1)/2}{{n}^{2}} (\mathrm{P}({\widehat{Y}}_{i{j}_{1}}^{*}=1, {\widehat{Y}}_{i{j}_{2}}^{*}=1) -{\pi }^{2})= \frac{\pi -{\pi }^{2}}{n} + \frac{k-1}{2n} (\mathrm{P}({\widehat{Y}}_{i{j}_{1}}^{*}=1, {\widehat{Y}}_{i{j}_{2}}^{*}=1) -{\pi }^{2}),$$

where

$$\mathrm{P}({\widehat{Y}}_{i{j}_{1}}^{*}=1, {\widehat{Y}}_{i{j}_{2}}^{*}=1) {=\left(1-p\right)}^{k}{\left(1-{S}_{p}\right)}^{3}{\left(1-p\right)}^{2}+\left(1-{\left(1-p\right)}^{k}\right){S}_{e}{\left({S}_{e}p+\left(1-{S}_{p}\right)\left(1-p\right)\right)}^{2}{=\left(1-p\right)}^{k+2}{\left(1-{S}_{p}\right)}^{3}+\left(1-{\left(1-p\right)}^{k}\right){S}_{e}{\left({S}_{e}p+\left(1-{S}_{p}\right)\left(1-p\right)\right)}^{2}.$$

Therefore,

$$V\left({\widehat{\pi }}^{D}\right)=\frac{1}{n}\left(\pi -{\pi }^{2}+\frac{k-1}{2}{\left(1-p\right)}^{k+2}{\left(1-{S}_{p}\right)}^{3}+\left(1-{\left(1-p\right)}^{k}\right){S}_{e}{\left({S}_{e}p+\left(1-{S}_{p}\right)\left(1-p\right)\right)}^{2}\right).$$

Keeping k fixed, as $J\to \infty , n\to \infty ,$ and $\sqrt{n}\left({\widehat{\pi }}^{D}-\pi \right)\to N(0, C)$, where

$$C=\left(\pi -{\pi }^{2}+\frac{k-1}{2}{\left(1-p\right)}^{k+2}{\left(1-{S}_{p}\right)}^{3}+\left(1-{\left(1-p\right)}^{k}\right){S}_{e}{\left({S}_{e}p+\left(1-{S}_{p}\right)\left(1-p\right)\right)}^{2}\right).$$

Appendix C: Derivation of the properties of ${\widehat{{\varvec{p}}}}^{{\varvec{D}}}$

From (9), we have $\frac{d\pi }{dp}=\left({S}_{e}+{S}_{p}-1\right)\left(\left(1-{S}_{p}\right)k{\left(1-p\right)}^{k-1}+{S}_{e}\right).$ Using the delta-method, we can write that.

${\widehat{\pi }}^{D}-\pi \approx \left({\widehat{p}}^{D}-p\right)\frac{d\pi }{dp}.$ As long as ${S}_{e}+{S}_{p}\ne 1,$ this shows that ${\widehat{p}}^{D}$ is a consistent estimator of p, and, moreover, $\sqrt{n}\left({\widehat{p}}^{D}-p\right)\to N(0, C^{\prime})$, where ${C}^{^{\prime}}=C/\left|\frac{d\pi }{dp}\right|.$

Appendix D: Derivation of the properties of ${\widehat{{\varvec{p}}}}_{{\varvec{T}}}-{\widehat{{\varvec{p}}}}_{{\varvec{P}}}$

The estimates ${\widehat{p}}_{T}$ and ${\widehat{p}}_{P}$ will be obtained by plugging in ${\widehat{\pi }}^{D}$ in both of the following two equations, and solving:

$$\pi = \left(1 - {S}_{p}^{T}- {S}_{e}^{T}\right)\left[\left(1 -{S}_{p}^{T}\right){(1-{p}_{T})}^{k} - {p}_{T}{S}_{e}^{T}\right]+ \left(1-{S}_{p}^{T}\right){S}_{e}^{T}$$

(C.1)

$$\pi = \left(1 - {S}_{p}^{P}- {S}_{e}^{P}\right)\left[\left(1 -{S}_{p}^{P}\right){(1-{p}_{P})}^{k} - {p}_{P}{S}_{e}^{P}\right]+ \left(1-{S}_{p}^{P}\right){S}_{e}^{P}$$

(C.2)

This tells us,

$${\widehat{p}}_{T}-{p}_{T} \approx ({\widehat{\pi }}^{D}-\pi )/ \frac{d\pi }{d{p}_{T}},\mathrm{and }{\widehat{p}}_{P}-{p}_{P} \approx ({\widehat{\pi }}^{D}-\pi )/ \frac{d\pi }{d{p}_{P}}.$$

In other words,

$$\left({\widehat{p}}_{T}-{\widehat{p}}_{P}\right)-\left({p}_{T}-{p}_{P}\right)\approx \left({\widehat{\pi }}^{D}-\pi \right)\left(\frac{1}{\frac{d\pi }{d{p}_{T}}}-\frac{1}{\frac{d\pi }{d{p}_{P}}}\right).$$

This tells us that ${\widehat{p}}_{T}-{\widehat{p}}_{P}$ will be consistent for ${p}_{T}-{p}_{P}$ for large sample sizes, and moreover,

$$\sqrt{n}\left(({\widehat{p}}_{T}-{\widehat{p}}_{P})-\left({p}_{T}-{p}_{P}\right)\right)\to N(0, C"),\mathrm{ where }C"=C\left|\frac{1}{\frac{d\pi }{d{p}_{T}}}-\frac{1}{\frac{d\pi }{d{p}_{P}}}\right|.$$