Energetic boundary element method for accurate solution of damped waves hard scattering problems

Abstract

The paper deals with the numerical solution of 2D wave propagation exterior problems including viscous and material damping coefficients and equipped by Neumann boundary condition, hence modeling the hard scattering of damped waves. The differential problem, which includes, besides diffusion, advection and reaction terms, is written as a space–time boundary integral equation (BIE) whose kernel is given by the hypersingular fundamental solution of the 2D damped waves operator. The resulting BIE is solved by a modified Energetic Boundary Element Method, where a suitable kernel treatment is introduced for the evaluation of the discretization linear system matrix entries represented by space–time quadruple integrals with hypersingular kernel in space variables. A wide variety of numerical results, obtained varying both damping coefficients and discretization parameters, is presented and shows accuracy and stability of the proposed technique, confirming what was theoretically proved for the simpler undamped case. Post-processing phase is also taken into account, giving the approximate solution of the exterior differential problem involving damped waves propagation around disconnected obstacles and bounded domains.

1 Introduction

Wave propagation problems are widely studied because they model a variety of phenomena in everyday life. In this context, while elastic forces tend to maintain the oscillatory motion, the transient effect vanishes because of energy dissipation process, referred to as damping. Usually, the dissipation is generated by the interaction between the waves and the propagation medium. On the other side, for instance in mechanical systems, since damping has the effect of reducing the amplitude of vibrations, it is desirable to have some amount of damping in order to faster achieve an equilibrium configuration. Hence, damping is whether an unavoidable presence in physical reality or a desired characteristic in industrial design (see e.g., the applicative papers [1,2,3,4]).

For these reasons, it is interesting to consider damping terms into the modeling partial differential equations (PDEs): well-known examples are, for instance, the Klein–Gordon or the Telegraph equations (see e.g. [5] and references therein). For what concerns their approximate resolution, while the application of advanced numerical techniques, such as finite element (FEM) and finite difference (FDM) methods, is well established, the Boundary element method (BEM) analysis of dissipation through damped wave equation rewritten as a boundary integral equation (BIE) is a relatively recent research topic [6,7,8] and not yet sufficiently investigated. Note that BEMs are ideally suited for solving problems defined in unbounded domains, such as wave propagation scattering by finite obstacles, because they (i) rewrite the problem over the bounded obstacle and (ii) implicitly fulfill prescribed solution behavior at infinity. Let us further remark that for the numerical solution of this kind of problems, one needs consistent approximations and accurate simulations even on large time domains of analysis.

In principle, both frequency domain [9, 10] and time domain [11, 12] BEM can be used for hyperbolic initial-boundary value problems. Space–time BEM has the advantage that it directly gives the unknown time-dependent quantities; in the case of unbounded domain problems, this is very beneficial. Let us note that Dirichlet absorbing boundary condition methods (see [13,14,15,16,17]) share the same feature. For space–time BEM, the construction of the BIEs, via boundary integral representation formula of the PDE solution, uses the fundamental solution of the hyperbolic differential operator at hand, if available, and jump relations [18]. The mathematical background of time-dependent BIEs is summarized by Costabel in [19].

This paper deals with the numerical solution of wave propagation problems exterior to open arcs in the plane, including viscous and material damping coefficients into the PDE, and equipped by Neumann boundary condition and homogeneous initial conditions. The numerical study of damped waves hard scattering model is a challenging task due to the presence of advection and reaction terms, and the adopted methodology generalizes what has been done in [20] for the much simpler undamped case. The differential problem is written as a space–time BIE whose kernel is given by the hypersingular fundamental solution of the 2D damped waves operator. The integral problem is then solved by a modified energetic BEM, appeared for the first time in its original form in [21]. Here, a suitable kernel treatment is introduced for the efficient evaluation of the discretization linear system matrix entries represented by space–time quadruple integrals with hypersingular kernel in space variables having no analytical time integration available, differently from the undamped case.

The paper is structured as follows: at first, we present the differential model problem on an unbounded 2D domain and its BIE energetic weak formulation. Section 3 briefly summarizes, for reader’s convenience, the main features of Energetic BEM discretization which leads to a final linear system having a lower triangular block Toeplitz matrix. Section 4 highlights the new approach introduced for the evaluation of quadruple space–time integrals with hypersingular damped kernel, giving some details about the adopted quadrature schemes, while in Sect. 5, a wide variety of significant results are presented and discussed, showing, from a numerical point of view, stability and accuracy of the proposed technique, theoretically proved for the undamped case in [20]. Post-processing phase is also taken into account, giving the numerical solution of the exterior differential problem involving damped waves propagation around disconnected obstacles and bounded domains. Conclusions and ongoing research are reported in the last Section.

2 Model problem and its hypersingular BIE energetic weak formulation

In a 2D Cartesian reference system for space variables, we will consider the Neumann problem for the damped wave equation in a bounded time interval [0, T], exterior to an obstacle given by an open arc $\varGamma \subset \mathbb {R}^2$:

$$\begin{aligned}&\Big [\varDelta u-\frac{1}{c^2}\;u_{tt}-\frac{2D}{c^2}u_t-\frac{P}{c^2} u\Big ](\mathbf{x},t)=0,\quad \quad \mathbf{x}\in \mathbb {R}^2\setminus \varGamma ,\, t\in (0,T], \end{aligned}$$

(1)

$$\begin{aligned}&u(\mathbf{x},0)=u_t(\mathbf{x},0) =0, \;\;\quad \quad \quad \qquad \qquad \qquad \qquad \mathbf{x}\in \mathbb {R}^2\setminus \varGamma , \end{aligned}$$

(2)

$$\begin{aligned}&q(\mathbf{x},t){:}{=}\frac{\partial u}{\partial \mathbf{n} }(\mathbf{x},t) = {\bar{q}}(\mathbf{x},t), \qquad \qquad \qquad \qquad \quad \mathbf{x} \in \varGamma ,\quad t \in (0,T], \end{aligned}$$

(3)

where c is the propagation velocity of a perturbation inside the domain, $D\ge 0$ and $P\ge 0$ are the viscous and material damping coefficients, respectively. Denoting by $\varGamma ^-$ and $\varGamma ^+$ the lower and upper faces of the obstacle, n stands for the normal unit vector defined in $\mathbf{x}\in \varGamma$, oriented from $\varGamma ^-$ to $\varGamma ^+$; further, the datum ${\bar{q}}$ represents the opposite of the normal derivative of the incident wave along $\varGamma$, i.e., ${\bar{q}}=- \partial u^I/\partial \mathbf{n }$. In the acoustic framework, the exterior Neumann problem defines the scattering of a plane wave at a hard obstacle [22].

Remark When $D=P=0$, the PDE (1) collapses to the classic wave equation and the considered model problem can be also conceived as the scattering problem by a crack in an unbounded elastic isotropic medium $\Omega =\mathbb {R}^2 \setminus \varGamma$. As usual, the total displacement field can be represented as the sum of the incident field (the wave propagating without the crack) and the scattered field; this latter, under suitable invariance hypothesis, satisfies the Neumann scalar problem (1)–(3) (see e.g., [23]).

Let us consider the double-layer representation of the solution of (1)–(3) (in the particular case of an open arc, the Neumann boundary condition fixes also the jumps of the solution and therefore the only representation formula is the double-layer potential representation [19]):

$$\begin{aligned} u(\mathbf{x},t)= \int _{\varGamma } \int _0^t \frac{\partial G}{\partial \mathbf{n}}_{{\varvec{\xi }}}(r,t-\tau )\, \varphi (\varvec{\xi },\tau )\,\text {d}\tau \, \text {d}\gamma _{{\varvec{\xi }}}, \quad \quad \mathbf{x} \in \mathbb {R}^2 \setminus \varGamma , \quad t \in (0,T], \end{aligned}$$

(4)

where the unknown density $\varphi =[u]_\varGamma$ represents the time history of the jump of u along $\varGamma$,

$$\begin{aligned} G(r,t-\tau )= \left\{ \begin{array}{rl} \frac{c}{2\pi }\,\text {e}^{-D(t-\tau )} \,\frac{\cos \Big (\frac{\sqrt{P-D^2}}{c}\sqrt{c^2(t-\tau )^2-r^2}\,\Big )}{\sqrt{c^2(t-\tau )^2-r^2}}\,H[c\,(t-\tau )-r],&{}P\ge D^2,\\ \\ \frac{c}{2\pi }\,\text {e}^{-D(t-\tau )} \,\frac{\cosh \Big (\frac{\sqrt{D^2-P}}{c}\sqrt{c^2(t-\tau )^2-r^2}\,\Big )}{\sqrt{c^2(t-\tau )^2-r^2}}\,H[c\,(t-\tau )-r], &{}P\le D^2 \end{array} \right. \end{aligned}$$

(5)

is the fundamental solution of the 2D damped wave operator, with $H[\cdot ]$ the Heaviside distribution, and $r{:}{=}\Vert \mathbf{r}\Vert _2=\Vert \mathbf{x}-{\varvec{\xi }}\Vert _2$.

Definition (5) is an extension of fundamental solutions found in [24,25,26], where only the viscous damping coefficient was taken into account, and it has been verified with the use of Mathematica software.

The case $P>D^2$ defines the so-called underdamping configuration, the case $P<D^2$ the overdamping configuration, while the ideal separation state $P=D^2$, referred to the vanishing of both $\cos (\cdot )$ and $\cosh (\cdot )$ arguments, is called critical damping. Furthermore, if we consider $D=P=0$, we recover the fundamental solution of the wave equation in 2D without damping, i.e.,

$$\begin{aligned} G_0(r,t-\tau )=\frac{c}{2\pi }\,\frac{H[c\,(t-\tau )-r]}{\sqrt{c^2(t-\tau )^2-r^2}}. \end{aligned}$$

(6)

Note that the solution of the differential problem can be evaluated at any point outside the obstacle and at any time instant from (4), with a post-processing phase once the density function $\varphi (\mathbf{x},t)$ has been recovered.

To this aim, applying a directional (normal) derivative w.r.t. $\mathbf{x}$ in (4), performing a limiting process for $\mathbf{x}$ tending to $\varGamma$ and using the assigned Neumann boundary condition (3), we obtain the hypersingular space–time BIE

$$\begin{aligned} \int _{\varGamma } \int _0^t \frac{\partial ^2 G}{\partial \mathbf {n_\mathbf{x}} \partial \mathbf {n_{{\varvec{\xi }}}}}(r,t-\tau ) \varphi (\varvec{\xi },\tau )\,\text {d}\tau \, \text {d}\gamma _{{\varvec{\xi }}} = {\bar{q}}(\mathbf{x},t), \qquad \mathbf{x} \in \varGamma ,\;t \in [0,T], \end{aligned}$$

(7)

in the unknown $\varphi (\mathbf{x},t)$, which can be written with the compact notation

$$\begin{aligned} {\mathcal {D}}\varphi = {\bar{q}}. \end{aligned}$$

(8)

The equivalence of (8) with the initially given differential model problem (1)–(3) has been stated for general time-dependent problems in [19].

In order to properly manage equation (8), we introduce the following results.

Proposition 1

Defining the auxiliary kernel ${\tilde{G}}(r,t-\tau )$ as

$$\begin{aligned} \left\{ \begin{array}{rl} \frac{\sqrt{P-D^2}}{2\pi }\,\mathrm{e}^{-D(t-\tau )} \,\sin \Big (\frac{\sqrt{P-D^2}}{c}\sqrt{c^2(t-\tau )^2-r^2}\,\Big )\,H[c\,(t-\tau )-r], &{}P\ge D^2,\\ \\ -\frac{\sqrt{D^2-P}}{2\pi }\,\mathrm{e}^{-D(t-\tau )} \,\sinh \Big (\frac{\sqrt{D^2-P}}{c}\sqrt{c^2(t-\tau )^2-r^2}\,\Big )\,H[c\,(t-\tau )-r], &{}P\le D^2, \end{array} \right. \end{aligned}$$

(9)

representation formula (4) can be rewritten explicitly for $\mathbf{x} \in \mathbb {R}^2\setminus \varGamma$ and $t \in (0,T]$ as

$$\begin{aligned} u(\mathbf{x},t)= & {} \int _{\varGamma } \int _0^t \frac{\mathbf{r}\cdot \mathbf{n_{{\varvec{\xi }}}}}{r}\,\left\{ G(r,t-\tau )\left[ \frac{\varphi _\tau (\varvec{\xi },\tau )+D\varphi (\varvec{\xi },\tau )}{c}+ \frac{\varphi (\varvec{\xi },\tau )}{c(t-\tau )+r}\right] + {\tilde{G}}(r,t-\tau ) \frac{\varphi (\varvec{\xi },\tau )}{c(t-\tau )+r}\right\} \nonumber \\&\times \,\mathrm{d}\tau \, \mathrm{d}\gamma _{{\varvec{\xi }}}. \end{aligned}$$

(10)

Proof

Let us consider the case $P\ge D^2$; starting from the definition of the double-layer potential in the right-hand side of (4), we observe that

$$\begin{aligned}&\frac{\partial G}{\partial \mathbf{n} _{\varvec{\xi }}}(r,t-\tau )=\frac{\partial G}{\partial r} (r,t-\tau )\,\frac{\partial r}{\partial \mathbf{n} _{\varvec{\xi }}}=\frac{c}{2\,\pi }\,\text {e}^{-D(t-\tau )},\\&\frac{\partial }{\partial r} \Big [\cos \Big (\frac{\sqrt{P-D^2}}{c}\sqrt{c^2(t-\tau )^2-r^2}\,\Big )\,\frac{1}{\sqrt{c(t-\tau )+r}}\,\frac{H[c(t-\tau )-r]}{\sqrt{c(t-\tau )-r}}\Big ]\,\frac{\partial r}{\partial \mathbf{n} _{\varvec{\xi }}}\\&\quad =\frac{c}{2\,\pi }\,\,\text {e}^{-D(t-\tau )} \Big [\frac{\sqrt{P-D^2}}{c}\sin \Big (\frac{\sqrt{P-D^2}}{c}\sqrt{c^2(t-\tau )^2-r^2}\,\Big )\,\frac{r\,H[c(t-\tau )-r]}{c^2(t-\tau )^2-r^2}\\&\qquad -\frac{1}{2}\,\cos \Big (\frac{\sqrt{P-D^2}}{c}\sqrt{c^2(t-\tau )^2-r^2}\,\Big )\,\frac{1}{c(t-\tau )+r}\,\frac{H[c(t-\tau )-r]}{\sqrt{c^2(t-\tau )^2-r^2}}\\&\qquad +\cos \Big (\frac{\sqrt{P-D^2}}{c}\sqrt{c^2(t-\tau )^2-r^2}\,\Big )\,\frac{1}{c\,\sqrt{c(t-\tau )+r}}\,\frac{\partial }{\partial \tau }\,\frac{H[c(t-\tau )-r]}{\sqrt{c(t-\tau )-r}}\Big ]\,\frac{\partial r}{\partial \mathbf{n} _{\varvec{\xi }}}. \end{aligned}$$

Now, considering the integration over $\varGamma \times (0,t)$ of the above expression multiplied by $\varphi (\varvec{\xi },\tau )$, integrating in the sense of distributions the term containing the derivative with respect to $\tau$ and then expressing explicitly

$$\begin{aligned} \frac{\partial }{\partial \tau }\Big [ \text {e}^{-D(t-\tau )}\cos \Big (\frac{\sqrt{P-D^2}}{c}\sqrt{c^2(t-\tau )^2-r^2}\,\Big )\,\frac{1}{c\,\sqrt{c(t-\tau )+r}}\Big ], \end{aligned}$$

one finally deduces the thesis. When $P< D^2$ we can proceed in the same manner, remembering that $\cos ({i}\,\cdot )=\cosh (\cdot )$ and $\sin ({i}\,\cdot )={i}\,\sinh (\cdot )$, being i the imaginary unit. $\square$

Proposition 2

The space–time hypersingular integral operator ${\mathcal {D}}$ admits the following explicit

expression:

$$\begin{aligned} {\mathcal {D}}\varphi (\mathbf{x},t)= & {} \int _{\varGamma } \int _0^t \left\{ \left( \frac{{\mathbf{n}_\mathbf{x}}\cdot {\mathbf{n}_{\varvec{\xi }}}}{r}-\frac{ \mathbf{r}\cdot \mathbf{n}_\mathbf{x}\,\mathbf{r}\cdot {\mathbf{n}_{\varvec{\xi }}}}{r^3}\right) \right. \nonumber \\&\times \left[ G(r,t-\tau )\left( \frac{\varphi _\tau (\varvec{\xi },\tau )+D\varphi (\varvec{\xi },\tau )}{c}+ \frac{\varphi (\varvec{\xi },\tau )}{c(t-\tau )+r}\right) +{\tilde{G}}(r,t-\tau )\frac{\varphi (\varvec{\xi },\tau )}{c(t-\tau )+r}\right] \nonumber \\&\quad -\frac{ \mathbf{r}\cdot \mathbf{n}_\mathbf{x}\,\mathbf{r}\cdot {\mathbf{n}_{\varvec{\xi }}}}{r^2}\left[ G(r,t-\tau ) \bigg (\frac{1}{c^2}[\varphi _{\tau \tau }(\varvec{\xi },\tau )+2D\varphi _\tau (\varvec{\xi },\tau )+D^2\varphi (\varvec{\xi },\tau )]\right. \nonumber \\&\quad +2\,\frac{\varphi _\tau (\varvec{\xi },\tau )+D\varphi (\varvec{\xi },\tau )}{c[c(t-\tau )+r]}+\left( \frac{3}{[c(t-\tau )+r]^2}-\frac{P-D^2}{c^2}\frac{c(t-\tau )-r}{c(t-\tau )+r}\right) \varphi (\varvec{\xi },\tau )\bigg )\nonumber \\&\left. \left. \quad +{\tilde{G}}(r,t-\tau )\left( 2\,\frac{\varphi _\tau (\varvec{\xi },\tau )+D\varphi (\varvec{\xi },\tau )}{c[c(t-\tau )+r]} +\frac{3\varphi (\varvec{\xi },\tau )}{[c(t-\tau )+r]^2}\right) \right] \right\} \,\mathrm{d}\tau \, \mathrm{d}\gamma _{{\varvec{\xi }}}. \end{aligned}$$

(11)

Proof

Applying ${\partial }/{\partial \mathbf{n} _\mathbf{x}}$ to the integrand function in (10), after some analytical manipulations, similar to what has been shown in the proof of Proposition 1, (11) is straightforwardly deduced. $\square$

Note that the expressions in the right-hand sides of (10) and (11) generalize formulas given for the case of undamped waves ($P=D=0$) and for $c=1$ in [20].

Problem (8) is then set in a weak form. Its energetic weak formulation can be deduced observing that, multiplying the PDE (1) by $u_t$, integrating over $[0,T]\times (\mathbb {R}^2\setminus \varGamma )$ and using integration by parts in space, one obtains that the energy of the solution u at the final time of analysis T, defined by

$$\begin{aligned} \mathcal {E}(u,T){:}{=}\frac{1}{2}\int _{\mathbb {R}^2\setminus \varGamma }\Big [\Vert \nabla _\mathbf{x} u(\mathbf{x},T)\Vert ^2+\frac{1}{c^2}u_t^2(\mathbf{x},T)+\frac{P}{c^2}u^2(\mathbf{x},T)+\frac{4D}{c^2}\int _0^T u_t^2(\mathbf{x},t)\text {d}t\Big ]\text {d}\gamma _\mathbf{x} \end{aligned}$$

(12)

can be rewritten as

$$\begin{aligned} \mathcal {E}(u,T)= \int _{\varGamma } \int _0^T [u_t]_\varGamma (\mathbf{x},t)\,\frac{\partial u}{\partial {\mathbf{n}_\mathbf{x}}}(\mathbf{x},t)\,\text {d}t\,\text {d}\gamma _\mathbf{x}\,= \int _{\varGamma } \int _0^T \varphi _t(\mathbf{x},t)\,{\mathcal {D}}\varphi (\mathbf{x},t)\,\text {d}t\,\text {d}\gamma _\mathbf{x}. \end{aligned}$$

(13)

Hence, projecting (8) by means of test functions $\psi$, derived w.r.t. time and belonging to the same functional space of the unknown density $\varphi$, we can write the energetic weak problem:

find $\varphi \in H^1([0,T];H^{1/2}_0(\varGamma ))$ such that $\forall \psi \in H^1([0,T];H^{1/2}_0(\varGamma ))$

$$\begin{aligned} \int _{\varGamma }\int _0^T {\mathcal {D}}\varphi (\mathbf{x},t)\,\psi _t(\mathbf{x},t)\, \text {d}t\,\text {d}\gamma _\mathbf{x} =\int _{\varGamma }\int _0^T {\bar{q}}(\mathbf{x},t)\,\psi _t(\mathbf{x},t)\, \text {d}t\,\text {d}\gamma _\mathbf{x}. \end{aligned}$$

(14)

Remark The theoretical analysis of the quadratic form coming from the left-hand side of (14) was carried out for the undamped case ($P=D=0$) in [20]: under suitable hypothesis, coercivity was proved in an infinite-dimensional subspace $H_{\varDelta x}$ of $H^1([0,T];H^{1/2}_0(\varGamma ))$ depending on a piece-wise linear semi-discretization in space variables. Fixing trivial damping parameters in (11)and indicating by ${\mathcal {D}}_0$ the hypersingular integral operator so obtained for the undamped case, it holds

$$\begin{aligned} \int _{\varGamma }\int _0^T {\mathcal {D}}_0\varphi (\mathbf{x},t)\,\varphi _t(\mathbf{x},t)\, \text {d}t\,\text {d}\gamma _\mathbf{x}\ge C\,\Vert \varphi \Vert ^2_{L^2((0,T);L^2(\varGamma ))} \qquad \forall \varphi \in H_{\varDelta x}, \end{aligned}$$

with $C=C(\varDelta \,x,T^{-2})$ (see [20] for the great amount of technical details). This property allowed us to deduce stability and convergence of the related space–time Galerkin approximate solution. For the more involved case of non-trivial damping coefficients, these properties are only conjectured, but they will be checked from a numerical point of view with intensive tests on several benchmarks discussed in Sect. 5.

3 Energetic BEM discretization

In the following, we will briefly summarize the main steps in the discretization of energetic weak problem (14).

For time discretization, we consider a uniform decomposition of the time interval [0, T] with time step $\varDelta t=T/N_{\varDelta t}$, $N_{\varDelta t}\in \mathbb {N}^{+}$ generated by the $N_{\varDelta t +1}$ time-knots: $t_k=k \varDelta t, k=0, \ldots , N_{\varDelta t}$ and we choose piece-wise linear time shape functions defined by

$$\begin{aligned} v_k(t)=R(t-t_k)-2R(t-t_{k+1})+R(t-t_{k+2}), \qquad k=0,\ldots , N_{\varDelta t}-1, \end{aligned}$$

(15)

where $R(t-t_k){:}{=}\frac{t-t_k}{\varDelta t}H[t-t_k]$ is the ramp function.

For the space discretization, we introduce on the obstacle a mesh constituted by $M_{\varDelta x}$ straight elements $e_1,\ldots ,e_{M_{\varDelta x}}$, with $2 l_i{:}{=}length (e_i)$ $\le \varDelta x$, $e_i \cap e_j=\emptyset$ if $i\ne j$ and such that $\bigcup _{i=1}^{M_{\varDelta x}} \overline{e}_i$ coincides with $\overline{\varGamma }$ if the obstacle is (piece-wise) linear, or is a suitable approximation of $\overline{\varGamma }$, otherwise. The functional background compels one to choose space shape functions belonging to $H^1_0(\varGamma )$; hence we use standard piece-wise linear polynomial boundary element functions $w_j(\mathbf {x}),\,j=1,\ldots ,M_{\varDelta x}-1$, related to the introduced mesh and vanishing at the endpoints of $\varGamma$, even if higher degree Lagrangian basis can be employed. Hence, the approximate solution of the problem at hand will be expressed as

$$\begin{aligned} \varphi (\mathbf {x},t)\simeq \sum _{k=0}^{N_{\varDelta t}-1} \sum _{j=1}^{M_{\varDelta x}-1} \alpha _j^{(k)} \,w_j(\mathbf {x})\,v_k(t). \end{aligned}$$

(16)

The Galerkin BEM discretization coming from energetic weak formulation (14) produces the linear system

$$\begin{aligned} A\,\alpha =b, \end{aligned}$$

(17)

of order $(M_{\varDelta x}-1)\cdot N_{\varDelta t}$, where $\alpha =\left( \alpha ^{(k)} \right)$, $k =0, \ldots , N_{\varDelta t}-1$, with $\alpha ^{(k)} =\left( \alpha _j^{(k)} \right)$, $j=1, \ldots ,M_{\varDelta x}-1$, and matrix A has a block lower triangular Toeplitz structure, owing, respectively, to the choice (15) and the fact that involved kernels depend on the difference between t and $\tau$. Each block has dimension $M_{\varDelta \,x}-1$, which for 2D problems is typically low. The solution of (17) is obtained by a block forward substitution, being the diagonal block non-singular. A FFT-based algorithm for the fast resolution of this kind of structured linear systems can be used to speed up the computation, as suggested in [27].

4 Handling hypersingular kernel space–time integration in matrix entries evaluation

In order to avoid a heavy notation in the explanation of the fundamental issues involved in the evaluation of the entries of matrix A, we consider, at first, the geometrical case of a straight obstacle $\varGamma$. In this setting, the BIE (8) reduces to

$$\begin{aligned} \int _{\varGamma } \int _0^t \frac{1}{r}\left[ \!G(r,t-\tau )\left( \frac{\varphi _\tau (\varvec{\xi },\tau )+D\varphi (\varvec{\xi },\tau )}{c}+ \frac{\varphi (\varvec{\xi },\tau )}{c(t-\tau )+r}\right) \,{+}\,{\tilde{G}}(r,t-\tau )\frac{\varphi (\varvec{\xi },\tau )}{c(t-\tau )+r}\!\right] \! \,\text {d}\tau \, \text {d}\gamma _{{\varvec{\xi }}}\,{=}\,{\bar{q}}(\mathbf{x},t) \end{aligned}$$

(18)

and, in (17), matrix entries coming from the energetic weak formulation of (18) are quadruple integrals of the form

$$\begin{aligned}&\int _{\varGamma }w_i(\mathbf {x})\int _{\varGamma }\frac{w_j({\varvec{\xi }})}{r}\int _0^T v_{h,t}(t)\int _0^t \left[ G(r,t-\tau )\left( \frac{v_{k,\tau }(\tau )+D\,v_k(\tau )}{c}+ \frac{v_k(\tau )}{c(t-\tau )+r}\right) \right. \nonumber \\&\quad \left. +\tilde{G}(r,t-\tau )\frac{v_k(\tau )}{c(t-\tau )+r}\right] \text {d}\tau \, \text {d}t\, \text {d}\gamma _{{\varvec{\xi }}} \,\text {d}\gamma _\mathbf{x}. \end{aligned}$$

(19)

Specifying the choice made for time basis function, quadruple integral (19) results, after some analytical manipulations, in a linear combination of integrals of the form

$$\begin{aligned}&-\frac{1}{(\varDelta t)^2} \int _{\varGamma }w_i(\mathbf {x})\int _{\varGamma }w_j(\mathbf {\varvec{\xi }})\frac{H[c(t_h-t_k)-r]}{r} \nonumber \\&\quad \times \int _{t_k+\frac{r}{c}}^{t_h} \int _{t_k}^{t-\frac{r}{c}}\left[ G(r,t-\tau )\left( \frac{1+D\,(\tau -t_k)}{c}+ \frac{\tau -t_k}{c(t-\tau )+r}\right) +{\tilde{G}}(r,t-\tau )\frac{\tau -t_k}{c(t-\tau )+r}\right] \text {d}\tau \, \text {d}t\, \text {d}\gamma _{{\varvec{\xi }}} \,\text {d}\gamma _\mathbf{x}.\nonumber \\ \end{aligned}$$

(20)

In the case of the undamped wave equation, the analysis of the space hypersingularity $O(1/r^2)$ of the integrand function has been performed in detail in [20]; furthermore, the presence in the kernels of the Heaviside distribution $H[c\,(t-\tau )-r]$, which represents the wavefront, and of the square root $\sqrt{c^2(t-\tau )^2-r^2}$ can cause numerical troubles that in [28] have been solved by suitable splitting of the outer integral over $\varGamma$ and using quadrature schemes which regularize integrand functions with mild singularities. We stress the fact that all the above-recalled space singularities appear after analytical integration in time variables.

Unfortunately, these analytical time integrations are no more possible on the damped kernel but we expect for the problem at hand a singular behavior similar to the one just described. Therefore, we consider the first term of the expansion of $G(r,t-\tau )$ with respect to damping parameters, centered in $P=D=0$, i.e., the undamped kernel $G_0(r,t-\tau )$ defined in (6), and we subtract and add back this term to the damped fundamental solution. In this way, we can split (20) as

$$\begin{aligned}&\!\!\! -\frac{1}{(\varDelta t)^2}\!\! \int _{\varGamma }w_i(\mathbf {x})\!\int _{\varGamma }w_j({\varvec{\xi }})\frac{H[c(t_h-t_k)-r]}{r}\! \int _{t_k+\frac{r}{c}}^{t_h}\! \int _{t_k}^{t-\frac{r}{c}}\left\{ \!\Bigg [ G(r,t-\tau )-G_0(r,t-\tau )\Bigg ]\right. \nonumber \\&\quad \times \left. \left( \frac{1+D\,(\tau -t_k)}{c}+ \frac{\tau -t_k}{c(t-\tau )+r}\right) + {\tilde{G}}(r,t-\tau )\frac{\tau -t_k}{c(t-\tau )+r}\right\} \text {d}\tau \,\text {d}t\, \text {d}\gamma _{{\varvec{\xi }}} \,\text {d}\gamma _\mathbf{x} \nonumber \\&\quad - \frac{1}{(\varDelta t)^2} \int _{\varGamma }w_i(\mathbf {x})\int _{\varGamma }w_j({\varvec{\xi }})\frac{H[c(t_h-t_k)-r]}{r}\nonumber \\&\quad \times \int _{t_k+\frac{r}{c}}^{t_h} \int _{t_k}^{t-\frac{r}{c}} G_0(r,t-\tau ) \left( \frac{1+D\,(\tau -t_k)}{c}+ \frac{\tau -t_k}{c(t-\tau )+r}\right) \text {d}\tau \, \text {d}t\, \text {d}\gamma _{{\varvec{\xi }}} \,\text {d}\gamma _\mathbf{x}. \end{aligned}$$

(21)

After analytical double time integration in the second quadruple integral of (21), we finally obtain the following expression for (20):

$$\begin{aligned} -\frac{1}{(\varDelta t)^2} \int _{\varGamma }w_i(\mathbf {x})\int _{\varGamma }w_j(\mathbf {\varvec{\xi }})\frac{H[c(t_h-t_k)-r]}{r^2} [r\,F_1(r,t_h,t_k)-F_2(r,t_h,t_k)]\, \text {d}\gamma _{{\varvec{\xi }}} \,\text {d}\gamma _\mathbf{x}, \end{aligned}$$

(22)

where

$$\begin{aligned} F_1(r,t_h,t_k):= & {} \int _{t_k+\frac{r}{c}}^{t_h} \int _{t_k}^{t-\frac{r}{c}} \bigg \{ [G(r,t-\tau )-G_0(r,t-\tau )]\nonumber \\&\times \left( \frac{1+D\,(\tau -t_k)}{c}+ \frac{\tau -t_k}{c(t-\tau )+r}\right) +{\tilde{G}}(r,t-\tau )\frac{\tau -t_k}{c(t-\tau )+r}\bigg \} \text {d}\tau \, \text {d}t \end{aligned}$$

(23)

and

$$\begin{aligned} F_2(r,t_h,t_k):= & {} \frac{1}{8\pi c^3}\bigg \{[-2cr+Dr^2+2Dc^2(t_h-t_k)^2][r \log -r\log (c(t_h-t_k) \nonumber \\&+\sqrt{c^2(t_h-t_k)^2-r^2})]-c(2c-3rD)(t_h-t_k)\sqrt{c^2(t_h-t_k)^2-r^2}\bigg \}. \end{aligned}$$

(24)

Proposition 3

In (22), it holds:

$$\begin{aligned} \lim _{r\rightarrow 0}\, [r\,F_1(r,t_h,t_k)-F_2(r,t_h,t_k)]=\frac{(t_h-t_k)^2}{4\pi } \end{aligned}$$

(25)

thus highlighting the hypersingular nature of space integration.

Proof

The limit of $F_2(r,t_h,t_k)$ can be evaluated straightforwardly from (24) and it turns out to be $-\frac{(t_h-t_k)^2}{4\pi }$. For what concerns the limit of $r\,F_1(r,t_h,t_k)$, we cannot perform, as already remarked, time integrations in (23) analytically; anyway, since we are interested in the behavior of the integrand function for vanishing r, we observe that in this case the time integration, which for $r>0$ must handle a weak singularity due to the presence of $[c^2(t-\tau )^2-r^2]^{-1/2}$, shows a stronger singularity in the neighborhood of $\tau =t$. Hence, if we expand the whole integrand function in (23) w.r.t. $r=0$ and $\tau =t$, we obtain, besides regular terms of polynomial type $r^\ell \,(t-\tau )^\iota , \ell \ge 0,\,\iota \ge 0$, which cannot develop outer space singularities, terms of the type $\frac{r^\ell }{(t-\tau )^{\iota +1}},\quad \ell \ge 0,\, \iota =0,\ldots ,\ell .$ These terms, after double time integration, show a space singular behavior at most of type $\log (r)$; therefore, $\lim _{r\rightarrow 0}\, r\,F_1(r,t_h,t_k)=0$ and the thesis follows. $\square$

Remark The above result assures that the difference between G and $G_0$ in (23) removes outer integration space hypersingularities. These singularities stem only after time integration in the second quadruple integral in (21). Moreover, we will have to deal only with weakly singular numerical time integration in (23) for $r>0$, since the case $r=0$ has been treated by means of the above analytical considerations.

For the general case of an open arc $\varGamma$ in the plane, we can proceed in the same manner, starting from the complete expression of the hypersingular integral operator in (11). Hence, we can finally state the following result.

Proposition 4

Using piece-wise linear time basis functions, matrix entries coming from the energetic weak formulation of (8) are of the form

$$\begin{aligned}&\!\sum _{\nu ,\eta ,\zeta =0}^{1} \frac{(-1)^{\nu +\eta +\zeta }}{(\varDelta t)^2} \left\{ -\int _{\varGamma }w_i(\mathbf {x})\int _{\varGamma }w_j(\mathbf {\varvec{\xi }})\left( {\mathbf{n}_\mathbf{x}}\cdot {\mathbf{n}_{\varvec{\xi }}}-\frac{ \mathbf{r}\cdot \mathbf{n}_\mathbf{x}\,\mathbf{r}\cdot {\mathbf{n}_{\varvec{\xi }}}}{r^2}\right) \frac{H[c(t_{h+\nu }-t_{k+\eta +\zeta })-r]}{r^2}\right. \nonumber \\&\quad \times \big [r\,F_1(r,t_{h+\nu },t_{k+\eta +\zeta })-F_2(r,t_{h+\nu },t_{k+\eta +\zeta })\big ]\, \mathrm{d}\gamma _{{\varvec{\xi }}} \,\mathrm{d}\gamma _\mathbf{x}\nonumber \\&\quad + \int _{\varGamma }w_i(\mathbf {x})\int _{\varGamma }w_j(\mathbf {\varvec{\xi }})\frac{ \mathbf{r}\cdot \mathbf{n}_\mathbf{x}\,\mathbf{r}\cdot {\mathbf{n}_{\varvec{\xi }}}}{r^2}\frac{H[c(t_{h+\nu }-t_{k+\eta +\zeta })-r]}{r^2}\nonumber \\&\quad \times \left. [r^2\,F_3(r,t_{h+\nu },t_{k+\eta +\zeta })-F_4(r,t_{h+\nu },t_{k+\eta +\zeta })]\, \mathrm{d}\gamma _{{\varvec{\xi }}} \,\mathrm{d}\gamma _\mathbf{x}\right\} , \end{aligned}$$

(26)

where $F_1(r,t_h,t_k)$ and $F_2(r,t_h,t_k)$ are defined in (23) and (24), respectively,

$$\begin{aligned} F_3(r,t_h,t_k):= & {} \int _{t_k+\frac{r}{c}}^{t_h}\int _{t_k}^{t-\frac{r}{c}}\Big \{[G(r,t-\tau )-G_0(r,t-\tau )]\nonumber \\&\times \Big (\frac{1}{c^2}[\delta (\tau -t_k) +2D+D^2(\tau -t_k)]+2\frac{1+D(\tau -t_k)}{c[c(t-\tau )+r]}\nonumber \\&+\Big (\frac{3}{[c(t-\tau )+r]^2}-\frac{P-D^2}{c^2}\frac{c(t-\tau )-r}{c(t-\tau )+r}\Big )(r-t_k)\Big )\nonumber \\&+\tilde{G}(r,t-\tau )\Big (2\frac{1+D(\tau -t_k)}{c[c(t-\tau )+r]}+\frac{3(\tau -t_k)}{[c(t-\tau )+r]^2}\Big )\Big \}\, \mathrm{d}\tau \;\mathrm{d}t, \end{aligned}$$

(27)

and

$$\begin{aligned} F_4(r,t_h,t_k):= & {} \frac{1}{8\pi c^4}\left\{ \big [-2c^2+4D\,c\,r-D^2(r^2+2c(t_h-t_k)^2)+2(P-D^2)\right. \nonumber \\&\times c(t_h-t_k)(c(t_h-t_k)+4r)+5(P-D^2)r^2\big ]\big [-r^2\log (r)+r^2\log (c(t_h-t_k)\nonumber \\&+\sqrt{c^2(t_h-t_k)^2-r^2})\big ]+\big [c(t_h-t_k)(-2c^2-4D\,c\,r+3D^2r^2\nonumber \\&- 7(P-D^2)r^2))-8(P-D^2)r^3\big ]\sqrt{c^2(t_h-t_k)^2-r^2}\,\Big \}. \end{aligned}$$

(28)

Moreover,

$$\begin{aligned} \begin{array}{l} \lim _{r\rightarrow 0}\, [r\,F_1(r,t_h,t_k)-F_2(r,t_h,t_k)]=\frac{(t_h-t_k)^2}{4\pi },\\ \\ \lim _{r\rightarrow 0}\, [r^2\,F_3(r,t_h,t_k)-F_4(r,t_h,t_k)]=\frac{(t_h-t_k)^2}{4\pi }, \end{array} \end{aligned}$$

thus highlighting the hypersingular nature of space integration in (26).

Using the standard element by element technique, the evaluation of every double integral (22) (the same treatment is applied to (26)) is reduced, up to the constant $-{1}/{(\varDelta t)^2}$, to the assembling of local contributions of the type

$$\begin{aligned} \int _0^{2 l_i} \tilde{w}_i(s) \int _0^{2 l_j}\tilde{w}_j(z) \frac{H[c(t_h-t_k)-r]}{r^2}\, [r\,F_1(r,t_h,t_k)-F_2(r,t_h,t_k)]\,\,\text {d}z\, \text {d}s, \end{aligned}$$

(29)

where $r=r(s,z)$ and $\tilde{w}_i,\,\tilde{w}_j$ define one of the Lagrangian basis functions in local space variables over the elements $e_i$ and $e_j$, respectively. Due to the hypersingularity $O(1/r^2)$ for $r\rightarrow 0$, the evaluation of double integrals of type (29) is troublesome when $e_i\equiv e_j$ and when $e_i, e_j$ are consecutive, and it has been performed similarly as in [28]. Anyway, for reader’s convenience, in the following we describe the double integration over coincident elements of the boundary mesh, i.e., $i=j$, which is the the most difficult case since hypersingularity appears at any point of $e_i$.

Let us start with an analysis of the double integration domain in (29) for $i=j$. In this case, the distance between the source and the field points can be written as $r=|s-z|$. Due to the presence of the Heaviside function $H[c(t_h-t_k)-r]$, the double integration domain is represented by the intersection between the square $[0,2\,l_i]^2$ and the strip defined by $|s-z|<c(t_h-t_k)$ where the Heaviside function is not trivial. Having set

$$\begin{aligned} M_s=\max (0,s-c(t_h-t_k)),\qquad m_s=\min (2l_i,s+c(t_h-t_k)), \end{aligned}$$

double integral (29) in this case becomes

$$\begin{aligned} \int _0^{2\,l_i} \tilde{w}_i(s) \int _{M_s}^{m_s}\tilde{w}_j(z)\, \frac{r\,F_1(r,t_h,t_k)-F_2(r,t_h,t_k)}{|s-z|^2}\,\text {d}z\, \text {d}s. \end{aligned}$$

(30)

The numerical quadrature in the variable s has been performed possibly subdividing the outer interval of integration in correspondence to the abscissas

$$\begin{aligned} s_1=c(t_h-t_k), \qquad s_2=2l_i-c(t_h-t_k). \end{aligned}$$

Note that if $c(t_h-t_k)>2l_i$ these points do not belong to the integration interval $[0,2l_i]$; if $c(t_h-t_k)=2l_i$ these points coincide with the endpoints of the integration interval; when $0<c(t_h-t_k)<2l_i$ and $c(t_h-t_k)\ne l_i$ both points belong to $[0,2l_i]$; at last, when $c(t_h-t_k)=l_i$ only one point belongs to the integration interval $(s_1=s_2)$. Almost all these geometrical situations are shown in Fig. 1.

Fig. 1

Double integration domain (coincident elements) for different values of $(t_h-t_k)$, having fixed $c=1$

Hence, (30) will be eventually decomposed into the sum of double integrals of the form

$$\begin{aligned} {\mathcal {I}}{:}{=}\int _a^b \tilde{w}_i(s) \int _{M_s}^{m_s}\tilde{w}_j(z) \frac{r\,F_1(r,t_h,t_k)-F_2(r,t_h,t_k)}{|s-z|^2}\,\,\text {d}z\;\text {d}s, \end{aligned}$$

(31)

where $[a,b]\subset [0,2l_i]$. Of course when no subdivision is needed, we will have to deal with only one double integral (31) where $[a,b]\equiv [0,2l_i]$.

At this stage, exploiting (25), we rewrite double integral (31) as follows:

$$\begin{aligned}&\mathcal {I}= \int _a^{b}\,\tilde{w}_i(s)\int _{M_s}^{m_s}\frac{1}{|z-s|} \frac{\tilde{w}_j(z)[r\,F_1(r,t_h,t_k)-F_2(r,t_h,t_k)]-\tilde{w}_j(s)\frac{(t_h-t_k)^2}{4\pi }}{|s-z|}\, \,\text {d}z\, \text {d}s \\&\qquad +\frac{(t_h-t_k)^2}{4\pi }\, \,\int _a^{b}\tilde{w}_i(s)\tilde{w}_j(s) \int _{M_s}^{m_s} \frac{1}{|s-z|^2}\,\text {d}z\, \text {d}s=:\mathcal {I}_1+\mathcal {I}_2. \end{aligned}$$

For the numerical evaluation of $\mathcal {I}_1$ we use:

Outer integral regularization procedure for integrand functions with endpoints mild singularities, coupled with Gauss–Legendre rule, as introduced and analyzed in [29]. This procedure depends on parameters p, q which suitably push the quadrature nodes towards the lower and upper endpoints of the integration interval, respectively ($p=q=1$ means standard Gauss–Legendre rule);

Inner integral interpolatory product rule [30] for $|s-z|^{-1}$ kernel, with Gauss–Legendre quadrature nodes and modified Gauss–Legendre weights absorbing the strong singularity.

Fixing $P=D=0$ and discretization parameters $2l_i=0.1$, $t_h-t_k=0.15,\,c=1$, $F_1(r,t_h,t_k)$ becomes trivial and it is possible to evaluate $\mathcal {I}_1$ analytically. Therefore, Table 1 reports the relative errors in the numerical evaluation of the integral $\mathcal {I}_1$, varying p and q and increasing the number of nodes in the outer integration; the inner integration has been performed with 16-nodes product rule, assuring single precision accuracy. Symbol ‘−’ means that the overall single precision accuracy in the evaluation of $\mathcal {I}_1$ has been achieved.

Table 1 Relative errors for different values of parameters p, q and increasing number of quadrature nodes in the outer integration of $\mathcal {I}_1$, for $P=D=0$

Further, Table 2 shows results for an example of evaluation of integral $\mathcal {I}_1$ in the presence of damping. Let us observe that in this case we have to evaluate numerically $F_1(r,t_h,t_k)$: time integration has been done by means of the above-cited regularization procedure [29] coupled with Gauss–Legendre rule, due to the presence of square root function $\sqrt{c^2(t_h-t_k)^2-r^2}$. The inner integration of $\mathcal {I}_1$ in z variable has been performed with 16-nodes product rule, as before. For the outer integration we have fixed $p=q=2$.

Table 2 reports the relative errors (evaluated w.r.t. a reference value obtained fixing 256 nodes in all quadrature rules) in the numerical integration of $\mathcal {I}_1$, varying the number of outer quadrature nodes and increasing the value of damping parameters. In this case, the stabilization worsens a little bit w.r.t. to the simpler case $P=D=0$ numerically analyzed before.

Table 2 Example of evaluation of integral $\mathcal {I}_1$: relative errors varying the number of outer quadrature nodes and increasing the value of damping parameters

For $\mathcal {I}_2$, after the inner analytical integration of the hypersingular kernel we have

$$\begin{aligned}&\mathcal {I}_2=\frac{(t_h-t_k)^2}{4\pi }\,\int _a^{b} \,\tilde{w}_i(s)\, \tilde{w}_j(s) \left[ \frac{1}{s-m_s}-\frac{1}{s-M_s}\right] \, \text {d}s=:\mathcal {I}_2^1+\mathcal {I}_2^2. \end{aligned}$$

$\mathcal {I}_2^1$ and $\mathcal {I}_2^2$ can be evaluated up to machine precision with the 2-points Gauss–Radau quadrature rule [31] for Hadamard finite part integrals if $M_s=a$, $m_s=b$ (as it is the case for the previously given numerical examples), otherwise with the standard Gauss–Legendre formula with a very low number of nodes.

For consecutive as well as disjoint boundary elements involved as double integration domain, the interest reader can proceed similarly as described in [28]. The overall accuracy of the adopted numerical integration schemes is based on the convergence properties of the above-cited basic quadrature rules and allows to obtain stable and convergent approximate BIE solutions, as we will show in the next Section.

5 Numerical results

In the following, we present an intensive numerical study of Energetic BEM applied to the analysis of 2D damped waves hard scattering by both connected and disconnected obstacles and considering not only open arcs but also bounded domains.

At first, we consider the model problem (1)–(3), fixing $\varGamma =\left\{ \mathbf{x}=(x,0)\,|\, x \in [0,1] \right\}$, $c=1$ and Neumann boundary datum coming from an incident plane wave $u^I(\mathbf{x},t)=f(t - \mathbf{k} \cdot \mathbf{x})$ propagating in direction $\mathbf{k}=(\cos \theta , \sin \theta )$, i.e.,

$$\begin{aligned} {\bar{q}}(\mathbf{x},t)=- \frac{\partial }{\partial \mathbf{n}_\mathbf{x}}f(t - \mathbf{k} \cdot \mathbf{x})\Big |_{\varGamma }. \end{aligned}$$

(32)

We show the results obtained for two different functions $f(\cdot )$, chosen also in [20] for the known asymptotic behavior of the solution, which allow us to validate the space–time approximate solution on $\varGamma$. In fact, at the Authors’ knowledge, no analytical space–time solution is available for the model problem taken into account. In particular, we will see how differently the solution of a scalar wave propagation problem behaves in the presence of damping terms w.r.t. the undamped case.

Firstly, we consider a plane harmonic wave, i.e., a wave which becomes harmonic after a fixed time:

$$\begin{aligned} f(t)=\left\{ \begin{array}{ll} 0 &{}\quad \mathrm{if} \quad t<0, \\ \\ \frac{1}{2}(1-\cos \omega t) &{}\quad \mathrm{if} \quad 0 \le t \le \frac{\pi }{\omega }, \\ \\ \sin \left( \frac{\omega t}{2} \right) &{} \quad \mathrm{if} \quad t \ge \frac{\pi }{\omega }, \end{array}\right. \end{aligned}$$

(33)

where $\omega$ represents the frequency. In this case the solution has to become harmonic too, with the same period as the incident wave, i.e., $2\pi /\widetilde{\omega }$, where $\widetilde{\omega }=\omega /2$. The fixed circular frequency $\omega = 8\pi$ is such that the wave length $\lambda =2\pi /\omega$ is equal to a quarter the crack length.

We choose a uniform decomposition of the crack $\varGamma$ in 20 subintervals ($\varDelta x=0.05$) and we decompose the observation time interval [0, 5] in 100 equal parts ($\varDelta t=0.05$).

In Fig. 2, for $\theta =\frac{\pi }{2}$ and $P=0,\,D=0$, we show the time harmonic behavior of the Crack Opening Displacement (COD) $\varphi$ at $x=0.25$ (left) and at $x=0.35$ (right), obtained starting from the energetic weak formulation. Note that the solution becomes immediately not trivial in both points, since the incident wave strikes the whole crack simultaneously.

In order to verify that the period of $\varphi$ coincides with the period of the incident wave, we show in Fig. 3 the approximated COD at time instants $t=1,3,5$, separated by multiples of the time period; note that, after the first considered time instant, the two successive curves perfectly match each other.

Fig. 2

$\varphi (0.25,t)$ (left) and $\varphi (0.35,t)$ (right) for $\theta =\pi /2$ and $P=0,\,D=0$

Fig. 3

COD at $t=1,3,5$ for $\theta =\pi /2$ and $P=0,\,D=0$

In Figs. 4, 5 (left) we show analogous results for $P=0,\, D=4$. Note that the presence of the non-trivial viscous damping coefficient changes the profile of the approximate solution, reducing the amplitude of the oscillations.

Fig. 4

$\varphi (0.25,t)$ (left) and $\varphi (0.35,t)$ (right) for $\theta =\pi /2$ and $P=0,\,D=4$

Fig. 5

COD at $t=1,3,5$ for $\theta =\pi /2$ and $P=0,\,D=4$ (left), $P=4,\,D=0$ (right)

In Fig. 5 (right), CODs at the above-considered time instants $t=1,3,5$ are reported for $P=4,\,D=0$. The profiles are very similar to the undamped case, but, due to the presence of the non-trivial material damping coefficient, the approximate solution presents a slightly more amplified oscillating behavior and at $t=3,\,5$ the related graphs are not yet completely overlapped, as one can see in Fig. 3. In Table 3 we show the variation of $\varphi (0.25,t),\, t=1,3,5$, for $D=0$ and different values of parameter P.

Table 3 $\varphi (0.25,t),\, t=1,3,5$, for different values of material damping parameter P, for $D=0$

Now, let us consider an incident plane linear wave, i.e., we fix in (32) $f(t)=0.5\,t\, H[t]$. In this case, when t tends to infinity, the Neumann datum (32) tends to ${\bar{q}}_{\theta }(\mathbf{x} )=0.5\,\mathbf{n}_\mathbf{x} \cdot (\cos \theta , \sin \theta )^\top = 0.5\,(0,1) \cdot (\cos \theta , \sin \theta )^\top =0.5\, \sin \theta =:{\bar{q}}_{\theta }$, independent of time and constant, so we expect that the approximate transient solution $\varphi (\mathbf{x},t)$ of BIE (7) on $\varGamma$ will tend to the BIE solution related to a simpler elliptic PDE.

When $P=0, D\ge 0$, we can discard in (1) the term depending on P and those derived w.r.t. time, for $t\rightarrow \infty$; we can therefore consider the following exterior Boundary Value Problem (BVP) for the Laplace equation:

$$\begin{aligned} \left\{ \begin{array}{ll} \varDelta u_\infty (\mathbf{x})=0, &{} \quad \mathbf{x}\in \mathbb {R}^2\setminus \varGamma , \\ q_\infty (\mathbf{x})={\bar{q}}_\theta , &{}\quad \mathbf{x}\in \, \varGamma ,\\ u_\infty (\mathbf{x})=O(\Vert \mathbf{x}\Vert _2^{-1}), &{} \quad \Vert \mathbf{x}\Vert _2\rightarrow \infty , \end{array}\right. \end{aligned}$$

(34)

and the related BIE on $\varGamma$, whose analytical solution is explicitly known and it reads $\varphi _\infty (x)=\sin \theta \,\sqrt{x(1-x)}$. Let us remark that the static solution remains the same for every value of D, when $P=0$, once $\theta$ is fixed.

For an incident angle $\theta =\pi /3$ and for discretization parameters fixed as $\varDelta x=0.05$ and $\varDelta t=0.05$, in Fig. 6 we show the approximate solution obtained by Energetic BEM, at the final time instant of analysis $T=5$, for $P=0$ and different values of the viscous damping parameter $D=0, 0.5, 1, 4$ (overdamping configuration), together with the reference Laplace BIE solution. The higher the value of D, the higher the gap between transient and steady-state solutions, meaning that, when we are in the presence of growing viscosity, more time is needed to see the overlapping between the two corresponding plots, i.e., to reach the equilibrium, conceived as the solution of the stationary BIE.

Fig. 6

$\varphi (\mathbf{x},T)$ on $\varGamma$, for $P=0$ and different values of D, having fixed $\theta =\pi /3$, compared with $\varphi _\infty (x)$

In Fig. 7, we show the time history of the transient approximate solution obtained by Energetic BEM with $\varDelta x=0.0125$ and $\varDelta t=0.0125$ at some points of $\varGamma$ on the time interval [0, 10] for $P=0,\,D=0$, and for $\theta =\pi /3$ (left) and $\theta =\pi /6$ (right): let us note that the solution behaves differently at the beginning of the simulation at symmetric points of the obstacle w.r.t. $x=0.5$, but after $t=4$ it recovers a symmetric profile. The same feature can be observed on $\varGamma$ for different time instants until $t=4$, in Fig. 8, for $\theta =\pi /3$ (top) and $\theta =\pi /6$ (bottom): for short times, if the wave hits the obstacle with a non-perpendicular incident direction, different points of the obstacle are stressed at different time instants generating an asymmetric solution on $\varGamma$. When the wavefront has covered the whole crack, for growing times the transient solution converges to the symmetric static one, and therefore the asymmetry tends to disappear.

Fig. 7

Time history of the transient approximate solution at some points of $\varGamma$, for $\theta =\pi /3$ (left) and $\theta =\pi /6$ (right)

Fig. 8

Transient approximate solution on $\varGamma$ at different time instants, for $\theta =\pi /3$ (top) and $\theta =\pi /6$ (bottom)

In Fig. 9, the surface of the approximate solution in space and time variables is plotted for $P=0,\, D=1$, $\theta =\pi /2$ (top), and $\theta =\pi /6$ (bottom), together with the corresponding surface representing the difference between transient and analytic static solutions, on the time interval [0, 6]. Also here there is the evidence that when the wavefront of the incident wave is not perpendicular to the obstacle, different points of $\varGamma$ are stricken at different time instants at the beginning of the simulation.

Fig. 9

Surfaces of approximate solution and its difference with the static one, for $P=0,\, D=1$, $\theta =\pi /2$ (top) and $\theta =\pi /6$ (bottom)

In order to observe longtime behavior of the Energetic BEM solutions and to numerically check longtime stability of the energetic formulation (14), we choose a uniform decomposition of $\varGamma$ in 10 subintervals $(\varDelta \, x=0.1)$ and enlarge the observation time interval, fixing $T=15$ and $\varDelta t=0.1$. In Fig. 10, for $\theta =\pi /3$, $P=0$ and different values of $D\ge 0$, the graphs report the time history of $\Vert \varphi (\cdot ,t)-\varphi _\infty (\cdot )\Vert _{L^1(\varGamma )}$, i.e., the time history of the difference in $L^1(\varGamma )$ norm between the approximate transient solution and the analytical stationary one related to the Laplace BVP (34). The fastest convergence is related to the critical damping configuration; the error order, which for growing time becomes the same for all values of D, is of course related to the fixed discretization parameters.

Fig. 10

Convergence of damped BIE solution, for $P=0$ and $D\ge 0$

In this respect, in Fig. 11, we show the time history of $\Vert \varphi (\cdot ,t)-\varphi _\infty (\cdot )\Vert _{L^1(\varGamma )}$ on the time interval [0, 8] for $P=0$, $D=0, 0.125, 0.25$ and different discretization parameters, having fixed $\theta =\pi /3$: the smaller $\varDelta x$ and $\varDelta t$, the smaller the gap between the approximate transient solution and the equilibrium state, for growing t. The evidence from Fig. 11 (and from the great amount of numerical simulations not shown here for brevity) is that the error decay is $O(\varDelta x)+O(\varDelta t)$, as already found in [20] in the 2D undamped case and theoretically proved in [5] for 1D damped problems.

Fig. 11

Convergence of damped BIE solution, for different values of discretization parameters, having fixed $\theta =\pi /3$, for $P=0$ and $D=0$ (left), $D=0.125$ (center), $D=0.25$ (right)

Further, even if the space–time analytical solution is not known, we have studied the space–time energy norm of the approximate solutions. Remembering (13), this norm is defined by

$$\begin{aligned} \Vert \varphi \Vert _{\mathcal {E}}^2{:}{=}<{\mathcal {D}}\varphi ,\varphi _t>_{L^2(\varGamma \times [0,T])}. \end{aligned}$$

(35)

In Table 4, we show the values of (35), having fixed $[0,T]=[0,10]$, $\theta =\pi /3$, $P=0$, and $D=0, 0.125, 0.25$, for diminishing discretization parameters. We observe that the energy norms are converging to a limit value which can be conceived as the energy norm of the exact space–time BIE solution. Let us note that limit values are similar because, apart from an initial different transient phase due to different viscous damping parameters, the limit stationary solution is the same for the three problems here considered. Moreover, they are reasonably lower for higher damping parameters.

Table 4 $\Vert \varphi \Vert _{\mathcal {E}}^2$ on the time interval [0, 10], for $P=0$, different viscous damping parameters and diminishing space–time mesh size. The total amount of degrees of freedom of the discrete Energetic BEM problem is also reported

When $P>0$ we can discard in (1) the terms derived w.r.t. time, for $t\rightarrow \infty$; hence, for any value of $D\ge 0$, we can consider the following exterior BVP for the Helmholtz equation:

$$\begin{aligned} \left\{ \begin{array}{ll} \varDelta u_\infty (\mathbf{x})+k^2u_\infty (\mathbf{x})=0, &{}\quad \mathbf{x}\in \mathbb {R}^2\setminus \varGamma , \\ q_\infty (\mathbf{x})={\bar{q}}_\theta , &{}\quad \mathbf{x}\in \, \varGamma ,\\ u_\infty (\mathbf{x})=O(\Vert \mathbf{x}\Vert _2^{-1}), &{} \quad \Vert \mathbf{x}\Vert _2\rightarrow \infty , \end{array}\right. \end{aligned}$$

(36)

with $k^2=-P$. The corresponding BIE solution $\varphi _\infty (x)$ on $\varGamma$ assumes the same behavior of the steady-state BIE solution related to the Laplace BVP and, of course, it changes for different values of material damping coefficient P.

For an incident angle of $\pi /3$ and for discretization parameters fixed as $\varDelta x=0.05$ and $\varDelta t=0.05$, in Fig. 12 (left column) we show the approximate solution obtained by Energetic BEM, at the final time instant of analysis $T=5$, for $D=0$ and different values of the material damping parameter $P= 0.5, 1, 4$ (underdamping configuration), together with the corresponding reference Helmholtz approximate solution obtained by standard Galerkin BEM with the same space discretization parameter (right column). The higher the value of P, the smaller the maximum value of the transient and steady-state solutions. The accordance between the corresponding plots is perfectly visible.

Fig. 12

$\varphi (\mathbf{x},T)$ on $\varGamma$, for $D=0$ and different values of P (left), together with the corresponding Helmholtz BIE static approximate solution (right), having fixed $\theta =\pi /3$

In order to observe longtime behavior of the above transient solutions and to numerically check longtime stability of the energetic formulation (14), we choose a uniform decomposition of $\varGamma$ in 10 subintervals $(\varDelta \, x=0.1)$ and enlarge the observation time interval, fixing $T=15$ and $\varDelta t=0.1$.

Looking at the graphs reporting the time history of $\Vert \varphi (\cdot ,t)-\varphi _\infty (\cdot )\Vert _{L^1(\varGamma )}$, shown in Fig. 13 for $D=0,\, P\ge 0$, we observe the expected convergence of each approximate transient solution to the corresponding approximate stationary one obtained using the same space discretization parameter. In particular, curves reveal a growing number of oscillations for growing $P>0$ (underdamping configuration), but the same global decay of the undamped case, which presents a monotone convergence after $t=6$ time instant. Note that the oscillations are due to intersections between approximate transient solutions and corresponding approximate stationary ones; they can be interpreted as oscillations of diminishing amplitude of each damped solution around its own equilibrium configuration.

Fig. 13

Convergence of damped BIE solution, for $D=0$ and $P\ge 0$

In Fig. 14, the surface of the approximate solution in space and time variables is plotted for $P=1,\, D=0$, $\theta =\pi /2$ (left), and $\theta =\pi /6$ (right), on the time interval [0, 6]. Also here there is the evidence that when the wavefront of the incident wave is not perpendicular to the obstacle, the transient Energetic BEM solution behaves differently at different points of $\varGamma$ at the beginning of the simulation.

Fig. 14

Surfaces of approximate solution, for $P=1,\,D=0$, $\theta =\pi /2$ (left) and $\theta =\pi /6$ (right)

Further, we consider numerical results for two critical damping configurations: the case $D=0,\, P=0$, related to the undamped hard scattering, already shown in Fig. 6 and the case $D=1,\, P=1$, shown in Fig. 15, both for $\theta =\pi /3$. In both cases, the approximate solutions, plotted on $\varGamma$ at $T=5$, obtained by Energetic BEM with discretization parameters fixed as $\varDelta x=0.05$ and $\varDelta t=0.05$, reveal optimal accuracy w.r.t. the corresponding stationary solutions, visible directly in Fig. 6 in the case $D=0,\, P=0$ and comparing Fig. 15 with the Helmholtz BIE solution reported in Fig. 12 for $P=1$.

Fig. 15

$\varphi (\mathbf{x},T)$ on $\varGamma$ for the critical damping configuration $D=1,\,P=1$, having fixed $\theta =\pi /3$

Fig. 16

Surfaces of approximate solution, for $P=D=1$, $\theta =\pi /2$ (left) and $\theta =\pi /6$ (right)

Fig. 17

Approximated transient BIE solutions for $P=0,\,D=0,\,0.1$ and BIE static solution on $\varGamma$ related to the Laplace BVP (34) (left), approximated transient BIE solutions for $P=0.1,\,D=0,\,0.1$ (right), for $\theta =\pi /6$ and $T=20$

Fig. 18

Time history of $\varGamma$ midpoint solution for $P=0,\,D=0,\,0.1$ (left) and for $P=0.1,\,D=0,\,0.1$ (right), for $\theta =\pi /6$

Fig. 19

Behavior of the approximated transient solution on $\varGamma$ in the first time instant of analysis (left) and for growing time (right), for $P=0.1,\,D=0$, and for $\theta =\pi /6$

Similarly as before, in Fig. 16, the surface of the approximate solution in space and time variables is plotted for $P=1,\, D=1$, $\theta =\pi /2$ (left) and $\theta =\pi /6$ (right), on the time interval [0, 6]. Also in this critical damping configuration Energetic BEM produces stable solutions.

All the above considerations written for a flat obstacle can be done in case of a curvilinear $\varGamma$. At first, we show results related to a semicircular obstacle, with unitary radius, discretized by 20 equal straight elements. The time interval [0, 20] is discretized by 200 uniform time steps. The assigned Neumann datum (32) with $f(t)=0.5\,t\, H[t]$ and $\theta =\pi /6$ becomes independent of time when t tends to infinity, i.e., ${\bar{q}}_{\theta }(\mathbf{x} )=0.5\,\mathbf{n}_\mathbf{x} \cdot (\cos \theta , \sin \theta )^\top$. Hence for $P=0$ we expect a convergence of the transient BIE solution to the solution of the BIE related to (34) with boundary datum ${\bar{q}}_{\theta }(\mathbf{x})$, shown in Fig. 17 on the left, together with the approximated transient BIE solution at $T=20$, obtained by Energetic BEM fixing $P=0$ and $D=0,\,0.1$. In the same Fig. 17 on the right, a similar plot is shown, involving damping parameters $P=0.1$ and $D=0,\,0.1$; in this case both approximate transient solutions are expected to tend to the same stationary Helmholtz BIE solution over the semicircular arc. The overlapping is very good. In Fig. 18, the time history of $\varGamma$ midpoint solution in the previous parameters case is presented. Note that for $D=0$, transient solution is still slightly oscillating, while damped solution has already reached a stationary configuration at the end of the time interval of analysis. At last, in Fig. 19, for $P=0.1,\,D=0$ we plot the behavior of the approximated transient solution on $\varGamma$ in the first time instants of analysis on the left and for growing time on the right. Note that for $t=14$ and $t=20$ the graphs are nearly overlapped.

Fig. 20

Images of the last two curvilinear obstacles

Fig. 21

Transient approximate solution at time T, together with reference Laplace BIE solution, for $\beta =10^{-4}$ (left) and for $\beta =1$ (right)

Fig. 22

Temporal profile of the incident wave in the last examples

Fig. 23

Total recovered displacement around breakwater obstacle for $P=0, D=0$

Fig. 24

Total recovered displacement around breakwater obstacle for $P=0, D=1$

Fig. 25

Total recovered displacement around breakwater obstacle for $P=0, D=2$

Now, fixing the temporal incident wave profile as $f(t)=-\,0.5\,t\, H[t]$, let us consider the following obstacles:

$$\begin{aligned} \varGamma _\beta =\left\{ \mathbf{x}=(x,\beta \sin (\pi x))|x \in [-\,1,1] \right\} , \quad \beta =10^{-4}, 1 \end{aligned}$$

whose images are reported in Fig. 20, stricken perpendicularly by the considered plane linear wave. These obstacles are non-uniformly meshed by a uniform decomposition of the parametrization interval in 20 subintervals. For $\beta =10^{-4}$, the time interval of analysis [0, 10] is uniformly subdivided by using $\varDelta t=0.1$; for $\beta =1$ the time interval of analysis is doubled as well as the number of time mesh intervals. Fixing $P=0,\, D=0.01$, we expect that, for growing time, the approximate transient BIE solution tends to the corresponding Laplace BIE stationary one, as happened in the previously analyzed cases.

In Fig. 21, we show the transient approximate solutions at the final time instant T of analysis, together with reference stationary solution, for $\beta =10^{-4}$ (left) and for $\beta =1$ (right). Note that for $\varGamma _{10^{-4}}$, which is almost flat, the approximate solution profile is analogous to those obtained for the straight crack, while for $\beta =1$ the approximate solution changes its behavior over the obstacle $\varGamma _1$.

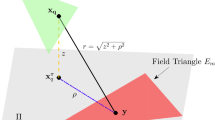
At last, we present some results involving the total displacement field $u(\mathbf{x} ,t)$ obtained by the superposition of the incident wave $u^I(\mathbf{x} ,t)$ and the reflected and diffracted waves caused by the presence of an obstacle in the plane. The temporal profile of the incident wave, from which we have deduced the Neumann datum (32) on $\varGamma$, is shown in Fig. 22 and it is similar to that one considered in [32, 33].

In the first simulation, Energetic BEM is applied in the case of a disconnected obstacle. In particular, the incident plane wave strikes perpendicularly a breakwater obstacle, made by five disjoint aligned or parallel segments each of length 0.5. The observation time interval is [0, 3]. As uniform temporal discretization step we use $\varDelta \,t=0.1$ and every segment is uniformly approximated by 5 boundary elements. The total recovered displacement in a square around the obstacle at time instants $t=0.2+j\,0.3,\, j=0, \ldots , 8$ is presented in Fig. 23 for $P=0,\, D=0$. These results show how the plane wave reaches the obstacle and how $\varGamma$ degenerates the wavefront. Reflected waves are evident in the lower half of the square. As time increases, the wavefront recovers and the scattering effect caused by the obstacle on the plane wave diminishes. As one can see, the adopted approximation technique furnishes satisfactory results. In Figs. 24, 25, we show analogous results for $P=0,\, D=1$ and $P=0,\, D=2$, respectively: the higher the value of D, the lower the effects of reflection and diffraction around the disconnected obstacle. The wavefront is, however, overall weakened.

The proposed methodology can handle also closed boundaries. In the following simulation, the same incident plane wave strikes a unitary circle. The observation time interval is [0, 4]. As uniform temporal discretization step we use $\varDelta \,t=0.1$ and the boundary of the circle is uniformly approximated by 80 straight boundary elements. Several snapshots related to the total recovered displacement in a square around the plane convex domain are shown in Fig. 26 for $P=D=0$. In Fig. 27 for $P=1,\,D=0$, the positive material damping coefficient amplifies the recovering of the wavefront at the top of the circle, producing circular waves that are not present in the undamped case. Further, in Fig. 28 related to the critical damping configuration $P=1,\,D=1$, the positive viscosity weakens all phenomena around the circle visible in the previous figure.

Fig. 26

Total recovered displacement around the circular obstacle for $P=D=0$

Fig. 27

Total recovered displacement around the circular obstacle for $P=1,\,D=0$

Fig. 28

Total recovered displacement around the circular obstacle for $P=1,\,D=1$

6 Conclusions

We have considered the numerical solution of 2D damped wave propagation exterior problems equipped by Neumann boundary condition, which model hard scattering phenomena. A modified version of Energetic BEM has been applied, in order to take into account the non-analytical time integrability of the hypersingular damped kernel here involved. The original version of this method was already considered in the case of undamped wave equations, revealing, also from theoretical point of view, its accuracy and stability. Numerical results obtained in the damped scenario confirm that these properties are maintained in presence of dissipation. Next steps will involve BEM–FEM coupling for this kind of model problems.