Dynamics of a stage-structured SI model for food adulteration with media-induced response function

Abstract

In this work, an eco-epidemic predator–prey model with media-induced response function for the interaction of humans with adulterated food is developed and studied. The human population is divided into two main compartments, namely, susceptible and infected. This system has three equilibria; trivial, disease-free and endemic. The trivial equilibrium is forever an unstable saddle position, while the disease-free state is locally asymptotically stable under a threshold of delay parameter $\tau$ as well as ${\mathcal {R}}_0<1$. The sufficient conditions for the local stability of the endemic equilibrium point are further explored when $\min \{{\mathcal {R}}_0,{\mathcal {R}}_0^*\}>1$ . The conditions for the occurrence of the stability switching are also determined by taking infection delay time as a critical parameter, which concludes that the delay can produce instability and small amplitude oscillations of population masses via Hopf bifurcations. Further, we study the stability and direction of the Hopf bifurcations using the center manifold argument. Furthermore, some numerical simulations are conducted to validate our analytical findings and discuss their biological inferences. Finally, the normalized forward sensitivity index is used to perform the sensitivity analysis of ${\mathcal {R}}_0$ and ${\mathcal {R}}_0^*$.

1 Introduction

In our daily life, there are many unhygienic and contaminated things which affect our health. The fruits and vegetables, which we eat now, also became adulterated and may have a severe effect on human health. The interaction between adulterated foods and human is similar to a prey–predator interaction. This interaction may be decreased exponentially with the spreading of media awareness.

In a recent scenario, adulteration is a serious concern and normally applies to supplementing adulterated matter to the drink or food, which is intended to be sold to increase the quantity of the product, which is done either for earning more money in short time or by carelessness in protection, processing, storing, transportation, marketing, etc. The adulteration in fruits or vegetables increases the impurities in it, which will be hazardous for human health. Our body needs a continuous supply of calories and nutrients for the healthy growth of cells, tissues, and organs, and for this purpose, we use adulterated vegetables or fruits continuously. The presence of adulterants in fruits and vegetables, like arsenic, lead, copper, calcium carbide, malachite green, wax coating, washing powder, and brick powder, causes several deadly diseases, like cancer, brain hemorrhage, hormonal imbalances, appendicitis, liver disorder, digestive problems, and gastric problems as cited in [1, 2]. Some of them are already present in our body in balanced measure, but in excess, it will become poisonous. Thus, adulteration in fruits and vegetables becomes a paramount problem for our society.

Many provisions have been made by the government to control the problem of adulteration in fruits and vegetables and to control the disease spread by them, but whether these are being followed or not remains uncertain. However, the media has played an essential role in the promotion of these provisions and making conscious people aware of this problem. Media, being the best source of information, can not only change the individuals’ role but also increases the governmental health administration engagement to regulate the diseases spread by the consumption of adulterated food. The most prominent source of knowledge about food adulteration is mass media, especially television (65%). The public obtained many food scandals proved by media rather than supervision officials, which seems to be playing an increasingly essential role in exposing food-safety problems [3]. Media also makes people acquainted with the diseases and preventive practices, and informed population start practices like social distancing, vaccination, etc. and try to minimize their risks of becoming infected. These behavioral shifts triggered by media may happen in an unanticipated epidemic pattern [4]. Recent studies recommended that education and watching TV have a meaningful impact in restricting the spread of HIV/AIDS among married couples in Bangladesh [5, 6]. For other diseases like childhood diseases, Malaria, Cholera, and Pandemic influenza, propagation can be limited media-induced awareness (e.g., social networking sites, newspaper, TV) and further interpersonal conversation can modify the response of population in the presence of the prevailing disease [7, 8]. Thus, the media play an important role in reducing the problem of food adulteration and in controlling the diseases spread by adulteration. In last decade, several mathematical models have been developed in controlling of infectious diseases with media awareness [9,10,11,12], but no one has paid attention to mathematical models for the dynamics of diseases spread by the consumption adulterated foods.

Naturally, the diseases can be spread when the human population come into contact with adulterated food and eat it. This types of interaction in the literature are commonly known as prey–predator interaction. The first prey–predator model was introduced by Lotka and Volterra [13, 14]; after that many prey–predator models have been formulated by ecologists and mathematicians to understand the dynamics of interacting populations [15,16,17,18]. Dynamics of prey–predator models are generally delineated by a functional response, which is the number of prey successfully attacked by a per predator as a function of prey density [19]. Skalski and Gilliam [20] suggested that there are only three primary functional responses which can provide better descriptions of the dynamics of predator–prey interaction by presenting statistical evidence.

Here, we will study a new response function other than these, which will be influenced by media and known as media-induced response function. In this study, we have taken adulterated food as prey, while the human population as a predator population. Further, the human population is classified into two classes, namely susceptible and infected. The propaganda of interaction mainly affects the effective contact rate of susceptible individuals, and it can increase the awareness of prevention and reduce the number of contact of susceptible by adjusting the media awareness. Hence, the media-induced response function is defined as a functional response, which is the number of prey successfully attacked by a per susceptible predator in the presence of infected predator with media effect as a function of prey and infected predator densities. In the absence of media effect, the response function will be linear, and once the outbreak of adulteration increases, the number of infections also increases. So in the presence of media, the susceptible persons restrict themselves from eating adulterated food. Hence the response function exponentially decreases. Thus the media-induced response function is more suitable and realistic to study the effect of food adulteration on the human population.

The susceptible person may become infected by eating adulterated food. Thus conversion from susceptible to infected is not instantaneous, and actually, it requires a period, after that the susceptible may become infected. So, based on this concept, we consider an eco-epidemic model, where the delay period partitioned the human population into two stages: the early and later stages. Assume that the individuals in the early stage can transfer to the later stage. When susceptible human population eats the adulterated food, it will be counted in the early stage as it takes a constant time to develop the infection inside the susceptible population and then transfers into the later stage, i.e., infected individual class through a delay term. In the last decade, several researchers have increased their attention on the epidemic models with multiple phases of infections, where infectivity passes through consecutive phases of infection [21,22,23,24]. Thus, we believe that this is the first time where an eco-epidemic prey–predator model with media-induced response function and multiples stages through time delay is considered to study the dynamics of diseases spread by food adulteration.

The paper is organized as follows: Sect. 2 deals with the development of a mathematical model. The system dynamics and the existence of equilibria are discussed in Sect. 3. The stability analysis is determined in Sect. 4. The stability and direction of Hopf bifurcation are studied in Sect. 5. Further, the numerical simulations and discussion are given in Sect. 6. Sensitivity analysis of the threshold ${\mathcal {R}}_0$ is performed in Sect. 7. Finally, a conclusion is presented in the last section.

2 Model development

In this section, we will develop a prey–predator model with media-induced interaction of adulterated food and human population, where the adulterated food will be used as a prey population while human as a predator population. Further, the predator will be divided into two compartments, namely susceptible/latently infected and infected. Here it is assumed that all the newborns are susceptible/latently infected and can be infected through the consumption of adulterated food, and this will be the only source of infection in the human population. Moreover, it is assumed that the infected predator population is only infected, but not infectious, and they cannot spread any disease. Let x(t), y(t), and z(t) be densities of prey, latently infected and infected human/predator population, respectively, at time t. The basic assumptions of our model are as follows:

• (A1) The prey population is growing in a logistic manner with an intrinsic growth rate r and carrying capacity K.

• (A2) The predation of adulterated foods by the susceptible human is influenced through the information spread by media, which is represented in terms of the media-induced response function $\beta \text {e}^{-mz(t)}x(t)$, where $\beta$ is the predation rate and m is the density of media awareness corresponding to the predator population. This term represents the predation, which influences through the information spread by media in proportion to the infected person. Thus, when the media increases awareness, the predation rate exponentially decreases. Hence, media-induced response function is exponentially decreasing due to media awareness in the presence of infective person (as suggested in [25]).

• (A3) In this paper, we discussed about only those susceptible human population, whose growth is completely dependent on adulterated food. Hence the growth of this susceptible population is proportional to the predation rate $\beta f(x(t),z(t))y(t)$), with proportionality constant k as conversion rate. The same population dies out naturally with mortality rate $d_1$.

• (A4) The term $\beta \text {e}^{-mz(t)}x(t)y(t)$ does not represent the incidence or disease transmission. It shows the predation, where $k\beta \text {e}^{-mz(t)}x(t)y(t)$ represents the growth of susceptible predator in form of energy conversion. Also, a fraction of this population dies out naturally with the rate $d_1$ and the remaining part of susceptible human population becomes infected after a time period $\tau$ as the conversion from one stage to another is not instantaneous (similar to that considered by several researchers in [26,27,28], where the predator has two stages: immature and mature). Hence the term $k\beta \text {e}^{-d_1\tau }f(x(t-\tau ),z(t-\tau ))y(t-\tau )$ represents the total number of infected persons, who joined the susceptible predator at the time $t-\tau$, where $0<\text {e}^{-d_1\tau }\le 1$. If we put $\tau = 0$ in the model, the susceptible population becomes extinct and it immediately becomes infected. In this case, we have to considered only two-dimensional system, i.e., adulterated food and infected human.

• (A5) The infected predator dies out naturally with mortality rate $d_2$.

Keeping the above assumptions in mind, our proposed mathematical model is ruled by the following system of differential equations:

$$\begin{aligned} \begin{aligned}&\frac{\text {d}x(t)}{\text {d}t}\,=\,rx(t)\left( 1-\frac{x(t)}{K} \right) -\beta \text {e}^{-mz(t)}x(t) y(t),\\&\frac{\text {d}y(t)}{\text {d}t}\,=\,k\beta \text {e}^{-mz(t)}x(t)y(t)-d_1y(t)-k\beta \text {e}^{-d_1\tau }\text {e}^{-mz(t-\tau )}x(t-\tau )y(t-\tau ),\\&\frac{\text {d}z(t)}{\text {d}t}\,=\,k\beta \text {e}^{-d_1\tau }\text {e}^{-mz(t-\tau )}x(t-\tau )y(t-\tau )-d_2z(t). \end{aligned} \end{aligned}$$

(2.1)

All the system parameters are positive and their description is given in Table 1.

Table 1 Parameters descriptions of the proposed system (2.1)

The initial population densities for system (2.1) take the form:

$$\begin{aligned} \begin{array}{l} x(t)=\phi (t), ~~y(t)=\psi _1(t), ~~z(t)=\psi _2(t),~~ t\in [-\tau ,~0],\\ \phi (t) \ge 0,~\psi _1(t),~\psi _2(t)\ge 0, \ \ \phi (0)> 0, ~\psi _1(0),~\psi _2(0) > 0, \end{array} \end{aligned}$$

(2.2)

where $\phi ,~\psi _1,~\psi _2\in C ([-\tau ,~0],~R_+^3)$. From the second equation of system (2.1), we get

$$\begin{aligned}y(t)=\int _{-\tau }^0 k\beta \text {e}^{d_1s} \text {e}^{-mz(t+s)}x(t+s)y(t+s)\text {d}s.\end{aligned}$$

Thus, we can impose the following continuity condition:

$$\begin{aligned} \psi _1(0)=\int _{-\tau }^0 k\beta \text {e}^{d_1s}\text {e}^{-m\psi _2(s)}\phi (s)\psi _1(s) \text {d}s. \end{aligned}$$

(2.3)

Assume the continuous solution of (2.1) is $X(t)=\left( x(t),y(t),z(t)\right) ^\mathrm{T}$, is defined as $X: R_+\rightarrow R_+^3$ and is also Lipschitzian in a compact set $R_+$ with initial conditions (2.2) and (2.3). Therefore, [29, Theorem 2.3] ensures that the system (2.1) with initial conditions (2.2) and (2.3) has a unique solution in $R_+^3$.

3 Positivity, Boundedness, and existence of equilibria

The positivity indicates that species are persistent and boundedness means a natural restriction to growth because of limited resources. Hence, we can establish the following lemma:

Lemma 3.1

All solutions of set of equations (2.1) along with (2.2) are positive for all $t\ge 0.$

Proof

Suppose (x(t), y(t), z(t)) is any solution of system (2.1) with initial conditions (2.2). For $0\le t\le \tau$, the last equation of (2.1) gives

$$\begin{aligned}\frac{\text {d}z}{\text {d}t}\ge -d_2 z (t).\end{aligned}$$

Clearly $z(t)\ge z(0)\text {e}^{-d_2t}\triangleq z_*(t)>0$ for all $t\ge 0$. Now first differential equation of (2.1), ${\forall }t\ge t_0$ for some $t_0>0$, we get

$$\begin{aligned}\frac{\text {d}x}{\text {d}t}\ge r x(t)\left( 1-\frac{x(t)}{K}\right) -\beta \text {e}^{-mz_*(t)}x(t)y(t),\end{aligned}$$

which gives

$$\begin{aligned}x(t)\ge x(0)\exp \left( \int _{0}^{t}\left[ r\left( 1-\frac{x(u)}{K}\right) -\beta \text {e}^{-m z_*(u)}y(u)\right] \text {d}u\right) \ge 0.\end{aligned}$$

For $0\le t\le \tau$, the second equation of system (2.1) can be written as

$$\begin{aligned} \frac{\text {d}y}{\text {d}t}\ge -d_1y(t)-k\beta \text {e}^{d_1\tau }f\left( x(t-\tau ),z(t-\tau )\right) y(t-\tau ).\end{aligned}$$

Let v(t) be the solution of

$$\begin{aligned} \frac{\text {d}v}{\text {d}t}= -d_1v(t)-k\beta \text {e}^{d_1\tau }f\left( x(t-\tau ),z(t-\tau )\right) v(t-\tau ),\ \ v(0)=y(0).\end{aligned}$$

We have $y(t)\ge v(t)$ on $0\le t \le \tau$, clearly,

$$\begin{aligned}v(t)=\text {e}^{-d_1t}\left[ y(0)-\int _0^t k\beta \text {e}^{d_1(s-\tau )}f(x(s-\tau ),z(s-\tau ))y(s-\tau )\text {d}s\right] .\end{aligned}$$

Hence

$$\begin{aligned} v(\tau )=\text {e}^{-d_1\tau }\left[ \int _{-\tau }^0 k\beta \text {e}^{d_1\xi }f(x(\xi ),z(\xi ))y(\xi ) \text {d}\xi -\int _0^{\tau } k\beta \text {e}^{d_1(s-\tau )}f(x(s-\tau ),z(s-\tau ))y(s-\tau )\text {d}s\right] . \end{aligned}$$

We thus have $v(\tau ) = 0$, and therefore $y(t)\ge 0$ for $t\in [0,\ \tau ]$. By induction, we can show that $y(t) \ge 0$ for all $t\ge 0$. $\square$

Lemma 3.2

The solutions of set of equations (2.1) along with (2.2) and (2.3) are bounded.

Proof

Let $V(t)=kx(t)+y(t)+z(t)$ and ${\bar{d}}=\min \{1,d_1,d_2\}$, we have

$$\begin{aligned} \frac{\text {d}V}{\text {d}t} = rk\left( 1-\frac{x(t)}{K} \right) x(t)-d_1y(t)-d_2z(t) \le (r+1)kx(t)-\frac{rkx^2(t)}{K}-{\bar{d}}V(t). \end{aligned}$$

This gives

$$\begin{aligned}\frac{\text {d}V}{\text {d}t}+{\bar{d}} V(t) \le (r+1)kx(t)-\frac{rkx^2(t)}{K}\le M_0,\end{aligned}$$

where $M_0=[{(r+1)^2kK}]/{4r}$. Thus $V(t)\le M_0/{\bar{d}}+\left( V(0)-M_0/{\bar{d}}\right) \text {e}^{-{\bar{d}}t}\rightarrow M_0/{\bar{d}}:=M \ \ \text{ as } \ \ t\rightarrow \infty$, i.e., $x(t)\le M, \ y(t)\le M, \ z(t)\le M$ for sufficiently large t and hence the system (2.1) is bounded. $\square$

Now, we find all biologically as well as feasibly relevant equilibria admitted by the system. There are three possible equilibria for the model (2.1):

• (i) Trivial equilibrium $E_1= (0,0,0)$, which always exists.

• (ii) Disease-free or human-free equilibrium $E_2= (K,0,0)$, which also always exists.

• (iii) Endemic equilibrium $E_3= (x^*, y^*, z^*)$ exists whenever $\min \{{\mathcal {R}}_0, {\mathcal {R}}_0^*\} >1$, where

  $$\begin{aligned} {\mathcal {R}}_0=kK\beta (1-\text {e}^{-d_1\tau })/d_1, \end{aligned}$$

  (3.1)

  and

  $$\begin{aligned} {\mathcal {R}}_0^*=8d_2\text {e}^{d_1\tau }/mrkK. \end{aligned}$$

  (3.2)

The existence of $E_1$ and $E_2$ is trivial, hence omitted. Here, we discuss only the existence of endemic equilibrium in detail. If endemic equilibrium point $E_3(x^*,y^*,z^*)$ exists, it must satisfy the equations:

$$\begin{aligned} \begin{aligned}&rx\left( 1-\frac{x}{K}\right) -\beta \text {e}^{-mz}xy=0,\\&k\beta \text {e}^{-mz}xy-d_1y-k\beta \text {e}^{-d_1\tau }\text {e}^{-mz}xy=0,\\&k\beta \text {e}^{-d_1\tau }\text {e}^{-mz}xy-d_2z=0. \end{aligned} \end{aligned}$$

(3.3)

Clearly, if there exists a positive equilibrium, it is a positive solution of

$$\begin{aligned} y= & {} \frac{r}{\beta \text {e}^{-mz}}\left( 1-\frac{d_1}{kK\beta \text {e}^{-mz}(1-\text {e}^{-d_1\tau })}\right) :=G(z),\nonumber \\ y= & {} \frac{d_2z(1-\text {e}^{-d_1\tau })}{d_1\text {e}^{-d_1\tau }}:=H(z). \end{aligned}$$

(3.4)

To find sufficient conditions for the uniqueness of a positive solution of (3.4), we follow the work of Lie et al. cited in [30], which provides that

$$\begin{aligned} G(0)=\frac{r}{\beta }\left( 1-\frac{1}{{\mathcal {R}}_0}\right) ,\qquad H(0)={0}\quad \text {and}\quad G(0)>H(0)\quad \text {if}\;{\mathcal {R}}_0>1. \end{aligned}$$

Thus, the two curves G(z) and H(z) have at least one positive intersection. In order to determine the number of other positive intersections, we consider the tangency of the above two curves G(z) and H(z). If the two curves intersect, it must have $G(z)=H(z)$ and $G'(z)=H'(z)$, i.e.,

$$\begin{aligned} \frac{r}{\beta \text {e}^{-mz}}-\frac{r}{\beta \text {e}^{-2mz}{\mathcal {R}}_0}=\frac{d_2z(1-\text {e}^{-d_1\tau })}{d_1\text {e}^{-d_1\tau }}, \end{aligned}$$

(3.5)

and

$$\begin{aligned} \frac{r}{\beta \text {e}^{-mz}}-\frac{2r}{\beta \text {e}^{-2mz}{\mathcal {R}}_0}=\frac{d_2(1-\text {e}^{-d_1\tau })}{md_1\text {e}^{-d_1\tau }}. \end{aligned}$$

(3.6)

The difference of equations (3.5) and (3.6) provides

$$\begin{aligned} \frac{r}{\beta \text {e}^{-2mz}{\mathcal {R}}_0}=\left( z-\frac{1}{m}\right) \frac{d_2\left( 1-\text {e}^{-d_1\tau }\right) }{d_1\text {e}^{-d_1\tau }}. \end{aligned}$$

(3.7)

Substituting the above value in (3.5), we obtain that

$$\begin{aligned} \frac{r}{\beta \text {e}^{-mz}}-(z-\frac{1}{m})\frac{d_2(1-\text {e}^{-d_1\tau })}{d_1\text {e}^{-d_1\tau }}=\frac{d_2z(1-\text {e}^{-d_1\tau })}{d_1\text {e}^{-d_1\tau }}, \end{aligned}$$

(3.8)

which implies that

$$\begin{aligned} \left( 2z-\frac{1}{m}\right) \frac{d_2(1-\text {e}^{-d_1\tau })}{d_1\text {e}^{-d_1\tau }}=\frac{r}{\beta \text {e}^{-mz}}. \end{aligned}$$

(3.9)

Squaring both sides of (3.9), we get

$$\begin{aligned} \left( 2z-\frac{1}{m}\right) ^2\frac{d_2^2(1-\text {e}^{-d_1\tau })^2}{d_1^2\text {e}^{-2d_1\tau }}=\frac{r^2}{\beta ^2 \text {e}^{-2mz}}. \end{aligned}$$

(3.10)

From (3.7) and (3.10), we get

$$\begin{aligned} \left( 2z-\frac{1}{m} \right) ^2=\frac{r\text {e}^{-d_1\tau }kK}{d_2}\left( z-\frac{1}{m} \right) . \end{aligned}$$

(3.11)

Let $\alpha ={1}/{m}$, $\delta =({rkK\text {e}^{-d_1\tau }})/{d_2}$, then we have

$$\begin{aligned} z=\frac{(4\alpha +\delta )\pm \sqrt{\delta (\delta -8\alpha )}}{8}. \end{aligned}$$

(3.12)

Let $m_0=(8d_2\text {e}^{d_1\tau })/(rkK)$. It can be simply determined that (3.12) has no root for $0<m<m_0$, and hence the system (2.1) has a unique endemic equilibrium. For $m=m_0$, (3.12) has one unique root and the system (2.1) has one endemic equilibrium point of multiplicity at least two. Again, if $m>m_0$, then (3.12) has two roots and hence the system (2.1) has three endemic equilibria. Thus, the existence of unique endemic equilibrium is stated in the following:

Lemma 3.3

If ${\mathcal {R}}_0>1$ and $0<m<m_0$ (i.e., ${\mathcal {R}}_0^*>1$) or $\min \{{\mathcal {R}}_0,{\mathcal {R}}_0^*\}>1$, then the system (2.1) has a unique endemic equilibrium point $E_3(x^*, y^*, z^*)$.

The above lemma suggests that a unique endemic equilibrium point exists whenever the delay parameter crosses a threshold $\left( \text{ i.e., } \tau >\tau _*:=\max \{\ \tau _1,\tau _2\}\right)$, where

$$\begin{aligned} \tau _1=\frac{1}{d_1}\log \left( 1+\frac{d_1}{kK\beta -d_1}\right) , \ \ \tau _2=\frac{1}{d_1}\log \left( \frac{mrkK}{8d_2} \right) .\end{aligned}$$

4 Stability analysis

In this part, we perform the local stability analysis and existence of the Hopf bifurcation for the model (2.1), which is governed by a crucial threshold ${\mathcal {R}}_0$. Clearly the characteristic equation of trivial equilibrium $E_1(0,0,0)$ takes the form $(\lambda -r)(\lambda +d_1)(\lambda +d_2)=0$, and hence $E_1$ is an unstable saddle. Further the characteristic equation for $E_2(K,0,0)$ is given as

$$\begin{aligned}(\lambda +r)(\lambda +d_2)\left( \lambda -kK\beta (1-\text {e}^{-d_1\tau }\text {e}^{-\lambda \tau })+d_1\right) =0.\end{aligned}$$

It is clear that $\lambda = -r$ and $\lambda =-d_2$ are always two negative eigenvalues. All other eigenvalues are given by the solutions of equation $\lambda - kK\beta (1-\text {e}^{-d_1\tau }\text {e}^{-\lambda \tau })+d_1=0$. If $kK\beta (1-\text {e}^{-d_1\tau })-d_1<0$, i.e., ${\mathcal {R}}_0<1$, one can easily check that the graph $f_1(\lambda )=\lambda$ and $f_2(\lambda )=kK\beta (1-\text {e}^{-d_1\tau }\text {e}^{-\lambda \tau })-d_1$ must intersect at a negative value of $\lambda$, and hence the predator-free equilibrium $E_2$ is locally asymptotically stable provided that ${\mathcal {R}}_0<1$, i.e., for all $\tau \in (0,\tau _1)$.

Now the characteristic equation of endemic equilibrium $E_3(x^*,y^*,z^*)$ takes the form

$$\begin{aligned} \lambda ^3+a_2(\tau )\lambda ^2+a_1(\tau )\lambda +a_0(\tau )+\left[ b_2(\tau )\lambda ^2+b_1(\tau )\lambda +b_0\right] \text {e}^{-\lambda \tau }=0, \end{aligned}$$

(4.1)

where

$$\begin{aligned}a_0(\tau )= & {} d_2k\beta x^* \text {e}^{-mz^*}\left[ \beta y^* \text {e}^{-mz^*}-\frac{rx^*}{K}\text {e}^{-d_1\tau }\right] ,\\ a_1(\tau )= & {} k\beta {x^*}\text {e}^{-mz^*}\left[ \beta y^* \text {e}^{-m z^*}-\frac{rx^*}{K}\text {e}^{-d_1\tau }\right] -d_2\text {e}^{-d_1\tau }+\frac{rx^*d_2}{K}, \\ a_2(\tau )= & {} \frac{r}{K}x^*+(d_1+d_2)-k\beta x^*\text {e}^{-mz^*}, \\ b_0(\tau )= & {} k\beta {x^*}\text {e}^{-mz^*}\text {e}^{-d_1\tau }(d_2+d_1my^*)\left[ \frac{rx^*}{K}-\beta y^*\text {e}^{-mz^*}\right] , \\ b_1(\tau )= & {} k\beta {x^*}\text {e}^{-mz^*}\text {e}^{-d_1\tau }(1+my^*)\left[ \frac{rx^*}{K}-\beta y^*\text {e}^{-mz^*}+\frac{d_2+d_1my^*}{1+my^*}\right] , \\ b_2(\tau )= & {} k\beta x^*\text {e}^{-mz^*}\text {e}^{-d_1\tau }(1+my^*).\end{aligned}$$

The above equation can be rewritten as

$$\begin{aligned} P(\lambda ,\tau )+Q(\lambda ,\tau )\text {e}^{-\lambda \tau }=0, \end{aligned}$$

(4.2)

where

$$\begin{aligned} P(\lambda ,\tau )=\lambda ^3+a_2(\tau )\lambda ^2+a_1(\tau )\lambda +a_0(\tau ), \qquad Q(\lambda ,\tau )= b_2(\tau )\lambda ^2+b_1(\tau )\lambda +b_0(\tau ). \end{aligned}$$

(4.3)

Lemma 3.3 ensures the existence of a unique endemic equilibrium for $\tau >\tau _*$. Therefore, existence of purely imaginary roots of the characteristic equation (4.1) is established for $\tau >\tau _*$ by using the geometric criterion for delay-dependent coefficients  [31], which is stated as follows:

Lemma 4.1

Equation (4.2) has a pure imaginary root $\lambda =\mathrm{i}\omega \ (\omega >0)$ for $\tau \in I$ with I defined in (4.6), if all the properties given in [31] are satisfied.

Proof

For $\tau \in I$, it is clear that

(i):

$P(0,\tau )+Q(0,\tau )= ({rd_1d_2x^*})/{K}+d_1mk\beta x^*y^*\text {e}^{-mz^*}\left[ ({rx^*})/{K} - r\beta y^*\text {e}^{-mz^*}\right] \ne 0$.

(ii):

$P(\text {i}\omega ,\tau )+Q(\text {i}\omega ,\tau )=-(a_2+b_2)\omega ^2+a_0+b_0+\text {i}[-\omega ^3+(a_1+b_1)\omega ]\ne 0$.

(iii):

The definitions of $P(\lambda ,\tau )$ and $Q(\lambda ,\tau )$ suggest that

$$\begin{aligned} \lim \ \sup \{|Q(\lambda ,\tau )/P(\lambda ,\tau )|\ : \ |\lambda |\rightarrow \infty ,\ Re\,\lambda \ge 0 \}=0<1. \end{aligned}$$

(iv):

Let F be defined as $F(\omega ,\tau )=|P(\mathrm{i}\omega ,\tau )|^2-|Q(\mathrm{i}\omega ,\tau )|^2$, where

$$\begin{aligned} |P(\text {i}\omega ,\tau )|^2= & {} \omega ^6 +\left( a_2^2-2a_1\right) \omega ^4+\left( a_1^2-2a_0a_2\right) \omega ^2+a_0^2, \\ |Q(\text {i}\omega ,\tau )|^2= & {} b_2^2\omega ^4 +\left( b_1^2-2b_0b_2\right) \omega ^2+b_0^2. \end{aligned}$$

We have

$$\begin{aligned} F(\omega )=\omega ^6+A(\tau )\omega ^4+B(\tau )\omega ^2+C(\tau )=0, \end{aligned}$$

(4.4)

with

$$\begin{aligned}A(\tau )= & {} a_2^2-b_2^2-2a_1, \\ B(\tau )= & {} a_1^2-b_1^2-2a_0a_2+2b_0b_2, \\ C(\tau )= & {} a_0^2-b_0^2. \end{aligned}$$

Let $\chi =\omega ^2,$ then (4.4) is rewritten as follows:

$$\begin{aligned} \chi ^3+A\chi ^2+B\chi +C=0. \end{aligned}$$

(4.5)

Let $D=\left( \frac{g}{2}\right) ^2+\left( \frac{h}{3}\right) ^3$, where $h=B-\frac{1}{3}A^2,\ g=\frac{2}{27}A^3-\frac{1}{3}AB+C$. Thus, there are three cases for the existence of solution of (4.5).

• (a) Equation (4.5) has a pair of complex roots and a real root when $D>0$. The positivity condition of the real root is given by

  $$\begin{aligned}\chi _1=\root 3 \of {-\frac{g}{2}+\sqrt{D}}+\root 3 \of {-\frac{g}{2}-\sqrt{D}}-\frac{A}{3}.\end{aligned}$$

• (b) Again for $D=0$, (4.5) has all real roots, with two being equal. Moreover, if $A>0$, it has only one positive real root, $\chi _1=2\root 3 \of {-\frac{g}{2}}-\frac{A}{3}$. Otherwise for $A<0$, there exists a positive root $\chi _1=2\root 3 \of {-\frac{g}{2}}-\frac{A}{3}$ for $\root 3 \of {-\frac{g}{2}}>\frac{A}{3}$, and there exist three positive roots for $\frac{A}{6}<\root 3 \of {-\frac{g}{2}}<-\frac{A}{3}$, given by

  $$\begin{aligned}\chi _1=2\root 3 \of {-\frac{g}{2}}-\frac{A}{3}, \ \ \chi _2=-\root 3 \of {-\frac{g}{2}}-\frac{A}{3}.\end{aligned}$$

• (c) If $D<0$, there are three distinct real roots given as

  $$\begin{aligned} \chi _1= & {} 2\sqrt{\frac{|h|}{3}}\cos \left( \frac{\varphi }{3}\right) -\frac{A}{3}, \\ \chi _2= & {} 2\sqrt{\frac{|h|}{3}}\cos \left( \frac{\varphi +2\pi }{3}\right) -\frac{A}{3}, \\ \chi _3= & {} 2\sqrt{\frac{|h|}{3}}\cos \left( \frac{\varphi +4\pi }{3}\right) -\frac{A}{3}, \end{aligned}$$

  where $\varphi =\arccos {({-g}/{2\sqrt{({|h|}/{3})^3}})}$ has to be calculated in radians. Furthermore, if $A>0$, there exists only one positive root. Otherwise, if $A<0$, there may exist either one or three positive real roots. If there is only one positive real root, it is equal to $\max \{\chi _1,\chi _2,\chi _3\}$.

Hence, the sign of the discriminant D of (4.5) determines the number of positive roots. Hence, the existence of at least one positive real root is given in the following region:

$$\begin{aligned} I=\left\{ \tau>\tau _*: \chi (\tau )>0 \text{ is } \text{ a } \text{ root } \text{ of } (4.5)\right\} . \end{aligned}$$

(4.6)

Thus (4.4) has at least two real roots $\omega _{\pm }(\tau )=\pm \sqrt{\chi (\tau )}$ for all $\tau \in I$. Since the function $F(\omega )$ is a sixth-degree polynomial, it has at most six real zeros for all $\tau \in I$.

(v):

From implicit function theorem each root of $F(\omega ,\tau )=0$ is continuous and differentiable in I, because $F(\omega ,\tau )$ is differentiable with respect to $\omega$ and continuous in $\omega$ and $\tau$ .

Hence, all the conditions given in [31] are satisfied, and thus the Lemma 4.1 ensures the existence of purely imaginary roots of characteristic equation (4.2) for all $\tau \in I$. $\square$

Now assume that $\lambda =\mathrm{i}\omega \ (\omega >0)$ is a purely imaginary characteristic root of (4.2). By substituting $\lambda =i\omega$ into (4.2) and separating real and imaginary parts, we obtained the following transcendental equations:

$$\begin{aligned} a_2\omega ^2-a_0= & {} (b_0-b_2\omega ^2)\cos \omega \tau +b_1\omega \sin \omega \tau ,\nonumber \\ \omega ^3-a_1\omega= & {} b_1\omega \cos \omega \tau -(b_0-b_2\omega ^2)\sin \omega \tau . \end{aligned}$$

(4.7)

It follows from (4.7) that

$$\begin{aligned} \cos (\omega \tau )= & {} \displaystyle \frac{(a_2\omega ^2-a_0)(b_0-b_2\omega ^2)+(\omega ^3-a_1\omega )(b_1\omega )}{(b_0-b_2\omega ^2)^2+(b_1\omega )^2},\nonumber \\ \sin (\omega \tau )= & {} \displaystyle \frac{(a_2\omega ^2-a_0)(b_1\omega )-(\omega ^3-a_1\omega )(b_0-b_2\omega ^2)}{(b_0-b_2\omega ^2)^2+(b_1\omega )^2}. \end{aligned}$$

(4.8)

As cited in [31], a well and unique $\theta (\tau )\in [0,2\pi ]$, ${\forall }\tau \in I$, is defined by

$$\begin{aligned} \cos \theta _\pm (\tau )= & {} \displaystyle \frac{b_1\omega _\pm (\omega _\pm ^3-a_1\omega _\pm )+(a_2\omega _\pm ^2-a_0)(b_0-b_2\omega _\pm ^2)}{(b_1\omega _\pm )^2+(b_0-b_2\omega _\pm ^2)^2},\nonumber \\ \sin \theta _\pm (\tau )= & {} \displaystyle \frac{b_1\omega _\pm (a_2\omega _\pm ^2-a_0)-(\omega _\pm ^3-a_1\omega _\pm )(b_0-b_2\omega _\pm ^2)}{(b_1\omega _\pm )^2+(b_0-b_2\omega _\pm ^2)^2}. \end{aligned}$$

(4.9)

One can check that $\mathrm{i}\omega ^*$ with $\omega ^*=\omega (\tau ^*)>0$ is a purely imaginary root of (4.2) if and only if $\tau ^*$ is a roots of $S_n$ defined by following map:

$$\begin{aligned} S_n^\pm (\tau )=\tau -\frac{\theta _\pm (\tau )+2n\pi }{\omega _\pm (\tau )}, \quad n\in N. \end{aligned}$$

Following Beretta and Kuang [31], we can state a theorem as given below:

Theorem 4.2

The characteristic equation (4.1) has a pair of simple pure imaginary roots $\lambda =\pm \text {i}\omega (\tau ^*)$ at $\tau ^*\in I$, provided $S_n(\tau ^*)=0$ for some $n\in N_0$. This pair of simple conjugate pure imaginary roots crosses the imaginary axis from left to right if $\delta (\tau ^*)>0,$ and right to left if $\delta (\tau ^*)<0,$ where

$$\begin{aligned}\delta (\tau ^*)=\mathrm{sign}\left\{ \left. \frac{\mathrm{d}Re(\lambda )}{\mathrm{d}\tau }\right| _{\lambda =\mathrm{i}\omega _+(\tau ^*)}\right\} =\mathrm{sign}\left\{ \left. \frac{\mathrm{d}S_n(\tau )}{\mathrm{d}\tau }\right| _{\tau =\tau ^*}\right\} .\end{aligned}$$

Here, we can easily find that $S_n(0)<0$ and $S_n(\tau )>S_{n+1}(\tau )$ ${\forall }\tau \in I$, $n\in N_0$. Thus, if $S_0$ has no zero in I, the function $S_n$ also has no zero in I and if the function $S_n$ has positive zeros, denoted by $\tau _n^j$ for some $\tau \in I,\ n\in N_0$, then without loss of generality, we may assume that ${\text {d}S_n(\tau _n^j)}/{\text {d}\tau }\ne 0\ \text{ with }\ S_n(\tau _n^j)=0$ and applying the similar logic as in [31], it is obtained that the stability switches occur at the zeros of $S_0(\tau )$, denoted by $\tau _0^j$. Thus using [29], we can conclude the dynamics of stability switches in the following theorem:

Theorem 4.3

The local behavior of the system (2.1) at endemic equilibrium $E_3$ is described as follows:

• 1. If the function $S_0(\tau )$ has no positive zero in I, then the endemic equilibrium $E_3(x^*,y^*,z^*)$ is locally asymptotically stable for all $\tau > \tau _*$ or ${\mathcal {R}}_0>1$, $0<m<m_0$.

• 2. If the function $S_n(\tau )$ has some positive zeros at $\tau _1^*$, $\tau _2^*,\tau _3^*\ldots$ in I for some $n\in N_0$, then $E_3$ is locally asymptotically stable for $\tau \in (\tau _*,\tau _1^*)\cup (\tau _2^*,\tau _3^*)\cup \ldots$ and unstable with existence of a Hopf bifurcation for $\tau \in (\tau _1^*,\tau _2^{*})\cup (\tau _3^*,\tau _4^{*})\cup \ldots$, i.e., stability switching occurs from stability–instability–stability and so on.

5 Criticality and stability of Hopf bifurcation

In the previous section, we have got some sufficient conditions under which a class of periodic solutions bifurcated from the steady state of the system (2.1), when the delay is more than the critical level $\tau ^*$. Now we shall study the direction of these Hopf bifurcations and stability of bifurcated periodic solutions using the method discussed in  [32]. Using Appendix A, we can compute the following values:

$$\begin{aligned} \begin{aligned} C_1(0)&=\frac{\text {i}}{2\omega ^*\tau ^*}\left( g_{20}g_{11}-2|g_{11}|^2-\frac{|g_{02}|^2}{3} \right) +\frac{g_{21}}{2},\\ \mu _2&=\frac{Re\{C_1(0)\}}{Re\{\lambda '(\tau ^*)\}},\qquad \beta _2=2\,Re\{C_1(0)\},\qquad T_2=\frac{I_m\{C_1(0)\}+\mu _2I_m\{ \lambda '(\tau ^*)\}}{\omega ^*\tau ^*}, \end{aligned} \end{aligned}$$

(5.1)

which determine the behavior of periodic solution in the center manifold at $\tau ^*$, i.e., again if $\mu _2 > 0 \ (\mu _2 < 0)$, then the Hopf bifurcation is supercritical (subcritical) and the bifurcating periodic solution exists for $\tau > \tau ^*\ (\tau < \tau ^*)$; $\beta _2$ determines the stability of the bifurcating periodic solution: the bifurcating periodic solution is stable (unstable) if $\beta _2 < 0 \ (\beta _2 > 0)$ and, finally, the period increases (decreases) if $T_2 > 0 \ (T_2<0)$.

Fig. 1

Time series plot for $\tau =1.48<\tau _1$ for ${\mathcal {R}}_0=0.990496<1$

6 Numerical simulations and discussions

Our analytical results indicate that the time delay must be accountable for the observed regular cycles of disease occurrence. To examine the effect of time delay on the system (2.1), let us consider the following model:

$$\begin{aligned} \begin{aligned} \frac{\text {d}x(t)}{\text {d}t}&=0.4 x(t)\left( 1-\frac{x(t)}{10} \right) -\beta \text {e}^{-mz(t)}x(t)y(t),\\ \frac{\text {d}y(t)}{\text {d}t}&=k\beta \text {e}^{-mz(t)}x(t)y(t)-0.1y(t) -k\beta \text {e}^{-d_1\tau } \text {e}^{-mz(t-\tau )}x(t-\tau )y(t-\tau ),\\ \frac{\text {d}z(t)}{\text {d}t}&=k\beta \text {e}^{-d_1\tau } \text {e}^{-mz(t-\tau )}x(t-\tau )y(t-\tau )-d_2z(t). \end{aligned} \end{aligned}$$

(6.1)

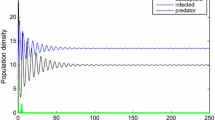
Here, some numerical results of system (6.1) will be discussed at different parametric values of $\tau ,\ m,\ \beta , \ k,\ d_2$. Let $m=2,\ \beta =0.24, \ k=0.3,\ d_2=0.2$, then it is clear that all the solutions of (6.1) are positive and bounded. A disease-free or human-free equilibrium point $E_2(10,0,0)$ exists and it is locally asymptotically stable for all $\tau <\tau _1=1.49532$ or ${\mathcal {R}}_0<1$. If we choose $\tau =1.48<\tau _1$, then ${\mathcal {R}}_0=0.990496<1$, and hence the equilibrium point $E_2(10,0,0)$ satisfies usual analytical criteria for stable equilibrium points (see Fig. 1). The equilibrium point $E_2(10,0,0)$ is not feasible for the society, as the human population may never be extinct in reality. Hence our main objective in this paper is to determine the situation where the human population will survive with minimal effect of adulterated foods on his health. Let us take $\tau _*=\max \{\tau _1,\tau _2\}$, where

$$\begin{aligned} \tau _1=\frac{1}{d_1}\log \left( 1+\frac{d_1}{kK\beta -d_1}\right) \quad \text {and}\quad \tau _2=\frac{1}{d_1}\log \left( \frac{mrkK}{8d_2} \right) . \end{aligned}$$

We can see that all the key parameters including predation rate $\beta$, media effect m, carrying capacity K, growth rate r, death rates $d_1,\ d_2$, and conversion rate k are involved in the above threshold condition. This allows us to address the effect of controlling parameter $\tau$ as well as adulterated food on human health. For $m=2$; $\tau _2=4.05465$, in this case a unique endemic equilibrium $E_3(x^*,y^*,z^*)$ exists for all $\tau >4.05465$. Moreover, all the conditions of the Lemma 4.1 are satisfied for all $\tau \in (4.05465\ 23.3547]$ and at least one pair of pure imaginary roots of characteristic equation (4.2) exists, for which $S_0$ has four zeros at $\tau _1^*=5.083 ,\ \tau _2^*= 10.197$, $\tau _3^*=13.168$ and $\tau _4^*=22.838$. Thus Theorem 4.3 ensures the switching of stability of endemic equilibrium point $E_3(x^*,y^*,z^*)$ at $\tau _1^*=5.083 ,\ \tau _2^*= 10.197$, $\tau _3^*=13.168$ and $\tau _4^*=22.838$. The endemic equilibrium is locally asymptotically stable for all $\tau \in (4.05465 \ 5.083)\cup [10.197 \ 13.168)\cup [22.838\ 23.3547]$ and unstable with existence of a Hopf bifurcation in $[5.083\ 10.197)\cup [13.168\ 22.838)$. Choosing $\tau =4.4>\tau _*=4.05465$, endemic equilibrium $E_3(8.8040,0.4498,0,4069)$ exists and locally asymptotically stable for ${\mathcal {R}}_0=2.56294>1$ (see Fig. 2).

Fig. 2

The trajectory is approaching to the endemic equilibrium $E_3(8.8040,0.4498,0,4069)$ for $\tau =4.4>\tau _*$ and ${\mathcal {R}}_0>1$

Further, the periodic fluctuations in disease occurrence arise for a different range of delay parameter $\tau$, which ensure that the stability of endemic equilibrium is switching from stability–instability–stability–instability–stability (see Fig. 3).

Fig. 3

The periodic fluctuations in disease occurrence for delay parameter $\tau$ in $(\tau _*\ 23.3547]$, a–c represent stability switching from stability–instability–stability at $\tau =5$, $\tau =5.5$ and $\tau =10.5$, respectively, d–f represent stability switching from instability–stability–instability at $\tau =13.1$, $\tau =13.3$, and $\tau =23$, respectively

Similarly, it is observed that the predator coefficient $\beta$, and the coefficient of media effect m can influence the dynamics of the system (2.1). Figures 4 and 5, respectively, show the effect of predation rate and media coefficient on destabilization of endemic equilibrium $E_3$ (Fig. 6).

Fig. 4

Approaching towards the periodic fluctuations in disease occurrence with predation rate $\beta =0.25$

Fig. 5

Approaching towards the periodic fluctuations in disease occurrence with media awareness coefficient $\mu =2.2$

Fig. 6

Declination of infected population with increasing media effect for $\tau =4.4$

Thus the above numerical simulations suggest that the usually delay parameter destabilized the steady state, whereas substantial delays have a stabilizing one. On the other hand, high predation and media awareness can destabilize the steady state. As the spread of infections depends on different factors, therefore, real-time information diffusion about the risk factors of disease through media has a positive impact on controlling the transmission of infectious diseases because of behavior, making them aware of the condition.

7 Sensitivity analysis

For real-life application, more attention should be paid towards highly sensitive parameters because these type of parameters will produce significant qualitative changes by a slight variation in their respective values. Thus, in this section, we discuss the sensitivity analysis of ${\mathcal {R}}_0$ and ${\mathcal {R}}^*_0$ using normalized forward sensitivity index, which is defined as follows:

Definition

(see [33]) The normalized forward sensitivity index of a variable, x, which depends upon a parameter, y, is defined as

$$\begin{aligned} \gamma ^{x}_{y}=\frac{\delta x}{\delta y}\times \frac{y}{x}. \end{aligned}$$

By taking the numerical values of all the parameters, the normalized forward sensitive indices for ${\mathcal {R}}_0$ and ${\mathcal {R}}^*_0$ are calculated in Table 2.

Table 2 The sensitivity indices for ${\mathcal {R}}_0$ and ${\mathcal {R}}^*_0$

From the above, it reveals that the parameters $K, \beta , k,$ and $\tau$ have a positive impact on ${\mathcal {R}}_0$, which means that when these parameters increase (or decrease) by keeping the others are constant, then the value of ${\mathcal {R}}_0$ will also increase (or decrease). Similarly, the parameter $d_1$ has a negative impact on ${\mathcal {R}}_0$, i.e., when the value of $d_1$ increases (or decreases) while others are being constant, then the value of ${\mathcal {R}}_0$ decreases (or increases). On the other hand, parameters r, K, m, and k have negative impact on ${\mathcal {R}}^*_0$ while $d_1, d_2,\ \text {and}\ \tau$ have positive impact. For example, 10% increase (or decrease) in $\tau$ will produce $9.278 \%$ increase (or decrease) in ${\mathcal {R}}_0,$ and 10% increase (or decrease) in $d_1$ will produce $0.722 \%$ decrease (or increase) in ${\mathcal {R}}_0.$ Moreover, it can be easily seen that the parameters, which have either a positive or a negative impact on ${\mathcal {R}}_0$ and ${\mathcal {R}}^*_0$, are most sensitive. Therefore, these parameters should be dealt very carefully as they play an adaptive role in disease outbreak.

8 Conclusions

Over the last few decades, it has been observed that food adulteration has a severe effect on human health. The adulteration is applying not only in the food but also in all things. Hence humans have nothing else to eat except adulterated items. Therefore, we have proposed an eco-epidemic prey–predator model for contaminated food and human with media awareness in the form of media-induced response function, where the growth of human is completely dependent on adulterated foods and due to consumption of these adulterants, human is assumed to be infected, and thus the predator population was divided into two compartments: susceptible and infected. The conversion from the susceptible to infected cannot be instantaneous. It requires a period, after that the susceptible become infected. In the analysis, it has obtained that the system has three equilibria, namely, trivial, boundary, and interior. The trivial equilibrium is an unstable saddle point, while the boundary equilibrium point is locally asymptotically stable for ${\mathcal {R}}_0<1$, i.e., for $\tau <\tau _1$, which shows that due to adulterants if the conversion of the susceptible population into infected is in short time, then both the populations will become extinct. In the next, by taking the delay as a bifurcation parameter, we have obtained certain sufficient conditions on the existence of the switching stability of the positive steady state. It shows that the delay can induce a small amplitude oscillations of population densities, i.e., Hopf bifurcations, by applying the geometric approach for stability switches on the characteristic equation with delay-dependent parameters. It has been recognized that the time-varying delay-dependent parameters play an important role in the dynamics of disease propagation and the endemic steady state has a periodic fluctuation in disease occurrence arise for different ranges of delay parameter $\tau$, which ensure that the stability of endemic equilibrium is switching, whereas large delays have a stabilizing effect. Furthermore, by employing the center manifold argument, the Hopf bifurcations’ direction and stability have ascertained. Finally, the sensitivity analysis of threshold ${\mathcal {R}}_0$ and ${\mathcal {R}}_0^*$ is performed, which shows that media helps in lowering the predation rate of adulterated foods as the predation rate is highly sensitive. Thus, when predation is reduced, the conversion rate of k will also be reduced.

Moreover, we have proposed a new media-induced response function in the form of media awareness to represent the interaction between adulterated food and human, which is exponentially decreasing with the increase of media awareness, as in the presence of media, the susceptible persons restrict themselves from eating the adulterated food. This response function is beneficial to know the various effects of food adulteration either by the predation or media awareness. The thresholds of predation rate $\beta$ and media effect coefficient m suggest to consume adulterated food at a low quantity, otherwise due to higher quantity the system may destabilize. Since adulteration in fruits and vegetables is a paramount problem for our society, the present work can be helpful in terms of showing the impact of media awareness on adulteration along with the behavioral change in population.

Appendix A

By the change of variables $x_1(t)=x(t)-x^*, \ x_2(t)=y(t)-y^*,\ x_3(t)=z(t)-z^*,\ {\bar{x}}_i(t)=x_i(\tau t),\ \tau =\tau ^*+\mu$ and dropping the bars for simplifications of notations, system (2.1) is transformed into a functional differential equation in $C=C([-1,0],R^3)$ as

$$\begin{aligned} {\dot{x}}(t)=L_\mu (x_t)+F(\mu ,x_t), \end{aligned}$$

(A.1)

where $x(t)=(x_1(t),x_2(t),x_3(t))^\mathrm{T}\in R^3$ and for $\phi =(\phi _1,\phi _2,\phi _3)^\mathrm{T}\in C$, $L_\mu :C\rightarrow R,\ F : C \times R\rightarrow R$, respectively, are given by

$$\begin{aligned} L_\mu (\phi )= & {} (\tau ^*+\mu )\left( \begin{array}{ccc} r(1-\frac{2x^*}{K})-\beta \text {e}^{-mz^*}y^* &{} -\beta \text {e}^{-mz^*}x^* &{} m\beta \text {e}^{-mz^*}x^*y^*\\ k\beta \text {e}^{-mz^*}y^* &{} k\beta \text {e}^{-mz^*}x^*-d_1 &{} -mk\beta \text {e}^{-mz^*}x^*y^*\\ 0 &{} 0 &{} -d_2 \end{array}\right) \left( \begin{array}{ccc} \phi _1(0)\\ \phi _2(0)\\ \phi _3(0) \end{array}\right) \\&+\,(\tau ^*+\mu )\left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ -\zeta y^* &{} -\zeta x^* &{} m\zeta x^*y^*\\ \zeta y^* &{} \zeta x^* &{}-m\zeta x^*y^* \end{array} \right) \left( \begin{array}{ccc} \phi _1(-1)\\ \phi _2(-1)\\ \phi _3(-1) \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned} F(\mu ,\phi )=(\tau ^*+\mu )\left( \begin{array}{ccc} \varDelta _1\\ \varDelta _2\\ \varDelta _3 \end{array}\right) + H.O.T., \end{aligned}$$

where

$$\begin{aligned} \zeta= & {} k\beta \text {e}^{-d_1(\tau +\mu )}\text {e}^{-mz^*}, \\ \varDelta _1= & {} -\frac{r\phi _1^2(0)}{K}+\beta \text {e}^{-mz^*}[my^*\phi _1(0)\phi _3(0)+mx^*\phi _2(0)\phi _3(0)-\phi _1(0)\phi _2(0)], \\ \varDelta _2= & {} k\beta \text {e}^{-mz^*}(\phi _1(0)\phi _2(0)-my^*\phi _1(0)\phi _3(0)-mx^*\phi _2(0)\phi _3(0))\\&+ \zeta (my^*\phi _1(-1)\phi _3(-1)+mx^*\phi _2(-1)\phi _3(-1)-\phi _1(-1)\phi _2(-1), \\ \varDelta _3= & {} -\zeta (my^*\phi _1(-1)\phi _3(-1)+mx^*\phi _2(-1)\phi _3(-1)-\phi _1(-1)\phi _2(-1). \end{aligned}$$

By the Riesz representation theorem, there exists a $3\times 3$ matrix $\eta (\theta ,\mu ):[-1,0]\rightarrow R^3$ whose elements are of bounded variation such that

$$\begin{aligned} L_\mu \phi =\int _{-1}^{0}\phi (\theta )\text {d}\eta (\theta ,\mu ), \ \ \theta \in C. \end{aligned}$$

(A.2)

In fact, we can choose

$$\begin{aligned} \eta (\theta ,\mu )= & {} (\tau ^*+\mu )\left( \begin{array}{ccc} r\left( 1-\frac{2x^*}{K}\right) -\beta \text {e}^{-mz^*}y^* &{} -\beta \text {e}^{-mz^*}x^* &{} m\beta \text {e}^{-mz^*}x^*y^*\\ k\beta \text {e}^{-mz^*}y^* &{} k\beta \text {e}^{-mz^*}x^*-d_1 &{} -mk\beta \text {e}^{-mz^*}x^*y^*\\ 0 &{} 0 &{} -d_2 \end{array} \right) \delta (\theta )\nonumber \\&-(\tau ^*+\mu )\left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ \zeta y^* &{} -\zeta x^* &{} m\zeta x^*y^*\\ \zeta y^* &{} \zeta x^* &{}-mk\zeta x^*y^* \end{array} \right) \delta (\theta +1), \end{aligned}$$

(A.3)

where $\delta$ is a Dirac delta function. For $\phi \in C^1([-1,0],R^3),$ let us define

$$\begin{aligned} A(\mu )\phi =\left\{ \begin{array}{ll} \frac{\text {d}\phi (\theta )}{\text {d}\theta }, &{} \quad \theta \in [-1,0),\\ \int _{-1}^{0} \phi (s) \text {d}\eta (s,\mu ), &{} \quad \theta =0, \end{array}\right. \end{aligned}$$

(A.4)

and

$$\begin{aligned} R(\mu )\phi =\left\{ \begin{array}{ll}0,&{}\quad \theta \in [-1,0),\\ F(\mu ,\phi ),&{} \quad \theta =0. \end{array}\right. \end{aligned}$$

(A.5)

Then the system (A.1) is equivalent to the following operator equation:

$$\begin{aligned} {\dot{u}}(t)=A(\mu )u_t+R(\mu )u_t, \end{aligned}$$

(A.6)

where $u=(x_1,x_2,x_3)^\mathrm{T}$ and $u_t=u(t+\theta )$ for $\theta \in [-1,0].$

For $\psi \in C^1([-1,0],(R^3)^*),$ define

$$\begin{aligned} A^*\psi (s)=\left\{ \begin{array}{ll} \frac{-\text {d}\psi (s)}{\text {d}s},&{} \quad s \in [-1,0),\\ \int _{-1}^{0}\psi (-t) \text {d}\eta ^\mathrm{T}(t,0),&{}\quad s=0, \end{array}\right. \end{aligned}$$

(A.7)

and a bilinear form

$$\begin{aligned} \langle \psi (s),\phi (\theta )\rangle ={\bar{\psi }}(0)\phi (0)-\int _{-1}^{0}\int _{\xi =0}^{\theta }{\bar{\psi }}(\xi -\theta )\text {d}\eta (\theta )\;\phi (\xi )\text {d}\xi , \end{aligned}$$

(A.8)

where $\eta (\theta )=\eta (\theta ,0).$ Then A(0) and $A^*$ are adjoint operators. From the discussion in previous section, we know that $\pm \text {i}\omega ^*\tau ^*$ are eigenvalues of A(0) and therefore they are also eigenvalues of $A^*$, corresponding to $\mathrm{i}\omega ^*\tau ^*$ and $-\text {i}\omega ^*\tau ^*$, respectively.

Suppose that $q(\theta )=(1,\alpha ,\gamma )^\mathrm{T}\text {e}^{\text {i}\theta \omega ^*\tau ^*}$ is the eigenvector of A(0) corresponding to $\text {i}\omega ^*\tau ^*,$ then $A(0)q(\theta )=\text {i}\omega ^*\tau ^*q(\theta ).$ It follows from the definition of A(0) and $\eta (\theta ,\mu )$ that

$$\begin{aligned} \tau ^*\left( \begin{array}{ccc} \text {i}\omega ^*+\beta \text {e}^{-mz^*}y^*-r(1-\frac{2x^*}{K}) &{} \beta \text {e}^{-mz^*}x^* &{} p_1\\ k\beta \text {e}^{-mz^*}y^*(\text {e}^{-d_1\tau ^*-1}) &{} \text {i}\omega ^*+k\beta \text {e}^{-mz^*}x^*(\text {e}^{-d_1\tau ^*-1})+1 &{} p_2\\ -k\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}y^* &{} -k\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}x^* &{} p_3 \end{array}\right) q(0)=0, \end{aligned}$$

where

$$\begin{aligned} p_1= & {} -m\beta \text {e}^{-mz^*}x^*y^*,\\ p_2= & {} -mk\beta \text {e}^{-mz^*}x^*y^*(\text {e}^{-d_1\tau ^*-1})\\ p_3= & {} \text {i}\omega ^*+mk\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}x^*y^*+d_2. \end{aligned}$$

Then, we can easily obtain $q(0)=(1,\alpha ,\gamma )^\mathrm{T},$ where

$$\begin{aligned} \alpha= & {} \frac{\gamma (\text {i}\omega ^*+mk\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}x^*y^*+d_2)-(k\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}y^*)}{k\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}x^*y^*},\\ \gamma= & {} \frac{k\text {e}^{-d_1\tau ^*}(r(1-\frac{2x^*}{K})-\text {i}\omega ^*)}{d_2+\text {i}\omega ^*}. \end{aligned}$$

Again, let $q^*(\theta )=D(1,\alpha ^*,\gamma ^*)\text {e}^{-\text {i}\theta \omega ^*\tau ^*}$ be the eigenvector of $A^*$ corresponding to $-\text {i}\omega ^*\tau ^*,$ then similarly we can obtain that

$$\begin{aligned} \alpha ^*= & {} \frac{\gamma ^*(-\text {i}\omega ^*+mk\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}x^*y^*+d_2)-mk\beta \text {e}^{-mz^*}x^*y^*}{mk\beta \text {e}^{-mz^*}x^*y^* (\text {e}^{-d_1\tau ^*}-1)},\\ \gamma ^*= & {} \frac{mx^*(r(1-\frac{2x^*}{K})+\text {i}\omega ^*)}{d_2-\text {i}\omega ^*}. \end{aligned}$$

By (A.8), we get

$$\begin{aligned} \langle q^*(s),q(\theta )\rangle= & {} {\bar{D}}(1,{\bar{\alpha }}^*,{\bar{\gamma }}^*)(1,\alpha ,\gamma )^\mathrm{T} -\int _{-1}^{0}\int _{\xi =0}^{\theta }{\bar{D}}(1,{\bar{\alpha }}^*,{\bar{\gamma }}^*)\text {e}^{-\text {i}\omega ^*\tau ^*(\xi -\theta )}\text {d}\eta (\theta )(1,\alpha ,\gamma )^\mathrm{T}\text {e}^{\text {i}\omega ^*\tau ^*\xi }\,\text {d}\xi \\= & {} {\bar{D}}\left[ 1+\alpha {\bar{\alpha }}^*+\gamma {\bar{\gamma }}^*-(1,{\bar{\alpha }}^*,{\bar{\gamma }}^*)\int _{-1}^{0}\phi (\theta )\text {d}\eta (\theta )(1,\alpha ,\gamma )^\mathrm{T}\right] \\= & {} {\bar{D}}[1+\alpha {\bar{\alpha }}^*+\gamma {\bar{\gamma }}^*+\tau ^*({\bar{\gamma }}^*-{\bar{\alpha }}^*)(y^*+\alpha x^*-m\gamma x^*y^*) \, k\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{-\text {i}\omega ^*\tau ^*}]. \end{aligned}$$

Then we choose

$$\begin{aligned} {\bar{D}}=\frac{1}{1+\alpha {\bar{\alpha }}^*+\gamma {\bar{\gamma }}^*+\tau ^*({\bar{\gamma }}^*-{\bar{\alpha }}^*)(y^*+\alpha x^*-m\gamma x^*y^*)k\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{-\text {i}\omega ^*\tau ^*}}, \end{aligned}$$

such that $\langle q^*(s),q(\theta )\rangle =1$ and $\langle q^*(s),{\bar{q}}(\theta )\rangle =0.$ In the following, we use the ideas in Hassard et al. [32] to compute the coordinates describing center manifold $C_0$ at $\mu =0$. Define

$$\begin{aligned} z(t)=\langle q^*,x_t\rangle ,\ W(t,\theta )=x_t(0)-2\,Re[z(t)q(\theta )], \end{aligned}$$

(A.9)

on the center manifold $C_0,$ and we have

$$\begin{aligned} W(t,\theta )=W(z(t),{\bar{z}}(t),\theta )=W_{20}(\theta )\frac{z^2}{2}+W_{11}(\theta )z{\bar{z}}+W_{02}\frac{{\bar{z}}^2}{2}+\cdots , \end{aligned}$$

(A.10)

where z and ${\bar{z}}$ are local coordinates for $C_0$ in C in the direction of $q^*$ and ${\bar{q}}^*.$ Note that W is real if $x_t$ is real. We deal only with the real solution. For solution $x_t \in C_0$ of (A.6), since $\mu =0,$ we have

$$\begin{aligned} {\dot{z}}(t)=\mathrm{i}\omega ^*\tau ^*z+{\bar{q}}^*(0)F(0,W(z,{\bar{z}},0)+2\,Re\{zq(0)\}) {\mathop {=}\limits ^{\text {def}}}\mathrm{i}\omega ^*\tau ^*z+{\bar{q}}^*(0)F_0(z,{\bar{z}})=\mathrm{i}\omega ^*\tau ^*z+g(z,{\bar{z}}), \end{aligned}$$

where $g(z,{\bar{z}})={\bar{q}}^*(0)$, and

$$\begin{aligned} F_0(z,{\bar{z}})=g_{20}\frac{z^2}{2}+g_{11}z{\bar{z}}+g_{02}\frac{{\bar{z}}^2}{2}+g_{21}\frac{z^2{\bar{z}}}{2}+\cdots . \end{aligned}$$

(A.11)

From (A.9) and (A.10), we have

$$\begin{aligned}x_t(\theta )=(x_{1t}(\theta ),x_{2t}(\theta ),x_{3t}(\theta ))=W(t,\theta )+zq(\theta )+\bar{zq(\theta )},\end{aligned}$$

and

$$\begin{aligned}q(\theta )=(1,\alpha ,\beta )^\mathrm{T}\text {e}^{\mathrm{i}\theta \omega ^*\tau ^*}.\end{aligned}$$

Thus, we can easily obtain that

$$\begin{aligned} x_{1t}(0)= & {} z+{\bar{z}}+W_{20}^{(1)}(0)\frac{z^2}{2}+W_{11}^{(1)}(0)z{\bar{z}}+W_{02}^{(1)}(0)\frac{{\bar{z}}^2}{2}+O(|(z,{\bar{z}})|^3),\\ x_{2t}(0)= & {} \alpha z+\bar{\alpha z}+W_{20}^{(2)}(0)\frac{z^2}{2}+W_{11}^{(2)}(0)z{\bar{z}}+W_{02}^{(2)}(0)\frac{{\bar{z}}^2}{2}+O(|(z,{\bar{z}})|^3),\\ x_{3t}(0)= & {} \gamma z+\bar{\gamma z}+W_{20}^{(3)}(0)\frac{z^2}{2}+W_{11}^{(3)}(0)z{\bar{z}}+W_{02}^{(3)}(0)\frac{{\bar{z}}^2}{2}+O(|(z,{\bar{z}})|^3),\\ x_{1t}(-1)= & {} z\text {e}^{-\text {i}\theta \omega ^*\tau ^*}+{\bar{z}}\text {e}^{\mathrm{i}\theta \omega ^*\tau ^*}+W_{20}^{(1)}(-1)\frac{z^2}{2}+W_{11}^{(1)}(-1)z{\bar{z}}+W_{02}^{(1)}(-1)\frac{{\bar{z}}^2}{2}+O(|(z,{\bar{z}})|^3), \\ x_{2t}(-1)= & {} \alpha z\text {e}^{-\text {i}\theta \omega ^*\tau ^*}+\bar{\alpha z}\text {e}^{\mathrm{i}\theta \omega ^*\tau ^*}+W_{20}^{(2)}(-1)\frac{z^2}{2}+W_{11}^{(2)}(-1)z{\bar{z}}+W_{02}^{(2)}(-1)\frac{{\bar{z}}^2}{2}+O(|(z,{\bar{z}})|^3),\\ x_{3t}(-1)= & {} \gamma z\text {e}^{-\text {i}\theta \omega ^*\tau ^*}+\bar{\gamma z}\text {e}^{\mathrm{i}\theta \omega ^*\tau ^*}+W_{20}^{(3)}(-1)\frac{z^2}{2}+W_{11}^{(3)}(-1)z{\bar{z}}+W_{02}^{(3)}(-1)\frac{{\bar{z}}^2}{2}+O(|(z,{\bar{z}})|^3). \end{aligned}$$

From the definition of $F(\mu ,x_t),$ we have

$$\begin{aligned} g(z,{\bar{z}})= & {} \tau ^*{\bar{D}}(1,{\bar{\alpha }}^*,{\bar{\gamma }}^*)\left( \begin{array}{c} \varDelta _{11}\\ \varDelta _{22}\\ \varDelta _{33} \end{array}\right) \\= & {} \tau ^*{\bar{D}}\left\{ z^2\left[ -\frac{r}{K}+\beta \gamma my^*\text {e}^{-mz^*}(1-k{\bar{\alpha }}^*)+\alpha \beta \gamma mx^*\text {e}^{-mz^*}(1-k{\bar{\alpha }}^*)\right. \right. \\&-\alpha \beta \text {e}^{-mz^*}(1-k{\bar{\alpha }}^*)+mk\beta \gamma y^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{-2\mathrm{i}\theta \omega ^*\tau ^*}({\bar{\alpha }}^*-{\bar{\gamma }}^*)\\&+mk\alpha \beta \gamma x^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{-2\mathrm{i}\theta \omega ^*\tau ^*}({\bar{\alpha }}^*-{\bar{\gamma }}^*)\left. -k\alpha \beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{-2\mathrm{i}\theta \omega ^*\tau ^*}({\bar{\alpha }}^*-{\bar{\gamma }}^*)\right] \\&+z{\bar{z}}z_1+{\bar{z}}^2z_2+z^2{\bar{z}}z_3, \end{aligned}$$

where

$$\begin{aligned} \varDelta _{11}= & {} -\frac{r}{K}x_{1t}^2(0)+\beta \text {e}^{-mz^*}(my^*x_{1t}(0)x_{3t}(0)+mx^*x_{2t}(0)x_{3t}(0)-x_{1t}(0)x_{2t}(0)),\\ \varDelta _{22}= & {} k\beta \text {e}^{-mz^*}(x_{1t}(0)x_{2t}(0)-my^*x_{1t}(0)x_{3t}(0)-mx^*x_{2t}(0)x_{3t}(0))\\&+ k\beta \text {e}^{-d_1\tau ^*} \text {e}^{-mz^*}(my^*x_{1t}(-1)x_{3t}(-1)+mx^*x_{2t}(-1)x_{3t}(-1) -x_{1t}(-1)x_{2t}(-1)),\\ \varDelta _{33}= & {} -k\beta \text {e}^{-d_1\tau ^*} \text {e}^{-mz^*}(my^*x_{1t}(-1)x_{3t}(-1)+mx^*x_{2t}(-1)x_{3t}(-1) -x_{1t}(-1)x_{2t}(-1)), \\ z_1= & {} -\frac{2r}{K}+\beta (\gamma +{\bar{\gamma }}) my^*\text {e}^{-mz^*}(1-k{\bar{\alpha }}^*)+\beta (\alpha {\bar{\gamma }}+{\bar{\alpha }}\gamma ) mx^*\text {e}^{-mz^*}(1-k{\bar{\alpha }}^*)\\&-(\alpha +{\bar{\alpha }})\beta \text {e}^{-mz^*}(1-k{\bar{\alpha }}^*)+(\gamma +{\bar{\gamma }})mk\beta y^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}({\bar{\alpha }}^*-{\bar{\gamma }}^*)\\&+(\alpha {\bar{\gamma }}+{\bar{\alpha }}\gamma )mk\beta x^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}({\bar{\alpha }}^*-{\bar{\gamma }}^*)-(\alpha +{\bar{\alpha }})k\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}({\bar{\alpha }}^*-{\bar{\gamma }}^*), \\ z_2= & {} -\frac{r}{K}+\beta {\bar{\gamma }} my^*\text {e}^{-mz^*}(1-k{\bar{\alpha }}^*)+\beta {\bar{\alpha }}{\bar{\gamma }} mx^*\text {e}^{-mz^*}(1-k{\bar{\alpha }}^*)-{\bar{\alpha }}\beta \text {e}^{-mz^*}(1-k{\bar{\alpha }}^*)\\&+mk\beta {\bar{\gamma }} y^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{2\mathrm{i}\theta \omega ^*\tau ^*}({\bar{\alpha }}^*-{\bar{\gamma }}^*)+mk\beta {\bar{\alpha }}{\bar{\gamma }} x^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{2\mathrm{i}\theta \omega ^*\tau ^*}({\bar{\alpha }}^*-{\bar{\gamma }}^*)\\&-k{\bar{\alpha }}\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{2\mathrm{i}\theta \omega ^*\tau ^*}({\bar{\alpha }}^*-{\bar{\gamma }}^*), \\ z_3= & {} -\frac{r}{K}(2W_{11}^{(1)}(0)+W_{20}^{(1)}(0))+\beta my^*\text {e}^{-mz^*}(1-k{\bar{\alpha }}^*)(W_{11}^{(3)}(0)+\gamma W_{11}^{(1)}(0)\\&+\frac{1}{2}W_{20}^{(3)}(0)+\frac{{\bar{\gamma }}}{2}W_{20}^{(1)}(0))+\beta mx^*\text {e}^{-mz^*}(1-k{\bar{\alpha }}^*)(\alpha W_{11}^{(3)}(0)+\gamma W_{11}^{(2)}(0)\\&+\frac{{\bar{\alpha }}}{2}W_{20}^{(3)}(0)+\frac{{\bar{\gamma }}}{2}W_{20}^{(3)}(0))-\beta \text {e}^{-mz^*}(1-k {\bar{\alpha }}^*)(W_{11}^{(2)}(0)+\alpha W_{11}^{(1)}(0)\\&+\frac{1}{2}W_{20}^{(2)}(0)+\frac{{\bar{\alpha }}}{2}W_{20}^{(1)}(0))+mk\beta y^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}({\bar{\alpha }}^*-{\bar{\gamma }}^*)(\text {e}^{-\text {i}\theta \omega ^*\tau ^*}W_{11}^{(3)}(-1)\\&+\gamma \text {e}^{-\text {i}\theta \omega ^*\tau ^*}W_{11}^{(1)}(-1)+\frac{1}{2}\text {e}^{\mathrm{i}\theta \omega ^*\tau ^*}W_{20}^{(3)}(-1)+\frac{{\bar{\gamma }}}{2}\text {e}^{\mathrm{i}\theta \omega ^*\tau ^*}W_{20}^{(1)}(-1))\\&+mk\beta x^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}({\bar{\alpha }}^*-{\bar{\gamma }}^*)(\alpha \text {e}^{-\text {i}\theta \omega ^*\tau ^*}W_{11}^{(3)}(-1)+\gamma \text {e}^{-\text {i}\theta \omega ^*\tau ^*}W_{11}^{(2)}(-1)\\&+\frac{{\bar{\alpha }}}{2}\text {e}^{\mathrm{i}\theta \omega ^*\tau ^*}W_{20}^{(3)}(-1)+\frac{{\bar{\gamma }}}{2}\text {e}^{\mathrm{i}\theta \omega ^*\tau ^*}W_{20}^{(2)}(-1))-k\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}({\bar{\alpha }}^*-{\bar{\gamma }}^*)\\&(\text {e}^{\mathrm{i}\theta \omega ^*\tau ^*}W_{11}^{(2)}(-1)+\alpha \text {e}^{-\text {i}\theta \omega ^*\tau ^*}W_{11}^{(1)}(-1)+\frac{1}{2}\text {e}^{\mathrm{i}\theta \omega ^*\tau ^*}W_{20}^{(2)}(-1) +\frac{{\bar{\alpha }}}{2}\text {e}^{\mathrm{i}\theta \omega ^*\tau ^*}W_{20}^{(1)}(-1)). \end{aligned}$$

On comparing the coefficients with (A.11), we obtain that

$$\begin{aligned} g_{20}=2\tau ^*{\bar{D}}z_2,\qquad g_{11}=2\tau ^*{\bar{D}}z_1,\qquad g_{02}=2\tau ^*{\bar{D}}z_2\qquad g_{21}=2\tau ^*{\bar{D}}z_3. \end{aligned}$$

In order to determine $g_{21},$ we need to compute $W_{20}(\theta )$ and $W_{11}(\theta ).$ From (A.6) and (A.9), we have

$$\begin{aligned} {\dot{W}}={\dot{x}}_t-{\dot{z}}q-\dot{{\bar{zq}}}= \left\{ \begin{array}{ll} AW-2\,Re[{\bar{q}}^*(0)F_{0}q(\theta )],&{}\quad \theta \in [-1,0),\\ AW-2\,Re[{\bar{q}}^*(0)F_{0}q(\theta )]+F_{0},&{}\quad \theta =0, \end{array}\right. {\mathop {=}\limits ^{\mathrm{def}}}AW+H(z,{\bar{z}},\theta ), \end{aligned}$$

(A.12)

where

$$\begin{aligned} H(z,{\bar{z}},\theta )=H_{20}(\theta )\frac{z^2}{2}+H_{11}(\theta )z{\bar{z}}+H_{02}(\theta )\frac{{\bar{z}}^2}{2}+\cdots . \end{aligned}$$

(A.13)

Note that on center manifold $C_0$ near the origin ${\dot{W}}=W_{z}{\dot{z}}+W_{{\bar{z}}}\dot{{\bar{z}}}$, and thus we obtain

$$\begin{aligned} (A-2\mathrm{i}\omega ^*\tau ^*)W_{20}(\theta )=-H_{20}(\theta ), \ \ AW_{11}(\theta )=-H_{11}(\theta ). \end{aligned}$$

(A.14)

Comparing the coefficients with (A.13), we obtain the following:

$$\begin{aligned} H_{20}(\theta )-g_{20}q(\theta )-{\bar{g}}_{02}{\bar{q}}(\theta ),\ \ H_{11}(\theta )=-g_{11}q(\theta )-{\bar{g}}_{11}{\bar{q}}(\theta ). \end{aligned}$$

(A.15)

From (A.14), (A.15) and the definition of A,  we have

$$\begin{aligned}{\dot{W}}_{20}(\theta )=2\mathrm{i}\omega ^*\tau ^*W_{20}(\theta )+g_{20}q(\theta )+{\bar{g}}_{11}{\bar{q}}(\theta ).\end{aligned}$$

Noting that $q(\theta )=q(0)\text {e}^{\mathrm{i}\omega ^*\tau ^*\theta },$ hence

$$\begin{aligned} {\dot{W}}_{20}(\theta )=\frac{\mathrm{i}g_{20}}{\omega ^*\tau ^*}q(0)\text {e}^{\mathrm{i}\omega ^*\tau ^*\theta }+\frac{\mathrm{i}{\bar{g}}_{02}}{3\omega ^*\tau ^*}{\bar{q}}(0)\text {e}^{-2\mathrm{i}\omega ^*\tau ^*\theta }+E_1\text {e}^{2\mathrm{i}\omega ^*\tau ^*\theta }, \end{aligned}$$

(A.16)

where $E_1=(E_1^{(1)},E_1^{(2)},E_1^{(3)})\in R^3$ is a constant vector.

Similarly, from (A.14) and (A.15), we obtain

$$\begin{aligned} W_{11}(\theta )=-\frac{\mathrm{i}g_{11}}{\omega ^*\tau ^*}q(0)\text {e}^{\mathrm{i}\omega ^*\tau ^*\theta }+\frac{\mathrm{i}{\bar{g}}_{11}}{\omega ^*\tau ^*}{\bar{q}}(0)\text {e}^{-\text {i}\omega ^*\tau ^*\theta }+E_2, \end{aligned}$$

(A.17)

where $E_2=(E_2^{(1)},E_2^{(2)},E_2^{(3)})\in R^3$ is also a constant vector.

In the following we shall find out $E_1$ and $E_2.$ From the definition of A and (A.14), we can obtain

$$\begin{aligned} \int _{-1}^{0}W_{20}(\theta ) \text {d}\eta (\theta )=2\mathrm{i}\omega ^*\tau ^*W_{20}(0)-H_{20}(0), \end{aligned}$$

(A.18)

and

$$\begin{aligned} \int _{-1}^{0}W_{11}(\theta )\text {d}\eta (\theta )=-H_{11}(0), \end{aligned}$$

(A.19)

where $\eta (\theta )=\eta (0,\theta ).$ From (A.12) and (A.13), we have

$$\begin{aligned} H_{20}(0)= & {} -g_{20}q(0)-{\bar{g}}_{02}{\bar{q}}(0)+2\tau ^*\left( \begin{array}{ccc}H_1\\ H_2\\ H_3 \end{array}\right) , \end{aligned}$$

(A.20)

$$\begin{aligned} H_{11}(0)= & {} -g_{11}q(0)-{\bar{g}}_{11}{\bar{q}}(0)+2\tau ^*\left( \begin{array}{ccc} H_4\\ H_5\\ H_6 \end{array}\right) , \end{aligned}$$

(A.21)

where

$$\begin{aligned} H_1= & {} \frac{-r}{K}+\beta \gamma my^*\text {e}^{-mz^*}+\alpha \beta \gamma mx^*\text {e}^{-mz^*}-\alpha \beta \text {e}^{-mz^*},\\ H_2= & {} -k\beta \gamma my^*\text {e}^{-mz^*}-k\alpha \beta \gamma mx^*\text {e}^{-mz^*}+k\alpha \beta \text {e}^{-mz^*}\\&+mk\beta \gamma y^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{-2\mathrm{i}\theta \omega ^*\tau ^*}+mk\alpha \beta \gamma x^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{-2\mathrm{i}\theta \omega ^*\tau ^*}-k\alpha \beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{-2\mathrm{i}\theta \omega ^*\tau ^*},\\ H_3= & {} -mk\beta \gamma y^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{-2\mathrm{i}\theta \omega ^*\tau ^*}-mk\alpha \beta \gamma x^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{-2\mathrm{i}\theta \omega ^*\tau ^*} +k\alpha \beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}\text {e}^{-2\mathrm{i}\theta \omega ^*\tau ^*},\\ H_4= & {} \frac{-2r}{K}+2 Re({\gamma })\beta my^*\text {e}^{-mz^*}+2\beta Re({\alpha {\bar{\gamma }}}) mx^*\text {e}^{-mz^*}-2\beta Re({\alpha }) \text {e}^{-mz^*},\\ H_5= & {} -2k\beta Re({\gamma }) my^*\text {e}^{-mz^*}-2k\beta Re({\alpha {\bar{\gamma }}}) mx^*\text {e}^{-mz^*}+2k\beta Re({\alpha })\text {e}^{-mz^*}\\&+2\,Re({\gamma })mk\beta y^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}+2\,Re({\alpha {\bar{\gamma }}})mk\beta x^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}-2\,Re({\alpha })k\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*},\\ H_6= & {} -2\,Re({\gamma })mk\beta y^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}-2\,Re({\alpha {\bar{\gamma }}})mk\beta x^*\text {e}^{-d_1\tau ^*}\text {e}^{-mz^*} +2\,Re({\alpha })k\beta \text {e}^{-d_1\tau ^*}\text {e}^{-mz^*}. \end{aligned}$$

Substituting (A.16) and (A.17) into (A.18) and noticing that

$$\begin{aligned} \left( \text {i}\omega ^*\tau ^*I-\int _{-1}^{0}\text {e}^{2\mathrm{i}\omega ^*\tau ^*\theta }\text {d}\eta (\theta )\right) q(0)=0, \end{aligned}$$

and

$$\begin{aligned} \left( -\text {i}\omega ^*\tau ^*I-\int _{-1}^{0}\text {e}^{-\text {i}\omega ^*\tau ^*\theta }\text {d}\eta (\theta )\right) \bar{q(0)}=0, \end{aligned}$$

we obtain

$$\begin{aligned} \left( 2\mathrm{i}\omega ^*\tau ^*I-\int _{-1}^{0}\text {e}^{2\mathrm{i}\omega ^*\tau ^*\theta }\text {d}\eta (\theta )\right) E_1=2\tau ^*\left( \begin{array}{ccc} H_1\\ H_2\\ H_3 \end{array}\right) , \end{aligned}$$

which leads to

$$\begin{aligned}\left( \begin{array}{ccc} \sigma _{11} &{} \sigma _{12} &{} \sigma _{13}\\ \sigma _{21} &{} \sigma _{22} &{} \sigma _{23}\\ \sigma _{31} &{} \sigma _{31} &{} \sigma _{33} \end{array}\right) E_1 =2\left( \begin{array}{ccc} H_1\\ H_2\\ H_3 \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned} \sigma _{11}= & {} 2\mathrm{i}\omega ^*-r(1-\frac{2x^*}{K})-\beta \text {e}^{-mz^*}y^*,\\ \sigma _{12}= & {} \beta \text {e}^{-mz^*}x^*,\\ \sigma _{13}= & {} -m\beta \text {e}^{-mz^*}x^*y^*,\\ \sigma _{21}= & {} -k\beta e^{-mz^*}y^*(1+\text {e}^{-(d_1+2\mathrm{i}\omega ^*)\tau ^*}),\\ \sigma _{22}= & {} 2\mathrm{i}\omega ^*+d_1-k\beta \text {e}^{-mz^*}x^*(1+\text {e}^{-(d_1+2\mathrm{i}\omega ^*)\tau ^*}),\\ \sigma _{23}= & {} mk\beta \text {e}^{-mz^*}x^*y^*(1+\text {e}^{-(d_1+2\mathrm{i}\omega ^*)\tau ^*}),\\ \sigma _{31}= & {} k\beta \text {e}^{-mz^*}y^*\text {e}^{-(d_1+2\mathrm{i}\omega ^*)\tau ^*},\\ \sigma _{33}= & {} 2\mathrm{i}\omega ^*+d_2-mk\beta \text {e}^{-mz^*}x^*y^*\text {e}^{-(d_1+2\mathrm{i}\omega ^*)\tau ^*}. \end{aligned}$$

It follows that

$$\begin{aligned} E_1 =2\left( \begin{array}{ccc} \sigma _{11} &{} \sigma _{12} &{} \sigma _{13}\\ \sigma _{21} &{} \sigma _{22} &{} \sigma _{23}\\ \sigma _{31} &{} \sigma _{31} &{} \sigma _{33} \end{array}\right) ^{-1}\times \left( \begin{array}{ccc} H_1\\ H_2\\ H_3 \end{array}\right) . \end{aligned}$$

Similarly, substituting (A.17) and (A.18) into (A.19), we can get

$$\begin{aligned} E_2=2\left( \begin{array}{ccc} \delta _{11} &{} \beta \text {e}^{-mz^*}x^* &{} \sigma _{13}\\ \delta _{21} &{} d_1-k\beta \text {e}^{-mz^*}x^*(1+\text {e}^{-d_1\tau ^*}) &{} mk\beta \text {e}^{-mz^*}x^*y^*(1+\text {e}^{-d_1\tau ^*})\\ \delta _{31} &{} k\beta \text {e}^{-mz^*}x^*\text {e}^{-d_1\tau ^*} &{} d_2-mk\beta \text {e}^{-mz^*}x^*y^*\text {e}^{-d_1\tau ^*} \end{array}\right) ^{-1} \times \left( \begin{array}{ccc} H_4\\ H_5\\ H_6 \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned} \sigma _{11}= & {} -r(1-\frac{2x^*}{K})-\beta \text {e}^{-mz^*}y^*,\\ \sigma _{21}= & {} -k\beta \text {e}^{-mz^*}y^*(1+\text {e}^{-d_1\tau ^*}),\\ \sigma _{23}= & {} k\beta \text {e}^{-mz^*}y^*\text {e}^{-d_1\tau ^*}. \end{aligned}$$

Thus, we can determine $W_{20}$ and $W_{11}$ from (A.16) and (A.17).