Skip to main content
SpringerLink
Log in

The limits of Riemann solutions to Euler equations of compressible fluid flow with a source term

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

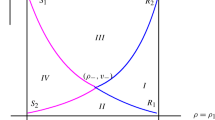
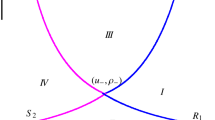
In this paper, we investigate the limits of Riemann solutions to the Euler equations of compressible fluid flow with a source term as the adiabatic exponent tends to one. The source term can represent friction or gravity or both in Engineering. For instance, a concrete physical model is a model of gas dynamics in a gravitational field with entropy assumed to be a constant. The body force source term is presented if there is some external force acting on the fluid. The force assumed here is the gravity. Different from the homogeneous equations, the Riemann solutions of the inhomogeneous system are non self-similar. We rigorously proved that, as the adiabatic exponent tends to one, any two-shock Riemann solution tends to a delta shock solution of the pressureless Euler system with a Coulomb-like friction term, and the intermediate density between the two shocks tends to a weighted \(\delta \)-mesaure which forms the delta shock; while any two-rarefaction-wave Riemann solution tends to a two-contact-discontinuity solution of the pressureless Euler system with a Coulomb-like friction term, whose intermediate state between the two contact discontinuities is a vacuum state. Moreover, we also give some numerical simulations to confirm the theoretical analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Chaplygin S (1904) On gas jets. Sci Mem Moscow Univ Math Phys 21:1–121

    Google Scholar 

  2. Tsien HS (1939) Two dimensional subsonic flow of compressible fluids. J Aeron Sci 6:399–407

    MathSciNet  MATH  Google Scholar 

  3. von Karman T (1941) Compressibility effects in aerodynamics. J Aeron Sci 8:337–356

    MathSciNet  MATH  Google Scholar 

  4. Shen C (2016) The Riemann problem for the pressureless Euler system with the Coulomb-like friction term. IMA J Appl Math 81:76–99

    MathSciNet  MATH  Google Scholar 

  5. Faccanoni G, Mangeney A (2012) Exact solution for granular flows. Int J Numer Anal Meth Geomech 37:1408–1433

    Google Scholar 

  6. Karelsky KV, Petrosyan AS, Tarasevich SV (2014) Nonlinear dynamics of magnet hydrodynamic flows of heavy fluid on slope in shallow water approximation. J Exp Theor Phys 146:352–367

    Google Scholar 

  7. Shen C (2016) The Riemann problem for the Chaplygin gas equations with a source term. Z Angew Math Mech 96:681–695

    MathSciNet  Google Scholar 

  8. Shen C, Sun M (2018) A distributional product approach to the delta shock wave solution for the one-dimensional zero-pressure gas dynamics system. Int J Nonlinear Mech 105:105–112

    Google Scholar 

  9. Savage SB, Hutter K (1989) The motion of a finite mass of granular material down a rough incline. J Fluid Mech 199:177–215

    MathSciNet  MATH  Google Scholar 

  10. Earnshaw S (1858) On the mathematical theory of sound. Philos Trans 150:1150–1154

    Google Scholar 

  11. Lu YG (2005) Existence of global entropy solutions to a nonstrictly hyperbolic system. Arch Ration Mech Anal 178:287–299

    MathSciNet  MATH  Google Scholar 

  12. Cheng Z (2008) Global entropy solutions to a variant of the compressible Euler equations. Appl Math Lett 21:410–415

    MathSciNet  MATH  Google Scholar 

  13. Klainerman S, Majda A (1981) Singular limits of quasilinear hyperbolic systems with large parameters and the incompressible limit of compressible fluids. Commun Pure Appl Math 34:481–524

    MathSciNet  MATH  Google Scholar 

  14. Oelschläger K (1991) On the connection between Hamiltonian many-particle systems and the hydrodynamical equation. Arch Ration Mech Anal 115:297–310

    MathSciNet  MATH  Google Scholar 

  15. Oelschläger K (1997) An integro-differential equation modelling a Newtonian dynamics and its scaling limit. Arch Ration Mech Anal 137:99–134

    MathSciNet  MATH  Google Scholar 

  16. Caprino S, Esposito R, Marra R, Pulvirenti M (1993) Hydrodynamic limits of the Vlasov equation. Commun Partial Differ Equ 18:805–820

    MathSciNet  MATH  Google Scholar 

  17. Cheng H, Yang H, Zhang Y (2010) Riemann problem for the Chaplygin Euler equations of compressible fluid flow. Int J Nonlinear Sci Numer Simul 11:985–992

    Google Scholar 

  18. DiPerna RJ (1973) Global solutions to a class of nonlinear hyperbolic systems of equations. Commun Pure Appl Math 26:1–28

    MathSciNet  MATH  Google Scholar 

  19. Li CZ (1982) Existence in the large for certain systems of quasi linear hyperbolic conservation laws. J Differ Equ 45:85–102

    Google Scholar 

  20. Pang Y, Zhang Y, Wen Y (2018) Delta shock wave to the compressible fluid flow with the generalized Chaplygin gas. Int J Nonlinear Mech 99:311–318

    Google Scholar 

  21. Sarrico COR, Paiva A (2017) The multiplication of distributions in the study of a Riemann problem in fluid dynamics. J Nonlinear Math Phys 24:328–345

    MathSciNet  MATH  Google Scholar 

  22. Song G, Xiao J (2009) Existence of global weak solutions to a special system of Euler equation with a source (II): general case. J Math Anal Appl 352:943–953

    MathSciNet  MATH  Google Scholar 

  23. Pudasaini SP (2012) A general two-phase debris flow model. J Geophys Res 117:F03010

    Google Scholar 

  24. Ghosh Hajra S, Kandel S, Pudasaini SP (2015) Lie symmetry solutions for two-phase mass flows. Int J Nonlinear Mech 77:325–341

    Google Scholar 

  25. Ghosh Hajra S, Kandel S, Pudasaini SP (2017) Optimal systems of Lie subalgebras for a two-phase mass flow. Int J Nonlinear Mech 88:109–121

    Google Scholar 

  26. Ghosh Hajra S, Kandel S, Pudasaini SP (2018) On analytical solutions of a two-phase mass flow model. Nonlinear Anal Real World Appl 41:412–427

    MathSciNet  MATH  Google Scholar 

  27. Pudasaini SP, Mergili M (2019) A multi-phase mass flow model. J Geophys Res Earth Surf 124:2920–2942

    Google Scholar 

  28. Daw DAE, Nedeljkov M (2016) Shadow waves for pressureless gas balance laws. Appl Math Lett 57:54–59

    MathSciNet  MATH  Google Scholar 

  29. Edwards CM, Howison SD, Ockendon H, Ockendon JR (2008) Non-classical shallow water flows. IMA J Appl Math 73:137–157

    MathSciNet  MATH  Google Scholar 

  30. Guo L, Li T, Yin G (2017) The limit behavior of the Riemann solutions to the generalized Chaplygin gas equations with a source term. J Math Anal Appl 455:127–140

    MathSciNet  MATH  Google Scholar 

  31. Guo L, Li T, Yin G (2017) The vanishing pressure limits of Riemann solutions to the Chaplygin gas equations with a source term. Commun Pure Appl Anal 16:295–309

    MathSciNet  MATH  Google Scholar 

  32. Sun M (2016) The exact Riemann solutions to the generalized Chaplygin gas equations with friction. Commun Nonlinear Sci Numer Simul 36:342–353

    MathSciNet  MATH  Google Scholar 

  33. Chen GQ, Liu H (2003) Formation of \({\delta }\)-shocks and vacuum states in the vanishing pressure limit of solutions to the Euler equations for isentropic fluids. SIAM J Math Anal 34:925–938

    MathSciNet  MATH  Google Scholar 

  34. Chen GQ, Liu H (2004) Concentration and cavitation in the vanishing pressure limit of solutions to the Euler equations for nonisentropic fluids. Physica D 189:141–165

    MathSciNet  MATH  Google Scholar 

  35. Li J (2001) Note on the compressible Euler equations with zero temperature. Appl Math Lett 14:519–523

    MathSciNet  MATH  Google Scholar 

  36. Ibrahim M, Liu F, Liu S (2019) Concentration of mass in the pressureless limit of Euler equations for power law. Nonlinear Anal Real World Appl 47:224–235

    MathSciNet  MATH  Google Scholar 

  37. Keyfitz BL (1999) Conservation laws, delta shocks and singular shocks. In: Grosser M, Hormann G, Kunzinger M, Oberguggenberger M (eds) Nonlinear theory of generalized functions. Research Notes in Mathematics, Chapman and Hall/CRC, Boca Raton, pp 99–111

    Google Scholar 

  38. Bouchut F (1994) On zero pressure gas dynamics. In: Advances in kinetic theory and computing. Adv Math Appl Sci, vol 22, World Sci Publ, River Edge, NJ, pp 171–190

  39. Li J, Zhang T, Yang S (1998) The two-dimensional Riemann problem in gas dynamics. Pitman Monographs and Surveys in Pure and Applied Mathematics, vol 98. Longman Scientific and Technical, Harlow

  40. Sheng W, Zhang T (1999) The Riemann problem for the transportation equations in gas dynamics. Memoirs of the Amer Math Soc, vol 137, AMS, Providence

  41. Yang H (1999) Riemann problems for a class of coupled hyperbolic systems of conservation laws. J Differ Equ 159:447–484

    MathSciNet  MATH  Google Scholar 

  42. Freistühler H, Bruce Pitman E (1992) A numerical study of a rotationally degenerate hyperbolic system. Part I. The Riemann problem. J Comput Phys 100:306–321

    MATH  Google Scholar 

  43. Kurganov A, Tadmor E (2000) New high-resolution central schemes for nonlinear conservation laws and convection diffusion equations. J Comput Phys 160:241–282

    MathSciNet  MATH  Google Scholar 

  44. Shu CW (1998) Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In: Quarteroni A (ed) Advanced numerical approximation of nonlinear hyperbolic equations. Lecture Notes in Mathematics, vol 1697, Springer, Berlin, pp 325–432

  45. Shen C, Sun M, Wang Z (2010) Limit relations for three simple hyperbolic systems of conservation laws. Math Methods Appl Sci 33:1317–1330

    MathSciNet  MATH  Google Scholar 

  46. Sun M (2018) The limits of Riemann solutions to the simplified pressureless Euler system with flux approximation. Math Methods Appl Sci 41:4528–4548

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to the four anonymous referees for their valuable comments and corrections, which have improved the original manuscript greatly. This work is supported by the Natural Science Foundation of Fujian Province of China (Grant No. 2019J01642).

Author information

Authors and Affiliations

  1. College of Mathematics and Computer Science, Fuzhou University, Fuzhou, 350108, China

    Shouqiong Sheng & Zhiqiang Shao

Authors
  1. Shouqiong Sheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhiqiang Shao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhiqiang Shao.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sheng, S., Shao, Z. The limits of Riemann solutions to Euler equations of compressible fluid flow with a source term. J Eng Math 125, 1–22 (2020). https://doi.org/10.1007/s10665-020-10066-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10665-020-10066-3

Keywords

Search

Navigation