1 Introduction

Quantifying correlations between stock indices and their derivatives is important to the understanding of the price discovery process between spot and derivative markets, and has practical values for investors and regulators to adjust investment strategies and strengthen the risk management of financial markets. According to the Efficient Markets Hypothesis (Fama, 1991; Shao et al., 2019), the indices should neither lead nor lag their derivatives. However, there is usually a mixed lead–lag structure among stock indices and their derivatives, due to the complexity and frictions of real markets, such as asymmetric information, liquidity and extreme events (Chan, 1992). With the advent of intelligent stock trading system that may result in the causal relations reflected on a smaller time scale (Ryu, 2012; Kim & Ryu, 2014), the literature starts to focus on the intraday lead–lag relations between the index and its derivatives.

The findings of the literature so far are diverse and inconsistent. There are some bivariate analysis showing that the derivatives led its index (Amin & Lee, 1997; Tse, 2001; Theissen, 2012; Fung et al., 2015; Ahn et al., 2019; Raju & Shirodkar, 2020). In contrast, other studies indicate the index played a price guiding role on its associated derivatives (Cao et al., 2014; Gaul & Theissen, 2015; Zhou & Wu, 2016). Besides, bidirectional causal relations between the index and its derivatives have been observed in recent studies (Cao et al., 2014; Gaul and Theissen 2015; Zhou and Wu 2016; Jiang et al., 2019). Further studies show that there exists a symmetric lead–lag relation between the options and the futures (Nam et al., 2006; Kang et al., 2006; Ren et al., 2019).

It has been noted that the lead–lag relations between the index and its derivatives vary over time, due to financial regulations (Jiang et al., 2001; Yu et al., 2012), political environment (Chan et al., 2009) and market condition (Li, 2008; Wang et al., 2017; Nuria et al., 2020; Yang & Shao, 2020). However, there is relatively limited empirical evidence of the dynamic lead–lag relations between the index and its derivatives in China at high-frequency time scale, which has the world’s biggest emerging financial market. In the present study, we investigate the intraday lead–lag relations between the index and its derivatives in the Chinese mainland, Hong Kong and US markets, and validates our results by using both the non-parametric thermal optimal path (TOP) method and the traditional vector error correction-information share (VECM-IS) model.

The empirical results of our paper indicate that the futures and options exhibit price leadership over the spot market, and the options is ahead of the futures on most trading days in all the three markets, consistent with Ren et al. (2019), Ahn et al. (2019) and Raju and Shirodkar (2020). Differing from the previous literature, our new findings on the reversal phenomenon of intraday lead–lag relations show that the relation between the derivative and its underlying index reverses when the index return has a significantly larger mean value, and the reversal phenomenon is also observed in the relations between the futures and options.

Compared to earlier studies, the main contributions of this study to the literature are as follows. First, we complement the work on the dynamic variation of intraday lead–lag relations between the index and its derivatives, and draw an explicit conclusion through a comprehensive study with broader coverage of research objectives and methodologies. Second, distinguishing from previous studies, our new findings on the reversal phenomenon of intraday lead–lag relations enrich the empirical research in this area.

The remainder of this paper is organized as follows. In Sect. 2, we introduce the TOP method and the VECM-IS model. Using 1-min data, we investigate the dynamic variation of intraday lead–lag relations among stock index-based futures, options and spot, and perform a multi-market comparison between the Chinese mainland, Hong Kong and US markets in Sect. 3. Section 4 concludes.

2 Methodology

We use two methods to identify the dynamic intraday lead–lag relations between the index and its derivatives, namely the TOP method and the VECM-IS method. The TOP method can capture the nonlinear lead–lag structures between economic variables (Sornette & Zhou, 2005), and the VECM-IS method can examine the dependence structure between two non-stationary time series (Wahab & Lashgari, 1993; Ghosh, 1993). Both methods have been widely and successfully applied to quantify the dependencies among various economic variables (Gong et al., 2016; Chen et al., 2016; Wang et al., 2017; Ren et al., 2019), and our study extends the application of these two methods in the detection of intraday lead–lag relation between financial series.

2.1 TOP Method

Compared to the traditional statistic methods, the main advantage of the TOP method is that it enables us to detect lagged dependence locally and is thus particularly useful when the dependence relation is nonlinear and changes intermittently (Zhou & Sornette, 2006). Supposing there are two standardized time series, donated as \(\{X(t_{1}): t_{1}=0, \ldots , N-1\}\) and \(\{Y(t_{2}): t_{2}=0, \ldots , N-1\}\). \(E_{X,Y}\) represents the distance matrix between \(X(t_{1})\) and \(Y(t_{2})\), and its element \(\varepsilon (t_{1},t_{2})\) can be calculated as

$$\begin{aligned} \varepsilon (t_{1},t_{2})=[X(t_{1})-Y(t_{2})]^{2}. \end{aligned}$$
(1)

Based on the distance matrix \(E_{X,Y}\), the key to investigating the lead–lag relationship is to minimize the total mismatch between \(X(t_{1})\) and \(Y(t_{2})\) by searching for a smooth mapping \(t_{1}\) \(\rightarrow \) \(t_{2}= \phi (t_{1})\). For example, if \(X(t_{1})\) is ahead of \(Y(t_{2})\) with \(k (k>0)\) units in time, they will have a mapping \(t_{1}=t_{2}+k\) that makes \(\varepsilon (t_{1},t_{2})=0\). Therefore, quantifying the lead–lag structures is equivalent to search for the mapping \(t_{1}\) \(\rightarrow \) \(t_{2}\) which can obtain the global minimization of the distance given by the following equation

$$\begin{aligned} Min_{\{\phi (t_{1}), t_{1}=0,1,2,\ldots ,N-1\}}\sum _{t_{1}=0}^{N-1}|X(t_{1})-Y(t_{2})|^{2}. \end{aligned}$$
(2)

For better understanding, we can interpret the distance matrix \(E_{X,Y}\) as the energy landscape, and the distance element is the energy corresponding to node \((t_{1},t_{2})\). In this case, the global minimization of Eq. (2) can be transformed into the search for the configuration with minimum energy. To make it convenient for solving the global minimization problem, we use the rotated coordinate system (x, t) to represent \((t_{1},t_{2})\) in the original coordinate system as

$$\begin{aligned} \begin{array}{l} x=t_{2}-t_{1},\\ t=t_{1}+t_{2}. \end{array} \end{aligned}$$
(3)
Fig. 1
figure 1

Illustration of the original coordinate plane \((t_{1}, t_{2})\) and the rotated frame (x, t). As depicted by the three red arrows, there are three possible paths allowed to move to \((\tau _{1} + 1, \tau _{2} + 1)\) in one step

Full size image

Figure 1 represents the rotated frame (x, t) and the original coordinate plane \((t_{1},t_{2})\). As depicted in the three red arrows in Fig. 1, there are three possible paths to reach \((\tau _{1} + 1, \tau _{2} + 1)\): either along the diagonal from \((\tau _{1},\tau _{2})\), or go vertically from \((\tau _{1} + 1, \tau _{2})\), horizontally from \((\tau _{1}, \tau _{2} + 1)\). In the original coordinate plane \((\tau _{1},\tau _{2})\), the path below (above) the diagonal corresponds to \(t_{1}>t_{2}\) (\(t_{1}<t_{2}\)). After the coordinate rotation according to Eq. (3), x measures the lead–lag structures between \(X(t_{1})\) and \(Y(t_{2})\). Specifically, \(x > 0\) implies that \(X(t_{1})\) is ahead of \(Y(t_{2})\); conversely, \(X(t_{1})\) lags behind \(Y(t_{2})\) when \(x < 0\).

In practical applications, both useful information and random noise are mixed in the real-world data, and thus the original time series decorated with noise may lead to misinterpretation of the lead–lag structures. To solve this problem, the thermal optimal path identified by the TOP method are allowed to deviate within a certain range near the absolute minimum energy path, which will make the results less sensitive to noise. Specifically, the robust lead–lag path is obtained as the weighted averaging of many paths, each assigned by the Boltzmann factor \(e^{-\varepsilon (x,t)/T}\). The Boltzmann factor can be interpreted as the probability of a given path with energy \(\varepsilon (x,t)\) above that of the path with absolute minimum energy, and the temperature T quantifies how much deviation from the minimum energy is allowed. A suitable value of T is helpful to discover the optimal thermal path. Too large value of T may result in the loss of important information on the genuine lead–lag pattern, while smaller T will increase the sensitivity of the path to noise.

The premise of searching for the thermal optimal path is to obtain the so-called partition functions G(x, t). From the movement scheme outlined in Fig. 1, the partition function G(x, t) for any lattice point can be determined recursively according to the following formula

$$\begin{aligned} G(x,t+1) = [G(x-1,t)+G(x+1,t)+G(x,t-1)]e^{-\varepsilon (x,t)/T}, \end{aligned}$$
(4)

where \(\varepsilon (t_{1},t_{2})\) is the element of the distance matrix defined in Eq. (1), which can also be considered as the energy. Through the recursive operation, the partition function G(x, t) and its sum \(G(t)=\sum _{x} G(x,t)\) can be obtained. Consequently, the ratio G(x, t)/G(t) implies the probability for a path to arrive at node (x, t). The optimal thermal average position \(\langle x(t)\rangle \) at time t can be defined as an average of all possible lead–lag configurations weighted by x, and its expression is as follows

$$\begin{aligned} \langle x(t)\rangle =\sum _{x} x G(x,t)/G(t). \end{aligned}$$
(5)

\(\langle x(t)\rangle \) can be interpreted as the average lead–lag relationship between \(X(t_{1})\) and \(Y(t_{2})\). A positive value of \(\langle x(t)\rangle \) implies that \(X(t_{1})\) is ahead of \(Y(t_{2})\), whereas a negative \(\langle x(t)\rangle \) means that \(Y(t_{2})\) leads \(X(t_{1})\).

What should be mentioned here is that the starting point should be set within m units from the origin (0, 0), and the end point requires to locate in m units from the top-right point (N, N) in the coordinate plane \((\tau _{1},\tau _{2})\). For the starting point and the end point, there are 2m+1 possible locations, respectively. Consequently, there are \((2m+1)^2\) possible paths starting from either points \((t_{1}=0,t_{2}=0)\), \((t_{1}=0,t_{2}=j)\) or \((t_{1}=j,t_{2}=0)\) and ending at \((t_{1}=N,t_{2}=N)\), \((t_{1}=N,t_{2}=N-j)\) or \((t_{1}=N-j,t_{2}=N)\), where \(j=1,2,\ldots ,m\). For a certain pair of starting and end points, its average distance (energy) \(e_{T}(x_{0})\) can be determined by the following equation

$$\begin{aligned} e_{T}=\frac{1}{2N-|x_{0}|-|x_{n}|-1}\sum _{t=|x_{0}|}^{2N-|x_{n}|-1}\sum _{x}\varepsilon (x,t)G(x,t)/G(t). \end{aligned}$$
(6)

Among the \((2m+1)^2\) possible paths, the path configuration with the minimum energy \(e_{T}(x_{0})\) is generally considered to be the global optimal path between \(X(t_{1})\) and \(Y(t_{2})\).

For the parameter selection criterion, we determine the optimal values of T and m according to the optimal solutions of the optimal thermal average position. In terms of our research purpose, T should not be too large to prevent the loss of a large amount of effective information, and too small value of T should also be avoided for the reason that too much spurious noise may be accompanied by overfitting. For parameter m, we first obtain a proper value of m for each trading day when \(\langle x(t)\rangle \) tends to stabilize, then choose a suitable quantile of those m values for all trading days as the optimal value of m, namely \(Q_{n}\). The quantile \(Q_{n}\) of variable m refers to the real number that satisfies the condition \(p(m \le Q_{n})= \alpha \). \(Q_{n}\) can satisfy the requirements of parameter m for most trading days, which can also improve the computational efficiency compared with the case that the selected optimal parameter is larger than the m values of all trading days.

2.2 VECM and IS Model

In literature, some traditional linear regression analysis methods, known as the VECM and the IS model, have been widely applied to investigate the casual relation between two time series. Supposing there are n cointegrated I(1) price series, denoted as \(P_{it}\) (\(i=1,2,\ldots ,n\)). The error correction terms \(z_{t}\) can be defined as the linearly independent differences of the price series, namely

$$\begin{aligned} z_{t}= \left[ \begin{array}{ccc} P_{1t}-P_{2t}\\ P_{1t}-P_{3t}\\ \vdots \\ P_{1t}-P_{nt}\\ \end{array} \right] . \end{aligned}$$
(7)

The analysis starts with the estimation of the following VECM

$$\begin{aligned} \Delta P_{t}=\alpha \beta ^\mathrm {'} P_{t-1}+\sum _{j=1}^{k} \Phi _{j} \Delta P_{t-j}+e_{t}, \end{aligned}$$
(8)

where \(\beta ^\mathrm {'} P_{t-1}=z_{t-1}\); \(\alpha \) is an \(n \times (n-1)\) error correction coefficient matrix, which quantifies how much the prices response to the deviation from the long-term equilibrium; \(\phi _{j}\) represents an \(n \times n\) autoregressive coefficients matrix, reflecting the short-term price movements due to the market imperfection; k is the lag length of the model; \(e_{t}\) is an \(n \times 1\) vector of serially uncorrelated disturbances, which is normally distributed with zero-mean and covariance matrix \(\Omega =\sigma _{ij}\).

On the basis of VECM, Hasbrouck (1995) developed the IS model to further quantify the relative contributions of derivatives and spot to price discovery. The main idea of the IS model lies in the fact that the information shares are calculated to measure the relative contribution of each market to the overall variance of innovations to the common factor. The VECM equation can also be expressed as the vector moving average (VMA) form

$$\begin{aligned} \Delta P_{t}=\Psi (L) e_{t}, \end{aligned}$$
(9)

where \(\Psi (L)\) denotes a matrix polynomials, and L is the lag operator. \(\Psi (L)e_{t}\) is defined as the long-term impact of innovations on the price of each market. Besides, the single integer form of VMA can be expressed as

$$\begin{aligned} P_{t}= \Psi (1) \left( \sum _{s=1}^{t} e_{s}\right) +\Psi ^\mathrm {*}(L) e_{t}, \end{aligned}$$
(10)

where \(\Psi (1)\) is calculated as the sum of moving average coefficients, and \(\Psi ^*(L)\) is a matrix composed of lagged polynomial.

The long-term impacts of innovations on all market prices are identical under the condition that each row of the impact matrix has the same elements. Therefore, Eq. (10) can then be transformed into the following form

$$\begin{aligned} P_{t}=\iota \psi \left( \sum _{s=1}^{t}e_{s}\right) +\Psi ^\mathrm {*}(L)e_{t}, \end{aligned}$$
(11)

where \(\iota \psi =\Psi (1)\); \(\iota \) is an \(n \times 1\) vector of ones, and \(\psi \) is a \(1 \times n\) vector of the impact matrix; \(\iota \psi (\sum _{s=1}^{t}e_{s})\) is the common factor, which measures the long-term impacts of innovations, and \(\Psi ^\mathrm {*}(L)e_{t}\) reflects the transitory effect. The increment \(\psi e_{t}\) depicts the common permanent impact of shock on prices, and its variance is denoted as \(Var(\psi e_{t})=\psi \Omega \psi ^\mathrm {'}\). The IS value of a particular market is calculated as \(Var(\psi e_{t})\) divided by the innovation variance in that market. In order to eliminate the contemporaneous correlation, Hasbrouck (1995) applied the Cholesky factorization of \(\Omega = QQ^\mathrm {'}\) to deal with the error correlation structure, where Q is a lower triangular matrix. Consequently, the information share of the \(j^{th}\) market can be expressed as

$$\begin{aligned} IS_{j}=\frac{(\psi Q_{j})^2}{\psi \Omega \psi ^\mathrm {'}}, (j=1,2,\ldots ,n). \end{aligned}$$
(12)

It is worth mentioning that the IS for each market is not unique, and it varies with different orderings of variables (Chen et al., 2016). In practical calculation, the scope of IS value can be obtained in the majority of the cases (Huang, 2002; Ates & Wang, 2005). In accordance with Baillie et al. (2002), the average of the lower and upper bounds is adopted to denote the information share in our analysis.

3 Data and Results

3.1 Data

This paper focuses on the dynamic variation of the intraday lead–lag relations between the index and its derivatives of the Chinese mainland market. To test the universality of empirical results, we also select the Hong Kong and US markets as two representive global mature markets to conduct a comparative study. Since there exists significant risk spillovers between the Chinese mainland and Hong Kong markets due to the stock connect programs of Shanghai-Hong Kong and Shenzhen-Hong Kong (Chen et al., 2021), we select it as a representative market and compare the intraday lead–lag relations between theses two markets. As one of the biggest global mature markets, other markets are both influenced by the US market (Ren et al., 2019; Yuan & Jin, 2021; Jin & Guo, 2021; Li & Chen, 2021). Therefore we choose it as a representative of the global mature markets.

The sampling data of SSE 50 index and its associated futures and ETF options are retrieved from the Wind database, see http://www.wind.com.cn. The Hang Seng Index (HSI) and its related futures and options are selected as the research objects of the Hong Kong market, and the stock index and derivatives analyzed in the US market include the spot, futures and options based on the Standard and Poor 500 (S&P 500) Index. The datasets used in the latter two markets are from the Bloomberg database, see http://www.bloomberg.cn. According to the trading rules, there are four types of contacts available for trading on the derivatives markets in mainland China and Hong Kong. Somewhat differently, there are eight contracts of S&P 500 index futures and options currently traded within a period of two years. Therefore, we select the most active contracts with the largest daily trading volume, commonly regarded as the main contracts, to construct the price sequences of futures and options. In reality, the current month contract is always filtered out as the main contract. If it reaches the delivery date, it will generally be substituted by next month contract, thus ensures the continuity of data.

The high frequency data of closing prices for 1-min intervals are used in our analysis, and the sampling periods are selected as follows. Since the SSE 50 index futures was issued on April 16, 2015, we therefore choose one of the sampling periods in the market of mainland China to be from April 16, 2015 to June 30, 2016. Another sampling period is from January 3, 2017 to January 18, 2018 in the Chinese mainland market and the Hong Kong market. To cover the same trading period among multiple markets, a sub-period from September 1, 2017 to January 18, 2018 is chosen in the study of the US market. In line with the majority of studies (Chiang & Fong, 2001; Cao et al., 2014), we study the lead–lag relations during the simultaneous intraday trading hours of the index and derivatives markets, i.e., from 9: 30 to 11: 30 and from 13: 00 to 15: 00 (Beijing Time) in the Chinese mainland market, from 9: 30 to 12: 00 and from 13: 00 to 16: 00 (Beijing Time) in the Hong Kong market, and from 9: 30 to 16: 00 (American Eastern Time) in the US market.

Suppose P(t) represents the closing price of the stock index or its derivative at time t, the logarithmic return R(t) of the stock index or its derivative can be calculated as follows

$$\begin{aligned} R(t)=\ln P(t)-\ln P(t-1). \end{aligned}$$
(13)

We thus obtain the logarithmic return series of SSE 50 index and its index futures and ETF options, denoted as \(R_{i}(t)\), \(R_{f}(t)\) and \(R_{o}(t)\), respectively. In a similar fashion, the returns of HSI and its associated futures and options are denoted as \(R_{i,HK}(t)\), \(R_{f,HK}(t)\), \(R_{o,HK}(t)\), and the returns of S&P 500 index, futures and options are denoted as \(R_{i,US}(t)\), \(R_{f,US}(t)\) and \(R_{o,US}(t)\), respectively. We have performed the Augmented Dicky-Fuller (ADF) test on the logarithmic price series of all indices and derivatives for each trading day, and found that not all of the time series are stationary. On the other hand, the return series are tested and shown to be stationary, and are therefore integrated.

Fig. 2
figure 2

Frequency distribution of the daily mean values of 1-min returns of SSE 50 index, HSI, S&P 500 index and their derivatives

Full size image

Figure 2 illustrates the frequency distribution of the daily mean value of 1-min returns of SSE 50 index, HSI, S&P 500 index and their derivatives. General statistics of the 1-min returns for all three stock indices and their derivatives during the sampling periods are also shown in Table 1, including mean, minimum, maximum, standard deviation, skewness and kurtosis. In all three markets, the mean values of 1-min returns of options are larger than those of the index and futures, and the standard deviations indicate that the intraday returns of options are more volatile compared with the spot and futures markets. The values of skewness show that the returns of the SSE 50 index futures and its underlying index are right-skewed (positive skewness), while the SSE 50 ETF options is left-skewed (negative skewness).

Table 1 Summary statistics of the 1-min returns of SSE 50 index, HSI, S&P 500 index and their derivatives
Full size table

It is worth to note that there may be a disparity between the closing price of the current day and the opening price of the following day. Therefore, this study does not carry out cross-day calculation for the 1-min data and treat the data from each day as a sub-sample. The trading of the index and its derivatives will be suspended when the stock index hits the daily upward or downward price fluctuation limits in the Chinese mainland stock market, which can lead to a lack of partial data. In order to ensure the availability of the data for the index and its derivatives in simultaneous trading times, we remove the trading days on which the daily limit was hit.Footnote 1 To ensure the comparability of the sub-sample data among different trading days, we choose a classical normalization: their mean is first subtracted and then divided by their standard deviation.

3.2 Results of the TOP Method

We begin by studying the intraday relation between 50 index and its derivative futures based on the TOP method. Treating the return series \(R_{i}(t)\) and \(R_{f}(t)\) as \(X(t_{1})\) and \(Y(t_{2})\), the intraday average lead–lag relation is calculated for each trading day. According to the principles of parameter selection mentioned in the last paragraph of Sect. 2.1, we calculate the values of \(\langle x(t)\rangle \) with parameters m ranging from 1 to 35, and obtain a proper value of m when \(\langle x(t)\rangle \) begins to stabilize for each trading day. On this basis, we select the third quartile \((Q_{3})\) of m values of the whole investigated trading days as the optimal parameter for the sake of the implementability of computation. \(Q_{3}\) can satisfy the requirements of parameter m for 75% sample trading days. Figure 3a shows the distribution of the proper values of m between the SSE 50 index and its related futures of the investigated trading days. One can see that the optimal parameter m is equal to 21. Together with the variation tendency of \(\langle x(t)\rangle \) with \(T=1, 2, 3\) and 4, we find that the values of \(\langle x(t)\rangle \) are relatively stable when m and T are set to be 21 and 3, respectively (Gong et al., 2016; Ren et al., 2019).

Fig. 3
figure 3

Distribution of the proper values of m among SSE 50 index-based spot, futures and ETF options when \(\langle x(t)\rangle \) tends to be stable for each day from the analysis using the TOP method. a The boxplot of the proper values of m between the index and the futures; b The boxplot of the proper values of m between the index and the ETF options; c The boxplot of the proper values of m between the futures and the ETF options

Full size image
Fig. 4
figure 4

Lead–lag relations among SSE 50 index-based spot, futures and ETF options obtained from the TOP method. a presents the lead–lag relation between the spot and the futures with optimal parameters \(m=21\) and \(T=3\); b presents the lead–lag relation between the spot and the ETF options with optimal parameters \(m=28\) and \(T=3\); c presents the lead–lag relation between the futures and the ETF options with optimal parameters \(m=19\) and \(T=3\)

Full size image

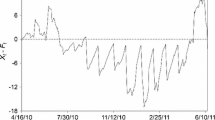
In order to show the intraday lead–lag relations intuitively, we average the thermal average position \(\langle x(t)\rangle \) for each trading day as the daily thermal average position, denoted by \(\langle x(t)\rangle _{d}\). Considering the sharp rise or fall at the terminal of \(\langle x(t)\rangle \) due to the starting and ending points constraints, we remove the initial and the last 10 min of \(\langle x(t)\rangle \) when calculating \(\langle x(t)\rangle _{d}\). A positive (negative) \(\langle x(t)\rangle _{d}\) indicates the price fluctuations of stock index leads (lags) those of the index futures on that day. Figure 4a shows the calculation results of \(\langle x(t)\rangle _{d}\) between the index and the futures, and each point corresponds to the daily thermal average position. One can observe that the index futures exhibits price leadership over the spot market on most trading days, except for a few days when the spot plays a leading role for the futures. Since the fluctuation of \(\langle x(t)\rangle \) within each day is relatively small, it is appropriate to adopt \(\langle x(t)\rangle _{d}\) to represent the intraday lead–lag relation for each trading day.

Figure 4b shows that the options plays a leading role for its corresponding index on most trading days during the period under study. However, the return of the index are also found to lead that of the options on a few days, and these trading days mostly coincide with those when the index return leads the futures return, meaning that the price guidance function of the index has greatly enhanced within these trading days. Figure 4c presents the daily thermal average position between the SSE 50 index futures and its associated ETF options. In a similar fashion, the return of the ETF options leads that of the index futures when \(\langle x(t)\rangle _{d}>0\), and vice versa. One can see from Fig. 4c that the ETF options plays a price guiding role for the futures on a relatively larger number of trading days, which is slightly smaller than the number of trading days when the options leads the index shown in Fig. 4b.

Fig. 5
figure 5

Lead–lag relations among HSI-based spot, futures and options obtained from the TOP method. a The lead–lag relation between the index and the futures with optimal parameters \(m=23\) and \(T=3\); b The lead–lag relation between the index and the options with optimal parameters \(m=32\) and \(T=3\); c The lead–lag relation between the futures and the options with optimal parameters \(m=23\) and \(T=3\)

Full size image

To conduct a comparative study among multiple markets, we here also analyze the intraday relations between HSI and its derivatives in the Hong Kong market, and the intraday relations of three pairs of return series in the US market. Figure 5 shows the lead–lag relations among the HSI spot, futures and options obtained from the TOP method. Figure 5a presents the lead–lag positions between HSI and its related futures, and we find that the return of HSI futures leads that of HSI for about 20 min on most trading days during the period under study, and lags on a relatively small number of trading days. From Fig. 5b, the price movements of the index options lead those of its spot for about 30 min on most trading days. We also observe that on a few trading days in mid-June 2017 and after September 2017, the intraday relation between the spot and the options reverses. Figure 5c shows that the options return is ahead of the futures return for about 23 min on most trading days, except several days in mid-June 2017 and after September 2017. The above analysis suggests that the price movements of the options lead those of the futures by 23 min, and the price changes in the futures market are ahead of those in the spot market by 20 min, which is generally consistent with the order of the lead–lag relation and the average lead minutes between the futures and the options.

Figure 6 show the intraday lead–lag relations among the S&P 500 spot, futures and options obtained from the TOP method. From Fig. 6a, we can see that the index futures exhibits price leadership over its underlying index on most trading days. Figure 6b indicate that the index options plays a leading role in the spot market on most trading days during the investigated period. Furthermore, Fig. 6c show the price movements of the options lead those of the futures in general, and their lead–lag relation reverses on a few trading days.

Fig. 6
figure 6

Lead–lag relations among S&P 500 index-based spot, futures and options obtained from the TOP method. a The lead–lag relation between the index and the futures with parameters \(m=17\) and \(T=3\); b The lead–lag relation between the index and the options with parameters \(m=29\) and \(T=3\); c The lead–lag relation between the futures and the options with parameters \(m=13\) and \(T=3\)

Full size image

In summary, the results of the TOP method show that the futures and options exhibit price leadership over the spot market, and the options is ahead of the futures on most trading days in the Chinese mainland market, which are generally in line with the results in Hong Kong and US markets. These conclusions are consistent with Ren et al. (2019), Ahn et al. (2019) and Raju and Shirodkar (2020).

3.3 Results of the VECM-IS Model

In this section, we use the VECM-IS model to test the robustness of the lead–lag relations obtained from the TOP method in the three markets. Three pairs of the original return series, namely \(R_{i}(t)\) and \(R_{f}(t)\), \(R_{i}(t)\) and \(R_{o}(t)\), \(R_{f}(t)\) and \(R_{o}(t)\), are proved to be cointegrated, therefore the VECM framework can be established to further estimate the Hasbrouck IS values. The IS values of the index, futures and options for each trading day are calculated, and the daily IS distribution obtained from these three pairs of original return series.

In the Chinese mainland market, from Fig. 7a, one can observe that the IS distribution of the SSE 50 index is slightly left-skewed, while the IS distribution of the SSE 50 index futures is slightly right-skewed. Within each trading day, one may infer that the stock index exhibits price leadership over its corresponding futures if the IS of the index is larger than that of the futures. On the contrary, if the IS of the futures appears to exceed that of its underlying index, the futures plays a price guiding role on the spot market. The above analysis suggests that the trading days on which the futures leads its underlying index account for a relatively larger portion of the whole investigated period than the trading days with reverse lead–lag relations. The trading days with reverse lead–lag relations revealed by the VECM-IS model mostly coincide with the reverse trading days obtained from the TOP method. Similarly, the right-skewed distribution of the SSE 50 ETF options in Fig. 7b shows strong evidence that the return of the ETF options leads that of its corresponding spot on more trading days compared to the case of their reverse lead–lag relations. From the upper subgraph in Fig. 7c, the options also shows a stronger price leadership than the futures.

Fig. 7
figure 7

The IS distribution of SSE 50 index, SSE 50 index futures and SSE 50 ETF options obtained from the VECM-IS model. a The IS distribution of the index and the futures calculated by using \(R_{i}(t)\) and \(R_{f}(t)\); b The IS distribution of the index and the ETF options calculated by using \(R_{i}(t)\) and \(R_{o}(t)\); c The IS distribution of the futures and the ETF options calculated by using \(R_{f}(t)\) and \(R_{o}(t)\)

Full size image

In the Hong Kong market, Fig. 8a shows that the IS distribution of HSI futures is right-skewed, indicating that the price movements of the futures lead those of the spot on most trading days. Similarly, the IS distribution of HSI options is slightly right-skewed in the bottom subgraph of Fig. 8b (the upper subgraph of Fig. 8c), which means that the number of trading days on which the options shows price leadership is larger than the number of trading days with reverse lead–lag relations. One can infer that the order of contributions of the three products is as follows: HSI options, HSI futures and HSI, which is verified by the results derived from the TOP method.

Fig. 8
figure 8

The IS distribution of HSI, HSI futures and HSI options obtained from the VECM-IS model. a The IS distribution of the spot and the futures calculated by using \(R_{i,HK}(t)\) and \(R_{f,HK}(t)\); b The IS distribution of the spot and the options calculated by using \(R_{i,HK}(t)\) and \(R_{o,HK}(t)\); c The IS distribution of the futures and the options calculated by using \(R_{f,HK}(t)\) and \(R_{o,HK}(t)\)

Full size image

In the US market, from Fig. 9a, we can see that the index futures exhibits price leadership over its underlying index on most trading days. Figure 9b indicate that the index options plays a leading role in the spot market on most trading days during the investigated period. Furthermore, Fig. 9c show the price movements of the options lead those of the futures in general, and their lead–lag relation reverses on a few trading days. These results are consistent with those of the Chinese mainland and Hong Kong markets.

Fig. 9
figure 9

The IS distribution of S&P 500 index, S&P 500 index futures and S&P 500 index options obtained from the VECM-IS model. a The IS distribution of the spot and the futures calculated by using \(R_{i,US}(t)\) and \(R_{f,US}(t)\); b The IS distribution of the spot and the options calculated by using \(R_{i,US}(t)\) and \(R_{o,US}(t)\); c The IS distribution of the futures and the options calculated by using \(R_{f,US}(t)\) and \(R_{o,US}(t)\)

Full size image

3.4 Comparison of the Results of Two Methods and Three Markets

To better compare the results obtained from the TOP method and the VECM-IS model, we summarizes the results presented in Figs. 4, 5, 6, 7, 8 and 9. Table 2 mainly contains the results of the three pairs of products in the different markets, namely, index and futures, index and options, futures and options. Given that the intraday lead–lag relations vary on different trading days, we display the results of each pair of products separately in two different lead–lag directions, for instance, index leads futures, and futures leads index. In each direction of the lead–lag relation, we give the proportion of trading days accounted for the entire sample, the average lead–lag minutes, the mean values of the returns of the two products, and the p value of the mean comparison test between these two return series.

In the Chinese mainland market, the futures is found to lead the index on 66% trading days of the whole period for about 20 min by the TOP method. The result from the VECM-IS model indicates that the futures leads the index for about 5 min on 71.69% trading days, which is generally consistent with the relation obtained from the TOP method. Both methods show that the relation between the index and its associated futures reverses on a relatively few trading days. To further understand the difference between the index and the futures in these two cases of lead–lag relations, we carry out a one-tailed paired T-test for the means of \(R_{i}(t)\) and \(R_{f}(t)\) in each case of the lead–lag relation. The original hypothesis is that the mean value of \(R_{i}(t)\) is larger than that of \(R_{f}(t)\) when the futures leads the index. At the 1% significance level, the p value of the T-test listed in Table 2 implies that the null hypothesis should be rejected. This suggests that the mean of \(R_{f}(t)\) is significantly larger than that of \(R_{i}(t)\) when the futures market plays a price guiding role for the spot. In addition, the lead–lag relation between the index and futures markets reverses when the index return has a significantly larger mean value than the futures return.

Table 2 Summary of the lead–lag relations between index and its derivatives
Full size table

In a similar fashion, the index-based options is found to lead its underlying index on 63.62% of the trading days obtained from the TOP method, and the corresponding proportion of the trading days having the same lead–lag direction obtained from the VECM-IS model is 80.67%. The p value of the T-test indicates that the mean of the options return is significantly larger than that of the index return when the ETF options leads its underlying index. On the other hand, in the case of the opposite lead–lag relation, the spot market has a larger mean value of return than the options market. For the relation between the ETF options and the index futures, the options leads the futures on most trading days within the analytical framework of the VECM-IS and TOP. The p value of the T-test further indicates that the mean value of \(R_{o}(t)\) is significantly larger than that of \(R_{f}(t)\) when the options is ahead of the futures. On the contrary, the futures return has a significantly larger mean value than the options return on a few trading days with reverse relation. In addition, it is worth to emphasize that the lead–lag relations among the SSE 50 index-based spot, futures and ETF options are consistent in terms of the order of the lead–lag relations and the average lead minutes.

In the Hong Kong market, both methods show strong evidences that the futures and the options exhibit price leadership over the stock market, and the options are ahead of futures on most trading days in our investigated periods. The order of the lead–lag relations and the average lead minutes between HSI and its associated futures and options are consistent. In addition, the lead–lag relations obtained from both methods show the similar reversal phenomenon: the derivatives lead the index in general, however their relation reverses when the index return has a significantly larger mean value, which is also the case for the relation between the futures and the options. We note that the proportion of trading days in each direction of the lead–lag relations and the average lead minutes obtained from these two methods show slight quantitative differences.

In the US market, both methods confirm the conclusion that the index options shows the price leadership over the futures market, and the futures leads its underlying index on most trading days, which is consistent in terms of the order of the lead–lag relations and the average lead minutes. In general, both the options and the futures play guiding roles in the price movements of spot market, but the relation reverses when the index return has a significantly larger mean value. Similar reversal phenomenon is also observed in the relation between the futures and the options. However, the proportion of trading days in each direction of the lead–lag relations and the average lead minutes obtained from these two methods show slight quantitative differences.

We now give a brief summary and interpretation for the relations between the index and its derivatives in three markets. This study provides strong evidence that both the index futures and the options exhibit price leadership over their underlying stock index in three markets, and their lead–lag relations vary sensitively with the changes of market condition. When the spot market has a significantly larger average return than the derivatives market, the price leadership of the derivatives weakens. In this case, investors are inclined to pay excessive attention to the price movements of the stock index to adjust their intraday investment strategies. As a result, the derivatives’ prices cannot efficiently reflect the relevant information, and the investors might be difficult to obtain market expectations from the derivatives market.

In addition, there are slight quantitative differences in the intraday lead–lag relations in the three markets. The results obtained from both methods show that the proportion of the trading days on which the options leads the index and the proportion of the trading days on which the options leads the futures are both higher in the Hong Kong and US markets, which may be due to the better price discovery function of the options in mature markets. The lead–lag minutes obtained from the two methods also have slight differences, for example, the average lead–lag minutes obtained from the TOP method are generally larger than that obtained from the VECM-IS model.

3.5 Robustness Tests

Considering the impact of extreme events on the lead–lag relationship among stock index-based spot, futures and options, we also use the data in a new period of time from September 1, 2017 to December 31, 2020 that covers the outbreak of the Covid-19, to perform the robustness test for the Chinese mainland market. In addition, the dynamic intraday lead–lag relations between the index and futures during the new period are consistent with the previous results for the Hong Kong and US markets. To save space, we do not present the results during the new period in these two markets here.

Figures 10 and 11 show the lead–lag relations among the SSE 50 index, futures and options obtained from the TOP and VECM-IS methods during the new period, respectively. In this period, we also find that the futures and options exhibit price leadership over the spot market, and the options are ahead of the futures on most trading days in the Chinese mainland market. Table 3 gives the summary of the lead–lag relations between index and its derivatives during the new sampling period in the Chinese mainland market. One can see that the same reversal phenomenon is also observed in the relations between the derivative and its underlying index, and the relations between the futures and the options, when there has a significantly larger mean value of the index and futures respectively. Our findings for the intraday lead–lag relations among the SSE 50 index, futures and options after considering the impact of extreme events are therefore robust.

Fig. 10
figure 10

Lead–lag relations among SSE 50 index-based spot, futures and ETF options obtained from the TOP method during the new sample period. a The lead–lag relation between the spot and the futures with optimal parameters \(m=19\) and \(T=3\); b The lead–lag relation between the spot and the ETF options with optimal parameters \(m=25\) and \(T=3\); c The lead–lag relation between the futures and the ETF options with optimal parameters \(m=22\) and \(T=3\)

Full size image
Fig. 11
figure 11

The IS distribution of SSE 50 index, SSE 50 index futures and SSE 50 ETF options obtained from the VECM-IS model during the new sampling period. a The IS distribution of the index and the futures calculated by using \(R_{i}(t)\) and \(R_{f}(t)\); b The IS distribution of the index and the ETF options calculated by using \(R_{i}(t)\) and \(R_{o}(t)\); c The IS distribution of the futures and the ETF options calculated by using \(R_{f}(t)\) and \(R_{o}(t)\)

Full size image
Table 3 Summary of the lead–lag relations between index and its derivatives during the new sampling period
Full size table

3.6 Pair Trading Strategy

In this section, we construct a pair trading strategy (Gatev et al., 2006; Gupta & Chatterjee, 2020) using the data of spot and futures based on their intraday lead–lag relationships obtained from the TOP method. For each trading day, we align the price series of the spot and futures based on their lead–lag orders. For example, we use the spot prices during the time period \([0,N-\langle x(t)\rangle _{if}]\) and the futures prices during the time period \([\langle x(t)\rangle _{if}+1,N]\) to perform the pair trading, when the spot leads futures by \(\langle x(t)\rangle _{if}\) minutes at t day. If the price spread between the aligned sequences of spot and futures exceeds the threshold at \(t^{'}\) minute, we will buy/sell the spot at \(\langle x(t)\rangle _{if}\) minutes and then sell/buy the futures at \(t^{'}+\langle x(t)\rangle _{if}\) minute, and close the position when the prices spread have reverted. Following Gatev et al. (2006), we open a position at \(t^{'}\) minute when the pair prices diverge by more than 1.5 times of the historical standard deviation, which is calculated by using the price spreads during the time period \([t^{'}-151,t^{'}-1]\). We set the transaction cost equals to zero, and set the maximum time period to hold the position equals to 30 min, i.e., we will close the position at \(t^{'}+30\) minute if the price spread has not reverted.

We use the data in the time period from April 16, 2015 to December 31, 2020 for the mainland China market, and the data in the time period from September 1, 2017 to December 31, 2020 for the Hong Kong and US markets, to test performance of our pair trading strategy (henceforth referred to as PTS). Table 4 gives the results of descriptive statistics for the daily returns of the pair trading strategy and the corresponding spot index. One can see that the mean and cumulative values of the daily returns of the pair trading strategy for three markets are all larger than that of the corresponding spot index in the three markets. The sharpe ratio of the pair trading strategy is also larger than that of the corresponding spot index in the three markets. In addition, the values of skewness show that the returns of the pair trading strategy are more right-skewed in the three markets. These results indicate that the pair trading strategy based on the lead–lag relationships can get better performance than the corresponding spot index.

Table 4 Summary of the returns of the pair trading strategy and the corresponding spot index
Full size table

In summary, inconsistent with the Efficient Markets Hypothesis (Fama, 1991; Shao et al., 2019), our research based on high-frequency data suggests that the futures and options exhibit price leadership over the spot market, and the options is ahead of the futures on most trading days in all three markets. These findings complement the work (Ren et al., 2019; Ahn et al. 2019; Raju & Shirodkar, 2020) on the dynamic variation of intraday lead–lag relations between the index and its derivatives. In addition, there is a reversal phenomenon of the relation between the derivative and its underlying index, which is different from previous studies and enriches the empirical research in this area.

4 Conclusion and Discussion

Based on high-frequency data, this is the first study on the dynamic variation of intraday lead–lag relations between SSE50 index and its newly issued index futures and ETF options in China. A comparative study between Chinese mainland, Hong Kong and US markets is performed to reveal the similarities and differences of the intraday lead–lag relations. Interestingly, the reversal phenomenon of the intraday lead–lag relations is uncovered in all three markets for the first time to our knowledge. Our study gives relatively robust conclusions on the intraday lead–lag relationship, demonstrated by the novel TOP method and the conventional VECM-IS model, both of which give mutually corroborated results. The universal stability result in the three markets shows strong evidence that both the futures and the options exhibit price leadership over their underlying index, and the price leadership of the options is stronger than the futures. The relations found on most trading days during our investigated period are consistent with the general conclusions, namely the derivatives play a leading role on its spot market (Chan, 1992; Fung et al., 2015; Kang et al., 2006). Another interesting result found in all three markets is that the relation between the derivative and its spot reverses when the index return has a significantly larger mean value, which is also observed in the relation between the futures and the options. One cause may be related to the fact that when the spot market has a significantly larger average return than the derivatives market, investors tend to adjust their intraday investment strategies according to the performance of the stock market. In this case, the derivatives’ prices cannot efficiently reflect the market information, thus it might be difficult for investors to obtain market expectations from the derivatives market. The difference between the intraday lead–lag relations obtained from these two methods in three markets is the proproportion of the trading days in each direction of the lead–lag relations and the average lead minutes which show slight quantitative difference. Finally, we construct a pair trading strategy using the data of spot and futures based on the above empirical conclusions, and the strategy after considering the intraday lead–lag relationships outperforms the corresponding spot index.

Our conclusions have great practical value for market participants. Our pair trading strategy based on the intraday lead–lag relationships provides investors with great ideas for adjust their intraday investment strategies and manage portfolio risk. For market regulators, our results indicate that the newly issued SSE 50 index-related futures and ETF options are not the real behind-the-scenes driver of the A-share market crash in June 2015. Conversely, when the stock market crashes, the operation of derivatives indeed benefits the pricing efficiency and the stability of the stock market. This could have certain referential significance for regulators to establish a risk warning mechanism according to the lead–lag structures between stock index and its derivatives. Compared with the mature market, the price discovery function of options in the Chinese mainland market is weaker, and regulators should further strengthen the construction of the options market, such as diversifying the options products and increasing the breadth of market participants. In addition, regulators could consider relaxing the trading restrictions in Chinese futures and options markets, which can further improve the efficiency of price discovery of markets and provide investors with more opportunities for asset allocation.

Future research will continue to explore the predictability of the current or future state of the index and its derivatives based on their dynamic intraday lead–lag relations, and the influencing factors like liquidity (Chung et al., 2011) and market conditions (Wang et al., 2017) could be taken into consideration. We can also consider the impact of exogenous events on the dynamic intraday lead–lag relations between the index and its derivatives, e.g., the Sino-US trade war and the escalation of the COVID-19. In addition, we can further expand our pair trading strategy by adjusting the model parameters or improving the research method of the lead–lag relationship, to obtain better performance in future research.