Abstract
The paper presents decomposition of impulse response functions (IRFs) as a new diagnostic tool for dynamic stochastic general equilibrium (DSGE) models. This method works with any DSGE model of arbitrary complexity or theoretical background. It is also applicable to any policy transmission channels. We illustrate it with monetary transmission mechanisms in two New Keynesian general equilibrium models: QUEST_III model of the European Commission and Smets–Wouters model of the USA economy. For that purpose, we use DYNARE platform for solving the models and provide a MATLAB file for IRFs decomposition. The underlying software can handle decomposition of IRFs using both the first-order and the second-order approximation of Taylor series to equilibrium relations. An IRF aggregates partial contributions of all state variables to impulse responses of a model’s variable to a stochastic shock. The IRF decomposition identifies individual contributions of state variables and marks each particular channel that a policy shock uses to propagate throughout the model. We show in two illustrated cases that monetary transmission channels might be quite distinct even if DSGE models employ the same (Taylor) policy rule and reveal similar IRFs. More specifically, IRFs initiated by a monetary shock might misrepresent the pure interest rate impact on some variables. Decomposition of monetary IRFs casts more light on flexibility needed in an economy to contain negative impact of a monetary shock.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
For the later discussion, it is important to notice that the policy function provides the optimal values of the control variables as a function of the state variables. The state variables are those variables whose values are already determined by agents’ actions in period t − 1 or set in period t by an exogenous process. The control variables in period t are those variables whose values rational agents choose in that period in order to maximize an objective function under constraints.
For indices \(i=1,\ldots , {\bar{i}}\), \(j=1,\ldots , {\bar{j}}\), and \(l=1,\ldots , {\bar{l}}\) that represent state and control variables, and exogenous shocks, respectively, matrix G has the following dimension \(\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {\bar{{i}}x\bar{{i}}}\quad &{} {\bar{{i}}x\bar{{j}}}\quad &{} {\bar{{i}}x\bar{{l}}} \\ {\bar{{j}}x\bar{{i}}}\quad &{} {\bar{{j}}x\bar{{j}}}\quad &{} {\bar{{j}}x\bar{{l}}} \\ {\bar{{l}}x\bar{{i}}}\quad &{} {\bar{{l}}x\bar{{j}}}\quad &{} {\bar{{l}}x\bar{{l}}} \\ \end{array} }} \right] \), while matrix \({\varvec{\Gamma }}\) is much more structured \(\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\bar{i}}x{\bar{i}}^{2} \quad &{} {\bar{i}}x{\bar{i}} \cdot {\bar{j}} \quad &{} {\bar{i}}x{\bar{i}} \cdot {\bar{l}} \quad &{} {\bar{i}}x{\bar{i}} \cdot {\bar{i}} \quad &{} {\bar{i}}x{\bar{j}}^{2} \quad &{} {\bar{i}}x{\bar{j}} \cdot {\bar{l}} \quad &{} {\bar{i}}x{\bar{l}} \cdot {\bar{i}} \quad &{} {\bar{i}}x{\bar{l}} \cdot {\bar{j}} \quad &{} {\bar{i}}x{\bar{l}}^{2} \\ {\bar{j}}x{\bar{i}}^{2} \quad &{} {\bar{j}}x{\bar{i}} \cdot {\bar{j}} \quad &{} {\bar{j}}x{\bar{i}} \cdot {\bar{l}} \quad &{} {\bar{j}}x{\bar{j}} \cdot {\bar{i}} \quad &{} {\bar{j}}x{\bar{j}}^{2} \quad &{} {\bar{j}}x{\bar{j}} \cdot {\bar{l}} \quad &{} {\bar{j}}x{\bar{l}} \cdot {\bar{i}} \quad &{} {\bar{j}}x{\bar{l}} \cdot {\bar{j}} \quad &{} {\bar{j}}x{\bar{l}}^{2} \\ {\bar{l}}x{\bar{i}}^{2} \quad &{} {\bar{l}}x{\bar{i}} \cdot {\bar{j}} \quad &{} {\bar{l}}x{\bar{i}} \cdot {\bar{l}} \quad &{} {\bar{l}}x{\bar{i}} \cdot {\bar{i}} \quad &{} {\bar{l}}x{\bar{j}}^{2} \quad &{} {\bar{l}}x{\bar{j}} \cdot {\bar{l}} \quad &{} {\bar{l}}x{\bar{l}} \cdot {\bar{i}} \quad &{} {\bar{l}}x{\bar{l}} \cdot {\bar{j}} \quad &{} {\bar{l}}x{\bar{l}}^{2} \\ \end{array} }} \right] \) and \({\hat{x}}_t \otimes {\hat{x}}_t =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {{\bar{i}} x{\bar{i}} ,}\quad &{} {{\bar{i}} x{\bar{j}} ,}\quad &{} {{\bar{i}} x{\bar{l}} ,}\quad &{} {{\bar{j}} x{\bar{i}} ,}\quad &{} {{\bar{j}} x{\bar{j}} ,}\quad &{} {{\bar{j}} x{\bar{l}} ,}\quad &{} {{\bar{l}} xi,}\quad &{} {{\bar{l}} x{\bar{j}} ,}\quad &{} {{\bar{l}} x{\bar{l}} } \\ \end{array} }} \right] ^{{\prime }}\).
To download the QUEST III source code an email request should be sent to Marco Ratto, https://ec.europa.eu/jrc/en/econometric-statistical-software. We downloaded it on 20 July 2013.
We obtained DYNARE source codes for this model from the DYNARE forum at the web site address: http://www.dynare.org/phpBB3/viewtopic.php?f=1&t=3750.
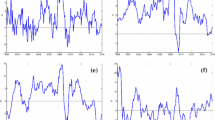
Of course, the sum of decomposed IRFs must be equal to the aggregate IRF. That is not visually obvious due to different graph scales.
We set \(\rho _3^{{ ucap}} = 0.90\).
The source code of this function is available on request by email to miroljub.labus@belox.rs.
In our example from Fig. 1, we use the following irf_decomposition(’E_GY’,’E_EPS_M’,0.01,6,20,1).
References
Adjemian, S., Bastani, H., Karame, F., Juillard, M., Maih, J., & Mihoubi, F., et al. (2011). DYNARE: Reference manual, version 4. DYNARE working papers, CEPREMAP. http://www.dynare.org.
Anderson, G. (2008). Solving linear rational expectations models: A horse race. Computational Economics, 31(2), 95–113. doi:10.1007/s10614-007-9108-0.
Blanchard, O. J., & Kahn, C. M. (1980). The solution of linear difference models under rational expectations. Econometrica, 48(5), 1305–1311.
Clarida, R. H., Gali, J., & Gertler, M. (1999). The science of monetary policy: A new Keynesian perspective. Journal of Economic Literature, 37(December), 1661–1707. doi:10.2139/ssrn.155910.
Collard, F., & Juillard, M. (2001). Accuracy of stochastic perturbation methods: The case of asset pricing models. Journal of Economic Dynamics & Control, 25. http://pages.stern.nyu.edu/~dbackus/GE_asset_pricing/computation/CollardJuillardstochperturbationJEDC01.pdf.
Hamilton, J. D. (1994). Time series analysis. Princeton University Press. doi:10.2307/1270781.
Hansen, G. D. (1985). Indivisible labor and the business cycle. Journal of Monetary Economics, 16(3), 309–327. doi:10.1016/0304-3932(85)90039-X.
Judd, K. L. (1998). Numerical methods in economics. MIT Press. https://mitpress.mit.edu/books/numerical-methods-economics.
Judd, K. L., & Jin, H.-H. (2002). Perturbation methods for general dynamic stochastic models. Working paper, pp. 1–44. http://web.stanford.edu/~judd/papers/PerturbationMethodRatEx.pdf.
King, R. G., Plosser, C. I., & Rebelo, S. T. (1988). Production, growth and business cycles. Journal of Monetary Economics, 21, 195–232.
King, R. G., Plosser, C. I., & Rebelo, S. T. (2002). Production, growth and business cycles?: Technical appendix. Computational Economics, 20(1–2), 87–116.
King, R. G., & Watson, M. W. (2002). System reduction and solution algorithms for singular linear difference systems under rational expectations. Computational Economics, 20(1–2), 57–86. doi:10.1023/A:1020576911923.
Klein, P. (2000). Using the generalized Schur form to solve a multivariate linear rational expectations model. Journal of Economic Dynamics and Control, 24(10), 1405–1423. doi:10.1016/S0165-1889(99)00045-7.
Kydland, Finn E., & Prescott, E. C. (1982). Time to build and aggregate fluctuations. Econometrica, 50, 1345–1370. doi:10.2307/1913386.
Long, J. B., & Plosser, C. I. (1983). Real business cycles. Journal of Political Economy, 91(1), 39–69. doi:10.1016/0304-3932(88)90029-3.
Ljungqvist, L., & Sargent, T. J. (2000). Recursive macroeconomic theory (2nd ed.). Cambridge: MIT Press.
McCandless, G. (2008). The ABCs of RBCs: An introduction to dynamic macroeconomic models. Harvard University Press. http://www.amazon.com/dp/0674028147.
Ratto, M., Roeger, W., & in’t Veld, J. (2009). QUEST III: An estimated DSGE model of the euro area with fiscal and monetary policy. Economic Modelling, 26. doi:10.2765/86277.
Rotemberg, J. J., & Woodford, M. (1997). An optimization-based framework for the evaluation. In NBER macroeconomics annual 1997 (Vol. 12, pp. 297–361). http://www.nber.org/chapters/c11041.
Sims, C. (1980). Macroeconomics and reality. Econometrica, 48, 1–48.
Sims, C. (2002). Solving linear rational expectations models. Computational Economics, 20(1–2), 1–21. http://sims.princeton.edu/yftp/gensys/.
Smets, F., & Wouters, R. (2007). Shocks and frictions in US business cycles: A Bayesian DSGE approach. American Economic Review, 97(3), 586–606. doi:10.1257/aer.97.3.586.
Stokey, N. L., Lucas, R. E. J., & Prescott, E. C. (1989). Recursive methods in economic dynamics. Cambridge: Harvard University Press.
Uhlig, H. (2001). A toolkit for analysing nonlinear dynamic stochastic models easily. In R. Marimon & A. Scott (Eds.), Computational methods for the study of dynamic economies, (Chap 3). Oxford University Press. doi:10.1093/0199248273.003.0003.
Woodford, M. (2003). Interest and prices: Foundations of a theory of monetary policy. Princeton University Press. http://press.princeton.edu/titles/7603.html.
Acknowledgements
We thank to Marco Ratto for useful comments and research guidance. Of course, we are responsible for computation and findings.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Decomposition of IRFs to a monetary shock (right scale for lines of aggregate IRFs and left scale for bars of decomposed IRFs)
Decomposition of IRFs to a monetary shock in Smets–Wouters model
Impulse responses of capacity utilization to a monetary shock (right scale for lines of aggregate IRFs and left scale for bars of decomposed IRFs)
Impulse responses of output to a monetary shock—decomposed effects due to ten state variables
Rights and permissions
About this article
Cite this article
Labus, M., Labus, M. Monetary Transmission Channels in DSGE Models: Decomposition of Impulse Response Functions Approach. Comput Econ 53, 27–50 (2019). https://doi.org/10.1007/s10614-017-9717-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10614-017-9717-1