Spatiotemporal Spectral Analysis of Turbulent Structures and Pollutant Removal in Two-Dimensional Street Canyon

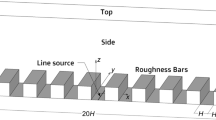
Abstract

This study expands the study conducted by Zhang et al. (Boundary-Layer Meteorol, 2022, Vol. 183, 97–123) to elucidate turbulent structures within an ideal two-dimensional street canyon, and determine their contribution to pollutant removal. In response to the limitations of the reference study wherein spanwise turbulent structures were not elucidated, an advanced technique called spectral proper orthogonal decomposition (SPOD) with two-dimensional Fourier transformation was applied in the current study. This approach combined proper orthogonal decomposition along the spatial streamwise and vertical directions and Fourier decomposition along the time and spatial spanwise direction. Using this technique, various fluctuation patterns were reasonably decomposed and visualised according to their scales. In addition, their intensities and contributions to pollutant removal were quantitatively analysed using the SPOD spectrum and cospectra. The time scales of most energetic modes were found to be proportional to their spanwise length scales, regardless of their scales and flow mechanisms. The ranges of the spanwise wavenumber and frequency, at which pollutant removal events occurred at the roof level, were specified. These ranges coincided with those of small-scale structures caused by Kelvin–Helmholtz instabilities. Further complex analysis of the correlation between large- and small-scale structures showed that large-scale structures have a high possibility of indirectly enhancing or weakening pollutant removal by amplifying or suppressing small-scale structures. This occurred stochastically along both time and spanwise directions. Quantitatively, the amplitude of small-scale structures was amplified or suppressed by 13–16% on average by high- or low-momentum fluids.

Appendices

Appendix 1: An Algorithm for Spectral Proper Orthogonal Decomposition with Two-Dimensional Fourier Transformation

An algorithm for the original SPOD was proposed by Towne et al. (2018) to enhance the convergence and enforceability of the estimation of modes and mode energies from the discrete velocity data. This algorithm combines Welch’s method for spectral estimation and the snapshot POD algorithm (Sirovich 1987). This algorithm is applicable for estimating modes and mode energies in SPOD with 2DFT, although some complements need to be made.

When the Fourier transform is applied over the y-coordinate on both sides of (8), it becomes:

$$ \int_{{{{ - L_{y} } \mathord{\left/ {\vphantom {{ - L_{y} } 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{{L_{y} } \mathord{\left/ {\vphantom {{L_{y} } 2}} \right. \kern-\nulldelimiterspace} 2}}} {{\mathbf{u^{\prime}}}e^{{ - i2{\uppi }\eta y}} dy} = \int_{ - \infty }^{ + \infty } {\sum\limits_{n} {a_{n} {{\varvec{\uppsi}}}_{n} } e^{{i2{\uppi }ft}} df}. $$

(18)

The right side shows the form of the original SPOD such that ${{\varvec{\uppsi}}}_{n}$ and $\lambda_{n}$ can be directly estimated using the algorithm proposed by Towne et al. (2018), whereas the input of the algorithm (the left side of (18)) is no longer the fluctuating velocity ${\mathbf{u^{\prime}}}$ — it is a one-dimensional Fourier transformation. Therefore, one can simply discretise the y-coordinate into y_j (j = 1, 2, …, N_y), and a discrete Fourier transform can be applied over the y-coordinate before the implementation of the original SPOD algorithm.

Based on this idea, the algorithm for SPOD with 2DFT is expressed as follows:

Step (i): Calculate the one-dimensional discrete Fourier transform of the fluctuation velocity ${\mathbf{u^{\prime}}}$ over the y-coordinate:

$$ \left[ {\begin{array}{*{20}c} {{\tilde{\mathbf{u}}}^{\prime } \left( {x,z,t;\eta _{1} } \right)} \\ {{\tilde{\mathbf{u}}}^{\prime } \left( {x,z,t;\eta _{2} } \right)} \\ \vdots \\ {{\tilde{\mathbf{u}}}^{\prime } \left( {x,z,t;\eta _{{N_{y} }} } \right)} \\ \end{array} } \right] = FFT\left( {\left[ {\begin{array}{*{20}c} {{\mathbf{u}}^{\prime } \left( {x,y_{1} ,z,t} \right)} \\ {{\mathbf{u}}^{\prime } \left( {x,y_{2} ,z,t} \right)} \\ \vdots \\ {{\mathbf{u}}^{\prime } \left( {x,y_{{N_{y} }} ,z,t} \right)} \\ \end{array} } \right]} \right), $$

(19)

where the fast Fourier transform (FFT) algorithm is recommended.

Step (ii): Replace ${\mathbf{u^{\prime}}}$ in the original SPOD algorithm by ${\tilde{\mathbf{u}}}^{\prime } \left( {x,z,t;\eta _{j} } \right)$, and obtain the mode ${{\varvec{\uppsi}}}_{n} \left( {x,z;\eta_{j} ,f} \right)$ and mode energies $\lambda_{n} \left( {\eta_{j} ,f} \right)$ with discrete frequency indices.

Step (iii): Repeat (ii) over j = 1, 2, …, N_y until the modes and mode energies at all discrete wavenumbers are obtained.

The original SPOD algorithm can be processed separately in steps (ii) and (iii) for each discrete wavenumber. Therefore, parallel processing is recommended to accelerate the computation. This does not contradict the energy cascade because statistics can be performed separately on non-independent variables. In addition, because ${\tilde{\mathbf{u}}}^{\prime } \left( {x,z,t;\eta _{j} } \right)$ consists of complex numbers, the modes are no longer symmetric with respect to f = 0. Both positive and negative f might be needed to be computed with the same wavenumber. However, because the mode energy is symmetric, and the mode and mode coefficients are conjugate symmetric with respect to the original point on the f-η plane, only two quadrants need to be considered.

Appendix 2: Cospectra in the Framework of Spectral Proper Orthogonal Decomposition with Two-Dimensional Fourier Transformation

The SPOD cospectrum between the streamwise and vertical velocity is defined as:

$$ S_{n}^{(uw)} \left( {x,z;\eta ,f} \right) = {\text{Re}} \left( {\lambda_{n} \psi_{n}^{(u)} \psi_{n}^{(w)*} } \right), $$

(20)

where $\psi_{n}^{(u)}$ and $\psi_{n}^{(w)}$ denote the u and w components of vector ${{\varvec{\uppsi}}}_{n}$, respectively. This cospectrum shows the planar density of the Reynolds shear stress on the f-η plane, and its integral equals the Reynolds shear stress at the spatial position (x, z); thus,

$$ {\text{E}}\left( {u^{\prime}w^{\prime}} \right) = \int_{ - \infty }^{ + \infty } {d\eta } \int_{ - \infty }^{ + \infty } {\sum\limits_{n} {S_{n}^{(uw)} } df} .$$

(21)

The SPOD cospectrum between the vertical velocity and concentration $c\left( {x,y,z,t} \right)$ is defined as:

$$ S_{n}^{(wc)} \left( {x,z;\eta ,f} \right) = {\text{Re}} \left( {\frac{{a_{n} \psi_{n}^{(w)} \hat{c^{\prime}}^{*} }}{{TL_{y} }}} \right), $$

(22)

where $\hat{c^{\prime}}$ denotes the 2DFT of $c^{\prime}$, whose spatial and temporal discretisation should be the same as the velocity. This cospectrum shows the planar density of the vertical turbulent mass flux on the f-η plane, and its integral equals the vertical turbulent mass flux at the spatial position (x, z); therefore,

$$ {\text{E}}\left( {w^{\prime}c^{\prime}} \right) = \int_{ - \infty }^{ + \infty } {d\eta } \int_{ - \infty }^{ + \infty } {\sum\limits_{n} {S_{n}^{(wc)} } df}. $$

(23)

These SPOD cospectra were estimated using Welch's method (Welch 1967), wherein the time signal was first divided into blocks, and the energy of the entire signal was estimated by averaging the energy values over all blocks. When computing $S_{n}^{(wc)}$, the block dividing and window function (if used) in the 2DFT of the concentration should be retained the same as the velocity when performing the SPOD algorithm. In the application, results in only two quadrants need to be computed because these cospectra are symmetric with respect to the original point on the f–η plane.

Appendix 3: Additional Remark in Plotting Spectra and Cospectra

In Figs. 2 and 5, the spectra and cospectra are shown by plotting the nondimensionalised value $f\eta S$ (where S can be either spectra or cospectra, see (13)–(15)) in the linear scale against the frequency/wavenumber in the logarithmic scale. This way of plotting is considered proper for quantitatively analysing the energy distributions. Note that the integrals of spectra or cospectra over frequency and wavenumber become energy values (see (12), (21), and (23)). For any integration range $\Omega_{f\eta }$ on the f-η plane, we can write the following transformation:

$$ \iint\limits_{{\Omega_{f\eta } }} {S{\kern 1pt} df{\kern 1pt} d\eta } = \left( {\ln 10} \right)^{2} \iint\limits_{{\Omega_{f\eta } }} {f\eta S{\kern 1pt} d(\log_{10} f){\kern 1pt} d(\log_{10} \eta )}, $$

(24)

where $\left( {\ln 10} \right)^{2}$ is a constant. This transformation indicates that plotting $f\eta S$ against $\log_{10} f$ and $\log_{10} \eta$ keeps the shapes of energy distributions undistorted in the provided figures of spectra and cospectra, and this is recommended in spectral analysis.

Data Availability Statements

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.