1 Introduction

The modelling of turbulent flow is a difficult task because of the complexity of the physical processes involved and the non-linearity of the governing equations. Turbulence is therefore generally described by statistical methods that involve solving a set of dynamical equations for the moments of the joint probability density functions (p.d.f.) of the velocity components and temperature. These methods are based on the so-called Reynolds-averaged Navier–Stokes models, which were first proposed by Reynolds. Similar models have been developed in many different fields, ranging from stellar astrophysics (Canuto 1992; Kupka and Montgomery 2002; Kupka 2003; Kupka and Robinson 2006), to oceanography (Canuto et al. 2001, 2002, 2007), and the planetary boundary layer (PBL), starting from the work of Mellor and Yamada (1974) to more complex higher order models (Canuto and Cheng 1994; Ferrero and Racca 2004; Cheng et al. 2005; Ferrero 2005; Gryanik et al. 2005; Ferrero and Colonna 2006; Ferrero et al. 2009, 2011).

Different closure relations can be found in the literature, and these can be divided into two categories: local and non-local models. The first category consists of models that include equation for the second-order moments and that either neglect or adopt a parametrization for the third-order moments (Mellor and Yamada 1982; Byggstoyl and Kollmann 1986; Jones and Musange 1988; Durbin 1993; Canuto and Cheng 1994; Speziale et al. 1996; Canuto et al. 1999; Trini Castelli et al. 2001, 2005). Unfortunately, local models are not sufficient to describe complex mixing processes such as those that occur in convection (Moeng and Wyngaard 1989; Holstag and Boville 1993), and locality is an approximation that is only justified when the turbulent mixing length is significantly smaller than the length scale of heterogeneity in the mean flow. In fact, turbulence in the convective boundary layer is associated with the non-local properties of the boundary layer as a whole (Holstag and Moeng 1991; Moeng and Sullivan 1994; Schmidt et al. 2006), which means that mixing is also present in regions of the boundary layer where there is no local production of turbulence due to the non-local effects of the vertical transport. In previous studies (Ferrero and Racca 2004; Ferrero 2005; Ferrero et al. 2009), we have shown that non-locality plays an important role in the shear-driven and stable boundary layers, despite the smaller-scale structures present in this kind of flow.

Non-locality has been included in local models either by means of parametrizations (Deardorff 1972; Holstag and Moeng 1991; Wyngaard and Weil 1991; Canuto et al. 2005), or by considering the dynamical equations for the third-order moments (Canuto 1992; Canuto and Cheng 1994; Zilitinkevich et al. 1999; Canuto et al. 2001; Cheng et al. 2005; Gryanik et al. 2005; Colonna et al. 2009; Ferrero et al. 2009, 2011), which, in Reynolds-stress formalism, represent the turbulent transport in the second-order-moment equations, and hence account for the non-locality of the turbulence. One shortcoming of these models is the large number of equations that need to be solved numerically, and the high computational demand. This can be a prohibitive task when the Reynolds-averaged Navier–Stokes models are included in circulation models in order to provide a detailed description of the boundary-layer phenomena. Although the PBL models entail, at most, one dynamical equation, that for turbulent kinetic energy (TKE), they are applied in situations such as in complex orographic terrain or the urban environment, i.e., in horizontally non-homogeneous areas, where, in principle, traditional boundary-layer parametrizations are no longer valid. In fact, deformations in turbulent fields that are induced by inhomogeneities modify the spatial distribution of turbulence, whose physical complexity demands the development of at least a second-order model (Ying et al. 1994; Ying and Canuto 1995, 1997; Cheng et al. 2020).

In a previous work (Ferrero et al. 2018), we analyzed the PBL schemes in the Weather Research and Forecasting model (Skamarock and Klemp 2008). Herein, we consider the Janjic (2001) model, which is one of the most commonly used boundary-layer models, and is based on a number of length scales obtained from a master length scale multiplied by some constants. We have evaluated the influence of these length scales on model performances. It is worth noting that these length scales rely on the pressure \((A_1,A_2)\) and dissipation terms \((B_1, B_2)\) in the original model equations (Mellor 1973), and account for the Rotta (1951a, 1951b) hypothesis of return-to-isotropy and the Kolmogorov (1941) hypothesis of local, small-scale isotropy. The pressure term was called the energy redistribution term by Rotta (1951a, 1951b) as one of its functions is to partition energy among the three components while not contributing to its total. The choice of these scales may therefore influence model performance in non-homogeneous conditions in which the redistribution of energy can also be different along the two horizontal components. Furthermore, the local isotropy hypothesis can be less realistic in horizontal non-homogeneous conditions, such as those considered here.

Below, model results obtained with different sets of constants are compared with sonic-anemometer measurements. The simulations were performed using a virtual machine called Chameleon Cloud. We introduce the formulation of the model in Sect. 2. The data used for the comparison and the model set-up are presented in Sect. 3, while the results are shown in Sect. 4. The main conclusions are drawn in Sect. 5.

2 Formulation of the Model

Janjic (2001) modified the Mellor–Yamada level-2.5 parametrization (Mellor and Yamada 1974, 1982), in order to identify the minimum conditions required for satisfactory performance in the full range of atmospheric forcing. This is achieved by imposing an upper limit on the master length scale, which is proportional to the square root of TKE and a function of the buoyancy and the wind shear. The TKE production/dissipation differential equation is solved iteratively over one timestep. The differential equation that is obtained by linearizing around the solution from of the previous iteration is solved at each individual iteration. Two iterations appear to be sufficient for satisfactory accuracy, and the computational cost is minor (Janjic 2001).

There is a set of empirical constants in the equations of the model, \((A_1, A_2, B_1,B_2, C_1) \) that should be determined, with each of these constants in the model multiplied by the so-called master length scale, providing a set of length scales that appear in the equations (Mellor and Yamada 1982).

In Mellor and Yamada (1982), the constants \(B_1\) and \(B_2\) are defined as

$$\begin{aligned} B_1= \left( \frac{R_B F_B^2}{Pr_t}\right) ^{3/2}, \;\; B_2=\frac{B_1}{R_B}, \end{aligned}$$
(1)

where \(F_B^2={u_*^2<\theta ^2>}/{<w\theta >^2}= 3.167441983\), \(Pr_t\) is the turbulent Prandtl number, and \(R_B={B_1}/{B_2}={16.6}/{10.1}\).

If we suppose (Mellor and Yamada 1982)

$$\begin{aligned} \gamma _1=\frac{1}{3}-2\dfrac{A_1}{B_1}=\frac{1}{3}-\dfrac{1}{9}, \end{aligned}$$
(2)

it is possible to calculate the other constants as

$$\begin{aligned} A_1= & {} \frac{B_1}{2} \left( \frac{1}{3}-\gamma _1 \right) , \end{aligned}$$
(3)
$$\begin{aligned} C_1= & {} \gamma _1-\frac{1}{(3 A_1)}B_1^{-1/3}, \end{aligned}$$
(4)

and

$$\begin{aligned} A_2=\frac{A_1 (\gamma _1-C_1)}{\gamma _1 Pr_t}. \end{aligned}$$
(5)

According to Mellor and Yamada (1982), the critical flux Richardson number is

$$\begin{aligned} Ri_{f_c}=\frac{B_1-6A_1}{B_1+3B_2+12A_1}. \end{aligned}$$
(6)

If \({P_b}\) is buoyancy production and \({P_s}\) is shear production, the flux Richardson number is

$$\begin{aligned} Ri_{f}=-\frac{P_b}{P_s}. \end{aligned}$$
(7)
Table 1 Sets of constants used in the simulations
Full size table

Different sets of constants can be found in the literature. In this work, we consider the sets from Mellor and Yamada (1982, MY82), Janjic (2001, BASE), and Trini Castelli et al. (1999, 2001, TCF). The values of the constants are listed in Table 1. The PR074 set of constants is obtained by modifying those of Janjic (2001) with an imposed \(Pr_t=0.74\) instead of \(Pr_t=1\). The value 0.74 was suggested by Kestin and Richardson (1963). Generally, it is possible to obtain a set of constants for any value of \(Pr_t\).

3 Data for Comparison and Model Set-up

3.1 Data for Comparison

For the sake of comparison, we have used the Urban Turbulence Project (UTP) (Mortarini et al. 2013; Trini Castelli et al. 2014) dataset, based on an experiment conducted on the outskirts of Turin, Italy, providing sonic-anemometer data at three different heights (5, 9, 25 m) above ground. A pre-processing procedure was carried out to give hourly mean wind speed and direction, as well as temperature and standard deviations of the velocity fluctuations, which were collected for more than one year. The period from 0600 UTC on 26 January to 1800 UTC on 31 January 2008 was considered, and the comparison was performed with data at a height of 25 m.

The site is located on the western edge of the Po Valley (northern Italy) at about 220 m above mean sea level (a.m.s.l.). A hill chain (maximum altitude of about 700 m a.m.s.l.) surrounds Turin on the eastern sector, while the Alps (whose crest line is about 100 km away) encircle it in the other three sectors. The city of Turin covers an area of about 130 km\(^2\) and has a population of about 900,000 inhabitants. The respective figures for the Turin conurbation area are 1100 km\(^2\) and 1,700,000 inhabitants. The area in which the instruments are located is in the southern outskirts of the town on grassy, flat terrain surrounded by buildings. There are buildings of about 30 m in height located 150 m away in the north-north-east direction, and sparse lower buildings (heights varying from 4 to 18 m) at a distance of 70–90 m in the other sectors. The site is characterized by horizontally non-homogeneous conditions. Surface roughness was estimated to be in the rough and very rough categories, depending on the incoming wind direction, and the urban fabric can be classified as being in the low-density class. Turin is characterized by frequent occurrences of low-wind-speed conditions. More than 80% of the data indicate a mean wind speed of < 1.5 m s\(^{-1}\) at 5 m, which is probably due to the shielding effect of the surrounding mountain and hill chains. The few cases of high wind speeds are related to the dry downslope slope flow from the Alps, the foehn, which occurs in the cold season typically about 15 times per year. The highest measurements almost correspond to the mean level of the surrounding roofs, and are thus only likely to be influenced a small amount by the buildings.

3.2 Simulations

The WRF model was run with five nested grids with horizontal spacings of 30000, 10000, 3333.33, 1111.11, 370.37 m, and 133 \(\times \) 133 grid points. All the grids have 35 vertical levels, up to an altitude of about 30000 m. The first vertical levels were at 0.2, 54, 132, 234, and 363 m, and there were eight levels in the first 1000 m in order provide enough resolution for comparisons between the model results and the observations, making it consistent with previous work (see for instance Kleczek et al. 2014; Ferrero et al. 2018). For the microphysics, we choose the WRF single-moment class 3 model (Hong et al. 2004), while the rapid radiative transfer model (Mlawer et al. 1997) was selected for the longwave radiation, and the Dudhia option (Dudhia 1989) was used for the shortwave radiation. The surface layer was simulated using the Janjic–Monin–Obukhov Eta (Janjic 1996) parametrization, while the Unified Noah land-surface model was used for the surface physics with the Kain–Fritsch (new eta) parametrization, (Kain 2004) for the cumulus parametrization, only to the first and second grids. No data were assimilated and the boundary conditions were provided by the National Oceanic and Atmospheric Administration Global Data Assimilation System reanalysis. The comparison with the observed data was carried out for a winter period of about 6 days. The prevailing meteorological conditions in winter are stable and are often characterized by low wind speed; and meteorological models generally have problems performing satisfactorily in these conditions. While the experimental campaign provides data at three different levels, these levels are too close to each other and to the ground to allow the vertical gradients to be analyzed. The meteorological fields were saved hourly. The meteorological variables were extracted from the finer grid fields and interpolated, both vertically and horizontally, to the sonic-anemometer position. In this way, we obtained a time series that could be compared with the observations.

In order to run the WRF model we used Cloud Computing, which has been defined as “a model that can provide convenient, on-demand network access to a shared pool of configurable computing resources (e.g., networks, servers, storage, applications, and services) that can be rapidly provisioned and released with minimal management effort or service-provider interaction” (Mell and Grance 2011). In other words, Cloud Computing can easily satisfy the huge amount of storage and computational power required by modern applications. This computational paradigm is now used in many fields, and users do not need to have any computing skill to use the cloud infrastructure itself. Moreover, in order to exploit different cloud infrastructures concurrently, the scientific literature has proposed various projects (Canonico et al. 2013; Canonico and Monfrecola 2016), some of which have made their source code available and have simple text–user interfaces, making the interactions with the major cloud infrastructures simple  (The UPO’s Distributed Computing Systems group 2020; Anglano et al. 2020). The advantages of using this system include flexibility and the possibility of setting up a virtual machine with specific characteristics and capacity needed for specific case. Furthermore, it is a low-cost and low-impact system. One aim of this work is, in fact, to investigate how well numerical weather prediction models run on this system. For our simulation, we used a virtual machine that runs Ubuntu 16.04 as its operating system and was equipped with 32 GB of system memory, eight cores, and 160 GB of storage.

4 Results

Below, the results are divided according to the weather and turbulence conditions in the cases of low-wind-speed, unstable, and stable conditions. Low-wind-speed conditions are defined as the cases in which the wind speed is < 1.5 m s\(^{-1}\) (Mortarini et al. 2013), while stability conditions are determined on the basis of the Obukhov length. It can be observed that the three data subsets are mutually exclusive when stable and unstable conditions are considered, but not concerning a low wind speed, which can arise in various stability conditions.

4.1 Low-Wind-Speed Conditions

Quantile–Quantile (Q–Q) plots for the various parametrizations shown in Table 1 for the wind speed, temperature, and TKE, in the case of low wind speed, can be observed in Fig. 1a. Although all of the models reproduce the distribution of wind speeds at low values, none are able to correctly reproduce the entire data distribution. The models provide wind speeds > 1.5 m s\(^{-1}\) for a considerable number of cases, where the corresponding measured values are lower than this threshold. As far as temperature is concerned, a general underestimation can be observed in all the models, without there being particular differences in one parametrization compared with the others. This underestimation has also been found previously (see for instance Kleczek et al. 2014; Ferrero et al. 2018), and may be attributed to limitations in the PBL models that do not explicitly determine the heat flux. This is usually corrected through the assimilation of measured data, which, in our case, was not carried out, as our aim is to verify the performance of the PBL models. The results obtained for TKE are perhaps even more interesting. In this case, we can observe how all the parametrizations, with the exception of the TCF model, underestimate the measured value. In fact, the TCF model satisfactorily reproduces the distribution of the observations.

The constant \(B_1\) is used in the following definition of the dissipation rate,

$$\begin{aligned} \epsilon = \frac{q^2}{B_1\; l}, \end{aligned}$$
(8)

where \(q^2\) is twice the TKE and l is the master length scale. Table 1 shows that the value of \(B_1\) prescribed by the TCF model is about double that found in the other sets of constants, which means that the dissipation of TKE is lower than in the other models, and that, consequently, more TKE is generated.

Fig. 1
figure 1

Quantile–Quantile plots for wind speed (m s\(^{-1}\)), temperature (K), and TKE (m\(^2\) s\(^{-2}\)), for a low-wind-speed, b unstable, and c stable conditions. Green: BASE, black: TCF, blue: PR074, red: MY82

Full size image
Table 2 Metrics for low-wind-speed conditions and for wind speed (U) and direction (Dir), for temperature (T) and TKE (e)
Full size table

These results are summarized in Table 2 which shows the values obtained for the statistical indices. The calculated and simulated average values, the bias b, and the correlation coefficient R have been taken into consideration in this analysis. The metrics have also been calculated for the wind direction and can be seen in the table. Since it is a cyclic variable, we checked whether the b values correspond to a real physical difference. All models overestimate the wind speed (negative bias) and underestimate the temperature by 6 K. Wind direction also shows a similar bias for all the models except for the TCF model, which yields a lower value. As for the TKE, a positive bias affects all the models but is lower for the TCF model. The correlation coefficient is very low for all of the variables and models, while R is slightly better for temperature.

4.2 Unstable Conditions

The Q–Q plots that correspond to the various simulations for the unstable cases are displayed in Fig. 1b for the wind speed, temperature and TKE. It can be seen that all of the models correctly reproducing the distribution of the observations for wind speed, but with a slight overestimation of the maximum values. The temperature, as in the previous case, is underestimated to the same extent by all of the models. However, this is not the case for the TKE, whose Q–Q plots differ according to the set of constants used. The TCF set of constants provides a remarkable result, with excellent agreement for all quantiles. Moreover, the result obtained by the PR074 model is also satisfactory, despite underestimating the maxima. The performance of the two other models is worse and shows a general underestimation. As in the case of low wind speed, it can be noted that the TCF model provided the highest value for the \(B_1\) constant. Furthermore, the PR074 set of constants includes a \(B_1\) value that is higher than those of the MY82 and BASE sets of constants.

Table 3 Metrics for unstable conditions and for wind speed (U) and direction (Dir), for temperature (T) and TKE (e)
Full size table

The results for the metrics are presented in Table 3 for unstable cases, illustrating that the best performance for wind speed and direction, in terms of the bias, is provided by the TCF set of constants, while this model gives a bias for the temperature that is slightly higher than that of the other models. As for the TKE, the TCF model overestimates it, while the other models underestimate the measured value. The PR074 set of constants provides the best result.

4.3 Stable Conditions

The Q–Q plots for the stable cases are presented in Fig. 1c. The distribution of wind speeds is well reproduced by all of the models which, conversely, underestimate that of the temperature equally. Even the TKE is underestimated regardless of the set of constants used. The TCF set of constants provides slightly better performance in this case. Table 4 indicates that the PR074 model overestimates the wind speed, which is, however, underestimated in the other cases. For the wind direction, all of the sets of constants show a large bias. It is interesting to note that the difficulty that the models have in simulating the wind direction here is neither observed under unstable conditions nor at low wind speeds. This fact may be related to sub-mesoscale motion, which induces horizontal oscillations in the wind direction (Cava et al. 2019). Except for temperature, the correlation coefficient is very low for all of the variables and models.

Table 4 Metrics for stable conditions and for wind speed (U) and direction (Dir), for temperature (T) and TKE (e)
Full size table

4.4 Bootstrap Test

In order to demonstrate that a given model configuration is better than the alternatives, attention should be paid to demonstrating the statistical significance of the results. We performed a bootstrap test on the bias of the wind speed and TKE. We computed the metric for two models and noted the difference. This step was then repeated \(10^4\) times, and each time the dataset was reshuffled via resampling with replacement. This bootstrap procedure yielded a p.d.f. of the metric differences; if the value zero is not in the tails of the distribution, the difference in skill between the two models is not significant (Wilks 2011).

The results show that the different sets of constants do not provide statistical significance for the bias and for the different meteorological conditions (stable, unstable, and low wind speed) for wind speed. This result is to be expected as the PBL model is the same in all the cases, and only the scales of the turbulence can be directly influenced by modifying the value of the constants. As for the TKE, the results of the bootstrap test are shown in Fig. 2 for low-wind-speed, unstable, and stable conditions. The p.d.f. of the difference in the bias of the model pairs is shown with each model corresponding to a set of constants, as listed in Table 1.

On the one hand, for low-wind-speed conditions (black line in Fig. 2), it can be seen that the difference in the bias is significant for the BASE and TCF models, and the TCF and MY82 models, and to a lesser extent for the TCF and PR074 models. On the other hand, the bias differences in the other models are not significant. Thus, the TCF set of constants provides a bias whose statistics differs significantly from the bias given by all the other sets of constants. Similar results are obtained for unstable conditions (red line in Fig. 2) and stable conditions (blue line in Fig. 2). The only set of constants that provides significant differences in the bias, compared with the others, is the TCF model.

Fig. 2
figure 2

Probability density functions of the difference in bias for the TKE for the model combinations a BASE–TCF, b BASE–PR074, c BASE–MY82, d TCF–PR074, e TCF–MY82, and f PR074–MY82

Full size image

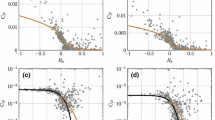
4.5 Normalized Mean Square Error Versus Fractional Bias

Figure 3 shows the normalized mean square error versus the fractional bias (Chang and Hanna 2004), which are often used as a single plot to indicate overall relative model performance, for the three meteorological conditions considered. The two indexes are defined as

$$\begin{aligned} FB= & {} 2\frac{({\overline{C}}_o - {\overline{C}}_p)}{({\overline{C}}_o + {\overline{C}}_p)}, \end{aligned}$$
(9)
$$\begin{aligned} NMSE= & {} \frac{\overline{(C_{o} - C_{p})^2}}{{\overline{C}}_p {\overline{C}}_p}, \end{aligned}$$
(10)

where \(C_{o} \) are the observations, \(C_{p}\) the model predictions, and the overline indicates the average. A perfect model would have \(FB = NMSE = \mathrm{zero}\). The minimum NMSE value, (i.e. without any unsystematic errors) for a given FB (Chang and Hanna 2004) is also reported (continuous line) in Fig. 3

$$\begin{aligned} NMSE = \frac{4 FB^{2}}{4-FB^{2}}. \end{aligned}$$
(11)

It can be seen that the best performance is obtained for temperature whose values are all close to the origin of the graph. However, it should be noted that this result does not reflect the systematic underestimation that was previously observed. Since the values of FB and NMSE are normalized by the average absolute temperatures in the observation and forecast samples, their numerical values are very low. This depends merely on the measurement unit (K) used for temperature. As far as wind speed is concerned, the results are similar under the three meteorological conditions, except for the underestimation shown in low-wind-speed conditions. The wind direction has a higher NMSE value in stable conditions than under other conditions. There are no noticeable differences between the different models for wind speed and direction, and for temperature. By contrast, there are differences in the results provided by the different sets of constants for the TKE. The best performance is found for TCF constants under low-wind-speed and stable conditions, while the PR074 constants provide the best results for unstable conditions. It can be noted that all models reproduce observations for the TKE in stable conditions with large errors, which reflects the fact that the values of the constants are generally not calibrated for such conditions. Similarly, the results in low-wind-speed conditions are worse than those in unstable conditions. It is worth noting that, while the literature on turbulence in unstable or neutral conditions is very rich, stable and low-wind-speed conditions are still challenging fields of research.

Fig. 3
figure 3

Plots of NMSE versus the fractional bias FB based on the wind speed (squares), temperature (triangles), and TKE (diamonds) for a low-wind-speed, b unstable, and c stable conditions. The continuous line represents the minimum possible NMSE value for a given value of FB

Full size image

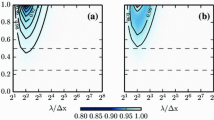
4.6 Taylor Diagrams

Comparing the performance of the four models using a Taylor diagram, in which the radial distance between the centre of the model symbol and the origin indicates the normalized standard deviation may be worthwhile. The distance from the centre of the model symbol to the large solid circle indicates normalized root-mean-square error. The cosine of the angle formed by the horizontal axis and segment normalized standard deviation indicates the correlation coefficient. A black open circle on the horizontal axis indicates the perfect model. Figure 4 shows the Taylor diagram for the different meteorological conditions and the four models. Generally speaking, the results show very low correlation, albeit slightly better for temperature, as indicated by the alignment of different models along the vertical axis. The Taylor diagrams reflect the low correlation coefficient found in the statistical analyses. It is worth noting that we have compared the model results with data from a single measurement station, which can be very difficult to reproduce. The results can probably be improved by assimilating the observations, as is generally done in the operative models. However, herein, we are interested in comparing the performance of PBL models and, for this reason, we cannot force the model results by using assimilation. Very small differences appear for the wind speed, while some discrepancies are found for the TKE. In addition to the observations made above, the points representing the different models are very close to each other for wind speed and temperature. On the one hand, as has already been shown, the differences in the bias for wind speed in the models is not significant. On the the other hand, the Taylor diagrams for the TKE show remarkable differences in model performance. This also means that turbulence is determined mainly by the PBL models, which include the TKE equation, and less by the mean quantities. The TCF set of constants shows the largest normalized standard deviation and the closest to the perfect model value of unity under all atmospheric conditions. The lowest normalized root-mean-square error is found for the BASE constants, and found to be between 1.0 and 1.5.

Fig. 4
figure 4

Taylor diagrams; green: BASE, black: TCF, blue: PR074, red: MY82

Full size image

5 Discussion and Conclusions

5.1 General Conclusion

We present the influence of length scales on the performance of the Janjic (2001) PBL models. As these length scales are generally based on sets of constants that take different values depending on the author, different results are obtained when varying the set of constants. This is especially true for the TKE, which is clearly the most sensitive to the choice of PBL model. Nonetheless, statistical analyses reveal some differences in the results obtained using the different sets of constants for the other quantities considered (wind speed and direction, temperature). In particular, an improved TKE can be obtained by suitably varying the length scales. The best results for the TKE are found using the TCF set of constants, as also found by Tomasi et al. (2019). It is worth noting that this set of constants was derived from data measured in non-homogeneous conditions (Trini Castelli et al. 1999). The length scales rely on the pressure \((A_1, A_2)\) and dissipation terms \((B_1, B_2)\) in the original model equations (Mellor 1973), and account for the Rotta (1951a, 1951b) hypothesis of return to isotropy and the Kolmogorov (1941) hypothesis of local, small-scale isotropy. In the model, the larger the \(A_1/B_1\) ratio, the greater the anisotropy. From Table 1, we can see that this ratio is similar for all of the models except for the TCF set of constants, which gives a slightly higher value, and may indicate that this set of constants is more able to take the inhomogeneities into account than the others. The values of B1 and B2, which are much higher for the TCF set of constants than for the other sets, suggest that the dissipation, both of TKE and temperature variance, is also higher, allowing more TKE to be produced.

5.2 Dependency on the Prandtl and Richardson Numbers

We have also found that the results depend on the value of the turbulent Prandtl number, which in turn depends on the constants considered. The results seem to suggest that lower \(Pr_t\) values allow better model performance to be obtained. We find that the TCF constants give the lowest values of the critical Richardson number, \(Ri_{f_c}\), which may indicate that turbulence is more suppressed using this set than using the others. Nevertheless, it has been demonstrated that turbulence also persists at higher Richardson numbers in the stable boundary layer (Canuto et al. 2008; Ferrero et al. 2011). In Mellor and Yamada (1982), the model constant \(A_1\) is related to the momentum flux and \(A_2\) to the buoyancy flux. As a consequence, if \(A_1/A_2\) \(\gg 1\), as in the TCF case, mechanical turbulence prevails over the buoyancy term, meaning that turbulence can persist even in the presence of a negative heat flux under stable conditions.

5.3 Dependency on the Low-Wind-Speed and Stability Conditions

The differences in model skill in stable, unstable, and low-wind-speed conditions show that unstable conditions give large standard deviations, particularly in the case of the TCF models (Fig. 4). The largest NMSE value and bias for the TKE are found under stable conditions (see Figs. 1, 3 and Tables 2, 3, 4). Under low-wind-speed conditions, TKE performance is satisfactory at least when the TCF set of constants is used, although all of the models have difficulty reproducing the wind-speed distribution (Fig. 1). It is worth noting that these considerations may only be valid when discussing days in winter. Stable and low-wind-speed conditions are more common in winter and these are the conditions that we have focused on, as meteorological models generally have problems providing satisfactory performance under these conditions.

5.4 Final Remarks

Although the experimental campaign has provided data at three different levels (5, 9, 25 m), these are too close to the ground to allow the vertical gradients to be analyzed. Nevertheless, the results of this work show that the choice of the set of constants can make an important difference. The degree of anisotropy and the dissipation rate of TKE and temperature variance depend on the constant values whose proper selection improves the performance of the model in conditions that are different from those assumed in the usual PBL models, such as conditions of horizontal inhomogeneity. Finally, it is worth mentioning that these simulations were carried out using a cloud computing system, which has many advantages, including reduced costs and scalability.