Lawson schemes for highly oscillatory stochastic differential equations and conservation of invariants

Abstract

In this paper, we consider a class of stochastic midpoint and trapezoidal Lawson schemes for the numerical discretization of highly oscillatory stochastic differential equations. These Lawson schemes incorporate both the linear drift and diffusion terms in the exponential operator. We prove that the midpoint Lawson schemes preserve quadratic invariants and discuss this property as well for the trapezoidal Lawson scheme. Numerical experiments demonstrate that the integration error for highly oscillatory problems is smaller than that of some standard methods.

1 Introduction

In this paper, we consider Stratonovich stochastic differential equations (SDEs) in which the drift and diffusion terms can be split into linear and non-linear parts,

$$\begin{aligned} \mathrm {d}X(t)&=\left( A_0X(t) + g_0(X(t))\right) \mathrm {d}t\nonumber \\&\quad + \sum _{m=1}^M \left( A_mX(t) + g_m(X(t))\right) \circ \mathrm {d}W_m(t), ~X(t_0) =X_{0}, \end{aligned}$$

(1.1)

where $t\in I$, $W_m(t)$, $m=1,\dotsc ,M$, denote independent, one-dimensional Wiener processes, and the SDE is solved on the interval $I=[t_0,T]$. We assume that SDE (1.1) has a unique solution for $X_0\in {\mathbb {R}}^{d}$ and that $g_m\in C^{1}({\mathbb {R}}^d,{\mathbb {R}}^d)$, $m=0,\dotsc ,M$. To simplify the notation, we define $W_0(t)=t$, so that (1.1) can be written as

$$\begin{aligned} \mathrm {d}X(t) = \sum _{m=0}^M \left( A_mX(t) + g_m(X(t))\right) \circ \mathrm {d}W_m(t), \quad t\in I, \quad X(t_0)=X_{0}. \end{aligned}$$

(1.2)

We will also assume that the matrices $A_m \in {\mathbb {R}}^{d\times d}$, $m=0,\dotsc ,M$, are constant, and moreover chosen such that the following commutativity assumption is satisfied:

Assumption 1

(Commutativity)

$$\begin{aligned}{}[A_l,A_k] =A_lA_k - A_kA_l = 0 \qquad \text {for all} \qquad l,k = 0,1,\dots ,M. \end{aligned}$$

To satisfy this assumption, it is sometimes convenient to split the linear parts of the problem, and let some of it be included in the $g_m$ functions.

Applications satisfying Assumption 1 are, e. g., [9] the FitzHugh–Nagumo equation with multiplicative noise, the Lotka-Volterra system and SDEs resulting from spectral spatial discretization of stochastic partial differential equations (SPDEs) with diagonal noise.

Exponential methods for solving such problems have in particular been applied in the SPDE setting, mostly, but not exclusively for problems with additive noise. Cohen [4] proposed an exponential method for stochastic oscillators, Yang et al. [21] suggested one for damped Hamiltonian systems. Recently, Erdoǧan and Lord [9] presented a quite general approach for constructing exponential integrators for (1.2) with multiplicative noise. One of the strategies presented there is an adaptation of a method introduced for ordinary differential equations (ODEs) by Lawson [17] to SDEs of the form (1.2). The idea is to transform the system by the fundamental solution of the linear part, solve the transformed system by a scheme of preference, and then transform back again. In the ODE literature, this is also referred to as an integrating factor method (Cox and Matthews [18], Maday et al. [6]). This is the procedure which will be applied in this paper, and which is described in detail in Sect. 2. We are essentially interested in studying highly oscillatory problems, and to show that the Lawson methods can attain good accuracy with larger step sizes than what can be obtained by standard stochastic methods. We will also show that the Lawson methods can, under reasonable assumptions, maintain conservation properties of the underlying scheme. Let us demonstrate the ideas of the paper by an introductory example.

Example 1.1

(The non-linear Kubo oscillator) As a starting point, consider the linear Kubo oscillator

$$\begin{aligned} \mathrm {d}X(t) = \begin{pmatrix} 0 &{} -\omega \\ \omega &{} 0 \end{pmatrix} X(t) \mathrm {d}t+ \begin{pmatrix} 0 &{} -\sigma \\ \sigma &{} 0 \end{pmatrix} X(t) \circ \mathrm {d}W(t) \end{aligned}$$

(1.3)

which models a simple oscillator perturbed by a stochastic term and appears in nuclear magnetic resonance and molecular spectroscopy (Goychuk [15], Kubo [10]). The exact solution of this problem starting at $({\tilde{t}},X({\tilde{t}}))$ for ${\tilde{t}}\in I$ is given by

$$\begin{aligned} X(t) = e^{L^{{\tilde{t}}}(t)}X({\tilde{t}}), \end{aligned}$$

where the fundamental solution $e^{L^{{\tilde{t}}}(t)}$ is a rotation matrix,

$$\begin{aligned} e^{L^{{\tilde{t}}}(t)} = \begin{pmatrix} \cos {\alpha ^{{\tilde{t}}}(t)} &{} -\sin {\alpha ^{{\tilde{t}}}(t)} \\ \sin {\alpha ^{{\tilde{t}}}(t)} &{} \cos {\alpha ^{{\tilde{t}}}(t)} \end{pmatrix} \text { with } \alpha ^{{\tilde{t}}}(t) = \omega (t-{\tilde{t}})+\sigma (W(t)-W({\tilde{t}})). \end{aligned}$$

Clearly, the exact solution $X(t)=(X_1(t),X_2(t))^\top$ of the linear problem is norm-preserving, i. e. satisfies the invariant

$$\begin{aligned} {\mathcal {I}}(X(t)) = X_1^2(t)+X_2^2(t) = \text {constant} \quad \text {for all } t. \end{aligned}$$

(1.4)

Cohen [4] proposed an extension to the Kubo oscillator by including a non-linear, skew-symmetric drift term, see also Laurent and Vilmart [16]. We extend this further, with non-linear terms in both the drift and diffusion, in addition to including multidimensional noise:

$$\begin{aligned} \begin{aligned} \mathrm {d}X(t) \!= \!\sum _{m=0}^M \left[ \omega _m \begin{pmatrix} 0 &{}\!{} -1 \\ 1 &{}\!{} 0 \end{pmatrix} X(t) \!+\! \begin{pmatrix} 0 &{}\!{} -U_m(X(t)) \\ U_m(X(t)) &{}\!{} 0 \end{pmatrix} X(t) \right] \! \circ \! \mathrm {d}W_m(t)\quad \quad \end{aligned}\end{aligned}$$

(1.5)

with $U_m:{\mathbb {R}}^2 \rightarrow {\mathbb {R}}$ and $\omega _m \in {\mathbb {R}}$. The solutions of these problems all preserve the invariant (1.4), see Sect. 3.1 for details. We are interested in studying to which extent a numerical approximation will be able to follow the fast oscillations of the linear parts, as well as how well the invariant (1.4) is preserved. In this example, the following three methods (described in detail in Sect. 2) have been applied to the SDE (1.5):

• The standard implicit stochastic midpoint rule (“Midpoint”), which is known to preserve quadratic invariants (Hong et al. [12], Milstein et al. [20]).

• The method proposed by Cohen [4] (“TDSL”) for highly oscillatory SDEs. This is a drift Lawson scheme based on the trapezoidal rule, but it does not preserve the invariant for the non-linear problem.

• A Lawson scheme based on the implicit midpoint rule (“MFSL”). Details of this scheme are given in Sect. 2, and in Sect. 3.1 it is proved that this scheme preserves the quadratic invariant ${\mathcal {I}}$.

In our example we will use $M=2$ and

$$\begin{aligned} U_0(X)&= \frac{1}{5}(X_1 + X_2)^5, ~ U_1(X)=0, ~ U_2(X)=\frac{1}{3}(X_1+X_2)^3,\\&\quad ~ \omega _0= 10, ~ \omega _1=10, ~ \omega _2=0, \end{aligned}$$

and the SDE is integrated from 0 to 1, using step size $h=2^{-5}$.

Fig. 1

Numerical trajectory of the non-linear Kubo oscillator. Blue: reference solution, blue circle: value at $t=1$. Red triangles: numerical approximation, red circle: value at $t=1$ (color figure online)

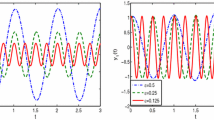
The numerical results are presented in Fig. 1. According to this, the implicit midpoint rule (“Midpoint”) preserves the invariant, it is however not able to resolve the fast oscillations. The method proposed by Cohen [4] (“TDSL”) resolves the oscillations well, but the solution drifts away from the manifold. The Lawson midpoint rule (“MFSL”) both stays on the manifold and resolves the high oscillations. This example is further exploited in Sect. 4.

The outline of this paper is as follows: In Sect. 2 we derive the midpoint and trapezoidal stochastic Lawson schemes. In Sect. 3 it is proved that, under reasonable assumptions, the Lawson transformation preserves linear and quadratic invariants, and consequently, if the underlying scheme preserves such invariants, so will the corresponding Lawson scheme. Section 4 is devoted to numerical experiments.

2 Stochastic Lawson schemes

In this section we will shortly outline how to derive the stochastic Lawson (SL) schemes, with particular emphasis on the implicit midpoint and the trapezoidal Lawson scheme.

Consider the linear SDE

$$\begin{aligned} \mathrm {d}{\hat{X}}(t) = \sum _{m=0}^M A_m {\hat{X}}(t) \circ \mathrm {d}W_m(t) \end{aligned}$$

(2.1)

and let

$$\begin{aligned} W^{{\tilde{t}}}(t) = ( W_m(t)-W_m({\tilde{t}}))_{m=0}^M\qquad \text { and }\qquad L{(W^{{\tilde{t}}}(t))} = \sum _{m=0}^M A_m W_m^{{\tilde{t}}}(t). \end{aligned}$$

Under the commutativity condition (Assumption 1), $e^{L{(W^{{\tilde{t}}}(t))}}$ and $A_m$ commute for $m=0,\dotsc ,M$, and the exact solution of the SDE (2.1) through the point $({\tilde{t}},{\hat{X}}({\tilde{t}}))$ is given by (see Arnold [3, Chapter 8.5])

$$\begin{aligned} {\hat{X}}(t) = e^{L{(W^{{\tilde{t}}}(t))}}{\hat{X}}({\tilde{t}}). \end{aligned}$$

(2.2)

This can easily be verified by the chain rule for Stratonovich integrals (see e.g. Ikeda and Watanabe [13, Chapter III, Theorem 2.1]),

$$\begin{aligned} \mathrm {d}{\hat{X}}(t)&=e^{L{(W^{{\tilde{t}}}(t))}}\sum _{m=0}^M A_m\circ \mathrm {d}W_m(t){\hat{X}}({\tilde{t}})\\&=\sum _{m=0}^M A_me^{L{(W^{{\tilde{t}}}(t))}}{\hat{X}}({\tilde{t}})\circ \mathrm {d}W_m(t)=\sum _{m=0}^M A_m{\hat{X}}(t)\circ \mathrm {d}W_m(t). \end{aligned}$$

We will now outline the procedure for constructing Lawson schemes. Let discretization points $t_0<t_1<\dots <t_N=T$ be given and denote the approximations by the Lawson scheme at time $t_n$ by $Y_n$, $n=0,\dots ,N$. Start from a point $(t_n,Y_n)$ and consider the locally transformed variable

$$\begin{aligned} V^n(t) = e^{-L^{n}(t)} X(t) \qquad \text {and thus} \qquad X(t) = e^{L^n(t)}V^n(t), \end{aligned}$$

(2.3)

where $L^n(t)=L{{(W^{t_n}(t))}}$. Applying again the chain rule for Stratonovich integrals results under Assumption 1 in

$$\begin{aligned} \mathrm {d}V^n(t)&=e^{-L^{n}(t)}\left( {-}\sum _{m=0}^{M}A_m\circ \mathrm {d}W_m(t)X(t){+} \sum _{m{=}0}^M \left( A_mX(t) {+} g_m(X(t))\right) \circ \mathrm {d}W_m(t) \right) \\&= e^{-L^n(t)}\sum _{m=0}^M g_m(X)\circ \mathrm {d}W_m(t), \end{aligned}$$

which can be written as a non-autonomous, non-linear SDE in the transformed variable $V^n(t)$,

$$\begin{aligned} \mathrm {d}V^n(t)&= \sum _{m=0}^M e^{-L^n(t)}g_m(e^{L^n(t)}V^{n}(t)) \circ \mathrm {d}W_m(t) \nonumber \\&=\sum _{m=0}^M{{\hat{g}}}_m(W^n(t),V^n(t)) \circ \mathrm {d}W_m(t), \qquad V^n(t_n)= V^n_n = Y_n, \end{aligned}$$

(2.4)

where $W^n = W^{t_n}$ and ${{\hat{g}}}_m({y},V^n(t))=e^{-L{(y)}}g_m(e^{L{(y)}}V^{n}(t))$. One step from $(t_n,Y_n)$ to $(t_{n+1},Y_{n+1})$ with a Lawson scheme is now just one step of some appropriate one-step method applied to the autonomous version

$$\begin{aligned} \mathrm {d}{\bar{V}}^n(t) = \sum _{m=0}^M {\bar{g}}_m({\bar{V}}^n(t)) {\circ } \mathrm {d}W_m(t), \quad {\bar{g}}_m = (\delta _{0,m},\ldots ,\delta _{M,m},{{{\hat{g}}}^{\top }_m})^{\top } \end{aligned}$$

(2.5)

of the transformed system (2.4), with ${\bar{V}}^n(t) = (W^n(t)^\top ,{V^n}(t)^\top )^{\top }$ and $\delta _{i,j} = {\left\{ \begin{array}{ll} 1, &{} i=j, \\ 0, &{} i\ne j, \end{array}\right. }$ giving $V^n_{n+1}$, followed by a back-transformation $Y_{n+1}=e^{L^n(t_{n+1})}V^n_{n+1}$ (see Debrabant et al. [8] for details). Due to the construction of the methods, the convergence properties of the underlying methods are retained (Debrabant et al. [8]). Specifically, we have the following theorem:

Theorem 2.1

(Convergence of stochastic Lawson methods [8]) Let Assumption (1) hold, let X be the solution of SDE (1.2), $Y_n$ be the result of the stochastic Lawson method ($n=0,\dots ,N$), ${\bar{V}}^0$ be the exact solution of (2.5) (with $n=0$), and ${\bar{V}}^0_{n}=({W^0_n}^\top ,{V^0_n}^\top )^{\top }$ for $n=0,\dots ,N$ be its approximation obtained by applying the underlying SRK method with step sizes $h_i=t_{i}-t_{i-1}$, $i=1,\dots ,N$. Further, let $h_{N,max}=\max _{i=1}^Nh_i$.

• 1. Assume that $W^0_n=W^0(t_n)$ and that the underlying SRK method is of mean square order p, i. e. there exists a $c\in {\mathbb {R}}$ such that for all $N\in {\mathbb {N}}$ and all $n\in \{0,1,\dots ,N\}$ it holds that $\sqrt{{{{\,\mathrm{E}\,}}}( \Vert {V}^0_n - {V}^0(t_n)\Vert _2^2)} \le ch_{{N,max}}^p$. Then the stochastic Lawson method is strong convergent of order p, i. e., there exists a ${\tilde{c}} \in {\mathbb {R}}$ such that for all $N\in {\mathbb {N}}$ and all $n\in \{0,1,\dots ,N\}$ it holds that

  $$\begin{aligned} {{{\,\mathrm{E}\,}}}\Vert Y_n - X(t_n)\Vert _2 \le {\tilde{c}}h_{{N,max}}^p. \end{aligned}$$

  (2.6)

• 2. Assume that

  • (a) $A_m$ for $m> 0$ are skew-symmetric (cmp. Assumption 2 below),

  • (b) ${\bar{V}}^0_n$ is of weak order ${\tilde{p}}$, i.e. for all ${\tilde{f}}\in C^{2({\tilde{p}}+1)}_P({\mathbb {R}}^{M+1}\times {\mathbb {R}}^{d},{\mathbb {R}})$ there exists a $c\in {\mathbb {R}}$ such that for all $N\in {\mathbb {N}}$ and all $n\in \{0,1,\dots ,N\}$ it holds that $|{{{\,\mathrm{E}\,}}}({\tilde{f}}({\bar{V}}^0_n) - {\tilde{f}}({\bar{V}}^0(t_n))| \le ch_{{N,max}}^{{\tilde{p}}}$,

  • (c) $W^0_{n,0}=W_0(t_n)=t_n$.

  Then the stochastic Lawson method is of weak order ${\tilde{p}}$, i. e., for all $f\in C^{2({\tilde{p}}+1)}_P{({\mathbb {R}}^{d},{\mathbb {R}})}$ there exists some constant $c_f > 0$ such that for all $N\in {\mathbb {N}}$ and all $n\in \{0,1,\dots ,N\}$ it holds

  $$\begin{aligned} | {{{\,\mathrm{E}\,}}} f(Y_{{n}}) - {{{\,\mathrm{E}\,}}}f(X(t_{{n}}))| \le c_{{f}} h_{{N,max}}^{{\tilde{p}}}. \end{aligned}$$

  (2.7)

In this paper, only Lawson schemes based on the implicit trapezoidal and midpoint rules will be discussed. These two methods, applied to (2.5), are given by

$$\begin{aligned} V_{n+1}^n&= V^n_n + \sum _{m=0}^M \bigg ({{\hat{g}}}_m({0},V^n_n)+ {{\hat{g}}}_m(\Delta W^n,V^n_{n+1})\bigg ) \frac{\Delta W^n_m}{2}, \end{aligned}$$

(2.8)

respectively

$$\begin{aligned} V^n_{n+1}&= V^n_n + \sum _{m=0}^M {{\hat{g}}}_m\left( {\frac{\Delta W^n}{2}},\frac{V^n_{n}+V^n_{n+1}}{2} \right) \Delta W^n_m, \end{aligned}$$

(2.9)

where the stochastic increments are $\Delta W_m^n = W_m(t_{n+1})-W_m(t_n)$, $m=0,\dotsc ,M$, and we used that $W^n(t_n)=0\in {\mathbb {R}}^{M+1}$ and $W^n(t_{n+1})=\Delta W^n$. Under appropriate conditions on the smoothness and boundedness of the ${{\hat{g}}}_m$ (e. g. for mean square convergence of order up to one that ${{\hat{g}}}_0+\frac{1}{2}\sum _{m=1}^M{{\hat{g}}}_m'{{\hat{g}}}_m$ and ${{\hat{g}}}_1,\dots ,{{\hat{g}}}_M$ satisfy a global Lipschitz condition and are, together with all the associated elementary differentials up to order three, of linear growth), these approximations will be of mean square order $p=0.5$ ($p=1$ for commutative noise) and weak order ${\tilde{p}}=1$, see e. g. Debrabant and Kværnø [7], Hong et al. [12], Kloeden and Platen [14], Milstein and Tretyakov [19]. Note that for methods that conserve a bounded manifold, smooth functions g can be replaced by smooth bounded functions being zero outside a suitable ball, see e.g. Cohen [5].

Applying the back-transformation results in the two Lawson methods of interest in this paper:

Trapezoidal Lawson rule:

$$\begin{aligned} Y_{n+1}&= e^{\Delta L^n}Y_n + \sum _{m=0}^M \bigg (e^{\Delta L^n}g_m(Y_n)+g_m(Y_{n+1}) \bigg ) \frac{\Delta W_m^n}{2}, \end{aligned}$$

(2.10)

Midpoint Lawson rule:

$$\begin{aligned} Y_{n+1}&= e^{\Delta L^n}Y_n + \sum _{m=0}^M e^{\frac{\Delta L^n}{2}} g_m\left( \frac{e^{\frac{\Delta L^n}{2}}Y_n + e^{-\frac{\Delta L^n}{2}}Y_{n+1}}{2} \right) \Delta W^n_m, \end{aligned}$$

(2.11)

where $\Delta L^n = L^n(t_{n+1}) = \sum _{m=0}^M A_m \Delta W_m^n$.

We would like to emphasize that there is some freedom in how to choose the matrices $A_m$ in the SDE (1.2) and thus the Lawson methods (2.10) and (2.11), as for any $A_m\in {\mathbb {R}}^{d\times d}$ an integrand ${\tilde{A}}_mX + {\tilde{g}}_m(X)$ can be written as

$$\begin{aligned} {\tilde{A}}_mX + {\tilde{g}}_m(X) = A_mX + \overbrace{({\tilde{A}}_m-A_m)X+{\tilde{g}}_m(X)}^{=:g_m(X)}, \end{aligned}$$

see also Debrabant et al. [8]. The matrices $A_m$ have to be chosen such that Assumption 1 is satisfied. Different splittings lead to different schemes. The underlying numerical scheme is restored by setting all the linear parts $A_m$ to 0 ($m=0,1,\dotsc ,M$). In a drift stochastic Lawson scheme (DSL), only the linear drift term is included in the exponential, that is $A_0\not =0$ and $A_m=0$ for $m=1,\dotsc ,M$. The exponential $e^{\Delta L^n}=e^{h_{{n+1}}A_0}$ is computed only once, and the DSL schemes can be quite efficient. The scheme suggested by Cohen [4] (denoted by TDSL in the present article) is an example of a DSL scheme based on the trapezoidal rule (2.10). If $A_m\not =0$ for at least one $m\not =0$, the scheme is denoted as a full stochastic Lawson scheme (FSL). In this case the exponentials depend on the stochastic increments and have to be calculated for each step, so the performance of the FSL schemes depends on how efficient this can be done.

For a continuous splitting between the linear and the non-linear part, see Erdoğan and Lord [9].

3 Preservation of invariants

Hong et al. [12] studied preservation of linear and quadratic invariants for SDEs. In particular, they showed that the stochastic midpoint rule (as a representative for the Gauss methods), preserves quadratic invariants. The aim of this section is to extend these results to the stochastic Lawson (SL) schemes. It is also well known that the standard trapezoidal rule almost preserves quadratic invariants for deterministic differential equations, see e.g. Hairer et al. [11, Example V.4.2]. This property does unfortunately not extend to the stochastic trapezoidal rule in general; we will study under which conditions it does hold. The commutativity condition Assumption 1 is always assumed to be satisfied throughout this section.

In the following, we first investigate when stochastic Lawson schemes preserve quadratic invariants before briefly commenting on the preservation of linear invariants.

3.1 Preservation of quadratic invariants

In this section we study when the SDE (1.2) for a $D\in {\mathbb {R}}^{d\times d}$ satisfies the quadratic invariant

$$\begin{aligned} {\mathcal {I}}(X(t)) {:}{=} X(t)^{\top } D X(t) = {\mathcal {I}}(X(t_0)), \end{aligned}$$

(3.1)

and the ability of the numerical schemes to preserve it. Without loss of generality we will assume that $D=D^{\top }$. For the rest of this section we will use a combination of the following assumptions:

Assumption 2

The matrices $A_m\in {\mathbb {R}}^{d\times d}$, $m=0,\dots ,M$, are skew-symmetric and commute with D.

Assumption 3

For all $X\in {\mathbb {R}}^d$ and $m=0,\dots ,M$ we have $X^{\top } D g_m(X)=0$.

The necessity of these two assumptions can be seen by applying the chain rule for Stratonovich integrals and using the symmetry of D to obtain

$$\begin{aligned} \begin{aligned} \mathrm {d}{\mathcal {I}}(X(t)) = 2\sum _{m=0}^{M} \bigg (X(t)^{\top }D A_m X(t) + X(t)^{\top } D g_m(X(t))\bigg ) \circ \mathrm {d}W_m. \end{aligned}\end{aligned}$$

To preserve ${\mathcal {I}}(X(t))$ we need both terms to be zero, the first is zero if Assumption 2 holds and the second is zero if Assumption 3 holds. In summary, it holds (see e.g. Hong et al. [12]):

Lemma 3.1

Under Assumptions 2 and 3, the SDE 1.2 has a quadratic invariant, i. e. its solution X(t) fulfills (3.1).

We now prove that the invariant (3.1) is preserved under transformations (2.3):

Lemma 3.2

Let Assumption 2 be fulfilled. Then it holds for ${\mathcal {I}}$ defined in (3.1) that

$$\begin{aligned} {\mathcal {I}}(v) = {\mathcal {I}}(e^{L^n(t)}v), \qquad \text {for all } v \in {\mathbb {R}}^d. \end{aligned}$$

(3.2)

Proof

By (3.1) and using that $A_m$, $m=0,\dots ,M$, are skew-symmetric (by Assumption 2) and $e^{L^n(t)}$ thus orthogonal, we obtain

$$\begin{aligned} {\mathcal {I}}(e^{L^n(t)}v)= v^{\top } e^{-L^n(t)} D e^{L^n(t)} v \end{aligned}$$

which, using that all $A_m$ commute with D (by Assumption 2) simplifies to

$$\begin{aligned} {\mathcal {I}}(e^{L^n(t)}v)= v^{\top } D v = {\mathcal {I}}(v). \end{aligned}$$

$\square$

We can then prove that the transformed system preserves the same invariant as the original one:

Lemma 3.3

Let Assumptions 1 to 3 hold. Then the transformed system (2.4) with solution $V^n(t)$ preserves the same invariant as the original system (1.2) with solution X(t), i.e.

$$\begin{aligned} {\mathcal {I}}(V^n(t)) = {\mathcal {I}}(X(t))={\mathcal {I}}(X(t_0)). \end{aligned}$$

(3.3)

Proof

By (2.3) it holds for $V^n(t)$ that (under Assumption 1)

$$\begin{aligned} {\mathcal {I}}(X(t)) = {\mathcal {I}}(e^{L^n(t)}V^n(t)). \end{aligned}$$

Lemma 3.2 implies then ${\mathcal {I}}(X(t)) = {\mathcal {I}}(V^n(t)).$ By Lemma 3.1 we can conclude that (3.3) holds. $\square$

We are now ready to state the main result of this section:

Theorem 3.1

Let Assumptions 1 to  3 hold and let $Y_n$ denote the discrete time approximation of (1.2) at time point $t_n$ using an SL scheme with an underlying numerical one-step method that preserves quadratic invariants. Then the SL scheme preserves the same quadratic invariant as (1.2), i.e.

$$\begin{aligned} {\mathcal {I}}(Y_n) = {\mathcal {I}}(X(t))={\mathcal {I}}(X(t_0)). \end{aligned}$$

(3.4)

Requirements for stochastic Runge–Kutta methods to preserve quadratic invariants are given in Hong et al. [12]. Strictly speaking, those results only apply to autonomous systems, it is however straightforward to extend them to the nonautonomous transformed SDE (2.4). We can then conclude with the following Corollary :

Corollary 3.1

Under the assumptions of Theorem 3.1 the midpoint stochastic Lawson scheme preserves the quadratic invariants (3.1).

Proof

(of Theorem 3.1) This follows directly by applying a numerical one-step method that preserves quadratic invariants to the transformed system: Let $V^{n}_{n+1}$ be the numerical approximation at time $t_{n+1}$ of the SDE (2.4). By Lemma 3.3 and the scheme preserving quadratic invariants, it holds that

$$\begin{aligned} {\mathcal {I}}(V^{n}_{n+1})={\mathcal {I}}(V^n(t_n))={\mathcal {I}}(X(t))={\mathcal {I}}(X(t_0)). \end{aligned}$$

By Lemma 3.2 and the definition of $Y_{n+1} = e^{\Delta L^n}V^n_{n+1}$ it follows that

$$\begin{aligned} {\mathcal {I}}(Y_{n+1})={\mathcal {I}}(V^{n}_{n+1})={\mathcal {I}}(X(t))={\mathcal {I}}(X(t_0)), \end{aligned}$$

which finishes the proof. $\square$

It is well known that the standard trapezoidal rule almost preserves quadratic invariants for deterministic differential equations, see e.g. Hairer et al. [11, Example V.4.2]. This property does unfortunately not extend to the stochastic trapezoidal rule in general. But if all the drift and diffusion terms are linear and included in the L operator, a similar result can be obtained, which is also a good argument for using full stochastic Lawson schemes instead of the drift ones.

Theorem 3.2

Let Assumptions 1 to 3 hold, let $g_m\equiv 0$ for $m=1,\dots ,M$ in the SDE (1.2) (all diffusion terms are linear and commute) and let $Y_n$ denote its discrete time approximation using the trapezoidal FSL scheme with equidistant step sizes h. Then

$$\begin{aligned} {\mathcal {I}}(Y_{n}) - {\mathcal {I}}(Y_0) = -\frac{1}{4} \left( g_0(Y_n)^{\top }Dg_0(Y_n)- g_0(Y_0)^{\top }Dg_0(Y_0) \right) h^2. \end{aligned}$$

(3.5)

Proof

The trapezoidal Lawson rule (2.10) can be considered as composed by two half steps, one with an exponential forward Euler step, and one with an exponential backward Euler step, as follows:

$$\begin{aligned} {\hat{Y}}_n&= e^{\frac{1}{2} \Delta L^n}Y_n + e^{\frac{1}{2} \Delta L^n} \sum _{m=0}^{M}g_m(Y_n)\frac{\Delta W^n_m}{2}, \end{aligned}$$

(3.6)

$$\begin{aligned} Y_{n+1}&= e^{\frac{1}{2} \Delta L^n}{\hat{Y}}_n + \sum _{m=0}^{M}g_m(Y_{n+1})\frac{\Delta W^n_m}{2}. \end{aligned}$$

(3.7)

Doing one more half step with the forward Euler method gives

$$\begin{aligned} {\hat{Y}}_{n+1}&= e^{\frac{1}{2} \Delta L^{n+1}}Y_{n+1} + e^{\frac{1}{2} \Delta L^{n+1}} \sum _{m=0}^{M}g_m(Y_{n+1})\frac{\Delta W^{n+1}_m}{2} \\&= e^{\frac{1}{2} (\Delta L^n+\Delta L^{n+1})} {\hat{Y}}_n + e^{\frac{1}{2} \Delta L^{n+1}}\sum _{m=0}^{M}g_m(Y_{n+1}) \frac{\Delta W_m^n + \Delta W_m^{n+1}}{2}, \end{aligned}$$

which together with (3.7) could be considered as one step of a modified version of the midpoint rule starting from ${\hat{Y}}_n$, and we would like to see if it conserves quadratic invariants: By Assumption 2, $e^{\Delta L^n}$ is orthogonal and commutes with D, so

$$\begin{aligned}&{\hat{Y}}_{n+1}^{\top }D{\hat{Y}}_{n+1} = {\hat{Y}}_n^{\top }D{\hat{Y}}_n + \sum _{m=0}^MY_{n+1}^{\top } D g_m(Y_{n+1}) (\Delta W_m^n+\Delta W_m^{n+1}) \nonumber \\&\quad + \sum _{m,r=0}^M g_r(Y_{n+1})^{\top } D g_m(Y_{n+1}) \frac{(\Delta W_r^{n+1}-\Delta W_r^{n})({\Delta } W_m^{n+1}+{\Delta } W_m^{n})}{4}, \end{aligned}$$

(3.8)

where we also used Assumption 1 and that by (3.7) it holds that $e^{\frac{1}{2} \Delta L^n}{\hat{Y}}_n = Y_{n+1} - \sum _{r=0}^{M}g_r(Y_{n+1})\frac{\Delta W^n_r}{2}.$ The second term of (3.8) vanishes since $Y^{\top }Dg(Y)=0$ for all $Y\in {\mathbb {R}}^d$ by Assumption 3. Due to the last term, the quadratic invariant is not preserved in general. Since $\Delta W_0=h$, if $g_m=0$ for $m=1,\dotsc M$ the last sum is 0, and ${\hat{Y}}_{n+1}^{\top }D{\hat{Y}}_{n+1} = {\hat{Y}}_n^{\top }D{\hat{Y}}_n$, which by (3.1) can be written as ${\mathcal {I}}({\hat{Y}}_{n+1})={\mathcal {I}}({\hat{Y}}_{n})$. It follows that

$$\begin{aligned} {\mathcal {I}}(Y_{n+1}) - {\mathcal {I}}(Y_0)&= {\mathcal {I}}(Y_{n+1}) - {\mathcal {I}}({\hat{Y}}_{n})+{\mathcal {I}}({\hat{Y}}_{n})-{\mathcal {I}}({\hat{Y}}_0) + {\mathcal {I}}({\hat{Y}}_0) - {\mathcal {I}}({Y}_0) \\&= {\mathcal {I}}(Y_{n+1}) - {\mathcal {I}}({\hat{Y}}_{n}) + {\mathcal {I}}({\hat{Y}}_0) - {\mathcal {I}}({Y}_0). \end{aligned}$$

Direct computations show that

$$\begin{aligned} {\mathcal {I}}({\hat{Y}}_0)-{\mathcal {I}}(Y_0)&= \frac{1}{4} g_0(Y_0)^{\top }Dg_0(Y_0)h^2, \\ {\mathcal {I}}(Y_{n+1}) - {\mathcal {I}}({\hat{Y}}_{n})&= -\frac{1}{4} g_0(Y_{n+1})^{\top }Dg_0(Y_{n+1})h^2, \end{aligned}$$

and in conclusion

$$\begin{aligned} {\mathcal {I}}(Y_{n}) - {\mathcal {I}}(Y_0) = -\frac{1}{4} \left( g_0(Y_n)^{\top }Dg_0(Y_n)- g_0(Y_0)^{\top }Dg_0(Y_0) \right) h^2. \end{aligned}$$

$\square$

Notice that a similar argument can also be used as a direct proof of Corollary 3.1: One step of the stochastic midpoint Lawson scheme is composed by one half step of the exponential backward Euler scheme followed by one half step of the exponential forward Euler scheme, both using the same stochastic increments $\Delta W^n_m/2$, so the last sum of (3.8) is 0.

Notice also that if the quadratic invariant is associated to a bounded manifold, i. e., the eigenvalues of D are all positive, then the proof of Theorem 3.2 implies that under the conditions given there, there exists a constant c such that

$$\begin{aligned} |{\mathcal {I}}(Y_{n}) - {\mathcal {I}}(Y_0)|\le c h^2 \end{aligned}$$

for all $n=0,1,\dots ,N$ and h sufficiently small.

3.2 Preservation of linear invariants

For completeness we also study when the SDE (1.2) preserves linear invariants

$$\begin{aligned} {\tilde{{\mathcal {I}}}}(X(t)) = r^{\top }X(t) = {\tilde{{\mathcal {I}}}}(X(t_0)) \end{aligned}$$

(3.9)

for an $r\in {\mathbb {R}}^{d}$ and the ability of the numerical schemes to preserve it as well.

As we did for quadratic invariants, we calculate $\mathrm {d}{\tilde{{\mathcal {I}}}}(X(t))$,

$$\begin{aligned} \mathrm {d}{\tilde{{\mathcal {I}}}}(X(t)) = \sum _{m=0}^{M} \left( r^{\top } A_m X(t) + r^{\top }g_m(X(t))\right) \circ \mathrm {d}W_m(t). \end{aligned}$$

Thus for the SDE (1.2) to preserve linear invariants we need the following two assumptions to be fulfilled:

Assumption 4

The matrices $A_m$, $m=0,\dots ,M$, satisfy $r\in \text { Null}(A_m^{\top })$.

Assumption 5

For all $X\in {\mathbb {R}}^d$ and $m=0,\dots ,M$ we have $r^{\top } g_m(X)=0$.

We now note that by Assumption 4 we have that

$$\begin{aligned} r^{\top } e^{L^n(t)} = r^{\top }. \end{aligned}$$

Using this property, Lemmas 3.2 and 3.3 and Theorem 3.1 extend directly to linear invariants.

4 Numerical examples

In this section four different stochastic Lawson schemes are tested numerically and compared with the standard midpoint rule: The trapezoidal DSL (TDSL), the trapezoidal FSL (TFSL), the midpoint DSL (MDSL) and the midpoint FSL (MFSL). All schemes are of weak order 1, and of strong order 1 for SDEs with commutative noise, otherwise of strong order 0.5. The methods are tested on two oscillatory problems preserving quadratic invariants. The error versus step size for different degrees of oscillatory behaviour is measured, as well as the ability of the schemes to preserve the invariants. Finally, the methods are tested on a stochastic Fermi–Pasta–Ulam–Tsingou (FPUT) problem. This is highly oscillatory, but does not preserve quadratic invariants exactly. The main findings of the experiments are:

• The SL schemes resolve the oscillatory behaviour better than the midpoint rule. For small linear diffusion terms, there are no significant differences between the DSL and the FSL schemes. For high noise problems, the FSL schemes are superior.

• The midpoint SL schemes preserve quadratic invariants.

• The trapezoidal FSL scheme almost preserves quadratic invariants for linear diffusions, but not for non-linear diffusions.

• The overhead caused by calculating the exponentials is insignificant, even for the FSL-schemes.

In all cases, the underlying non-linear algebraic equations of the implicit methods are solved by Newton’s method with tolerance $10^{-12}$.

4.1 Stochastic rigid body problem

The first example is the classical rigid body problem perturbed with linear skew-symmetric drift and diffusion terms, see e.g. Abdulle et al. [1], Anmarkrud and Kværnø [2] and Cohen [4]. The SDE is given by

$$\begin{aligned} \begin{aligned} \mathrm {d}X= \omega \begin{pmatrix} 0 &{} 1 &{} 0\\ -1 &{} 0 &{}0 \\ 0&{}0&{}0 \end{pmatrix}X \mathrm {d}t&+ \begin{pmatrix} 0 &{} X_3 / I_3 &{} -X_2 / I_2 \\ -X_3 / I_3 &{} 0 &{} X_1 / I_1 \\ X_2 / I_2 &{} -X_1 / I_1 &{} 0 \end{pmatrix} X \mathrm {d}t\\&+ \sigma \begin{pmatrix} 0 &{} 1 &{} 0\\ -1 &{} 0 &{}0 \\ 0&{}0&{}0 \end{pmatrix}X \circ \mathrm {d}W, \end{aligned} \end{aligned}$$

(4.1)

with, following the above references,

$$\begin{aligned} I_1 = 2, \quad I_2=1, \quad I_3=2/3, \quad t_0=0 \quad \text{ and } \quad X(0) = (\cos (1.1), 0, \sin (1.1))^{\top }.\nonumber \\ \end{aligned}$$

(4.2)

Different values of the parameters $\omega$ and $\sigma$ are chosen to investigate the schemes’ response on problems with oscillatory drift and/or diffusion terms.

First, we want to see how well the methods respond to different degrees of oscillatory behaviour. The following two experiments are carried out:

• (a) The oscillatory drift and diffusion terms contribute equally much to the solution, thus there can be a significant amount of noise in the system. The values used in the experiments are $\omega =\sigma \in \{1,5,10\}$.

• (b) The noise term is small ($\sigma =0.3$), but the drift term causes no oscillations ($\omega =0$), average ($\omega =10$) or very high oscillations ($\omega =100$). When $\omega =0$, the DSL schemes coincide with their underlying schemes. The choice of $\sigma$ corresponds to the one used by Cohen [4].

The integration interval is [0, 1] and the problem is solved with step sizes $\log _2(h)\in \{-11,\ldots ,-3\}$, and the strong error is calculated at the end of the interval. The reference solution is computed by the MFSL scheme, using $h_{\text {ref}}=2^{-17}$. In each case, the results are based on 1000 independent simulations of the underlying Wiener process. The results are given in Fig. 2. The $95\%$-confidence intervals are in all cases found to be less than $12\%$ of the corresponding error value.

Fig. 2

The stochastic rigid body problem: Strong error versus step size for different values of $\sigma$ and $\omega$

The results of experiment (a) are shown in Fig. 2a. In this experiment, there is a significant contribution to the solution from the noise term. All schemes demonstrate an acceptable performance when $\omega =\sigma =1$, the case with slow oscillations. For higher values of $\omega$ and $\sigma$ the FSL schemes are superior. In the case of $\sigma =\omega =10$, only the FSL-schemes are able to produce reliable solutions for $h>2^{-7}$. This behaviour is as expected, since the FSL schemes solve the oscillatory parts of the problem exactly.

The results of experiment (b) are given in Fig. 2b. Here, the oscillatory noise is quite small, and the oscillations are dominated by the contribution from the linear drift in all cases but $\omega =0$. For $\omega =0$, we observe no significant differences between the methods. The dominating part here is the nonlinear drift term, which is handled similarly by the schemes. For higher values of $\omega$, all the SL schemes yield similar results, and all are superior to the midpoint rule. In particular the SL schemes are able to resolve the high oscillations for larger step sizes, up to $h=2^{-6}$ even when $\omega =100$. The midpoint rule fails to give reliable results for step sizes above approximately $h=2^{-9}$ in this case. All schemes exhibit, as expected, strong order 1 for sufficiently small step sizes.

In Fig. 3 we depict the computational efforts, measured as wall-clock time per batch of 25 paths versus the strong error averaged over all batches. Somewhat surprisingly, the FSL schemes are slightly cheaper in terms of computational work per step. All the methods are implicit, thus the efforts of solving the nonlinear equations dominate. The computational overhead required for calculating the exponentials for the FSL methods seems in this example to be outweighted by the fact that there is no diffusion term to calculate in the right hand side of the equation, as it is absorbed in the exponential.

Fig. 3

The stochastic rigid body problem: Wall-clock time per batch of 25 paths versus accuracy for different values of $\sigma$ and $\omega$

We will next see how well the methods preserve invariants, also over long time integration. In the case of the stochastic rigid body problem (4.1), Assumptions 2 and 3 are satisfied, and by Lemma 3.1 the exact solution of (4.1) preserves the invariant

$$\begin{aligned} {\mathcal {I}}(X(t)) = X(t)^{\top } X(t) \end{aligned}$$

(4.3)

and thus, when using the given initial values, stays on the unit sphere. The matrices $A_0$ and $A_1$ commute, so the requirements of Corollary 3.1 are satisfied and the MDSL and MFSL schemes should preserve the invariant. As $g_1(x)=0$ the requirements for Corollary 3.2 are satisfied, and the TFSL scheme nearly preserves the invariant, and the weak order with respect to I is 2. This is clearly demonstrated in Fig. 4, the weak order is one for the TDSL scheme and two for the TFSL scheme. For the small noise problem, the error from the drift term dominates, and the order, in particular for larger values of h, is then close to 2. The midpoint schemes preserve the invariant exact and are not included in the figure.

Fig. 4

The stochastic rigid body problem: Weak error of I versus step size for different values of $\sigma$ and $\omega$

Fig. 5

The stochastic rigid body problem: The invariant ${\mathcal {I}}(Y_n)$

Lastly, as $g_0(x)\ne 0$, Theorem 3.1 in Cohen [4] does not apply, and we expect the TDSL scheme to drift off. To confirm this, two extreme cases from the experiments above have been chosen, that is $\omega =\sigma =10$, and $\omega =100$ and $\sigma =0.3$. The SDE is solved on the interval [0, 100], using the step size $h=25/2^{10}$. Fig. 5 shows the value of the invariant ${\mathcal {I}}(Y_n)$. For visibility, only each 128th step is plotted. In Fig. 6, we zoom in onto the interval [60, 70], for better visibility neglecting the TFSL method and for the midpoint methods plotting only every 6th value. Notice that the drift of the TDSL schemes is severe in the experiments with much noise, while in the case of small noise, it is reasonably small.

Fig. 6

The stochastic rigid body problem: The invariant ${\mathcal {I}}(Y_n)$

To this aim, the stochastic rigid problem is solved by the TFSL scheme over the interval [0, 100] for different step sizes, with 1000 independent simulations. Figure 7 shows the maximum average deviation over the interval, clearly demonstrating the second order of the deviation predicted by Corollary 3.2. The parameters used in this experiment are $\omega =10$ and $\sigma =0.3$.

Fig. 7

The stochastic rigid body problem with $\omega =10$ and $\sigma =0.3$: Maximum average deviation on the interval [0, 100] versus step size when solved by the TFSL method. p denotes the numerically determined order of convergence

4.2 Non-linear Kubo oscillator

We next study the methods applied to a problem with multiple noise terms. To this aim, the non-linear Kubo oscillator, already introduced in Sect. 1, is chosen. The SDE is

$$\begin{aligned} \mathrm {d}X(t) = \sum _{m=0}^M \left[ \omega _m \begin{pmatrix} 0 &{} -1 \\ 1 &{} 0 \end{pmatrix} X(t) + \begin{pmatrix} 0 &{} -U_m(X(t)) \\ U_m(X(t)) &{} 0 \end{pmatrix} X(t) \right] \circ \mathrm {d}W_m(t)\qquad \end{aligned}$$

(4.4)

with $U_m:{\mathbb {R}}^2 \rightarrow {\mathbb {R}}$. In the current experiments, $M=2$ and the nonlinear terms are

$$\begin{aligned}&U_0(X) = \frac{1}{5}(X_1 + X_2)^5, ~ U_1(X)=0,\\&~ U_2(X)=\frac{1}{3}(X_1+X_2)^3,~ \omega _0= \omega , ~ \omega _1=\sigma , ~ \omega _2=0, \end{aligned}$$

thus there are two independent diffusion terms, one linear and one non-linear. These are scaled to ensure that the highly oscillatory parts come from the linear terms. As in the rigid body case, $\omega$ and $\sigma$ vary to investigate how the schemes respond to highly oscillatory parts in the drift and / or diffusion terms. The experiment setup is as for the stochastic rigid problem:

• (a) Equal contribution from drift and diffusion: The parameters used in the experiments are $\omega =\sigma \in \{1,5,10\}$,

• (b) Small linear diffusion: The parameters are $\sigma =0.3$ and $\omega \in \{1,10,50\}$.

The integration interval is [0,1], $X(0)=(1,0)^\top$, and the SDE is solved with step sizes $\log _2(h)\in \{-15,\ldots ,-8$} and with 1000 independent simulations. The reference solutions are computed by the MFSL scheme using $h_{\text {ref}}=2^{-21}$. The strong error at the end point is shown in Fig. 8. The $95\%$-confidence intervals have been calculated and span in all cases less than $15\%$ of the corresponding error values.

Fig. 8

The Kubo oscillator: Strong error versus step size for different values of $\sigma$ and $\omega$

Fig. 9

The Kubo oscillator: Wall-clock time per batch of 25 paths versus accuracy for different values of $\sigma$ and $\omega$.

The case in which $\sigma =\omega$ is presented in Fig. 8a. Again, there are no significant differences between the methods for $\sigma =\omega =1$ and the strong order is 0.5 as expected. For higher values of $\sigma$ and $\omega$, the advantage of the FSL methods for larger step sizes is evident. In the cases of the midpoint and the DSL schemes, the error is dominated by the linear stochastic diffusion term, thus causing the first order behaviour. This term is incorporated in the exponentials of the FSL schemes and will there thus not contribute to the errors. For problems with small linear noise contributions in Fig. 8, all the SL schemes outperform the midpoint scheme for the oscillatory cases, when $\omega \in \{10,50\}$.

For step sizes larger than $h=2^{-8}$, the Newton solver frequently failed to solve the underlying nonlinear algebraic equations, in particular for the TDSL scheme. The computational efforts depicted in Fig. 9 again demonstrate that there are only small differences in execution time between the methods, thus the more accurate methods are also the most efficient ones in terms of wall-clock terms versus accuracy.

Fig. 10

The Kubo oscillator: Weak error of I versus step size for different values of $\sigma$ and $\omega$

We next investigate how well the numerical solution preserves quadratic invariants. Assumptions 2 and 3 are satisfied, and by Lemma 3.1 the exact solution of (4.4) is norm-preserving, thus

$$\begin{aligned} {\mathcal {I}}(X(t)) = X(t)^{\top } X(t) \end{aligned}$$

(4.5)

is constant, and the solution will stay on a circle. The matrices $A_0$, $A_1$ and $A_2$ trivially commute; thus Corollary 3.1 applies and all the midpoint based methods are expected to preserve the invariant. As $g_2(x)\ne 0$, Corollary 3.2 no longer applies. We thus expect to see a weak order one for the two trapezoidal SL schemes, which is exactly what is observed in Fig. 10.

Finally, we want to study how well the quadratic invariants are preserved over time. Using each of the schemes, one solution path is calculated on the interval [0, 50], using step size $h = 2^{-5}$. The following two sets of parameters are chosen: $\omega =\sigma =10$ and $\omega =100$ and $\sigma =0.3$. The values of ${\mathcal {I}}(Y_n)$ are shown in Fig. 11. Again, for visibility, only every 40th step is plotted.

Fig. 11

The non-linear Kubo oscillator: Evaluation of the invariant ${\mathcal {I}}(Y_n)$

In both cases, the mid-point based schemes preserve the invariant, while there is a significant drift-off for the two trapezoidal based schemes. The case $\omega =\sigma =10$ is the example depicted in Fig. 1, although there, the integration interval is only [0, 1]. In Fig. 11, where the integration is done over longer time, the drift-off leaves the TDSL scheme basically useless. The midpoint based methods preserve the invariant. In the low noise case, the drift-off is almost the same for the two trapezoidal schemes, and again, there is none or little drift-off in the midpoint schemes.

4.3 Stochastic Fermi–Pasta–Ulam–Tsingou problem

Finally, we would like to test the SL schemes by applying them to a more complex highly oscillatory problem. To this aim, a stochastic modification of the famous deterministic Fermi–Pasta–Ulam–Tsingou (FPUT) problem as described in Hairer et al. [11, Chapter I.5] is considered. The deterministic problem is defined by the Hamiltonian

$$\begin{aligned} \begin{aligned} {\mathcal {I}}_0(x,y)&= \sum _{m=1}^{M} J_m + \frac{1}{4} \left( (x_{0,1}-x_{1,1})^4 + (x_{0,M}+x_{1,M})^4 \right) \\ {}&\quad + \frac{1}{4}\sum _{m=1}^{M-1} \left( x_{0,m+1}-x_{1,m+1}-x_{0,m}-x_{1,m}\right) ^4, \end{aligned}\end{aligned}$$

(4.6)

where

$$\begin{aligned} J_m=\frac{1}{2} \left( y_{0,m}^2 + y_{1,m}^2\right) + \frac{\omega ^2}{2} x_{1,m}^2. \end{aligned}$$

In our example, stochastic noise of strength $\sigma _mJ_m$ is added to each of the springs. The resulting system is a 4M dimensional SDE:

$$\begin{aligned} \begin{aligned} dx_{0,m}&= y_{0,m}\mathrm {d}t+ \sigma _m y_{0,m}\circ \mathrm {d}W_m, \\ dx_{1,m}&= y_{1,m} \mathrm {d}t+ \sigma _m y_{1,m}\circ \mathrm {d}W_m, \\ dy_{0,m}&= (- g_m + g_{m+1})\mathrm {d}t, \\ dy_{1,m}&= (-\omega ^2 x_{1,m} + g_{m} + g_{m+1})\mathrm {d}t-\sigma _m \omega ^2 x_{1,m} \circ \mathrm {d}W_m \end{aligned}\end{aligned}$$

for $m=1,\ldots ,M$, where

$$\begin{aligned} g_1&= (x_{0,1}-x_{1,1})^3,\\ g_m&= (x_{0,m}-x_{1,m}-x_{0,m-1}-x_{1,m-1})^3, \qquad m=2,\ldots ,M, \\ g_{M+1}&= -(x_{0,M}+x_{1,M})^3. \end{aligned}$$

Let $X={\big (}(x_{0,m})_{m=1}^M,(x_{1,m})_{m=0}^M,(y_{0,m})_{m=1}^M,(y_{1,m})_{m=0}^M{\big )}^\top$. The complete system can be written as a semi-linear SDE

$$\begin{aligned} \begin{aligned} \mathrm {d}X= (A_0X+g_0(X))\mathrm {d}t+ \sum _{m=1}^M A_m X \circ \mathrm {d}W_m, \end{aligned}\end{aligned}$$

(4.7)

where $A_m$ are $4M\times 4M$ block matrices given by

$$\begin{aligned} \begin{aligned} A_m = \begin{pmatrix} 0 &{}{} 0 &{}{} D_m &{}{} 0 \\ 0 &{}{} 0 &{}{} 0 &{}{} D_m \\ 0 &{}{} 0 &{}{} 0 &{}{} 0 \\ 0 &{}{} -\omega ^2D_m &{}{} 0 &{}{} 0 \end{pmatrix}, \end{aligned} \end{aligned}$$

(4.8)

where $D_m = \sigma _m \text {diag}\{0,\dotsc ,1,\dotsc ,0\}$, with the nonzero element in position m, for $m=1,\ldots ,M$, and $D_0=I_M$, the identity matrix of dimension $M\times M$. The matrices $A_m$ satisfy Assumption 1, so the SL schemes are applicable. For the same reason, the expected strong order is 1 for all methods considered. Assumptions 2 and 3 are not satisfied, so there is no quadratic invariant to preserve.

For the simulations we have used $M=3$, $\omega =50$, $\sigma _m$ $=\sigma$ for all m, with $\sigma \in \{0.02, 0.2\}$, and initial values

$$\begin{aligned} x_{0,1}(0)=y_{0,1}(0)=1, \quad x_{1,1}(0)=\omega ^{-1}, \quad y_{1,1}(0)=1. \end{aligned}$$

The remaining initial values are all zero. Once again, we measure the strong error based on 1000 simulations. The SDE is solved over the interval [0, 1], and the reference solutions are computed by the MFSL scheme with $h_{\text {ref}}=2^{-17}$. The results are presented in Fig. 12. The $95\%$-confidence intervals have been calculated and in all cases they span less than $14\%$ of the shown mean values.

Fig. 12

Convergence of the TDSL, TFSL, MDSL, MFSL and implicit midpoint rule for the stochastic Fermi–Pasta–Ulam–Tsingou problem

Fig. 13

Wall-clock time per batch of 25 paths versus accuracy of the TDSL, TFSL, MDSL, MFSL and implicit midpoint rule for the stochastic Fermi–Pasta–Ulam–Tsingou problem

Fig. 14

Weak convergence of $I_1$, $I_2$, $I_3$ and ${{\tilde{I}}}=I_1+I_2+I_3$ for the TDSL, TFSL, MDSL, MFSL and implicit midpoint rule for the stochastic Fermi–Pasta–Ulam–Tsingou problem

Fig. 15

Wall-clock time per batch of 1250 paths versus weak error of ${{\tilde{I}}}=I_1+I_2+I_3$ for the TDSL, TFSL, MDSL, MFSL and implicit midpoint rule for the stochastic Fermi–Pasta–Ulam–Tsingou problem

In all cases the Lawson schemes perform significantly better than the implicit midpoint rule. For small values of $\sigma$ the two FSL schemes are only slightly better than the two DSL schemes. For larger values of $\sigma$, the FSL schemes outperform the DSL schemes. This is in line with what was observed for the Kubo oscillator in Fig. 8. But even in the small noise case, the feasible step sizes of the Lawson schemes are larger than the feasible step sizes for the implicit midpoint rule - the convergence deteriorates for the implicit midpoint rule approximately when $h=2^{-6}$, whereas the convergence of the Lawson schemes only deteriorates around $h=2^{-3}$, the SL schemes thus allowing to use much larger step sizes than the implicit midpoint rule. For larger values of $\sigma$, the midpoint rule is in practice useless for the step sizes applied here.

The work-precision diagram Fig. 13 again demonstrates that even for this slightly larger problem the higher accuracy of the SL schemes, in particular the FSL schemes, compensates for the disadvantage of the additional computational work required for the calculation of the matrix exponentials. In the current example, the TFSL method is slightly the most efficient.

Finally, we consider the weak convergence of the methods when applied to calculate the total oscillatory energy ${{\tilde{I}}}=\sum _{j=1}^{M}I_j$, where the oscillatory energy of the j-th string is given by $I_j=\frac{1}{2}(y_{1,j}^2+\omega ^2x_{1,j}^2)$ for the FPUT problem, and the result is presented in Fig. 14. In the small noise case, when $\sigma =0.02$, the error is clearly dominated by the diffusion term, and the order of the method is close to the deterministic order two. Still, the FSL schemes are significantly more accurate than the midpoint rule, although the difference between those again is minuscule. When the noise level increases to $\sigma =0.2$, the midpoint and the DSL schemes perform almost the same, while the errors of the FSL schemes are significantly smaller. We also observe the order two behaviour of the trapezoidal FSL scheme, although, as already mentioned, no quadratic invariants are conserved in this case. However, in the case where $g_m=0$ for $m=1,\dotsc ,M$, the transformed system (2.5) is in fact an SDE with additive noise, for which the weak order of the trapezoidal rule is two, see e. g. Milstein and Tretyakov [19]. In Fig. 15 we observe how this makes the trapezoidal FSL scheme the most efficient what concerns the weak error.

5 Conclusion

In this paper, we proved that stochastic Lawson schemes under suitable conditions preserve linear and quadratic invariants. We proved that the trapezoidal stochastic Lawson scheme nearly preserves quadratic invariants if the diffusion terms are linear and fully included in the exponential. These results have been verified by numerical experiments.

For stochastic differential equations with highly oscillatory drift and diffusion we numerically demonstrated that full stochastic Lawson schemes allow for larger step-sizes than standard schemes, in the sense of being able to resolve high frequency oscillations. All methods are implicit, and in our implementations, the cpu-time used for solving the nonlinear systems was dominant compared to the time used to evaluate the matrix exponentials, and in terms of accuracy versus computational work, the more accurate methods were the most efficient. This, of course, depends heavily on the problem at hand, for larger problems with more demanding matrix exponential evaluations, the drift Lawson methods might turn out to be preferable.