Skip to main content
SpringerLink
Log in

A generalization of Filon–Clenshaw–Curtis quadrature for highly oscillatory integrals

  • Published:
BIT Numerical Mathematics Aims and scope Submit manuscript

Abstract

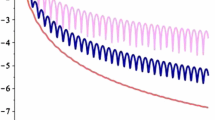
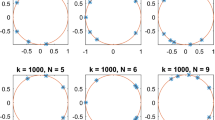
The Filon–Clenshaw–Curtis method (FCC) for the computation of highly oscillatory integrals is known to attain surprisingly high precision. Yet, for large values of frequency \(\omega \) it is not competitive with other versions of the Filon method, which use high derivatives at critical points and exhibit high asymptotic order. In this paper we propose to extend FCC to a new method, FCC\(+\), which can attain an arbitrarily high asymptotic order while preserving the advantages of FCC. Numerical experiments are provided to illustrate that FCC\(+\) shares the advantages of both familiar Filon methods and FCC, while avoiding their disadvantages.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Asheim, A., Huybrechs, D.: Complex Gaussian quadrature for oscillatory integral transforms. IMA J. Numer. Anal. 33(4), 1322–1341 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  2. Deaño, A., Huybrechs, D., Iserles, A.: The kissing polynomials and their Hankel derminants. Tech. rep., DAMTP, University of Cambridge (2015)

  3. Domínguez, V.: Filon–Clenshaw–Curtis rules for a class of highly-oscillatory integrals with logarithmic singularities. J. Comput. Appl. Math. 261, 299–319 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  4. Domínguez, V., Graham, I.G., Kim, T.: Filon–Clenshaw–Curtis rules for highly oscillatory integrals with algebraic singularities and stationary points. SIAM J. Numer. Anal. 51(3), 1542–1566 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  5. Domínguez, V., Graham, I.G., Smyshlyaev, V.P.: Stability and error estimates for Filon–Clenshaw–Curtis rules for highly oscillatory integrals. IMA J. Numer. Anal. 31(4), 1253–1280 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  6. Gao, J., Iserles, A.: Error analysis of the extended Filon-type method for highly oscillatory integrals. To appear in Research in the Mathematical Sciences (2017)

  7. Gradshteyn, I.S., Ryzhik, I.M.: Table of Integrals, Series, and Products, 7th edn. Elsevier, Amsterdam. Translated from the Russian, Translation edited and with a preface by Alan Jeffrey and Daniel Zwillinger, With one CD-ROM. Windows, Macintosh and UNIX (2007)

  8. Huybrechs, D., Vandewalle, S.: On the evaluation of highly oscillatory integrals by analytic continuation. SIAM J. Numer. Anal. 44(3), 1026–1048 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  9. Iserles, A.: On the numerical quadrature of highly-oscillating integrals. I. Fourier transforms. IMA J. Numer. Anal. 24(3), 365–391 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  10. Iserles, A., Nørsett, S.P.: On quadrature methods for highly oscillatory integrals and their implementation. BIT 44(4), 755–772 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  11. Iserles, A., Nørsett, S.P.: Efficient quadrature of highly oscillatory integrals using derivatives. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 461(2057), 1383–1399 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  12. Levin, D.: Fast integration of rapidly oscillatory functions. J. Comput. Appl. Math. 67(1), 95–101 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  13. Olver, S.: Moment-free numerical integration of highly oscillatory functions. IMA J. Numer. Anal. 26(2), 213–227 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  14. Piessens, R.: Computing integral transforms and solving integral equations using Chebyshev polynomial approximations. J. Comput. Appl. Math. 121(1-2), 113–124 (2000). Numerical analysis in the 20th century, Vol. I, Approximation theory

  15. Piessens, R., de Doncker-Kapenga, E., Überhuber, C.W., Kahaner, D.K.: QUADPACK, Springer Series in Computational Mathematics, vol. 1. Springer, Berlin (1983). A subroutine package for automatic integration

  16. Piessens, R., Poleunis, F.: A numerical method for the integration of oscillatory functions. BIT 11(3), 317–327 (1971)

  17. Sloan, I.H., Smith, W.E.: Product integration with the Clenshaw–Curtis points: implementation and error estimates. Numer. Math. 34(4), 387–401 (1980)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an, China

    Jing Gao

  2. DAMTP, Centre for Mathematical Sciences, University of Cambridge, Cambridge, UK

    Arieh Iserles

Authors
  1. Jing Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Arieh Iserles
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jing Gao.

Additional information

Communicated by Tom Lyche.

The work is supported by the Projects of International Cooperation and Exchanges NSFC-RS (Grant No. 11511130052), the Key Science and Technology Program of Shaanxi Province of China (Grant No. 2016GY-080) and the Fundamental Research Funds for the Central Universities.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gao, J., Iserles, A. A generalization of Filon–Clenshaw–Curtis quadrature for highly oscillatory integrals. Bit Numer Math 57, 943–961 (2017). https://doi.org/10.1007/s10543-017-0682-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10543-017-0682-9

Keywords

Mathematics Subject Classification

Search

Navigation