Gradualism, natural selection, and the randomness of mutation–fisher, Kimura, and Orr, connecting the dots

Abstract

Evolutionary gradualism, the randomness of mutations, and the hypothesis that natural selection exerts a pervasive and substantial influence on evolutionary outcomes are pair-wise logically independent. Can the claims about selection and mutation be used to formulate an argument for gradualism? In his Genetical Theory of Natural Selection, R.A. Fisher made an important start at this project in his famous “geometric argument” by showing that a random mutation that has a smaller effect on two or more phenotypes will have a higher average fitness than a random mutation that has a larger phenotypic effect. Motoo Kimura’s demonstration that a gene’s probability of fixation depends on both the selection coefficient and the effective population size shows that Fisher’s argument for gradualism was mistaken. Here we analyze Fisher’s argument and explain how Kimura’s theory leads to a conclusion that Fisher did not anticipate. We identify a fallacy that reasoning about fitness differences and their evolutionary consequences should avoid. We then distinguish forward-directed from backward-directed versions of gradualism. The backward-directed thesis about a single mutation may be correct, but the forward-directed thesis is not. After that we consider a sequence of random mutations that all affect the same cluster of phenotypes and Allen Orr’s idea that there is an optimal sequence of mutation sizes, moving from larger to smaller as the population approaches a fixed optimum. This provides a likelihood justification for a forward-directed version of gradualism when there is a fixed optimum, but it also provides an argument against forward-directed gradualism if the optimum shifts substantially as the population evolves. Finally, we consider whether genome-wide association studies (GWASs) can furnish empirical evidence that bears on the truth of gradualism. The version of gradualism that GWASs directly bear on concerns the phenotypic effect size of a gene after it arises by mutation and has reached an appreciable frequency, not the phenotypic size of the mutation event itself.

Appendices

Appendix 1: the probability that a random mutation will improve fitness

In Fig. 1, let r be the radius of a circle centered on X and d be the radius of the circle centered on the optimum.⁵ We use the law of cosines to find w, the distance from the phenotype resulting from $\theta$ to the optimum:

$${w}^{2}={r}^{2}{+d}^{2}-2rd\mathrm{cos}\theta$$

As we want to know the probability that this mutation is advantageous ($w<d$) and given that all values are positive distances,

$${d}^{2}>{r}^{2}+{d}^{2}-2rd \mathrm{cos\theta }$$

Rearranging and cancelling terms we find,

$$\mathrm{cos}\theta >\frac{r}{2d}$$

Taking the arccosine to find the angles,

$$\mathrm{arccos}\left(\frac{r}{2d}\right)>\theta >-\mathrm{arccos}\left(\frac{r}{2d}\right)$$

As both the positive and negative angles are equal, the total angle will be $2\mathrm{arccos}\left(\frac{r}{2d}\right)$. Dividing by the full circle, $2\pi ,$ we get the proportion of the full circle which improves fitness,

$$\begin{array}{*{20}c} {\frac{{\arccos \left( \frac{r}{2d} \right)}}{\pi }} \\ \end{array}$$

(1)

Note that when $r>2d$, there will be no solutions to this formula. In this case the circle centered on X will fully encompass the circle centered at the optimum, and thus all mutations will decrease fitness.

Appendix 2: the expected degree of improvement, given that the mutation improves fitness

We begin again with the law of cosines, where the mutation is of size r, but this time we solve for w, the fitness distance resulting from a mutation $\theta$.

$$w=\sqrt{{r}^{2}+{d}^{2}-2rd\mathrm{cos}\theta }$$

The improvement (decrease in fitness distance), $\Delta w$, from mutation $\theta$ will be equal to $d-w$. Thus,

$$\Delta w=d-\sqrt{{r}^{2}+{d}^{2}-2rd\mathrm{cos}\theta }$$

To find the expected improvement given that the mutation improves fitness we integrate over the $\theta$ resulting in advantage and average over all $\theta$ resulting in advantage. For the full circle we would integrate from/to $\pm \mathrm{arccos}\left(\frac{r}{2d}\right),$ but as both the positive and negative portions are equal and we are only concerned with proportion, we simply integrate from 0 to the positive angle and divide by $\mathrm{arccos}\left(\frac{r}{2d}\right)$ rather than $2\mathrm{arccos}\left(\frac{r}{2d}\right)$.

$$\begin{array}{*{20}c} {E\Delta w|{\text{adv}} = \frac{{\int\nolimits_{0}^{{\arccos \left( \frac{r}{2d} \right)}} {} d - \sqrt {r^{2} + d^{2} - 2rd\cos \theta } d\theta }}{{\arccos \left( \frac{r}{2d} \right)}}} \\ \end{array}$$

(2)

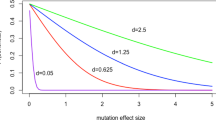
Figure 6 shows the ratio of the expected improvement in fitness for a big mutation of size (0.1)f and the expected improvement in fitness of a small mutation of size 0.1, where f > 1. As can be seen, the ratio is not always greater than 1. The ratio begins to drop off when the big mutation is larger than d and begins to “overshoot” the optimum. Eventually, this overshooting becomes so deleterious that small is more advantageous than big.

Appendix 3: a random mutation’s expected improvement in fitness

To find the expected fitness from a random mutation, we take the average of all possible mutations of size r. This is done by first integrating over all possible $\theta$ (0 to $2\pi$) and then dividing by the full circle ($2\pi$):

$$\begin{array}{*{20}c} {E\Delta w = \frac{{\int\limits_{0}^{2\pi } {d - \sqrt {r^{2} + d^{2} - 2rd\cos \theta } d\theta } }}{2\pi }} \\ \end{array}$$

(3)

This is shown in Fig. 

Fig. 6

Ratio of expected changes in fitness given large advantageous mutation of size (0.1)f and small advantageous mutation of size 0.1

3.

Appendix 4: the full formula for (area of spherical cap)/(area of sphere) for an n-dimensional sphere

We begin with the formula for a spherical cap and sphere (Li 2011). n is the number of dimensions, r is the radius, and I the regularized incomplete beta function.

$${A}_{n}^{cap}\left(r\right)=\frac{1}{2}{A}_{n}\left(r\right)\text{ I}\left[{\mathrm{sin}}^{2}\Phi ;\frac{n-1}{2},\frac{1}{2}\right]$$

We divide the formula for the area of the spherical cap by the area of the full n-sphere to find the proportion of the sphere covered by the cap:

$$\frac{{A}_{n}^{cap}\left(r\right)}{{A}_{n}\left(r\right)}=\frac{\frac{1}{2}{A}_{n}\left(r\right) I\left[{\mathrm{sin}}^{2}\Phi ;\frac{n-1}{2},\frac{1}{2}\right]}{{A}_{n}\left(r\right)}$$

The areas of the sphere, ${A}_{n}\left(r\right)$ cancel, leaving us with:

$$\frac{{A}_{n}^{cap}\left(r\right)}{{A}_{n}\left(r\right)}=\frac{1}{2} I\left[{\mathrm{sin}}^{2}\Phi ;\frac{n-1}{2},\frac{1}{2}\right]$$

Using trigonometric identities and the results from Appendix 1, we find, ${\mathrm{sin}}^{2}\Phi$:

$$\begin{aligned} \sin^{2} {\uptheta } = & 1 - \cos^{2} {\uptheta } \\ = & 1 - \cos^{2} \left( {\arccos \left( \frac{r}{2d} \right)} \right) \\ = & 1 - \frac{{r^{2} }}{{4d^{2} }} \\ \end{aligned}$$

(4)

Thus our final result for the probability of an advantageous mutation in n-dimensions is:

$$\begin{array}{*{20}c} {\frac{{A_{n}^{cap} \left( r \right)}}{{A_{n} \left( r \right)}} = \frac{1}{2}I\left[ {1 - \frac{{r^{2} }}{{4d^{2} }};\frac{n - 1}{2},\frac{1}{2}} \right]} \\ \end{array}$$

(5)

As in Appendix 1, this formula will not be valid for $r>2d$. At $r>2d$ all $\uptheta$ will take the organism further from the optimum (and thus be disadvantageous). Hartl and Taubes (1996) arrive at the same result, but express it as a fraction of integrals:

$$\frac{{\int }_{0}^{r/2d}{\mathrm{sin}}^{n-1}\uptheta d\uptheta }{{\int }_{0}^{\uppi }{\mathrm{sin}}^{n-1}\uptheta d\uptheta }$$

Appendix 5: Probability of fixation for a mutation of size r

The selection coefficient, s, for a mutation B is given by:

$$\mathrm{s}={\mathrm{W}}_{\mathrm{B}}-{\mathrm{W}}_{\mathrm{A}}$$

where W_A is the fitness of the wild type and W_B the fitness of the mutant. From Appendix 2, let the fitness distance to optimum of the wild type be 1, and $\mathrm{w}$ be the distance to optimum for the mutant. Halving the distance to optimum doubles the fitness, reducing distance by 2/3 triples it, and so on, thus:

$$\frac{{\mathrm{W}}_{\mathrm{B}}}{{\mathrm{W}}_{\mathrm{A}}}=\frac{1}{\mathrm{w}}$$

Choosing the wild type as our reference, we let ${\mathrm{W}}_{\mathrm{A}}=1$, thus:

$${\mathrm{W}}_{\mathrm{B}}=\frac{1}{\mathrm{w}}$$

Substituting these values into the definition of s:

$$\mathrm{s}=\frac{1}{\mathrm{w}}-1$$

Substituting for w by the formula from Appendix 2:

$$\mathrm{s}=\frac{1}{\sqrt{{\mathrm{r}}^{2}+1-2\mathrm{rcos\theta }}}-1$$

The probability of fixation for a randomly mating diploid population of size ${N}_{e}$ is given by Kimura (1962):

$$\mathrm{u}=\frac{1-{\mathrm{e}}^{-2\mathrm{s}}}{1-{\mathrm{e}}^{-4{\mathrm{N}}_{\mathrm{e}}\mathrm{s}}}$$

Substituting the above value for s into Kimura’s formula and using the ‘exp’ notation for clarity [$\mathrm{exp}\left(\mathrm{x}\right)={\mathrm{e}}^{\mathrm{x}}$],

$$\mathrm{u}=\frac{1-\mathrm{exp}\left(-2\left(\frac{1}{\sqrt{{\mathrm{r}}^{2}+1-2\mathrm{rcos\theta }}}-1\right)\right)}{1-\mathrm{exp}\left(-4{\mathrm{N}}_{\mathrm{e}}\left(\frac{1}{\sqrt{{\mathrm{r}}^{2}+1-2\mathrm{rcos\theta }}}-1\right)\right)}$$

To find the expected probability of fixation for a random mutation of size r, we integrate the probability densities from the above formula over all mutations $\uptheta$ and divide by all possible mutations (effectively summing the probability densities for all possible mutations and dividing by the number of possible mutations to find an average probability):

$$\mathrm{Eu}=\frac{{\int }_{0}^{\uppi }\frac{1-\mathrm{exp}\left(-2\left(\frac{1}{\sqrt{{\mathrm{r}}^{2}+1-2\mathrm{rcos\theta }}}-1\right)\right)}{1-\mathrm{exp}\left(-4{\mathrm{N}}_{\mathrm{e}}\left(\frac{1}{\sqrt{{\mathrm{r}}^{2}+1-2\mathrm{rcos\theta }}}-1\right)\right)}\hspace{0.17em}\mathrm{d\theta }}{\uppi }$$

Letting ${\mathrm{N}}_{\mathrm{e}}=10$, we plot this curve in Fig. 

Fig. 7

Expected probability of fixation given size of mutation

7. This plot is valid for all $\mathrm{r}\ge 0$. The greatest probability of fixation for occurs when $r=0.7274$. Thus a mutation smaller than or larger than $r=0.7274$ will have a lower average probability of fixation. This value is remarkably stable, going to 0.7304 as ${\mathrm{N}}_{\mathrm{e}}\to \infty$. Thus smaller mutations do not have a higher average probability of fixation than bigger mutations.