The arithmetic mean of what? A Cautionary Tale about the Use of the Geometric Mean as a Measure of Fitness

Abstract

Showing that the arithmetic mean number of offspring for a trait type often fails to be a predictive measure of fitness was a welcome correction to the philosophical literature on fitness. While the higher mathematical moments (variance, skew, kurtosis, etc.) of a probability-weighted offspring distribution can influence fitness measurement in distinct ways, the geometric mean number of offspring is commonly singled out as the most appropriate measure. For it is well-suited to a compounding (multiplicative) process and is sensitive to variance in offspring number. The geometric mean thus proves to be a predictively efficacious measure of fitness in examples featuring discrete generations and within- or between-generation variance in offspring output. Unfortunately, this advance has subsequently led some to conclude that the arithmetic mean is never (or at best infrequently) a good measure of fitness and that the geometric mean should accordingly be the default measure of fitness. We show not only that the arithmetic mean is a perfectly reasonable measure of fitness so long as one is clear about what it refers to (in particular, when it refers to growth rate), but also that it functions as a more general measure when properly interpreted. It must suffice as a measure of fitness in any case where the geometric mean has been effectively deployed as a measure. We conclude with a discussion about why the mathematical equivalence we highlight cannot be dismissed as merely of mathematical interest.

Introduction

It is notoriously difficult to make the concept of fitness in evolutionary population biology precise. Among the advances that have been made toward clarifying it is the realization that some simple summary statistics, such as the arithmetic mean of a probability distribution over reproductive output, do not always accurately capture the concept of fitness. Beatty and Finsen (1989), Brandon (1990), and Sober (2001), among others, have shown why it is often preferable to use more informative measures of fitness. The geometric mean has been singled out as particularly important in this regard since it is attentive to the variance or “spread” of data and has a realistic biological interpretation with known implications for evolutionary dynamics. This correction was as welcome as it was overdue. It emphasizes the importance of being precise about what exactly it is that such measures should lead us to expect. The fact that “expected reproductive output” and “expected reproductive success” can be decoupled was a key revelation because it sanctioned the possibility that an individual could have high (multigenerational) reproductive success despite a low expected reproductive output. However, a peculiar tendency has subsequently emerged within philosophy of biology. It is not at all uncommon to read or hear that one should always defer to the geometric mean as the default summary measure of fitness. The purpose of this paper is to show that the arithmetic mean can be a perfectly reasonable measure of fitness so long as one is clear about what it refers to. In fact, it must suffice as a measure of fitness in any case where the geometric mean has been effectively deployed as a measure. It is not our aim, however, to introduce a new or alternative measure of fitness into the existing literature. Rather, we wish to clarify a ubiquitous but potentially confusing feature of any sophisticated fitness measure and elaborate on why the mathematical equivalence we highlight cannot be dismissed as merely of mathematical interest. The points argued for in this paper may consequently be of interest to propensity theorists who would like to better understand the mathematical underpinnings of token fitness (i.e., fitness as a measurable property of individual organisms), in addition to those who believe that fitness ascriptions are best reserved for trait types. For present purposes, we remain neutral on this issue.

Background: limits of the arithmetic mean

Philosophers have hailed the propensity interpretation of fitness (hereafter ‘PIF’) as a major achievement (Brandon 1978; Mills and Beatty 1979). It was developed as a response to the common practice of defining and measuring fitness as the realized or actual reproductive output of an individual (Mills and Beatty 1979; Millstein 2016).¹ Doing so creates insurmountable difficulties for evolutionary theorizing. As noted by several early critics, perhaps most provocatively by Popper (1974), if evolution via natural selection is depicted as “the survival of the fittest” (a la Herbert Spencer) and the “fittest” are defined as “those that actually survive and reproduce,” the concept of fitness becomes tautologous. It is accordingly rendered empirically unfalsifiable and explanatorily impotent. The fittest individuals in a population just happen to be those that survive and produce the most offspring, irrespective of the reasons for their having done so. As such, reproductive output would no longer be reliable evidence upon which to infer the character states that are better able to meet ecological challenges to survival. This is clearly an unwelcome consequence, one that was foreshadowed by Michael Scriven’s (1959) example involving identical twins (i.e., physical duplicates in the philosophical sense) who exhibit differential viability (e.g., one survives while the other dies by way of lightning strike). There is no selectively relevant difference, as in heritable character state variation(s), that can account for the twins’ distinct evolutionary fates. Therefore, there must be more to fitness than actual survival and reproductive output.

Those who introduced the PIF (Brandon 1978; Mills and Beatty 1979) recognized that fitness must be empirically sensitive to actual lifetime reproductive output without being exhaustively defined by it. Crucial for the PIF’s success was its distinguishing two desiderata that any definitional analysis (or explication) of fitness must address. On the one hand, a definition of fitness should justify use of the concept as a causal parameter in explanations for why some character states or trait variants (and the organisms that exemplify them) are more prevalent than competing character states or trait variants in a population. On the other hand, an adequate definition of fitness should inform or (at least) be consistent with measures of fitness that accurately predict the direction and magnitude of relative frequency changes or mean phenotype values due to natural selection.

Mills and Beatty’s (1979) and Brandon’s (1978) proposals shared two key components designed to meet these desiderata. The metaphysical or ontological component addressed the former desideratum by depicting fitness as a probabilistic dispositional property or “propensity.” Fitness is thereby an intrinsic and objective feature of a token organism, albeit one that finds expression only in the organism’s relation to specified selective environments. The epistemological component addressed the second desideratum by acknowledging the mathematical function(s) used to estimate this propensity. It is estimated via a probability-weighted average over reproductive outcomes for an individual after a specified period. The major shift in thinking about fitness that was ushered in with the PIF involved reidentifying the individual organisms constituting a population as members of sets. The sets that are most relevant to explanation in evolutionary population biology are composed of individuals who exhibit the same character state or trait variant (e.g., blue feather coloration as opposed to red; diploid genotype AA rather than Aa or aa). This shift to type identification based on variation in what is otherwise a uniform selective environment (i.e., background conditions equally or randomly experienced by all) is what makes it possible for individuals of the same type to (probabilistically) realize different reproductive outcomes. Two or more organisms of the same type can do so while still maintaining the same dispositional tendency. This possibility severs the problematic definitional link between an individual’s actualized reproductive contribution and its fitness.²

However, the PIF faces a number of problems. In addition to those who have directly questioned the characterization of fitness as a propensity (Abrams 2007; Ariew and Ernst 2009; Walsh 2007, 2010; Bourrat 2017), the metaphysical status of propensities in general has come under heavy scrutiny (Hájek 2019; Rosenthal 2010; Strevens 2011). Despite its importance, we shall ignore this strand of criticism. Our focus is restricted to the epistemic advances inherited by philosophers of biology from the work of Beatty and Finsen (1989), Brandon (1990), and Sober (2001). Drawing on insights from theoretical biology (Gillespie 1977; Levins 1968; Lewontin and Cohen 1969; Thoday 1953), these critics have, in various ways, questioned the very possibility of measuring fitness accurately via the assignment of a single, unchanging numerical value. Early formulations of PIF (Mills and Beatty 1979; Brandon 1978) generally took it for granted that the fitness of an individual could be determined statistically by deriving the offspring contribution from a probability-weighted distribution over reproductive output for the individual. Unfortunately, as noted by Beatty and Finsen (1989), Brandon (1990), and Sober (2001), summarizing the probability distribution with the arithmetic mean offspring contribution (or the “expectation”) often leads to erroneous prediction. The arithmetic mean can be an insufficient measure of fitness because it ignores occasionally crucial information about the probability distribution over reproductive output. Notably, it does not account for the higher mathematical moments of statistical distributions (e.g., variance, skew, kurtosis). Such simplification or oversight cannot be justified on the grounds of parsimony, or in the sense of these moments being nothing more than intriguing mathematical artifacts. The higher moments of a distribution often have realistic interpretations corresponding to causally relevant features of the organism–environment systems that affect the predictive efficacy of fitness measures. Variance, for instance, can represent the effects of demographic stochasticity or environmental stochasticity.³ The former is due to within- and between-generation differences in number or timing of offspring. The latter occurs with fluctuations in the biotic and abiotic components of the selective environment. Both are known to influence ecological and evolutionary dynamics (Lande et al. 2003; Lenormand et al. 2009; Takacs and Bourrat 2021).

Properly computing the mean number of offspring: a few examples

A vignette adapted from Wagenaar and Timmers (1979, p. 241) demonstrating the common misperception of exponential growth can convey the practical importance of using the geometric mean. Envision a boy who would one day take his father’s place as the mandarin whose assignment it was to oversee the imperial water garden. When this boy was still quite young, his father declared that a newly constructed pond within the garden was to contain duckweed. As a gesture of unyielding paternal love, he permitted his son to plant the first duckweeds in the pond. There was, however, a caveat. Emperor’s fiat had it that the most aesthetically appealing situation was one in which duckweed occupied no more than half the pond’s total surface area. Any more than this and the mandarin in charge would forever “sleep with the duckweed.” When the boy, now a mandarin, turned 70 years of age, he proudly observed that the pond was 1/8 covered with duckweed. Never once did he worry about the growth of the duckweed exceeding the emperor’s strict limit. After all, he had a lifetime’s worth of observations that seemed to suggest it would not happen anytime soon. His once routine checks on the pond thus became increasingly infrequent and eventually ceased altogether. However, unbeknownst to this boy-become-mandarin was the fact that the duckweed doubled every five years. So, to the great consternation of the complacent mandarin, and the equally great satisfaction of the neglected duckweeds, the pond would be more than half covered come the time of his eighty-first birthday. A commonsense notion of “expectation,” as in what one might expect to happen after unreflectively applying the arithmetic mean (to duckweed growth), can set a dangerous precedent.

An example of intergenerational reproductive variance among competing character states inspired by Beatty and Finsen (1989) illustrates the necessity of heeding the geometric mean in a more mathematically rigorous way. Suppose we have two selectively relevant character states (or trait variants), A and B, in a population. By stipulation, these are mutually exclusive and exhaustive. The species exhibiting this character is asexual, and individuals must breed true to form (i.e., progenitors give rise only to descendants of the same type). Let us also make the simplifying assumption that there are discrete (non-overlapping) generations. Type-A individuals can contribute either five or six offspring with equal probability, while type-B individuals can contribute either two or ten offspring with equal probability. However, all individuals of a type within a generation must give rise to the same number of offspring (i.e., there is no intragenerational variance). Census data gathered over eleven generations reveal the following (Table 1):

Table 1 Population Growth and Census Data for Two Competing Variants (See text for details.)

This simple case demonstrates how variance in offspring contribution among competing trait types can make a difference to their evolutionary trajectories or “fates.” In the first generation, the character states were equally prevalent in the population. Both had a frequency of 0.5. By the eleventh generation, character state A rose to a frequency of 0.88, while character state B plummeted to a frequency of 0.12. This appears (ceteris paribus) to be a classic case of directional selection favouring individuals who bear trait variant A, with variant B well on its way to extinction. Yet, this is inconsistent with what one would have predicted if the “expectation” or arithmetic mean number of offspring for each trait type was taken as a proxy for fitness. The values for arithmetic mean number of offspring suggest that B-type individuals have higher fitness (6.0) than their A-type counterparts (5.5). In this case, it is consequently wrong to use the arithmetic mean number of offspring as a predictive measure of fitness. The geometric mean provides us with a much better prediction, one that holds despite common-sense expectations to the contrary.

Unlike the arithmetic mean number of offspring, the geometric mean gives us a better result because it is sensitive to (“discounts for”) intergenerational variation in offspring output. The geometric mean is a measure of central tendency defined as the n-th root of the product of n numbers. For numbers x₁, x₂, …, x_n, it is defined as follows:

$${\left(\prod_{i=1}^{n}{x}_{i}\right)}^\frac{1}{n}=\sqrt[n]{\left({x}_{1}{x}_{2}\dots {x}_{n}\right)}$$

It can account for the fact that the reproductive contribution of B-type individuals varies dramatically around the arithmetic mean between generations. The derivation of the geometric mean number of offspring is particularly sensitive to those instances or generations where B-type individuals contribute just two offspring each. The long-term relative fitness cost incurred during such “bad years” (generations 1, 3, 5, 7, and 9 in Table 1) is not offset by the large gains that accrue during the “good years” (generations 0, 2, 4, 6, and 8 in Table 1). This is because the biological process of reproduction, as it pertains to the relative fitness of competing trait variants, is multiplicative. The growth of a lineage is a “compounding process” in the sense that the overall reproductive contribution of a type to the number of individuals who bear that type in a subsequent generation depends on the number of individuals with the type in the current generation. The reproductive contribution that B-type individuals could make toward increasing the relative frequency of their type in what is an otherwise “good (high fecundity) year” is diminished by its application to the outcome of a preceding “bad (low fecundity) year.” This is evident if one compares the difference between what the number of B-type individuals would have been if the population had grown according to the arithmetic mean (without variance) and the actual number of B-type individuals in Table 1 (third vs. first columns under variant B). This penalty becomes more pronounced with the passage of time. In Sisyphean fashion, the selective relief experienced by the B-type during the “good years” becomes increasingly shorter-lived as the hill to climb grows into a mountain.

The geometric mean number of offspring tracks the fitness cost associated with variance in finite populations. Other things (e.g., arithmetic means) being equal, character states with lower variance have a higher probability of increasing in frequency. This holds even when variance in offspring contribution is depicted as a within-generation (intragenerational) occurrence (Sober 2001). Higher mathematical moments (e.g., skew, kurtosis) of probability distributions over offspring contribution for competing trait types, although typically of lesser significance than variance, can generate similarly intractable problems for evolutionary predictions based on a single, static measure of fitness (Beatty and Finsen 1989; Gillespie 1977). To adequately recover fitness as a measurable propensity would seem to require extracting all information from the probability distribution over possible reproductive output.

Why the arithmetic mean nevertheless remains a good measure of fitness

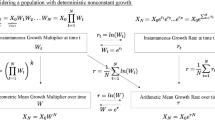
As discussed earlier, the case against using the arithmetic mean as a measure of fitness appears decisive. We now explain why the temptation to construe the situation as such should be resisted. The first step in justifying our reticence is to reiterate that evolutionary explanations are concerned typically with the growth of lineages generated by competing character state types. In other words, evolutionary population biology compares the growth rates of subpopulations distinguished by character state. Population growth is a compounding (multiplicative) process, a fact which figures prominently in the criticisms lodged by Beatty and Finsen (1989), Brandon (1990), and Sober (2001). Population abundance increases geometrically (if modelled in discrete time) or exponentially (if modelled in continuous time), rather than linearly (i.e., as if adding the same number of individuals in each generation). Although researchers in theoretical population biology rarely make this explicit, what many refer to when using expressions like “growth rate of the population” is the growth rate of the logarithm of population size. Conversion to a logarithmic scale is what enables them to recapture a linear approximation of (i.e., constant scaling factor for) population growth rate and, thereby, abundance in continuous time.

Returning to the example illustrated in Table 1 makes this distinction apparent. If the sole individual with character state type B in the first generation produces ten B-type offspring, each of whom produces two B-type offspring, this is equivalent to a situation where individuals produce $(10 \times 2)^{\frac{1}{2}} = \sqrt{20} =$4.47 offspring each generation, as opposed to $\frac{\left(10+2\right)}{2} = 6$ offspring each generation, as per the arithmetic mean.⁴ Note that the progenitor of this lineage will have 20 grand-offspring, just as if the population was multiplied by the geometric mean of $4.47$ each generation (e.g.,$\sqrt{20} \times \sqrt{20} = 20$) rather than the arithmetic mean of 6 (e.g., $6 \times 6 = 36$). As many have recognized, the proper way to average a geometric growth rate is accordingly to take the geometric mean of the multiplicative terms (i.e., the n-th root of n factors). However, the more general context for assessing population growth is logarithmic space. For to average over changes on a log scale is to average the proportional changes in population size across successive time steps rather than the absolute changes in population size.⁵ On a log scale, it is the arithmetic mean that provides the correct result. The logarithm of population size increases by $\frac{\mathrm{ln}\left(10\right)+\mathrm{ln}\left(2\right)}{2} = 1.50$ each generation (for a total increase of ln (20)).⁶ In contrast, use of the geometric mean on a log scale would lead one astray: $\sqrt{\mathrm{ln}(10)\times \mathrm{ln}(2)} = 1.26 \ne 1.50$. Thus, asserting that the geometric mean is “better than” or “superior to” the arithmetic mean can be just as problematic as adopting the arithmetic mean (of offspring output) when the quantity to be averaged (e.g., number of offspring vs. number of grand-offspring) is left unspecified. Neither Beatty and Finsen (1989) nor Brandon (1990) or Sober (2001) leave the quantity unspecified. The geometric mean is a statistical summary measure of number of offspring for them. It is a perfectly admissible measure of fitness in the types of cases that they discuss. Later in this section, we show how even this careful specification of the quantity measured can fall short for preserving the geometric mean as the “most generally applicable” or “default” measure of (relative) fitness.

Thus far, we have shown only that the arithmetic mean change in log population size is equivalent to the geometric mean number of offspring, not that the former is preferable to the latter. This result should not come as a surprise since computing fitness using the arithmetic mean of the log population size increase is strictly equivalent to computing it with the geometric mean of the multiplicative terms. By the basic properties of the log function, ${e}^{\frac{\mathrm{ln}\left(10\right)+\mathrm{ln}\left(2\right)}{2}} = {\left(2 \times 10\right)}^\frac{1}{2} = \sqrt{20}$, with Euler’s number e ≈ 2.718. It is always true for multiplicative (compounding) processes, irrespective of their deterministic or stochastic nature, that the arithmetic mean of the exponential growth rate is equivalent to the geometric mean of the multiplicative growth rate.⁷ In the absence of intergenerational fluctuation (i.e., when the population is multiplied by a constant growth rate every generation), the arithmetic and geometric means for number of offspring are equal⁸; therefore, this distinction proves unnecessary.

In and of itself, the foregoing mathematical equivalence is of little philosophical interest. Its importance only begins to take shape when noting how the equivalency between the geometric and exponential notation hints at a seminal link between evolutionary biology (e.g., population genetics) and population ecology. The dynamics of a closed biological population (i.e., its growth, decline, or stasis) ultimately consist of the very same births and deaths that are used to determine fitness values (Crow and Kimura 1970, p. 7; Hamilton 2011, pp. 185–188; Hartl and Clark 1997, pp. 216–218; Rice 2004, pp. 6–8). Where ${N}_{0}$ and ${N}_{t}$ are, respectively, the population size at an initial time 0 and a subsequent point in time t (e.g., the next generation), and ${e}^{rt}$ is the finite rate of increase represented in exponential form (with Euler’s number e), we have the integrated form of the well-known exponential equation for population growth that predicts population size: ${N}_{t} = {N}_{0}{e}^{rt}$. Deriving the average individual fitness of population members requires solving for r, the “intrinsic rate of increase” (or “Malthusian parameter”). A sequence of simple algebraic rearrangements followed by a transition to differential form shows how this can be done:

$${N}_{t} = {N}_{0}{e}^{rt}$$

(1)

$$\frac{{N}_{t}}{{N}_{0}}={e}^{rt}$$

(2)

$$ln\left(\frac{{N}_{t}}{{N}_{0}}\right)=\mathrm{ln}({e}^{rt})$$

(3)

$$\mathrm{ln}\left({N}_{t}\right)-\mathrm{ln}\left({N}_{0}\right)=rt$$

(4)

On the simplifying assumption that this population began with a single member (i.e., ${N}_{0} = 1$, so that $\mathrm{ln}\left({N}_{0}\right) = \mathrm{ln}\left(1\right) = 0$), we then have:

$$\mathrm{ln}\left({N}_{t}\right)=rt$$

(5)

$$\frac{\mathrm{ln}({N}_{t})}{t}=r$$

(6)

$$\frac{{dln(N}_{t})}{dt}=r=\frac{d\left({N}_{t}\right)}{dt}\frac{1}{{N}_{t}}$$

(7)

Two key points can be made with this formal apparatus in place. First, it makes explicit what is typically taken for granted by many theoretical population biologists; namely, that population growth rates are determined by change in the logarithm of population size. This is already evident on the left-hand side of the equation in step (4) and is transparent on the left-hand side of Eq. (7). Tracking change in the logarithm of population size is what licenses the arithmetic mean as a measure of fitness for a multiplicative process in continuous time (the importance of continuous time will be discussed momentarily). Second, the intrinsic rate of population increase (r) is equivalent to the per capita instantaneous change in population size.⁹ The second term in the rearrangement on the far right-hand side of Eq. (7), $\frac{1}{{N}_{t}}$ makes this clear. This represents the average contribution that each of the individuals constituting a population makes (per unit time) to the change in population size. Although commonly encountered as a general population level parameter in the context of population ecology (where individual variation is glossed over), it functions as an evolutionary measure of fitness when the “population” for which it is derived happens to be a subpopulation whose members share a unique character state or trait variant. For example, in population genetics, this value is typically referred to as a “genotype specific growth rate” or, more simply, “absolute fitness” and “Malthusian fitness” (Hamilton 2011, p.185; Hartl and Clark 1997, p. 218). Importantly, such subpopulations can consist of a single member (McGraw and Caswell 1996, p. 49; Wagner 2010, pp. 1359–1360; Fisher 1930, pp. 23–24). While it is not our aim to endorse fitness as a propensity of token organisms, it should be recognized that recasting the individual as a “subpopulation of one” or “invading novel mutant” with a probabilistic tendency to give rise to a lineage with some number of members given a specified duration of time is central to theoretical frameworks such as adaptive dynamics (Metz et al. 1992; Pence and Ramsey 2013; Tuljapurkar 1989).

In effect, what many population biologists do when they deploy these ecological measures in an evolutionary setting is to compare the intrinsic growth rates associated with lineages of trait types to derive relative fitness values. The geometric mean number of offspring, focusing as it does on reproductive output rather than growth rate, works well¹⁰ with discrete population growth and non-overlapping generations. Intrinsic growth rate is equal to reproductive output in such circumstances. However, this should not mislead us into thinking that reproductive output is the more general measure; it represents a “special case” of continuous time population growth.

Readers will surely have noticed that the example we provide (Table 1) involves a population that grows (reproduces) discretely with non-overlapping generations. In that particular case, it is perfectly acceptable to use the geometric mean number of offspring as a measure of fitness. Why, then, should an instantaneous measure of fitness (r) for continuous (i.e., non-generational) time be considered a more basic or fundamental measure? The deceptively simple but potentially confusing answer from population biology draws on calculus: the continuous model is equivalent to a discrete difference equation with an infinitely small time step. The preceding question then becomes “why prefer a measure of fitness based on an infinitely small time step?” The direct answer is that one must defer to an instantaneous or intrinsic rate of increase whenever the finite timescales over which we measure the fitness of competing character states are unequal. We now provide an example that shows why the instantaneous measure should be granted explanatory precedence.

Consider two closed human populations that exhibit unequal constant growth rates (i.e., birth and death rates remain constant).¹¹ Let us refer to these populations as P1 and P2, respectively. Reproduction in human populations does not occur in discrete generations. Humans reproduce “year round,” and generations overlap. We have no well-defined reproductive schedules. Suppose we have census data on the size (i.e., absolute abundance) of both populations. The catch is that the census data for P1 are taken once every 20 years, whereas the data for P2 reflect a 30-year census period. We want to know which population grows faster. How is a comparison to be drawn? The problem confronting the demographer in this case parallels the problem faced by an evolutionary population biologist who investigates distinct trait variants exhibiting divergent reproductive schedules with unequal time steps. Although this example involves uniform populations, it should not be forgotten that the “population” of importance for assessing relative fitness ultimately consists of subpopulations whose members are unified by their exhibiting the same character state or trait variant. However, let us momentarily set aside this complication and instead examine these two populations sans (intrapopulation) variation.

Growth in either of these populations can be modelled with a discrete difference equation wherein a population increases by a constant proportion, $g$, over the time step determined by its census period:

$$ N_{t + 1} = \, N_{t} + gN_{t} $$

(8)

Here, ‘$g$’ is the discrete growth factor.¹² Let us assume that P1, which has a time step of 20 years, grew by 20%. As such, g₁ = 0.20 for P1. P2, with its time step of 30 years, grew by 25%, so g₂ = 0.25 for P2. If each population exhibits a constant increase associated with its distinct census time, the population size for the following time step (N_t+1) could be modelled as in Eq. 8. This reflects the actual or realized increase in the population size over a single time step (20 years for P1; 30 years for P2). Simple algebraic rearrangement permits the following transformation:

$$ N_{t + 1} = \, N_{t} \left( {1 + g} \right) $$

(9)

The factor (1 + g) indicates the finite rate of increase and is more commonly denoted by λ. Substituting this notation into the difference equation yields a form that may be more familiar to readers:

$$ N_{t + 1} = \, \lambda N_{t} $$

(10)

If λ > 1, the population is growing. If 0 < λ < 1, the population is in decline. And if λ = 1, the population is at equilibrium, where birth and death rates are perfectly balanced. It is important to note that λ is equal to the ratio of the population size during the next time step (N_t+1) to the population size for the current time step (N_t): N_t+1/N_t = λ. It thus measures the proportional (contra absolute) change in population size from one year to the next. Given λ and an initial population size (N_t), we can with Eq. 10 predict the size of either population at any time step in the future. This can be done because the output of Eq. 10 (N_t+1) serves as the input (N_t) for the calculation of the subsequent time step (N_t+2). If we accordingly wanted to predict the population size two time steps into the future, we would do so as follows: N_t+2 = λ(N_t+1) = λ(λ N_t) = λ²N_t. Of course, this calculation could be repeated as many times as needed to reach a desired time step. The general solution to this recursion equation after t years (with N₀ as initial population size) is:

$$ N_{t} = \, \lambda^{t} N_{o} $$

(11)

Now, it is crucial to recognize that λ is necessarily associated with a particular time step in the equation, in this case a (discrete) census time of 20 years for P1 and 30 years for P2. Consequently, there may remain looming uneasiness concerning the seemingly arbitrary choice of a 20-year time step over a 30-year time step (or vice versa) as the proper duration over which to measure. Similar scepticism may very well infect any other proposed discrete duration for measurement.

How, then, can this anxiety be assuaged? Since λ is “time step-dependent” it cannot be changed by simple scaling. Recall that in our ongoing example for P1 (with a 20-year time step), we have g₁ = 0.20, which means that λ₁ takes a value of 1.20. To compare this against P2 (g₂ = 0.25, λ₂ = 1.25), which has a 30-year time step, one might naively assume that a straightforward rescaling procedure would suffice, whereby the finite rate of increase (λ₁) for P1 is multiplied by the number of 20-year periods in a 30-year time step (30/20 = 1.5): 1.20 × 1.5 = 1.80.¹³ But a λ₁ value of 1.20 with a 20-year time step is not equivalent to a λ₁ value of 1.80 with a 30-year time step. The latter value of λ₁ indicates an 80% increase in population size. It cannot be “scaled down” to recover the realized, constant 20-year increase of 20%. Therefore, it is no mere redescription of population growth on a different (e.g., 30-year) timescale.

Correctly changing the time step of λ₁ for explicit comparison of P1 against P2 involves a sequence of three steps. The first step requires converting λ₁ to r, the instantaneous or intrinsic rate of increase (or Malthusian parameter). In the limit, as the time step associated with λ₁ becomes infinitesimally small, it is the case that λ = e^r.¹⁴ Taking the natural logarithm of both sides makes the operation more obvious: r = ln(λ). Using the value of λ₁ for P1 from our example subsequently renders r = ln(1.20) = 0.182. The second step is to scale r to the appropriate time step. The unit of measure for this newly derived value for r is average number of offspring per individual per 20 years. It is still fit to a 20-year time step. Accordingly, we must scale this to a 30-year time step, which requires multiplying r by the number of 20-year periods in a 30-year period (30/20 = 1.5): 0.182 × 1.5 = 0.273 offspring per individual per 30 years. The third and final step is to convert the now appropriately scaled value of r back to λ₁ by using λ = e^r (from above): ${e}^{0.273}$ ≈ 1.314 offspring per individual per 30 years. The result can be checked for accuracy using Eq. 11: N_t = λ^tN_o. Notice that the 20-year finite rate of increase (λ₁ = 1.20) must meet the condition that, when multiplied by itself one and a half times (t = 1.5), it yields a 30-year finite rate of increase of 1.314. And so it does: ${1.20}^\frac{3}{2} = \sqrt{{1.20}^{3}} \approx 1.314$. This is the correctly scaled (with a 30-year time step) per capita contribution to the discrete rate of increase in P1. It can now be compared directly against the finite growth rate of P2 (λ₂ = 1.25). Comparing the two discrete rates reveals that P1 “increases more quickly than” (read “is fitter than”) P2 with a 30-year time step, contrary to initial appearances that suggested a per time step increase favouring P2 (g₂ = 0.25, λ₂ = 1.25) over P1 (g₁ = 0.20, λ₁ = 1.20).

So far, so good. A direct comparison could also have been drawn by calculating the geometric mean increase in population size (per capita number of offspring) for P1. In fact, we showed this in the second half of the preceding paragraph when we calculated that λ₁^t = 1.20^1.5 = ${1.20}^\frac{3}{2} = \sqrt{{1.20}^{3}} \approx 1.314$. A problem nevertheless remains. The direct comparison has been achieved at the cost of privileging the discrete 30-year time step for the measurement of fitness. Alternatively, we could just as easily have privileged P1’s discrete 20-year time step by rescaling P2’s finite growth rate over a 30-year period to a corresponding 20-year period using the three steps noted above. However, neither option suffices. Human populations reproduce continuously, and generations overlap. There are no discernible, discrete reproductive schedules when it comes to human populations. Whether it be a 20- or 30-year time step, a principled biological basis on which to base the choice is absent. These discrete time steps are “accidents of convention” or “occupational hazards” for the demographer. It would not be difficult to complicate the given scenario further by including many other populations, each with its own unique census time. This difficulty is only compounded when focus shifts to the continuous variation on display in evolutionary scenarios. It is not, for instance, difficult to imagine a situation where the only selectively relevant, heritable variation in a population turns out to be associated with a very large number of distinct and discrete times for reproduction. Moreover, it may be the case that no other division of the population into similarity classes is statistically more relevant to reproduction. In such cases, population biologists and demographers alike turn to a time-independent measure of growth rate: namely, the intrinsic or instantaneous rate of increase (r). We believe that this is the fulcrum on which many, if not most, sophisticated theoretical measures of fitness rest.

The preceding example demonstrates the explanatory primacy of the instantaneous or intrinsic rate of increase and, hence, the “derivative” nature of the finite rate of increase when comparing discrete growth rates for “uniform” populations (i.e., ones where there is no heritable trait variation) over unequal time steps. Since (by stipulation) these populations are not in genuine competition with one another, they do not form a genuine metapopulation in any theoretically interesting sense—only our demographer’s interest linked them. As emphasized at the outset, this simplified comparison of human populations is not a scenario of genuine interest for those measuring (relative) fitness. A relevant scenario for evolutionary biologists would involve a population consisting of at least two distinct heritable trait variants or character states. Recall, however, that competing trait variants are themselves characterized as (sub)populations in evolutionary population biology. The procedure for measuring fitness does not differ fundamentally from that shown in our demography-based example where the finite time step for population growth has been changed to permit direct comparison. Many cases of interest to evolutionary biologists require measuring the relative fitness of trait variants over unequal timescales. In fact, this so-called “timing of offspring” problem has served as a primary motivation for more recent, sophisticated philosophical accounts of fitness (Pence and Ramsey 2013). The principal difference, then, between our example from demography and an explicitly evolutionary scenario is that the fitnesses (growth rates) of trait variants (populations) must often be rescaled via their intrinsic rates of increase to facilitate comparative assessments of relative fitness. It goes without saying that there are more complex ways to formally model fitness, many of which are explicitly designed to address the scores of perturbing factors that might thwart accurate prediction. However, no matter how sophisticated these models may be, we believe that their functional forms are expansions of the foundational discrete and continuous models for population growth. Continuous growth and overlapping generations are now recognized as the norm in nature and exacerbate the need for intrinsic or instantaneous measures of fitness. It is high time for more philosophers to accept this measure as fundamental even if the classic examples in the philosophical literature on fitness (featuring discrete reproductive schedules and implicitly ergodic processes) do not make this apparent.

While some mathematical sophistication is unavoidable considering the topic under discussion, the degree introduced may appear daunting to some readers. We have restricted ourselves to what many population biologists would consider the minimal basis for more sophisticated models (of which there are many). Since such reassurance will likely come as cold comfort for those who remain perplexed by the mathematical models that inform the fitness literature, let us draw this section to a close with a concise summary of this seemingly excessive formalization. The mathematical models we deploy demonstrate three crucial points. The first of these is that the (exponential of the) arithmetic mean of log population size is necessarily equivalent to the geometric mean number of offspring over a specific timescale (e.g., a generation). The arithmetic mean in this specific sense must, consequently, be a predictively efficacious measure of fitness whenever the geometric mean of offspring output is. This shows that the arithmetic mean (again, in the sense just noted) must, at least, be “on equal footing” with the geometric mean of offspring output when it comes to being a summary measure of fitness in those cases that have traditionally preoccupied philosophers. The second point of importance is that both the exponential of the arithmetic mean change in log population size and the geometric mean of offspring output are measures of fitness as growth rate. The former is applicable to exponential increase in continuous time, and the latter for geometric increase in discrete time. Restricting focus to the cases discussed by Beatty and Finsen (1989), Brandon (1990), and Sober (2001), which parallel the case we present in Table 1, it is unnecessary to distinguish these measures. Calculating one yields just as good a predictor of evolutionary success (relative differential representation) as the other. However, all the cases they discuss involve reproduction over discrete time steps with no generational overlap. Such cases represent only a minority of those in nature. Most organisms, humans included, exhibit overlapping generations and continuous population growth. Therefore, in the majority of cases, we need a measure of fitness as growth rate that enables us to make principled comparisons of reproductive output over discrete but unequal time steps (e.g., distinct “census times”). Resolving this difficulty requires a measure of fitness as instantaneous or intrinsic growth rate (e.g., Malthusian fitness), which does not arbitrarily privilege one temporal period of measurement over another. The third point is just that the more generally applicable, continuous time measure of fitness as intrinsic growth rate must be measured via the arithmetic mean since it involves a log scaled value.

Why does this matter?

Many philosophers of biology understand that population growth is a multiplicative process which lends to measurement via the geometric mean. There is no shortage of examples demonstrating this. Peter Godfrey-Smith, for instance, states that “[w]hen the outcomes of trials are combined in a multiplicative way, the predictor of long-term success in a representative sequence of trials is not the arithmetic mean payoff […] but the geometric mean payoff” (1996, p. 222). Further, few (if any) of the central contributors to the philosophical literature on fitness are oblivious to the fact that ignoring higher mathematical moments of a probability distribution over possible offspring can adversely affect prediction. Here is but a small sample of their respective appreciation:

What Gillespie, and this example, show is, in effect, that expected offspring contribution is just one component of fitness, variance is another. (Beatty and Finsen 1989, p. 25)

Beatty and Finsen (1989) show that the skew of a distribution of offspring numbers, as well as the mean and variance, also matters. That is why in the above definition of A*(O,E), the function f(Ε,σ²) is a dummy function in the sense that the form it takes can be specified only after the details of the selection scenario have been specified. (Brandon 1990, p. 20 [footnote 16])

In principle, fitness may depend on all the details of the probability distribution. (Sober 2001, p. 34)

[C]areful reading of some of Gillespie’s papers shows that even when he proposes that fitness can be taken to be a function of expectation and variance, complex functions of higher statistical moments would still be needed to provide a precise definition of fitness. (Abrams 2009, pp. 752–753)

Considering such acknowledgments, it is worth emphasizing that nowhere in the foregoing has it been our intention to suggest that Beatty and Finsen, Brandon, or Sober were (or are) completely unaware of the mathematical equivalency we highlight. In fact, on rare occasions, there appears to be some recognition of it. For example, Sober (2001, p. 34) alludes to the findings of Lewontin and Cohen (1969), who make it explicit that “if we consider a continuous time model, the discrepancy between geometric and arithmetic mean disappears” (p. 1059). Rather, our broad aim is to correct a misunderstanding that threatens to link otherwise sophisticated treatments with less nuanced counterparts in the literature. Successfully accomplishing this requires debunking the near consensus view that the geometric mean is often better than the arithmetic mean of log growth rate for tracking fitness. This is simply not the case when fitness is characterized as growth rate.

Measurement problems arise when fitness is reified as number of offspring. The geometric mean number of offspring provides a predictively adequate measure of fitness when reproductive contribution occurs over discrete time steps. But it is only under very restrictive assumptions (non-overlapping generations and no intra- or intergenerational variance) that expected reproductive output over consecutive generations can be a predictive measure of fitness. Fitness construed as a continuous growth rate is a more general measure. It also suffices for tracking multiplicative change over time. However, fitness is not measured by way of the geometric mean when continuous growth rates are used. Instead, one must use the arithmetic (mean of) growth rate in such cases. From that, one could potentially recover the geometric mean of offspring output. Because it is calculated as an arithmetic mean in continuous time, intrinsic growth rate (or Malthusian fitness) can assume any frequency of compounding, including continuous compounding. It thus has the flexibility to accommodate any change of temporal scale when assessing (relative) reproductive performance. Fitness qua growth rate thereby has broader explanatory scope and application.

Let us momentarily pause to take stock. Conceiving of fitness as a continuous growth rate presents several distinct advantages. First, its generality promises to unify measures of fitness that are otherwise potentially inconsistent. Beatty and Finsen (1989) and Sober (2001) cautioned that short-term selective advantage does not entail long-term selective advantage. They sought to distinguish a short-term notion of “expected reproductive output” (over a single time step) from a longer-term notion of “expected reproductive success” (over more than a single time step). Accordingly, an individual might have high expected reproductive output but relatively low multigenerational reproductive success (e.g., as with the progenitor B-type individual in Table 1). Measuring fitness as (relative) growth rate circumvents the need for such a distinction. Doing so has the capacity to capture the average reproductive contribution for members of a growing lineage at any point in the (not too distant) future. If fitness is to be commensurate with evolutionary success, any metric that tracks such success should correspond to fitness. For instance, in the example offered by Beatty and Finsen (1989), as well as in Table 1 above, we observe a two-generation cycle for the variance in number of offspring. By computing fitness in terms of the expected number of grand-offspring, we can track long-term evolutionary success. However, this measure does not represent a general proxy for fitness. That is, we could have found ourselves in a situation involving a cycle of three or more generations. There is no principled reason for favouring the number of grand-offspring over the number of offspring or, for that matter, any other time step as the appropriate one over which to compute. This difficulty can arise despite assuming discrete generation times and deterministic cycles in the intergenerational variance. When those assumptions are not met, the problem of which timescale to use when computing fitness becomes even more substantial (Doulcier et al. 2021). However, measuring fitness as a growth rate evades such problems.

The second advantage is closely related to the first. While some species (e.g., periodical cicadas in the genus Magicicada) have readily delineated reproductive schedules and generation times, others (e.g., Homo sapiens) do not (Williams and Simon 1995). In the latter type of case, which is arguably the norm in nature, there lingers the ever-present danger that fitness assessments will be undertaken over arbitrary and, thus, possibly erroneous durations (Ahmed and Hodgkin 2000; Crow and Kimura, 1956). As emphasized by some (Pence and Ramsey 2013), this concern can be allayed if one shifts from a generational timeframe and frequency of measurement to an absolute (continuous) timeframe. Yet, again, this advantage is only available to continuous time models that measure fitness as a constant growth rate, which is, in turn, calculated as the arithmetic mean change in log population size.

In what substantive sense, then, does the demonstration of mathematical equivalence amount to anything more than the satisfaction of an idle curiosity? We have already noted how use of the arithmetic mean on a log scale can sidestep problems associated with inconsistency or arbitrariness of timescale for measurement. Uncritical deference to the geometric mean over the arithmetic mean as a measure of fitness also threatens to gloss over more fundamental ontological and explanatory concerns. Use of the geometric mean as a proxy for fitness relies on reproductive output measured in discrete time steps; therefore, its range of explanation is also much constrained. More specifically, its application presumes that reproducibility of a trait type (character state) entails the production of distinct (token) descendants. However, organisms that physically increase in size but produce no discernible offspring, such as the quaking aspen (see Bouchard 2008, 2011), accordingly cannot undergo evolution via natural selection (Van Valen 1976, 1989). The geometric mean demands a “full-blooded” sense of reproduction insofar as it implies that natural selection cannot occur unless there is, at minimum, fission of a focal progenitor. Yet, curtailing explanatory scope in this way is, to put it mildly, questionable. Biological entities exhibiting variations that enable them to persist more reliably than competitors (e.g., neurons less prone to apoptosis or neuronal configurations reinforced via synaptic pruning; see Garson, 2019), albeit without any subsequent physical growth or production of offspring, are similarly excluded.¹⁵ This view of natural selection as involving persistence and growth in addition to reproduction has been systematically defended by Frédéric Bouchard (2004, 2008, 2011). The foregoing types of biological entity are sometimes depicted as being non-paradigmatically Darwinian (Godfrey-Smith 2009) or simply mentioned in passing as problematic outliers for selective explanation.¹⁶ The continuous growth rate framework for fitness offers the quantitative means to (sensibly) withhold such contentious qualitative judgments and naturally provides some grist for Bouchard’s mill.¹⁷ The abstract notion of growth encompasses not only cases where entities reproduce and merely persist but also cases where entities expand.

The fitness qua growth rate framework provides a way to extend selective explanation to what are otherwise peculiar biological entities by presenting us with the means to measure the general phenomenon of (relative) growth. Growth in population size (abundance) is just one manifestation of this; others include an individual’s growth in terms of physical size or a biological entity’s ability to persist. Measuring fitness via growth rate in the latter, less paradigmatic cases can make fitness a property of an individual. This might be reason enough for disapproval in the minds of some. However, a sophisticated attempt to develop this framework is what, for example, Charles Pence and Grant Ramsey (2013, pp. 864–867) have already provided via deriving a measure for token fitness (i.e., fitness as a measurable property of individual organisms) from adaptive dynamics (for an introduction to this approach, see Brännström et al. 2013). One cannot begin to understand the project that they and others have undertaken unless fitness is refashioned as pertaining to the growth rates of (sub)populations. Some (Pence and Ramsey 2013, 2015; Ramsey 2006) argue for the explanatory priority of lineages of descendants engendered by a focal individual, while others contend that unifying a lineage under the auspices of a trait variant provides a more faithful characterization of evolutionary explanation (Sober 2013). Sensible disagreements no doubt abound. But the ascriptive flexibility on which debate turns presupposes that population level parameters in ecology (e.g., population growth rates) must relate to evolutionary parameters (e.g., fitness).

Conclusion

Beatty and Finsen (1989), Brandon (1990), and Sober (2001) provided noteworthy corrections to early formulations of the PIF. Although clearly acknowledging that other moments of a probability-weighted offspring distribution are relevant to characterizing and measuring fitness, the geometric mean was nevertheless singled out as a particularly important summary statistic or proxy measure. This was predominantly a consequence of the toy examples that were used to show the perils of its neglect. Such examples were deliberately simplified ones that rely on discrete generation times and, consequently, lend to proper measurement via the geometric mean of offspring output. An unwelcome consequence of this is that many now assume that the arithmetic mean cannot in any sense be an adequate measure of fitness. Not only is this assumption unfounded—it is also potentially misleading in theoretically substantive ways. When assessing competing trait types or individuals to generate predictive measures of evolutionary trajectory, theoreticians typically compare the relative growth rates of competing (sub)populations distinguished by trait type. The most general mathematical context for assessing growth rate is in continuous time on a logarithmic scale. Crucially, it is the arithmetic mean that provides the correct measure on that scale. The discrete generation timeframe and geometric mean measure that accompanies it is a derivative case of this more general framework. If the geometric measure is taken as basic, we run the risk of reifying reproductive output and limiting ourselves to a conception of fitness that appears to be unjustifiably truncated. Thus, clarifying how and why the arithmetic mean can be an appropriate measure of fitness removes at least one obstacle toward what is perhaps a more unificatory theory. What devils there may be will undoubtedly be found in the details. For now, let us begin by recognizing why using arithmetic mean to characterize fitness should not be unduly de-emphasized or ignored.