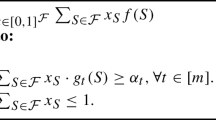A new mixed-integer programming formulation for the maximally diverse grouping problem with attribute values

Abstract

The paper presents a new mixed-integer programming formulation for the maximally diverse grouping problem (MDGP) with attribute values. The MDGP is the problem of assigning items to groups such that all groups are as heterogeneous as possible. In the version with attribute values, the heterogeneity of groups is measured by the sum of pairwise absolute differences of the attribute values of the assigned items, i.e. by the Manhattan metric. The advantage of the version with attribute values is that the objective function can be reformulated such that it is linear instead of quadratic like in the standard MDGP formulation. We evaluate the new model formulation for the MDGP with attribute values in comparison with two different MDGP formulations from the literature. Our model formulation leads to substantially improved computation times and solves instances of realistic sizes (for example the assignment of students to seminars) with up to 70 items and three attributes, 50 items and five attributes, and 30 items and ten attributes to (near) optimality within half an hour.

1 Introduction

The maximally diverse grouping problem (MDGP) is the problem of assigning a set of items, $i,j \in I$, to groups, $g \in G$, such that each group gets the same or a similar number of items assigned and the sum of pairwise distances $d_{ij}$ between all items assigned to the same group is maximized. Thus, for equal-sized groups the heterogeneity inside groups is maximized, which leads also to similar groups.

Although the MDGP is in its general version formulated with arbitrary distances $d_{ij}$, common applications like the assignment of students to seminars use attribute values $av_i^a$ for all students and attributes. Examples are grades or other performance scores or zero-one attributes (e.g. for international or non-international). Given these attribute values, the distances are computed as $d^a_{ij} = |av_i^a - av_j^a|$, i.e. by the Manhattan metric, for all attributes $a \in A$ and items/students $i,j \in I$.

In this paper, we consider the MDGP where $d^a_{ij} = |av_i^a - av_j^a|$ for attribute values $av_i^a \in {\mathbb {Q}}_{\ge 0}$ and use results of Schulz (2021b) to introduce a new mixed-integer programming formulation for the problem setting. We prove that our formulation leads to the same optimal objective values as the standard formulation. Our computational results show that this formulation outperforms the standard formulation and the model formulation by Papenberg and Klau (2021) for the MDGP by far. Moreover, we outline how the approach by Schulz (2021b) for the balanced MDGP, i.e. the problem of finding a best balanced solution among all optimal MDGP solutions, can be adapted if there is no MDGP solution fulfilling Assumption 1 (compare page 6) for every attribute or if not equal-sized groups are considered.

The paper is organised as follows: In Sect. 2, the relevant literature is reviewed. Afterwards, we give a formal problem description in Sect. 3. Our mixed-integer programming (MIP) formulation is introduced in Sect. 4. The MIP is compared with the standard formulation and the model by Papenberg and Klau (2021) in a computational study in Sect. 5. The paper closes with a conclusion (Sect. 6).

2 Literature review

The MDGP has been investigated in different settings in the literature. Weitz and Lakshminarayanan (1997) showed that it is mathematically equivalent to VLSI design (group highly connected modules onto the same circuit) and exam scheduling (assigning exam blocks to days). In a further paper, Weitz and Lakshminarayanan (1998) mentioned the assignment of students to project groups as a possible application.

Assignments of students are a common application of grouping problems. In an early work, Beheshtian-Ardekani and Mahmood (1986) assigned students to project groups. In more recent works, students were assigned to study groups (Krass and Ovchinnikov, 2010), work groups (Caserta and Vo, 2013), and multiple teaching groups (on the basis of preferences; Heitmann and Brüggemann (2014)). Johnes (2015) published a review on operations research in education and considered amongst others the assignment of students to courses. Dias and Borges (2017) applied the MDGP to assign students to teams. Students are mostly assigned according to their academic performance (overall average grade or grades in specific courses) to groups. Furthermore, students can be distributed to groups according to their gender to reach an equally distribution of male, female, and third gender students. Moreover, international students can be distributed equally over all groups. All these measures can be implemented as attribute values (e.g. attribute value 0 for male, 1 for female, and 2 for third gender, or 0 for non-international and 1 for international). Mingers and O’Brien (1995), Krass and Ovchinnikov (2006), Krass and Ovchinnikov (2010), and Caserta and Voß (2013) assign students to groups according to binary attributes.

Baker and Benn (2001) investigated in a case study how pupils in a school should be assigned to tutor groups such that the groups are as similar as possible. Criteria are the gender, the ability level, ethnic minority groups, feeder schools, and special educational needs of pupils. All of them can also be represented by attribute values. Rubin and Bai (2015) considered the problem of assigning individuals to teams to make the teams as similar as possible. Schulz (2021b) extended the MDGP (in the version with attribute values) by such a balancing component.

Homogeneity over different days and therefore heterogeneity inside days is also helpful to distribute workload evenly over days. This is, for example, important in surgery scheduling to avoid overtime (surgery durations can be represented by attribute values). Overtime minimization is a frequently investigated objective in surgery scheduling (compare the review by Cardoen et al. (2010)). Schulz (2021c) assigned surgeries to days such that the days are balanced according to the surgery durations. Schulz and Fliedner (2021) analyzed the intra-day assignment of surgeries to starting times and rooms according to several balancing criteria. Papenberg and Klau (2021) used the fact that die MDGP aims at homogeneity over groups and heterogeneity inside groups in psychology to partition data sets into equivalent parts.

The MDGP is NP-hard (Feo and Khellaf, 1990) which may be the reason why only a few exact solution approaches for the MDGP were investigated. Gallego et al. (2013) presented a computational study with the standard formulations of both problem variants presented in Sect. 3.1 ((1)–(4) and (1)–(2), (4)–(5), respectively), where only instances with up to 12 items could be solved to optimality within 1800s (general $d_{ij}$). Papenberg and Klau (2021) introduced an exact MDGP formulation for the setting with equal-sized groups (compare Sect. 3.2) based on a work by Grötschel and Wakabayashi (1989). They could solve instances with 28 items in 950s and instances with 30 items in nearly 10000s to optimality.

Schulz (2021b) investigated the MDGP with attribute values. The author proved that the set of optimal solutions for the MDGP with attribute values equals for at most two attributes the set of feasible solutions of a special system of equations (for more than two attributes this does not hold in general). He searched for the best balanced solution amongst all optimal solutions of the MDGP with attribute values in the case if there is a solution fulfilling Assumption 1 (compare page 7) for every attribute. We explain the ideas of this paper further in Sect. 4, where we work with them. Schulz (2021a) generalised this research for the case in which no MDGP solution fulfilling Assumption 1 for every attribute exists. The paper considered also only equal-sized groups. Schulz (2021a) solved instances with up to 15 items and 5 attributes to optimality within 600s (version with equal sized-groups; (1–4)).

In contrast to exact approaches, the MDGP has been solved by a variety of heuristic solution approaches. Fan et al. (2011) applied a hybrid genetic algorithm to it. An artificial bee colony algorithm has been investigated for the MDGP by Rodriguez et al. (2013). Gallego et al. (2013) developed a tabu search algorithm with strategic oscillation. Tabu search in an iterated version was considered by Palubeckis et al. (2015). Moreover, Brimberg et al. (2015) applied a skewed general variable neighbourhood search algorithm to solve the MDGP, Lai and Hao (2016) iterated maxima search, and Singh and Sundar (2019) a hybrid genetic algorithm. Lai et al. (2020) implemented a neighbourhood decomposition based variable neighbourhood search and a tabu search algorithm to solve the MDGP. A recent review on metaheuristics applied to solve grouping problems can be found in Ramos-Figueroa et al. (2020).

Brimberg et al. (2017) solved the clique partitioning problem as an MDGP. A similar class of problems are dispersion problems. In contrast to the MDGP, only a single group of a given size is selected. Dispersion problems are considered for example in Fernández et al. (2013), Aringhieri et al. (2015), and Amirgaliyeva et al. (2017).

3 Problem description

In this paper, we consider a set of items $i,j \in I$, a set of groups $g \in G$, and a set of attributes $a \in A$ as given. Each item has an attribute value $av_i^a \in {\mathbb {Q}}_{\ge 0}$ for each attribute $a \in A$. Given them, we compute the distances between each pair of items for each attribute according to the Manhattan metric as

$$\begin{aligned} d_{ij}^a = |av_i^a - av_j^a|. \end{aligned}$$

Note that it is no restriction to consider non-negative attribute values. As $d^a_{ij}$ measures only differences between them, we can add a constant $c^a = \max _{i \in I:0>av_i^a} \{ |av_i^a| \}$ to all attribute values of attribute a without changing the $d^a_{ij}$ values since

$$\begin{aligned} d_{ij}^a = |av_i^a - av_j^a| = |av_i^a + c^a - av_j^a - c^a| = |(av_i^a + c^a) - (av_j^a + c^a)|. \end{aligned}$$

In the following subsections, we present the standard formulation of the MDGP (Sect. 3.1) and the formulation by Papenberg and Klau (2021) (Sect. 3.2).

3.1 Standard formulation

The standard integer programming formulation for the MDGP with equal-sized groups is (compare e.g. Gallego et al. (2013), Singh and Sundar (2019) or Schulz (2021a)):

$$\begin{aligned}&\max \; \sum _{a \in A} \sum _{g \in G} \sum _{i \in I} \sum _{j \in I: j>i} d^a_{ij} x_{ig} x_{jg} \\&\text {with the constraints}\nonumber \end{aligned}$$

(1)

$$\begin{aligned}&\sum _{g \in G} x_{ig} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall i \in I \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{i \in I} x_{ig} = |I|/|G| \quad \quad \quad \quad \quad \quad \quad \forall g \in G \end{aligned}$$

(3)

$$\begin{aligned}&x_{ig} \in \{ 0,1 \} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad ~ \forall i \in I,g \in G \end{aligned}$$

(4)

$x_{ig}$ is a binary variable which equals to one if item i is assigned to group g and is zero otherwise. Objective function (1) maximizes the pairwise differences between each pair of items assigned to the same group according to all attributes. Constraints (2) ensure that each item is assigned to exactly one group while Constraints (3) take care that all groups are equal-sized. Constraints (4) are the binary constraints for the x variables.

Several authors (Fan et al., 2011; Gallego et al., 2013; Singh and Sundar, 2019; Lai et al., 2020) relax (3) to

$$\begin{aligned} l_g \le \sum _{i \in I} x_{ig} \le u_g \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall g \in G, \end{aligned}$$

(5)

where $l_g$ is a lower bound and $u_g$ an upper bound for the number of items in group g. In this paper, we consider as a start the more restricted case with (3) and relax it afterwards to (5).

Objective function (1) is quadratic. Thus, we have to linearize it to use an off-the-shelf solver for mixed-integer programming. Therefore, we introduce a new set of variables $z_{ijg}$, $i,j \in I$ with $i<j$ and $g \in G$, such that the variable $z_{ijg}$ is one if items i and j are assigned to group g and zero otherwise. Then, we replace (1) by

$$\begin{aligned} \max \; \sum _{a \in A} \sum _{g \in G} \sum _{i \in I} \sum _{j \in I: i<j} d^a_{ij} z_{ijg} \end{aligned}$$

(6)

and add the constraints

$$\begin{aligned}&z_{ijg} \le x_{ig} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall i,j \in I: i<j, g \in G \end{aligned}$$

(7)

$$\begin{aligned}&z_{ijg} \le x_{jg} \quad \quad \quad \quad \quad \quad \quad \quad \quad ~~\, \forall i,j \in I: i<j, g \in G \end{aligned}$$

(8)

$$\begin{aligned}&z_{ijg} \ge x_{ig} + x_{jg} - 1 \quad \quad \quad \quad ~\, \forall i,j \in I: i<j, g \in G \end{aligned}$$

(9)

$$\begin{aligned}&z_{ijg} \in [0,1] \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall i,j \in I:i<j, g \in G \end{aligned}$$

(10)

Objective function (6) replaces the product of variables in (1) by the new variable $z_{ijg}$. This variable has to be one if items i and j are assigned to group g and zero else. Since $0 \le z_{ijg} \le 1$ (10), Constraints (7) and (8) set $z_{ijg} = 0$ if item i or item j is not assigned to group g. Constraints (9) set $z_{ijg} = 1$ if items i and j are assigned to group g.

Model (1)–(4) contains symmetric solutions. Given a solution, swapping the group assignments of all items assigned to two different groups $g_1$ and $g_2$ with $\sum _{i \in I} x_{ig_1} = \sum _{i \in I} x_{ig_2}$ leads to a different solutions which is structurally identical because the two groups have the same size. In the case with equal-sized groups, this symmetry results in |G|! structurally identical solutions. The following set of inequalities avoids symmetric solutions by sorting homogeneous groups in increasing order of the smallest index of their assigned items (Salem and Kieffer (2020)): $x_{11} = 1$ and

$$\begin{aligned} x_{ig} \le \sum _{j = 1}^{i-1} x_{j,g-1} \forall i \in \{2, ..., |I|\}, g \in \{ 2, ..., |G|\} \end{aligned}$$

(11)

In objective function (1) as well as in (6), $d_{ij}$ is only counted if both items i and j are assigned to the same group. This means that at the moment when an item i is assigned to a group—for example in a branch-and-bound procedure—, we are not (fully) aware of the consequences. If i is the first item assigned to the group, this has even no immediate influence on the objective value. If i is not the first but also not the last item assigned to the group, we know that certain $d_{ij}^a$ values are realized but it is still possible that we have to add a large $d_{ij}^a$ value later if the corresponding item j is added to the same group. This might lead to unprofitable decisions at early stages in the branch-and-bound tree. Thus, although objective function (6) is linearized, its quadratic character still influences the search process. We reduce this drawback by a reformulation of the model in Sect. 4.

3.2 Formulation by Papenberg and Klau (2021)

The model formulation by Papenberg and Klau (2021) is based on a work by Grötschel and Wakabayashi (1989). We adapt it here for the multi-attribute case. It uses binary variables ${\bar{x}}_{ij}$, $i,j \in I$, $i<j$, which are one if items i and j are assigned to the same group and zero else. The model formulations is:

$$\begin{aligned}&\max \; \sum _{a \in A} \sum _{i \in I} \sum _{j \in I: j>i} d^a_{ij} {\bar{x}}_{ij} \\&\text {with the constraints} \nonumber \end{aligned}$$

(12)

$$\begin{aligned}&-{\bar{x}}_{ij} + {\bar{x}}_{ik} + {\bar{x}}_{jk} \le 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad ~ \forall i,j,k \in I: i<j<k \end{aligned}$$

(13)

$$\begin{aligned}&{\bar{x}}_{ij} - {\bar{x}}_{ik} +{\bar{x}}_{jk} \le 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall i,j,k \in I: i<j<k \end{aligned}$$

(14)

$$\begin{aligned}&{\bar{x}}_{ij} +{\bar{x}}_{ik} - {\bar{x}}_{jk} \le 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall i,j,k \in I: i<j<k \end{aligned}$$

(15)

$$\begin{aligned}&\sum _{j \in I: i<j} {\bar{x}}_{ij} + \sum _{j \in I:j<i} {\bar{x}}_{ji} = \frac{|I|}{|G|} - 1 \quad \quad \,\,\,\!~ \forall i \in I \end{aligned}$$

(16)

$$\begin{aligned}&{\bar{x}}_{ij} \in \{ 0,1 \} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \,\forall i,j \in I: i<j \end{aligned}$$

(17)

Constraints (13)–(15) are transitivity constraints which ensure that two items are in the same group if both of them are in the same group with a third item. Constraints (16) form equal-sized groups with $\frac{|I|}{|G|}$ items each. Given an item i, it has to be in the same group with $\frac{|I|}{|G|} - 1$ further items to ensure that the group size is $\frac{|I|}{|G|}$. Finally, Constraints (17) are the binary constraints. Note that this model formulation does not contain symmetric solutions, as variables do not have a group index. Note further that $|I| \cdot |G| < \frac{|I|(|I|-1)}{2}$ is equivalent to $2|G| < |I|-1$. This means that the model formulation by Papenberg and Klau (2021) has more binary variables than the standard formulation if at least three items are assigned to the same group. Moreover, the model is restricted to equal-sized groups. Varying group sizes could be implemented by bounding the left side of (16) to both sides, but then all groups have the same lower and upper bound. If lower and upper bounds for group sizes vary, we would need a set of variables which indicate the assignment of items to groups.

4 New mixed-integer programming formulation

First, we investigate the case with equal-sized groups (Sect. 4.1), i.e. model (1)–(4) to introduce the ideas and get familiar with the notation. Afterwards, we generalize the findings and consider varying group sizes, i.e. model (1)–(2) and (4)–(5), in Sect. 4.2.

4.1 Equal-sized groups

As mentioned above a disadvantage of the problem formulation (1)–(4) is that the share of an item i in the objective function, for example expressed by

$$\begin{aligned} \sum _{a \in A} \sum _{g \in G: x_{ig} = 1} \sum _{j \in I} \frac{d_{ij}^a \cdot x_{jg}}{2}, \end{aligned}$$

depends on the decision which of the other items are assigned to the same group.

To overcome this drawback, Schulz (2021b) introduced an assignment of the items to blocks $k \in K$ with $|K| = |I|/|G|$ (|K| is the number of items per group) for each attribute according to

Assumption 1

Let |G| be the number of groups. Then, the |G| items with the largest attribute values according to the considered attribute are assigned to the first block, the |G| items with the next largest attribute values according to the considered attribute are assigned to the second block, and so on.

Moreover, a binary parameter $b_{ki}^a$ is introduced which is 1 if item i is according to attribute a assigned to block k and 0 else. Schulz (2021b) (Theorem 1 in that paper) proved that the set of optimal solutions for (1)–(4) equals the set of feasible solutions for (2), (4), and

$$\begin{aligned} \sum _{i \in I: b_{ki}^a = 1} x_{ig} = 1 \quad \quad \forall a \in A, g \in G, k \in K \end{aligned}$$

(18)

if blocks are determined according to Assumption 1 and one of the following two criteria is fulfilled:

• 1. $|A| = 1$,

• 2. $|A| > 1$ and the assignment according to Assumption 1 is unique (no two items with identical attribute values are assigned to different blocks regarding the corresponding attribute).

Schulz (2021b) proved also that the set of feasible solutions for (2), (4), and (18) might be empty if $|A| > 2$ (Theorem 3 in that paper).

With the help of the block notation (parameter $b_{ki}^a$), the optimal objective value for (1)–(4) can be calculated, if the set of feasible solutions for (2), (4), and (18) is not empty (a proof can be found in Schulz (2021b)), as

$$\begin{aligned} \sum _{a \in A} \sum _{g \in G} \sum _{i \in I} \sum _{j \in I: i<j} d^a_{ij} x_{ig} x_{jg} = \sum _{a \in A} \sum _{k \in K} \sum _{i \in I} b_{ki}^a c_k av_i^a \end{aligned}$$

(19)

with

$$\begin{aligned} c_k = {\left\{ \begin{array}{ll} {\bar{c}}_k &{} \text {if } k \le \left\lceil \frac{|K|}{2} \right\rceil \\ -{\bar{c}}_k &{} \text {else,} \end{array}\right. } \end{aligned}$$

(20)

where

$$\begin{aligned} {\bar{c}}_k = 2 \cdot \max \left( \frac{|K|}{2} - k, k - \frac{|K|}{2} - 1 \right) + 1 \end{aligned}$$

(21)

if |K| is even and

$$\begin{aligned} {\bar{c}}_k = 2 \cdot \left| k - \left\lceil \frac{|K|}{2} \right\rceil \right| \end{aligned}$$

(22)

if |K| is odd.

Fig. 1

${\bar{c}}_k$ values (left) and $c_k$ values (right)

Figure 1 illustrates ${\bar{c}}_k$ (left side of the figure) and $c_k$ (right side of the figure) values for small numbers of blocks. The first row states the number of blocks. The numbers below are the ${\bar{c}}_k$ and $c_k$ values, respectively, in increasing order of the block number. If $|K| = 2$, (21) leads to ${\bar{c}}_1 = {\bar{c}}_2 = 1$. If $|K| = 3$, (22) leads to ${\bar{c}}_1 = 2$, ${\bar{c}}_2 = 0$, and ${\bar{c}}_3 = 2$. It can easily be seen that ${\bar{c}}_k$ values are symmetric. The same is true for $c_k$ values but with a different algebraic sign.

Let us consider an example for (19). Let $|K| = 4$, $|A| = 1$. Four items with attribute values $av^1_1 = 8$, $av^1_2 = 5$, $av^1_3 = 4$, and $av^1_4 = 1$ are assigned to the one considered group. Then,

$$\begin{aligned}&\sum _{a \in A} \sum _{g \in G} \sum _{i \in I} \sum _{j \in I: i<j} d^a_{ij} x_{ig} x_{jg} \nonumber \\ {=}&\sum _{i \in I} \sum _{j \in I: i<j} |av^1_i - av^1_j| \nonumber \\ {=}&|8-5| + |8-4| + |8-1| + |5-4| + |5-1| + |4-1| \nonumber \\ {=}&(8-5) + (8-4) + (8-1) + (5-4) + (5-1) + (4-1) \nonumber \\ {=}&\underbrace{(8-5) + (5-1)}_{= (8-1)} + \underbrace{(8-4) + (4-1)}_{= (8-1)} + (8-1) + (5-4) \nonumber \\ {=}&3 \cdot (8-1) + 1 \cdot (5-4) \nonumber \\ {=}&3 \cdot 8 - 3 \cdot 1 + 1 \cdot 5 - 1 \cdot 4 \nonumber \\ {\mathop {=}\limits ^{(21)}}&{\bar{c}}_1 \cdot 8 + {\bar{c}}_2 \cdot 5 - {\bar{c}}_3 \cdot 4 - {\bar{c}}_4 \cdot 1 \nonumber \\ {\mathop {=}\limits ^{(20)}}&c_1 \cdot 8 + c_2 \cdot 5 + c_3 \cdot 4 + c_4 \cdot 1 \nonumber \\ {=}&\sum _{k \in K} \sum _{i \in I} b^1_{ki} c_k av^1_i \nonumber \\ {=}&\sum _{a \in A} \sum _{k \in K} \sum _{i \in I} b^a_{ki} c_k av^a_i \end{aligned}$$

(23)

with $b^1_{ki}$ according to Assumption 1, i.e. $b^1_{11} = 1$, $b^1_{22} = 1$, $b^1_{33} = 1$, $b^1_{44} = 1$, and $b^1_{ki} = 0$ else. Equation (23) shows us why we should assign items to blocks according to Assumption 1. Each $c_k$ value with $k \le \left\lceil \frac{|K|}{2} \right\rceil$ is multiplied with exactly one $d^a_{ij}$ such that each item i is considered exactly once ($d^a_{ii} = |av^a_i - av^a_i| = 0$). Because of our definition of $d^a_{ij}$ and the fact that $c_1> c_2> ... > c_{\left\lceil \frac{|K|}{2} \right\rceil }$, it is optimal to multiply the largest $c_k$ value, i.e. $c_1$, with the largest $d^a_{ij}$ value, i.e. the difference of the largest and the smallest attribute value assigned to the group. This means, we assign the item with the largest attribute value to the first block and the item with the smallest attribute value to the last block. If we repeat this with all remaining items until all items are assigned, we get the assignment according to Assumption 1.

Note that the right side of (19) is independent of $x_{ig}$. Because of (2), item i is assigned to exactly one group such that

$$\begin{aligned} \sum _{a \in A} \sum _{k \in K} \sum _{i \in I} \sum _{g \in G} b_{ki}^a c_k av_i^a x_{ig} = \sum _{a \in A} \sum _{k \in K} \sum _{i \in I} b_{ki}^a c_k av_i^a. \end{aligned}$$

In (19), the objective value is independent of the assignment of items to groups, which underlines that the set of optimal solutions for (1)–(4) equals the set of feasible solutions for (2), (4), and (18). However, we are only sure that (19) is valid if $|A| = 1$ or $|A| = 2$. For $|A| > 2$, in contrast, we are not sure that (19) is valid (Schulz (2021b), Theorems 2 and 3); there might be no feasible solution for (2), (4), and (18)).

The right side of (19) has in comparison to the left side the advantage that the share of item i in the objective value, i.e. $\sum _{a \in A} \sum _{k \in K} b_{ki}^a c_k av_i^a$, is independent of the assignment of all other items. The idea of this paper is to replace $b_{ki}^a$ by a variable, i.e. make the assignment of items to blocks to an endogenous decision. By this, we overcome the drawback that we do not know whether there is a solution fulfilling (19) if $|A| > 2$.

So, we replace $b_{ki}^a$ (in combination with $x_{ig}$) by a new variable $y_{kig}^a$ which is 1 if item i is assigned to group g and according to attribute a to block k and 0 else. This makes the assignment of items to blocks to an endogenous decision, which is only allowed if the assignment is feasible regarding to (2) and (4). This does not only ensure feasibility, the resulting model formulation is, moreover, equivalent to the standard MDGP formulation ((1)–(4); compare Theorem 1).

The new model formulation is

$$\begin{aligned}&\max \; \sum _{a \in A} \sum _{i \in I} \sum _{g \in G} \sum _{k \in K} c_k av_i^a y_{kig}^a \\&\text {with the constraints} \nonumber \\&(2), (4)&\nonumber \end{aligned}$$

(24)

$$\begin{aligned}&\sum _{i \in I} y_{kig}^a = 1 \quad \quad \quad \quad \quad \quad \quad \! \forall a \in A, g \in G, k \in K \end{aligned}$$

(25)

$$\begin{aligned}&\sum _{k \in K} y_{kig}^a = x_{ig} \quad \quad \quad \quad \quad ~~\forall a \in A, i \in I, g \in G \end{aligned}$$

(26)

$$\begin{aligned}&0 \le y_{kig}^a \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall a \in A, i \in I, g \in G, k \in K \end{aligned}$$

(27)

Objective function (24) adds up the shares of all items for all attributes. Although the items are evaluated independently from each other (no $d_{ij}^a$ values), they are only at the first glance independent because the assignment of items to blocks depends on the other items assigned to the same group. Constraints (25) ensure that each group and each block gets for each attribute exactly one item assigned according to which the share in the objective value is determined. Moreover, each item is assigned to exactly one block for each attribute (Constraints (26)). Therefore, $|K| = |I|/|G|$ items are assigned to each group. Constraints (26) set in combination with Constraints (27) also the range of the $y_{kig}^a$ variables. Their value can be between zero and one if item i is assigned to group g. Otherwise they must be zero. The proof of Theorem 1 shows that there is an optimal solution in which all y variables are zero or one.

Theorem 1 proves that the model formulation (2), (4), and (24)–(27) is equivalent to the standard MDGP formulation with attribute values (1)–(4).

Theorem 1

Let $|K| = |I|/|G|$. Then, the model formulation (2), (4), and (24)–(27) is equivalent to the formulation (1)–(4) in the sense that both model formulations lead to the same objective value for any feasible assignment of the $x_{ig}$ variables.

Proof

Let any feasible solution of (1)–(4) be given. Due to (3) exactly $|K| = |I|/|G|$ items are assigned to each group. In the following, we decompose the instance into one instance per combination of attributes and groups, i.e. given $a \in A$ and $g \in G$. This reduced instance consists of all items assigned to the fixed group g, i.e. the items with $x_{ig} = 1$ in the solution of (1)–(4). Since we consider only a single attribute, we know from Schulz (2021b) that (19) holds with $b^{a}_{ki}$ according to Assumption 1. Set $y^{a}_{kig} = b^{a}_{ki}$ with the fixed $a \in A$ and $g \in G$. Then, (19) implies

$$\begin{aligned} \sum _{i \in I} \sum _{j \in I: i<j} d^{a}_{ij} x_{ig} x_{jg} = \sum _{k \in K} \sum _{i \in I} c_k av_i^{a} y^{a}_{kig}. \end{aligned}$$

As $b^{a}_{ki}$ is binary, $0 \le y^{a}_{kig}$ for all $i \in I$ with $x_{ig} = 1$ and $k \in K$ (compare (27)). Since the number of blocks equals the number of items in our reduced instance, exactly one item is assigned to each block. Thus, $\sum _{i \in I:x_{ig}=1} y^{a}_{kig} = 1$ for all $k \in K$ (compare (25)) and $\sum _{k \in K} y^{a}_{kig} = x_{ig} = 1$ for all $i \in I$ with $x_{ig} = 1$ holds (compare (26)).

We can repeat the procedure for every pair (a, g) with $a \in A$ and $g \in G$. Together,

$$\begin{aligned} \sum _{a \in A} \sum _{g \in G} \sum _{i \in I} \sum _{j \in I: i<j} d^a_{ij} x_{ig} x_{jg} = \sum _{a \in A} \sum _{i \in I} \sum _{g \in G} \sum _{k \in K} c_k av_i^a y^a_{kig}, \end{aligned}$$

and (25), (26), and (27) are fulfilled. Moreover, (25) leads to

$$\begin{aligned} \begin{aligned}&\sum _{k \in K} \sum _{i \in I} y_{kig}^a = |K| \\ {\mathop {\Longrightarrow }\limits ^{(26)}} \;&\sum _{i \in I} x_{ig} = |K| = |I|/|G|, \\ \end{aligned} \end{aligned}$$

as $|K| = |I|/|G|$, for all $g \in G$ in every feasible solution of (2), (4), and (24)–(27). Thus, every assignment of $x_{ig}$ variables which is feasible for (2), (4), and (24)–(27) is also feasible for (1)–(4). Together the theorem follows. $\square$

The idea of the proof is that it is still optimal to assign the items assigned to a group in decreasing order of their attribute values to the blocks (compare (23) and the following explanations). This means that, given fixed $x_{ig}$ variables, (1)–(4) and (2), (4), and (24)–(27) are solved optimally if we assign for each attribute and each group g the items assigned to that group, i.e. with $x_{ig} = 1$, in decreasing order of their attribute values to the blocks (set $y^a_{kig}$ accordingly). If (2), (4), and (18) has a feasible solution, $y^a_{kig} = b^a_{ki} \cdot x_{ig}$ holds in an optimal solution for all $i \in I$, $a \in A$, $k \in K$, and $g \in G$ ($b^a_{ki}$ according to Assumption 1). If not, a pair of items i and j with $b^a_{ki} = b^a_{kj} = 1$ for an $a \in A$ and a $k \in K$ exists which are assigned to the same group ($x_{ig} = x_{jg} = 1$ for a $g \in G$). Thus, (18) is not fulfilled for all $a \in A$, $g \in G$, and $k \in K$. In other words, our model (2), (4), and (24)–(27) decides in the assignment of the y variables which block constraints (18) should be violated, if necessary, such that (1) is maximized. Thereby, we avoid the drawback of the block constraints that there might be no feasible solution but still benefit from the formulation on the right side of (19).

Let us consider an example. Let $|A| = 3$, $|I| = 4$, and $|G| = 2$. Let the attribute values be like in Table 1. If we assign the items according to Assumption 1 to blocks, items 1 and 2 are assigned to the first block according to the first attribute, i.e. $b_{11}^1 = b_{12}^1 = 1$ and $b_{23}^1 = b_{24}^1 = 1$. For the second attribute we get $b_{11}^2 = b_{13}^2 = 1$ and $b_{22}^2 = b_{24}^2 = 1$. For the third attribute items 1 and 4 are in the first block, i.e. $b_{11}^3 = b_{14}^3 = 1$ and $b_{22}^3 = b_{23}^3 = 1$. This means that item 1 is for the first attribute with item 2 in one block, for the second attribute with item 3 and for the third attribute with item 4. Thus, there is no feasible solution fulfilling (2), (4), and (18).

Table 1 Attribute values for the example

There are three possibilities to assign four items to two groups with two items each. They are

$$\begin{aligned} \begin{aligned}&x_{11} = x_{21} = 1: |1-1| + |1-0| + |0.01-0| = 1.01 \\&x_{32} = x_{42} = 1: |0-0| + |1-0| + |0-0.01| = 1.01, \\&\\&x_{11} = x_{31} = 1: |1-0| + |1-1| + |0.01-0| = 1.01 \\&x_{22} = x_{42} = 1: |1-0| + |0-0| + |0-0.01| = 1.01, \\ \end{aligned} \end{aligned}$$

and

$$\begin{aligned}&x_{11} = x_{41} = 1: |1-0| + |1-0| + |0.01-0.01| = 2 \nonumber \\&x_{22} = x_{32} = 1: |1-0| + |0-1| + |0-0| = 2, \end{aligned}$$

(28)

where the right side equals the sum of pairwise differences over all attributes of the two items assigned to the group ($\sum _{a=1}^3 \sum _{i=1}^4 \sum _{j:j>i} d_{ij}^a x_{ig}x_{ig}$). Hence, the third solution has the largest objective value such that the model sets $x_{11} = x_{41} = x_{22} = x_{32} = 1$ (beside symmetry) which fulfills (2) and (4).

As we assign two items to each group, $c_1 = 1$ and $c_2 = -1$ (compare (20) and (21)). Thus, (24) is maximized if we set $y_{kig}^a$ variables such that the item with the larger attribute value of the group is in block one and the item with the smaller attribute value of the group is in block two. Hence, the model sets $y_{111}^1 = y_{111}^2 = y_{111}^3 = y_{122}^1 = y_{222}^2 = y_{122}^3 = y_{232}^1 = y_{132}^2 = y_{232}^3 = y_{241}^1 = y_{241}^2 = y_{241}^3 = 1$ and all remaining $y_{kig}^a$ variables to zero. Then, (25)–(27) are fulfilled and (24) equals

$$\begin{aligned} \begin{aligned}&c_1 \cdot (av_1^1 + av_2^1 + av_1^2 + av_3^2 + av_1^3 + av_2^3) \\&\qquad + c_2 \cdot (av_3^1 + av_4^1 + av_2^2 + av_4^2 + av_3^3 + av_4^3) \\&\quad = 1 \cdot (1 + 1 + 1 + 1 + 0.01 + 0) - 1 \cdot (0 + 0 + 0 + 0 + 0 + 0.01) \\&\quad = 4.01 - 0.01 = 4, \\ \end{aligned} \end{aligned}$$

which equals the sum in (28). If we compare $b_{ki}^a$ and $y_{kig}^a$, $y_{kig}^a \ne b_{ki}^a \cdot x_{ig}$ for items 2 and 4 and attribute 3. While item 4 is assigned to block 1 according to Assumption 1, the model assigns item 2 to block 1 (can also be item 3). Thus, the model selects the block constraints (18) which should be violated if necessary (here both block constraints of attribute 3).

4.2 Varying group sizes

We adapt the approach of the previous subsection in this subsection to investigate the relaxation of (3) to (5) and obtain our reformulation of (1)–(2) and (4)–(5).

We replace $c_k$ and ${\bar{c}}_k$ in the following by $c_{k{\bar{k}}}$ and ${\bar{c}}_{k{\bar{k}}}$, respectively, because individual groups may contain a different number of items. This means that ${\bar{c}}_{k{\bar{k}}} = {\bar{c}}_k$ for $|K| = {\bar{k}}$ in (21) and (22), respectively, and all $k \in K$. Correspondingly, $c_{k{\bar{k}}} = c_k$ for $|K| = {\bar{k}}$ in (20) and all $k \in K$. Note that ${\bar{k}} \le \max _g u_g$.

Moreover, we introduce the binary variable $w_{g{\bar{k}}}$ which is one if group g has ${\bar{k}}$ blocks, i.e. g has ${\bar{k}}$ assigned items. Variable $y^a_{kig}$ is replaced by variable ${\bar{y}}^a_{kig{\bar{k}}}$ which is defined continuously between zero and one but is one if item i is assigned to block k in group g and group g has ${\bar{k}}$ assigned items. Both variables, w and ${\bar{y}}$, are for all $g \in G$ only defined for $l_g \le {\bar{k}} \le u_{g}$. Moreover, we fix ${\bar{y}}^a_{kig{\bar{k}}} = 0$ for $k > {\bar{k}}$.

By this, we get the following model formulation:

$$\begin{aligned}&\max \; \sum _{a \in A} \sum _{i \in I} \sum _{g \in G} \sum _{l_g \le {\bar{k}} \le u_g} \sum _{k = 1}^{{\bar{k}}} c_{k{\bar{k}}} av_i^a {\bar{y}}_{kig{\bar{k}}}^a \end{aligned}$$

(29)

$$\begin{aligned}&(2), (4) \nonumber \\&\sum _{i \in I} \sum _{l_g \le {\bar{k}} \le u_g} {\bar{y}}_{kig{\bar{k}}}^a \le 1 \quad \quad \quad \quad \quad \,\,\,\,\forall a \in A, g \in G, k \in K: k \le u_g \end{aligned}$$

(30)

$$\begin{aligned}&\sum _{l_g \le {\bar{k}} \le u_g} \sum _{k \in K:k \le {\bar{k}}} {\bar{y}}_{kig{\bar{k}}}^a = x_{ig} \quad \quad \quad \! \forall a \in A, i \in I, g \in G \end{aligned}$$

(31)

$$\begin{aligned}&0 \le y_{kig{\bar{k}}}^a \le w_{g{\bar{k}}} \quad \quad \quad \quad \quad \quad \quad \quad \,\,\forall a \in A, i \in I, g \in G, \nonumber \\&\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \qquad \quad {\bar{k}} \in \{ l_g, ..., u_g \}, k \in K: k \le {\bar{k}} \end{aligned}$$

(32)

$$\begin{aligned}&\sum _{l_g \le {\bar{k}} \le u_g} {\bar{k}} \cdot w_{g{\bar{k}}} = \sum _{i \in I} x_{ig} \!\quad \quad \quad \quad \forall g \in G \end{aligned}$$

(33)

$$\begin{aligned}&\sum _{l_g \le {\bar{k}} \le u_g} w_{g{\bar{k}}} = 1 \quad \quad \quad \!\,\,\quad \qquad \quad \quad \, \forall g \in G \end{aligned}$$

(34)

$$\begin{aligned}&w_{g{\bar{k}}} \in \{ 0,1\} \quad \quad \quad \quad \quad \,\, \qquad \quad \quad \quad \, \forall g \in G, l_g \le {\bar{k}} \le u_g \end{aligned}$$

(35)

The model sets $x_{ig}$ variables to assign items to groups. Thereby, it ensures that at least $l_g$ and at most $u_g$ items are assigned to group $g \in G$ (33). Because of (33)–(35), $w_{g{\bar{k}}}$ indicates the number of items in group g. Given $w_{g{\bar{k}}}$, (32) fixes ${\bar{y}}_{kig{\bar{k}}}^a$ for all but one ${\bar{k}}$ (dependent on g) to zero. So, $\sum _{l_g \le {\bar{k}} \le u_g} (\cdot )$ includes only one non-zero addend in (29)–(31) such that they set ${\bar{y}}^a_{kig{\bar{k}}}$ in line with (24)–(26) and the argumentation in the proof of Theorem 1.—Note that we fix ${\bar{y}}^a_{kig{\bar{k}}} = 0$ for $k > {\bar{k}}$. Thus, (30) is an equality for $k \le {\bar{k}}$ and the left side of (30) is zero for $k > {\bar{k}}$.—Hence, the largest attribute values within each group are multiplied with the largest $c_{k{\bar{k}}}$ values in (29). By this, we are able to prove the following theorem which is an analogon to Theorem 1.

Theorem 2

The model formulation (2), (4), and (29)–(35) is equivalent to the formulation (1)–(2) and (4)–(5) in the sense that both model formulations lead to the same objective value for any feasible assignment of the $x_{ig}$ variables.

Proof

Let any feasible solution of (1)–(2) and (4)–(5) be given. In the following, we decompose the instance into one instance per combination of attributes and groups, i.e. given $a \in A$ and $g \in G$. This reduced instance consists of all items assigned to the fixed group g, i.e. the items with $x_{ig} = 1$ in the solution of (1)–(2) and (4)–(5). Since $x_{ig}$ variables are fixed, we can set $w_{g{\bar{k}}} = 1$ for ${\bar{k}} = \sum _{i \in I} x_{ig}$ and zero for all other ${\bar{k}}$s. Thus, (33)–(35) are fulfilled. Furthermore, (32) fixes $y^a_{kig{\bar{k}}}$ to zero for all but one ${\bar{k}}$ and all $a \in A, i \in I, g \in G,$ and $k \in K$. Thus, ${\bar{k}}$ is fixed in (29)–(31). Given the fixed ${\bar{k}}$, it follows by the same argumentation as in the proof of Theorem 1 that both model formulations, (1)–(2) and (4)–(5) as well as (2), (4), and (29)–(35), have the same objective value for the given solution.

It remains to show that each feasible solution of (2), (4), and (29)–(35) is also feasible for (1)–(2) and (4)–(5). As $w_{g{\bar{k}}}$ is binary (35), $w_{g{\bar{k}}} = 1$ for exactly one $l_g \le {\bar{k}} \le u_g$ for all $g \in G$ due to (34). By this, (33) implies that $l_g \le \sum _{i \in I} x_{ig} \le u_g$ for all $g \in G$. Thus, (5) is fulfilled. Since (2) and (4) are part of both model formulations, a feasible solution of (2), (4), and (29)–(35) is also feasible for (1)–(2) and (4)–(5). $\square$

The model formulation (2), (4), and (29)–(35) is clearly a generalization of the setting with equal-sized groups ((2), (4), and (24)–(27)). However, we need a further set of binary variables $w_{g{\bar{k}}}$ for the number of items within each group. Thus, there is a further generalization of (2), (4), and (24)–(27) but a special case of (2), (4), and (29)–(35) where we do not need $w_{g{\bar{k}}}$ variables. If we set $l_g = n_g = u_g$, i.e. fix the number of items assigned to each group (not necessarily with $n_g = n_{g'}$ for all $g, g' \in G$), $\sum _{l_g \le {\bar{k}} \le u_g} (\cdot )$ contains only one addend such that $w_{g,n_g} = 1$ due to (34). So $w_{g{\bar{k}}}$ is already determined such that the model can be reformulated to omit $w_{g{\bar{k}}}$ variables. Together with $w_{g{\bar{k}}}$, ${\bar{k}}$ is known for each g. Thus, ${\bar{k}}$ can be omitted in the definition of $y^a_{kig{\bar{k}}}$ (compare (32)).

5 Computational study

This section describes our computational study which is divied into two parts. In the first part, we consider equal-sized groups and compare the model formulations (1)–(4), called standard, (12)–(17), called Papenberg and Klau, and (2), (4), and (24)–(27), called blocks. In the second part, we consider the case with varying group sizes and the most general formulations of standard ((1)–(2) and (4)–(5)) and blocks ((2), (4), and (29)–(35)). The models were implemented in GAMS (version 32.0) and solved by CPLEX (version 12.10). The standard model was implemented in the linearized version, i.e. we used the formulations (2)–(4) and (6)–(10) and (2) and (4)–(10), respectively. The symmetry breaking constraints (11) were added to the standard model as well as to the blocks model when equal-sized groups are considered. The computational study was executed on a single AMD EPYC 7302 core with 2.99GHz. Section 5.1 describes the composition, Sect. 5.2 the results for the case with equal-sized groups, and Sect. 5.3 the results for the case with varying group sizes.

5.1 Composition

We tested the models with instances with 10, 20, 30, 40, 50, 60, 70, and 80 items. All of them were distributed into 2 and 5 groups. Starting with 20 items they were also distributed in 10 groups. 60, 70, and 80 items were further distributed into 15 groups and 80 items into 20 groups. For the case with equal-sized groups we used only those settings where the number of items divided by the number of groups is integer. All settings were tested in 30 runs each for 3, 5, and 10 attributes. Attribute values were determined according to a [0,1] uniform distribution. Considering [0,1] values is no restriction, as we are only interested in their absolute differences and each other interval can be normalized to [0,1] without changing the relation of two attribute values. Before we determined the range for the group sizes ($l_g$ and $u_g$) for the second part of the computational study, we distributed the items randomly to the groups according to the following procedure to ensure that there is a feasible assignment: First, we draw $|G|-1$ uniform integers between 1 and $|I|-|G|$. They were sorted in increasing order and we computed the differences between 0 and the first, the first and the second, and so on and added 1 to all of them. Moreover, we computed the difference between the sum of them and |I|. Thereby, we ensured that each difference is positive. In total, this leads to |G| numbers which sum up to |I|. Finally, we set $n_1$ equal to the first of them, $n_2$ equal to the second, and so on. Afterwards, we determined $l_g$ and $u_g$. We set $l_g = \max (1,n_g - {\mathcal {U}}\left\{ 0,\lceil n_g \cdot 0.05 \rceil \right\} )$ and $u_g = n_g + {\mathcal {U}}\left\{ 0,\lceil n_g \cdot 0.05 \rceil \right\}$, i.e. the group size interval is determined uniformly and bounded by about 10% around $n_g$. We interrupted the search after 30 minutes (1800 seconds) if no solution was proved to be optimal like it was done by Gallego et al. (2013).

Table 2 Results for three attributes

Table 3 Results for five attributes

Table 4 Results for ten attributes

5.2 Results (equal-sized groups)

Tables 2–4 present the results with equal-sized groups split according to the number of attributes. The tables are structured as follows: The first two columns indicate the parameter setting. The next six columns show the results for the blocks model (average objective value, average computation time in seconds, average gap in percent, average objective value of the relaxed model, number of feasible solutions found, and number of optimal solutions found). The next six columns present the same classifications numbers for the standard model, the last six for the model by Papenberg and Klau. Note that average objective values contain only instances where the corresponding model found a feasible solution. Average gaps contain only instances where the corresponding model found a feasible but no proven optimal solution.

Table 2 presents the results for three attributes. The model formulations blocks and standard found for all instances a feasible solution. The formulation by Papenberg and Klau found also for all settings beside the one with 70 items and 5 groups a feasible solution. However, for the setting with 70 items and 5 groups no feasible solution was found. Having a closer look on the problem setting, finding a feasible solution is easy because any assignment with exactly |I|/|G| items in each group is feasible. The reason why we have not found a feasible solution for the model formulation by Papenberg and Klau seems to be that CPLEX used the whole 1800s in the root node such that no solution was detected (also for five and ten attributes).

blocks terminated for almost all instances up to 60 items with a proven optimal solution within 1800s and terminated also for larger instances often with a proven optimal solution before the time limit was reached. The two other formulations, however, found only optimal solutions for small instance sizes up to 20 (standard) and 30 items (Papenberg and Klau), respectively. Both models reached comparable results regarding the number of optimally solved instances.

Considering the solution gap for the instances for which we found feasible solutions but could not prove optimality, the model formulation by Papenberg and Klau clearly outperformed the standard formulation. For the blocks model the gap was almost zero for all instances which could not be solved to proven optimality. The required computation times confirm the results for the three model formulations.

In total, we can conclude that the blocks model leads for instances with three attributes to the best results in comparison with the standard model and the formulation by Papenberg and Klau. If we solve the blocks model but relax (4), i.e. with $0 \le x_{ig} \le 1$ for all $i \in I$ and $g \in G$ instead of (4), we find a reason for it. Column 6 shows the average objective values for the relaxed model of blocks, column 12 the corresponding average objective values for the standard model and column 18 for the formulation by Papenberg and Klau (relaxing (17)). Relaxing blocks leads to substantially better upper bounds for the objective value than relaxing standard. Relaxing the formulation by Papenberg and Klau leads to slightly worse upper bounds than the blocks formulation. However, the difference between the average optimal objective value and the average optimal objective value of the relaxed model is still large. Thus, we can assume that we have to fix a large number of $x_{ig}$ variables to zero or one before we get tight upper bounds by relaxing the remaining binary constraints in a branch-and-bound procedure. This may also explain why larger instances could not be solved reliably to optimality.

Tables 3 and 4 show the results for five and ten attributes, respectively. For the standard model the results are similar for all three numbers of attributes. The performance of the blocks model decreases. The larger the number of attributes is the lower is the number of solutions where we proved optimality within 1800s. However, the gap is still comparably small with under 5% on average. In contrast, the formulation by Papenberg and Klau leads to better results regarding the number of proven optimal solutions found and the gap the larger the number of attributes is. Interestingly, the model by Papenberg and Klau requires less computation time if the number of attributes increases. For both of the other models computation times increase if the number of attributes increases. Because of this the model by Papenberg and Klau is faster than blocks for some settings with up to 30 items—especially if the number of attributes increases.

5.3 Results (varying group sizes)

Tables 5–7 present the results regarding the setting with varying group sizes. Analogous to Sect. 5.2 the tables are split according to the number of attributes. The tables are structured as in Sect. 5.2. As the formulation by Papenberg and Klau works only for equal-sized groups, we consider only the blocks and the standard formulation in this subsection.

Table 5 presents the results for three attributes. Both model formulations found for almost all instances a feasible solution but the blocks model found clearly more proven optimal solutions. For up to 50 items even all instances could be solved to optimality while standard could only solve instances with two groups or 10 items to optimality. This results also in smaller computation times for the blocks model in comparison with the standard model. Moreover, the blocks formulation reached small gaps after 1800s for up to 70 items and gaps up to 8.1% on average for instances with up to 80 items.

Table 6 examines the performance of the models for five attributes. For five attributes blocks still managed to find feasible solutions for almost all instances but had trouble in proving optimality for larger numbers of groups (at least 5) in combination with larger numbers of items (at least 40). From 60 items on the model further struggled with instances with two groups. Nevertheless, there is again a transition where the model found less optimal solutions but reached small gaps (40 or 50 items and 5 or 10 groups, and 60, 70 or 80 items and 2 or 5 groups).

Table 5 Results for three attributes

Table 6 Results for five attributes

Table 7 Results for ten attributes

The trend confirms for ten attributes (Table 7). Although blocks still found in at least 75% of the instances a feasible solution in each setting (23 out of 30 for 80 items and 2 groups), it found only for small instances up to 20 items always a proven optimal solution. Accordingly, the gaps increased for larger instances. However, there is again a transition where the model did not manage to find proven optimal solutions for all instances but reached small gaps (25 items and 10 groups, 30 or 40 items and 5 groups, and 50 items and 2 groups). The development of the solution quality for standard is similar as in the setting with equal-sized groups although the model is able to prove some solutions to be optimal for larger instances with two groups. A reason could be that $l_g$ and $u_g$ and therefore the group size is determined randomly such that some instances might be particularly easy to solve if one of the groups has only a small number of items assigned while the other one has a large number of assigned items. In comparison with the setting with equal-sized groups, the blocks model had more difficulties with the setting with varying group sizes which results in less instances which could be solved to proven optimality within 1800s and larger gaps for those which could not be solved to proven optimality.

6 Conclusion

We introduced a new mixed-integer programming formulation for the MDGP with attribute values. As common applications like the assignment of students to groups (grades, gender, international or not) or surgery scheduling (surgery duration) use attribute values, this is an interesting special case of the MDGP. Nevertheless, using the Manhattan metric is a limitation of our study. Our MIP clearly outperforms comparable approaches for instances with attribute values. Moreover, it is able to solve instances of realistic size, for example in the assignment of students to seminars—e.g. 40 students assigned to two seminar groups or 20 students within a seminar assigned to working groups with two or four students each—in reasonable time to (near) optimality.

As our model formulation is able to solve larger instances to near optimality, the model can help to evaluate heuristic approaches for the general MDGP by testing them on the version with attribute values even for a larger number of attributes.

This paper shows that it is worth to have a closer look on the data structure of the MDGP. Thus, a direction for future research may also be to investigate how instances with binary or integer attributes or other special data structures and their combinations over several attributes, which occur in practical applications, can be tackled by made-to-measure solution approaches.