Decision space robustness for multi-objective integer linear programming

Abstract

In this article we introduce robustness measures in the context of multi-objective integer linear programming problems. The proposed measures are in line with the concept of decision robustness, which considers the uncertainty with respect to the implementation of a specific solution. An efficient solution is considered to be decision robust if many solutions in its neighborhood are efficient as well. This rather new area of research differs from robustness concepts dealing with imperfect knowledge of data parameters. Our approach implies a two-phase procedure, where in the first phase the set of all efficient solutions is computed, and in the second phase the neighborhood of each one of the solutions is determined. The indicators we propose are based on the knowledge of these neighborhoods. We discuss consistency properties for the indicators, present some numerical evaluations for specific problem classes and show potential fields of application.

1 Introduction

In industrial or economical applications, a computed optimal or efficient solution may be subject to small changes or deviations during its implementation. These deviations may be due to technical, political, and/or strategic reasons, which are generally not known beforehand and which are thus not included in the optimization model. As a consequence, a solution obtained with an optimization method may, in practice, not be implementable, or may be affected with severe drawbacks.

In this paper, we focus on multi-objective integer programming problems that have a discrete solution set. Implementation uncertainties then relate to specific variables or, for example, items that were selected for a knapsack solution, but that become unavailable when the solution is to be implemented. In this situation, we can try to anticipate the potential failure of (parts of) solutions and incorporate appropriate robustness measures into the optimization process.

Dealing with uncertainty or, more general, with the imperfect knowledge of data in single and multi-objective optimization is not new. Imperfect knowledge about data and models in general is mainly due to four aspects: the arbitrariness when, for example, we opted for a specific objective function or constraint among several others that would be also adequate; the uncertainty since we are using methods, tools, and approaches for modeling and anticipating an unknown future; the imprecision related with the tools we are using to measure objects; and, the ill-determination related with the fact that we are modeling some aspects that are possibly not well determined and defined (for more details see, for example, Roy et al., 2014).

Dealing with the imperfect knowledge about the whole model in single and multi-objective optimization is rather a Herculean task. Researchers have been concentrating their attention mainly on the imperfect knowledge of some type of data, i.e., the model parameters. For single-objective optimization we can mention three fundamental references: Ben-Tal et al. (2009), Kouvelis and Yu (1997), and Birge and Louveaux (1997).

In multi-objective optimization there is a long tradition for dealing with the imperfect knowledge of data and several approaches have been proposed in the literature. For a survey about different concepts of robustness in multi-objective optimization see, for example, Ide and Schöbel (2016). The following is a brief and non-exhaustive summary of main approaches found in the literature: stochastic programming (Inuiguchi et al., 2016; Słowiński et al., 1990); fuzzy/possibilistic programming (Adeyefa and Luhandjula, 2011; Inuiguchi et al., 2016; Słowiński et al., 1990); interval programming (Oliveira and Henggeler-Antunes, 2007); parametric programming (Dellnitz and Witting, 2009; Witting et al., 2013); minimax like programming (Aissi et al., 2009; Ehrgott et al., 2014); set valued optimization (Ide and Köbis, 2014); and, Monte Carlo simulation (Mavrotas et al., 2015). The different approaches have in common to find solutions which are more or less robust with respect to changes in some parameters which occur in the constraints and/or objectives of an optimization problem. We refer to this as parameter robustness in the following. In this context, a solution that is more or less immune to parameter changes is a robust solution.

If, however, the uncertainty is an intrinsic property of the variables, we talk about decision space robustness, also denoted as implementation or variable robustness (see, for example, Beyer et al., 2007). Very recently, Eichfelder et al. (2015, 2017, 2019) introduced and made some studies about the concept of uncertainty with respect to the implementation of variable values in continuous multi-objective optimization. This problem is, however, not limited to the continuous case. In project selection a project might be canceled during the implementation and the corresponding investment is free to be spent on an other project. In a routing problem an edge or a node along the shortest path might be blocked requiring a local detour. In a job assignment problem, a certain assignment is not implementable and has to be substituted.

All these applications have in common that one is not willing to completely discard a once chosen optimal solution only because one single component of it is not available/blocked/fails or would be affected with severe drawbacks. The repair of a solution can be considered as replacing the chosen solution by a neighboring one. The robustness measures that we discuss in this paper are motivated by the following questions:

• Are there enough feasible neighbors around the selected efficient solution that may be used to replace it in case an impossibility occurs at the moment of its implementation?

• Are there enough efficient neighbors around the selected efficient solution?

• Are there enough high quality neighbors around the selected efficient solution? This leads to a second question: How good should be the quality of the neighbors in the worst case or the average case?

The purpose of this paper is to answer the questions by presenting ways of measuring the robustness in multi-objective discrete optimization problems. In this attempt, the paper covers a variety of MOILP problems with a combinatorial structure with applications in a vast range of areas.

This paper is organized as follows. Section 2 summarizes the fundamental concepts, their definitions, and the adopted notation. Section 3 presents several robustness indicators for MOILP problems, some numerical results, theoretical properties of the indicators and a fundamental distinction between robustness and representation. In Sect. 4 the proposed robustness concepts are applied in the context of representation problems and decision making using Electre Tri-C. Finally, some concluding remarks and avenues for future research are provided.

2 Concepts, definitions, and notation

This section is devoted to the presentation of the problem, the main concepts of dominance and efficiency, as well as the concepts of neighborhood and adjacency. It ends with the introduction of an illustrative example.

2.1 Problem formulation

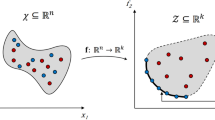
A general multi-objective optimization problem can be stated as follows.

$$\begin{aligned} {\displaystyle \max _{x \in X} f(x)} \end{aligned}$$

(1)

where $f(x) = \big (f_1(x),\ldots ,f_p(x)\big )^\top$ is a vector-valued function such that $f: X\longrightarrow \mathbb {R}^p$ with $X \subseteq \mathbb {R}^n$. In this formulation $\mathbb {R}^n$ is called the decision space, while its subset X represents the feasible region. Each function $f_k$, for $k=1,\ldots ,p$, is a real-valued function such that $f_k\;:\; X \longrightarrow \mathbb {R}$, and $\mathbb {R}^p$ is referred to as the objective space.

In what follows we will restrict ourselves to discrete multi-objective optimization problems where the feasible region X can be defined as $X= P\, \cap \, \mathbb {Z}^n$, with $P=\{x\in \mathbb {R}^n :A\,x\leqq b,\; x\geqq 0\}$ being a polyhedron, i.e., the intersection of finitely many halfspaces.

The functions $f_k$, for $k=1,\ldots ,p$, are linear. They can be defined as follows: $f_k(x) = c^{k\top }\,x$, where $c^{k} = (c_{1}^{k},\ldots ,c_{n} ^{k})^\top \in \mathbb {R}^n$ is the vector of coefficients of the objective function $f_k$ for $k=1,\ldots ,p$. Within such a framework we are placed in the context of multi-objective integer linear programming. This problem can be presented in a more compact way, as follows.

$$\begin{aligned} {\displaystyle \max _{x \in X} C\,x,} \end{aligned}$$

(2)

where $C=(c^{1},\ldots ,c^{p})^\top \in \mathbb {R}^{p\times n}$ is a $p\times n$ matrix in which each row corresponds to a vector of coefficients $c^{k\top }$, for $k=1,\ldots ,p$.

The outcome vector of a feasible solution $x \in X$ is the image of x under the vector-valued function, i.e., f(x). The set $Z:= \{f(x):x \in X\} = f(X) \subseteq \mathbb {R}^p$ is the set of feasible outcome vectors in the objective or outcome space $\mathbb {R}^p$.

It is well-known that whenever $p \geqslant 2$ there is no canonical order in the objective space. For $z^{\prime }$, $z^{\prime \prime }\in \mathbb {R}^p$ the following vector componentwise order can thus be used.

$$\begin{aligned} z^{\prime } \geqq z^{\prime \prime }&\iff z^{\prime }_k \geqslant z^{\prime \prime }_k, \qquad k=1,\ldots ,p, \\ z^{\prime } \ge z^{\prime \prime }&\iff z^{\prime }_k \geqslant z^{\prime \prime }_k, \qquad k=1,\ldots ,p,\;\; \text {with}\;\; z^{\prime } \ne z^{\prime \prime },\\ z^{\prime }> z^{\prime \prime }&\iff z^{\prime }_k > z^{\prime \prime }_k, \qquad k=1,\ldots ,p. \end{aligned}$$

In multi-objective optimization dominance relations replace the canonical ordering structure of real numbers. Based on the componentwise order the concept of dominance allows to define a partial order in the objective space of a multi-objective problem and make a distinction between dominated and non-dominated vectors or points as it will be shown in the next section. For a general introduction to multiobjective optimization see (Ehrgott, 2005; Steuer, 1986).

2.2 Dominance and efficiency

Let $z^\prime , z^{\prime \prime } \in \mathbb {R}^p$ denote two outcome vectors. Then, $z^\prime$ dominates $z^{\prime \prime }$ if $z^\prime \ge z^{\prime \prime }$.

Let $\bar{z} \in Z$ denote a feasible outcome vector. Then, $\bar{z}$ is called a non-dominated vector if there does not exist another $z \in Z$ such that $z \ge \bar{z}$. Otherwise, $\bar{z}$ is a dominated outcome vector. Let $Z_{\text {N}}$ denote the set of all non-dominated outcome vectors or points.

A feasible solution $\bar{x} \in X$ is called efficient if there does not exist another $x \in X$ such that $f(x) = C x \ge f(\bar{x}) = C \bar{x}$. Otherwise, $\bar{x}$ is called inefficient. Let $X_{\text {E}}$ denote the set of all efficient solutions. In the following we assume that all problems we are looking at have a nonempty and bounded efficient set, i. e., they fulfill $X_{\text {E}}\ne \varnothing$ and $|X_{\text {E}}|<a$ for some $a\in \mathbb {Z}$.

A non-dominated outcome vector $\bar{z} \in Z_{\text {N}}$ is said to be supported non-dominated if there is a real vector $\lambda \in \mathbb {R}^p$ with $\lambda \ge 0$ such that $\lambda ^\top \, \bar{z} \geqslant \lambda ^\top \, z$ for all other feasible outcome vectors $z\in Z$. Otherwise, the non-dominated outcome vector is called unsupported non-dominated. Analogously, the preimage of a supported non-dominated vector is called supported efficient solution, while the preimage of an unsupported non-dominated vector is called unsupported efficient solution. Let the sets of supported non-dominated vectors, unsupported non-dominated vectors, supported efficient solutions, and unsupported efficient solutions be denoted, respectively by $Z_{\text {sN}}$, $Z_{\text {uN}}$, $X_{\text {sE}}$, and $X_{\text {uE}}$.

2.3 Adjacency and neighborhood

In order to investigate the relations and distances between feasible solutions in the decision space, we need to introduce three concepts: adjacency, adjacency graph, and neighborhood structure. We adopt two concepts of adjacency as suggested in Gorski et al. (2011): An LP-based definition of adjacency and a combinatorial definition of adjacency. For the first, we have to assume that all feasible solutions in X correspond to extreme points of the linear programming relaxation of the problem, i.e., $X=\text{ ext }\{x\in \mathbb {R}^n: Ax \le b\}$ with some integer constraint matrix A and right-hand-side b. This is, for example, satisfied for the standard ILP formulations of shortest path and assignment problems and, more generally, for all problems with binary variables and a totally unimodular constraint matrix. Then two feasible solutions $x',x''\in X$ are called adjacent if $x''$ can be obtained from $x'$ by applying a single pivot operation. The motivation for this adjacency concept is that in the continuous case, i.e., when considering a multi-objective linear programming problem, the set of all efficient extreme points of the polyhedral feasible set is a connected set, see Isermann (1977). This means that for every pair of efficient extreme points there exists a sequence of pivot operations such that all intermediate extreme points are also efficient. Note that every problem with a finite feasible set allows for such a formulation and that the resulting concept of adjacency depends on the given ILP formulation of the problem and is in general not unique.

A combinatorial definition of adjacency, on the other hand, operates directly on the combinatorial structure of the considered problem. It is thus formulated for multi-objective combinatorial optimization problems (MOCO), i.e., for MOIP problems that possess a combinatorial structure. Examples are knapsack and assignment problems as well as shortest path, spanning tree, and network flow problems. Adjacency in this sense is always problem specific. For example, in an instance of the knapsack problem two binary solutions $x',x''$ can be considered adjacent if they differ in at most two variable entries, where at most one of these entries is equal to $1$ in each of the two adjacent solutions. Similarly, two spanning trees $x',x''$ of a minimum spanning tree problem are usually called adjacent if $x''$ can be obtained from $x'$ by adding an edge and removing another edge from the obtained cycle. In some of these cases, a combinatorial definition of adjacency may in fact be equivalent to an appropriate LP-based definition of adjacency. We refer to Gorski et al. (2011) for more details. In both cases, we refer to the operation of moving from one feasible solution $x'$ to an adjacent feasible solution $x''$ as an elementary move.

The notion of adjacency imposes an interrelation between the feasible solutions in X which can be represented in terms of a so-called adjacency graph. The adjacency graph for a set of solutions X is a graph $G=({V},E)$ where each node in V represents one solution in X and vice versa. Two vertices $v_{x^{\prime }}$ and $v_{x^{\prime \prime }}$ are connected by an edge $[v_{x^{\prime }}, v_{x^{\prime \prime }}] \in E$ if and only if the corresponding solutions ${x^{\prime }}$ and ${x^{\prime \prime }}$ are adjacent.

The neighborhood of a feasible solution x, denoted by ${\mathcal {N}}(x)$, is a subset of $X$ containing all feasible solutions $x^{\prime }$ that are adjacent to x. The solutions $x^{\prime }\in {\mathcal {N}}(x)$ are also called neighbors of x. In the following neighboring solutions will be considered as substitutes for a failing or blocked solution. Thereby, we distinguish two modelling approaches for the underlying uncertainty set: On one hand we may be required to exchange one item, where it does not matter which item. On the other hand we consider that individual items may fail and may be replaced by chosing an appropriate substitute from ${\mathcal {N}}(x)$ that does not contain this particular item. Both concepts are related to recoverable robustness, see, e.g., Kasperski and Zieliński (2017). The second can be considered as a special case of an interdiction problem where the interdiction sets contain subsets of cardinality one (see, e.g., Adjiashvili et al., 2014 for the more general approach of bulk robustness).

2.4 Illustrative example

To illustrate the neighborhood structure of a combinatorial optimization problem we use a bi-objective cardinality constrained optimization problem (CCP), which is also denoted as selection problem, c.f. Kasperski and Zieliński (2017):

$$\begin{aligned} \begin{array}{rl} \max \;\, f_1(x) \; = &{} \sum _{j=1}^n c^1_j \, x_j \\ \max \;\, f_2(x) \; = &{} \sum _{j=1}^n c^2_j \, x_j \\ \text {s. t.} &{} \sum _{j=1}^n x_j=\ell \\ &{} x_j\in \{0,1\},\quad j=1,\dots ,n \end{array} \end{aligned}$$

(CCP)

The feasible set of problem (CCP) is denoted by $X:=\{x\in \{0,1\}^n\,:\, \sum _{j=1}^n x_j=\ell \}$. We define one elementary move as swapping two variables, i.e., two feasible solutions $x$ and $x^\prime$ are adjacent if there exist $p,q\in \{1,\ldots ,n\}$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} x_p=0 \;\;\text {and}\;\; x^\prime _p=1&{} \text {for}\;\; p\in \{1,\ldots ,n\}, \\ x_q=1 \;\;\text {and}\;\; x^\prime _q=0&{} \text {for}\;\; q\in \{1,\ldots ,n\}\setminus \{p\}, \;\text {and} \\ x_j=x^\prime _j &{}\text {for all}\;\; j\in \{1,\ldots ,n\}\setminus \{p,q\} \end{array}\right. } \end{aligned}$$

Note that every vertex $v_{{x}}$ in $G$ has the same degree $|\mathcal {N}({x})| = \ell (n-\ell )$, i.e., the same number of neighbors.

Consider the following numerical example of a bi-objective cardinality constrained problem with 10 items:

$$\begin{aligned} \begin{array}{rrl} \max &{} f_1(x) &{}=\; (9, 5, 3, 5, 10, 5, 9, 9, 8, 4) \,x \\ \max &{}f_2(x) &{}=\; (6, 10, 10, 3, 8, 5, 3, 2, 4, 4)\,x \\ \mathrm {s.t.} &{} \displaystyle \sum _{i=1}^{10} x_i &{}=\; 5 \\ &{} x_i &{}\in \;\{0,1\} \quad \forall i\in \{1,\ldots ,10\}. \end{array} \end{aligned}$$

(3)

The set of non-dominated solutions for the previous problem is the following. The outcome vectors are given in descending lexicographical order with respect to the first objective function value.

$$\begin{aligned} \begin{array}{rl} Z_{\text {N}}=&\big \{(45,23),(42,29),(41,31),(38,32),(37,33),(36,37),(35,38),(32,39)\big \} \end{array} \end{aligned}$$

The sets of supported non-dominated and unsupported non-dominated outcome vectors are $Z_{\text {sN}}= \{z^1,\,z^3,\,z^6,\,z^7,\,z^8\}$ and $Z_{\text {uN}}= \{z^2,\,z^4,\,z^5\}$, respectively (see Fig. 1).

The set of corresponding efficient solutions is as follows.

$$\begin{aligned} \begin{array}{rl} X_{\text {E}}= &{} \bigl \{ (1000101110), (1100101100), (1100101010), (1100111000),\, \\ &{} \;\;\, (1100110010), (1110101000), (1110100010), (1110110000)\bigr \} \end{array} \end{aligned}$$

Analogously, the sets of supported efficient and unsupported efficient solutions are, respectively, the following, $X_{\text {sE}}= \{x^1,\,x^3,\,x^6,\,x^7,\,x^8\}$ and $X_{\text {uE}}= \{x^2,\,x^4,\,x^5\}$.

Let us now consider an efficient solution, say $x^3 \in X_{\text {E}}$ and determine its neighborhood $\mathcal {N}(x^3)$, which consists of $\ell (n-\ell )= 25$ solutions. The image of its neighborhood $z\bigl (\mathcal {N}(x^3)\bigr )$ is illustrated in the objective space in Fig. 2.

Fig. 1

The set of feasible, supported non-dominated (squares) and unsupported non-dominated (circles) outcome vectors for the illustrative example in Sect. 2.4

Fig. 2

The neighborhood of solution $x^3$ in the objective space (illustrative example in Sect. 2.4)

3 Robustness indicators for MOILP problems

In this section we introduce two main classes of robustness indicators for MOILP problems. The first subsection is devoted to a feasibility based robustness indicator, while the second subsection presents some efficiency based indicators. The section ends with a continuation of the example (3) introduced in Sect. 2.4.

3.1 Feasibility based indicators

In case of failure of an efficient solution, the feasibility based robustness indicator answers the question on the number of alternative neighboring solutions, which could be used to substitute. The motivation for our indicator comes from the fact that if, for some reason, we cannot implement exactly the solution x, we should be able to implement a neighboring solution $x' \in \mathcal {N}(x)$. Thus, the higher the cardinality of the neighborhood of a solution the more robust the solution (the larger the number of alternatives available for replacing it). In that sense, counting the number of feasible neighbors is a measure of robustness for a given efficient solution.

Definition 1

(Feasibility robustness indicator) Let $x\in X$ denote a feasible solution. Then the number of feasible neighbors of $x$

$$\begin{aligned} I^{cf}(x)=|\mathcal {N}(x)|, \end{aligned}$$

is called feasibility robustness indicator of $x$ w.r.t. $\mathcal {N}(x)$.

Large values of $I^{cf}$ correspond to more robust solutions having large numbers of feasible neighboring substitute solutions. Note that all solutions in the neighborhood of $x$ are considered as substitutes regardless of the containing elements. Alternative concepts taking failure of individual items into account are considered in Definitions 5 and 6, below.

In the case of problem (CCP) we have that $I^{cf}(x)=|\mathcal {N}(x)|=\ell \,(n-\ell )$ is constant, for all $x\in {X}$. Thus, feasibility robustness yields no meaningful result for (CCP). However, in problems with more complex combinatorial structure the number of feasible neighbors can vary significantly over the efficient set (cf. bi-objective shortest path example in Sect. 3.3).

3.2 Efficiency based indicators

Efficiency based indicators go beyond feasibility based robustness indicators and take into account not only the number of feasible solutions in the neighborhood but also their quality. Counting the number of efficient neighbors is a measure of robustness for a given efficient solution and allows to define a class of indicators. Another general class of indicators is defined by taking into account the relative distance of neighboring solutions from the Pareto-front.

3.2.1 Cardinality based efficiency indicator

Let $x \in X$ denote a feasible solution, and let $\mathcal {N}({x})$ denote the set of neighbors of $x$. The number of neighbors that are efficient is an indicator of how well the solutions in the neighborhood of $x$ perform with respect to the dominance ordering.

Definition 2

(Efficiency robustness indicator) Let $x\in X$. Then the number of efficient neighbors of $x$

$$\begin{aligned} I^{ce}(x)=|\mathcal {N}(x)\cap X_{\text {E}}|, \end{aligned}$$

is called efficiency robustness indicator of $x$ w.r.t. $\mathcal {N}(x)$ and $X_{\text {E}}$.

Large values of $I^{ce}$ correspond to more robust solutions having large numbers of efficient neighboring substitute solutions. Thereby all neighboring efficient solutions are considered as potential substitute solutions.

3.2.2 $\varepsilon$-robustness indicator

Let ${x}\in X$ and let $\mathcal {N}({x})$ denote the set of the neighbors of $x$. The $I^\varepsilon ({x})$ indicator measures the highest outcome criterion-wise degradation with respect to $Z_{\text {N}}$ over the complete set of neighbors of $x$. The smaller the value of $I^\varepsilon ({x})$ is the more robust $x$ is with respect to this indicator. Since this degradation is measured as a stretching factor with the origin as reference point we will assume from now on that $f(x)>0$ for all $x\in X$.

Definition 3

($\varepsilon$-robustness indicators) Let $x\in X$. Then

$$\begin{aligned} I^\varepsilon (x) = \max _{\begin{array}{c} \hat{x} \in \mathcal {N}({x}) \end{array}} \left\{ \min _{z \in Z_{\text {N}}} \left\{ \max _{k\in \{1,\dots ,p\}} \left\{ \frac{z_k}{f_k(\hat{x})} \right\} \right\} \right\} , \end{aligned}$$

is called $\varepsilon$-robustness indicator of $x$ w.r.t. $\mathcal {N}(x)$ and $Z_{\text {N}}$.

The value of the $\varepsilon$-robustness indicator of an efficient solution $x$ is the smallest scalar such that each image of a neighboring solution which is stretched by this scalar dominates at least one non-dominated point (the smaller $I^\varepsilon (x)$ the more robust $x$ is). One might wonder why we are not considering the stretching factor to make any neighboring point non-dominated, which would be reasonable from an application point of view. However, the determination of this factor is difficult since it would involve a disjunctive formulation (better in at least one objective function). Note the $\varepsilon$-robustness indicator takes the worst case into account, i.e., it measures the quality of the worst neighboring solution. This is particularly meaningful if no second stage optimization problem is solved to determine the best substitute solution.

The $\varepsilon$-robustness indicator is defined in analogy to the $\varepsilon$-indicator as used in representation and approximation algorithms (see, e.g., Zitzler et al., 2003). However, $\varepsilon$-indicator of a representative subset $R\subseteq Z_n$ follows a different paradigm:

$$\begin{aligned} \max _{z \in Z_{\text {N}}} \left\{ \min _{\hat{x}\in R} \left\{ \max _{k\in \{1,\dots ,p\}} \left\{ \frac{z_k}{f_k(\hat{x})} \right\} \right\} \right\} \end{aligned}$$

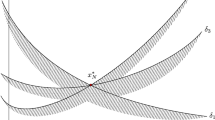
The value of the $\varepsilon$-indicator is the scalar stretching factor such that each point in the non-dominated set is dominated by at least one stretched non-dominated point in the representation. For a graphical comparison of $\varepsilon$-robustness indicator and $\varepsilon$-indicator see Fig. 3.

Note that in the $\varepsilon$-robustness indicator the worst substitute solution within the neighborhood is considered. This relates to the situation, where an broken optimal solution is replaced by an arbitrary substitute solution within its neighborhood. This is in contrast to the concept of recoverable robustness where a second-stage problem is solved to optimality to find a substitute, see e.g. Kasperski and Zieliński (2017).

Another approach using an additive $\varepsilon$-indicator within robust two-stage optimization is presented in Hollermann et al. (2020). Thereby, in each scenario the distance between the ideal Pareto-front for this scenario and the Pareto-front obtained by extending the first stage decision is minimized.

Fig. 3

Comparison of $\varepsilon$-robustness indicator $\varepsilon$ and $\varepsilon$-indicator $\varepsilon ^{\text {rep}}$. In both cases the same two points $z'$ and $z''$ are selected as an illustrative example for images of neighboring solutions or for a representative subset, respectively. In the illustration both points $z'$ and $z''$ are streched by the same factor such that at least one point is dominated by each or all points are dominated by at least one, respectively

Instead of considering the worst case, i.e., the maximal stretching factor required for a solution in the neighborhood, the $\varepsilon$-average-robustness indicator takes the average stretching factor into account. This can compensate neighboring solutions quite far away from the Pareto front if the majority of neighbors is efficient or close to the Pareto front.

Definition 4

($\varepsilon$-average-robustness indicator) Let $x\in X$. Then

$$\begin{aligned} I^{\Sigma \varepsilon }(x) = \frac{1}{|\mathcal {N}({x})|} \sum _{\begin{array}{c} \hat{x} \in \mathcal {N}({x}) \end{array}} \min _{z\in Z_{\text {N}}} \left\{ \max _{k\in \{1,\dots ,p\}} \left\{ \frac{z_k}{f_k(\hat{x})} \right\} \right\} , \end{aligned}$$

is called $\varepsilon$-average-robustness indicator of $x$ w.r.t. $\mathcal {N}(x)$ and $Z_{\text {N}}$.

In some applications, it may be meaningful to assume that, whenever an item becomes unavailable in an efficient solution $x$, it is replaced by the best possible alternative. In this case, we can consider an item-wise $\varepsilon$-robustness indicator as follows. Let $j\in \{1,\ldots ,n\}$ such that $x_j=1$, then ${\mathcal {N}^j}({x})$ denotes the set of neighbors of $x$, in which the j-th variable has value 0, i.e., $N^j(x):=\{\hat{x}\in N(x):\hat{x}_j=0\}$. The $I_{D}^\varepsilon ({x})$ indicator measures the highest outcome criterion-wise degradation with respect to $Z_{\text {N}}$, assuming that whenever a variable should be replaced, the best possible replacement will be used.

Definition 5

(Interdiction $\varepsilon$-robustness indicator) Let $x \in X$. Then

$$\begin{aligned} I_{D}^\varepsilon (x) = \max _{j\in \{1,\ldots ,n\} } \left\{ \min _{\hat{x} \in {\mathcal {N}^j}({x})} \left\{ \min _{z \in Z_{\text {N}}} \left\{ \max _{k\in \{1,\dots ,p\}} \left\{ \frac{z_k}{f_k(\hat{x})} \right\} \right\} \right\} \right\} , \end{aligned}$$

is called interdiction $\varepsilon$-robustness indicator of $x$ w.r.t. $\mathcal {N}(x)$ and $Z_{\text {N}}$.

Also in the case of interdiction robustness indicators we take an average case analysis into account by defining the interdiction $\varepsilon$-average-robustness indicator.

Definition 6

(Interdiction $\varepsilon$-average-robustness indicator) Let $x\in X\setminus \{0\}$, let $J:=\{j\in \{1,\ldots ,n\}:x_j=1\}$ and let $\varphi _j\in (0,1]$ denote a multiplier that reflects the probability or cost of replacing an item j, $j\in \{1,\dots ,n\}$ selected in $x$ when it gets unavailable. Then

$$\begin{aligned} I_{D}^{\Sigma \varepsilon }(x) = \frac{1}{\sum \limits _{j\in J} \varphi _{j}} \sum _{j\in J} \varphi _{j}\left( \min _{\hat{x} \in {\mathcal {N}^j}({x})} \left\{ \min _{z\in Z_{\text {N}}} \left\{ \max _{k\in \{1,\dots ,p\}} \left\{ \frac{z_k}{f_k(\hat{x})} \right\} \right\} \right\} \right) \end{aligned}$$

is called interdiction $\varepsilon$-average-robustness indicator of $x$ w.r.t. $\mathcal {N}(x)$ and $Z_{\text {N}}$.

Note that the multiplier $\varphi _j$ may reflect a probability, a weight, or in the case of our cardinality constrained knapsack problem we may choose $\varphi _j=1/\ell$, for $j=1,\ldots ,n$.

3.2.3 $\varepsilon$-robustness indicators for minimization problems

For minimization problems the $\varepsilon$-robustness indicators introduced in Sect. 3.2.2 above have to be defined with respect to a prespecified reference point $z^r$ that is strictly dominated by images of feasible points ($z^r> z$ for all $z \in Z$), or that is strictly dominated by all points that relevant for the problem at hand. We exemplarily state the formulation for the $\varepsilon$-robustness indicator introduced in Definition 3:

$$\begin{aligned} I^\varepsilon (x) = \max _{\begin{array}{c} \hat{x} \in \mathcal {N}({x}) \end{array}} \left\{ \min _{z \in Z_{\text {N}}} \left\{ \max _{k\in \{1,\dots ,p\}} \left\{ \frac{z^r_k-z_k}{z^r_k-f_k(\hat{x})} \right\} \right\} \right\} . \end{aligned}$$

All other indicators introduced in Sect. 3.2.2 can be reformulated analogously.

3.3 Illustration at bi-objective CCP and shortest path problems

Before we investigate the properties of the robustness indicators introduced above we evaluate all of them on the example introduced in Sect. 2.4. The computation of the robustness indicators is straight forward based on the determination of the neighborhood of the respective solution. The results are presented in Table 1.

Table 1 Robustness indicators for the example (3) introduced in Sect. 2.4. The best value of the respective robustness indicator is highlighted in bold

In order to show the effect of decision space robustness indicators for different combinatorial structures we additionally investigate a small real-life bi-objective shortest path problem, see Fig. 4. This graph represents the street map of the western hillside of the center of the city of Coimbra, connecting the old downtown (left side) to the campus Pólo I of the University of Coimbra (right side). This data was retrieved from Open Street Map with a python script using OSMnx API (Boeing, 2017), and corresponds to a rectangular area with coordinates $(40.20642, -8.42944)$ and $(40.20923, -8.42540)$ and network of type walk. The leftmost circle corresponds to the source, a crossing between Ferreira Borges street and Arco Almedina street at $(40.208897, -8.4290758)$, and the rightmost circle corresponds to the destination, the Paãßo Real at the University of Coimbra at $(40.2078443, -8.4260833)$. The length of each street segment was taken from Open Street Map with OSMnx API and the elevation of each location corresponding to a blue circle in Fig. 4 was retrieved with Open Topo Data API (https://api.opentopodata.org). There is a total of 77 locations and 186 street segments.

The walking paths between these two locations are a well-known tourist attraction in old town of Coimbra. The streets are not only narrow but also very steep. Although the length of a typical walking path between source and destination is less than 1 km, it implies a difference of 60 m in elevation.

Fig. 4

Real-life shortest path example

In our example, we consider the problem of finding a path from source to destination that minimizes both the total length and the sum of the positive slopes. For the computation of the solpe of an arc we take the ascent quadratically into account. A total of 10280 feasible (simple) paths between source and destination were computed, from which only four were efficient, as shown in the four plots in Fig. 5. The resulting total lengths (in meters) and total slopes as well as the decision space robustness indicator values are given in Table 2. The reference point z was computed as the total length of the longest feasible path plus one meter (2206.93 m) and the total slope of the steepest feasible path plus one (50.06). The neighborhood definition used to compute the decision space robustness indicators is given in Ehrgott and Klamroth (1997) and Gorski et al. (2011), that is, two paths are neighbors if their symmetric difference of their arc set in the residual graph corresponds to a single cycle. For the $I_{D}^{\Sigma \varepsilon }$ indicator, we used the same value of $\phi _j$ for every street segment, equals to the reciprocal of the total number of street segments.

Fig. 5

Four efficient paths for the shortest path example

Figure 5 indicates that $p^1$ and $p^2$ are neighboring paths, as well as $p^3$ and $p^4$, the former being shorter but steeper than the latter (see columns length and slope in Table 2). The difference of 4 m between $p^1$ and $p^2$ and between $p^3$ and $p^4$ is only due to a small detour that can be observed in the top-right corner of each plot in Fig. 5.

Table 2 suggests that paths $p^1$ and $p^2$ are more robust than $p^3$ and $p^4$ with respect to $I^{cf}$. Therefore, $p^1$ and $p^2$ contain more alternative detours in case some road segment becomes blocked. However, paths $p^3$ and $p^4$ are more robust with respect to $I^{\varepsilon }(p)$ and $I^{\Sigma \varepsilon }(p)$, that is, they are better with respect to the worst case quality of their neighboring paths.

Table 2 Total length, slope and decision space robustness indicators of the four efficient paths in Fig. 5

3.4 Comparison to decision robustness in the continuous case

In Eichfelder et al. (2017) decision robustness is considered for continuous multi-objective optimization problems. Since our robustness indicators significantly differ from the set-valued optimization approach suggested therein, we will show the differences and highlight why our indicators are better suited for the discrete structure of MOILPs. In the continuous case the set of realizations of a solution $x$ is assumed to be a compact set containing $x$, which we can identify with an appropriately chosen neighborhood $\mathcal {U}(x)$.

According to Eichfelder et al. (2017), a solution $x$ is called decision robust feasible if all of its realizations are feasible, i.e., $\mathcal {U}({x})\subset X$. Furthermore, a solution $x^*\in \hat{X}=\{x\in X:\mathcal {U}({x})\subset X\}$ is called decision robust efficient if there is no $x'\in \hat{X}\setminus \{x^*\}$ such that

$$\begin{aligned} f\bigl (\mathcal {U}({x'})\bigr ) \subset f\bigl (\mathcal {U}({x^*})\bigr ) + \mathbb {R}^p_+. \end{aligned}$$

In other words, a solution $x^*$ is denoted as decision robust efficient, if there is no other solution $x'\in \hat{X}\setminus \{x^*\}$ such that for all $x''\in \mathcal {U}(x')$ there exists an $x\in \mathcal {U}(x^*)$ such that $f(x) \le f(x'')$.

Applying this definition to discrete optimization problems is problematic, since discrete neighborhoods are not local like in the continuous case. Depending on the definition of neighborhood and the problem structure all neighborhoods of feasible solutions might contain infeasible solutions. Moreover, the discrete neighborhood of a solution often covers a significantly large part of the feasible region. In the assignment problem, for example, the distance between any pair of solutions is at most two elementary swaps, i.e., changes along alternating paths (Gorski et al., 2011). Thus, the images of the solutions in the neighborhood might be spread considerably in objective space. Consequently, the majority of solutions would be decision robust w.r.t. to the set-valued definition, because not all realizations are dominated by realizations of another solution. However, in the discrete case it is not possible to consider smaller neighborhoods than the ones defined by basic swaps. Consequently, we relaxed both concepts decision feasibility robustness and decision efficiency robustness to gradual indicators.

3.5 Properties of robustness indicators

This section provides some theoretical properties of the proposed indicators and the relationship between the three types of indicators. The most well-known unary requirements an indicator must fulfill are quite natural and easy to check. Despite these two aspects, it is important to consider them as properties of our indicators in this paper.

Proposition 1

(Existence) All the proposed indicators always exist and are well-defined, but they are not unique with respect to the feasible solutions $x \in X$ (i.e., two or more solutions can have the same indicator value).

Proof

It is easy to see from the definitions that all the indicators are well-defined formulas. Particularly, the denominator in the $\varepsilon$-robustness indicators ($I^{\varepsilon }(x)$, $I^{\Sigma \varepsilon }(x)$, $I_{D}^{\varepsilon }(x)$, $I_{D}^{\Sigma \varepsilon }(x)$) is larger than zero, as $f_k(x)>0$ for all $x\in X$ by assumption. In general, the indicators are not unique, i.e., they are non-injective, since several solutions can have the same indicator value as can be seen in Table 1.

Proposition 2

(Symmetry) All the proposed indicators are symmetric with respect to any permutation of the components and/or elements of their input.

Proof

Let us take for example indicator $I_{D}^{\varepsilon }(x)$, which has as input the solution $x = (x_1,\ldots ,x_j,\ldots ,x_n)$, the neighborhoods $\mathcal {N}^j(x)$, for $j=1,\dots ,n$, and the set of non-dominated points $Z_{\text {N}}$. It is easy to see that for any $x$ re-ordered as $x^{\pi } = (x_{\pi (1)},\ldots ,x_{\pi (j)},\ldots ,x_{\pi (n)})$, where $\pi :\{1,\ldots ,n\}\rightarrow \{1,\ldots ,n\}$ is an arbitrary permutation of the indices, the value of the indicator does not change. The same applies to any permutation of the elements of the sets $\mathcal {N}^j(x)$, for $j=1,\dots ,n$, and $Z_{\text {N}}$.

Proposition 3

(Scale invariance) Indicators $I^{\varepsilon }(x)$, $I^{\Sigma \varepsilon }(x)$, $I^{\varepsilon }_{D}(x)$, and $I^{\Sigma \varepsilon }_{D}(x)$ are positively homogeneous with respect to the coefficients of the matrix C, i.e., any multiplication with a positive scalar of the coefficients of the matrix, $\alpha \, C$, does not have impact on the values of any of these indicators. However, these indicators are not stable with respect to translations of the coefficients of C (i.e., linear affine transformations).

Proof

Positive homogeneity is only related with the aggregation operator:

$$\begin{aligned} \max \left\{ \frac{z_k}{f_k(\hat{x})}\right\} \end{aligned}$$

It is very easy to see that multiplying both $z_k$ and $c^{k\top }$ by $\alpha >0$ does not change the aggregation value since the operator is still the same:

$$\begin{aligned} \frac{\alpha \, z_k}{\alpha f_k(\hat{x})} = \frac{z_k}{f_k(\hat{x})}. \end{aligned}$$

The indicators are not stable with respect to linear affine transformations, which can be easily seen from the definition.

Proposition 4

If $I^\varepsilon ({x}) = 1$ then $|\mathcal {N}({x})| = |\mathcal {N}({x})\cap X_{\text {E}}|$.

Proposition 5

The relations between the following pairs of indicators hold.

$$\begin{aligned} I^{ce}(x)&\leqslant I^{cf}(x),&I_D^\varepsilon (x)&\leqslant I^\varepsilon (x), \\ I^{\Sigma \varepsilon }(x)&\leqslant I^{\varepsilon }(x),&I_D^{\Sigma \varepsilon }(x)&\leqslant I_D^{\varepsilon }(x). \end{aligned}$$

4 Fields of applications for the robustness indicators

The proposed robustness indicators can be considered as a tool to evaluate the quality of efficient solutions in an a-posteriori analysis. This additional quality measure can be utilized in different ways. Two possible approaches will be covered in this section.

Due to the possibly large number of non-dominated points (and efficient solutions) decision makers are confronted with huge amount of mathematically incomparable alternatives. The burden of the decision maker can be significantly reduced by the selection of a representative subset of non-dominated points/efficient solutions (see e.g., Sayın, 2000; Vaz et al., 2015). In an a-posteriori algorithm to determine a representation, decision space robustness can be integrated as an additional quality criterion, ensuring robustness of the representation.

Instead of leaving the decision to a human decision maker it is also possible to use automatic tools, so called decision support systems, to select the most preferred efficient solutions. Since the robustness of a solution can be considered as a quality criterion, it should be integrated in the process of decision making.

4.1 Decision space robust representations

We aim at the computation of a representative subset $R\subseteq X_{\text {E}}$ of efficient solutions, which has a fixed cardinality of $|R|=k$, optimizes some representation quality measure and is “decision space robust”. However, the decision space robustness indicators proposed in Sect. 3 gradually measure the robustness of a single solution. We thus extend this solution-wise definition to sets of solutions. Since every single solution in a representative subset should be a valuable choice for the decision maker, each one should satisfy a certain robustness level. This consideration leads us to a worst case analysis:

Definition 7

Let $R\subseteq X_{\text {E}}$ be a subset of efficient solutions and let

$I(x)\in \{ -I^{cf}(x), -I^{ce}(x), I^\varepsilon (x), I^{\Sigma \varepsilon }(x), I^\varepsilon _D(x)\}$ denote a decision space robustness indicator. Then the respective decision space robustness of $R$ is

$$\begin{aligned} I(R)=\max _{x\in R} I(x) \end{aligned}$$

Since $I^{cf}$ and $I^{ce}$ are to minimized (while the other indicators are to be maximized), we use here their negative values.

Most representation quality measures are based on points in the objective space. Since we are considering representative sets of the efficient set $R\subseteq X_{\text {E}}$ in the decision space, we adapt the definitions of uniformity, coverage, and $\varepsilon$-indicator (Sayın, 2000; Zitzler et al., 2003) to our notation. Note that the representation quality is increasing with increasing values of uniformity, thus we will use (contrary to the original definition) its negative value to obtain three minimization quality measures $Q^U$, $Q^C$, and $Q^\varepsilon$.

$$\begin{aligned}&\mathrm{Uniformity}&Q^U(R)=&-\min _{r^i,r^j \in R, r^i \ne r^j} \Vert f(r^i) - f(r^j) \Vert \\&\mathrm{Coverage}&Q^C(R)=&\max _{z\in Z_{\text {N}}} \, \min _{r \in R} \, \Vert f(r)-z \Vert \\&{\varepsilon }-\mathrm{Indicator}\quad&Q^\varepsilon (R)=&\max _{z \in Z_{\text {N}}} \, \min _{r \in R} \max _{k \in \{1,\ldots ,p\}} \frac{z_k}{f_k(r)} \end{aligned}$$

Definition 8

(Bi-objective robust representation problem)

Let $Q\in \{Q^U,Q^C,Q^\varepsilon \}$ denote one of the representation quality measures uniformity, coverage, or $\varepsilon$-indicator, and let $I(x)\in \{-I^{cf}(x), -I^{ce}(x), I^\varepsilon (x), I^{\Sigma \varepsilon }(x),\, I^\varepsilon _D(x)\}$ denote a decision space robustness indicator. Then, the bi-objective robust representation problem is defined as

$$\begin{aligned} \begin{array}{rl} \displaystyle \min &{}{I(R)} \\ \,\min &{} {Q(R)}\\ \mathrm {s.\,t.} &{} |R| = k\\ &{} R \subseteq X_{\text {E}}\end{array} \end{aligned}$$

(RRP)

Since the worst case robustness value $I(R)=\max _{x\in R} I (x)$ is attained by (at least) one efficient solution in the representation, it is possible to solve (RRP) by a sequence of $|X_{\text {E}}|$ $\varepsilon$-constraint scalarizations, which can be rewritten by considering only sufficiently robust solutions:

In case of bi-objective integer programming problems (RRP-$\varepsilon$) can be solved in polynomial time in the number of efficient solutions. Efficient algorithms based on dynamic programming to solve such representation problems for bi-objective discrete optimization problems are suggested in Vaz et al. (2015). The approaches make use of the 1D strucuture of the nondominated set of bi-objective problems.

We use the numerical example (3) introduced in Sect. 2.4 to evaluate the bi-objective representation problem (RRP) with respect to coverage and $\varepsilon$-robustness.

$$\begin{aligned} \min _{\begin{array}{c} R \subseteq X_{\text {E}}\\ |R| = 3 \end{array}} \Bigl (I^\varepsilon (R),\; Q^C(R)\Bigr ) \end{aligned}$$

(4)

The bi-objective representation problem (4) has eleven efficient representations mapping to three nondominated points (w.r.t. coverage and $\varepsilon$-robustness), see Fig. 6. Since solution $z^1$ which is important to yield a small coverage radius (c.f. Fig. 6), has a rather high $\varepsilon$-robustness indicator value, the two quality measures are conflicting. On the other hand, the three most robust solutions ($z^3,z^6,z^7$) do not cover the non-dominated set well (c.f. Fig. 6).

Fig. 6

Three nondominated representations w.r.t. coverage and $\varepsilon$-robustness indicator. The supported non-dominated points are depicted as squares, unsupported non-dominated as circles, which are filled black if the respective is in the robust representative subset. The grey circles indicate the coverage radii

4.2 A composite qualitative robustness index

This section is devoted to composite qualitative robustness indices that can be used for assessing the robustness of each efficient solution, $x\in X_{\text {E}}$, with respect to (most of) the indicators presented in this paper. We will exemplify this by applying a simplified version of Electre Tri-C (Almeida-Dias et al., 2010). In this simplified version we consider one criterion per indicator and we do not make use of discriminating and veto thresholds. The method can be illustrated through the data in Table 1, by removing index $I^{cf}(\cdot )$ since its value is the same for all the solutions. The remaining indices are thus our criteria. The notation $g_1,\ldots ,g_5$ will be used to represent them in this context, where $g_j(x)$ denotes the performance of an efficient solution $x\in X_{\text {E}}$ on criterion $g_j$, for $j=1,\ldots ,5$ (we will use the subscript j to avoid confusion with components of the vector of variables x). For the sake of simplicity we assume without loss of generality that all the criteria are to be minimized. In the context of our illustrative problem (3), we thus multiply the data of the first column by $-1$. The performance table can be presented in the following Table 3 (see also Table 1).

Table 3 Performance for the example problem (3) introduced in Sect. 2.4

The Electre Tri-C method (Almeida-Dias et al., 2010) is a pairwise comparison method with the objective to form an outranking relation for all ordered pairs of efficient solutions (hereafter we use the term actions instead of solutions), and then explore this relation by assigning the actions to categories. In the following, we will discuss the two main steps of the Electre Tri-C method, i.e., outranking and classification, in more detail and illustrate them using the data of Table 3.

4.2.1 Pairwise comparison and outranking

In the simplified version of Electre Tri-C, there are only three possibilities when comparing an ordered pair of actions $(x,\hat{x}) \in X_{\text {E}}\times X_{\text {E}}$ on each criterion $g_j$, for $j=1,\ldots ,n$ (recall that all the criteria are to be minimized):

• x is at least as good as (outranks) $\hat{x}$ ($x \succsim _j \hat{x}$), iff $g_j(x) \leqslant g_j(\hat{x})$;

• x is strictly preferred to $\hat{x}$ ($x \succ _j \hat{x}$), iff $g_j(x) < g_j(\hat{x})$;

• x is indifferent to $\hat{x}$ ($x \sim _j \hat{x}$), iff $g_j(x) = g_j(\hat{x})$.

The weight or relative importance (weights can also be interpreted as the voting power of the criterion) of each criterion $g_j$, denoted by $w_j\in [0,1]$, with $\sum _{j=1}^{n}w_j=1$ is a fundamental preference parameter that impacts the outranking relation. In what follows, we consider the same normalized weight for each criterion, i.e., $w_j=1/5=0.2$, for $j=1,\ldots ,5$ in the example problem.

4.2.2 Categorization

In our example, we consider only three categories: “low robustness ($C^1$)”, “medium robustness ($C^2$)”, and “high robustness ($C^3$)” in order to qualitatively classify the eight efficient actions by taking into account all the criteria (indices) in a composite (aggregated) way.

Each category is represented by a representative/central element, say $\hat{x}^1$ for the category $C^1$ of the lowest robustness level; $\hat{x}^2$ for the category $C^2$ with the medium robustness level; and $\hat{x}^3$ for the category $C^3$ of the highest robustness level. In the example problem, we can consider the following data for each one of these central actions (let us assume that the actions are “well” separated according to the separability properties of the method). These values are obtained by taking into account the range of each criterion in Table 3, but possibly also some additional information on the quality of the given actions in the respective criterion. For example, the range of the values of $g_1$ are given by $g_1(x)\in [-6,-2]$ for $x\in X_{\text {E}}$, where actually the worst attained value of $-2$ might still be quite good as compared to other non-listed actions. This information is used for defining the first components of the representative actions of each category. Since we are minimizing, the value $-1$ is a rather bad value for an action, $-3$ is a medium value, and $-5$ is a good value for $g_1$. We proceed in the same way for the other components and set

$$\begin{aligned} g(\hat{x}^{1})&= (-1, 1.260, 1.047, 1.120, 1.041)\\ g(\hat{x}^{2})&= (-3, 1.230, 1.037, 1.100, 1.033)\\ g(\hat{x}^{3})&= (-5, 1.200, 1.027, 1.080, 1.028). \end{aligned}$$

4.2.3 Implementation

The first step in the method is to construct a comprehensive outranking relation by taking into account all the criteria at the same time (i.e, by aggregating them). For such a purpose a degree of credibility between an ordered pair of actions, $(x, \hat{x})$, denoted by $\sigma (x, \hat{x})$, is computed. In the simplified version of the method, this degree of credibility is computed only by the power of the coalition of criteria for which x outranks $\hat{x}$, i.e,

$$\begin{aligned} {\displaystyle \sigma (x, \hat{x}) = \sum _{\{j\,:\, g_j(x) \leqslant g_j(\hat{x})\}}w_j}. \end{aligned}$$

This is a fuzzy number since $\sigma (x, \hat{x}) \in [0,1]$, which represents the degree to which x outranks $\hat{x}$. In other words, it specifies the fraction of votes favorable to x over $\hat{x}$. The degrees of credibility between the solutions of our example are shown in Table 4.

For example, we compare the performance lists of $x^4$ and $\hat{x}^2$, taking into account their performances $g(x^4) = (\mathbf {-5}, \mathbf {1.185185},$ 1.042190, 1.129032, 1.045390) and $g(\hat{x}^2) = (-3, 1.230, \mathbf {1.037}, \mathbf {1.100}, \mathbf {1.033})$, respectively. Action $x^4$ is better in the first two criteria and worse in the other three. Thus, $\sigma (x^4,\hat{x}^2) = 0.2 + 0.2 = 0.4$ (the fraction of votes favorable to $x^4$ against $\hat{x}^2$ is 0.4) and $\sigma (\hat{x}^2, x^4) = 0.2 + 0.2 + 0.2= 0.6$ (with similar interpretation).

Table 4 Credibility degrees $\sigma (x, \hat{x})$ and $\sigma (\hat{x}, x)$

In order to transform the fuzzy numbers into crispy ones, we can use a kind of cutting or majority level, denoted by $\lambda$, which may be interpreted as a majority level like in voting theory. For example, if $\lambda \geqslant 0.55$ we only accept an outranking where the coalition of criteria has a majority over 55% (in our example, $x^4$ does not outrank $\hat{x}^2$ since $\sigma (x^4,\hat{x}^2) < 0.55$, but $\hat{x}^2$ outranks $x^4$ since $\sigma (\hat{x}^2,x^4) \geqslant 0.55$). After the application of such a $\lambda$ cutting level we can devise the following comprehensive relations for an ordered pair of alternatives (these relations will further be used to compare the solutions against the characteristic central action and in the assignment procedures in order to assign them to the most adequate category(ies)):

• x outranks $\hat{x}$ ($x \succsim _\lambda \hat{x}$) iff $\sigma (x, \hat{x}) \geqslant \lambda$;

• x is preferred to $\hat{x}$ ($x \succ _\lambda \hat{x}$) iff $\sigma (x, \hat{x}) \geqslant \lambda$ and $\sigma (\hat{x}, x) < \lambda$;

• $\hat{x}$ is preferred to x ($\hat{x} \succ _\lambda x$) iff $\sigma (\hat{x}, x) \geqslant \lambda$ and $\sigma (x, \hat{x}) < \lambda$;

• $\hat{x}$ is indifferent to x ($\hat{x} \sim _\lambda x$) iff $\sigma (x, \hat{x}) \geqslant \lambda$ and $\sigma (\hat{x}, x) \geqslant \lambda$;

• $\hat{x}$ is incomparable to x ($\hat{x} \Vert _\lambda x$) iff $\sigma (x, \hat{x}) < \lambda$ and $\sigma (\hat{x}, x) < \lambda$.

Back to our example, since the central action $\hat{x}^2$ is preferred to $x^4$, we use the (reverse strict preference) notation $x^4\prec _\lambda \hat{x}^2$. Table 5 presents the preference relations between solutions and central actions and it will be useful to understand the mechanism of the assignment procedures (the relations depend on the chosen $\lambda$; in this case we choose $\lambda =0.55$).

Table 5 Preference relations with central actions

From these relations Electre Tri-C (Almeida-Dias et al., 2010) makes use of two assignment procedures conjointly to assign the actions to an interval of categories (the best situation occurs when the two procedures produce the same assignment). The categories are, in our case, $C^1 \prec C^2 \prec C^3$: they are ordered from the worst to the best and they are characterized by $\hat{x}^1$, $\hat{x}^2$, and $\hat{x}^3$, respectively. The two procedures need the definition of a selection function of the form

$$\begin{aligned} {\rho (x,\hat{x}) = \min \{\sigma (x,\hat{x}),\sigma (\hat{x},x)\}}. \end{aligned}$$

In our example, ${\rho (x^4,\hat{x}^2) = \min \{\sigma (x^4,\hat{x}^2),\sigma (\hat{x}^2,x^4)\}} = \{0.4, 0.6\}=0.4$. Table 6 below presents the computations for all the solutions.

Table 6 The values of $\rho (x,\hat{x})$

The two procedures can be presented as follows.

Algorithm 1

(Descending procedure) Choose $\lambda \in [0.5,1]$. Decrease k from 3 to the first value k such that $\sigma (x,\hat{x}^k) \geqslant \lambda$ (i.e, $x \succsim _\lambda \hat{x}^k$), or set k to 0 if such a value does not exist.

• 1 For $k=3$, select $C^3$ as a possible category to assign action x.

• 2 For $0< k < 3$, if $\rho (x,\hat{x}^k) > \rho (x,\hat{x}^{k+1})$, then select $C^k$ as a possible category to assign x; otherwise, select $C^{k+1}$.

• 3 For $k = 0$, select $C^1$ as a possible category to assign x.

If we continue with our example for $\lambda = 0.55$, the first k for which $\sigma (x^4,\hat{x}^k) \geqslant 0.55$ is for $k=1$. We are in Case 2 of Algorithm 1, but since we do not have $\rho (x^4,\hat{x}^1)=0.4 > \rho (x,\hat{x}^2)=0.4$, then $x^4$ will be assigned to $C^2$.

Algorithm 2

(Ascending procedure) Choose $\lambda \in [0.5,1]$. Increase k from 1 to the first value k such that $\sigma (\hat{x}^k,x) \geqslant \lambda$ (i.e, $\hat{x}^k \succsim _\lambda x$), or set k to 4 if such a value does not exist.

• 1 For $k=1$, select $C^1$ as a possible category to assign action x.

• 2 For $1< k < 4$, if $\rho (x,\hat{x}^k) > \rho (x,\hat{x}^{k-1})$, then select $C^k$ as a possible category to assign x; otherwise, select $C^{k-1}$.

• 3 For $k = 4$, select $C^3$ as a possible category to assign x.

If we follow the procedure for our example for $\lambda = 0.55$, the first k for which $\sigma (\hat{x}^k,x^4) \geqslant 0.5$ is for $k=2$. We are in Step 2, but since we do not have $\rho (x^4,\hat{x}^2)=0.4 > \rho (x,\hat{x}^1)=0.4$, then $x^4$ will be assigned to $C^1$.

The results are as follows (note that the previous tables change when changing the values of $\lambda$), when using the two procedures conjointly:

• Assignments with $\lambda =0.55$:

  $$\begin{aligned} {\displaystyle C^1=\{x^1,x^4\},\;\; C^2=\{x^4,x^5,x^8\},\;\;C^3=\{x^2,x^3,x^6,x^7\}.} \end{aligned}$$

  All the actions are precisely assigned, except $x^4$ which can be of low and medium robustness.

• Assignments with $\lambda =0.65$:

  $$\begin{aligned} {\displaystyle C^1=\{x^1,x^4\},\;\; C^2=\{x^4,x^5,x^8\},\;\;C^3=\{x^2,x^3,x^6,x^7\}.} \end{aligned}$$

  The assignments are the same, even with a higher cutting level.

• To show the impact of the cutting level, we also computed the assignments for $\lambda =0.85$ (even though very high cutting levels are of little practical relevance):

  $$\begin{aligned} {\displaystyle C^1=\{x^1,x^4,x^5\},\;\; C^2=\{x^7,x^8\},\;\;C^3=\{x^2,x^3,x^4,x^5,x^6,x^7\}.} \end{aligned}$$

  Note that at this very high cutting level, the actions $x^4$ and $x^5$ can not be clearly assigned, i.e., the method provides uncertainty about the robustness of these solutions at this cutting level.

If we look at the indicator values for the actions, the assignments for $\lambda =0.55$ (and also for $\lambda =0.65$) make sense. We can say, that $x^2$, $x^3$, $x^6$, and $x^7$ are quite robust actions, while $x^1$ is an action with low robustness.

5 Concluding remarks

In this paper we adopt the concept of decision space robustness to multiobjective integer linear programming problems. In many practical applications, the computed optimal solutions can not be exactly implemented in reality. By identifying possible sets of alternative realizations in appropriately chosen neighborhoods, we propose robustness indicators that assess the quality of the considered solution under slight deviations. This can be applied to support decision making and the selection of a most preferred and simultaneously robust solution. We exemplify such an approach using the Electre Tri-C method. Moreover, robustness indicators can be extended to sets of solutions, such that the robustness of different representations of the efficient set can be evaluated and optimized.

From a computational perspective, the computation of neighborhoods of solutions usually requires the a priori computation of the complete efficient set or feasible set, respectively, which is usually very costly. However, depending on the problem structure, this neighborhood information can be obtained already during the solution process, for example, in dynamic programming type algorithms (see, e.g., Correia et al., 2018). In this paper we made use of the neighbors of the investigated solution to define the robustness indicators. Analogously, it is possible to define a $k$-order neighborhood, where the neighbors of $x$ are at most $k$ elementary moves away from x and define the indicators accordingly. Future research could also address possible advantages of using neighborhood search techniques, despite the fact that the efficient set of multiobjective integer linear programming problems is not connected in general (Gorski et al., 2011).