Sufficient conditions for the existence of a sample mean of time series under dynamic time warping

Abstract

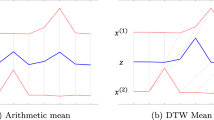
Time series averaging is an important subroutine for several time series data mining tasks. The most successful approaches formulate the problem of time series averaging as an optimization problem based on the dynamic time warping (DTW) distance. The existence of an optimal solution, called sample mean, is an open problem for more than four decades. Its existence is a necessary prerequisite to formulate exact algorithms, to derive complexity results, and to study statistical consistency. In this article, we propose sufficient conditions for the existence of a sample mean. A key result for deriving the proposed sufficient conditions is the Reduction Theorem that provides an upper bound for the minimum length of a sample mean.

Appendix

A Proof of Example 9

Proof

From the Reduction Theorem follows that it is sufficient to consider candidate solutions of length one and two. Thus, it is sufficient to consider the restricted Fréchet functions F₁ and F₂. In addition, it is sufficient to assume that all warping paths are compact (see Example 25). Then the set §P_m,n with m,n ∈ {1,2} consists of exactly one warping path. Suppose that x = (x₁), y = (y₁,y₂) and z = (z₁,z₂). Then the squared DTW distances are of the form δ(x,z)² = d(x₁,z₁) + d(x₁,z₂)δ(y,z)² = d(y₁,z₁) + d(y₂,z₂).

We proceed with considering a slightly modified setting using the local distance function $d^{\prime }(a, a^{\prime }) = (a-a^{\prime })^{2}$ for all $a, a^{\prime } \in \mathcal {A}$. Under this setting, we denote the DTW distance by $\delta ^{\prime }$ and the restricted Fréchet functions by $F^{\prime }_{1}$ and $F^{\prime }_{2}$. The function $F^{\prime }_{1}(x)$ at time series x = (x₁) is of the form

$$ \begin{array}{@{}rcl@{}} F^{\prime}_{1}(x) = \underbrace{(x_{1} - 1)^{2} + (x_{1} - 1)^{2}}_{= \delta^{\prime}(x, x^{(1)})} + \underbrace{(x_{1} - 1)^{2} + (x_{1} + 1)^{2}}_{= \delta^{\prime}(x, x^{(2)})}. \end{array} $$

The function $F^{\prime }_{1}$ is convex and differentiable with respect to x₁. Taking the gradient, setting to zero and solving yields the unique solution x₁ = 0.5. Thus, z = (0.5) is the restricted sample mean of $\mathcal {X}$ on §T₁ with Fréchet variation $F^{\prime }_{1}(z) = 3$.

For a given x = (x₁,x₂), a similar calculation with

$$ \begin{array}{@{}rcl@{}} F^{\prime}_{2}(x) = (x_{1} - 1)^{2} + (x_{2} - 1)^{2} + (x_{1} - 1)^{2} + (x_{2} + 1)^{2} \end{array} $$

gives z = (1,0) as the unique restricted sample mean on $\mathcal {T}_{2}$ with Fréchet variation $F^{\prime }_{2}(z) = 2$. By combining both results, we conclude that z = (1,0) is an unrestricted sample mean of $\mathcal {X}$ with total variation $F^{\prime *} = 2$.

Next, we assume the original local distance function d on §A as defined in Example 9. Again, we first consider time series x = (x₁) of length one. Then we have $F_{1}(x) = F^{\prime }_{1}(x)$ if x₁≠ 0 and F₁(x) = 4 if x₁ = 0. Thus, z = (0.5) is the restricted sample mean of $\mathcal {X}$ on $\mathcal {T}_{1}$ with Fréchet variation F₁(z) = 3.

Now, we consider time series of length two. Let x_ε = (1,ε) for some $\varepsilon \in \mathbb {R}$. Then

$$ \begin{array}{@{}rcl@{}} \lim_{\varepsilon \to 0} F(x_{\varepsilon}) = 2 \end{array} $$

(5)

but F(x₀) = 4. Suppose there is a restricted sample mean z = (z₁,z₂) on $\mathcal {T}_{2}$. From (5) follows that F(z) ≤ 2. If at least one element of z is zero, we have F(z) ≥ 4. This contradicts our assumption that z is a sample mean. Thus, the elements of z are both non-zero. Then we have $F_{2}(z) = F^{\prime }_{2}(z)$. Recall that the unique minimizer of $F^{\prime }_{2}$ has a zero element. This yields the contradiction $2 < F^{\prime }_{2}(z) = F_{2}(z) \leq 2$. Consequently, the function F₂ has no minimizer. Thus, the unrestricted Fréchet function F never attains its infimum 2 and therefore $\mathcal {X}$ has no sample mean. □