A novel two-channel continuous-time time-interleaved 3rd-order sigma-delta modulator with integrator-sharing topology

Abstract

This paper presents a 3rd-order two-path continuous-time time-interleaved (CTTI) delta-sigma modulator which is implemented in standard 90 nm CMOS technology. The architecture uses a novel method to resolve the delayless feedback path issue arising from the sharing of integrators between paths. By exploiting the concept of the time-interleaving techniques and through the use time domain equations, a conventional single path 3rd-order discrete-time (DT) ΔΣ modulator is converted into a corresponding two-path discrete-time time-interleaved (DTTI) counterpart. The equivalent CTTI version derived from the DTTI ΔΣ modulator by determining the DT loop filters and converting them to the equivalent continuous-time loop filters through the use of the Impulse Invariant Transformation. Sharing the integrators between two paths of the reported modulator makes it robust to path mismatch effects compared to the typical time-interleaved modulators which have individual integrators in all paths. The modulator achieves a dynamic range of 12 bits with an OverSampling Ratio of 16 over a bandwidth of 10 MHz and dissipates only 28 mW of power from a 1.8-V supply. The clock frequency of the modulator is 320 MHz but integrators, quantizers and DACs operate at 160 MHz.

1 Introduction

The rapid growth of the portable communication device markets such as audio systems and consumer electronics has been led to an increasing demand for low power high resolution ADC designs over the last decade [1]. The ΔΣ modulator can achieve a very high resolution analog-to-digital conversion for relatively low-bandwidth signals through the use of the oversampling and the noise shaping technique. It is known that ΔΣ modulators do not require precise analog components and sharp cut-off frequencies for their analog anti-aliasing filters. The noise-shaping loop filter of a ΔΣ modulator can be implemented as a DT structure by using Switched-Capacitor (SC) techniques or as CT one through active-RC or gm-c filters. The SC circuits are insensitive to clock jitter and the frequency response of the noise-shaping filter can be accurately set by capacitor ratios [2].

The signal bandwidth the ΔΣ modulators can deal with is narrow and is restricted by the OSR and technology deployed. To increase the signal bandwidth the modulator can process, a variety of methods are used: the first one is to increase the order of the modulator, but at a price, where the stability problem requires to be dealt with very carefully [2]. The second is to increase the number of bits for the quantizer, which makes the design of the modulator more complicated [1]. The third is to increase the sampling frequency. However, the major disadvantage of the third method is the technology limitations. The fourth method that is one of the more practical ways is to deploy a CT loop filter coupled with the time-interleaving technique [3].

This paper is organized as follows. In Sect. 2, the CT ΔΣ modulators and the concept of the impulse-invariant transformation are reviewed. In Sect. 3, a single-path DTTI ΔΣ modulator is derived from a 3rd-order conventional DT ΔΣ modulator through the use of the time domain equations and it is converted to its equivalent CTTI ΔΣ modulator. The delayless feedback path problem and our proposed solution are both discussed in detail in this section. In Sect. 4, MATLAB simulation results are presented. In Sect. 5, circuit design and simulations are reviewed. Finally, conclusions are given in Sect. 6.

2 Continuous-time ΔΣ modulator

The CT ΔΣ modulators benefit from operating at higher sampling frequencies in comparison to their DT counterparts. The errors of the sample-and-hold circuit are shaped by the loop filter and the CT ΔΣ modulators have an implicit anti-aliasing filter in their forward signal path; However, CT ΔΣ modulators suffer from several drawbacks: excess loop delay, jitter sensitivity and RC time constant variations.

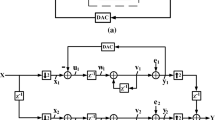
One way to convert a DT ΔΣ modulator to an equivalent CT ΔΣ modulator is the impulse-invariant transformation [1]. Another is the use of the modified z-transform [1]. To set the scene for our work, we shall stick to the straight forward implementation method of the impulse-invariant transformation. A DT and a CT ΔΣ modulator are shown in Fig. 1, and are said to be equivalent when their quantizer inputs are equal at the sampling instants.

$$q\left( n \right) = \left. {q_{c} \left( t \right)} \right|_{t = nT} \quad {\text{for all n}}$$

(1)

Fig. 1

The block diagrams of a the DT ΔΣ modulator and b the CT ΔΣ modulator [1, 4, 5]

This condition would be satisfied if the impulse responses of the open-loop diagrams in Fig. 2 were equal at the sampling times. As a result (1) translates directly into (2) [1]:

$$Z^{ - 1} \left\{ {H_{dDAC} \left( z \right)H_{d} \left( z \right)} \right\} = \left. {\varLambda^{ - 1} \left\{ {H_{cDAC} \left( s \right)H_{c} \left( s \right)} \right\}} \right|_{t = nT}$$

(2)

Fig. 2

a The open-loop DT ΔΣ modulator and b the open-loop CT ΔΣ modulator [1, 4, 5]

Because $H_{dDAC} \left( z \right) = 1$, Eq. (2) can be simplified to give (3):

$$Z^{ - 1} \left\{ {H_{d} \left( z \right)} \right\} = \left. {\varLambda^{ - 1} \left\{ {H_{cDAC} \left( s \right)H_{c} \left( s \right)} \right\}} \right|_{t = nT}$$

(3)

The transformation in (3) is called the impulse-invariant transformation where $Z^{ - 1}$, $\varLambda^{ - 1}$, $H_{cDAC} \left( s \right)$, $H_{d} \left( z \right)$ and $H_{c} \left( s \right)$ represent the inverse Z-transform, the inverse Laplace transform, the CT DAC transfer function, the DT and the CT loop filter respectively [1, 3]. Depending on the output waveform of the CT DAC, there would be an exact mapping between the DT and the CT ΔΣ modulator. The popular feedback-DAC waveforms have rectangular shapes. The time and frequency (Laplace) domain responses of these waveforms are [1, 3]:

$$h_{cDAC} \left( t \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\alpha T \le t \le \beta T,} \hfill & {0 \le \alpha ,\beta \le 1} \hfill \\ {0,} \hfill & {otherwise} \hfill & {} \hfill \\ \end{array} } \right.$$

(4)

$$H_{cDAC} \left( s \right) = \frac{{e^{ - \alpha Ts} - e^{ - \beta Ts} }}{s}$$

(5)

As illustrated in Fig. 1b, the input signal $x\left( t \right)$ of the CT ΔΣ modulator is CT but its output $y\left( n \right)$ is a DT signal. Consequently defining a pure s-domain Signal Transfer Functions (STF) for the CT ΔΣ modulator is impossible. To calculate the STF and the Noise Transfer Function (NTF), the loop filter $H_{c} \left( s \right)$ and implicit sampler are relocated across the summation point and placed in front of the CT ΔΣ modulator and in the feedback path as shown in Fig. 3a. The NTF of the CT ΔΣ modulator is the same as its DT counterpart. Thus, the NTF remains unchanged [1]:

$$NTF\left( {j2\pi f} \right) = \frac{1}{{1 + H_{d} \left( {e^{j2\pi f} } \right)}}$$

(6)

Fig. 3

a An equivalent representation of the CT ΔΣ modulator and b another equivalent representation of the CT ΔΣ modulator [4, 5]

Figure 3b shows another equivalent representation of the CT ΔΣ modulator. It consists of an Anti-Aliasing Filter (AAF), a sampler and an NTF of its DT equivalent. The STF of the CT ΔΣ modulator will be [4, 5]:

$$\begin{array}{*{20}c} {STF\left( {j2\pi f} \right) = } \\ \end{array} \underbrace {{H_{c} \left( {j2\pi f} \right)}}_{AAF}\underbrace {{e^{ - j\pi fT} \frac{{\sin \left( {\pi fT} \right)}}{\pi f}}}_{Sampler}\underbrace {{\frac{1}{{1 + H_{d} \left( {e^{j2\pi f} } \right)}}}}_{NTF}$$

(7)

According to [4], the effect of “sinc” term is negligible and neglected in this work for the purpose of comparison between the CT modulator with its DT counterpart.

3 Time-interleaved ΔΣ modulator

The procedure for the design of a ΔΣ modulator is based on choosing: the order and architecture of the ΔΣ modulator, the OSR and the number of bits for the quantizer. By using the time-interleaving technique and M interconnected parallel modulators that are working concurrently, the effective sampling rate and the OSR become M times the clock rate and the OSR of each modulator respectively [8, 9]. It should be noted that the required resolution can be acquired without increasing the order of the modulator or the number of bits for the quantizer and also without utilizing a state of the art technology.

3.1 Derivation of TI ΔΣ modulator

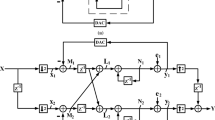
The 3rd-order two-path DTTI ΔΣ modulator is derived directly from the time domain node equations of its conventional DT ΔΣ modulator as shown in Fig. 4 [15,16,17]. It is assumed that the DAC in the feedback loop is ideal, therefore $H_{DAC} (z) = 1$. The time domain equations of the modulator are written for two consecutive time slots as (2n)th and (2n + 1)th as follows [10]:

$$v_{1} \left( {2n} \right) = ax\left( {2n - 1} \right) - ay\left( {2n - 1} \right) + v_{1} \left( {2n - 1} \right)$$

(8.a)

$$v_{2} \left( {2n} \right) = bv_{1} \left( {2n - 1} \right) - by\left( {2n - 1} \right) + v_{2} \left( {2n - 1} \right)$$

(8.b)

$$v_{3} \left( {2n} \right) = cv_{2} \left( {2n - 1} \right) - cy\left( {2n - 1} \right) + v_{3} \left( {2n - 1} \right)$$

(8.c)

$$y\left( {2n} \right) = Q\left[ {v_{3} \left( {2n} \right)} \right]$$

(8.d)

and

$$v_{1} \left( {2n + 1} \right) = ax\left( {2n} \right) - ay\left( {2n} \right) + v_{1} \left( {2n} \right)$$

(9.a)

$$v_{2} \left( {2n + 1} \right) = bv_{1} \left( {2n} \right) - by\left( {2n} \right) + v_{2} \left( {2n} \right)$$

(9.b)

$$v_{3} \left( {2n + 1} \right) = cv_{2} \left( {2n} \right) - cy\left( {2n} \right) + v_{3} \left( {2n} \right)$$

(9.c)

$$y\left( {2n + 1} \right) = Q\left[ {v_{3} \left( {2n + 1} \right)} \right]$$

(9.d)

where $Q\left[ . \right]$ represents the quantization function. The input $x\left( n \right)$ is distributed between two channels through an input demultiplexer which operates at twice the clock frequency of each channel. The input $x\left( n \right)$ is relabelled as follows:

$$x_{1} \left( n \right) = x\left( {2n} \right), x_{2} \left( n \right) = x\left( {2n - 1} \right)$$

(10)

Fig. 4

A 3rd-order conventional single-loop DT ΔΣ modulator

Similarly, the other nodes of the modulator are relabelled:

$$v_{11} \left( n \right) = v_{1} \left( {2n} \right),\quad v_{12} \left( n \right) = v_{1} \left( {2n - 1} \right)$$

(11.a)

$$v_{21} \left( n \right) = v_{2} \left( {2n} \right),\quad v_{22} \left( n \right) = v_{2} \left( {2n - 1} \right)$$

(11.b)

$$v_{31} \left( n \right) = v_{3} \left( {2n} \right),\quad v_{32} \left( n \right) = v_{3} \left( {2n - 1} \right)$$

(11.c)

$$y_{1} \left( n \right) = y\left( {2n} \right),\quad y_{2} \left( n \right) = y\left( {2n - 1} \right)$$

(11.d)

By sharing only one set of integrators, the input demultiplexer is removed and the input $x\left( n \right)$ is shared between channels. Hence Eq. (10) results in (12) as follows:

$$x_{1} \left( n \right) = x_{2} \left( n \right) = x\left( n \right)$$

(12)

Equation sets (13) and (14) are derived by substituting equation set (11) and Eq. (12) into equation sets (8) and (9) respectively as follows:

$$v_{11} \left( n \right) = ax\left( n \right) - ay_{2} \left( n \right) + v_{12} \left( n \right)$$

(13.a)

$$v_{21} \left( n \right) = bv_{12} \left( n \right) - by_{2} \left( n \right) + v_{22} \left( n \right)$$

(13.b)

$$v_{31} \left( n \right) = cv_{22} \left( n \right) - cy_{2} \left( n \right) + v_{32} \left( n \right)$$

(13.c)

$$y_{1} \left( n \right) = Q\left[ {v_{31} \left( n \right)} \right] = Q\left[ {cv_{22} \left( n \right) - cy_{2} \left( n \right) + v_{32} \left( n \right)} \right]$$

(13.d)

and

$$v_{12} \left( {n + 1} \right) = ax\left( n \right) - ay_{1} \left( n \right) + v_{11} \left( n \right)$$

(14.a)

$$v_{22} \left( {n + 1} \right) = bv_{11} \left( n \right) - by_{1} \left( n \right) + v_{21} \left( n \right)$$

(14.b)

$$v_{32} \left( {n + 1} \right) = cv_{21} \left( n \right) - cy_{1} \left( n \right) + v_{31} \left( n \right)$$

(14.c)

$$y_{2} \left( {n + 1} \right) = Q\left[ {v_{32} \left( {n + 1} \right)} \right]$$

(14.d)

Equation set (14) can be rewritten as equation set (15):

$$v_{12} \left( n \right) = ax\left( {n - 1} \right) - ay_{1} \left( {n - 1} \right) + v_{11} \left( {n - 1} \right)$$

(15.a)

$$v_{22} \left( n \right) = bv_{11} \left( {n - 1} \right) - by_{1} \left( {n - 1} \right) + v_{21} \left( {n - 1} \right)$$

(15.b)

$$v_{32} \left( n \right) = cv_{21} \left( {n - 1} \right) - cy_{1} \left( {n - 1} \right) + v_{31} \left( {n - 1} \right)$$

(15.c)

$$y_{2} \left( n \right) = Q\left[ {v_{32} \left( n \right)} \right]$$

(15.d)

Equation set (16) is derived by further substituting equation set (13) into equation set (14).

$$v_{12} \left( n \right) = 2ax\left( {n - 1} \right) - ay_{1} \left( {n - 1} \right) - ay_{2} \left( {n - 1} \right) + v_{12} \left( {n - 1} \right)$$

(16.a)

$$v_{22} \left( n \right) = abx\left( {n - 1} \right) + 2bv_{12} \left( {n - 1} \right) - by_{1} \left( {n - 1} \right) - b\left( {1 + a} \right)y_{2} \left( {n - 1} \right) + v_{22} \left( {n - 1} \right)$$

(16.b)

$$v_{32} \left( n \right) = bcv_{12} \left( {n - 1} \right) + 2cv_{22} \left( {n - 1} \right) - cy_{1} \left( {n - 1} \right) - c\left( {1 + b} \right)y_{2} \left( {n - 1} \right) + v_{32} \left( {n - 1} \right)$$

(16.c)

The DTTI ΔΣ modulator which is shown in Fig. 5 is derived directly from the time domain equation sets (13) and (16).

Fig. 5

A 3rd-order two-path DTTI ΔΣ modulator with shared integrators

The motive behind sharing one set of integrators is to eliminate the instability that can arise due to the DC offset mismatch of the two individual integrator set based two channel interleaving case [8, 15, 17]. The DTTI ΔΣ modulators require an input demultiplexer which samples the input signal at the highest clock frequency of the DTTI ΔΣ modulator and distributes it between channels. This fast demultiplexer is a limiting factor for the performance of the DTTI ΔΣ modulators. This architecture does not require an input demultiplexer and the input signal is shared between channels [1, 8]. Removing the input demultiplexer has no effect on the NTF of the DTTI ΔΣ modulator but it causes some notches in its STF at the following frequencies $0.5F_{clk} , 1.5F_{clk} , 2.5F_{clk} , 3.5F_{clk} , \ldots$ which is shown in Fig. 10 where $F_{clk}$ is the clock frequency of the DTTI ΔΣ modulator [9].

3.2 Delayless feedback path problem in TI ΔΣ modulator

This is the issue that forms the focus of this paper which to our best knowledge, has not been effectively solved and reported in the open literature. This is the issue which makes implementation of the multi-path TI ΔΣ modulators with shared integrators impractical and it is called the “delayless feedback path” problem that comes from Eq. (13.c) in which $v_{31} \left( n \right)$ (the input of quantizer Q1) is directly linked to $y_{2} \left( n \right)$. This means that the output of the second quantizer (Q2) is connected to the input of another quantizer (Q1) without any delay [11]! One method to eliminate the delayless path is to move this feedback to the digital domain instead of performing it in the analog domain [11]. The disadvantage of this method is that the first quantizer (Q1) requires more comparators than the number of the comparators in the second quantizer (Q2) [11]. The second method is to use a sample-and-hold in front of the first quantizer (Q1) and quantizing the signal when the output of DAC2 is ready [3]. This method requires a complicated timing generator, a sample-and-hold and also faster integrators. The third method which is our proposed novel method is based on an error correction technique. An error is intentionally induced in the analog domain through the use of the output of DAC2 as shown in Fig. 7 then the error is substantially corrected in the digital domain which effectively eliminates the delayless feedback path. To better understand how this works we shall perform a step by step mathematical analysis of what happens. The timing diagram as depicted in Fig. 6 shows the delay from the outputs of quantizers Q1 and Q2 and their propagation through to the outputs of DAC1 and DAC2 as $\delta$. As a result the output of DAC2 that is sampled at the nth time slot is $y_{2} \left( {n - 1} \right)$ where in theory we should have had $y_{2} \left( n \right)$. To overcome this inconsistency we look at the input and output of Q1, as depicted in Fig. 5. Quantizer Q1 quantizes the signal $v_{31} \left( n \right)$ as follows:

$$y_{1} \left( n \right) = Q\left[ {v_{31} \left( n \right)} \right]$$

(17)

Fig. 6

The outputs of Q1, Q2, DAC1 and DAC2

Equation (18) is derived by substituting (13.c) into (17):

$$y_{1} \left( n \right) = Q\left[ {cv_{22} \left( n \right) - cy_{2} \left( n \right) + v_{32} \left( n \right)} \right]$$

(18)

The output of DAC2 is used in (19) and Eq. (18) is rewritten as:

$$y_{1} \left( n \right) = Q\left[ {cv_{22} \left( n \right) - cy_{2} \left( {n - 1} \right) + v_{32} \left( n \right)} \right] + cy_{2} \left( {n - 1} \right) - cy_{2} \left( n \right)$$

(19)

The output of Q1 is called $y_{1e} \left( n \right)$ in (20):

$$y_{1} \left( n \right) = y_{1e} \left( n \right) + cy_{2} \left( {n - 1} \right) - cy_{2} \left( n \right)$$

(20)

$$error = c\Delta y = c\left( {y_{2} \left( n \right) - y_{2} \left( {n - 1} \right)} \right)$$

(21)

$$Y_{1} \left( z \right) = Y_{1e} \left( z \right) - c\left( {1 - z^{ - 1} } \right)Y_{2} \left( z \right)$$

(22)

As stated in (20), $y_{1e} \left( n \right)$ (the output of Q1) requires to be corrected before it is applied to the input of DAC1; otherwise it causes instability in the modulator as it will change the modulators dynamics by increasing its order.

A first order differencer block $(1 - z^{ - 1}$) is used to perform this correction as described in (22). Equation (22) illustrates the point that Q1 is able to quantize its input without any additional circuit in the analog domain by merely using the output of DAC2. The differencer block $(1 - z^{ - 1}$) only corrects the error in Eq. (20) and it has no effect on the quantization error or the signal in the proposed structure. The proposed 3rd-order two-path DTTI ΔΣ modulator with shared integrator is shown in Fig. 7.

Fig. 7

The proposed 3rd-order two-path DTTI ΔΣ modulator with shared integrators

The signal swing at the input of quantizer Q1 is increased in the first and the proposed methods because scaling is not an option and it will lead to loss of signal-to-noise ratio (SNR). Based on exhaustive simulation results, the first and the proposed method require 48 and 32 comparators for quantizer Q1 respectively, in comparison to the second method which requires only 16 comparators as depicted in Table 1. The significant advantages and disadvantages of all three methods have been summarized in Table 1.

Table 1 Comparison of the first, the second and the proposed method

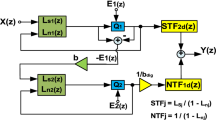
3.3 Derivation of continuous-time TI (CTTI) ΔΣ modulator

The CTTI ΔΣ modulator equivalent of the DTTI ΔΣ modulator of Fig. 7 is obtained in three steps as follows [13]: The first step is to determine the loop filters of the DTTI ΔΣ modulator. In this design, the DTTI ΔΣ modulator has six loop filters $(FF_{1d} (z), FF_{2d} (z), H_{1d} (z), H_{2d} (z), H_{3d} (z)$ and $H_{4d} (z))$ and can be determined with the help of the symbolic toolbox of MATLAB. These loop filters for the DTTI ΔΣ modulator are depicted in Fig. 8a. The second step is to convert the DT loop filters into their equivalent CT loop filters by using the impulse-invariant transformation [1, 3, 9]. The equivalent CTTI ΔΣ modulator is shown in Fig. 8b where the DT loop filters of Fig. 8a have been replaced with their equivalent CT loop filters $FF_{1c} \left( s \right), FF_{2c} \left( s \right), H_{1c} \left( s \right), H_{2c} \left( s \right), H_{3c} \left( s \right)$ and $H_{4c} \left( s \right)$. The third step is to convert the modulator of Fig. 8b into a 3rd order CTTI ΔΣ modulator as shown in Fig. 9. Two DACs with non-retrun-to-zero (NRZ) implementation and intentional delay of $0.25T \left( {T = 1/160\;{\text{MHz}}} \right)$ have been used. To overcome the excess-loop delay issue, two additional feedback paths from the outputs of DAC1 and DAC2 to the input of quantizer Q1 and Q2 are used [7]. The loop filters of the modulator shown in Fig. 9 can be determined and matched to the loop filters in Fig. 8b to determine the coefficients $f_{c1} ,$ $f_{c2} ,$ $f_{c3} ,$ $f_{c4} ,$ $f_{c5} ,$ $f_{c6} ,$ $f_{c7} ,$ $f_{c8} ,$ $f_{c9}$ and $f_{c10}$. This is achieved by using the symbolic toolbox of MATLAB, as the algebra is complex and it is very easy to make a mistake with.

Fig. 8

The block diagrams of a a DTTI ΔΣ modulator and b a CTTI ΔΣ modulator which show their loop filters

Fig. 9

The proposed 3rd-order two-path CTTI ΔΣ modulator with shared integrators

The OSR of the overall modulator shown in Fig. 9 from $x\left( t \right)$ to $y\left( n \right)$ is 16 and has been designed to operate at 320 MHz clock frequency for a 10 MHz signal bandwidth. The resolution of Q1 and Q2 are 5 and 4 bits respectively. After correcting the error as stated by Eq. (21) in the digital domain, $y_{1} \left( n \right)$ will be 4 bits in length. Therefore, DAC1 and DAC2 both require 4 bit DACs. To simplify the design, generally, the coefficient $c$ scaling the first order differencer $(1 - z^{ - 1} )$ in the digital domain should be chosen to be a number which is a power of two. This choice results in replacing the potentially complicated multiplier with a simple hard-wired shift.

3.4 STFs and NTFs of the DTTI and CTTI ΔΣ modulator

The signal and noise transfer functions of the DTTI ΔΣ modulator of Fig. 8a is formulated by performing the following algebraic analysis:

$$Y\left( z \right) = Y_{1} \left( {z^{2} } \right)z^{ - 1} + Y_{2} \left( {z^{2} } \right)$$

(23)

$$Y\left( z \right) = STF_{d} \left( z \right)X\left( z \right) + NTF_{1d} \left( z \right)E_{1} \left( z \right) + NTF_{2d} \left( z \right)E_{2} \left( z \right)$$

(24)

$$NTF_{1d} \left( z \right) = \frac{{H_{3d} \left( {z^{2} } \right) + \left( {1 - H_{4d} \left( {z^{2} } \right)} \right)z^{ - 1} }}{DEN\left( z \right)}$$

(25)

$$NTF_{2d} \left( z \right) = \frac{{(1 - H_{1d} \left( {z^{2} } \right)) + H_{2d} \left( {z^{2} } \right)z^{ - 1} }}{DEN\left( z \right)}$$

(26)

$$DEN\left( z \right) = \left( {1 - H_{1d} \left( {z^{2} } \right)} \right)\left( {1 - H_{4d} \left( {z^{2} } \right)} \right) - H_{2d} \left( {z^{2} } \right)H_{3d} \left( {z^{2} } \right)$$

(27)

$$STF_{d} \left( z \right) = FF_{1d} \left( {z^{2} } \right)NTF_{1d} \left( z \right) + FF_{2d} \left( {z^{2} } \right)NTF_{2d} \left( z \right)$$

(28)

Where $STF_{d} \left( z \right), NTF_{1d} \left( z \right)$ and $NTF_{2d} \left( z \right)$ represent the signal transfer function from $x\left( t \right)$ to $y\left( n \right)$, the noise transfer function from $e_{1} \left( n \right)$ to $y\left( n \right)$ and the noise transfer function from $e_{2} \left( n \right)$ to $y\left( n \right)$ respectively. The $z^{2}$ terms in (23) show the effect of the up-samplers in the modulator. The NTFs of the DTTI ΔΣ modulator of Fig. 8a and its equivalent CTTI ΔΣ modulator of Fig. 8b are the same. To derive the STF of the CTTI ΔΣ modulator $\left( {STF_{c} \left( s \right)} \right)$, both $NTF_{1d} \left( z \right)$ and $NTF_{2d} \left( z \right)$ are used and the $STF_{c} \left( s \right)$ is given in (29):

$$STF_{c} \left( s \right) = FF_{1c} \left( s \right)NTF_{1d} \left( z \right) + FF_{2c} \left( s \right)NTF_{2d} \left( z \right)$$

(29)

By substituting $z = e^{j2\pi f}$ and $s = j2\pi f$ in (25)–(28), the STF of the DTTI and CTTI ΔΣ modulator are plotted in Fig. 10. Since both $NTF_{1d} \left( z \right)$ and $NTF_{2d} \left( z \right)$ have an identical amplitude, only $NTF_{1d} \left( z \right)$ is plotted in Fig. 11 and is compared to the NTF of the conventional DT ΔΣ modulator of Fig. 4.

Fig. 10

The signal transfer functions of the DTTI and the CTTI ΔΣ modulators

Fig. 11

The noise transfer functions of the CTTI and the conventional DT ΔΣ modulators

4 MATLAB simulation results

The proposed CTTI ΔΣ modulator has been simulated using the SIMULINK toolbox of MATLAB and all non-idealities such as finite dc gain and bandwidth of the opamps, the DAC mismatches, offsets of the quantizers and the clock jitter of the DACs have been modelled and their effects on the performance of the modulator have been investigated [6, 14]. All specifications of the CTTI ΔΣ modulator have been summarized in Table 2.

Table 2 The specifications of the CTTI ΔΣ modulator

The output spectrum of this CTTI ΔΣ modulator is compared with the conventional DT and the DTTI ΔΣ modulators in Fig. 12. The output spectra of the DTTI and CTTI ΔΣ modulators are the same and their in-band noise are shaped more than the conventional DT ΔΣ modulator. The SNDRs of the conventional DT, the DTTI and CTTI ΔΣ modulator are 57.50, 78.47 and 78.54 dB respectively. Therefore in this particular case, the SNDRs of the TI ΔΣ modulators are improved by 21 dB. As can be seen in Fig. 12, non-idealities have not been included in this comparison.

Fig. 12

The output spectra of the conventional DT, the DTTI and the CTTI ΔΣ modulator for a 2.4462 MHz input with clock frequencies of 160, 320 and 320 MHz respectively

Figures 13 and 14 show the SNDR of the CTTI ΔΣ modulator versus the matching of the DAC1 and DAC2 coefficients respectively. The minimum matching requirements for the coefficients of DAC1, $f_{c1} ,$ $f_{c3} ,$ $f_{c5} ,$ $f_{c7}$ and $f_{c9}$ are 10, 7, 4, 4 and 4 bits respectively and for the coefficients of DAC2, $f_{c2} ,$ $f_{c4} ,$ $f_{c6} ,$ $f_{c8}$ and $f_{c10}$ they are 10, 7, 4, 4 and 4 bits respectively. The requirements can be easily achieved by the current steering DACs. The coefficient $c$ has the minimum matching requirement which is 4bits between the analog and the digital domain as shown in Fig. 14. Hence there will be no need to use the Data-Weighted Averaging (DWA) block if the coefficients of DAC1 and DAC2 meet the minimum matching requirements. This will make the circuit design of the ΔΣ modulator easier as a result.

Fig. 13

The SNDR versus the matching of the DAC1 coefficients

Fig. 14

The SNDR versus the matching of the DAC2 coefficients

5 Circuit Design and Simulation

The modulator circuit has been designed using the 90 nm CMOS TSMC technology with the supply voltage of 1.8-V. Figure 15 shows the block diagram of the 3rd-order two-path CTTI ΔΣ modulator. The operating frequency of the two quantizers, DACs and all other blocks except for the output multiplexer is 160 MHz but the output multiplexer operates at 320 MHz. The OSR of the modulator is 16, allowing a maximum input signal bandwidth of 10 MHz. The major circuit blocks of the modulator include three active-RC integrators, ten 4-bit current steering DACs, one 4-bit and one 5-bit flash ADC, two summation circuits, a clock generator, a biasing circuit, an output multiplexer and a digital error correction block ($1 - z^{ - 1}$).

Fig. 15

Block diagram of the 3rd-order CTTI ΔΣ modulator

As can be seen in Fig. 15, three active-RC integrators have been used and RC time constant varies up to 50% in CMOS technologies. A tunable capacitor array will be used to tune up the RC time constant of the integrators and to compensate for process variations [12].

One popular opamp architecture is a two-stage Miller-compensation opamp which has been utilized for the first, second and third integrator and opamp4 and is shown in Fig. 16. A PMOS input differential pair is used as the input stage for two reasons: First, the second pole is determined by the transconductance of the input transistors of the second stage and the NMOS transistor is faster than the PMOS one therefore the whole opamp will be more stable. Second, the input and output common mode voltage of the opamp is set to be 0.8 V instead of VDD/2 (0.9 V). The tail transistor in the first stage will have more VDS voltage and will not be pushed to triode region. The benefit of using PMOS transistors as input in the differential pair is low flicker noise, but in our wideband design, the flicker noise is of less concern.

Fig. 16

Schematic of a opamp and b comparator of the 3rd-order CTTI ΔΣ modulator

This modulator requires two ADCs. The first ADC has 5 bits resolution and 31 comparators and the second ADC has 4 bits resolution and 15 comparators. As shown in Fig. 16, each latched comparator is composed of a single preamplifier stage and a latch. The preamplifier is used to amplify the input signal and to minimize the input capacitance of the comparator. The preamplifier stage isolates the latch and the resistor ladder; therefore it reduces the kick-back noise seen in reference string during switching times of the comparator. The latch is used to compare the two amplified input signals coming from the preamplifier and to provide a digital rail-to-rail output signal.

The whole CTTI ΔΣ modulator has been simulated with an input frequency of $F_{in} = 1.005\;{\text{MHz}}$, an amplitude of $1.6V_{pp}$ (− 2 dBFS) and a sampling rate of 320 MHz across process corners and temperatures. Due to the excessive long simulation times, these circuit simulation results were obtained by using only 16,384-point FFTs. Since the signal bandwidth is 10 MHz, up to 512 frequency bins will be included in the calculation of the SNDR. The circuit-level simulations have been run to make sure that the modulator is stable across process corners and temperatures. The SNDR of the modulator obtained from circuit simulations in TT 27 °C, FF 120 °C and SS − 40 °C are 75.3, 75.9 and 74.5 dB respectively.

The output spectrum obtained from the circuit simulation at TT corner and 27 °C temperature is shown in Fig. 17. From the output spectrum shown in Fig. 17, it can be seen that big tones reside at around the half clock frequency (160 MHz). Those tones are images and are created due to utilizing the time-interleaving technique in the modulator. Those tones are dangerous because they fold back the out-of-band noise into the band of interest and hence increase the in-band noise floor. The image tone located at $0.5F_{clk} - F_{in}$ has − 35.3 dB amplitude and should be attenuated enough in the decimation filter following this modulator.

Fig. 17

The output spectra of the CTTI ΔΣ modulator for a 1.005 MHz input with clock frequencies of 320 MHz simulated in TT corner and 27 °C

6 Conclusions

In this paper the design of a 3rd-order CTTI ΔΣ modulator with one set of integrators in the 90 nm CMOS TSMC technology has been presented. A novel method to resolve the delayless feedback path issue has been proposed, designed, implemented and tested to demonstrate the novel approach [18]. The results obtained from the circuit simulations confirm what was expected from the theory behind the proposed method and works very well without any noticeable degradation in the output performance. The designed circuit has furthermore been demonstrated in simulation to achieve a dynamic range of 12 bits with an OverSampling Ratio (OSR) of 16 over a bandwidth of 10 MHz and dissipates only 28 mW of power from a 1.8-V supply. The clock frequency of the modulator is 320 MHz but the integrators, quantizers and DACs operate at 160 MHz.