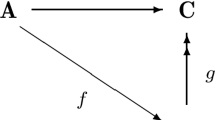
Let A be a universal algebra and H its subalgebra. The dominion of H in A (in a class {ie304-01}) is the set of all elements a ∈ A such that every pair of homomorphisms f, g: A → ∈ {ie304-02} satisfies the following: if f and g coincide on H, then f(a) = g(a). A dominion is a closure operator on a set of subalgebras of a given algebra. The present account treats of closed subalgebras, i.e., those subalgebras H whose dominions coincide with H. We introduce projective properties of quasivarieties which are similar to the projective Beth properties dealt with in nonclassical logics, and provide a characterization of closed algebras in the language of the new properties. It is also proved that in every quasivariety of torsion-free nilpotent groups of class at most 2, a divisible Abelian subgroup H is closed in each group 〈H, a〉 generated by one element modulo H.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
J. R. Isbell, “Epimorphisms and dominions,” Proc. Conf. Cat. Algebra, La Jolla 1965, Springer-Verlag, New York (1966), pp. 232–246.
J. R. Isbell, “Epimorphisms and dominions. IV,” J. London Math. Soc., II. Ser., 1, 265–273 (1969).
A. Magidin, “Dominions in varieties of nilpotent groups,” Comm. Alg., 28, No. 3, 1241–1270 (2000).
B. Mitchell, “The dominion of Isbell,” Trans. Am. Math. Soc., 167, 319–331 (1972).
D. Saracino, “Amalgamation bases for nil-2 groups,” Alg. Univ., 16, 47–62 (1983).
H. E. Scheiblich, “On epics and dominions of bands,” Semigroup Forum, 13, 103–114 (1976/77).
A. Budkin, “Dominions in quasivarieties of universal algebras,” Stud. Log., 78, Nos. 1/2, 107–127 (2004).
P. V. Higgins, “Epimorphisms and amalgams,” Coll. Math., 56, No. 1, 1–17 (1988).
A. I. Mal'tsev, “Quasiprimitive classes of abstract algebras,” Dokl. Akad. Nauk SSSR, 108, No. 2, 187–189 (1956).
S. A. Shakhova, “Lattices of dominions in quasivarieties of Abelian groups,” Algebra Logika, 44, No. 2, 238–251 (2005).
S. A. Shakhova, “Distributivity conditions for lattices of dominions in quasivarieties of Abelian groups,” Algebra Logika, 45, No. 4, 484–499 (2006).
A. Budkin, “Lattices of dominions of universal algebras,” Algebra Logika, 46, No. 1, 26–45 (2007).
L. L. Maksimova, “Modal logics and varieties of modal algebras: Beth properties, interpolation, and amalgamation,” Algebra Logika, 31, No. 2, 145–166 (1992).
L. L. Maksimova, “Projective Beth properties in modal and superintuitionistic logics,” Algebra Logika, 38, No. 3, 316–333 (1999).
L. L. Maksimova, “Intuitionistic logic and implicit definability,” Ann. Pure Appl. Log., 105, Nos. 1–3, 83–102 (2000).
L. L. Maksimova, “Restricted interpolation and the projective Beth property in equational logic,” Algebra Logika, 42, No. 6, 712–726 (2003).
V. A. Gorbunov, Algebraic Theory of Quasivarieties, Sib. School Alg. Log. [in Russian], Nauch. Kniga, Novosibirsk (1999).
A. I. Mal'tsev, Algebraic Systems [in Russian], Nauka, Moscow (1970).
A. I. Budkin, Quasivarieties of Groups [in Russian], Altai State Univ., Barnaul (2002).
A. I. Budkin and V. A. Gorbunov, “Toward a theory of quasivarieties of algebraic systems,” Algebra Logika, 14, No. 2, 123–142 (1975).
M. I. Kargapolov and Yu. I. Merzlyakov, Fundamentals of Group Theory [in Russian], Nauka, Moscow (1982).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Algebra i Logika, Vol. 47, No. 5, pp. 541–557, September–October, 2008.
Rights and permissions
About this article
Cite this article
Budkin, A.I. Dominions of universal algebras and projective properties. Algebra Logic 47, 304–313 (2008). https://doi.org/10.1007/s10469-008-9029-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10469-008-9029-6