Influence of Collaterals on True FFR Prediction for a Left Main Stenosis with Concomitant Lesions: An In Vitro Study

Abstract

With the aim of assisting interventional cardiologists during decision making for revascularization, reduced-order (0D) approaches have been developed to predict the true fractional flow reserve (FFR_True) of individual stenoses in multiple-lesion arrangements. In this study, a general equation was derived to predict the FFR_True of a left main (LM) coronary stenosis with downstream lesions, one in the left anterior descending (LAD) and the other in the left circumflex (LCx) artery, and distinct collateral circulations supplying each daughter artery. An in vitro model mimicking the fractal nature of LM bifurcation trees with collateral branches was developed to validate the FFR values obtained with the prediction model (FFR ^Model_Pred ). Our results demonstrated that: (1) considering collaterals significantly improved the FFR ^Model_Pred estimation for a moderate LM stenosis with two downstream lesions as compared to computations with no collateral consideration (p < 0.001): mean absolute error |FFR ^Model_Pred  − FFR_True| ± SD was equal to 0.02 ± 0.01 vs. 0.04 ± 0.02 respectively, and (2) Deviations from FFR_True for LM stenoses are correlated to both, downstream lesion severities and collateral developments. The present study supports the hypothesis that collateral circulations supplying the LAD and LCx must be considered when predicting the FFR_True of an LM stenosis with downstream lesions.

Appendix

Derivation of the General True FFR Prediction Equation for an LM Stenosis with Two Downstream Lesions and Two Collateral Circulations Supplying the LAD and LCx

Background

Pijls et al.18 described the flow in a single stenosed coronary artery supplied by a collateral circulation. They found and validated the two following relationships:

$$ Q_{\rm S}^{{\prime }} = \frac{{P_{\rm d}^{{\prime }} - P_{\rm W}^{{\prime }} }}{{P_{\rm d} - P_{\rm W} }} Q_{\rm S} $$

(A.1)

$$ {\text{and}}\;Q_{\rm S} = \frac{{P_{\rm d} - P_{\rm W} }}{{P_{\rm a} - P_{\rm W} }} Q_{\rm S}^{\rm N} , $$

(A.2)

where ($P_{\rm d} ,P_{\rm d}^{{\prime }}$), ($P_{\rm W} ,P_{\rm W}^{{\prime }}$) and ($Q_{\rm S} ,Q_{\rm S}^{{\prime }}$) are the distal pressures, wedge pressures and hyperemic coronary flows going through the stenosis before and after revascularization, respectively. Q ^N_S is the normal coronary artery flow. Superscript ‘N’ will be used for normal state (State N) or healthy configuration (i.e., without stenoses).

Proposed Model

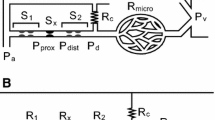
After removing the two downstream lesions R_1S and R_2S (State A′, Fig. 1b), the distal pressures of the treated lesions are both equal to the distal pressure of the LM stenosis (i.e., $P_{\rm 1d}^{{\prime }} = P_{\rm 2d}^{{\prime }} = P_{\rm m}^{{\prime }}$). Moreover, the coronary occlusion pressures $P_{{1{\text{W}}}}^{{\prime }} \;{\text{and}}\;P_{{2{\text{W}}}}^{{\prime }}$ are assumed to be different for each coronary branch (Fig. 1b). By considering the previous relationships (Eqs. (A.1) and (A.2)) for LAD and LCx coronary arteries supplied by their own collateral circulation (Fig. 1), one can write:

$$ Q_{\rm 1S}^{{\prime }} = \frac{{P_{\rm m}^{{\prime }} - P_{\rm 1W}^{{\prime }} }}{{P_{\rm 1d} - P_{\rm 1W} }} Q_{\rm 1S} , Q_{\rm 2S}^{{\prime }} = \frac{{P_{\rm m}^{{\prime }} - P_{\rm 2W}^{{\prime }} }}{{P_{\rm 2d} - P_{\rm 2W} }} Q_{\rm 2S} $$

(A.3a,b)

with

$$ Q_{\rm 1S} = \frac{{P_{\rm 1d} - P_{\rm 1W} }}{{P_{\rm a} - P_{\rm 1W} }} Q_{\rm 1S}^{\rm N} \;{\text{and}}\;Q_{\rm 2S} = \frac{{P_{\rm 2d} - P_{\rm 2W} }}{{P_{\rm a} - P_{\rm 2W} }} Q_{\rm 2S }^{\rm N} $$

(A.4a,b)

By substituting Eq. (A.4a) into Eq. (A.3a) and Eq. (A.4b) into Eq. (A.3b) one can obtain:

$$ Q_{\rm 1S}^{{\prime }} = \frac{{P_{\rm m}^{{\prime }} - P_{\rm 1W}^{{\prime }} }}{{P_{\rm a} - P_{\rm 1W} }} Q_{\rm 1S}^{\rm N} \;{\text{and}}\;Q_{\rm 2S}^{{\prime }} = \frac{{P_{\rm m}^{{\prime }} - P_{\rm 2W}^{{\prime }} }}{{P_{\rm a} - P_{\rm 2W} }} Q_{\rm 2S}^{\rm N} $$

(A.5a,b)

Since the LM stenosis resistance R_m does not vary from State A (Fig. 1a) to State A′ (Fig. 1b) and because it was assumed that the flow through a resistance satisfies Poiseuille’s law (i.e., Resistance = Pressure gradient/Flow), one can derive the following relationship:

$$ R_{\text{m}} = \frac{{P_{\text{a}} - P_{\text{m}} }}{{Q_{\text{m}} }} = \frac{{P_{\text{a}}^{{\prime }} - P_{\text{m}}^{{\prime }} }}{{Q_{\text{m}}^{{\prime }} }} \;{\text{or}}\;\frac{{P_{\text{a}} - P_{\text{m}} }}{{P_{\text{a}}^{{\prime }} - P_{\text{m}}^{{\prime }} }} = \frac{{Q_{\text{m}} }}{{Q_{\text{m}}^{{\prime }} }} = \frac{{Q_{{1{\text{S}}}} + Q_{{2{\text{S}}}} }}{{Q_{{ 1 {\text{S}}}}^{{\prime }} + Q_{{ 2 {\text{S}}}}^{{\prime }} }} $$

(A.6a,b)

Substituting Eqs. (A.4a,b) and (A.5a,b) into Eq. (A.6b) yields to:

$$ \frac{{P_{\rm a} - P_{\rm m} }}{{P_{\rm a}^{{\prime }} - P_{\rm m}^{{\prime }} }} = \frac{{\frac{{\left( {P_{\rm 1d} - P_{\rm 1W} } \right) Q_{\rm 1S}^{\rm N} }}{{P_{\rm a} - P_{\rm 1W} }} + \frac{{\left( {P_{\rm 2d} - P_{\rm 2W} } \right) Q_{\rm 2S}^{\rm N} }}{{P_{\rm a} - P_{\rm 2W} }} }}{{\frac{{\left( {P_{\rm m}^{{\prime }} - P_{\rm 1W}^{{\prime }} } \right) Q_{\rm 1S}^{\rm N} }}{{P_{\rm a} - P_{\rm 1W} }} + \frac{{\left( {P_{\rm m}^{{\prime }} - P_{\rm 2W}^{{\prime }} } \right) Q_{\rm 2S}^{\rm N} }}{{P_{\rm a} - P_{\rm 2W} }}}} $$

(A.7)

In this model the collateral flow index (CFI), which describes how developed is the collateral circulation, is calculated as ${\text{CFI}}_{1} = P_{{1{\text{W}}}} /P_{\text{a}} = P_{{1{\text{W}}}}^{{\prime }} /P_{\text{a}}^{{\prime }}$ for the myocardial resistance supplied by the LAD (R₁) and as ${\text{CFI}}_{2} = P_{{2{\text{W}}}} /P_{\text{a}} = P_{{2{\text{W}}}}^{{\prime }} /P_{\text{a}}^{{\prime }}$ for the myocardial resistance supplied by the LCx (R₂). Notice that CFI₁ and CFI₂ do not vary from State A to State A′.18

Dividing the numerators and denominators on both sides of Eq. (A.7) by P_a and $P_{\rm a}^{{\prime }}$ respectively, allows us to obtain the following relationship:

$$ \frac{{1 - \text{FFR}_{\rm App} }}{{1 - \text{FFR}_{\rm Pred} }} = \frac{{\frac{{\left( {\text{FFR}_{\rm G1} - \text{CFI}_{1} } \right) Q_{\rm 1S}^{\rm N} }}{{P_{\rm a} - P_{\rm 1W} }} + \frac{{\left( {\text{FFR}_{\rm G2} - \text{CFI}_{2} } \right) Q_{\rm 2S}^{\rm N} }}{{P_{\rm a} - P_{\rm 2W} }} }}{{\frac{{\left( {\text{FFR}_{\rm Pred} - \text{CFI}_{1} } \right) Q_{\rm 1S}^{\rm N} }}{{P_{\rm a} - P_{\rm 1W} }} + \frac{{\left( {\text{FFR}_{\rm Pred} - \text{CFI}_{2} } \right) Q_{\rm 2S}^{\rm N} }}{{P_{\rm a} - P_{\rm 2W} }}}} $$

(A.8)

where FFR_App = P_m/P_a, ${\text{FFR}}_{\text{Pred}} = P_{\rm m}^{{\prime }} /P_{\text{a}}^{{\prime }},$ FFR_G1 = P_1d/P_a and FFR_G2 = P_2d/P_a (see “Materials and Methods” section for FFR definitions).

Then, dividing by P_a the numerator and denominator of the right side term of Eq. (A.8), gives:

$$ \frac{{1 - \text{FFR}_{\rm App} }}{{1 - \text{FFR}_{\rm Pred} }} = \frac{{\left( {1 - \text{CFI}_{2} } \right)\left( {\text{FFR}_{\rm G1} - \text{CFI}_{1} } \right) Q_{\rm 1S}^{\rm N} + \left( {1 - \text{CFI}_{1} } \right)\left( {\text{FFR}_{\rm G2} - \text{CFI}_{2} } \right) Q_{\rm 2S}^{\rm N} }}{{\left( {1 - \text{CFI}_{2} } \right)\left( {\text{FFR}_{\rm Pred} - \text{CFI}_{1} } \right) Q_{\rm 1S}^{\rm N} + \left( {1 - \text{CFI}_{1} } \right)\left( {\text{FFR}_{\rm Pred} - \text{CFI}_{2} } \right) Q_{\rm 2S}^{\rm N} }} $$

(A.9)

To isolate FFR_Pred, Eq. (A.9) transforms as follow:

$$ \text{FFR}_{\rm Pred} = \frac{{Q_{\rm 1S}^{\rm N} \left( {1 - \text{CFI}_{2} } \right)\left( { \text{FFR}_{\rm G1} - \text{CFI}_{1} \text{FFR}_{\rm App} } \right) + Q_{\rm 2S}^{\rm N} \left( {1 - \text{CFI}_{1} } \right)\left( {\text{FFR}_{\rm G2} - \text{CFI}_{2} \text{FFR}_{\rm App} } \right)}}{{Q_{\rm 1S}^{\rm N} \left( {1 - \text{CFI}_{2} } \right)\left( { 1 - \text{FFR}_{\rm App} + \text{FFR}_{\rm G1} - \text{CFI}_{1} } \right) + Q_{\rm 2S}^{\rm N} \left( {1 - \text{CFI}_{1} } \right)\left( {1 - \text{FFR}_{\rm App} + \text{FFR}_{\rm G2} - \text{CFI}_{2} } \right)}} $$

(A.10)

Finally, dividing the numerator and denominator of the right side term of Eq. (A.10) by $Q_{\rm 2S}^{\rm N}$ and defining “k” as the flow ratio $Q_{\rm 1S}^{\rm N} /Q_{\rm 2S}^{\rm N},$ allow us to obtain the original predictive equation for the true hemodynamic significance of the LM lesion (i.e., Eq. (1)).

The parameter “k” represents the flow ratio between LAD and LCx branches for a non-pathological LM bifurcation (i.e., at healthy configuration without collaterals). This is when no stenotic lesions (R_m, R_1S and R_2S) are present (i.e., when FFR_G1 = FFR_G2 = FFR_App = 1) and when both collateral circulations supplying the LAD and LCx are poorly developed (i.e., when CFI₁ = CFI₂ ≈ 0).

Flow-Diameter Scaling Law for “k” Calculation

From Kassab’s group work6 it is know that flows and diameters in a vascular tree follow the next relationship:

$$ \left[ {\frac{{Q_{\rm stem} }}{{Q_{\rm max} }}} \right] = \left[ {\frac{{D_{\rm stem} }}{{D_{\rm max} }}} \right]^{7/3} , $$

(A.11)

where Q_stem and D_stem are the flow and diameter of the “stem” or branch of interest (LAD or LCx for this example). Q_max and D_max are the flow and diameter of the most proximal stem (LM in this case).

The following expressions are obtained for healthy LAD and LCx flows:

$$ Q_{\rm 1S}^{\rm N} = Q_{\rm m}^{\rm N} \left( {\frac{{D_{\rm LAD}^{7/3} }}{{D_{\rm LM}^{7/3} }}} \right) $$

(A.12)

$$ Q_{\rm 2S}^{\rm N} = Q_{\rm m}^{\rm N} \left( {\frac{{D_{\rm LCx}^{7/3} }}{{D_{\rm LM}^{7/3} }}} \right) $$

(A.13)

Finally,

$$ k = \frac{{Q_{\rm 1S}^{\rm N} }}{{Q_{\rm 2S}^{\rm N} }} = \left( {\frac{{D_{\rm LAD} }}{{D_{\rm LCx} }}} \right)^{{\frac{7}{3}}} $$

(A.14)

Experimental Estimation of “k” for the In Vitro Validation

In this model each coronary branch plus its collateral is considered as an individual path to bring blood to a specific myocardial resistance. The total myocardial flow for R₁ and R₂ can be expressed as follows: Q₁ = Q_1S + Q_1C and Q₂ = Q_2S + Q_2C (see Fig. 1c).

In “healthy configuration” collateral circulations $Q_{\rm 1C}^{\rm N}$ and $Q_{\rm 2C}^{\rm N}$ are considered negligible and normal coronary flows $Q_{\rm 1S}^{\rm N}$ and $Q_{\rm 2S}^{\rm N}$ are equal to normal myocardial flows $Q_{1}^{\rm N}$ and $Q_{2}^{\rm N},$ respectively.18 So, at normal state it is assumed that $Q_{\rm 1S}^{\rm N} /Q_{\rm 2S}^{\rm N} = Q_{1}^{\rm N} /Q_{2}^{\rm N}.$

Moreover, at State A′ (Fig. 1d), the flow ratio $Q_{1}^{{\prime }} /Q_{2}^{{\prime }}$ is equal to the ratio of the myocardial resistances R₂/R₁ because $Q_{1 }^{{\prime }} = \left( {P_{\rm m}^{{\prime }} - P_{\rm v}^{{\prime }} } \right)/R_{1}$ and $Q_{2 }^{{\prime }} = \left( {P_{\rm m}^{{\prime }} - P_{\rm v}^{{\prime }} } \right)/R_{2}.$ Similarly, at “normal state” (i.e., State N) Poiseuille’s law allows us also to write: $Q_{1 }^{\rm N} = \left( {P_{\rm a}^{\rm N} - P_{\rm v}^{\rm N} } \right)/R_{1}$ and $Q_{2 }^{\rm N} = \left( {P_{\rm a}^{\rm N} - P_{\rm v}^{\rm N} } \right)/R_{2}$ making the flow ratio $Q_{1}^{\rm N} /Q_{2}^{\rm N}$ equal to R₂/R₁ as well. In the end, if the myocardial resistances remain unchanged for a patient, one has:

$$ k = \frac{{Q_{\rm 1S}^{\rm N} }}{{Q_{\rm 2S}^{\rm N} }} = \frac{{Q_{1}^{\rm N} }}{{Q_{2}^{\rm N} }} = \frac{{Q_{1 }^{{\prime }} }}{{Q_{2}^{{\prime }} }}. $$

(A.15)