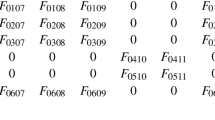Abstract
The purpose of this paper is to propose and develop a large strain embedded finite element formulation that can be used to explicitly model axonal fiber bundle tractography from diffusion tensor imaging of the brain. Once incorporated, the fibers offer the capability to monitor tract-level strains that give insight into the biomechanics of brain injury. We show that one commercial software has a volume and mass redundancy issue when including embedded axonal fiber and that a newly developed algorithm is able to correct this discrepancy. We provide a validation analysis for stress and energy to demonstrate the method.












Similar content being viewed by others
References
Assaf, Y., and O. Pasternak. Diffusion tensor imaging (DTI)-based white matter mapping in brain research: a review. J. Mol. Neurosci. 34(1):51–61, 2008.
Bayly, P. et al. Measurement of brain biomechanics in vivo by magnetic resonance imaging. In: Application of Imaging Techniques to Mechanics of Materials and Structures: Proceedings of the 2010 Annual Conference on Experimental and Applied Mechanics, vol. 4, T. Proulx, Ed. Springer, 2013, pp. 117–128.
Belytschko, T., W. K. Liu, B. Moran, and K. Elkhodary. Nonlinear Finite Elements for Continua and Structures. New York: Wiley, 2013.
De Geeter, N., L. Dupré, and G. Crevecoeur. Modeling transcranial magnetic stimulation from the induced electric fields to the membrane potentials along tractography-based white matter fiber tracts. J. Neural Eng. 13(2):026028, 2016.
Murray, D. W., and A. A. Elwi. Nonlinear analysis of axisymmetric reinforced concrete structures. Structural engineering report SER 87 | SER-ID SER87, 1980. https://doi.org/10.7939/R3T14TR1F.
Fish, J. The s-version of the finite element method. Comput. Struct. 43(3):539–547, 1992.
Fish, J., and T. Belytschko. Elements with embedded localization zones for large deformation problems. In: Computational Structural Mechanics & Fluid Dynamics, edited by A. K. Noor, and D. L. Dwoyer. Pergamon: Elsevier, 1988, pp. 247–256.
Garimella, H. T., Yuan, H. Johnson, B. D., Slobounov, S. L., and R. H. Kraft. A two-fiber anisotropic constitutive model of human brain with intravoxel heterogeneity of fiber orientation using diffusion spectrum imaging (DSI). In ASME 2014 International Mechanical Engineering Congress and Exposition, 2014, pp. V003T03A011–V003T03A011.
Garimella, H. T., and R. H. Kraft. Modeling the mechanics of axonal fiber tracts using the embedded finite element method. Int. J. Numer. Methods Biomed. Eng. 33(5):e2823, 2017.
Garimella, H. T., and R. H. Kraft. A new computational approach for modeling diffusion tractography in the brain. Neural Regen. Res. 12(1):23, 2017.
Garimella, V. An embedded element based human head model to investigate axonal injury. PhD Thesis, Pennsylvania State University, 2017.
Garimella, H. T., A. Przekwas, and R. H. Kraft. Do blast-induced skull flexures result in axonal deformation? PloS ONE 13(3):e0190881, 2018.
Giordano, C., S. Zappalà, and S. Kleiven. Anisotropic finite element models for brain injury prediction: the sensitivity of axonal strain to white matter tract inter-subject variability. Biomech. Model. Mechanobiol. 16(4):1269–1293, 2017.
Gleichgerrcht, E., J. Fridriksson, C. Rorden, and L. Bonilha. Connectome-based lesion-symptom mapping (CLSM): a novel approach to map neurological function. NeuroImage Clin. 16:461–467, 2017.
Guertler, C. A., R. J. Okamoto, J. L. Schmidt, A. A. Badachhape, C. L. Johnson, and P. V. Bayly. Mechanical properties of porcine brain tissue in vivo and ex vivo estimated by MR elastography. J. Biomech. 69:10–18, 2018.
Guy, J., E. A. Ellis, K. Kelley, and G. M. Hope. Spectra of G ratio, myelin sheath thickness, and axon and fiber diameter in the guinea pig optic nerve. J. Comp. Neurol. 287(4):446–454, 1989.
Hagmann, P., et al. Mapping the structural core of human cerebral cortex. PLoS Biol. 6(7):e159, 2008.
Helmut, H. Development of a Continuum-Mechanics-Based Tool for 3D Finite Element Analysis of Reinforced Concrete Structures and Application to Problems of Soil-Structure Interaction. Graz: Graz University of Technology, 2002.
Iarve, E. V., D. H. Mollenhauer, E. G. Zhou, T. Breitzman, and T. J. Whitney. Independent mesh method-based prediction of local and volume average fields in textile composites. Compos. Part Appl. Sci. Manuf. 40(12):1880–1890, 2009.
Jiang, W.-G., S. R. Hallett, M. R. Wisnom, et al. Development of domain superposition technique for the modelling of woven fabric composites. In: Mechanical Response of Composites, edited by P. P. Camanho. Dordrecht: Springer, 2008, pp. 281–291.
Johnson, C. L., et al. Local mechanical properties of white matter structures in the human brain. NeuroImage 79:145–152, 2013.
Makarov, S., A. P. Leone, and A. Nummenmaa. Researching fiber networks: computational modeling of complex fibrous tissue geometries. IEEE Pulse 8(4):58–61, 2017.
Mori, S., and J. Zhang. Principles of diffusion tensor imaging and its applications to basic neuroscience research. Neuron 51(5):527–539, 2006.
Ohyama, D., Kurashiki, T., Watanabe, Y., Fujita, Y., and M. Zako. Estimation of mechanical behavior of braided composites based on mesh superposition method. In: 18th International Conference on Composite Materials, Jeju island, Korea, 2011.
Shattuck, D. W., and R. M. Leahy. BrainSuite: an automated cortical surface identification tool. Med. Image Anal. 6(2):129–142, 2002.
Sporns, O., G. Tononi, and R. Kötter. The human connectome: a structural description of the human brain. PLoS Comput. Biol. 1(4):e42, 2005.
Tabatabaei, S., and S. V. Lomov. Eliminating the volume redundancy of embedded elements and yarn interpenetrations in meso-finite element modelling of textile composites. Comput. Struct. 152:142–154, 2015.
Tabatabaei, S., S. V. Lomov, and I. Verpoest. Assessment of embedded element technique in meso-FE modelling of fibre reinforced composites. Compos. Struct. 107:436–446, 2014.
Toosy, A. T., O. Ciccarelli, G. J. Parker, C. A. Wheeler-Kingshott, D. H. Miller, and A. J. Thompson. Characterizing function–structure relationships in the human visual system with functional MRI and diffusion tensor imaging. Neuroimage 21(4):1452–1463, 2004.
Werring, D., C. Clark, G. Parker, D. Miller, A. Thompson, and G. Barker. A direct demonstration of both structure and function in the visual system: combining diffusion tensor imaging with functional magnetic resonance imaging. Neuroimage 9(3):352–361, 1999.
Zako, M., Kurashiki, T., Kubo, F., and M. Imura. A multi-scale analysis for structural design of fibrous composites–M3 method. In: 15th international conference on composite materials (ICCM-15), CD ed., Durban, 2005.
Zhao, W., Y. Cai, Z. Li, and S. Ji. Injury prediction and vulnerability assessment using strain and susceptibility measures of the deep white matter. Biomech. Model. Mechanobiol. 16(5):1709–1727, 2017.
Acknowledgment
The authors gratefully acknowledge the support provided by CFDRC, Inc. under a sub-contract funded by the Department of Defense, Department of Health Program through Contract W81XWH-14-C-0045, the U.S. Army Research Laboratory (ARL) at the Aberdeen Proving Grounds under Contract W15P7T-10-D-D416, the Defense Health Agency under the Contract W81XWH-14-C-0045 and the US Department of Defense through the Contracts W15P7T-10-D-D416, W81XWH-17-C-0216, DOTC-17-01-INIT0086. Neuroimaging data show in Fig. 2 was provided by The Pennsylvania State University Center for Sports Concussion Research and Service, University Park, USA. The authors thank Dr. Sam Slobounov and Dr. Brian D. Johnson for the data provided. We would also like to acknowledge The Pennsylvania State University Social, Life, and Engineering Sciences Imaging Center (SLEIC), High Field MRI Facility for providing access to the imaging equipment. The authors also thank The Pennsylvania State University Institute for Cyberscience for providing the computational resources required for this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Associate Editor Raj K. Prabhu oversaw the review of this article.
Harsha T. Garimella and Ritika R. Menghani are co-first authors.
Appendix
Appendix
How Does Our Element Level Corrections Compare to the Transverse Isotropic Constitutive Modeling?
In this section, we will look into some of the implementation details of selected areas of this finite element formulation—that are specific to the embedded element technique.
Transformation Matrix
This matrix can be used to transform a tensor from one coordinate system to another coordinate system. Let’s assume that the first coordinate system is represented by the basis \(\left( {m_{1} ,m_{2} ,m_{3} } \right)\) and the second coordinate system is represented by the basis \(\left( {e_{1} ,e_{2} ,e_{3} } \right)\), then the transformation matrix to transform a tensor from first coordinate system to the second coordinate system can be defined as:
i.e., if a tensor in the first coordinate system is \({\varvec{\upsigma}}_{m}\) and the same tensor in the second coordinate system is \({\varvec{\upsigma}}_{e}\), then
This matrix is frequently used in transforming a tensor of interest from fiber to matrix coordinate systems and vice versa.
Adding Embedded Fiber Mass to the Host Element Mass
For implementation purposes, an element level direct lumped mass matrix was used. The below-listed procedure explains the detailed calculation of global mass matrix using the host as well as the embedded element information.
-
1.
Calculate the host element mass using the volume and density information
-
2.
Calculate the total fiber volume embedded in this particular host element
-
3.
Calculate the fiber mass using its volume (Step-2) and using the material model information.
-
4.
Calculate the effective element mass by adding the host and embedded element masses.
-
5.
Divide this effective element mass among all the host element nodes equally and form an element level diagonal mass matrix.
-
6.
Scatter this element level mass matrix into a global mass matrix and repeat this step for all the elements.
Deformation in the Embedded Elements
Since the displacements of the embedded nodes are assumed to be a function of the displacements of the host nodes, it can be shown that the deformation gradient of the embedded elements will be same as that of the host element.
But, since \({\text{u}}_{\text{embed}} = \left[ {\mathbf{N}} \right]{\text{u}}_{{n,{\text{host}}}}\) and \({\mathbf{B}} = \frac{{\partial \left[ {\text{N}} \right]}}{{\partial {\text{X}}_{\text{host}} }}\),
Therefore, we can see that the above Eq. (22) can be extended such that
In the above equations, \(\varvec{ }{\mathbf{F}}_{\text{host}}\) represents the deformation gradient of the host element,\(\varvec{ }{\mathbf{F}}_{{{\mathbf{embed}}}}\) represents the deformation gradient of the embedded element,\(\varvec{ }{\text{x}}_{\text{host}}\) represents the current configuration of the host element, \(\varvec{ }{\text{X}}_{{{\mathbf{host}}}}\) represents the reference configuration of the host element, \({\text{u}}_{\text{host}}\) represents the continuum displacement of the host domain,\(\varvec{ }{\text{u}}_{{n,{\text{host}}}}\) represents the nodal displacements of the host domain, \(\varvec{ }{\text{u}}_{\text{embed}} \varvec{ }\) represents the nodal displacement vector of the embedded elements, \({\mathbf{B}}\) represents the strain displacement matrix and \(\varvec{ }\left[ {\mathbf{N}} \right]\) represents the shape function matrix of the host element.
Adding the Nodal Force Contribution from the Embedded Fibers Back to That of the Host Elements
Adding the nodal force vector of the truss element to the host–parent element is not straight forward and involves a complicated procedure. The overall methodology adopted here can be classified into multiple steps:
-
1.
Calculating integration points
-
2.
Calculating the internal nodal force vector.
Calculating Integration Points
This step involves a calculating the integration points and moving between coordinate systems. Note that this step in explained in the context of truss elements embedded in hexahedral host elements. Here, we have three coordinate systems. First one is the global coordinate system (coordinate system in which the host and embedded meshes are defined). The second one is the iso-parametric coordinate system of the host element. And the third one is the iso-parametric coordinate system of the embedded fiber. We will designate these systems as G (global system), LH (iso-parametric coordinate system of the host element) and LE (iso-parametric coordinate system of the embedded fiber), respectively for our future discussion. Since we will be integrating over the fiber volume to calculate the internal nodal force vector contribution from the embedded fibers and adding it to the nodal force vector from the host element, we need the integration points of the embedded fibers calculated in the LH coordinate system (iso-parametric coordinate system of the host element). This can be done using an iterative solver. In our library, we have currently implemented the Newton–Raphson solver for this purpose. More information on the mapping of integration points or the Newton–Raphson solving can be obtained from the dissertation work by Hartl.18
Calculating the Internal Nodal Force Vector of the Embedded Fiber
Once the fiber integration points are calculated in the host element coordinate system, the nodal force vector can be calculated by integrating over the fiber volume using the following equation:
In the above equation, \(n_{\xi }\) represents the number of Gauss quadrature points, and \(wts\left( \xi \right)\) represents the Gaussian weights of the particular quadrature point.
Calculating the Stress Along the Fiber
As seen in the above sub-section, both the host and embedded elements will have the same deformation gradient. Therefore, the Cauchy stress tensor calculated using the deformation gradient and the embedded fiber material properties will be transformed into the fiber coordinate system (a unit vector along the fiber axis forms the basis of this coordinate system), and the corresponding fiber stress will be calculated.
where F is the deformation gradient and \({\varvec{\upsigma}}_{\text{fiber}}\) is the fiber Cauchy stress tensor calculated in the host element coordinate system.
Calculating the Strain Along the Fiber
The deformation gradient tensor can be used to calculate the strain projected along the fiber using the following equations:
where C is the right Cauchy-Green deformation tensor, \(\lambda_{\text{fiber}}\) is the stretch along the fiber, a0 is the unit vector along the fiber direction and \(\varepsilon_{\text{fiber}}\) is the strain along the fiber.
EEMA Energy Plot
Since embedded element technique has been formulated using the finite element method, it would be essential for the energy to be conserved. Appendix Figure A1 shows a system and its corresponding energy plot. As expected, the total energy of the system remains zero throughout the span of the simulation.
Rights and permissions
About this article
Cite this article
Garimella, H.T., Menghani, R.R., Gerber, J.I. et al. Embedded Finite Elements for Modeling Axonal Injury. Ann Biomed Eng 47, 1889–1907 (2019). https://doi.org/10.1007/s10439-018-02166-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10439-018-02166-0