Abstract
In this paper, I propose a tractable model of sovereign default and the inter-state spillovers emanating from default. A coalition of nations may choose to insure against default, and the behavior of the coalition is used to examine the magnitude of the international spillovers. A voting structure for the coalition is proposed to examine idiosyncratic spillovers. The model is calibrated to the recent Greek Debt crisis to understand the spillovers from a default, and the moral hazard effect of the Troika. I find that spillover effects are large. If the rest of the world defaulted, this would create a loss equivalent to a permanent 9% decrease in government spending. Counterfactual experiments reveal that default would be prevalent without the IMF, suggesting that the own-penalty to defaulting has decreased since the IMF’s creation.






Similar content being viewed by others
Notes
I design the model with sufficient generality to capture any of the various motivations the IMF might have for preventing a sovereign default. These might include financial contagion, trade disruptions, or even non-economic costs.
An example would be the US debt ceiling.
This is stronger than necessary for the Townsend result to hold. All that is needed is that \(\frac{\partial ^2 u(g, c)}{\partial g \partial c} \le 0\), or that public and private consumption are substitutes.
This tax rate is taken as given. This simplification prevents governments from taxing their way out of a crisis. Holding the tax rate constant is plausible. For example, in the U.S. federal revenues are about 15 to 19 percent of GDP over time. See https://fred.stlouisfed.org/series/FYFRGDA188S. Revenue as a percentage of GDP tends to go down during a recession, lending further credence to the assumption that governments cannot tax their way out of a budget crisis.
Because the utility function is additively separable, shutting down private credit markets will not affect the solvency decisions of governments.
A extension to this model would be to allow the default to impact total factor productivity, not welfare. This would allow for interesting mechanics in terms of debt crisis contagion. The current specification has a tractability advantage, and it also captures non-economic costs to default such as social unrest.
In reality, the IMF assigns voting shares to nations roughly proportional to their GDP. In the model, nations are atomless. Because in recent history, defaulting nations have all commanded a small percentage of world GDP (the largest in the last two decades being Russia’s 1998 default when it represented \(.9\%\) of world GDP), atomlessness is not unrealistic and steady state analysis can be performed when calibrating the model.
France, a large and developed nation, was the first country to receive a bailout in 1947.
Less than one tenth of one percent of the Fund’s value is spent on salaries and administrative expenses.
See appendix for a game theoretic view of the IMF in which nations vote for \(\theta \). This allows for analysis of idiosyncratic spillovers resulting from a default.
As I will describe in the computational section, It is possible to compute IMF’s involvement directly by simply finding the ratio of interventions to crisis. Both methods are used.
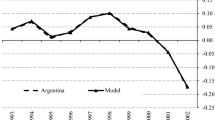
I assume that without a bailout, Greece would default with probability 1. Therefore, any chance of repayment comes solely from the chance of receiving a bailout. In this case an interest rate of 29.24 on ten year bonds gives a value of \(\theta = .8\).
In a two by two transition matrix, it is easy to show that the mean and variance for the coefficient estimates of the steady state matrix do not exist.
Several international organizations are structured in this way. The EMU requires unanimous consent on major issues. Similarly, when the Troika negotiated the Greek bailout, participation of all parties appeared necessary.
I use the word pure carefully here. Nations are choosing a probability, not an action, therefore, choosing one probability would be a pure strategy. A mixed strategy would be the choice of a distribution over probabilities to announce.
References
Bernanke, B.S.: Bankruptcy, liquidity, and recession. Am. Econ. Rev. 71(2), 155–159 (1981)
Bulow, J.I., Rogoff, K.S.: Sovereign debt: is to forgive to forget? (1988)
Calomiris, C.W.: The imf’s imprudent role as lender of last resort. Cato J. 17, 275 (1997)
Cruces, J.J., Trebesch, C.: Sovereign defaults: the price of haircuts. Am. Econ. J. Macroecon. 5(3), 85–117 (2013)
Diamond, P.A.: National debt in a neoclassical growth model. Am. Econ. Rev. 55(5), 1126–1150 (1965)
Fernandez, R., Rosenthal, R.W.: Strategic models of sovereign-debt renegotiations. Rev. Econ. Stud. 57(3), 331–349 (1990)
Fischer, S.: On the need for an international lender of last resort. J. Econ. Perspect. 13(4), 85–104 (1999)
Gale, D., Hellwig, M.: Incentive-compatible debt contracts: the one-period problem. Rev. Econ. Stud. 52(4), 647–663 (1985)
Glasserman, P., Young, H.P.: Contagion in financial networks. J. Econ. Lit. 54(3), 779–831 (2016)
Hart, O.: Different approaches to bankruptcy. Technical rep, National Bureau of Economic Research (2000)
Hart, O., Moore, J.: Default and renegotiation: a dynamic model of debt. Q. J. Econ. 113(1), 1–41 (1998)
Herranz, N., Krasa, S., Villamil, A.P.: Entrepreneurs, risk aversion, and dynamic firms. J. Polit. Econ. 123(5), 1133–1176 (2015)
Leland, H.: Predictions of expected default frequencies in structural models of debt. In: Venice Conference on Credit Risk (2002)
Masson, P.R.: Contagion: monsoonal effects, spillovers, and jumps between multiple equilibria. International Monetary Fund (1998)
Mehra, R., Prescott, E.C.: The equity premium: a puzzle. J. Monet. Econ. 15(2), 145–161 (1985)
Oatley, T., Yackee, J.: American interests and imf lending. Int. Polit. 41(3), 415–429 (2004)
Reinhart, C.M., Rogoff, K.S.: This Time is Different: Eight Centuries of Financial Folly. Princeton University Press, Princeton (2009)
Martins-da Rocha, V.F., Vailakis, Y.: Borrowing in excess of natural ability to repay. Rev. Econ. Dyn. 23, 42–59 (2017)
Rosenthal, R.W.: On the incentives associated with sovereign debt. J. Int. Econ. 30(1–2), 167–176 (1991)
Stone, R.W.: The political economy of imf lending in Africa. Am. Polit. Sci. Rev. 98(04), 577–591 (2004)
Tauchen, G.: Finite state Markov-chain approximations to univariate and vector autoregressions. Econ. Lett. 20(2), 177–181 (1986)
Thacker, S.C.: The high politics of imf lending. World Polit. 52(01), 38–75 (1999)
Townsend, R.M.: Optimal contracts and competitive markets with costly state verification. J. Econ. Theory 21(2), 265–293 (1979)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Computational Appendix: Markov transition matrix
To estimate a Markov transition matrix from continuous data, the seminal work researchers turn to is Tauchen (1986). Alternatively, one may also take the “brute force approach” and simply estimate the transition probabilities directly. However, this model presented several characteristics that made the standard approaches challenging. First, a large transition matrix is needed because the fineness of the matrix determines how precisely interest rates can be estimated (through \(F(\gamma ^*)\)). Second, because this is a model of default, rare negative shocks are pivotal in determining behavior. Finally, because I intend to do steady state analysis, I need the steady state produced by the matrix (especially at these negative shocks) to be consistent with the data.
Standard approaches are wanting for various reasons. Tauchen imposes a linear structure behind the transition probabilities, which can make for strange steady states and tails of the distribution of shocks. The brute force method runs into a data problem, so the estimates of the transition matrix will be inexact. Further, if statistics on the resulting steady state distribution vector are desired they will be computationally challenging to get, if they exist at all.Footnote 13 Here, I propose an alternative technique which can be used to calculate large transition matrices with an eye towards the steady state vector which it will produce.
Let \(\varGamma \) be a length T sequence of annual growth rates and let \(\gamma _t\) be the number t element of \(\varGamma \). Bin these rates into n number of states \(\{s_1, s_2, ..., s_n\} = S\), and call the resulting sequence \({\bar{\varGamma }}\). Call the distribution of the aggregate frequency in each state \({\hat{\mathbf {d}}}\). Thus, \({\hat{\mathbf {d}}}\) is a probability mass function with value
Consider \({\hat{\mathbf {d}}}\), an estimate of the steady state distribution. The resulting estimated transition matrix must produce \({\hat{\mathbf {d}}}\) as its steady state. Each element \({\hat{\mathbf {d}}}_i\) of the vector \({\hat{\mathbf {d}}}\) is a parameter estimate of the frequency of this realization occurring in steady state. The standard error is
Let \(\varvec{M}\) be an n by n transition matrix such that \(\varvec{M}_{i,j}\) is the probability of transitioning to state j if one is in state i. If M has steady state \({\hat{\mathbf {d}}}\), then it must satisfy
Being a transition matrix, of course it must also satisfy
where \(\varvec{\mathbb {1}}\) is a n by 1 vector of ones. Because the problem requires the expected growth rate to be rising in the current state in a first order stochastic dominance sense,
To estimate a transition matrix in a computationally feasible way, I minimize least squares under these linear constraints. The objective is therefore:
In doing this, I have essentially tacked a middle road. I biased the transition matrix, compared to that produced by the brute force method, by constraining it to fit the steady state distribution. This insures me moments of the parameter estimates of the steady state distribution. On the other hand, I have not “biased” the estimation so much as the Tauchen method would, because I merely impose first order stochastic dominance on the rows of the transition matrix, not a linear form.
To estimate the transition matrix, I used IMF data on annual growth rates from a panel of 110 countries. To solve the problem, I used IBM’s CPLEX software. Solving a 30 by 30 matrix (900 variables, 120 constraints) can be done in less than .005 seconds on a desktop (Fig. 7).
You can see that it is undefined at some lower states due to incidences of the low realization occurring at the end or beginning of a nation’s sequence of shocks. It is clear that the preferred specification has a wider spread, which is helpful in the model.
Appendix: Voting and the IMF
While the view of the coalition as a planner induces a straightforward interpretation of its behavior by way of the underlying externalities which motivate it, such a monolithic structure does not allow for heterogeneity in the international spillovers. To this end, consider a political economy for the coalition.
Suppose that the coalition is composed of \(j = 1...n\) members who each receive an idiosyncratic utility penalty resulting from the default of a country. Each country, with knowledge of this penalty, announces a probability of voting to approve the bailout. I consider the case in which unanimous consent is required to approve a bailout because crisp theoretical results are produced.Footnote 14
Therefore, the probability of a bailout being issued is
Payoffs in this game are given by
Suppose all \(U_j\) are strictly concave in \(\theta \) and each coalition member j has a unique \(\theta ^*_j\) where \(U_j\) is maximized. Also, suppose at least two coalition members have different ideal \(\theta ^*_j\) values.
I consider pure strategies.Footnote 15
Suppose there exists a nation j such that its desired outcome \(\theta ^*_j < \theta ^*_i\) for all \(i \ne j\).
Proposition 4
The unique pure strategy Nash equilibrium occurs when the nation desiring the lowest \(\theta \) plays that value, and all other nations choose \(\theta _j = 1\).
This equilibrium is highly illustrative. Because nations only differ in \(u^{ij}\), their idiosyncrasies in \(\theta ^*_j\) are determined through \(u^{ij}\). We end up with two cases
-
1.
If default is decreasing in \(\theta \) at \({\hat{\theta }}\), then the \(u_{ij}\) implied by the chosen \({\hat{\theta }}\) is an upper bound for the coalition members’ \(u^{ij}\).
-
2.
If default is increasing in \(\theta \) at the observed level \({\hat{\theta }}\), then the \(u^{ij}\) which motivates \({\hat{\theta }}\) is the lowest \(u^{ij}\) in the coalition. That is, the coalition members’ \(u^{ij}\) values are bounded below by the \(u^{ij}\) implied by solving the coalitions problem as was done in the computational section.
Following from this, if we find ourselves in the second case, and we observe an increase in \(\theta \) (though either lower interest rates, or in increased incidence of bailouts), one can infer that the underlying spillovers have increased.
Appendix: Proofs
1.1 Proof of Proposition 1
Part one: It is straight forward to show. First we must note that our expectation of \(\gamma '\) increases in \(\gamma \) because of the FOSD assumption. Defining
T maps increasing functions to increasing functions, so \( V^S(b',y',\gamma ',x', \zeta )\) is increasing in \(\gamma '\), and \(E[ V^S(b',y',\gamma ',x', \zeta ) ]\) is increasing in \(\gamma \). A similar argument can be made for \(V^D\)
Finally, suppose that for a small increase in \(\gamma \), the additional output is consumed completely. There must be an increase in u, because it is increasing in both arguments, and \({\tilde{V}}^S\) must increase by at least as much.
Part two: For any \(\{b, \ell , y, x, \zeta \}\) such that \(\gamma \in D(b, \ell )\), define \(g^S \) as the optimal policy solving \(\tilde{V^S}\), and \(g^D = \tau (1 - \frac{\zeta ' - \zeta }{y})y\).
Note that the difference between the last two terms must be positive because an increase in output tomorrow for an unstained nation can be consumed or used to payoff debt, where an increase in output for a stained nation can only be used for consumption (public or private). Also, as output increases, debt must weakly decrease in equilibrium so \(V^{S,1} \frac{\partial b}{\partial \gamma }\) is positive.
There are two cases. If \(g^S < g^D\) then by \(\frac{\partial ^2 u}{\partial g \partial c} < 0\) the first four terms are positive.
If \(g^S > g^D\) then clearly \(g^D\) is obtainable while remaining solvent. If \(g^S\) then \(u(g^S,c) > u(g^S,c)\). \(V^S(b, y, \gamma , x, \zeta ) > V^D(b,y,\gamma , x, \zeta ) - u^{ii}\), so \({\tilde{V}}^S> {\tilde{V}}^D\), a contradiction of \(\gamma \in D(b, \ell )\).
1.2 Proof of Theorem 1
Proof
If the default set is empty, or spans the support of F the theorem is vacuously true. Now suppose that for a given \(b_t\), \({\tilde{D}} \subset Y\). This implies that in every period, there exists some value \(y^*\), with a conjoined \(\gamma ^*\) at which \(V^S(b, y^*, \gamma ,x) < V^D(b,y^*,\gamma ^*)\) and some other value \(y'\) at which \(V^S > V^D\). Because both functions are increasing in y, but \(V^S\) increases faster, it must be that \(y<y'\). Because we have continuity of the value functions, the intermediate value theorem implies that \(\exists \gamma ^*\) such that \(V^S = V^D\). By the same argument used to order y and \(y'\), we conclude that for any \(y \in V^D\), \(y<y^*\). \(\square \)
1.3 Proof of Proposition 2
Proof
Recall that \({\bar{b}}\) and \(u^{ii}\) scale in \(\gamma \) and \(\gamma ^{1-\sigma }\) respectively, so the right hand side of the value function changes by a factor of \(\gamma ^{1-\sigma }\).
Suppose current bonds b and current output y go to \(\gamma b\) and \(\lambda y\) respectively. Let spending go to \(\gamma g\) and next period bonds \(\gamma b'\). This satisfies the budget constraint and the default set remains unaltered.
Optimality of \(V^s(\gamma b, \gamma y, \gamma )\) therefore implies
Finally, letting \({\tilde{b}} = b/\gamma \) and \({\tilde{y}} = y/\gamma \)
Therefore, we have
A similar argument can be made for \(V^D\). \(\square \)
1.4 Proof of Theorem 2
Proof
Suppose to the contrary that \({\bar{b}}_r > {\tilde{b}}\). This implies that the debt level at which interest rates go to infinity is higher than the level guaranteed by the IMF. However, if the IMF cannot make a loan above \({\tilde{b}}\), this implies that it would not be paid back \({\tilde{b}}\). Therefore, the interest rate at \({\tilde{b}}\) goes to infinity. But at \({\bar{b}}_r\), interest rates go to infinity, and \({\bar{b}}_r > {\tilde{b}}\). A contradiction
Now suppose that \({\bar{b}}_r < {\tilde{b}}\). This implies that the IMF is willing to make a loan at \({\bar{b}}_r\). But in that case, with \(\theta \) probability, the loan will be repaid. Therefore interest rates cannot go to infinity at \({\bar{b}}\), a contradiction. Therefore we conclude \({\bar{b}}_r\) = \({\tilde{b}}\). \(\square \)
1.5 Proof of Proposition 3
Proof
The two equations which link \(r^i _{t+1}\) and \(\gamma ^*_t\) are as follows:
The first equation says that at \(\gamma ^*\) for a given level of debt \(b_t\), the nation must be indifferent between choosing solvency and insolvency before any IMF action is considered. This is merely the definition of \(\gamma ^*\). Note that holding b constant, the mapping generated from \([r^i(b')\) to \(\gamma ^*(b)]\) is continuous and passes through the origin. That is to say, if interest rates are zero, no nation need default because debt can simply be rolled over without cost. As \(\theta \) increases, \(V^S\) increases faster than \(V^D\).
Observe that at \(\gamma ^*\), for the first equality to hold, government spending must be higher for the defaulting nation than the solvent nation. This is because \(\beta E W^S(b, \gamma , x) > \beta E V^D - u^{ii}\), and utility is increasing. Because u is concave, as \(\theta \) increases, \(\gamma ^*\) must decrease.
Now, note that the second equation will cross the point \((r^0,0)\). In other words, at the risk free rate, the nation never defaults. It is easy to show that the graph of the function in \([r_i, \gamma ^*]\) is increasing and concave. If \(\theta \) is zero, it approaches \(\gamma ^*\) asymptotically. If \(\theta \) is strictly greater than zero, their exists a \(r^i_{max}\) such that \(\gamma ^*(r^i,\cdot ) = \gamma _{max}\). This \(r^i_{max}\) is the highest interest rate attainable in equilibrium. Clearly, as \(\theta \) increases, the same interest rate must be supported by a higher level of risk, so \(\gamma ^*\) increases.
To attack existence, note that as \(\theta \) approaches 1, graph of \(r^i\) and \(\gamma ^*\) produced by the first equation approaches \(\gamma ^*(r_i,\cdot ) = 0\) for all \(r^i\). This is to say, if \(\theta \) goes to 1 then \(V^S - V^D\) goes to infinity. To maintain the equality, \(\gamma ^*\) approaches 0. Finally, equation 1 must be satisfied if \(r^i\) and \(\gamma ^*\) are equal to zero.
The graph of \(r^i\) and \(\gamma ^*\) produced by the second equation clearly becomes vertical as \(\theta \) approaches 1. This equation is satisfied when \(r^i = r^0\) and \(\gamma ^* = 0\). Because these functions are continuous and defined on a closed graph, a lending equilibrium must exist.
Therefore, increasing \(\theta \) sufficiently high guarantees both existence of a lending equilibrium, and uniqueness of this equilibrium.
Finally, I show the derivation of the implementability condition in the IMF’s Ramsay Problem. This condition is given as:
Taking derivatives of the solvent nation’s problem Lagrangian with respect to spending today, spending tomorrow, and debt gives:
Where \(\varLambda \) is the Lagrange multiplier on the budget constraint and \(\chi \) is the Lagrange multiplier on the borrowing constraint.Substituting the first two equations into the third gives the desired result. \(\square \)
1.6 Proof of Proposition 4
Proof
Existence is trivial. The lowest \(\theta _j\) nation is getting it’s maximizing value of \(\theta \), so it will not deviate. All other nations can only deviate to make \(\theta \) lower, so by concavity, they will not do so. Uniqueness is similarly straight forward. Suppose by way of contradiction that some arbitrary collection \(\{\theta _1, \theta _2,...,\theta _n\}\) such that \(\theta _j \le \theta _k < 1\) is an equilibrium. For the lowest \(\theta ^*_j\) member not to deviate, \(\prod \theta _i = \theta ^*_{j,min}\). But in that case, all other players desire a higher \(\theta \). Nation k will deviate and increase its choice \(\theta _k\), so we have reached a contradiction. \(\square \)
Rights and permissions
About this article
Cite this article
Rudderham, R. Birds of a feather: separating spillovers from shocks in sovereign default. Ann Finance 17, 353–378 (2021). https://doi.org/10.1007/s10436-021-00392-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10436-021-00392-6