Interval exchange transformations and low-discrepancy

Abstract

In Masur (Ann Math 115(1):169–200, 1982) and Veech (J Anal Math 33:222–272, 1978), it was proved independently that almost every interval exchange transformation is uniquely ergodic. The Birkhoff ergodic theorem implies that these maps mainly have uniformly distributed orbits. This raises the question under which conditions the orbits yield low-discrepancy sequences. The case of $n=2$ intervals corresponds to circle rotation, where conditions for low-discrepancy are well-known. In this paper, we give corresponding conditions in the case $n=3$. Furthermore, we construct infinitely many interval exchange transformations with low-discrepancy orbits for $n \ge 4$. We also show that these examples do not coincide with LS-sequences if $S \ge 2$.

1 Introduction

Low-discrepancy sequences are an essential tool for high-dimensional numerical integration. Three families of low-discrepancy sequences are classically used for that purpose, namely Kronecker sequences, digital sequences and Halton sequences (compare [7], see also [9]). From an ergodic point of view, Kronecker sequences are of particular interest: They are realized as orbits of circle rotations which are in turn the simplest examples of interval exchange transformations (two intervals). This raises the question whether further examples of low-discrepancy sequences can be constructed by interval exchange transformations with $n > 2$ intervals.

In this paper, we at first draw a complete picture for interval exchange transformations with three intervals and give criteria when their orbits yield low-discrepancy sequences. For most combinatorial data, also the case $n=3$ corresponds to usual circle rotations but there exists a specific choice of combinatorial data which is different. We draw our attention solely to the latter class of examples. These can be regarded as the first return maps of a circle rotation on some interval $[0,\lambda )$ with $\lambda > 0$ to [0, 1). Therefore, our approach consists in considering low-discrepancy sequences in arbitrary intervals and their restriction to [0, 1).

Inspired by the algebraic relations used to define LS-sequences (see [1]), we then present a canonical construction of further low-discrepancy sequences as orbits of interval exchange transformations with at least four intervals. These examples are similar to Kronecker sequences and give further insight into the interaction of low-discrepancy and ergodicity which has been recently discussed, e.g., in [2, 4, 15]. Moreover, it should be mentioned here that to our best knowledge these examples are the first explicitly known interval exchange transformations which have low-discrepancy orbits besides circle rotations and the single example given in [2].

2 Discrepancy theory

2.1 (Star-)discrepancy in arbitrary intervals

Usually, the concept of discrepancy is applied to sequences $S=(\omega _n)_{n \ge 0}$ in $[0,1)^d$. It may, however, be generalized to arbitrary intervals $I=[\alpha _1,\beta _1) \times \cdots \times [\alpha _d,\beta _d)$ with $- \infty< \alpha _i< \beta _i < \infty$ for all $i = 1, \ldots , d$ in the following way: Let $S = (\omega _n)_{n \ge 0}$ be a sequence in I. The star-discrepancy of its first N points is given by

$$\begin{aligned} D_{N,I}^{*}(S) = \sup _{B^* \subset I} \left| \frac{A_N(B^*,S)}{N} - \frac{\lambda _d(B^*)}{\lambda _d(I)} \right| , \end{aligned}$$

where the supremum is taken over all intervals of the form $B^*=[\alpha _1,b_1)\times \cdots \times [\alpha _d,b_d)$ with $\alpha _i< b_i < \beta _i$ for all i and where $\lambda _d$ denotes the d-dimensional Lebesgue measure and $A_N(B,S) := \# \left\{ n \ \mid \ 0 \le n \le N, \omega _n \in B \right\}$. Note that the definition is consistent with the usual definition of star-discrepancy for $I=[0,1)^d$ and that we still have $0 \le D_{N,I}^{*}(S) \le 1$. Whenever we consider the d-dimensional unit-interval we leave away I in the definition of star-discrepancy, $D_N^*(S)$. The following proposition asserts that the star-discrepancy of a sequence is invariant under scaling.

Proposition 2.1

Let $S=(\omega _n)_{n \ge 0}$ be a sequence in I with discrepancy $D_{N,I}^*(S)$. Then, the component-wise scaled sequence

$$\begin{aligned} \widetilde{S} := \left( -\alpha _1 + \frac{1}{\beta _1 - \alpha _1} z_{1,n}, \ldots , -\alpha _d + \frac{1}{\beta _d - \alpha _d} z_{d,n} \right) _{n \ge 0} \end{aligned}$$

has discrepancy $D_N^*(\widetilde{S}) = D_{N,I}^*(S)$ in $[0,1)^d$.

Proof

This can be proved by a direct calculation. For an interval $B^* = [0,b_1) \times \cdots \times [0,b_d) \subset [0,1)^d$ we set $C^*=[\alpha _1,\alpha _1 + b_1(\beta _1 - \alpha _1)) \times \cdots \times [\alpha _d, \alpha _d + b_d(\beta _d - \alpha _d)) )$. Thus, we have

$$\begin{aligned} \left| \frac{A_N(B^*,\widetilde{S})}{N} - \lambda (B^*) \right|&= \left| \frac{A_N(B^*,\widetilde{S})}{N} - \frac{\lambda (C^*)}{(\beta _1 - \alpha _1) \cdot \, \cdots \, \cdot (\beta _d - \alpha _d)} \right| \\&= \left| \frac{A_N(C^*,S)}{N} - \frac{\lambda (C^*)}{\lambda (I)} \right| . \end{aligned}$$

Taking the supremum over all intervals $B^*$ implies the claim. $\square$

If we restrict to the case $d=1$ and if $D_N^*(S)$ satisfies

$$\begin{aligned} D_{N}^*(S) = O(N^{-1}\log N) \end{aligned}$$

then $S \subset [0,1)$ is called a low-discrepancy sequence. In dimension one this is the best possible rate of convergence as it was proved in [10], that there exists a constant c with

$$\begin{aligned} D_N^*(S) \ge c N^{-1} \log N. \end{aligned}$$

The constant c fulfills $0.06< c < 0.223$ but its precise value is still unknown (see, e.g., [7]). A theorem of Weyl states that a sequence of points $S=(\omega _n)_{n \ge 0}$ is uniformly distributed if and only if

$$\begin{aligned} \lim _{N \rightarrow \infty } D_{N}^*(S) = 0. \end{aligned}$$

Thus, the only candidates for low-discrepancy sequences are uniformly distributed sequences. For a discussion of the situation in higher dimensions, see, e.g., [9, Chapter 3].

Corollary 2.2

Let $S=(\omega _n)_{n \ge 0}$ be a sequence in $I=[\alpha _1,\beta _1)$. Then, we have $D_{N,I}^*(S) \ge c N^{-1} \log N$ with $0.06< c < 0.223$.

Thus, it makes sense to speak of low-discrepancy sequences in an arbitrary interval $I=[\alpha _1,\beta _1) \times \cdots \times [\alpha _d,\beta _d)$. Accordingly, the discrepancy of the first N points of a sequence $S=(\omega _n)_{n \ge 0}$ in I is defined by

$$\begin{aligned} D_{N,I}(S) := \sup _{B \subset [0,1)} \left| \frac{A_N(B,S)}{N} - \frac{\lambda _d(B)}{\lambda _d(I)} \right| , \end{aligned}$$

where the supremum is taken over all subintervals $B = [a_1,b_1) \times \cdots \times [a_d,b_d)$ with $\alpha _i \le a_i< b_i < \beta _i$ for all i. It is straightforward to see that $D_{N,I}^*(S) \le D_{N,I}(S) \le 2^d D_{N,I}^*(S)$.

2.2 Low-discrepancy in subintervals

The low-discrepancy property of a sequence is often regarded as being as uniformly distributed as possible. We aim to make this statement more precise here. Let $(\omega _n)_{n \ge 0}$ be a low-discrepancy sequence in the interval I and let $I_1 \subset I$ be a half-open subinterval with its left endpoint included. Since $(\omega _n)_{n \ge 0}$ is uniformly distributed, there are infinitely many $\omega _i$ in $I_1$. Hence, the numbers

$$\begin{aligned} i_0 := \min \left\{ j \in {\mathbb {N}}_0 | \omega _j \in I_1 \right\} , \quad i_j := \min \left\{ j \in {\mathbb {N}}_0 | j > i_{j-1}, \omega _j \in I_1 \right\} \ (j \ge 1) \end{aligned}$$

form an infinite sequence $(i_j)_{j \ge 0}$ in ${\mathbb {N}}_0$. As a consequence, the subsequence $(\omega ^1_j)_{j \ge 0} := (\omega _{i_j})_{j \ge 0}$ is well-defined and lies in $I_1$. It is called the restriction of $(\omega _n)_{n \ge 0}$ to $I_1$. By this construction, low-discrepancy is preserved.

Proposition 2.3

Let $I_1 \subset I$ be an arbitrary half-open subinterval and let $(\omega _n)_{n \ge 0}$ be a low-discrepancy sequence in I. Then, the restriction $(\omega ^1_n)_{n \ge 0}$ is a low-discrepancy sequence in $I_1$.

Proof

In order to facilitate notation, we leave away the indexes of sequences in this proof. The low-discrepancy of $\omega$ in I implies

$$\begin{aligned} \left| \frac{A_N(\omega ,I_1)}{N} - \lambda (I_1) \right| \le c \frac{\log N}{N} \end{aligned}$$

(1)

for all $N \in {\mathbb {N}}$ with fixed $c \in {\mathbb {R}}$ independent of N. Now let $N_1 \in {\mathbb {N}}$ be arbitrary and choose $N \ge N_1$ such that $N_1 = {A_N(\omega ,I_1)}$. We need to bound the following quantity

$$\begin{aligned} \widetilde{D}_{N_1,I^*}^*&:= \sup _{I^* \subset I_1} \left| \frac{A_{N_1}(\omega ^1,I^*)}{N_1} - \frac{\lambda (I^*)}{\lambda (I_1)}\right| \\&\le \sup _{I^* \subset I_1} \left| \frac{A_{N_1}(\omega ^1,I^*)}{N_1} - \frac{N\lambda (I^*)}{N_1}\right| + \sup _{I^* \subset I_1} \left| \frac{N\lambda (I^*)}{N_1} - \frac{\lambda (I^*)}{\lambda (I_1)}\right| . \end{aligned}$$

For every subinterval $I^* \subset I_1$, we have

$$\begin{aligned} A_{N_1}(\omega ^1,I^*) = A_{N}(\omega ,I^*) \end{aligned}$$

yielding

$$\begin{aligned} \widetilde{D}_{N_1,I^*}^*&\le \frac{N}{N_1} \sup _{I^* \subset I_1} \left| \frac{A_{N}(\omega ,I^*)}{N} - \lambda (I^*)\right| + \frac{N}{N_1} \sup _{I^* \subset I_1} \frac{\lambda (I^*)}{\lambda (I_1)} \left| \lambda (I_1) - \frac{N_1}{N}\right| \\&= \frac{N}{N_1} \sup _{I^* \subset I_1} \left| \frac{A_{N}(\omega ,I^*)}{N} - \lambda (I^*)\right| + \frac{N}{N_1} \sup _{I^* \subset I_1} \frac{\lambda (I^*)}{\lambda (I_1)} \left| \frac{A_N(\omega ,I_1)}{N} - \lambda (I_1) \right| \\&{\mathop {\le }\limits ^{(1)}} \frac{N}{N_1} c \frac{\log N}{N} + \frac{N}{N_1} \cdot 1 \cdot c \frac{\log N}{N}. \end{aligned}$$

Therefore, it suffices to bound $N/N_1$. We show here that for sufficiently large N the expression $N_1/N$ is arbitrarily close to a positive constant. Indeed, this claim follows from

$$\begin{aligned} \left| \frac{N_1}{N} - \lambda (I_1) \right| = \left| \frac{A_N(\omega ,I_1)}{N} - \lambda (I_1) \right| \le c \frac{\log N}{N}. \end{aligned}$$

since $\lambda (I_1)$ is some positive constant that does not depend on N and $\log N / N$ converges to zero. This completes the proof. $\square$

2.3 Kronecker sequences

A classical example of low-discrepancy sequences is Kronecker sequences: given $z \in {\mathbb {R}}$, let $\left\{ z \right\} := z - \lfloor z \rfloor$ denote the fractional part of z. A Kronecker sequence is a sequence of the form $(z_n)_{n \ge 0} = (\left\{ n z \right\} )_{n \ge 0}$. If $z \notin {\mathbb {Q}}$ and z has bounded partial quotients in its continued fraction expansion, the sequence $(z_n)$ has low-discrepancy in [0, 1). More precisely, the following statement holds:

Theorem 2.4

[3, Corollary 1.65] Let $z \in {\mathbb {R}}$ be irrational with continued fraction expansion $z =[a_0;a_1;a_2;\ldots ]$. Then, the sequence $(\left\{ n z \right\} )_{n \ge 0}$ is low-discrepancy if and only if the moving average

$$\begin{aligned} a_m^{(1)} = \frac{1}{m} \sum _{j=1}^m a_j \end{aligned}$$

is a bounded sequence.

The sequence $(z_n)_{n \ge 0}$ corresponds to the rotation of the unit circle by the angle $2 \pi z$ if we identify [0, 1) with ${\mathbb {R}}/ {\mathbb {Z}}$. Furthermore, it is the simplest example of an interval exchange transformation (see Chapter 3).

2.4 LS-sequences

Another way to construct uniformly distributed sequences goes back to the work of Kakutani [5] and was later on generalized in [14] in the following sense.

Definition 2.5

Let $\rho$ denote a non-trivial partition of [0, 1). Then, the $\rho$-refinement of a partition $\pi$ of [0, 1), denoted by $\rho \pi$, is defined by subdividing all intervals of maximal length positively homothetically to $\rho$.

The resulting sequence of partitions is denoted by $\left\{ \rho ^n \pi \right\} _{n \in {\mathbb {N}}}$. We now turn to a specific class of examples of $\rho$-refinement which was introduced in [1].

Definition 2.6

Let $L \in {\mathbb {N}}, S \in {\mathbb {N}}_0$ and $\beta$ be the solution of $L \beta + S \beta ^2 = 1$. An LS-sequence of partitions $\left\{ \rho _{L,S}^n \pi \right\} _{n \in {\mathbb {N}}}$ is the successive $\rho$-refinement of the trivial partition $\pi = \left\{ [0,1) \right\}$ where $\rho _{L,S}$ consists of $L+S$ intervals such that the first L intervals have length $\beta$ and the successive S intervals have length $\beta ^2$.

The partition $\left\{ \rho _{L,S}^n \pi \right\}$ consists of intervals only of length $\beta ^n$ and $\beta ^{n+1}$. Its total number of intervals is denoted by $t_n$, the number of intervals of length $\beta ^n$ by $l_n$ and the number of intervals of length $\beta ^{n+1}$ by $s_n$. A specific ordering of the endpoints of the partition yields the LS-sequence of points.

Definition 2.7

Given an LS-sequence of partitions $\left\{ \rho _{L,S}^n \pi \right\} _{n \in {\mathbb {N}}}$, the corresponding LS-sequence of points $(\xi ^n)_{n \in {\mathbb {N}}}$ is defined as follows: Let $\Lambda _{L,S}^1$ be the first $t_1$ left endpoints of the partition $\rho _{L,S} \pi$ ordered by magnitude. Given $\Lambda _{L,S}^n = \left\{ \xi _1^{(n)}, \ldots , \xi _{t_n}^{(n)} \right\}$ an ordering of $\Lambda _{L,S}^{n+1}$ is then inductively defined as

$$\begin{aligned} \Lambda _{L,S}^{n+1}&= \left\{ \xi _1^{(n)}, \ldots , \xi _{t_n}^{(n)},\psi _{1,0}^{(n+1)} \left( \xi _1^{(n)}\right) , \ldots , \psi _{1,0}^{(n+1)} \left( \xi _{l_n}^{(n)}\right) , \ldots , \psi _{L,0}^{(n+1)} \left( \xi _1^{(n)}\right) , \right. \\&\left. \quad \ldots , \psi _{L,0}^{(n+1)} \left( \xi _{l_n}^{(n)}\right) , \psi _{L,1}^{(n+1)} \left( \xi _1^{(n)}\right) , \ldots , \psi _{L,1}^{(n+1)} \left( \xi _{l_n}^{(n)}\right) , \ldots , \psi _{L,S-1}^{(n+1)} \left( \xi _1^{(n)}\right) , \right. \\&\left. \quad \ldots , \psi _{L,S-1}^{(n+1)} \left( \xi _{l_n}^{(n)}\right) \right\} , \end{aligned}$$

where

$$\begin{aligned} \psi ^{(n)}_{i,j}(x) = x + i\beta ^n + j\beta ^{n+1}, \quad x \in {\mathbb {R}}. \end{aligned}$$

As the definition of LS-sequences might not be completely intuitive at first sight, we illustrate it by an explicit example.

Example 2.8

For $L=S=1$ the LS-sequence is the so-called Kakutani–Fibonacci sequence (see [2]). We have

$$\begin{aligned} \Lambda ^1_{1,1}&= \left\{ 0, \beta \right\} \\ \Lambda ^2_{1,1}&= \left\{ 0, \beta , \beta ^2 \right\} \\ \Lambda ^3_{1,1}&= \left\{ 0, \beta , \beta ^2, \beta ^3, \beta + \beta ^3 \right\} \\ \Lambda ^4_{1,1}&= \left\{ 0, \beta , \beta ^2, \beta ^3, \beta + \beta ^3, \beta ^4,\beta +\beta ^4,\beta ^2+\beta ^4 \right\} \end{aligned}$$

and so on.

More precisely, LS-sequences are not only uniformly distributed but in many cases even low-discrepancy.

Theorem 2.9

(Carbone [1]) If $L \ge S$, then the corresponding LS-sequence has low-discrepancy.

It has been pointed out that for parameters $S=0$ and $L=b$, the corresponding LS-sequence coincides with the classical van der Corput sequences. In [15], it was proven that LS-sequences for $S=1$ coincide with symmetrized Kronecker sequences up to permutation and that neither van der Corput sequences nor Kronecker sequences occur for $S \ge 2$.

3 Interval exchange transformations

Let $I \subset {\mathbb {R}}$ be an interval of the form $[0,\lambda ^*)$ and let $\left\{ I_\alpha | \alpha \in \mathcal {A} \right\}$ be a finite partition of I into subintervals indexed by some finite alphabet $\mathcal {A}$. An interval exchange transformation is a map $f: I \rightarrow I$ which is a translation on each subinterval $I_\alpha$. It is determined by its combinatorial data and its length data. The combinatorial data consist of two bijections $\pi _0, \pi _1: \mathcal {A} \rightarrow \left\{ 1,\ldots ,n \right\}$, where n is the number of elements of $\mathcal {A}$ and the length data are numbers $(\lambda _\alpha )_{\alpha \in \mathcal {A}}$ with $\lambda _\alpha > 0$ and $\lambda ^* = \sum _{\alpha \in \mathcal {A}} \lambda _\alpha$. The number $\lambda _\alpha$ is the length of the subinterval $I_\alpha$ and the pair $\pi = (\pi _0,\pi _1)$ describes the ordering of the subintervals before and after the map f is iterated. In analytical terms, consider for $\epsilon \in \left\{ 0, 1 \right\}$ the maps $j_\epsilon$ which are given on $I_\alpha$ by

$$\begin{aligned} j_\epsilon (x) = x + \sum _{\pi _\epsilon (\beta ) < \pi _\epsilon (\alpha )} \lambda _\beta . \end{aligned}$$

(2)

The interval exchange transformation corresponding to the combinatorial and length data equals $f = j_1 \circ j_0^{-1}$. It can also be described completely by its translation vector w with components

$$\begin{aligned} w_\alpha = \sum _{\pi _1(\beta )<\pi _1(\alpha )} \lambda _\beta - \sum _{\pi _0(\beta )<\pi _0(\alpha )} \lambda _\beta . \end{aligned}$$

Note that combinatorial data are not uniquely determined by f (see, e.g., [13, Example 1.3]). For $\mathcal {A} = \left\{ A, B \right\}$ and $\pi _0(A) = \pi _1(B) = 1$ and $\pi _1(A) = \pi _0(B) = 2$, the interval exchange transformation becomes the rotation of ${\mathbb {R}}/ \lambda ^* {\mathbb {Z}}$ by $\lambda _B$.

If the combinatorial data satisfy

$$\begin{aligned} \pi _0^{-1}(\left\{ 1, \ldots , k \right\} ) = \pi _1^{-1}(\left\{ 1, \ldots , k \right\} ) \end{aligned}$$

(3)

for some $k < n$, the interval exchange transformation splits into two interval exchange transformations of simpler combinatoric. The analysis of interval exchange transformations is therefore usually restricted to admissible combinatorial data, for which (3) does not hold for any $k < n$. Further details on interval exchange transformation can be found, e.g., in [8, 13, 16].

Recently, it has been discussed in some articles, see, e.g., [2, 4, 15], that there is a connection between interval exchange transformations and low-discrepancy.

Theorem 3.1

[2, Theorem 17] For $L=S=1$ the LS-sequence coincides with an orbit of an ergodic interval exchange transformation $T: [0,1) \rightarrow [0,1)$ consisting of infinitely many intervals.

In [15], this theorem was improved in two senses: First it is possible to generalize the result to arbitrary L, and second the interval exchange map can be further simplified by using only two intervals instead of infinitely many. Note that neither of the cited theorems claims uniqueness.

Theorem 3.2

[15, Theorem 1.7] For $S=1$ and arbitrary L, the LS-sequence coincides with an orbit of an interval exchange transformation $T: [0,1) \rightarrow [0,1)$ consisting of two intervals.

3.1 The case $n=3$

We will show next that also the second simplest examples of interval exchange transformations, i.e., $n=3$, yield low-discrepancy sequences in [0, 1). In that case, the argumentation is based on Proposition 2.3.

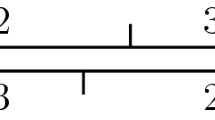
Assume that $\mathcal {A} = \left\{ A,B,C \right\}$. Without loss of generality, we have $\pi _0(A) = 1, \pi _0(B) = 2, \pi _0(C) = 3$. Only 3 of the 6 bijections $\pi _1: \mathcal {A} \rightarrow \left\{ 1,2,3\right\}$ yield admissible combinatorial data. Two of these choices for $\pi _1$ yield again rotations on the circle ${\mathbb {R}}/\lambda ^* {\mathbb {Z}}$ (see, e.g., [16]) and therefore Kronecker sequences. The case we are interested in is thus (compare Fig. 1)

$$\begin{aligned} \pi _1(A) = 3,\pi _1(B)= 2, \pi _1(C) = 1. \end{aligned}$$

According to [16, Section 2], the corresponding interval exchange transformation $f: I \rightarrow I$ can be described as follows: Let $\hat{I} :=[0,\lambda ^* + \lambda _B]$ and $T: \hat{I} \rightarrow \hat{I}$ be defined as the rotation of ${\mathbb {R}}/ (\lambda ^* + \lambda _B) {\mathbb {Z}}$ by $\lambda _B + \lambda _C$. Then, for $y \in [0,\lambda _A)$ or $y \in [\lambda _A + \lambda _B, \lambda ^*)$ we have $f(y) = T(y)$. For $y \in [\lambda _A, \lambda _A + \lambda _B)$, the identity $f(y)= T^2(y)$ holds. Therefore, f is the first return map of T in I. In other words, the sequence $(f^n(y))_{n \ge 0}$ is the restriction of $(T^n(y))_{n \ge 0}$ to I. From Proposition 2.3 and Theorem 2.4, we thus deduce.

Fig. 1

Interval exchange transformation for $n=3$

Theorem 3.3

Given $\mathcal {A} = \left\{ A,B,C \right\}$, the combinatorial data

$$\begin{aligned} \pi _0(A) = 1, \pi _0(B) = 2, \pi _0(C) = 3, \quad \pi _1(A) = 3,\pi _1(B)= 2, \pi _1(C) = 1, \end{aligned}$$

and the length data $\lambda _A, \lambda _B, \lambda _C$, the corresponding interval exchange transformation $f: [0,\lambda ^*) \rightarrow [0,\lambda ^*)$ yields a low-discrepancy sequence $(f^n(y))_{n \ge 0}$ for all $y \in [0, \lambda ^*)$ if and only if $\frac{\lambda _B+\lambda _C}{\lambda ^* + \lambda _B}$ is irrational and has bounded moving average of its continued fraction expansion.

In particular, if we choose $\lambda _A,\lambda _B,\lambda _C$ such that $\lambda ^* = 1$, then $(f^n(y))_{n \ge 0}$ is a (classical) low-discrepancy sequence in [0, 1) which comes from the restriction of a low-discrepancy sequence in $[0,1+\lambda _B)$. By [9, Corollary 3.5], the rate of convergence of star-discrepancy is expected to be the better the smaller the coefficients in the continued fraction expansion of $\tfrac{\lambda _B+\lambda _C}{1 + \lambda _B}$ are. Hence, for a fair comparison with the case $n=2$, i.e., the circle rotation by $\gamma$, we should impose

$$\begin{aligned} \frac{\lambda _B+\lambda _C}{1 + \lambda _B} = \gamma . \end{aligned}$$

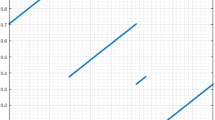
The additional condition lowers the degree of freedom to 1. We may, e.g., choose $\lambda _C$ with $\lambda _C < \min (\tfrac{\gamma }{1-\gamma },\tfrac{1-\gamma }{\gamma })$ arbitrarily and by that automatically fix $\lambda _A$ and $\lambda _B$. In Fig. 2, we plot the star-discrepancy of the orbit arising from the circle rotation by the golden mean $\gamma = \tfrac{\sqrt{5}-1}{2}$ in comparison with the case $n=3$ with $\lambda _C = \gamma / 2$ and $\lambda _C = \gamma / 4$, respectively. Taking into account the graph of $\log (N)/N$, we clearly see that all sequences are indeed low-discrepancy. Although the star-discrepancies have similar asymptotic behavior, there seems to be more variation for the case $n=3$. Yet, the degree of freedom for the choice of $\lambda _C$ allows for optimization of star-discrepancy.

Fig. 2

Comparison of star-discrepancies up to $N = 2.000$

3.2 The general case

Under some rather mild conditions, interval exchange transformations yield low-discrepancy sequences for $n=2,3$. Still the requirements imposed in Theorem 3.3 are strictly stronger than the so-called Keane condition (compare [13, Chapter 3]). Nevertheless, there is reasonable hope that a similar result can be proven also for $n \ge 4$ due to Birkhoff’s ergodic theorem and the following theorem proven independently by Masur [8] and Veech [12]. Let the combinatorial data be fixed and almost every refer to the choice of length data with respect to the Lebesgue measure.

Theorem 3.4

(Masur, Veech) Almost every interval exchange transformation is uniquely ergodic.

Generalizing Theorem 1.7 in [15] we may, however, not expect to get LS-sequences with $S \ge 2$ by this construction.

Theorem 3.5

For arbitrary L and $S \ge 2$, the corresponding LS-sequence of partitions does not coincide with an orbit of any interval exchange transformation.

Proof

Let L and $S \ge 2$ be fixed. We have

$$\begin{aligned} \beta ^{n+2} = \frac{\beta ^{n+1}-L\beta ^n}{S} \end{aligned}$$

(4)

and the denominator grows arbitrarily large with increasing n. Suppose that the claim is not true and let $(\lambda _\alpha )_{\alpha \in \mathcal {A}}$ denote the length data of the corresponding interval exchange transformation and x be an arbitrary point in [0, 1). We see from (2) that every point in the orbit of x may be written as a linear combination of x and the $(\lambda _\alpha )_{\alpha \in \mathcal {A}}$ with integral coefficients. This contradicts (4) because by construction the LS-sequence contains $\beta ^l$ for all $l \in {\mathbb {N}}$. $\square$

Still the algebraic relation $L \beta + S \beta ^2 = 1$, which is a main ingredient for the definition of LS-sequences, can be used to get interval exchange transformations potentially yielding low-discrepancy sequences. Recall the fact that every interval exchange transformation can be normalized by choosing $\mathcal {A} = \left\{ 1, \ldots , d \right\}$ and $\pi _0 = {\mathrm{Id}}$ (see [13]). If we set $\lambda _i = \beta$ for $i=1,\ldots , L$ and $\lambda _i = \beta ^2$ for $i = L+1, \ldots , L+S$ and let $\pi _1$ be arbitrary, then the intervals before applying f correspond to the intervals of $\rho _{L,S}$. The orbit of every left endpoint of $\rho _{L,S}$ is contained in the set

$$\begin{aligned} \mathcal {J}_{L,S} :&= \left\{ \left\{ m \beta + n \beta ^2\right\} \ | \ m,n \in {\mathbb {Z}}\right\} \\&= \left\{ \left\{ m \beta + n \beta ^2\right\} \ | \ m,n \in {\mathbb {Z}}, 0 \le n < S \right\} \\&= \bigcup _{n=0}^{S-1} \left\{ \left\{ m \beta + n \beta ^2\right\} \ | \ m \in {\mathbb {Z}}\right\} . \end{aligned}$$

By Dirichlet’s approximation theorem, the set $\mathcal {J}_{L,S}$ is dense in [0, 1]. Therefore, it can be equipped with an ordering that turns it into a low-discrepancy sequence. The key point of the following proposition is that such an ordering can be explicitly constructed for $\mathcal {J}_{L,S}$.

Proposition 3.6

There exists an explicitly constructible ordering of $\mathcal {J}_{L,S}$ such that the corresponding sequence of points is low-discrepancy.

Proof

It follows from Lagrange’s Theorem on continued fractions that $\beta$ has eventually periodic continued fraction expansion, see, e.g., [11]. Therefore, for each $n \in {\mathbb {Z}}$ and arbitrary $N \in {\mathbb {N}}$, the set

$$\begin{aligned} \mathcal {J}_{L,S}^n := \left\{ \left\{ m \beta + n \beta ^2\right\} \, | \ m \in {\mathbb {Z}}\right\} \end{aligned}$$

(with the natural ordering inherited from ${\mathbb {N}}$) has discrepancy $D_N(\mathcal {J}_{L,S}^n) \le c \log {N} /N$ for some $c \in {\mathbb {R}}$ by Theorem 2.4. Now, we define a sequence $(x_i)$ of the left endpoints of $\mathcal {J}_{L,S}$ by

$$\begin{aligned} x_i := \left\{ \lfloor i / S \rfloor \beta + (i - kS) \beta ^2 \right\} \quad \text {for} \ kS \le i < (k+1)S, \ k \in {\mathbb {N}}_0 \end{aligned}$$

The triangle inequality for discrepancies (see [6, Theorem 2.6]) implies that $(x_i)$ is indeed a low-discrepancy sequence. $\square$

Next, we show how to construct interval exchange transformations which have an orbit that coincides with $\mathcal {J}_{L,S}$ as a set. The example for $n=4$ is illuminating.

Fig. 3

Interval exchange transformation for $n=4$

Example 3.7

Let $n=4$, $L=S=2$ and $2 \beta + 2\beta ^2 = 1$. We choose $\pi _1$ by setting $\pi _1(1)=2, \pi _1(2) = 4, \pi _1(3)= 1$ and $\pi _1(4) = 3$ (see Fig. 3). The corresponding interval exchange transformation $f_{2,2}$ is admissible with translation vector

$$\begin{aligned}&w_1 = \beta + \beta ^2, \quad w_2 = -\beta , \quad w_3 = \beta ^2 \quad w_4 = - \beta - \beta ^2. \end{aligned}$$

Note that $f_{2,2}(x) \ne x$ for all $x \in [0,1)$. For $x \in I_1$ we have $f_{2,2}(x) \in I_2$ or $f_{2,2}(x) \in I_3$. Furthermore, the following implications hold

$$\begin{aligned} x&\in I_2 \Rightarrow f_{2,2}(x) \in I_1\\ x&\in I_3 \Rightarrow f_{2,2}(x) \in I_4\\ x&\in I_4 \Rightarrow f_{2,2}(x) \in I_2. \end{aligned}$$

This means $f_{2,2}$ always maps an element of $I_2 \cup I_3$ to $I_1 \cup I_4$ and vice versa. Hence, the translation vector of $f_{2,2}^2$ is restricted to the following possibilities, where $\equiv$ stands for equivalence modulo 1:

$$\begin{aligned}&w_1 + w_2 = \beta + \beta ^2 - \beta = \beta ^2\\&w_1 + w_3 = \beta + \beta ^2 + \beta ^2 \equiv -\beta \\&w_3 + w_4 = \beta ^2 -\beta - \beta ^2 = - \beta \\&w_4 + w_2 = - \beta - \beta ^2 - \beta \equiv \beta ^2 \end{aligned}$$

We define the sequence $(x_n)_{n\in {\mathbb {Z}}}$ by $x_0 = 2\beta +\beta ^2$ and $x_k = f_{2,2}^k(x_0)$ for all $k \in {\mathbb {Z}}$ and claim that every pair $(x_{2k},x_{2k+1})$ is either of the form

$$\begin{aligned} \left( \left\{ (-k+1)\beta \right\} ,\left\{ (-k+2)\beta +\beta ^2\right\} \right) \quad \text {or} \quad \left( \left\{ (-k+2)\beta +\beta ^2\right\} , \left\{ (-k+1)\beta \right\} \right) . \end{aligned}$$

We prove this by induction on k. For $k=0$ the second possibility holds, i.e., $(x_{0},x_1) = (2\beta + \beta ^2,\beta )$. Now assume that the claim is true for k. At first, we consider the case $(x_{2k},x_{2k+1}) = (\left\{ (-k+1)\beta \right\} ,\left\{ (-k+2)\beta +\beta ^2\right\} )$. In view of the translation vector of $f_{2,2}^2$, the entry $x_{2k+2}$ is either equal to

$$\begin{aligned} \left\{ (-k+1)\beta - \beta \right\}&= \left\{ (-(k+1)+1)\beta \right\} =: y_{2k+2} \quad \text {or}\\ \left\{ (-k+1)\beta + \beta ^2 \right\}&= \left\{ (-(k+1)+2)\beta + \beta ^2 \right\} =: z_{k+2}. \end{aligned}$$

Since $x_{2k+3} = f_{2,2}(x_{2k+2}) \ne x_{2k+2}$, the entry $x_{2k+3}$ is $z_{2k+2}$ if $x_{2k+2} = y_{2k+2}$ and vice versa. The argumentation in the second case, namely $(x_{2k},x_{2k+1}) = (\left\{ (-k+2)\beta +\beta ^2\right\} ,\left\{ (-k+1)\beta \right\} )$ is similar. In summary, it follows that $\left\{ f_{2,2}^n(\beta ) \ | \ n \in {\mathbb {Z}}\right\}$ equals $\mathcal {J}_{L,S}$ as a set.

Although the combinatorial data in Example 3.7 are admissible, there is as few interaction between the $\beta$-part and the $\beta ^2$-part of the partition as possible. For arbitrary n, we specify $\pi _1$ by

$$\begin{aligned} \pi _1(i)&= i + 1, \quad i = 1, \ldots , L-1,\\ \pi _1(L)&= L+S,\\ \pi _1(L+1)&= 1,\\ \pi _1(i)&= i + 1, \quad i = L+2, \ldots L + S. \end{aligned}$$

Thus, the translation vector of the corresponding interval exchange transformation $f_{L,S}$ is

$$\begin{aligned} w_1&= (L-1)\beta + \beta ^2\\ w_i&= - \beta , \quad i = 2, \ldots , L,\\ w_i&= \beta ^2 , \quad i = L+1, \ldots L + S-1,\\ w_{L+S}&= -(S-1)\beta ^2-\beta . \end{aligned}$$

Now we fix an arbitrary $r \in {\mathbb {Z}}$ and choose $q_0 \in {\mathbb {Z}}$ such that $\left\{ -r\beta - q_0 \beta ^2 \right\} \in I_1$ but $\left\{ -r\beta - (q_0+1) \beta ^2 \right\} \notin I_1$ and set $x_0 = \left\{ -r\beta - q_0 \beta ^2 \right\} .$

Theorem 3.8

If $L \ge S$, then the orbit $\left\{ f_{L,S}^n(x_0) \ | \ n \in {\mathbb {Z}}\right\}$ equals $\mathcal {J}_{L,S}$ as a set.

Proof

In order to facilitate notation, we leave away brackets $\left\{ \cdot \right\}$, i.e., all expressions have to be interpreted modulo 1. The function $f_{L,S}$ maps

$$\begin{aligned} x_0 \mapsto (-r+(L-1))\beta - (q_0-1) \beta ^2 \end{aligned}$$

with $f_{L,S}(x_0) \in I_L$. This implies

$$\begin{aligned} f_{L,S}^i(x_0) = (-r+(L-1)-(i-1)) - (q_0-1) \beta ^2, \quad i = 1, \ldots , L. \end{aligned}$$

Note that $m \beta ^2 > \beta$ is equivalent to $m \ge L+1$ by the definition of L and S. Therefore, we again have $f_{L,S}(f_{L,S}^L(x_0)) \in I_L$ and the orbit continues as

$$\begin{aligned} f_{L,S}^i(x_0) = (-r+(L-1)-(i-1)) - (q_0-k) \beta ^2, \quad i = (k-1)L + 1, \ldots , kL \end{aligned}$$

until $k=L$. When applying $f_{L,S}$ once more, the orbit intersects $I_{L+1}$ instead of $I_L$, i.e.,

$$\begin{aligned} f_{L,S}^{L^2+1} = (-r+(L-1))\beta - (q_0-L-1)\beta ^2 \in I_{L+1}. \end{aligned}$$

For the next $S-1$ iterations, the term $\beta ^2$ is added such that

$$\begin{aligned} f_{L,S}^{L^2+1+i} = (-r+(L-1))\beta - (q_0-L-1+i)\beta ^2, \quad i = 1, \ldots , S-1. \end{aligned}$$

Since $f_{L,S}^{L^2+S} \in I_{K+S}$, the orbit jumps back to $I_L$ next. The distance between $f_{L,S}^{L^2+S+1}(x_0)$ and $(L-1)\beta$ is less than $\beta ^2$, and we have

$$\begin{aligned} f_{L,S}^{L^2+S+i} = (-r + (L-1) - i) \beta - (q_0-L-1)\beta ^2 , \quad i = 1, \ldots , L. \end{aligned}$$

Hence, after $L^2+L+S$ applications of $f_{L,S}$ the orbit reaches again $I_1$ and $f_{L,S}^{L^2+S+1}(x_0) < \beta ^2$. We are back in the same situation as at the start with $-r\beta -q\beta ^2$ replaced by $-(r+1)\beta - (q_0-L-1)$ and it is clear that every $y \in \mathcal {J}_{L,S}$ is contained in the orbit of $f_{L,S}$.

Corollary 3.9

If $L \ge S$, then sequence $(x_i)_{i \in {\mathbb {Z}}} = f_{L,S}^i(x_0)$ is a low-discrepancy sequence for all $x_0 \in [0,1)$.