1 Introduction

In several areas of society, it remains an open question whether a “hot hand” effect exists, according to which humans may temporarily enter a state during which they perform better than on average. While this concept may occur in different fields, such as among hedge fund managers and artists (Jagannathan et al. 2010; Liu et al. 2018), it is most prominent in sports. Sports commentators and fans — especially in basketball — often refer to players as having a “hot hand”, and being “on fire” or “in the zone” when they show a (successful) streak in performance. In the academic literature, the hot hand has gained great interest since the seminal paper by Gilovich et al. (1985), who investigated a potential hot hand effect in basketball. They found no evidence for its existence and attributed the hot hand to a cognitive illusion, much to the disapproval of many athletes and fans. Still, the results provided by Gilovich et al. (1985) have often been used as a primary example for showing that humans over-interpret patterns of success and failure in random sequences (see, e.g. Thaler and Sunstein 2009; Kahneman 2011).

During the last decades, many studies have attempted to replicate or refute the results of Gilovich et al. (1985), analysing sports such as volleyball, baseball, golf, and especially basketball. Bar-Eli et al. (2006) provide an overview of 25 studies on the hot hand, 11 of which were in favour of the hot hand phenomenon, while 13 studies provided evidence against the hot hand, and one study remained inconclusive. Several more recent studies, often based on large data sets, support the existence of the hot hand (see, e.g. Raab et al. 2012; Green and Zwiebel 2017; Miller and Sanjurjo 2018; Chang 2019). Notably, Miller and Sanjurjo (2018) show that the original study from Gilovich et al. (1985) suffers from a selection bias. Using the same data as in the original study by Gilovich et al. (1985), Miller and Sanjurjo (2018) account for that bias, and their results do reveal a hot hand effect. However, there are also recent studies which provide mixed results (see, e.g. Wetzels et al. 2016) or which do not find evidence for the hot hand, such as Morgulev et al. (2020). Thus, more than 30 years after the study of Gilovich et al. (1985), the existence of the hot hand remains highly disputed.

Moreover, the literature does not provide a universally accepted statistical modelling approach for the hot hand effect. While some studies regard it as serial correlation in outcomes (see, e.g. Gilovich et al. 1985; Dorsey-Palmateer and Smith 2004; Miller and Sanjurjo 2018), others consider it as serial correlation in success probabilities (see, e.g. Albert 1993; Wetzels et al. 2016; Ötting et al. 2020). The latter modelling approach translates into a latent (state) process underlying the observed performance — intuitively speaking, a measure for a player’s form — which can be elevated without the player necessarily being successful in every attempt. In our analysis, we follow this approach and hence consider state-space models (SSMs) to investigate the hot hand effect in basketball. Specifically, we analyse free throws from more than 9000 games played in the National Basketball Association (NBA), totalling in 110,513 observations. In contrast, Gilovich et al. (1985) use data on 2600 attempts in their controlled shooting experiment.

Free throws in basketball, or similar events in sports with game clocks, occur at unevenly spaced time points. These varying time lengths between consecutive attempts may affect inference on the hot hand effect if the model formulation does not account for the temporal irregularity of the observations. As an illustrative example, consider an irregular sequence of throws with intervals ranging from, say, two seconds to 15 minutes. For intervals between attempts that are fairly short (such as a few seconds), players will most likely be able to retain their form from the last shot. On the other hand, if several minutes elapse before players take their next shot, it becomes less likely that they are able to retain their form from the last attempt. However, we found that existing studies on the hot hand do not account for different interval lengths between attempts. In particular, studies investigating serial correlation in success probabilities usually consider discrete-time models that require the data to follow a regular sampling scheme and thus, cannot (directly) be applied to irregularly sampled data. In our contribution, we overcome this limitation by formulating our model in continuous time to explicitly account for irregular time intervals between free throws in basketball. Specifically, we consider a stochastic differential equation (SDE) as latent state process, namely the Ornstein-Uhlenbeck (OU) process, which represents the underlying form of players fluctuating continuously around their average performance.

In the following, Sect. 2 presents our data set and covers some descriptive statistics. Subsequently, in Sect. 3, the continuous-time SSM formulation for the analysis of the hot hand effect is introduced, while its results are presented in Sect. 4. We conclude our paper with a discussion in Sect. 5.

2 Data

We extracted data on all basketball games played in the NBA between October 2012 and June 2019 from https://www.basketball-reference.com/, covering both regular seasons and playoff games. For our analysis, we consider data only on free throw attempts as these constitute a highly standardised setting without any interaction between players, which is usually hard to account for when modelling field goals in basketball. Specifically, when considering field goals in basketball, several additional factors may affect the outcome of a shot, such as the position of the player, the position of the opposing team’s players, and the effort of the defence. If this information on a shot is ignored, a corresponding hot hand analysis might suffer from an omitted-variable bias.

We included all players who took at least 2000 free throws in the period considered, totalling in 110,513 free throws from 44 players. For each player, we included only those games in which he attempted at least four free throws to ensure that throws did not only follow successively (as players receive up to three free throws if they are fouled). In our analysis of the hot hand effect, we are interested in within-game variations in a player’s form. A single sequence of free throw attempts thus consists of all throws taken by one player in a given game, totalling in 15,075 throwing sequences with a median number of 6 free throws per game (min: 4; max: 39).

As free throws occur irregularly within a basketball game, the information on whether an attempt was successful needs to be supplemented by its time point \(t_k, k = 1,\ldots ,T\), where \(0 \le t_1 \le t_2 \le \ldots \le t_T\), corresponding to the time already played (in minutes) as indicated by the game clock. For each player p in his n-th game, we thus consider an irregular sequence of binary variables \(Y_{t_1}^{p,n}, Y_{t_2}^{p,n}, \ldots , Y_{t_{T_{p,n}}}^{p,n}\), with

$$\begin{aligned} Y_{t_k}^{p,n} = {\left\{ \begin{array}{ll} 1 &{} \text {if free throw attempt at time }t_k\text { is successful;} \\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

In our sample, the proportion of successful free throw attempts is obtained as 0.784. However, there is considerable heterogeneity in the players’ throwing success as the corresponding empirical proportions range from 0.451 (Andre Drummond) to 0.906 (Stephen Curry). Players can receive up to three free throws (depending on the foul) in the NBA, which are then thrown in quick succession, and the proportion of successful free throws differs substantially between the three attempts, with 0.769, 0.8, and 0.883 obtained for the first, second, and third free throw, respectively. To account for the position of the throw in a player’s set of (at most) three free throws, we hence include the dummy variables ft2 and ft3 in our analysis. In our sample, 54.5% of all free throws correspond to the first, 43.7% to the second, and only 1.8% to the third attempt in a set (cf. Table 1). Furthermore, as the outcome of a free throw is likely affected by intermediate information on the game — such as a close game leading to pressure situations — we consider several further covariates, which were also used in previous studies (see, e.g. Toma 2017; Morgulev et al. 2020). Specifically, we consider the current score difference (scorediff), a home dummy variable (home), and a dummy variable indicating whether the free throw occurred in the last 30 seconds of the quarter (last30). Corresponding summary statistics are shown in Table 1.

Table 1 Descriptive statistics of the covariates
Full size table

In Table 2, example throwing sequences used in our analysis are shown for free throws taken by LeBron James in five NBA games. These throwing sequences illustrate that free throw attempts often appear in clusters of two or three attempts at the same time (depending on the foul), followed by a time period without any free throws. Therefore, it is important to take into account the different lengths of the time intervals between consecutive attempts as the time elapsed between free throws affects a player’s underlying form.

Table 2 Throwing sequences of LeBron James
Full size table

3 Continuous-time modelling of the hot hand

3.1 State-space model specification

Following the idea that the throwing success depends on a player’s current (latent) form (see, e.g. Albert 1993; Wetzels et al. 2016; Ötting et al. 2020), we model the observed free throw attempts using a state-space model formulation as represented in Fig. 1. The observation process corresponds to the binary sequence of a player’s throwing success, while the state process can be interpreted as a player’s underlying form (or “hotness”). We further include the covariates introduced in Sect. 2 in the model, which possibly affect a player’s throwing success. In particular, we model the binary response of throwing success \(Y_{t_k}^{p,n}\) using a Bernoulli distribution with the associated success probability \(\pi _{t_k}^{p,n}\) being a function of the player’s current state \(S_{t_k}^{p,n}\) and the covariates. Dropping the superscripts p and n for notational simplicity from now on, we thus have

$$\begin{aligned} \begin{aligned} Y_{t_k} \sim \text {Bern}(\pi _{t_k}), \quad \text {logit}(\pi _{t_k}) =&S_{t_k} + \beta _{0,p} + \beta _1 \textit{home} + \beta _2 \textit{scorediff} \\&+ \beta _3 \textit{last30} + \beta _4 \textit{ft2} + \beta _5 \textit{ft3}, \end{aligned} \end{aligned}$$
(1)

where \(\beta _{0,p}\) is a player-specific intercept to account for differences between players’ average throwing success. To address the temporal irregularity of the free throw attempts, we formulate the stochastic process \(\{S_t\}_{t \ge 0}\) in continuous time. Furthermore, we require the state process to be continuous-valued to allow for gradual changes in a player’s form, rather than assuming a finite number of discrete states (e.g. three states interpreted as cold vs. normal vs. hot; cf. Wetzels et al. 2016; Green and Zwiebel 2017). In addition, the state process ought to be stationary such that in the long-run a player returns to his average form. A natural candidate for a corresponding stationary, continuous-valued and continuous-time process is the OU process, which is described by the following SDE:

$$\begin{aligned}{\text{d}}S_{t} = \theta (\mu - S_{t} ){\text{d}}t + \sigma {\text{d}}B_{t} ,\quad S_{0} = s_{0} ,\end{aligned}$$
(2)

where \(\theta > 0\) is the reversion parameter indicating the strength of reversion to the long-term mean \(\mu \in {\mathbb {R}}\), while \(\sigma > 0\) is the diffusion parameter controlling the strength of fluctuations, and \(B_t\) denotes the Brownian motion. We further specify \(\mu = 0\) to ensure that our model is identifiable, leading to the state process fluctuating around a player’s average form, given the current covariate values. In particular, positive values of the state process indicate higher success probabilities, whereas negative values indicate decreased throwing success, given the player’s average ability and the current game characteristics.

Fig. 1
figure 1

Dependence structure of our SSM: the throwing success \(Y_{t_k}\) is assumed to be driven by the underlying (latent) form of a player. To explicitly account for the irregular time intervals between observations, we formulate our model in continuous time

Full size image

As shown in Fig. 1, we model the hot hand effect as serial correlation in success probabilities as induced by the state process. Specifically, the observed free throw attempts are conditionally independent, given the underlying states, while the unobserved state process induces correlation in the observation process. Regarding the hot hand effect, the reversion parameter \(\theta\) of the OU process is thus of main interest as it governs the speed of reversion (to the average form). The smaller \(\theta\), the longer it takes for the OU process to return to its mean and hence the higher the serial correlation. To assess whether a model including serial dependence (i.e. an SSM) is actually needed to describe the structure in the data, we additionally fit a benchmark model without the underlying state variable \(S_{t_k}\) in Eq. (1). Consequently, the benchmark model corresponds to the absence of any hot hand effect, i.e. a standard logistic regression model. We compare the fit of both models to the data using a cross-validated likelihood score as suggested by Celeux and Durand (2008). While standard information criteria such as AIC and BIC are often considered for this purpose, it may very well be the case that they underpenalise the flexible parameters of the OU process in our SSM — a similar issue is well-known for nonparametric and mixed models (see, e.g. Hurvich et al. 1998; Müller et al. 2013). For the SSM considered here, it is anything but clear to what extent the latent states should be counted as parameters and contribute to the penalisation term (see, e.g. Auger-Méthé et al. in press). We circumvent these difficulties by instead using a cross-validated likelihood score to compare our models. We split the data set into 20 random samples, where 90% of each individual’s throwing sequences serve as training data, while the remaining 10% serve as test data. Fitting each model to the training data, we subsequently consider the out-of-sample log-likelihood on the remaining 10% of the throwing sequences to assess the models.

3.2 Statistical inference

The likelihood of the continuous-time SSM given by Eqs. (1) and (2) involves integration over all possible realisations of the continuous-valued state \(S_{t_k}\), at each observation time \(t_1, t_2, \ldots , t_T\). For simplicity of notation, let the integer \(\tau = 1, 2, \ldots , T\) denote the index of the observation in the time series, such that \(Y_{t_\tau }\) shortens to \(Y_\tau\) and \(S_{t_\tau }\) shortens to \(S_\tau\). Further, \(t_\tau\) represents the time at which the observation \(\tau\) was collected. Then the likelihood of a single throwing sequence \(y_1, \ldots , y_T\) is given by

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_T&= \int \ldots \int p(y_1, \ldots , y_T, s_1, \ldots , s_T) {\rm d}s_T \ldots {\rm d}s_1 \\&= \int \ldots \int p(s_1) \text {Pr}(y_1|s_1) \prod _{\tau =2}^T p(s_\tau | s_{\tau -1}) \text {Pr}(y_\tau |s_\tau ) {\rm d}s_T \ldots ds_1, \\ \end{aligned} \end{aligned}$$
(3)

where we assume that each player starts a game in his stationary distribution \(S_1 \sim {\mathcal {N}} \left( 0, \frac{\sigma ^2}{2\theta } \right)\), i.e. the stationary distribution of the OU process. Further, we assume \(Y_\tau\) to be Bernoulli distributed with corresponding state-dependent probabilities \(\text {Pr}(y_\tau |s_\tau )\) additionally depending on the current covariate values (cf. Eq. (1)), while the transition density of the state process \(p(s_\tau | s_{\tau -1})\) is normally distributed as determined by the conditional distribution of the OU process:

$$\begin{aligned} S_{\tau } | S_{\tau -1} = s \sim {\mathcal {N}}\left( \text {e}^{-\theta \varDelta _\tau } s, \quad \frac{\sigma ^2}{2\theta } \bigl (1- \text {e}^{-2\theta \varDelta _\tau }\bigr ) \right) , \end{aligned}$$
(4)

where \(\varDelta _\tau = t_{\tau } - t_{\tau -1}\) denotes the time difference between consecutive observations. Note that some of the observations actually occur at the exact same time according to the game clock, namely if fouled players are assigned two or three successive free throws. In such cases, the conditional distribution in Eq. (4) is given by \(S_{\tau } | S_{\tau -1} = s \sim {\mathcal {N}}(s, 0)\), for \(\varDelta _\tau = 0\), such that effectively, we assume a player’s underlying form to be the same for two or three successive attempts.

Due to the T integrals in Eq. (3), the likelihood calculation is intractable. To render its evaluation feasible, we approximate the multiple integral by finely discretising the continuous-valued state space as first suggested by Kitagawa (1987). The discretisation of the state space can effectively be seen as a reframing of the model as a continuous-time hidden Markov model (HMM) with a large but finite number of states, enabling us to apply the corresponding efficient machinery. In particular, we use the forward algorithm to calculate the likelihood, defining the possible range of state values as \([-2, 2]\), which we divide into 100 intervals. We chose the interval \([-2, 2]\) such that the essential range of possible values of the state process is covered. The latter can be examined by looking at the (estimated) stationary distribution of the OU process, which we also monitored while fitting the model. For the OU process, a possible choice of the interval range would be \(\bigl [-3\sigma /\sqrt{2\theta }, 3\sigma /\sqrt{2\theta }\bigr ]\) (corresponding to three times the standard deviation in either direction as suggested by Fridman and Harris 1998). For further details on the approximation of the likelihood via state discretisation, see Ötting et al. (2020) for discrete-time and Mews et al. (2020) for continuous-time SSMs.

As we are interested in within-game variations of a player’s form, we assume single throwing sequences of players to be mutually independent, conditional on the model parameters, such that the likelihood over all games and players is simply calculated as the product of the individual likelihoods. The model parameters, i.e. the reversion parameter and the diffusion coefficient of the OU process as well as the regression coefficients, are then estimated by numerically maximising the (approximate) joint likelihood. The resulting parameter estimators are unbiased and consistent — corresponding simulation experiments are shown in Mews et al. (2020).

4 Results

According to the cross-validated likelihood scores, the continuous-time model formulation including a potential hot hand effect is preferred over the benchmark model without any underlying state process. On average, the difference in the out-of-sample log-likelihood between the models is 3.8 in favour of the continuous-time SSM, with the latter scoring higher likelihoods in 17 out of 20 cross-validation sets. The parameter estimates of the OU process, which represents the underlying form of a player, as well as the estimated regression coefficients are shown in Table 3. In particular, the estimate for the reversion parameter \(\theta\) of the OU process is fairly small, thus indicating serial correlation in the state process over time. To be more specific, the autocorrelation function (ACF) of the OU process is proportional to exp(\(-\theta \varDelta\)), where \(\varDelta\) denotes the time interval, based on which we can deduce that exp\((-0.042 \cdot 71) \approx 0.05\). Consequently, the ACF decreases by 95% over a time interval of 71 minutes, indicating that the hot hand phenomenon occurs over a whole game. Given that an NBA game lasts 48 minutes, our results indicate that the correlation between a player’s form at the beginning and end of a game is still around 0.13 (cf. Fig. 2).

Table 3 Parameter estimates with 95% confidence intervals
Full size table
Fig. 2
figure 2

Continuous-time autocorrelation function of the OU process based on the estimated reversion parameter provided in Table 3. The shaded area corresponds to the 95% CI

Full size image

Based on the estimated parameters of the OU process, the corresponding stationary distribution is estimated as \({\mathcal {N}}\left( 0, 0.348^2 \right)\), indicating a rather small range of the state process. The latter becomes apparent also when simulating state trajectories based on the parameter estimates of the OU process (cf. Fig. 3). Still, the associated success probabilities, given that all covariate values are fixed to zero, vary considerably during the time of an NBA game (cf. right y-axis of Fig. 3). More specifically, the state process fluctuates between – 0.68 and 0.68 around 95% of the time, implying that for a player with median throwing success the corresponding success probabilities lie between 0.69 and 0.9, conditional on the covariates being equal to zero. In this specific case, a player’s underlying form thus changes his throwing success by up to – 12 and + 8 percentage points (the change in percentage points is not symmetrical around the average throwing success as we model the predictor on the logit scale, cf. Eq. (1)). While the state process and hence the resulting success probabilities slowly fluctuate around the average throwing success (given the covariates), the simulated state trajectories reflect the temporal persistence of the players’ underlying form. Thus, our results suggest that players can temporarily enter a state in which their success probability is considerably higher than their average performance, which provides evidence for a hot hand effect.

Fig. 3
figure 3

Simulation of possible state trajectories for the length of an NBA game based on the estimated parameters of the OU process. The red-dashed line indicates the intercept (here: the median throwing success over all players), around which the processes fluctuate. The right y-axis shows the success probabilities resulting from the current state (left y-axis), given that the explanatory variables equal 0. The graphs were obtained by application of the Euler-Maruyama scheme with initial value 0 and step length 0.01

Full size image

Regarding the estimated regression coefficients, the player-specific intercepts \({\hat{\beta }}_{0,p}\) range from -0.311 to 2.192 (on the logit scale), reflecting the heterogeneity in players’ throwing success. The estimates for \(\beta _1\) to \(\beta _5\) are displayed in Table 3 together with their 95% confidence intervals and the resulting odds ratios. The chance in making a free throw is slightly increased if the game is played at home (\(\beta _1\)) or if a free throw occurs in the last 30 seconds of a quarter (\(\beta _3\)), but both corresponding confidence intervals include the zero. In contrast, the confidence interval for the score difference (\(\beta _2\)) does not include the zero and its effect is positive, indicating that the odds to make a free throw increase by 3% per score the team is leading. The position of the throw, i.e. whether it is the first, second (\(\beta _4\)), or third (\(\beta _5\)) attempt in a row, has the largest effect of all covariates considered: compared to the first free throw, the odds of a hit increase considerably if it is the second or, in particular, the third attempt, i.e. an increase in odds of 25% and 52.3%, respectively, which was already indicated by the descriptive analysis presented in Sect. 2. However, this strong effect on the success probabilities is probably caused by the fact that three successive free throws are only awarded if a player is fouled while shooting a three-point field goal, which, in turn, is more often attempted by players who regularly perform well at free throws.

To further investigate how the hot hand may evolve during a game, we compute the most likely state sequences, corresponding to the underlying form of a player. Specifically, we seek

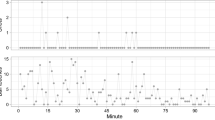
$$\begin{aligned} (s_{1}^*,\ldots ,s_{T}^*) = \underset{s_{1},\ldots ,s_{T}}{{\text {argmax}}} \; \Pr ( s_{1},\ldots ,s_{T} | y_{1},\ldots , y_{T} ), \end{aligned}$$

where \(s_{1}^*,\ldots ,s_{T}^*\) denotes the most likely state sequence given the observations. As we transferred our continuous-time SSM to an HMM framework by finely discretising the state space (cf. Sect. 3.2), we can use the Viterbi algorithm to calculate such sequences at low computational cost (Zucchini et al. 2016). Figure 4 shows the most likely states underlying the throwing sequences presented in Table 2. While the decoded state processes fluctuate around zero (i.e. the player’s average throwing success), the state values vary slightly over the time of an NBA game. Over all players and games, the decoded states range from \(-0.42\) (in a game of Josh Smith) to 0.46 (Andre Drummond), leading to changes in the success probabilities of about \(-10\) and \(+11.4\) percentage points, respectively, given the corresponding current game characteristics.

Fig. 4
figure 4

Decoded states underlying the throwing sequences of LeBron James shown in Table 2. Successful free throws are shown in yellow, missed shots in black

Full size image

The decoded state sequences in Fig. 4 further allow to illustrate the advantages and the main idea of our continuous-time modelling approach. For example, consider the throwing sequence in the second match shown, where LeBron James only made a single free throw of his first four attempts. The decoded state at throw number 3 is \(- 0.092\) (cf. Fig. 4) and the time passed between throw number 3 and 4 is 1.65 minutes (cf. Table 2). Thus, the value of the state process at throw number 4 is drawn from a normal distribution, given the decoded state of the previous attempt, with mean \(\text {e}^{- 0.042 \cdot 1.65} (- 0.092) = - 0.086\) and variance \(\frac{0.101^2}{2\cdot 0.042} (1 - \text {e}^{-2\cdot 0.042 \cdot 1.65}) = 0.016\) (cf. Eq. (4)). Accordingly, the value of the state process for throw number 5 is drawn from a normal distribution with mean \(- 0.050\) and variance 0.078, conditional on the decoded state of \(- 0.084\) at throw number 4 and a relatively long time interval of 12.22 minutes. As highlighted by these example calculations, the conditional distribution of the state process takes into account the interval length between consecutive attempts: the more time elapses, the higher the variance in the state process and hence, the less likely is a player to retain his form, with a tendency to return to his average performance.

5 Discussion

In our analysis of the hot hand, we used SSMs formulated in continuous time to model throwing success in basketball. Focusing on free throws taken in the NBA, our results provide evidence for a hot hand effect as the underlying state process exhibits some persistence over time. In particular, the model including a hot hand effect is preferred over the benchmark model without any underlying state process based on cross-validated likelihood scores. Although we provide evidence for the existence of a hot hand, the magnitude of the hot hand effect is rather small as the underlying success probabilities are elevated by only a few percentage points (cf. Figs. 3 and 4 ).

A clear advantage of the continuous-time modelling framework considered in this contribution is that it enables us to explicitly account for the unevenly spaced time points of free throws in basketball. As argued in Sect. 1, it seems intuitively plausible that players are more likely to retain their form the less time elapses between two consecutive attempts. Our modelling approach thus naturally mirrors these considerations by using the OU process to model the evolution of a player’s latent form over time, while accommodating varying interval lengths between observations. In contrast, SSMs operating in discrete time require that time intervals are of equal length and therefore, are not (directly) applicable to irregularly spaced observations in time. Although it is possible to temporally aggregate irregularly spaced data to generate regular (i.e. equidistant) time intervals between observations and thus, to render discrete-time models applicable, this approach comes with several drawbacks. For instance, the temporal aggregation of the data introduces subjectivity regarding the choice of the discrete-time modelling resolution and discards information on the exact observation times. Moreover, it has been shown that applying discrete-time models to data with irregularly spaced events can lead to biased estimates (see, e.g. Delsing et al. 2005; Barbour et al. 2013; de Haan-Rietdijk et al. 2017). Therefore, using continuous-time models to analyse irregularly spaced observations in time avoids the pitfalls mentioned above and, in addition, is conceptually appealing as the model’s interpretation does not depend on the time resolution of the data at hand.

A minor drawback of the analysis arises from the fact that there is no universally accepted statistical modelling approach for the hot hand. While we evaluate the magnitude of the hot hand effect based on the ACF (see Sect. 4), it is not clear how strong the autocorrelation in the state process should be to reflect a distinct hot hand pattern, rendering definite conclusions almost impossible. Based on the ACF, however, the magnitude of the estimated hot hand effect can easily be compared to other studies which consider (discrete- or continuous-time) SSMs to investigate autocorrelation in players’ underlying success probabilities. A further limitation of our approach is related to the general problem of disentangling the hot hand effect from possible model misspecifications. Although we include several covariates in our model, which were also used in previous studies on free throw shooting in basketball, we cannot rule out an omitted-variable bias. In addition, possible heterogeneity across players regarding covariate effects has not been considered in our analysis. Consequently, if player-specific effects or covariates which affect the outcome of a free throw are missing in our model, this may lead to biased estimates of the OU process and hence, to biased results on the hot hand effect.

In general, the modelling framework considered provides great flexibility with regard to distributional assumptions. In particular, the response variable is not restricted to be Bernoulli distributed (or Gaussian, as is often the case when making inference on continuous-time SSMs), such that other types of response variables used in hot hand analyses (e.g. Poisson) can be implemented by changing just a few lines of code. Our continuous-time SSM can thus easily be applied to other sports, and the measure for success does not have to be binary as considered here. For readers interested in adopting our code to fit their own hot hand model, the electronic supplement of this article provides the data and code used for the analysis.