On the robustness of potential-based flow networks

Abstract

Potential-based flows provide a simple yet realistic mathematical model of transport in many real-world infrastructure networks such as, e.g., gas or water networks, where the flow along each edge depends on the difference of the potentials at its end nodes. We call a network topology robust if the maximal node potential needed to satisfy a set of demands never increases when demands are decreased. This notion of robustness is motivated by infrastructure networks where users first make reservations for certain demands that may be larger than the actual flows sent later on. In these networks, node potentials correspond to physical quantities such as pressures or hydraulic heads and must be guaranteed to lie within a fixed range, even if the actual amounts are smaller than the previously reserved demands. Our main results are a precise characterization of robust network topologies for the case of point-to-point demands via forbidden node-labeled graph minors, as well as an efficient algorithm for testing robustness.

1 Introduction

A common feature of many infrastructure networks such as water, gas, electricity, telecommunication, and road networks is that their load heavily fluctuates due to changes in the demands of the transported commodities. As a consequence, the robustness of these networks with respect to changes in the demands is a major issue for network operators. Informally, a network is robust if it is feasible for a prescribed range of demand scenarios rather than a single situation only.

In the robust optimization literature, the robustness of networks has been mainly examined for the classical flow model of Ford and Fulkerson [15]. In this model, we are given a (directed) graph $G= (V,E)$ with vertex set V and edge set E. Every edge has a capacity. A flow assigns a value $x_e$ to each edge e such that the usual flow conservation constraints are satisfied and the capacity constraint of no edge is violated. The robustness of such a network is examined with respect to a set of demand scenarios. Each demand scenario specifies a balance vector (henceforth b-vector) that specifies a certain balance for each vertex of the graph. A network is robust for a given scenario set if for every b-vector from the set there exists a corresponding feasible flow in the network. Characterizations of robust networks and algorithms for their construction have been developed for the so-called network synthesis problem where the scenario set contains one b-vector for each pair of nodes and this vector is zero except for these two nodes; see, e.g., Chien [8], Gomory and Hu [17, 18], Gusfield [24], and Talluri [36]. Further models consider the case where the scenario set is a full-dimensional polyhedron, see Àlvarez-Miranda et al. [1], Buchheim et al. [6] and Cacchiani et al. [7]. Here, cutting plane methods are used for the design of robust networks.

The works and results above are mainly motivated by robustness requirements of telecommunication networks where edges correspond to server connections for which a hard capacity constraint is a reasonable assumption. In addition, the model of Ford and Fulkerson implicitly allows flow to be routed arbitrarily at intermediate vertices which is realistic in telecommunication networks. As discussed by Cacchiani et al. [7], these models are less suitable for the flow in physical networks such as gas, water, or power networks. Such networks are more difficult to handle, since the flow on an edge depends on physical properties of the network such as pressures in gas or water networks networks, or voltages in power networks. The flow then evolves based on these potentials and cannot be rerouted arbitrarily at intermediate vertices. Another issue is that, e.g., natural gas networks are controlled by network operators who sell the right to ship up to a fixed maximal amount of flow between a prescribed set of network nodes (cf. Grimm et al. [21] and Koch et al. [27]). Even in the simplest such model where network users acquire the transmission rights between pairs of distinct nodes, the set of actual demands below these maximal transmissions gives rise to a lower-dimensional set of demand scenarios that, to the best of our knowledge, has not been studied in the literature yet.

In this paper, we close both gaps, i.e., we study the robustness of infrastructure networks with respect to a natural model for physical flows under a natural robustness concept that requires robustness against all flows satisfying given maximal flow constraints. We adopt the classical potential-based flow model introduced by Birkhoff and Diaz [5]; see also Rockafellar [31] for a general treatment. This model is based on an undirected graph $G = (V,E)$ where each edge $e = \{u,v\}$ is endowed with potential loss functions $\psi _{u,v}$, $\psi _{v,u}$, and a resistance $\beta _{e}$ that govern the flow $x_{u,v}$ on edge e as a function of the difference of the potentials $\pi _u$ and $\pi _v$ at its endpoints via the equation $\beta _e \psi _{u,v}(x_{u,v}) = \pi _u - \pi _v$. Here positive flow values $x_{u,v}$ model flow from u to v while negative flow values model flow from v to u. Typical potential loss functions are of the form $\psi _{u,v}(x) = x_{u,v}|{x_{u,v}}|$ for gas networks and $\psi _{u,v}(x_{u,v}) = \text {sgn}(x_{u,v})|{x_{u,v}}|^{1.852}$ for water networks; see also Hendrickson and Janson [25] and Gross et al. [22] and the references therein. The potentials correspond to physical quantities like the pressures or the hydraulic heads at the nodes. Due to safety reasons, real-world networks have a bound ${\bar{\pi }}$ on the maximum potential that the network allows, i.e., only potential vectors $\pi \in [0,{\bar{\pi }}]^V$ are feasible.

Suppose a network operator has issued a set of licenses I where each license $i \in I$ specifies a source-sink pair $(s_i, t_i) \in V \times V$ and a demand $d_i \in \mathbb {R}_{\ge 0}$. The license allows that up to $d_i$ units of flow can be injected into the network at $s_i$ and the same amount of flow is then discharged at $t_i$. We stress that these are single-commodity networks and hence the flow units injected in $s_i$ do not actually have to be transported to $t_i$ if there are other injections and discharges in the network. Assuming that all licenses use their full volume, this leads to a b-vector defined as

$$\begin{aligned} b_v = \sum _{i \in I : s_i = v} d_i - \sum _{i \in I : t_i = v} d_i \quad \text { for all }v \in V. \end{aligned}$$

(1)

For a network operator, it is straightforward to check whether this b-vector can be realized by a feasible potential vector in the following way. As shown by Birkhoff and Diaz [5] and Collins et al. [10] for every b-vector, there is a unique potential vector $\pi \in \mathbb {R}^V$ with $\min _{v \in V} \pi _v = 0$ that yields a flow satisfying b and these flows can be computed with standard convex optimization techniques. If $\max _{v \in V} \pi _v$ does not exceed the bound ${\bar{\pi }}$, the b-vector can be realized in the network, otherwise the b-vector is infeasible.

However, each license i allows its holder to inject and discharge less than the maximal amount of $d_i$. Thus, network operators actually need to ensure that the whole set

$$\begin{aligned} {\mathcal {B}} = \biggl \{ b \in \mathbb {R}^V : b = \sum _{i \in I : s_i = v} d_i' - \sum _{i \in I : t_i = v} d'_i \;\;\text {with } d_i' \in [0,d_i] \text { for all } i \in I \biggr \} \end{aligned}$$

(2)

of b-vectors that may arise from partial usage of the licenses can be realized by a feasible potential vector.

In this paper, we are interested in identifying networks for which the feasibility of the b-vector in (1) implies the feasibility of the whole set of possible b-vectors in (2). This is desirable for network operators since it reduces the potentially challenging task of checking the feasibility of the whole set ${\mathcal {B}}$ to the easier task of checking the feasibility of a single b-vector. Since the upper bounds on the demands $d_i$ are subject to changes when new licenses are negotiated and also the coefficients $\beta _e$ are subject to changes as the physical properties of the edges change due to wear, impurities, dirt, or technical perturbations, we study this question in the most conservative way. Specifically, we consider network topologies that only specify a graph $G = (V,E)$, source-sink pairs $s_i$, $t_i$, $i \in I$, for some finite index set I, and the potential loss functions $\psi _{u,v}$, u, $v \in V$. We call such a network topology robust if for all demand vectors $d \in \mathbb {R}^I_{\ge 0}$, all resistances $\beta _e > 0$, $e \in E$, and all potential bounds ${\bar{\pi }}\ge 0$, the feasibility of the b-vector in (1) that arises from the complete fulfilment of licenses implies the feasibility of the whole set of b-vectors (2) that arises from partial fullfilment of lincenses. It is straightforward to verify that our notion of robustness is equivalent to the requirement that the maximal potential is monotonic in the demand, i.e., for two demand vectors d, $d' \in \mathbb {R}^I_{\ge 0}$ with $d'_i \le d_i$ for all $i \in I$ and two corresponding potential vectors $\pi$, ${\pi ' \in \mathbb {R}^V}$ with $\min _{v \in V} \pi _v = \min _{v \in V} \pi _v' = 0$, we have that ${\max _{v \in V} \pi _{v}' \le \max _{v \in V} \pi _{v}}$.

1.1 Results, techniques, and paper outline

Fig. 1

Non-robust potential flow network topologies

In this paper, we give a full characterization of robust network topologies. The remainder of this paper is organized as follows. We fix notation and formally introduce the problem in Sect. 2. Section 3 contains the main results of our paper. Before we explain the results obtained in this section, we give some intuition. Consider the two network topologies depicted in Fig. 1. The network in Fig. 1a consists of a single edge and two routing requests in opposite directions. It is easy to see that this network is not robust. Suppose there is a demand of one unit between $s_1$ and $t_1$ as well as another unit demand between $s_2$ and $t_2$. Using (1), this leads to an all-zero b-vector which can be realized with a maximal potential of ${\bar{\pi }} = 0$. On the other hand, decreasing either of the demands leads to a non-zero b-vector that requires an actual flow and, thus, a maximal potential ${\bar{\pi }} > 0$; see Lemma 4 for a formal proof of this result. Next, consider the network in Fig. 1b. A straightforward argument shows that also this network topology is not robust. For ease of exposition assume that all three edges have the same potential loss function and resistance. By symmetry, to send one unit of flow from $s_i$ to $t_i$ for all $i \in \{1,2,3\}$, we can choose a potential vector $\pi$ such that $\pi _{s_1} = \pi _{s_2}$ and $\pi _{t_1} = \pi _{t_3}$. On the other hand, if there is no demand between $s_2$ and $t_2$, we need $\pi _{s_2} = \pi _{t_2}$ to prevent flow on the edge $\{s_2,t_2\}$. One can show that this inevitably leads to an increase of the maximal potential in the network; see Lemma 5 for a formal proof of this result.

As our main result, we show that these type-1 and type-2 network topologies in Fig. 1 are essentially the only two networks that are non-robust for potential flow networks. For a formal statement of this result, we use the notion of node-labeled graph minors introduced by Friedman et al. [16] that extends the usual notion of a graph minor. To this end, we label each node with a subset of source labels ${\mathfrak {s}}_i$ and sink labels ${\mathfrak {t}}_i$ with $i \in I$. A graph is a minor of another graph if the former can be constructed from the latter by a sequence of edge contractions, edge deletions, and label deletions, where an edge contraction is defined such that the new node receives the union of the labels of its endpoints. With this definition, we show that a network topology is robust if and only if it neither contains a type-1 nor a type-2 network as a (node-labeled) minor; see Theorem 1 for a formal proof of this result. As an immediate corollary of our result, we obtain that networks with a single source or a single sink are robust; see Corollary 2.

To exhibit the explanatory power of our characterization, we demonstrate its consequences for tree and cycle networks in Sect. 4. Tree networks are particularly relevant since in the non-robust setting all minimal network designs are cycle-free. We show that a tree network is robust if and only if after contracting all edges that do not lie on an ${\mathfrak {s}}_i$-${\mathfrak {t}}_i$-path, the remaining edges can be oriented such that all paths from a source ${\mathfrak {s}}_i$ to a sink ${\mathfrak {t}}_i$ follow the orientation, and along every path in the tree the orientation of the edges flips at most once; see Theorem 2. We further give a characterization of robust networks consisting of a single cycle in terms of the ordering of the node labels along the cycle; see Theorem 3.

In Sect. 5, we study a variant of the model where each routing demand is specified by a b-vector itself rather than by demands between given source-sink pairs. This is motivated by the process of capacity nomination in the European gas market (cf. Grimm et al. [21] and Koch et al. [27]). Specifically, we assume that the network nodes are partitioned into potential sources S and potential sinks T, and that every routing demand is a balanced b-vector with the additional property that demands are non-positive for sources and non-negative for sinks. We show that in this model, a network topology is robust if and only if it contains a node that separates the sources from the sinks, i.e., every path between a source and a sink passes this node; see Theorem 4.

In Sect. 6, we give a polynomial time algorithm that determines whether a network topology is robust; see Theorem 5.

In Sect. 7, we present a case study that shows the consequences of our characterizations for the gas networks of Greece and Belgium. Specifically, we give a full characterization of the configurations of these networks that are robust in our sense.

1.2 Related work

The first mathematical treatment of potential-based flows is due to Birkhoff and Diaz [5]. They show the existence of a unique solution for various boundary value problems. Collins et al. [10] show that for each b-vector, there is a unique flow satisfying these node balances, and that this flow can be computed by solving a classical minimum cost network flow problem with convex cost functions. Maugis [28] considers the special case of homogenous networks where the potential loss function of each edge is of the form $\psi (x) = \alpha \,\text {sgn}(x) |{x}|^r$ for some $\alpha$, $r \in \mathbb {R}_{>0}$. For more results, we refer to the textbook by Rockafellar [31]. For a discussion how potential flow networks are used to model gas networks, water networks, and DC power networks, see Gross et al. [22] and the references therein. Szabó [35] analyzes how the maximum potential changes when inserting an additional edge, in particular, while maintaining the demands at every node, inserting an edge may increase the maximum potential.

Robust network flows have been studied mainly in the classical flow model of Ford and Fulkerson [15] where edges have a fixed capacity. The first investigation of robust network flows is for the network synthesis problem defined by Chien [8]. Given an undirected network with demands between pairs of nodes, the problem asks for minimal edge capacities such that for each pair of nodes there is a feasible flow satisfying the demand. The problem can be reformulated as a robust flow problem in the sense of Ben-Tal and Nemirowski [3] with a discrete scenario set by introducing a scenario for each pair of vertices; see also the textbook of Ben-Tal et al. [2] for a general introduction into robust optimization. Gomory and Hu [18] prove that the problem admits a linear programming formulation of polynomial size. The same authors also propose a strongly polynomial combinatorial algorithm for this problem (Gomory and Hu [17]). Gusfield [24] gives easier algorithms for the problem that produce solutions with better structure. Talluri [36] proposes further algorithms that yield networks with fewer edges than the algorithms by Gomory and Hu, and Gusfield. When the flow demands are integer the original algorithm of Gomory and Hu [17] produces a half-integral solution. Chou and Frank [9] and Sridhar and Chandrasekaran [34] propose combinatorial algorithms that produce integer solution when the input is integer. An algorithm that matches the flow requirements exactly is given by Kabadi et al. [26].

Gomory and Hu [19] discuss a generalization of the problem where different demands between nodes have to be satisfied for different time steps. Buchheim et al. [6] consider a further generalization where scenarios are arbitrary b-vectors and flows need to be integral. They show that minimizing the cost of a network satisfying all scenarios is $\mathsf {NP}$-hard even for three scenarios and linear capacity cost; they also propose a branch-and-cut-algorithm. Àlvarez-Miranda et al. [1] propose a heuristic for the problem based on linear programming techniques. Cacchiani et al. [7] propose an integer programming formulation that does not depend on the size of the scenario set. Without the integrality constraint, the problem is solvable by linear programming techniques as shown by Schmidt [32].

Minoux [29] studies a variant of the problem where in each scenario a multi-commodity flow needs to be sent and the set of scenarios is finite. Bienstock and Günlük [4] investigate a generalization where capacities are already given and need to be augmented. Duffield et al. [13] and Fingerhut et al. [14] study a infinite scenario set for multi-commodity flows, the so-called Hose polytope. Given upper bounds on the incoming and outgoing demands for each node, the Hose polytope contains all demand matrices (specifying a routing demand for each pair of vertices) obeying these bounds. When the routing has to be fixed before the scenario is released and the scenario set is a Hose polytope, the network design problem is known as virtual private network design. The optimal solution for such a problem is always a tree as shown by Goyal et al. [20] and Gupta et al. [23]. While the Hose polytope shares with the set of b-vectors defined in (2) the fact that it is a low-dimensional polytope whose inequalities are upper bounds on the demand, our set is fundamentally different from the Hose polytope in two important ways. First, we consider only single-commodity flows while the Hose polytope contains traffic matrices. Second, our upper bounds are upper bounds on demands between pairs of nodes and not upper bounds on the traffic of single vertices as in the Hose polytope.

2 Preliminaries

Let $G = (V,E)$ be an undirected graph. We assume that G is simple and connected. For a finite index set I, let $D \in (D_i)_{i \in I}$ with $D_i = (s_i,t_i) \in V \times V$ be a set of source-sink pairs. We call the tuple (G, D) a network topology. A flow in G is a vector $x \in \mathbb {R}^{V \times V}$ with $x_{u,v} = - x_{v,u}$ for all u, $v \in V$ and $x_{u,v} = 0$ for all u, $v \in V$ with $\{u,v\} \notin E$. A positive value $x_{u,v}$ indicates a movement of flow particles along edge $\{u,v\}$ from u to v, while a negative value models flow along this edge in the opposite direction from v to u. Let

$$\begin{aligned} {\mathcal {F}}:=\bigl \{ x \in \mathbb {R}^{V\times V} : \;\;&x_{u,v} = -x_{v,u} \text { for all }u,v \in V,\\&x_{u,v} = 0 \text { for all } u, v \in V\text { with }\{u,v\} \notin E\bigr \} \end{aligned}$$

denote the set of all flows in G. The balance vector ${{\,\mathrm{bal}\,}}( x) \in \mathbb {R}^V$ of a flow $x \in {\mathcal {F}}$ is defined by ${{\,\mathrm{bal}\,}}(x)_u :=\sum _{v \in V} x_{u,v}$ for all $u \in V$. Similarly, for a vector of demands $d \in \mathbb {R}_{\ge 0}^I$, the balance vector ${{\,\mathrm{bal}\,}}( d) \in \mathbb {R}^V$ is defined as

$$\begin{aligned} {{\,\mathrm{bal}\,}}(d)_u :=\sum _{i \in I :\, u = s_i} d_i - \sum _{i \in I :\, u = t_i} d_i\qquad \text {for all }u \in V. \end{aligned}$$

We say that a flow x satisfies a vector of demands d if ${{\,\mathrm{bal}\,}}( x) = {{\,\mathrm{bal}\,}}( d)$.

The flows considered in this paper are based on potential vectors $\pi \in \mathbb {R}^V$. For each edge $e = \{u,v\} \in E$, we are given potential loss functions $\psi _{u,v}$ and $\psi _{v,u}:\mathbb {R}\rightarrow \mathbb {R}$ and a resistance $\beta _{e} \in \mathbb {R}_{>0}$. The potential loss functions $\psi _{u,v}$ and $\psi _{v,u}$ model opposite orientations of the same physical principles. Thus, we have $\psi _{u,v}(z) = -\psi _{v,u}(-z)$ for all $\{u,v\} \in E$ and $z \in \mathbb {R}$. Intuitively, the potential loss functions and resistances describe the physics of the underlying network. Throughout this paper, we impose the following assumptions on the potential loss functions.

Assumption 1

For each $\{u,v\} \in E$, the potential loss function $\psi _{u,v}:\mathbb {R}\rightarrow \mathbb {R}$ satisfies the following properties:

• 1. $\psi _{u,v} \text { is continuous,}$

• 2. $\psi _{u,v} \text { is strictly increasing,}$

• 3. $\psi _{u,v}(0) = 0$.

The first two assumptions are standard and are required by Birkhoff and Diaz [5]. The third assumption is not required by them, but satisfied by all practical applications, including gas, DC power, and water networks; see Birkhoff and Diaz [5], Maugis [28], and Gross et al. [22]. Note that without this assumption, realizing a flow of zero on an edge may require a potential difference between its end points.

We denote the family of all functions satisfying Assumption 1 by $\varPsi$. We say that a flow x is induced by $\pi$ if, for each edge $e = \{u,v\}$, the difference of the node potentials of the end nodes equals the potential loss induced by the flow along e, i.e.,

$$\begin{aligned} \beta _{e} \psi _{u,v}\big (x_{u,v}\big ) = \pi _u - \pi _v. \end{aligned}$$

(3)

Since the potential loss functions $\psi _{u,v}$ are one-to-one, for a given potential vector $\pi \in \mathbb {R}^V$ with $(\pi _u - \pi _v)/\beta _e \in \psi _{u,v}(\mathbb {R})$ for all $e = \{u,v\}\in E$, there is a unique flow $x\in {\mathcal {F}}$ satisfying (3), which we denote by $x(\pi )$. For such a flow $x( \pi )$, the corresponding balance vector ${{\,\mathrm{bal}\,}}( x( \pi ))$ can be computed as

$$\begin{aligned} {{\,\mathrm{bal}\,}}\bigl ( x( \pi )\bigr )_u = \sum _{v \in V} x( \pi )_{u,v} = \sum _{v \in V: \{u,v\}\in E} \psi _{u,v}^{-1} \Bigl ( \tfrac{\pi _u - \pi _v}{\beta _{\{u,v\}}} \Bigr ) \end{aligned}$$

(4)

for all $u \in V$.

Since the right-hand side of (3) is a difference of node potentials, uniformly shifting the entries of a potential vector $\pi \in \mathbb {R}^V$ has no effect in terms of (3). Although in all applications potentials are non-negative, we find it mathematically more convenient to allow also for negative potentials and instead fix the potential of an arbitrary node $v_0\in V$ to 0. Let

$$\begin{aligned} \varPi _{v_0} :=\bigl \{ \pi \in \mathbb {R}^V : (\pi _u - \pi _v)/\beta _{\{u,v\}}\in \psi _{u,v}(\mathbb {R}) \text { for all } \{u,v\}\in E, \; \pi _{v_0} = 0\bigr \} \end{aligned}$$

be the set of such potential vectors and let $B :=\bigl \{ b \in \mathbb {R}^V : \sum _{v \in V} b_v = 0\bigr \}$ be the set of node balances that sum to 0. Under the above conditions on G and the potential loss functions $\psi _{u,v}$, for all $v_0 \in V$, the function $f:\varPi _{v_0} \rightarrow B$ defined as $f( \pi ) :=\bigl (f_u( \pi )\bigr )_{u \in V}$ with

$$\begin{aligned} f_u ( \pi ) :=\sum _{v \in V: \{u,v\}\in E} \psi _{u,v}^{-1} \Bigl ( \tfrac{\pi _u-\pi _v}{\beta _{\{u,v\}}} \Bigr )\end{aligned}$$

(5)

is bijective and continuous. In particular, the inverse function $f^{-1}:B \rightarrow \varPi _{v_0}$ exists and is also continuous; see, e.g., Birkhoff and Diaz [5]. This implies that there is a one-to-one correspondence between node balances $b \in B$ and potentials $\pi \in \varPi _{v_0}$.

For a potential vector $\pi \in \mathbb {R}^V$, we write

$$\begin{aligned} {{\,\mathrm{str}\,}}_G( \pi ) :=\max _{v \in V} \pi _v - \min _{v \in V} \pi _v. \end{aligned}$$

Intuitively, the stress of a potential vector is equal to the maximal potential after the potential vector is re-normalized such that $\min _{v \in V} \pi _v = 0$. Since in practical applications, the potentials need to be non-negative, the normalized potential vector with $\min _{v \in V} \pi _v = 0$ is the unique non-negative potential vector that minimizes the maximal potential.

Using a slight overload of notation, we define for a balance vector $b\in B$ the stress ${{\,\mathrm{str}\,}}_G( b)$ of the corresponding potential vector $\pi = f^{-1}( b)$ as

$$\begin{aligned} {{\,\mathrm{str}\,}}_G( b) :=\max _{v \in V} \bigl (f^{-1}( b)\bigr )_v - \min _{v \in V} \bigl (f^{-1}( b)\bigr )_v. \end{aligned}$$

Further overloading the notation, we write for a demand vector $d \in \mathbb {R}_{\ge 0}^I$

$$\begin{aligned} {{\,\mathrm{str}\,}}_G( d) :={{\,\mathrm{str}\,}}_G({{\,\mathrm{bal}\,}}( d)). \end{aligned}$$

It is straightforward to see that the stress of a balance vector $b \in B$ is invariant under the choice of $v_0$. If the network G is clear from the context, we omit the subscript and simply write ${{\,\mathrm{str}\,}}(\pi )$, ${{\,\mathrm{str}\,}}( b)$, and ${{\,\mathrm{str}\,}}( d)$.

3 Robust network topologies

In this section we introduce the concept of robustness of a network topology and give a full characterization of robust network topologies. We call a network topology robust if for all resistances a component-wise decrease of a demand vector d never leads to an increase of the stress.

Definition 1

A network topology (G, D) together with potential loss functions $\psi _{u,v}\in \varPsi$, for $\{u,v\}\in E$, is called robust if, for all resistances $\beta \in \mathbb {R}_{>0}^E$, the function ${{\,\mathrm{str}\,}}:\mathbb {R}_{\ge 0}^I \rightarrow \mathbb {R}_{\ge 0}$ is non-decreasing, i.e., for all demand vectors ${d'}, {d} \in \mathbb {R}_{\ge 0}^I$ with $d'\le d$ (component-wise), we have ${{\,\mathrm{str}\,}}( d')\le {{\,\mathrm{str}\,}}( d)$.

Remark 1

One may also want to consider a stronger form of robustness, where the monotonicity of the stress even holds for all potential loss functions $\psi _{u,v}$, $\{u,v\} \in E$. We call a network topology strongly robust if, for all $\beta \in \mathbb {R}_{>0}^E$ and for all $\psi _{u,v} \in \varPsi$, $\{u,v\} \in E$, the function ${{\,\mathrm{str}\,}}: \mathbb {R}_{\ge 0}^I \rightarrow \mathbb {R}_{\ge 0}$ is non-decreasing. As a byproduct of our analysis below, we prove that a network topology is robust if and only if it is strongly robust.

For our characterization of robust network topologies, we need the concept of a minor of a network topology which is obtained by a sequence of edge deletions, edge contractions, and deletions of source-sink pairs. To keep track of the location of the source-sink pairs, for every source $s_i\in V$ and every sink $t_i\in V$ we introduce labels ${\mathfrak {s}}_i$ and ${\mathfrak {t}}_i$, which can be inherited or deleted when constructing the minor; see Fig. 2 for an illustration. More formally, we use the concept of node-labeled graph minors in which the labels form a quasi-order (a reflexive and transitive binary operation) as introduced by Friedman et al. [16]. To this end, consider a node-labeled graph $G_{L}$ with label set $L :=\{{\mathfrak {s}}_i : i \in I\} \cup \{{\mathfrak {t}}_i : i \in I\}$, and define $\ell (v)\subseteq L$ to be the subset of labels attached to node $v\in V$. We choose as quasi-order on L the natural order given by the $\subseteq$-relation. The graph is well-labeled if, for all $i\in I$,

$$\begin{aligned} \Big |{\{v \in V : {\mathfrak {s}}_i \in \ell (v)\}}\Big | = \Big |{\{v \in V : {\mathfrak {t}}_i \in \ell (v)\}}\Big | \in \{0,1\}, \end{aligned}$$

i.e., labels ${\mathfrak {s}}_i$ and ${\mathfrak {t}}_i$ are used pairwise or not at all.

There is a bijection between network topologies and well-labeled graphs: For a given network topology (G, D), each node v obtains the label set $\ell (v) = \{{\mathfrak {s}}_i : i \in I \text { with } s_i = v\} \cup \{{\mathfrak {t}}_i : i \in I \text { with } t_i = v\}$. Conversely, each well-labeled graph defines a network topology using those node pairs $(s_i,t_i)$ with ${\mathfrak {s}}_i \in \ell (s_i)$ and ${\mathfrak {t}}_i \in \ell (t_i)$.

For a well-labeled graph, the contraction of an edge $e = \{u,w\} \in E$ is the operation that deletes e, merges u and w into a single node, and gives this node the label set $\ell (u) \cup \ell (w)$. We can delete a label pair ${\mathfrak {s}}_i,{\mathfrak {t}}_i$ by deleting the labels ${\mathfrak {s}}_i$ and ${\mathfrak {t}}_i$ from both L and the label sets they are contained in, and deleting i from I. We denote the resulting label and index sets by $\bar{L}$ and ${\bar{I}}$, respectively. Deletion of edges is defined analogously to the unlabeled case. A node-labeled graph $\bar{G}_{{\bar{L}}}$ is a minor of a labeled graph $G_{L}$, if the former can be constructed from the latter by a finite sequence of edge contractions, edge deletions, and label deletions.

Definition 2

Let (G, D) be a network topology and $G_{L}$ the corresponding well-labeled graph. Then a network topology $(\bar{G}, \bar{ D})$ is a minor of (G, D) if its corresponding well-labeled graph $\bar{G}_{{\bar{L}}}$ is a minor of $G_{L}$.

Due to their one-to-one correspondence, throughout this paper we use the notions of network topologies and well-labeled graphs interchangeably.

Fig. 2

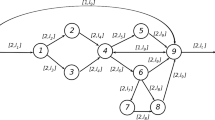
Original network topology (G, D) and one of its minors $(\bar{G}, \bar{ D})$. A possible sequence of contractions and deletions is as follows: contraction of edge $e_7$, deletion of edge $e_4$, deletion of edge $e_2$, contraction of edge $e_1$ and deletion of labels ${\mathfrak {s}}_1,{\mathfrak {t}}_1$

If $({\bar{G}}, {\bar{D}})$ is a minor of (G, D), then, in particular, ${\bar{G}}$ is an (ordinary unlabeled) minor of G; see, e.g., Diestel [12]. In particular, any node in a minor is obtained through a series of contractions and, thus, corresponds to a connected subgraph in the original graph. In addition, any two such connected subgraphs are disjoint.

Lemma 1

([12, Section 1.7]) Let (G, D) be a network topology and $({\bar{G}}, {\bar{D}})$ a minor, where $G = (V,E)$ and ${\bar{G}} = ({\bar{V}}, {\bar{E}})$. For ${\bar{v}}\in {\bar{V}}$, let $V({\bar{v}})\subseteq V$ be the subset of nodes in V contracted into ${\bar{v}}$ when creating the minor. Then, for every ${\bar{v}}\in {\bar{V}}$, the induced subgraph $G[V({\bar{v}})]$ is connected, and for any two ${\bar{v}}_1$, ${\bar{v}}_2\in {\bar{V}}$ with ${\bar{v}}_1 \ne {\bar{v}}_2$, we have $V({\bar{v}}_1) \cap V({\bar{v}}_2) = \emptyset$.

We proceed to show that a network topology is robust if and only if it contains neither of two special minors, called type-1 and type-2 networks depicted in Fig. 1. Since both of these networks are simple and connected, in the following, we can restrict our attention to simple and connected minors, which simplifies the analysis. The sequence of operations to obtain a simple and connected minor $(\bar{G}, {\bar{D}})$ of a network topology (G, D) can always be chosen such that all intermediate graphs are also simple and connnected. This follows from the observation that, whenever an edge contraction results in two parallel edges (which happens whenever we contract an edge on a cycle of length three), one can instead delete one of the two parallel edges before the contraction. Moreover, no intermediate graph can be disconnected as otherwise also $\bar{G}$ would be disconnected. As a consequence, when constructing a simple and connected minor, we only need to consider the following basic operations.

Definition 3

For a network topology (G, D) the following are basic operations:

• (a) deletion of an edge which lies on a cycle;

• (b) contraction of an edge which does not lie on a triangle (cycle of length three);

• (c) deletion of a pair of labels ${\mathfrak {s}}_i,{\mathfrak {t}}_i$.

We show that every simple and connected minor of a robust network topology (G, D) is robust. In order to prove this result, we need the following lemma. It states that, for each of the three operations above, we can adapt the vector of edge resistances $\beta$ such that the stress on the original network and the stress on the minor network are arbitrarily close to each other. The intuition behind the proof is that deletion or contraction of an edge can be approximated by giving the edge a very high or very low resistance, respectively. For given node potentials, this approximation distorts the node balances only by a very small amount. Then, by the continuity of the function $f^{-1}$ mapping node balances to potentials, one only needs to change the potentials (and thus, in particular, the stress on the network) by a very small amount to restore the original node balances.

Lemma 2

Let (G, D) be a network topology and $(\bar{G},\bar{ D})$ with ${\bar{G}} = (\bar{V}, \bar{E})$ and $\bar{ D} = (\bar{D}_i)_{i \in \bar{I}}$ a minor obtained by one basic operation. Then, for every $\bar{ d} \in \mathbb {R}^{\bar{I}}$, ${\bar{\beta }} \in \mathbb {R}_{>0}^{\bar{E}}$, and $\varepsilon > 0$, there exists $\beta \in \mathbb {R}_{>0}^E$ with $\beta _e = {\bar{\beta }}_e$ for all $e \in \bar{E} \subseteq E$ such that

$$\begin{aligned} |{{{\,\mathrm{str}\,}}_G( d) - {{{\,\mathrm{str}\,}}_{{\bar{G}}}}(\bar{ d})}| < \varepsilon , \end{aligned}$$

where $d\in \mathbb {R}_{\ge 0}^V$ is defined as $d_i :=\bar{d}_i$ for all $i \in \bar{I}$ and $d_i:=0$ for all $i\in I \setminus \bar{I}$.

Proof

The proof is trivial for the case that the basic operation deletes a pair of labels, so we only discuss the remaining two cases. Let $\bar{ d} \in \mathbb {R}^{\bar{I}}$, ${\bar{\beta }} \in \mathbb {R}_{>0}^{\bar{E}}$, and $\varepsilon > 0$. Let $e^* \in E \setminus \bar{E}$ be the edge which is deleted or contracted by the basic operation. Let $\beta \in \mathbb {R}^E$ with $\beta _e = {\bar{\beta }}_e$ for all $e\in \bar{E}$ and $\beta _{e^*}$ arbitrary. The value of $\beta _{e^*}$ will be determined later, depending on the basic operation performed to produce the minor. Let $v_0\in V \cap \bar{V}$, and let $f:\varPi _{v_0} \rightarrow B$ and $\bar{f}:{\bar{\varPi }}_{v_0} \rightarrow \bar{B}$ be the functions mapping potentials to balances as defined in (5) for the original graph G and its minor $\bar{G}$, respectively. Let $\pi :=f^{-1}\bigl ({{\,\mathrm{bal}\,}}( d)\bigr )$ and ${\bar{\pi }} :=\bar{ f}^{-1}\bigl ({{\,\mathrm{bal}\,}}(\bar{ d})\bigr )$ be the potentials corresponding to d and $\bar{ d}$, respectively. We show that one can choose $\beta _{e^*}$ such that

$$\begin{aligned} |{{{\,\mathrm{str}\,}}_G( d) - {{{\,\mathrm{str}\,}}_{{\bar{G}}}}(\bar{ d})}| = |{{{\,\mathrm{str}\,}}_G( \pi ) - {{{\,\mathrm{str}\,}}_{{\bar{G}}}}({\bar{\pi }})}| < \varepsilon . \end{aligned}$$

We distinguish two cases depending on the conducted basic operation on $e^*$.

First case: $e^*$ is deleted (and thus lies on a cycle). Then, $\bar{E} = E \setminus \{e^*\}$ and $\bar{V} = V$ and, by construction of d, ${{\,\mathrm{bal}\,}}( d) = {{\,\mathrm{bal}\,}}(\bar{{d}})$. For the potential vector ${\bar{\pi }} = \bar{ f}^{-1}\bigl ({{\,\mathrm{bal}\,}}(\bar{ d})\bigr )$, inserting edge $e^* = \{u,w\}$ into graph $\bar{G}$ only changes the balances of nodes u and w, namely by the amount of flow along edge $e^*$. For $b :=f({\bar{\pi }})$ we get

$$\begin{aligned} \Vert {b - {{\,\mathrm{bal}\,}}( d)}\Vert _{\infty } = \Vert {b - {{\,\mathrm{bal}\,}}(\bar{ d})}\Vert _{\infty }= \Vert {f({\bar{\pi }}) - \bar{ f}({\bar{\pi }})}\Vert _{\infty } = \left|\psi _{u,w}^{-1}\left( \frac{{\bar{\pi }}_u - {\bar{\pi }}_w}{\beta _{e^*}}\right) \right|. \end{aligned}$$

Since $\psi _{u,w}$ is continuous with continuous inverse and $\psi _{u,w}(0) = 0$, we obtain that $\Vert {b - {{\,\mathrm{bal}\,}}( d)}\Vert _{\infty } \rightarrow 0$ for $\beta _{e^*} \rightarrow \infty$. Since $f^{-1}$ is continuous as well, one can choose $\beta _{e^*}$ large enough such that

$$\begin{aligned} \Vert {\pi - {\bar{\pi }}}\Vert _{\infty } = \Vert {f^{-1}\bigl ({{\,\mathrm{bal}\,}}( d)\bigr ) - f^{-1}(b)}\Vert _{\infty } < \tfrac{1}{2} \varepsilon , \end{aligned}$$

and hence $|{{{\,\mathrm{str}\,}}_G( \pi ) - {{\,\mathrm{str}\,}}_{{\bar{G}}}({\bar{\pi }})}| < \varepsilon$.

Second case: $e^*$ is contracted (and thus does not lie on a triangle). For $e^* = \{u,w\}$, nodes u and w are contracted into a single node denoted by $v^*$. We have ${{\,\mathrm{bal}\,}}( d)_v = {{\,\mathrm{bal}\,}}(\bar{ d})_v$ for all $v\in V \setminus \{u,w\}$ and ${{\,\mathrm{bal}\,}}(\bar{ d})_{v^*} = {{\,\mathrm{bal}\,}}( d)_u + {{\,\mathrm{bal}\,}}( d)_w$. Consider the potential vector $\pi ^1 \in \mathbb {R}^V$ defined as

$$\begin{aligned} \pi ^{(1)}_v :={\left\{ \begin{array}{ll} {\bar{\pi }}_{v^*} &{} \text { if }v \in \{u,w\},\\ {\bar{\pi }}_v &{} \text { otherwise},\\ \end{array}\right. } \end{aligned}$$

and note that

$$\begin{aligned} {{\,\mathrm{str}\,}}_G( \pi ^{(1)}) = {{\,\mathrm{str}\,}}_{{\bar{G}}}({\bar{\pi }}). \end{aligned}$$

(6)

Let $b^{(1)} :=f( \pi ^{(1)})$. Then $b^{(1)}_v = {{\,\mathrm{bal}\,}}( d)_v$ for all $v\in V \setminus \{u,w\}$ and $b^{(1)}_u + b^{(1)}_w = {{\,\mathrm{bal}\,}}(\bar{ d})_{v^*} = {{\,\mathrm{bal}\,}}( d)_u + {{\,\mathrm{bal}\,}}( d)_w$. It is without loss of generality to assume that $b^{(1)}_w \le {{\,\mathrm{bal}\,}}( d)_w$ and, thus, $b^{(1)}_u \ge {{\,\mathrm{bal}\,}}( d)_u$. In order to restore the balances at u and w, we send a flow of value ${{\,\mathrm{bal}\,}}( d)_w - b^{(1)}_w$ from w to u along edge $e^* = \{u,w\}$, by decreasing the potential at u. To this end, let $\pi ^{(2)}\in \mathbb {R}^V$ be defined as

$$\begin{aligned} \pi ^{(2)}_v :={\left\{ \begin{array}{ll} \pi ^{(1)}_u - \beta _{e^*}\psi _{w,u}\bigl ({{\,\mathrm{bal}\,}}( d)_w - b^{(1)}_w\bigr ) &{} \text { if }v = u,\\ \pi ^{(1)}_v &{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

Note that

$$\begin{aligned} \pi ^{(2)} \rightarrow \pi ^{(1)} \quad \text {for } \beta _{e^*}\rightarrow 0. \end{aligned}$$

(7)

Let $b^{(2)} :=f( \pi ^{(2)})$. By construction, we have

$$\begin{aligned} b^{(2)}_w = {{\,\mathrm{bal}\,}}( d)_w \quad \text {and} \quad b^{(2)}_v = {{\,\mathrm{bal}\,}}( d)_v \quad \text {for all } v \in V \setminus (N(u)\cup \{u\}), \end{aligned}$$

(8)

where $N(u):=\{v\in V: \{u,v\}\in E\}$ is the set of neighbors of node u. However, by having decreased the potential at u, the balance of all neighbors of u has increased. For $v \in N(u) \setminus \{w\}$ we have

$$\begin{aligned} b^{(2)}_v - {{\,\mathrm{bal}\,}}( d)_v&= b^{(2)}_v - b^{(1)}_v \nonumber \\&= \psi _{v,u}^{-1}\left( \frac{\pi ^{(2)}_v \!-\! \pi ^{(2)}_u}{\beta _{\{v,u\}}} \right) - \psi _{v,u}^{-1}\left( \frac{\pi ^{(1)}_v \!-\! \pi ^{(1)}_u}{\beta _{\{v,u\}}} \right) \overset{(7)}{\longrightarrow } 0 \quad \text {for } \beta _{e^*}\rightarrow 0, \end{aligned}$$

(9)

by continuity of $\psi _{v,u}^{-1}$. Furthermore, since

$$\begin{aligned} \sum _{v\in V}\bigl (b_v^{(2)} - {{\,\mathrm{bal}\,}}(d)_v\bigr ) = \sum _{v\in V}b_v^{(2)} - \sum _{v\in V}{{\,\mathrm{bal}\,}}(d)_v = 0 - 0 = 0, \end{aligned}$$

we have

$$\begin{aligned} b^{(2)}_u - {{\,\mathrm{bal}\,}}( d)_u&= -\sum _{v\in V\setminus \{u\}}\big (b^{(2)}_v - {{\,\mathrm{bal}\,}}( d)_v\big ) \nonumber \\&\overset{(8)}{=} - \sum _{v \in N(u)\setminus \{w\}} \bigl (b^{(2)}_v - {{\,\mathrm{bal}\,}}( d)_v\bigr ) \overset{(9)}{\longrightarrow } 0 \quad \text {for } \beta _{e^*}\rightarrow 0. \end{aligned}$$

(10)

Equations (8), (9), and (10) imply $b^{(2)} - {{\,\mathrm{bal}\,}}( d)\rightarrow 0$ as $\beta _{e^*} \rightarrow 0$ and, hence,

$$\begin{aligned} \pi - \pi ^{(2)} = f^{-1}\bigl ({{\,\mathrm{bal}\,}}( d)\bigr ) - f^{-1}( b^{(2)}) \rightarrow 0 \quad \text {for } \beta _{e^*}\rightarrow 0, \end{aligned}$$

(11)

by continuity of $f^{-1}$. Altogether, by (6), (7), and (11), we get for $\beta _{e^*}$ small enough

$$\begin{aligned}&|{{{\,\mathrm{str}\,}}_G( \pi ) - {{\,\mathrm{str}\,}}_{{\bar{G}}}({\bar{\pi }})}| \\&\quad = |{{{\,\mathrm{str}\,}}_G( \pi ) \!-\! {{\,\mathrm{str}\,}}_G( \pi ^{(2)}) \!+\! {{\,\mathrm{str}\,}}_G( \pi ^{(2)}) \!-\! {{\,\mathrm{str}\,}}_G( \pi ^{(1)}) \!+\! {{\,\mathrm{str}\,}}_G( \pi ^{(1)}) \!-\! {{\,\mathrm{str}\,}}_{{\bar{G}}}({\bar{\pi }})}| < \varepsilon , \end{aligned}$$

which completes the proof. $\square$

We are now in the position to show that robustness of a network topology is closed under taking simple and connected minors.

Lemma 3

Every simple and connected minor of a robust network topology is robust.

Proof

Let (G, D) be a robust network topology. By contradiction, assume there is a non-robust minor $(\bar{G}, \bar{ D})$ with $\bar{G} = (\bar{V}, \bar{E})$ and $\bar{ D} = ({\bar{D}}_i)_{i \in \bar{I}}$, where $\bar{I} \subseteq I$ is the index set of the minor $(\bar{G}, \bar{D})$. Since $({\bar{G}}, {\bar{D}})$ is obtained by a sequence of basic operations, by considering the last minor in the sequence that is robust, we may assume that $(\bar{G}, \bar{ D})$ is obtained from (G, D) by one basic operation.

As $(\bar{G}, \bar{ D})$ is not robust, there are ${\bar{\beta }} \in \mathbb {R}_{>0}^{\bar{E}}$ and $\bar{ d} \le \bar{ d}' \in \mathbb {R}_{\ge 0}^{\bar{I}}$ for which

$$\begin{aligned} {{\,\mathrm{str}\,}}_{{\bar{G}}}(\bar{ d}) \ge {{\,\mathrm{str}\,}}_{{\bar{G}}}(\bar{ d}') + \varepsilon \end{aligned}$$

(12)

for some $\varepsilon > 0$.

For the network topology (G, D) with $G = (V,E)$ and $D = (D_i)_{i \in I}$ consider the demand vectors d, $d'\in \mathbb {R}_{\ge 0}^I$ with $d_i = {\bar{d}}_i$, $d'_i = {\bar{d}}_i'$ for all $i \in {\bar{I}}$ and $d_i = d_i' = 0$ for all $i\in I \setminus {\bar{I}}$. By construction, $d \le d'$. Lemma 2 implies the existence of $\beta \in \mathbb {R}^E$ with $\beta _e = {{\bar{\beta }}}_e$ for all $e\in {\bar{E}}\subseteq E$ such that $|{{{\,\mathrm{str}\,}}_G(d) - {{\,\mathrm{str}\,}}_{{\bar{G}}}(\bar{ d})}| < \varepsilon /2$ and $|{{{\,\mathrm{str}\,}}_G(d') - {{\,\mathrm{str}\,}}_{{\bar{G}}}(\bar{ d}')}| < \varepsilon /2$. Due to (12) it follows that ${{\,\mathrm{str}\,}}_G( d) > {{\,\mathrm{str}\,}}_G( d')$, contradicting the robustness of (G, D). $\square$

Before we prove the full characterization of robustness, we show that type-1 and type-2 network topologies are not robust.

Lemma 4

The type-1 network topology is not robust.

Proof

Consider the network in Fig. 1a with a demand vector d such that $d_1 = d_2 > 0$. Then there is no flow on the only edge $e = \{s_1,t_1\}$, and since $\psi _{s_1,t_1}(0) = 0$, it follows that ${{\,\mathrm{str}\,}}( d) = 0$.

Consider the demand vector $d'$ with $d'_1 = d_1$ and $d_2' = 0$, such that $d' \le d$. Since ${{\,\mathrm{bal}\,}}(d')_{s_1} = -{{\,\mathrm{bal}\,}}(d')_{t_1} = d_1 > 0$, $\psi _{s_1,t_1}(0) = 0$, and $\psi _{s_1,t_1}$ is strictly increasing, a positive potential difference between the two nodes is necessary in order to enforce a flow, which implies ${{\,\mathrm{str}\,}}( d') > 0$. $\square$

Lemma 5

The type-2 network topology is not robust.

Proof

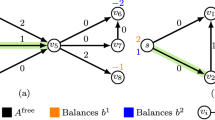
Consider the type-2 network in Fig. 3a. Let $\beta _{e_1} :=1/\psi _{v_1,v_2}(1)$, $\beta _{e_2} :=1/\psi _{v_3,v_2}(1)$, $\beta _{e_3} :=1/\psi _{v_3,v_4}(1)$, and consider the demand vector d with $d_i = 1$ for $i=1,2,3$. Let $\pi :=f^{-1}\bigl ({{\,\mathrm{bal}\,}}( d)\bigr )$. Then ${{\,\mathrm{str}\,}}(\pi ) = 1$; see Fig. 3b. The flow x induced by $\pi$ satisfies $x_{v_1,v_2} = x_{v_3,v_4} = 1$ and $x_{v_2,v_3} = -1$.

Consider the demand vector $d'$ with $d'_1 = d_3'= 1$ and $d_2' = 0$. Let $\pi ' :=f^{-1}\bigl ({{\,\mathrm{bal}\,}}( d')\bigr )$. Then ${{\,\mathrm{str}\,}}(\pi ') = 2$; see Fig. 3c. (Note that the flow $x'$ induced by $\pi '$ satisfies $x_{v_1,v_2} = x_{v_3,v_4} = 1$ and $x_{v_2,v_3} = 0$.) Hence, the type-2 network is not robust. $\square$

Fig. 3

The type-2 network with node potentials satisfying demands d and $d'$

We proceed to characterize the network topologies that have a type-1 network as a minor. To this end, we introduce the following notation. For an undirected graph $G = (V,E)$, a path P is a sequence of pairwise distinct nodes $(v_1,\dots , v_k)$ such that $\{v_i,v_{i+1}\}\in E$ for all $i\in \{1,\dots , k-1\}$. We denote by $V(P) :=\{v_1,\dots , v_k\}$ and $E(P) :=\bigl \{\{v_i,v_{i+1}\}: i\in \{1,\dots , k-1\}\bigr \}$ the node and edge set of P, respectively. Two paths P and $P'$ are called node-disjoint if $V(P)\cap V(P') = \emptyset$. For two nodes u, $v\in V$, we call a path $(v_1,\dots , v_k)$ a u-v-path if $v_1 = u$ and $v_k = v$. We denote the set of all u-v-paths in G by ${\mathcal {P}}^G_{u,v}$.

Furthermore, for a network topology (G, D) and two labels ${\mathfrak {u}},{\mathfrak {v}} \in L$ (of the corresponding well-labeled graph $G_{L}$), a ${\mathfrak {u}}$-${\mathfrak {v}}$-path is a u-v-path, where u and v are the nodes labeled by $\mathfrak u$ and ${\mathfrak {v}}$, respectively, i.e., ${\mathfrak {u}}\in \ell (u)$ and ${\mathfrak {v}}\in \ell (v)$. Correspondingly, we set ${\mathcal {P}}^G_{{\mathfrak {u}},{\mathfrak {v}}} :={\mathcal {P}}^G_{u,v}$. If the graph G is clear from the context, we sometimes omit the superscript and simply write ${\mathcal {P}}_{{\mathfrak {u}}, {\mathfrak {v}}}$ and ${\mathcal {P}}_{u,v}$.

Lemma 6

Let (G, D) be a network topology, $({\bar{G}},\bar{ D})$ a minor, and ${\mathfrak {u}}_1$, ${\mathfrak {v}}_1$, ${\mathfrak {u}}_2$, ${\mathfrak {v}}_2\in {\bar{L}} \subseteq L$ labels. If there exist two node-disjoint paths ${\bar{P}}_1\in {{\mathcal {P}}^{{\bar{G}}}_{{\mathfrak {u}}_1,{\mathfrak {v}}_1}}$ and ${\bar{P}}_2\in {\mathcal {P}}^{{\bar{G}}}_{{\mathfrak {u}}_2, {\mathfrak {v}}_2}$ in the minor ${\bar{G}}$, then there also exist two node-disjoint paths $P_1\in {\mathcal {P}}^G_{{\mathfrak {u}}_1,{\mathfrak {v}}_1}$ and $P_2\in {\mathcal {P}}^G_{{\mathfrak {u}}_2, {\mathfrak {v}}_2}$ in G.

Proof

Let ${\bar{P}}_1 \in {\mathcal {P}}^{{\bar{G}}}_{{\mathfrak {u}}_1,{\mathfrak {v}}_1}$ and ${\bar{P}}_2 \in {\mathcal {P}}^{{\bar{G}}}_{{\mathfrak {u}}_2,{\mathfrak {v}}_2}$ be node-disjoint paths. Denote the node sets of ${\bar{P}}_1$ and $\bar{P}_2$ by ${\bar{V}}_1$ and ${\bar{V}}_2$, respectively. By Lemma 1, $V_1 :=\bigcup _{\bar{v}\in {\bar{V}}_1}V({\bar{v}})\subset V$ and $V_2:=\bigcup _{{\bar{v}}\in {\bar{V}}_2}V({\bar{v}}) \subset V$ are disjoint, and both $G[V_1]$ and $G[V_2]$ are connected. Furthermore, ${\mathfrak {u}}_1,{\mathfrak {v}}_1 \in \bigcup _{v\in V_1}\ell (v)$ and ${\mathfrak {u}}_2, {\mathfrak {v}}_2\in \bigcup _{v\in V_2}\ell (v)$. Hence, there exist node-disjoint paths $P_1\in {\mathcal {P}}^G_{{\mathfrak {u}}_1, {\mathfrak {v}}_1}$ and $P_2\in {\mathcal {P}}^G_{{\mathfrak {u}}_2,{\mathfrak {v}}_2}$ in G. $\square$

Lemma 7

A network topology (G, D) contains a type-1 minor if and only if there exist i, $j \in I$ with $i \ne j$ and two node-disjoint paths $P \in {\mathcal {P}}^G_{{\mathfrak {s}}_i,{\mathfrak {t}}_j}$ and $P' \in {\mathcal {P}}^G_{{\mathfrak {s}}_j,{\mathfrak {t}}_i}$.

Proof

“$\Leftarrow$”: Suppose there are i, $j \in I$ with $i \ne j$ and two node-disjoint paths $P \in {\mathcal {P}}^G_{{\mathfrak {s}}_i\,{\mathfrak {t}}_j}$ and $P' \in {\mathcal {P}}^G_{{\mathfrak {s}}_j,{\mathfrak {t}}_i}$. Since G is connected, there exists a path Q connecting P and $P'$ with $\Big |{V(Q)\cap V(P)}\Big | = \Big |{V(Q)\cap V(P')}\Big | = 1$; see Fig. 4a. Consider the minor $(\bar{G},\bar{ D})$ which is obtained from (G, D) as follows: all edges in $E \setminus \bigl (E(P) \cup E(P') \cup E(Q)\bigr )$ are deleted and all edges in $E(P) \cup E(P')$ and all edges in E(Q) except for a single one are contracted. Further, all labels except ${\mathfrak {s}}_i$, ${\mathfrak {t}}_i$, ${\mathfrak {s}}_j$, and ${\mathfrak {t}}_j$ are deleted. This yields a type-1 network; see Fig. 4b.

Fig. 4

Node-disjoint paths $P \in {\mathcal {P}}_{{\mathfrak {s}}_i,{\mathfrak {t}}_j}$ and $P' \in {\mathcal {P}}_{{\mathfrak {s}}_j,{\mathfrak {t}}_i}$ imply the existence of a type-1 minor

“$\Rightarrow$”: Let (G, D) contain a type-1 minor $({\bar{G}}, {\bar{D}})$. The type-1 network obviously contains node-disjoint-paths ${\bar{P}} \in {\mathcal {P}}^{{\bar{G}}}_{{\mathfrak {s}}_i,{\mathfrak {t}}_j}$ and ${\bar{P}}' \in {\mathcal {P}}^{{\bar{G}}}_{{\mathfrak {s}}_j,{\mathfrak {t}}_i}$, namely paths consisting only of a single edge. Therefore, by Lemma 6, also the original network contains node-disjoint paths $P \in {\mathcal {P}}^G_{{\mathfrak {s}}_i,{\mathfrak {t}}_j}$ and $P' \in {\mathcal {P}}^G_{{\mathfrak {s}}_j,{\mathfrak {t}}_i}$. $\square$

In order to prove the general characterization of robust networks we need some preparation. For a graph $G = (V,E)$ and s, $t\in V$ with $s\ne t$, we call a flow $x\in {\mathcal {F}}$ an s-t-flow if ${{\,\mathrm{bal}\,}}( x)_s = - {{\,\mathrm{bal}\,}}( x)_t \ge 0$ and ${{\,\mathrm{bal}\,}}( x)_v = 0$ for all $v\in V \setminus \{s,t\}$. Furthermore, for two disjoint subsets U, $W\subset V$, let ${{\,\mathrm{}\,}}[U,W]:=\{\{u,w\}\in E: u\in U, w\in W\}$ be the cut between U and W.

Lemma 8

Let $G = (V,E)$ be a connected graph, $x \in {\mathcal {F}}$ an s-t-flow, and $\pi \in \mathbb {R}^V$ such that

$$\begin{aligned} {{\,\mathrm{sgn}\,}}(x_{u,v}) = {{\,\mathrm{sgn}\,}}(\pi _u - \pi _v) \qquad \text {for all } \{u,v\}\in E. \end{aligned}$$

(13)

Then the following holds:

• (a) $\pi _s \ge \pi _v \ge \pi _t$ for all $v\in V$.

• (b) The flow x can be decomposed into a sum of positive flows along a set of s-t-paths ${\mathcal {P}}\subseteq {\mathcal {P}}_{s,t}$, such that for every path $(v_1,\dots ,v_k)\in {\mathcal {P}}$ we have $x_{v_i,v_{i+1}} > 0$ for all $i \in \{1,\dots ,k-1\}$.

• (c) For all $c\in \mathbb {R}$, both the subgraph induced by $V_c^+:=\{v\in V: \pi _v \ge c\}$ and the subgraph induced by $V_c^-:=\{v\in V: \pi _v < c\}$ are connected.

Proof

We first show (a). Let ${\bar{\pi }} :=\max _{v \in V} \pi _v$ and assume by contradiction that $\pi _s < \bar{\pi }$. Let ${\bar{V}} :=\{v\in V: \pi _v = {{\bar{\pi }}}\}$. Since $s \notin \bar{V}$ and G is connected, there is $\{u,v\}\in E$ with $u\in {\bar{V}}$ and $v\in V \setminus {\bar{V}}$. By the maximality of $\pi _u$ and (13), we have $x_{u,w} \ge 0$ for all $w \in V$ and $x_{u,v} > 0$. Therefore,

$$\begin{aligned} {{\,\mathrm{bal}\,}}( x)_u = \sum _{w \in V}x_{u,w} \ge x_{u,v} > 0, \end{aligned}$$

contradicting the fact that x is an s-t-flow. Similarly, one can conclude that $\pi _t = \min _{v\in V}\pi _v$.

To show (b), note that by classical flow decomposition, the s-t-flow x decomposes into a sum of positive flows along a set of s-t-paths ${\mathcal {P}}$ and a set of cycles ${\mathcal {C}}$, such that all edges carry positive flow in the direction of the path or cycle. Assume by contradiction that ${\mathcal {C}}\ne \emptyset$ and $(v_1,\dots , v_k, v_1) \in {\mathcal {C}}$. Then (13) implies $\pi _{v_1}> \pi _{v_2}> \dots> \pi _{v_k} > \pi _{v_1}$, a contradiction.

To prove (c), we only need to consider values c with $\min _{v\in V}\pi _v<c\le \max _{v\in V}\pi _v$, since $V_c^+$ or $V_c^-$ is empty otherwise. Let $C :=[V_c^+,V_c^-]\subseteq E$ be the cut between $V_c^+$ and $V_c^-$. Consider $w_1$, $w_2\in V_c^+$ and a path $P \in {\mathcal {P}}_{w_1,w_2}$. We are done if all nodes of P are contained in $V_c^+$. Otherwise, P contains at least two edges of the cut C. Let $e_1 = \{u_1, v_1\}$ and $e_2 = \{u_2, v_2\}$ with $u_1$, $u_2 \in V_c^+$ and $v_1$, $v_2 \in V_c^-$ be the first and the last edge of P contained in C. By definition of $V^+_c$ and $V^-_c$, we have $\pi _{u_1} > \pi _{v_1}$ and thus $x_{u_1,v_1} > 0$. By (b), this implies the existence of an s-t-path $Q = (q_1,\ldots , q_k) \in {\mathcal {P}}$ containing edge $\{u_1,v_1\}$ such that $x_{q_i,q_{i+1}} > 0$ for all $i\in \{1,\ldots , k-1\}$. The path Q does not contain any other edge of C, since all edges in C carry positive flow from $V_c^+$ to $V_c^-$. Therefore, Q contains a subpath from s to $u_1$ whose nodes are all contained in $V_c^+$. By a similar argument, there exists a path from s to $u_2$ whose nodes are all contained in $V_c^+$. It follows that there exists a path from $w_1$ to $u_1$, from $u_1$ to s, from s to $u_2$, and from $u_2$ to $w_2$ only using nodes in $V_c^+$. Thus, the subgraph induced by $V_c^+$ is connected. Analogously, one can show that the subgraph induced by $V_c^-$ is connected.

$\square$

The following lemma gives a necessary condition on the potential vectors of flows in type-1-free networks. Recall that network topologies are, by definition, connected.

Lemma 9

Let (G, D) with $D = ((s_i,t_i))_{i\in I}$ be a network topology without a type-1 minor. Let $j\in I$, let $x \in {\mathcal {F}}$ be an $s_j$-$t_j$-flow, and let $\pi \in \mathbb {R}^V$ be such that x and $\pi$ fulfill (13). Then, $\pi _{s_i}\ge \pi _{t_i}$ for all $i\in I$.

Proof

By Lemma 8a, we have $\pi _{s_j} \ge \pi _v \ge \pi _{t_j}$ for all $v\in V$. By contradiction, suppose that $\pi _{t_i} > \pi _{s_i}$ for some $i\in I \setminus \{j\}$. Thus, we have $\pi _{s_j}\ge \pi _{t_i}> \pi _{s_i}\ge \pi _{t_j}$. Let $V^+ :=\{v\in V : \pi _v\ge \pi _{t_i}\}$ and $V^- :=V \setminus V^+$. Then, $s_j$, $t_i\in V^+$ and $t_j$, $s_i\in V^-$. By Lemma 8c, both $G[V^+]$ and $G[V^-]$ are connected. Therefore, there exist node-disjoint paths $P \in {\mathcal {P}}_{s_i,t_j}$ and $P' \in {\mathcal {P}}_{s_j, t_i}$. By Lemma 7, (G, D) contains a type-1 minor, a contradiction. $\square$

To complete our preparation for the main result, we prove a technical lemma whose conditions are sufficient to explicitly construct a type-2 minor.

Lemma 10

Let (G, D) be a network topology without a type-1 minor. Assume the node set V of G can be partitioned into $V = V^- \cup V^+$ with $V^-\cap V^+ = \emptyset$ such that all of the following conditions are satisfied:

• (a) Both $G[V^-]$ and $G[V^+]$ are connected.

• (b) There exist i, j, $k \in I$ with $s_i$, $t_i$, $t_j \in V^-$ and $s_j$, $s_k$, $t_k \in V^+$.

• (c) There exists a $t_i$-$s_k$-path which neither contains $s_i$ nor $t_k$.

Then (G, D) contains a type-2 minor.

Fig. 5

Construction of a type-2 network in the proof of Lemma 10. The dotted lines indicate the existence of a path from $s_i$ to $P^-_r$ in $G[V^-]$ and a path from $t_k$ to $P^+_r$ in $G[V^+]$ for all $r\in \{1, \ldots , m \}$

Proof

Let P be an $t_i$-$s_k$-path which neither contains $s_i$ nor $t_k$ and which uses a minimal number of edges of the cut ${{\,\mathrm{}\,}}[V^-,V^+]$. Let $P^-:=P\cap G[V^-]$ and $P^+:=P\cap G[V^+]$ be the parts of P which are contained in $G[V^-]$ and $G[V^+]$, respectively. Furthermore, let $P^-_1,\dots , P^-_m$ and $P^+_1,\dots ,P^+_m$ be the connected components of $P^-$ and $P^+$, where $t_i\in P^-_1$ and $s_k\in P^+_m$; see Fig. 5.

Due to the connectedness of $G[V^-]$, for any $r \in \{1,\dots ,m\}$, there exists a path from $s_i$ and to $P^-_{r}$ contained in $G[V^-]$. Note that any such path is node-disjoint from $P^-_{r'}$ for all $r'\in \{1,\ldots , m\} \setminus \{r\}$, since otherwise there exists a path between $P^-_{r}$ and $P^-_{r'}$ not containing $s_i$, and thus, there exists a $t_i$-$s_k$-path neither containing $s_i$ nor $t_k$ which uses fewer edges of the cut ${{\,\mathrm{}\,}}[V^-,V^+]$ than P, contradicting the minimality of P.

Let $P_{s_i}\subset G[V^-]$ be a path from $s_i$ to $P^-_1$, and let $P_{t_j}\subset G[V^-]$ be a path from $t_j$ to $P^- \cup P_{s_i}$. Then $P_{t_j}$ ends in $P^-_1$ since otherwise there exist node-disjoint $s_i$-$t_j$- and $t_i$-$s_j$-paths, which would imply the existence of a type-1 minor due to Lemma 7. To see this, assume for a contradiction that $P_{t_j}$ does not end in $P^-_1$. Then, either $P_{t_j}$ ends in $P_{s_i}$, and thus, there exists an $s_i$-$t_j$ path in $G[V^-]$ which is node-disjoint from $P^-_1$, or $P_{t_j}$ ends in $P^-_r$ for some $r\in \{2,\ldots , m\}$. By the argument above, there also exists a path from $s_i$ to $P^-_r$ in $G[V^-]$ which is node-disjoint from $P^-_1$. Hence, also in this case there exists an $s_i$-$t_j$-path in $G[V^-]$, which is node-disjoint from $P^-_1$. On the other hand, from $t_i$ one can follow $P^-_1$ to get to $V^+$. From there, due to the connectedness of $G[V^+]$, one can reach $s_j$ only using nodes in $V^+$.

Let $P_{t_k}\subset G[V^+]$ be a path from $t_k$ to $P^+_m$, and let $P_{s_j}\subset G[V^+]$ be a path from $s_j$ to $P^+ \cup P_{t_k}$. By a similar argument as before, it follows that $P_{s_j}$ ends in $P^+_m$.

Finally, let $e_i\in E(P_{s_i})$, $e_j\in E(P)\cap {{\,\mathrm{}\,}}[V_-,V_+]$, and $e_k\in E(P_{t_k})$. Then, deleting all labels except for ${\mathfrak {s}}_i$, ${\mathfrak {t}}_i$, ${\mathfrak {s}}_j$, ${\mathfrak {t}}_j$, ${\mathfrak {s}}_k$, ${\mathfrak {t}}_k$, deleting all edges in E except for the ones in the tree $T :=P \cup P_{s_i} \cup P_{t_j} \cup P_{s_j}\cup P_{t_k}$, and afterwards contracting all edges in $E(T)\setminus \{e_i,e_j,e_k\}$ yields a type-2 minor. $\square$

We can now prove the main result of this section.

Theorem 1

A network topology (G, D) is robust if and only if it neither contains a type-1 nor a type-2 minor.

Proof

“$\Rightarrow$”: If (G, D) contains a type-1 or type-2 minor, then, by Lemmas 4 and 5, (G, D) has a minor that it not robust. Lemma 3 implies that (G, D) is not robust.

“$\Leftarrow$”: For the reverse direction assume that (G, D) is not robust, i.e., there exist $\beta \in \mathbb {R}_{>0}^E$ and d, $d'\in \mathbb {R}_{\ge 0}^I$ with $d\le d'$ such that ${{\,\mathrm{str}\,}}( d') < {{\,\mathrm{str}\,}}( d)$. We can assume without loss of generality that there is $j \in I$ such that $d_j < d_j'$ and $d_i = d'_i$ for all $i \in I \setminus \{j\}$; otherwise, move from $d'$ to d by successively decreasing the demands $d'_i$ to $d_i$, one at a time, and identify a step which strictly increases the stress.

For the rest of the proof, assume that (G, D) does not contain a type-1 minor. Our goal is to construct node sets $V^-$ and $V^+$ fulfilling the requirements of Lemma 10 in order to prove that (G, D) contains a type-2 minor. To that end, define the potentials $\pi :=f^{-1}\bigl ({{\,\mathrm{bal}\,}}( d)\bigr )$, $\pi ' :=f^{-1}\bigl ({{\,\mathrm{bal}\,}}( d')\bigr )$, and let $x :=x(\pi )$, $x' :=x(\pi ')$ be the corresponding flows.

First, we consider nodes with highest or lowest potential. Let $V_{\max } \subseteq {{\,\mathrm{argmax}\,}}_{v\in V}\pi _v$ be a maximal subset of nodes for which $G[V_{\max }]$ is connected. Similarly, let $V_{\min } \subseteq {{\,\mathrm{argmin}\,}}_{v\in V}\pi _v$ be a maximal subset of nodes for which $G[V_{\min }]$ is connected.

Consider the flow and potential differences $\varDelta x :=x' - x$ and $\varDelta \pi :=\pi ' - \pi$. We define the sets $V^-$ and $V^+$ based on the potential differences $\varDelta \pi$ with respect to $V_{\min }$. Specifically, let c be the smallest potential difference among all nodes in $V_{\min }$, i.e., $c :=\min _{v\in V_{\min }}\varDelta \pi _v$, and define

$$\begin{aligned} V^+ :=\{v\in V: \varDelta \pi _v\ge c\} \qquad \text {and} \qquad V^- :=\{v\in V: \varDelta \pi _v< c\}. \end{aligned}$$

Clearly, $V^-$ and $V^+$ are disjoint and $V = V^- \cup V^+$.

Claim

The following holds.

• (a) $V_{\min }\subseteq V^+$ and $V_{\max } \subseteq V^-$.

• (b) Both $G[V^+]$ and $G[V^-]$ are connected.

• (c) $s_j\in V^+$ and $t_j\in V^-$.

Proof

(of the claim) We first show (a). The fact that $V_{\min }\subseteq V^+$ follows directly from the definition of $V^+$. In order to show $V_{\max }\subseteq V^-$ we assume for a contradiction that $\varDelta \pi _u \ge c$ for some $u\in V_{\max }$. Thus, there exists a node $v\in V_{\min }$ with $\varDelta \pi _u \ge \varDelta \pi _v$. But since ${{\,\mathrm{str}\,}}(\pi ) = \pi _u - \pi _v$, we get

$$\begin{aligned} {{\,\mathrm{str}\,}}( d')&= {{\,\mathrm{str}\,}}( \pi ') \ge \pi '_u - \pi '_v = {{\,\mathrm{str}\,}}( \pi ) + \varDelta \pi _u - \varDelta \pi _v \ge {{\,\mathrm{str}\,}}( \pi ) = {{\,\mathrm{str}\,}}( d), \end{aligned}$$

a contradiction.

To prove (b) and (c), we show that $\varDelta x$ and $\varDelta \pi$ satisfy the requirements of Lemma 8. Indeed, $\varDelta x$ is an $s_j$-$t_j$-flow of value $d_j' - d_j > 0$, and due to Eq. (3), we have for all $\{u,v\}\in E$:

$$\begin{aligned} {{\,\mathrm{sgn}\,}}(\varDelta x_{u,v})&= {{\,\mathrm{sgn}\,}}(x'_{u,v} - x_{u,v})\\&= {{\,\mathrm{sgn}\,}}\bigl (\psi _{u,v}^{-1}(\pi _u' - \pi _v') - \psi _{u,v}^{-1}(\pi _u - \pi _v)\bigr )\\&= {{\,\mathrm{sgn}\,}}\bigl ((\pi _u' - \pi _v') - (\pi _u - \pi _v)\bigr )\\&= {{\,\mathrm{sgn}\,}}(\varDelta \pi _u - \varDelta \pi _v), \end{aligned}$$

where for the third equality we used that, by Assumption 1, $\psi _{u,v}^{-1}$ is strictly increasing. This completes the proof of the claim. $\square$

By the last claim we have $s_j\in V^+$ and $t_j\in V^-$. In order to fulfill the requirements of Lemma 10, we need to find source-sink pairs $s_i$, $t_i \in V^-$ and $s_k$, $t_k\in V^+$ and a $t_i$-$s_k$-path which neither contains $s_i$ nor $t_k$. To that end, we define the following set $U^-\subseteq V^-$ via its complement: Let $V\setminus U^-$ be the set of nodes containing $V^+$ and all nodes that can be reached from $V^+$ without visiting any node of $V_{\max }$ (recall that $V_{\max }\subseteq V_-$). Then we have $V_{\max } \subseteq U^- \subseteq V^-$; see Fig. 6.

Claim

$G[U^-]$ is connected.

Proof

(of the claim) Let u, $v\in U^-$, $P \in {\mathcal {P}}_{u,v}$, and assume that P contains some node in $V\setminus U^-$. Let $\{\alpha ,{{\bar{\alpha }}}\}$ and $\{\omega ,{{\bar{\omega }}}\}$, with $\alpha$, $\omega \in U^-$ and ${{\bar{\alpha }}}$, ${{\bar{\omega }}} \in V\setminus U^-$, be the first and last edge of P in the cut $[U^-,V\setminus U^-]$. Then, $\alpha$, $\omega \in V_{\max }$ since otherwise $\alpha$ or $\omega$ could be reached from $V\setminus U^-$ without passing any node of $V_{\max }$, contradicting $\alpha$, $\omega \notin V\setminus U^-$ and the definition of $V\setminus U^-$. But since $G[V_{\max }]$ is connected, there is a path from u to v via $\alpha$ and $\omega$ by only using nodes within $U^-$. $\square$

Similarly, let $V\setminus U^+$ be the set of nodes which contains $V^-$ and all nodes that can be reached from $V^-$ without visiting any node of $V_{\min }$. Then, $V_{\min } \subseteq U^+ \subseteq V^+$. By the same line of arguments as before, $G[U^+]$ is connected. $\square$

Claim

There exist source-sink pairs $s_i\in U^-$, $t_i\in V^-\setminus U^-$, and $t_k\in U^+$, $s_k\in V^+\setminus U^+$.

Proof

(of the claim) Note that, by the definition of $U^-$, for every $\{u,v\}\in E$ with $u\in U^-$ and $v\in V\setminus U^-$, we have that $u\in V_{\max }$ and $v\notin V_{\max }$, and thus $x_{u,v} > 0$. Similarly, for every edge $\{u,v\}\in E$ with $u\in U^+$ and $v\in V\setminus U^+$, we have $x_{u,v} < 0$. Hence,

$$\begin{aligned} \sum _{v\in U^-}{{\,\mathrm{bal}\,}}(x)_v > 0 \qquad \text {and} \qquad \sum _{v\in U^+}{{\,\mathrm{bal}\,}}(x)_v < 0. \end{aligned}$$

(14)

As a consequence, there exists a source $s_i\in U^-$ with $t_i\notin U^-$. Likewise, there exists a sink $t_k\in U^+$ with $s_k\notin U^+$. Since $s_i\in U^-\subseteq V^-$, Lemma 9 implies that $\varDelta \pi _{t_i} \le \varDelta \pi _{s_i} < c$, and thus, $t_i\in V^-$. Similarly, we have $\varDelta \pi _{s_k} \ge \varDelta \pi _{t_k} \ge c$, and thus $s_k\in V^+$. $\square$

It remains to show that there exists a $t_i$-$s_k$ path which neither contains $s_i$ nor $t_k$. Consider the node set $W :=V\setminus (U^- \cup U^+)$. Then, by the last claim, it follows that $t_i$, $s_k\in W$ and $s_i$, $t_k\notin W$. The proof of the theorem is complete once we have shown that G[W] is connected.

Fig. 6

Illustration of the different node sets in the proof of Theorem 1

Claim

G[W] is connected.

Proof

(of the claim) Let $W_1,\dots ,W_q$ be the node sets of the connected components of G[W]. Assume for a contradiction that $q \ge 2$. By the definition of $V\setminus U^-$, the subgraph $G[V \setminus U^-]$ is connected. Thus, ${{\,\mathrm{}\,}}[U^+,W_{r}]\ne \emptyset$ for all $r\in \{1,\dots ,q\}$; see Fig. 6. Likewise, we have ${{\,\mathrm{}\,}}[U^-,W_{r}]\ne \emptyset$ for all $r\in \{1,\dots ,q\}$. Let R be set of all indices $r\in \{1,\dots , q\}$ for which there exists a source $s_{\ell }\in U^-$ with $t_{\ell }\in W_r$. We claim that for every $r\in R$ it holds that

$$\begin{aligned} \forall \, \ell '\in I: \quad s_{\ell '}\in W_r \;\Rightarrow \; t_{\ell '}\in W_r. \end{aligned}$$

(15)

Otherwise, there exists a source $s_{\ell '}\in W_{r}$ with $t_{\ell '} \notin W_{r}$. At the same time, by the definition of R, there exists a source $s_{\ell }\in U^-$ with $t_{\ell }\in W_{r}$. But since $q\ge 2$, the subgraph $G[V \setminus W_r]$ is connected, and hence there exist node-disjoint paths $P\in {\mathcal {P}}_{s_{\ell },t_{\ell '}}$ and $P'\in {\mathcal {P}}_{s_{\ell '},t_{\ell }}$. Thus, by Lemma 7, (G, D) contains a type-1 minor, a contradiction.

Set $W_R :=\bigcup _{r\in R} W_{r}$. Note, that for every edge $\{u,v\}\in E$ with $u\in U^-\cup W_R$ and $v\notin U^- \cup W_R$, we have $u\in V_{\max }$ or $v\in V_{\min }$, and hence $x_{u,v} > 0$. It follows that

$$\begin{aligned} \sum _{v\in U^-\cup W_R}{{\,\mathrm{bal}\,}}( x)_v > 0. \end{aligned}$$

Therefore, there exists a source $s_{\ell }\in U^-\cup W_R$ with $t_{\ell }\notin U^-\cup W_R$; in particular, $t_{\ell }\notin W_R$. Thus, (15) implies $s_{\ell }\notin W_R$, and hence $s_{\ell }\in U^-$. By the definition of R, it follows that $t_{\ell }\notin W_{r}$ for all $r\in \{1,\dots , q\}$, and hence $t_{\ell }\in U^+$. Therefore, $\varDelta \pi _{t_{\ell }} > \varDelta \pi _{s_{\ell }}$, a contradiction to Lemma 9. This completes the proof of the claim and the theorem. $\square$

As mentioned in Remark 1, as a consequence of Theorem 1, robustness and strong robustness are in fact equivalent.

Corollary 1

A network topology is robust if and only if it is strongly robust.

Proof

By Theorem 1, a network topology is robust if and only if it neither contains a type-1 nor a type-2 minor. This condition is independent of the choice of the functions $\psi _{u,v}$, $\{u,v\}\in E$. $\square$

Furthermore, we can conclude that every network topology containing only a single soure or a single sink is robust.

Corollary 2

Let (G, D) be a network topology with a single source or a single sink, i.e., $\Big |{\bigcup _{i \in I} \{s_i\}}\Big | = 1$ or $\Big |{\bigcup _{i \in I} \{t_i\}}\Big | = 1$. Then (G, D) is robust.

Proof

Every type-1 and every type-2 network contains at least two distinct sources and two distinct sinks. Thus, (G, D) does not contain a type-1 or type-2 network as a minor. By Theorem 1, (G, D) is robust. $\square$

To conclude this section, we prove two lemmas which turn out to be useful later. The first one states that in a network topology, edges which are not contained in any $s_i$-$t_i$-path never carry any flow. Based on this fact, the second lemma concludes that contracting these edges has no influence on the robustness of the network topology.

Lemma 11

Let (G, D) be a network topology, $d\in \mathbb {R}_{\ge 0}^I$, $\pi = f^{-1}\bigl ({{\,\mathrm{bal}\,}}( d)\bigr )$, and $x = x( \pi )$ the flow satisfying demands d. If $x_{u,v} \ne 0$ for some $e = \{u,v\}\in E$, then e is contained in an $s_i$-$t_i$-path for some $i\in I$.

Proof

We proceed by induction on $p( d):=\Big |{\{i\in I: d_i > 0\}}\Big |$. If $p( d) = 0$, then $x = 0$ and there is nothing to show. Now assume $p( d) > 0$, and consider $\{u,v\}\in E$ with $x_{u,v} \ne 0$. Let $j\in I$ with $d_j > 0$ and define $d'\in \mathbb {R}_{\ge 0}^I$ by $d'_j :=0$ and $d'_i :=d_i$ for all $i\in I\setminus \{j\}$. Let $\pi ':=f^{-1}\bigl ({{\,\mathrm{bal}\,}}( d')\bigr )$ and $x' :=x( \pi ')$ the flow satisfying demands $d'$. Note that $p( d') = p( d) -1$. If $x'_{u,v} \ne 0$, then, by induction, edge $\{u,v\}$ is contained in an $s_i$-$t_i$-path for some $i\in I$. Thus, we can assume that $x'_{u,v} = 0$. Let $\varDelta x :=x - x'$ and $\varDelta \pi :=\pi - \pi '$. Then $\varDelta x$ is an $s_j$-$t_j$-flow of value $d_j > 0$ and, due to Eq. (1) and Assumption 1, ${{\,\mathrm{sgn}\,}}(\varDelta x_{u,v}) = {{\,\mathrm{sgn}\,}}(\varDelta \pi _u - \varDelta \pi _v)$ for all $\{u,v\}\in E$. Furthermore, since $x_{u,v} \ne 0$ and $x'_{u,v} = 0$, we have $\varDelta x_{u,v} \ne 0$. Hence, by Lemma 8(b) we conclude that edge $\{u,v\}$ is contained in some $s_j$-$t_j$-path. $\square$

Lemma 12

Let (G, D) be a network topology and $({\bar{G}}, \bar{ D})$ its minor obtained by contracting all edges $e\in E$ that are not contained in any $s_i$-$t_i$-path, $i\in I$. Then (G, D) is robust if and only if $({\bar{G}}, \bar{ D})$ is robust.

Proof

“$\Rightarrow$”: This direction follows directly from Lemma 3.

“$\Leftarrow$”: Let $d\in \mathbb {R}_{\ge 0}^I$, $\pi :=f^{-1}\bigl ({{\,\mathrm{bal}\,}}( d)\bigr )$, and $x :=x( \pi )$ be the flow satisfying demands d. By Lemma 11, $x_{u,v} = 0$ and thus $\pi _u = \pi _v$ for all edges $e = \{u,v\}\in E$ which are not contained in any $s_i$-$t_i$-path, $i\in I$. Therefore, contracting these edges does not alter the stress on the network, i.e., ${{\,\mathrm{str}\,}}_G( d) = {{\,\mathrm{str}\,}}_{{\bar{G}}}( d)$. Thus, due to the robustness of $({\bar{G}}, \bar{ D})$, for every ${d}'\in \mathbb {R}_{\ge 0}^I$ with $d'\le d$, we have ${{\,\mathrm{str}\,}}_G( d') = {{\,\mathrm{str}\,}}_{{\bar{G}}}( d') \le {{\,\mathrm{str}\,}}_{{\bar{G}}}( d) = {{\,\mathrm{str}\,}}_G( d)$. Hence (G, D) is robust. $\square$

4 Robustness for special graph classes

For certain special classes of graphs, such as trees and cycles, we can give more explicit characterizations of robustness.

4.1 Robust tree topologies

For the case that the network is a tree, it turns out that robustness is closely related to the possibility to give an orientation to each edge of the tree such that the resulting directed graph is a so-called bi-arborescence (see Fig. 7) and the unique paths from a source to the corresponding sink follow this orientation.

We use the following terminology: A directed graph is an arc-tree if its underlying undirected graph is a tree. Furthermore, for a directed graph (V, A), a sequence of pair-wise distinct nodes $P = (v_1,\dots ,v_k)$ is a path if $(v_i, v_{i+1}) \in A$ or $(v_{i+1}, v_{i}) \in A$ for all $i=1,\dots ,k-1$, and P is a directed path if $(v_i, v_{i+1}) \in A$ for all $i=1,\dots ,k-1$. Denote the arc set of P by A(P). For two nodes $u,v\in V$, a (directed) path $(v_1,\dots ,v_k)$ is a (directed) u-v-path if $v_1 = u$ and $v_k = v$. An arc-tree (V, A) is called an arborescence if there exists a node $r\in V$, called root of the arborescence, such that, for every $v\in V$, there exists a directed r-v-path.

Definition 4

An arc-tree (V, A) is called a bi-arborescence if there exists a node $r\in V$, called root of the bi-arborescence, such that, for every $v\in V$, there exists a directed v-r-path or a directed r-v-path.

See Fig. 7 for an illustration. Note that any arborescence is also a bi-arborescence. In contrast to arborescences, however, the root of a bi-arborescence is not necessarily unique.

Fig. 7

Three examples of bi-arborescences

We give an alternative characterization of bi-arborescences in terms of changes of edge orientations along a path. To that end, for a directed graph (V, A) and a node $v\in V$, let $\delta ^{+}(v)\subseteq A$ be the set of arcs that start in v, and let $\delta ^{-}(v)\subseteq A$ be the set of arcs that end in v.

Definition 5

Let (V, A) be a directed graph and P a path. A node $v\in V$ with $\Big |{\delta ^{-}(v) \cap A(P)}\Big | = 2$ or $\Big |{\delta ^{+}(v) \cap A(P)}\Big | =2$ is called a flipping node of P. Moreover, the number

$$\begin{aligned} \varphi (P) :=\Big |{\{v\in V: v \text { is a flipping node of }P\}}\Big | \end{aligned}$$

is called the number of flips of path P.

Lemma 13

An arc-tree (V, A) is a bi-arborescence if and only if every path in (V, A) has at most one flip.

Proof

“$\Rightarrow$”: If (V, A) is a bi-arborescence, then, for any path P, the only possible flipping node of P is the node with minimal graph-theoretic distance to the root r; see Fig. 8a.

“$\Leftarrow$”: If $|{\delta ^-(v)}|\le 1$ for all $v\in V$, then (V, A) is an arborescence and thus a bi-arborescence. Otherwise, among all nodes u with $|{\delta ^-(u)}|\ge 2$ choose one such that there is no directed path from u to any other such node (this node exists due to the acyclicity of the graph). We call this node r and argue that (V, A) is a bi-arborescence with root r: Let $v\in V$ be arbitrary and let P be the unique r-v-path. If the first arc on P is in $\delta ^{+}(r)$, then P is a directed r-v-path since otherwise the first flipping node $r'$ on P would have two incoming arcs and could be reached from r, contradicting our choice of r; see Fig. 8b. If the first arc on P is in $\delta ^{-}(r)$, then reversing P yields a directed v-r-path, since otherwise adding the second arc in $\delta ^-(r)$ to P yields a path with at least two flips, a contradiction; see Fig. 8c. $\square$

Fig. 8

Illustration of the proof of Lemma 13

We proceed to give a characterization of robust trees. It will depend on the possibility to turn the tree into a bi-arborescence such that each $s_i$-$t_i$-path follows this orientation, i.e., each $s_i$-$t_i$-path is directed.

Definition 6

For a simple undirected graph (V, E), a set of arcs $A \subset V\times V$ is called an orientation of E if $|{A}| = |{E}|$ and $E = \{\{u,v\} : (u,v) \in A\}$. A network topology (T, D) is called tree topology if $T = (V,E)$ is a tree. A tree topology is robustly orientable if there exists an orientation A of E such that (V, A) is a bi-arborescence with a directed ${\mathfrak {s}}_i$-${\mathfrak {t}}_i$-path for every $i\in I$.

Lemma 14

Every minor of a robustly orientable tree topology is robustly orientable.

Proof

Let (T, D) be a robustly orientable tree topology. Note that after contracting an edge $e\in E$ or deleting a pair of labels ${\mathfrak {s}}_i,{\mathfrak {t}}_i$ the resulting network topology is still robustly orientable. Since T is a tree, every minor of (T, D) can be obtained by a finite sequence of edge contractions and label pair deletions. By induction, every minor of (T, D) is robustly orientable. $\square$

For a tree topology (T, D) denote by $P^T_i$ the unique ${\mathfrak {s}}_i$-${\mathfrak {t}}_i$-path in T, $i\in I$. We can now give a characterization of robust tree topologies.

Theorem 2

Let (T, D) be a tree topology and let $({\bar{T}}, \bar{ D})$ be the minor that is obtained from (T, D) by contracting all edges $e\in E$ with $e\notin \bigcup _{i\in I}E(P^T_i)$. Then (T, D) is robust if and only if $({\bar{T}}, \bar{ D})$ is robustly orientable.

Proof

By Lemma 12, (T, D) is robust if and only if $({\bar{T}}, \bar{ D})$ is robust. Thus, it remains to show that $({\bar{T}}, \bar{ D})$ is robust if and only if it is robustly orientable.

“$\Rightarrow$”: We show the contraposition. First, assume that there is no orientation ${\bar{A}}$ of ${\bar{E}}$ such that the arc-tree $({\bar{V}},{\bar{A}})$ contains a directed ${\mathfrak {s}}_i$-${\mathfrak {t}}_i$-path for every $i\in I$. Then, there exist i, $j\in I$ and an edge $e\in E(P^{{\bar{T}}}_i) \cap E(P^{{\bar{T}}}_j)$ such that e is traversed in opposite directions when going from ${\mathfrak {s}}_i$ to ${\mathfrak {t}}_i$ and from ${\mathfrak {s}}_j$ to ${\mathfrak {t}}_j$, respectively. Thus, contracting every edge in ${\bar{E}} \setminus \{e\}$ and deleting all labels except for ${\mathfrak {s}}_i, {\mathfrak {t}}_i, {\mathfrak {s}}_j, {\mathfrak {t}}_j$ yields a type-1 minor. By Theorem 1, $({\bar{T}}, \bar{ D})$ is not robust.

Second, assume there is an orientation ${\bar{A}}$ of ${\bar{E}}$ such that, for every $i\in I$, the arc-tree $({\bar{V}}, {\bar{A}})$ contains a directed ${\mathfrak {s}}_i$-${\mathfrak {t}}_i$-path, but $({\bar{V}}, {\bar{A}})$ is not a bi-arborescence. By Lemma 13, $({\bar{V}}, {\bar{A}})$ contains a path P with at least two flipping nodes. By considering subpaths, it is without loss of generality to assume that $P = (v_1, \dots , v_f, \dots , v_{f'},\dots ,v_r)$ has exactly two flipping nodes $v_{f}$ and $v_{f'}$ with $f > 1$ and $f' < r$. By potentially reversing the path, it is without loss of generality to assume that $|\delta ^-(v_f) \cap A(P)| = 2$ and $|\delta ^+(v_{f'}) \cap A(P)| = 2$. Let $a_i = (v_{f-1},v_{f})$, $a_j = (v_{f}, v_{f+1})$, and $a_k = (v_{f'}, v_{f'+1})$. By construction, when traversing P

• $a_i$ is traversed before $a_j$,

• $a_j$ is traversed before $a_k$,

• $a_i$ and $a_k$ are traversed along their orientation,

• $a_j$ is traversed against its orientation;

see Fig. 9 for an illustration.

Fig. 9

An arc-tree containing a type-2 minor, as described in the proof of Theorem 2

Furthermore, by the construction of the arc-tree $({\bar{V}}, {\bar{A}})$, there exist i, j, $k\in I$ such that, for every $\ell \in \{i,j,k\}$, the arc $a_{\ell }$ is contained in the directed ${\mathfrak {s}}_{\ell }$-${\mathfrak {t}}_{\ell }$-path. Let $e_i$, $e_j$, $e_k \in {\bar{E}}$ be the edges corresponding to the arcs $a_i$, $a_j$, $a_k\in {\bar{A}}$. Within $({\bar{T}}, \bar{ D})$, contracting all edges in ${\bar{E}} \setminus \{e_i,e_j,e_k\}$ and deleting all labels except for ${\mathfrak {s}}_i$, ${\mathfrak {t}}_i$, ${\mathfrak {s}}_j$, ${\mathfrak {t}}_j$, ${\mathfrak {s}}_k$, ${\mathfrak {t}}_k$ yields a type-2 minor. By Theorem 1, $({\bar{T}}, \bar{ D})$ is not robust.

“$\Leftarrow$”: Assume $({\bar{T}}, \bar{ D})$ is robustly orientable. Then, by Lemma 14, every minor of $({\bar{T}}, \bar{ D})$ is robustly orientable. But then $({\bar{T}}, \bar{ D})$ can neither contain a type-1 nor a type-2 minor, since these minors are clearly not robustly orientable. By Theorem 1, $({\bar{T}}, \bar{ D})$ is robust. $\square$

4.2 Robust cycles

Next, we give a characterization of robust cycles. We start by considering a necessary condition for robustness.

Lemma 15

Let (G, D) be a network topology such that G is a cycle. If (G, D) is robust, then, for all $i,j\in I$, every $s_i$-$t_j$-path contains $s_j$ or $t_i$.

Proof

If there exists an $s_i$-$t_j$-path which neither contains $s_j$ nor $t_i$, then there also exists an $s_j$-$t_i$-path which neither contains $s_i$ nor $t_j$. Thus, by Lemma 7, (G, D) contains a type-1 minor and is therefore not robust. $\square$

We can now give a full characterization of robust cycles. To that end, for a path $P = (v_1,\dots , v_k)$ we write $v_i \prec _P v_j$ if $i < j$.

Theorem 3

Let (G, D) be a network topology such that G is a cycle and $s_i\ne t_i$ for all $i\in I$. Then (G, D) is robust if and only if both of the following two conditions hold:

• (a) There exist two edges $\{u_1,v_1\},\{u_2,v_2\}\in E$ and two node-disjoint paths $P_u\in {\mathcal {P}}_{u_1,u_2}$, $P_v\in {\mathcal {P}}_{v_1,v_2}$ with $\{s_i: i \in I\}\subseteq V(P_u)$, $\{t_i: i \in I\}\subseteq V(P_v)$.

• (b) Moreover, there is no pair $i,j\in I$ such that $s_i \prec _{P_u} s_j$ and $t_j \prec _{P_v} t_i$.

Figure 10 shows examples of robust and non-robust cycles.

Fig. 10

The cycles in (a) and (b) are robust, whereas the cycles in (c) and (d) are not robust. The cycle in (c) violates Property (a) in Theorem 3. The cycle (d) violates Property (b) since $s_3 \prec _{P_u} s_2$ and $t_2 \prec _{P_v} t_3$

Proof

(of Theorem 3) “$\Rightarrow$”: By contradiction, first assume that (a) holds, but (b) does not hold. Then there exist i, $j\in I$ with $s_i \prec _{P_u} s_j$ and $t_j \prec _{P_v} t_i$. Consequently, there exist node-disjoint paths $P\in {\mathcal {P}}_{s_i,t_j}$ and $P'\in {\mathcal {P}}_{s_j,t_i}$. By Lemma 7, (G, D) contains a type-1 minor and is thus not robust, a contradiction.

Next, assume that (a) does not hold. Thus, there exist i, j, $k\in I$ such that the cycle G can be decomposed into the concatenation of four paths: $P_1 \in {\mathcal {P}}_{s_i,t_j}$, $P_2 \in {\mathcal {P}}_{t_j,s_k}$, $P_3 \in {\mathcal {P}}_{s_k,t_i}$, and $P_4 \in {\mathcal {P}}_{t_i,s_i}$; see Fig. 11.

Fig. 11

A cycle violating Property (a) of Theorem 3

Applying Lemma 15 to $s_i$ and $t_j$ implies that $s_j\in V(P_1)$. Applying Lemma 15 once more to $s_k$ and $t_j$ implies that $t_k\in V(P_2)$. But then there exists an $s_i$-$t_k$-path which neither contains $s_k$ nor $t_i$, contradicting Lemma 15.

“$\Leftarrow$”: Assume by contradiction that (G, D) is not robust. By Theorem 1, it contains a type-1 or a type-2 minor. First assume that (G, D) contains a type-2 minor. Then G is of the form shown in Fig. 12a where each of the paths $P_2$ and $P_4$ might be of length zero, whereas all of the paths $P_1$, $P_3$, $P_5$, and $P_6$ contain at least one edge. Consequently, Property (a) is not satisfied. Now, assume (G, D) contains a type-1 minor. Then G has one of the forms shown in Fig. 12b, c, where each of the paths $P_1$ and $P_3$ might be of length zero, whereas both of the paths $P_2$ and $P_4$ contain at least one edge. In the first case, Property (a) is violated. In the second case, if $P_1$ or $P_3$ has length zero, then Property (a) is violated, otherwise Property (b) is violated. $\square$

Fig. 12

The possible cases for non-robust cycles. In (a) the cycle contains a type-2 minor. In (b) and (c) it contains a type-1 minor

5 Robustness in the entry-exit model

Let $G = (V,E)$ be an undirected graph, and let S, $T\subset V$ be nonempty disjoint sets of sources and sinks, respectively. We call (G, S, T) an entry-exit topology. In this section we define robustness for entry-exit topologies and give a complete characterization of the class of robust entry-exit topologies by exploiting the results on robustness of network topologies proved in the previous sections.

The set of possible balance vectors is

$$\begin{aligned} B(S,T):= & {} \left\{ b \in \mathbb {R}^V :\; b_s \ge 0 \text { for all } s\in S,\; b_t \le 0 \text { for all } t\in T,\right. \\&\left. \sum _{v\in V} b_v = 0,\; b_v = 0 \text { for all } v\in V\setminus (S\cup T) \right\} . \end{aligned}$$

For b, $b' \in B(S,T)$ we write $b \preceq b'$ if $|{b_v}| \le |{b_v'}|$ for all $v\in V$.

Definition 7

An entry-exit topology (G, S, T) together with potential loss functions $\psi _{u,v}\in \varPsi$, for $\{u,v\}\in E$, is called robust if, for all $\beta \in \mathbb {R}_{>0}^E$, the function ${{\,\mathrm{str}\,}}:B(S,T) \rightarrow \mathbb {R}_{\ge 0}$ is non-decreasing with respect to $\preceq$, i.e., for all b, $b' \in B(S,T)$ with $b\preceq b'$ we have ${{\,\mathrm{str}\,}}(b)\le {{\,\mathrm{str}\,}}(b')$.

Note that in contrast to the definition of robustness of network topologies, where the stress function is required to be non-decreasing with respect to demands of given pairs of sources and sinks, the definition of robustness of entry-exit topologies requires the stress function to be non-decreasing with respect to demands that lie in the set B(S, T), i.e., demands that may involve any source or sink of the network.

We will show that robustness of an entry-exit topology is equivalent to robustness of a certain corresponding network topology. To that end, let

$$\begin{aligned} D(S,T) :=\bigl ((s,t): (s,t)\in S\times T\bigr ) \end{aligned}$$

be the tuple of all source-sink pairs with sources in S and sinks in T. Sticking to the notation of the previous sections, this means that $D(S,T) = (D_i)_{i\in I}$, where $I = S\times T$, and for $i\in I$ we have $D_i = (s_i,t_i)$. We state the following classic observation:

Observation 1

For each $b\in B(S,T)$ there is a $d\in \mathbb {R}_{\ge 0}^{S\times T}$ with ${{\,\mathrm{bal}\,}}(d) = b$.

Lemma 16

For every b, $b'\in B(S,T)$ with $b\preceq b'$, there exist d, $d'\in \mathbb {R}_{\ge 0}^{S\times T}$ with $d\le d'$ such that ${{\,\mathrm{bal}\,}}(d) = b$ and ${{\,\mathrm{bal}\,}}(d') = b'$.

Proof

Let b, $b'\in B(S,T)$ with $b\preceq b'$ and set $\varDelta b:=b'-b \in B(S,T)$. By Observation 1, let d, $\varDelta d \in \mathbb {R}_{\ge 0}^{S\times T}$ with ${{\,\mathrm{bal}\,}}(d) = b$ and ${{\,\mathrm{bal}\,}}(\varDelta d) = \varDelta b$, and set $d':=d + \varDelta d \in \mathbb {R}_{\ge 0}^{S\times T}$. Then $d\le d'$ and ${{\,\mathrm{bal}\,}}(d') = {{\,\mathrm{bal}\,}}(d) + {{\,\mathrm{bal}\,}}(\varDelta d) = b + \varDelta b = b'$.

$\square$

Lemma 17

An entry-exit topology (G, S, T) is robust if and only if the network topology $\bigl (G,D(S,T)\bigr )$ is robust in the sense of Definition 1.

Proof

“$\Rightarrow$”: Assume that (G, S, T) is robust, and let $d \le d'\in \mathbb {R}_{\ge 0}^{S\times T}$. Then,

$$\begin{aligned} {{\,\mathrm{bal}\,}}(d)_s&= \sum _{t\in T}d_{(s,t)} \le \sum _{t\in T}d'_{(s,t)} = {{\,\mathrm{bal}\,}}(d')_s \quad \text {for all }s\in S, \\ {{\,\mathrm{bal}\,}}(d)_t&= -\sum _{s\in S}d_{(s,t)} \ge -\sum _{s\in S}d'_{(s,t)} = {{\,\mathrm{bal}\,}}(d')_t \quad \text {for all }t\in T, \\ {{\,\mathrm{bal}\,}}(d)_v&= 0 = {{\,\mathrm{bal}\,}}(d')_v \quad \text {for all } v\in V \setminus (S \cup T). \end{aligned}$$

Thus, ${{\,\mathrm{bal}\,}}(d)\preceq {{\,\mathrm{bal}\,}}(d')$ and ${{\,\mathrm{bal}\,}}(d)$, ${{\,\mathrm{bal}\,}}(d')\in B(S,T)$. Since (G, S, T) is robust, it follows that ${{\,\mathrm{str}\,}}(d) = {{\,\mathrm{str}\,}}\bigl ({{\,\mathrm{bal}\,}}(d)\bigr ) \le {{\,\mathrm{str}\,}}\bigl ({{\,\mathrm{bal}\,}}(d')\bigr ) = {{\,\mathrm{str}\,}}(d)$, showing that $\bigl (G,D(S,T)\bigr )$ is robust.

“$\Leftarrow$”: Assume that $\bigl (G,D(S,T)\bigr )$ is robust, and let b, $b'\in B(S,T)$ with $b\preceq b'$. By Lemma 16 there exist $d,d'\in \mathbb {R}_{\ge 0}^{S\times T}$ with $d\le d'$, ${{\,\mathrm{bal}\,}}(d) = b$, and ${{\,\mathrm{bal}\,}}(d') = b'$. Since $\bigl (G,D(S,T)\bigr )$ is robust, it follows that ${{\,\mathrm{str}\,}}(b) = {{\,\mathrm{str}\,}}\bigl ({{\,\mathrm{bal}\,}}(d)\bigr ) \le {{\,\mathrm{str}\,}}\bigl ({{\,\mathrm{bal}\,}}(d')\bigr ) = {{\,\mathrm{str}\,}}(b')$, showing that (G, S, T) is robust. $\square$

As our main result of this section, we provide a complete characterization of robustness for entry-exit topologies. The following theorem states that an entry-exit topology is robust if and only if there is an articulation node separating sources from sinks, i.e., there exists a node $r \in V$ such that removing r from G disconnects G into two subgraphs $G_S$ and $G_T$ with $S\setminus \{r\}\subseteq V(G_S)$ and $T \setminus \{r\}\subseteq V(G_T)$.

Theorem 4

An entry-exit topology (G, S, T) is robust if and only if G contains an articulation node which separates the sources from the sinks.

Proof

By Lemma 17 it suffices to show that the network topology $\bigl (G, D(S,T)\bigr )$ is robust if and only if G contains an articulation node that separates the sources from the sinks.

“$\Rightarrow$”: Assume that there is no articulation node separating the sources from the sinks. Applying Menger’s Theorem to S and T yields the existence of s, $s' \in S$, t, $t' \in T$ such that there are two node-disjoint paths $P \in {\mathcal {P}}_{s,t}$ and $P' \in {\mathcal {P}}_{s',t'}$. For $i:=(s,t')\in I$ and $j:=(s',t)\in I$, we have that ${\mathcal {P}}_{s,t} = {\mathcal {P}}_{s_i,t_j}$ and ${\mathcal {P}}_{s',t'} = {\mathcal {P}}_{s_j,t_i}$. Consequently, Lemma 7 implies that $\bigl (G, D(S,T)\bigr )$ contains a type-1 minor. By Theorem 1, $\bigl (G, D(S,T)\bigr )$ is not robust.

“$\Leftarrow$”: Assume that $\bigl (G, D(S,T)\bigr )$ is not robust. Then Lemma 1 implies that $\bigl (G, D(S,T)\bigr )$ contains a type-1 or a type-2 minor. First, assume that $\bigl (G, D(S,T)\bigr )$ contains a type-1 minor. By Lemma 7, there exists $i = (s,t')\in I$ and $j = (s',t)\in I$ and node-disjoint paths $P\in {\mathcal {P}}_{s_i,t_j} = {\mathcal {P}}_{s,t}$ and $P'\in {\mathcal {P}}_{s_j,t_i} = {\mathcal {P}}_{s',t'}$. Consequently, there exists no articulation node between the sources and the sinks.

Next, assume that $\bigl (G, D(S,T)\bigr )$ contains a type-2 network $({\bar{G}}, \bar{ D})$ as a minor; see Fig. 1b. This type-2 minor contains node disjoint paths ${\bar{P}} \in {\mathcal {P}}^{{\bar{G}}}_{{\mathfrak {s}}_i,{\mathfrak {t}}_i}$ and ${\bar{P}}'\in {\mathcal {P}}^{{\bar{G}}}_{{\mathfrak {s}}_k,{\mathfrak {t}}_k}$. By Lemma 6, also $\bigl (G, D(S,T)\bigr )$ contains node-disjoint paths $P \in {\mathcal {P}}^{G}_{{\mathfrak {s}}_i,{\mathfrak {t}}_i}$ and $P'\in {\mathcal {P}}^{G}_{{\mathfrak {s}}_k,{\mathfrak {t}}_k}$ and can therefore not contain an articulation node separating the sources from the sinks. $\square$

6 Algorithmically determining the robustness of a network

After having fully characterized robust network topologies theoretically, we show in this section that the robustness of a network topology can be decided in polynomial time. Referring to Theorem 1, deciding the robustness of a network is equivalent to deciding whether a network has a type-1 or type-2 network as a minor. In this context, Robertson and Seymour [30] showed that, for a fixed graph ${\bar{G}}$, there is an algorithm which decides whether ${\bar{G}}$ is a minor of larger graph G in time polynomial in the size of G. Their result, however, is only known to hold for unlabeled graph minors, and a generalization of their result to labeled graph minors is beyond the scope of this work. Instead, to show that we can efficiently decide whether a graph has a type-1 or type-2 minor, we will use the following result of Robertson and Seymour [30].

Lemma 18

(Robertson and Seymour [30]) Let $G = (V,E)$ be an undirected graph, k a fixed natural number, and ${\mathcal {A}} = \{(u_1,v_1),\dots ,(u_k,v_k)\} \subseteq V\times V$. Then, the existence of node-disjoint paths $P_1\in \mathcal P_{u_1,v_1},\dots , P_k\in {\mathcal {P}}_{u_k,v_k}$ can be decided in time polynomial in the size of G.

For a set of node pairs ${\mathcal {A}} = \{(u_1,v_1),\dots , (u_k,v_k)\} \subseteq V\times V$, we call paths $P_1\in \mathcal P_{u_1,v_1},\dots , P_k\in {\mathcal {P}}_{u_k,v_k}$ internally node-disjoint if, for all i, $j\in \{1,\dots , k\}$ with $i\ne j$, we have $\bigl (V(P_i) \setminus \{u_i,v_i\}\bigr ) \cap V(P_j) = \emptyset$, i.e., all nodes in $V(P_i)$ and $V(P_j)$ are pairwise distinct, except for possibly $\{u_i,v_i\}\cap \{u_j,v_j\} \ne \emptyset$. Note that deciding whether a graph G contains internally node-disjoint paths $P_i\in \mathcal P^G_{u_i,v_i}$, for $i=1,\dots ,k$, can be easily reduced in polynomial time to deciding whether a certain slightly modified graph ${\hat{G}}$ contains node-disjoint paths ${\bar{P}}_i\in \mathcal P^{{\hat{G}}}_{{\hat{u}}_i,{\hat{v}}_i}$, where $({\hat{u}}_i,{\hat{v}}_i)$ are corresponding copies of the pairs $(u_i,v_i)$, $i=1,\dots ,k$. Let $\textsc {(Internally)NodeDisjointPaths}({\mathcal {A}})$ be the polynomial algorithm that decides whether there exist (internally) node-disjoint paths $P_i\in {\mathcal {P}}_{u_i,v_i}$, for $i=1,\dots ,k$.

Theorem 5

Deciding whether a network topology (G, D) is robust can be done in time polynomial in the input size of (G, D).

Proof

By Lemma 7, (G, D) contains a type-1 minor if and only if there exist i, $j\in I$ with two node-disjoint paths $P\in {\mathcal {P}}_{s_i,t_j}$ and $P'\in \mathcal P_{s_j,t_i}$. This can be decided in polynomial time by iterating over all i, $j\in I$ with $i\ne j$ and calling $\textsc {NodeDisjointPaths}\bigl (\{(s_i,t_j),(s_j,t_i)\}\bigr )$.

Moreover, if (G, D) does not contain a type-1 minor, we claim that the polynomial algorithm ContainsType2Minor correctly decides whether (G, D) contains a type-2 minor. To prove this claim, assume that (G, D) contains a type-2 minor $({\bar{G}}, {\bar{D}})$, but no type-1 minor. Denote the three edges of ${\bar{G}}$ by $e_i$, $e_j$, and $e_k$; see Fig. 13.

Fig. 13

The type-2 minor in the proof of Theorem 5

By Lemma 1, G contains a subtree for which contracting all edges except $e_i$, $e_j$, and $e_k$, and deleting all labels except for ${\mathfrak {s}}_i$, ${\mathfrak {t}}_i$, ${\mathfrak {s}}_j$, ${\mathfrak {t}}_j$, ${\mathfrak {s}}_k$, ${\mathfrak {t}}_k$ yields $({\bar{G}},{\bar{D}})$. Within this tree, let P be the path from $s_i$ to $t_k$, let $P_{t_j}$ and $P_{s_j}$ be the paths from $t_j$ to P and from $s_j$ to P, respectively, and let $P_{t_i}$ and $P_{s_k}$ be the paths from $t_i$ to $P\cup P_{t_j}$ and from $s_k$ to $P\cup P_{s_j}$, respectively. Finally, let $u_j\in V(P_{t_j})\cap V(P)$, $v_j\in V(P_{s_j}) \cap V(P)$, $u_i\in V(P_{t_i})\cap V(P\cup P_{t_j})$, and $v_k\in V(P_{s_k})\cap V(P \cup P_{s_j})$; see Fig. 14 for an illustration. Four cases can occur:

• 1. $u_i\notin V(P)$ and $v_k\notin V(P)$,

• 2. $u_i\in V(P)$ and $v_k\notin V(P)$,

• 3. $u_i\notin V(P)$ and $v_k\in V(P)$,

• 4. $u_i\in V(P)$ and $v_k\in V(P)$.

If $u_i\in V(P)$, then $u_i \preceq _P u_j$, since otherwise there exist node-disjoint $s_i$-$t_j$- and $s_j$-$t_i$ paths, and hence (G, D) would contain a type-1 minor. Similarly, $v_k\in V(P)$ implies $v_j\preceq v_k$. Therefore, in the $\ell$-th case, the path P is the union of internally node-disjoint paths for the pairs in ${\mathcal {B}}_\ell$, $\ell \in \{1,2,3,4\}$, where

$$\begin{aligned} {\mathcal {B}}_1&= \{(s_i,u_j),(u_j,v_j),(v_j,t_k)\}, \\ {\mathcal {B}}_2&= \{(s_i,u_i),(u_i,u_j),(u_j,v_j),(v_j,t_k)\}, \\ {\mathcal {B}}_3&= \{(s_i,u_j),(u_j,v_j),(v_j,v_k),(v_k,t_k)\}, \\ {\mathcal {B}}_4&= \{(s_i,u_i),(u_i,u_j),(u_j,v_j),(v_j,v_k),(v_k,t_k)\}. \end{aligned}$$

Moreover, if the $\ell$-th case occurs, then the union of P, $P_{t_i}$, and $P_{t_j}$, is the union of internally node-disjoint paths for the pairs in ${\mathcal {B}}_\ell \cup {\mathcal {C}}_\ell$, where

$$\begin{aligned} {\mathcal {C}}_1&= {\mathcal {C}}_3 = \{(u_j,u_i),(u_i,t_i),(u_i,t_j)\}, \\ {\mathcal {C}}_2&= {\mathcal {C}}_4 = \{(u_i,t_i),(u_j,t_j)\}. \end{aligned}$$

Finally, in the $\ell$-th case, the union of P, $P_{t_i}$, $P_{t_j}$, $P_{s_j}$, and $P_{s_k}$, is the union of internally node-disjoint paths for the pairs in ${\mathcal {A}}_\ell = \mathcal B_\ell \cup {\mathcal {C}}_\ell \cup {\mathcal {D}}_\ell$, where

$$\begin{aligned} {\mathcal {D}}_1&= {\mathcal {D}}_2 = \{(v_j,v_k),(v_k,s_j),(v_k,s_k)\}, \\ {\mathcal {D}}_3&= {\mathcal {D}}_4 = \{(v_j,s_j),(v_k,s_k)\}. \end{aligned}$$

Hence, for one $\ell \in \{1,2,3,4\}$, there exist internally node-disjoint paths for all pairs in ${\mathcal {A}}_\ell$. Since the algorithm iterates over all such sets and checks for the existence of internally node disjoint paths, it corresctly decides that the graph has a type 2 minor.

Fig. 14

Example of a tree T containing a type-2 minor. Here, $u_i\notin V(P)$ and $v_k\in V(P)$. Thus, T is the union of internally node-disjoint paths for the pairs in ${\mathcal {A}}_3$

On the other hand, assume that the algorithm returns true. Then, there exists a set of pairs ${\mathcal {A}}_\ell = {\mathcal {B}}_\ell \cup {\mathcal {C}}_\ell \cup {\mathcal {D}}_\ell$ of the form as defined above, such that the sets $\{s_i\}$, $\{t_i,t_j,u_i,u_j\}$, $\{s_j,s_k,v_j,v_k\}$, and $\{t_k\}$, are pairwise disjoint, and there exists internally node-disjoint paths for all pairs in ${\mathcal {A}}_\ell$. Let $T'$ be the union of these paths, and let $T\subseteq T'$ be a spanning tree of $T'$. Let P be the $s_i$-$t_k$-path in T, let $e_i$ and $e_k$ be the first and the last edge of P, respectively, and let $e_j$ be an edge of the $u_j$-$v_j$-path in T. Then, deleting from G all edges in $E\setminus E(T)$, afterwards contracting all edges in $E(T)\setminus \{e_i,e_j,e_k\}$, and finally deleting all labels except for ${\mathfrak {s}}_i$, ${\mathfrak {t}}_i$, ${\mathfrak {s}}_j$, ${\mathfrak {t}}_j$, ${\mathfrak {s}}_k$, ${\mathfrak {t}}_k$ yields a type-2 minor. $\square$

7 Case study

In order to illustrate our characterization of robust network topologies we consider two real-world gas networks, determine all possible robust network topologies, and give examples of non-robust network topologies. We analyze slightly simplified versions of the gas networks of Greece (see the GasLib-134 instance of the GasLib library [33]) and Belgium (see the paper by De Wolf and Smeers [11] for a thorough discussion on this network). The networks are illustrated in Fig. 15.

For each network, the data set consists of the network structure G, as well as the location of sources S, sinks T, and storages P. At sources, gas can be injected into the network, while at sinks, gas can be discharged. At storages, gas can be both injected and discharged. Based on this data we construct network topologies by introducing pairs $(s_i,t_i)$, $i\in I$, where we require that for each $i\in I$ we have $s_i\in S\cup P$, $t_i\in T\cup P$, and $T\subseteq \{t_i: i\in I\}$. The latter condition ensures that all sinks are delivered. Both for Belgium and Greece, the graph G is a tree, and thus, we can apply the results developed in Sect. 4.1. In particular, when computing the set of all robust network topologies, by Theorem 2, we can restrict ourselves to network topologies for which it is possible to give an orientation to the edges of the graph such that each $s_i$-$t_i$-path follows this orientation.

We use this fact to give the following compact representation of network topologies. Each edge $e\in E$ is given an orientation or remains unoriented. The resulting graph then represents the set of all network topologies (G, D), $D= (s_i,t_i)_{i\in I}$, such that for all $i\in I$ the unique path from $s_i$ to $t_i$ follows the orientation of the edges. When an edge e is unoriented, no $s_i$-$t_i$-path is allowed to pass e. We call such a representation a configuration. For instance, the configuration

represents the network topologies whose set of source-sink pairs is contained in the set

$$\begin{aligned} \bigl \{\{(v_1,v_2), (v_3,v_2)\}, \{(v_1,v_2)\}, \{(v_3,v_2)\}, \emptyset \bigr \}. \end{aligned}$$

We call a configuration robust if all network topologies that are represented by that configuration are robust. We further call a robust configuration maximal if all configurations representing a strict superset of network topologies are not robust. By Theorem 2, it follows that a configuration is robust if and only if (after contracting the unoriented edges) it does not contain a path with two flips.

Both for Belgium and Greece, we compute all maximal robust configurations and give examples of non-robust configurations. The robust configurations for Belgium are illustrated in Fig. 16. In the first two robust configurations, (a) and (b), gas is imported from Algeria. In (a) the storage in Loenhout operates as a source, whereas in (b) it serves as a sink and is filled up. In the third robust configuration, (c), gas is imported from Norway and both the storages in Dudzele and Loenhout operate as sinks. In the robust configurations (d)–(f) no gas is imported and all sinks are supplied by storages. Note that for the configurations to be robust, it is necessary that no gas is imported from Algeria and Norway at the same time, since otherwise there exists a path with two flips. Examples of this situation are shown in Fig. 17.

Fig. 15

Schematic plot of the Belgian and Greek gas networks

Fig. 16

All maximal robust configurations for the Belgian gas network

Fig. 17

Examples of non-robust configurations for the Belgian gas network

Fig. 18

All maximal robust configurations for the Greek gas network

Fig. 19

Examples of non-robust configurations for the Greek gas network

The robust configurations for Greece are illustrated in Fig. 18. In (a) gas is inserted at all three sources. Note that in this situation gas from Revythoussa can only supply sources in the very southwest in order to avoid a path with two flips. In (b) no gas is inserted at Sidirokastro. Thus, the sinks to the east are supplied by gas from Kipi. The third robust configuration is shown in (c). Here, all sinks are supplied by gas from Revythoussa and no gas is inserted at the other two sources. Whenever gas from Revythoussa is sent to the north, in order for the configuration to be robust, Revythoussa must be the only source at which gas is inserted. Otherwise, we obtain a path with two flips as illustrated in Fig. 19a, b.

8 Conclusion and outlook

In this paper we gave a full characterization of robust network topologies. We proved that a network topology is robust if and only if it neither contains a type-1 nor a type-2 network as a minor. Applying this general result, we derived very specific characterizations of robustness for special classes of network topologies. For trees, robustness turned out to be equivalent to the possibility to (after contracting edges which are not contained in any $s_i$-$t_i$-path) give an orientation to the edges such that the resulting directed graph is a bi-arborescence and every $s_i$-$t_i$-path follows that orientation. For cycles, we proved that a network topology is robust if and only if sources and sinks lie on two disjoint paths and the sources and their corresponding sinks occur in the same order on these two paths. Furthermore, we studied entry-exit topologies which can be interpreted as special cases of network topologies. We proved that an entry-exit topology is robust if and only if there exists an articulation node which separates the sources from the sinks. Finally, we devised an efficient algorithm determining the robustness of a given network topology.

We now discuss open problems for future research. In our definition of robustness the stress function of a network is required to be non-decreasing for all possible edge resistances of the network. Therefore, it could be possible that even though a network topology is not robust in our sense, for specific given edge resistances, the stress function is still non-decreasing. This is indeed the case for the following example. Consider the network topology in Fig. 20 which contains a type-2 minor.

Fig. 20

Even though the network topology is non-robust, for specific edge resistances the stress function can still be non-decreasing

Assume that $\beta _e = 1$ and $\psi _{u,v}$ is the identity for every edge $e = \{u,v\}$. Then the potential loss along an edge equals the amount of flow through that edge. Without loss of generality we can assume that the potential of $t_2$ is fixed to zero. Then the stress function ${{\,\mathrm{str}\,}}:\mathbb {R}_{\ge 0}^3 \rightarrow \mathbb {R}_{\ge 0}$ is given by

$$\begin{aligned} {{\,\mathrm{str}\,}}(d_1,d_2,d_3)&= \max (\pi _{s_1}, \pi _{s_3}) - \min (\pi _{t_1},\pi _{t_3}) \\&= \max (d_1, d_3+d_2) - \min (-d_1, - d_3 + d_2) \\&= \max (d_1, d_3 + d_2) + \max (d_1, d_3-d_2) \\&= {\left\{ \begin{array}{ll} 2d_1 &{} \text {if } d_1 \ge d_3 + d_2, \\ d_1+d_2+d_3 &{} \text {if } d_3+d_2 \ge d_1 \ge d_3-d_2, \\ 2d_3 &{} \text {if } d_3-d_2 \ge d_1, \end{array}\right. } \end{aligned}$$

which is a non-decreasing function. However, when doubling the resistances $\beta _{\{s_1,t_2\}}$ and $\beta _{\{s_2,t_3\}}$, and setting $d_1 = d_3 = 1$, then for all $d_2\in [0,1]$ we have

$$\begin{aligned} {{\,\mathrm{str}\,}}(d_1,d_2,d_3)&= \max (\pi _{s_1}, \pi _{s_3}) - \min (\pi _{t_1},\pi _{t_3}) \\&= \max (2d_1, d_3+d_2) - \min (-d_1, - 2d_3 + d_2) \\&= \max (2d_1, d_3 + d_2) + \max (d_1, 2d_3-d_2) \\&= \max (2, 1 + d_2) + \max (1, 2-d_2) \\&= 4 - d_2, \end{aligned}$$

which is a decreasing function in $d_2$.

A very interesting question would be to give a characterization and/or an efficient algorithm that determine whether a potential-based flow network with given edge resistances is robust in the sense that the stress function is non-decreasing. Furthermore, following the analysis of the qualitative property of monotonicity, another step would be to examine quantitively how much the stress of a network changes when demands are changing.