Abstract
In this work we review discontinuous Galerkin finite element methods on polytopal grids (PolydG) for the numerical simulation of multiphysics wave propagation phenomena in heterogeneous media. In particular, we address wave phenomena in elastic, poro-elastic, and poro-elasto-acoustic materials. Wave propagation is modeled by using either the elastodynamics equation in the elastic domain, the acoustics equations in the acoustic domain and the low-frequency Biot’s equations in the poro-elastic one. The coupling between different models is realized by means of (physically consistent) transmission conditions, weakly imposed at the interface between the subdomains. For all models configuration, we introduce and analyse the PolydG semi-discrete formulation, which is then coupled with suitable time marching schemes. For the semi-discrete problem, we present the stability analysis and derive a-priori error estimates in a suitable energy norm. A wide set of two-dimensional verification tests with manufactured solutions are presented in order to validate the error analysis. Examples of physical interest are also shown to demonstrate the capability of the proposed methods.
Similar content being viewed by others
1 Introduction
Multiphysics wave propagation in heterogeneous media is a very attractive research topic and, in recent decades, it has registered considerable interest in the mathematical, geophysical and engineering communities. Mathematical models for wave propagation phenomena range from the linear transport equation, to the non-linear system of Navier–Stokes equations. They appear in many different scientific disciplines, such as acoustic engineering [87], vibroacoustics [63], aeronautical engineering [39], biomedical engineering [58], and computational geosciences; see [38] for a comprehensive review.
Thanks to the ongoing development of increasingly advanced high-performance computing facilities, the use of digital twins models for solving wave propagation problems has given a notable impulse towards a deeper understanding of these phenomena. Numerical methods designed for wave simulations must simultaneously account for the following three distinguishing features: accuracy, geometric flexibility and scalability. Accuracy is essential to correctly reproduce the physical phenomenon, and allows to minimize numerical dispersion and dissipation errors that would deteriorate the quality of the solution. Geometric flexibility is required since the computational domain usually features complicated geometrical shapes as well as sharp media contrasts. Scalability is demanded to solve on parallel machines real computational models featuring several hundred of millions or even billions of unknowns.
In this work we consider wave propagation problems arising from geophysics and we discuss and analyze several models, with increasing complexity, employed in this scientific area. We first present models of elastodynamics, then of poro-elasticity, and finally coupled poro-elasto-acoustics models.
Elastodynamics and viscoelastodynamics models are typically used for the study of seismic waves that propagate across the globe and are generated by earthquakes, volcanic activity, or artificial explosions. As far as the elastodynamics equations are concerned, the most used numerical methods are finite differences [40, 66, 71], finite elements [25], finite volumes [32, 47, 48, 70], and spectral elements in either their conforming [54, 60, 85] or discontinuous setting [3, 44, 51].
Poro-elastodynamics models are used to describe the propagation of pressure and elastic waves through a porous medium. Pressure waves propagate through the saturating fluid inside pores, while elastic ones through the porous skeleton. In the pioneering work by Biot [26] general equations of waves propagation in poro-elastic materials were introduced. More recently, in [83] it is proposed a model of seismic waves in saturated soils, distinguishing between in-phase (fast) movements between solid and fluid and out-phase (slow) ones. Poro-elasto-acoustic problem model acoustic/sound waves impacting a porous material and consequently propagating through it. The coupling between acoustic and poro-elastic domains, realized by means of physically consistent transmission conditions at the interface, is discussed in [57] and [41].
There is a wide strand of literature concerning the numerical discretization of poro-elastic or poro-elasto-acoustic models. Here, we recall, e.g., the Lagrange Multipliers method [2, 52, 80], the Finite Element method [24, 53] the Spectral and Pseudo-Spectral Element method [68, 82], the ADER scheme [41, 45], the finite difference method [64], and the references therein.
The aim of this work is to introduce and analyze a discontinuous Galerkin method on polygonal/polyhedral (polytopal, for short) grids (PolydG) for the numerical discretization of multiphysics waves propagation through heterogeneous materials. The geometric flexibility and arbitrary-order accuracy featured by the proposed scheme are crucial within this context as they ensure the possibility of handling complex geometries and an intrinsic high-level of precision that are necessary to correctly represent the solutions.
For early results in the field of dG methods on polygonal/polyhedral grids we refer the reader to [4, 5, 22, 33,34,35, 43] for second-order elliptic problems, to [36] for parabolic differential equations, to [6,7,8] for flows in fractured porous media, and to [9] for fluid structure interaction problems; cf. also the review paper in the context of geophysical applications [10]. In the framework of dG methods for hyperbolic problems, we mention [56, 76] for scalar wave equations on simplicial grids and the more recent PolydG discretizations designed in [11] for elastodynamics problems, in [12] for non-linear sound waves, in [13, 14] for coupled elasto-acoustic problems, and in [15] for poro-elasto-acoustic wave propagation. Recently, a novel staggered DG scheme on unstructured grids has been proposed and analyzed for linear seismic wave propagation in [86].
The results of the present work review and extend the analysis conducted in [11] and [15]. In particular, in Section 5 we provide a novel stability estimate for the poro-elastic case requiring minimal regularity on problem data and showing explicitly the dependence on the model coefficients, final simulation time, and initial conditions. Additionally, in Section 6 we generalize the PolydG semi-discrete formulation derived in [15, Section 3] to the heterogeneous case, namely we allow all the model coefficients to be discontinuous over the computational domain.
The remaining part of the paper is structured as follows: in Section 2 we review the differential models for wave propagation in heterogeneous Earth’s media while in Section 3 we define the discrete setting used in the paper. The elastodynamic model and its numerical discretization through a PolydG method is recalled in Section 4, while Sections 5 and 6 discuss the numerical analysis of a PolydG method for wave propagation problems in poro-elastic and coupled poro-elastic-acoustic media, respectively. Sections 4, 5, and 6 contain at the end suitable verification test cases to validate the theoretical error bounds. Different numerical tests of physical interest are introduced and discussed in Section 7. Finally, in Section 8 we draw some conclusions and discuss some perspective about future work.
Notation
In the following, for an open, bounded domain \(D\subset \mathbb {R}^{d}, d=2, 3\), the notation L2(D) is used in place of [L2(D)]d, with d ∈{2,3}. The scalar product in L2(D) is denoted by (⋅,⋅)D, with associated norm ∥⋅∥D. Similarly, Hℓ(D) is defined as [Hℓ(D)]d, with ℓ ≥ 0, equipped with the norm ∥⋅∥ℓ,D, assuming conventionally that H0(D) ≡L2(D). In addition, we will use H(div,D) to denote the space of L2(D) functions with square integrable divergence. In order to take into account essential boundary conditions, we also introduce the subspaces
with ΓD ⊂ ∂D having strictly positive Hausdorff measure. Here, n denotes the unit outward normal vector to ∂D. Given \(k\in \mathbb {N}\) and a Hilbert space \(\mathbb {H}\), the usual notation \(C^{k}([0,T];\mathbb {H})\) is adopted for the space of \(\mathbb {H}\)-valued functions, k-times continuously differentiable in [0,T]. Finally, the notation \(x\lesssim y\) stands for x ≤ Cy, with C > 0 independent of the discretization parameters, but possibly dependent on the physical coefficients and the final time T.
2 Modelling Seismic Waves
A seismic event is the result of a sudden release of energy due to the rupture of a more fragile part of the Earth’s crust called the fault. The deformation energy, accumulated for tens and sometimes hundreds of years along the fault, is transformed into kinetic energy that radiates, in the form of waves, in all directions through the layers of the Earth. Seismic waves are therefore energy waves that produce an oscillatory movement of the ground during their passage. Seismic waves are subdivided into two main categories: volume waves and surface waves. The former can be decomposed into compression waves (P) and shear waves (S). The (faster) P waves are transmitted both in liquids and in solids, while the (slower) S waves travel only in solid media. P waves induce a ground motion aligned with the wave field direction while S waves induce ground a motion in a plane perpendicular to the wave propagation field.
More and more frequently mathematical models are used for the study and analysis of ground motion. The solution of these models through appropriate numerical methods can provide important information for the evaluation of the seismic hazard of a given region and for the planning of the territory in order to limit the socio-economic losses linked to the seismic event. In the following we consider the differential model that aims at describing the propagation of seismic wave within Earth’s interior.
Let Ω be a bounded domain modeling the portion of the Earth where the passage of seismic waves occurs, and let ∂Ω be its boundary that can be decomposed into three disjoint parts ΓD, ΓN, and ΓA. The values of the displacement (Dirichlet conditions), the values of tractions (Neumann conditions), and the values of fictitious tractions (absorbing conditions) are imposed on ΓD, ΓN, and ΓA, respectively. For a temporal interval (0,T], with T > 0, the equation governing the displacement field u(x,t) of a dynamically disturbed elastic medium can be expressed as
where ρ is the mass density, f defines a suitable seismic source and σ is the stress tensor that models the constitutive behaviour of the material. Possible definition for σ and f will be discussed in the sequel. Equation (1) is completed by prescribing suitable boundary conditions as well as initial conditions. For the latter, by choosing u(⋅,0) = ∂tu(⋅,0) = 0, we suppose the domain to be at rest at the initial observation time.
2.1 Seismic Waves in Viscoelastic Media
The stress tensor σ in (1) can be defined in different ways to properly model the behavior of the soil. Before presenting the main constitutive laws that can be adopted for seismic wave propagation analysis we introduce: (i) the strain tensor ε, defined as the symmetric gradient ε(u) = (∇u + ∇Tu)/2, and (ii) the fourth-order (symmetric and positive definite) stiffness tensor \(\mathbb {D}\), encoding the mechanical properties of the medium. It is expressed in term of the first and the second Lamé coefficients, namely λ and μ, respectively. For an elastic material the generalized Hooke’s law
defines the most general linear relation among all the components of the stress and strain tensor. In the most general case, i.e. a fully anisotropic material, (2) contains 21 material parameters. However in our case, i.e., for a perfectly isotropic material, (2) can be reduced as
where I is the identity tensor.
Pure elastic constitutive laws are not physically representative in the field of application of interest. A first model for visco-elastic media can be handled by modifying the equation of motion according to [62]. In the approach, the inertial term ρ∂ttu in (1) is replaced by ρ∂ttu + 2ρζ∂tu + ρζ2u where ζ is an attenuation parameter. As a matter of fact, with this substitution, i.e.,
all frequency components are equally attenuated with distance, resulting in a frequency proportional quality factor Q > 0 [69]. A second attenuation model is obtained by considering materials “endowed with memory” (cf., e.g., [59, 77]) in the sense that the state of stress at the instant t depends on all the deformations undergone by the material in previous times. This behaviour can be expressed through an integral equation of the form
where the stress σ is determined by the entire strain history. Implicit in this law is the dependence on time of the Lamé parameters λ and μ, cf. [61, 67]. For the mathematical and numerical analysis of viscoelastic problems with constitutive law expressed by (5), we refer to [78], where a spatial dG discretization is coupled with a trapezoidal-rectangle rule approximation of the history integral, and to [81], where a space-time dG method is presented. We remark that, by using (5) it is possible to obtain an almost constant quality factor Q in a suitable frequency range, cf. [67].
We conclude this section by addressing proper boundary conditions to supplement equation (4). Several conditions can be set to correctly define the interaction between the wave and the domain boundary. Dirichlet conditions are employed to prescribe the behaviour of the displacement field, i.e. u = gD on ΓD, while Neumann conditions σn = gN on ΓN represent the distribution of surface loads. Here n denotes the outward pointing normal unit vector with respect to ∂Ω.
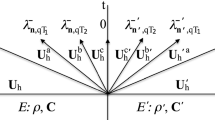
For geophysical applications, since the domain of interest Ω represents a portion of the Earth the following boundary conditions are commonly adopted: (i) free-surface condition, i.e. σn = 0 for the top Earth’s surface and (ii) transparent boundary conditions σn = t for the remaining lateral and bottom surfaces. The latter consists in modeling the absorbing boundary layers by introducing a fictitious traction term t = t(u,∂tu), consisting of a linear combination of displacement space and time derivatives. Examples can be found in [23, 72]. In Fig. 1 we report an illustrative example of domain Ω together with boundary conditions.
2.2 Seismic Waves in Porous Media
Modeling wave propagation through fluid-saturated porous rock is crucial for the characterization of the seismic response of geologic formations. In what follows, we assume that the porous medium is homogeneous and isotropic. In this case, the effects stemming from the interaction between the viscous fluid and the solid matrix have to be taken into account. In the framework of Biot’s poro-elasticity theory [26, 27], the total stress tensor \(\widetilde {\boldsymbol {\sigma }}\) additionally depends on the pore pressure p according to the following relation
with σ(u) defined as in (3) and 0 < β ≤ 1 denoting the Biot coefficient. Adding to the momentum balance equation (1) the inertial term corresponding to the filtration displacement w = ϕ(wf −u), where ϕ > 0 is the reference porosity and wf the fluid displacement, leads to
Here, the average density ρ is given by ρ = ϕρf + (1 − ϕ)ρs, where ρf > 0 is the saturating fluid density and ρs > 0 is the solid density. To derive Biot’s wave equations in Section 5, the rheology of the porous material (6) and the momentum balance (7) are combined with the dynamics of the fluid system described by Darcy’s law and the conservation of fluid mass in the pores.
Two major differences have been observed when dealing with poro-elastic media instead of elastic ones: (i) the attenuation due to wave-induced fluid flow and (ii) the presence of an additional compressional wave of the second kind (slow P-wave), which becomes a diffusive mode in the low-frequency range, cf. [38]. As observed in [45], this slow P-wave is mainly localized near the material heterogeneities or the source.
2.3 Modelling the Seismic Source
Seismic wave can be generated by different natural and artificial sources. Depending on the problem’s configuration, one can consider a single point-source, an incidence plane wave or a finite-size rupturing fault.
We can define a point-wise force f acting on a point x0 ∈Ω in the ith direction as
where ei is the unit vector of the ith Cartesian axis, δ(⋅) is the delta distribution, and f(⋅) is a function of time. The expression of f(⋅) can be selected among different waveforms. Here, we report one of the most employed one, i.e. the Ricker wavelet [75], defined as
where A0 is the wave amplitude, fp is the peak frequency of the signal and t0 is a fixed reference time.
To define a vertically incident plane wave one can consider a uniform distribution of body forces along the plane z = z0 of the form f(x,t) = f(t)eiδ(z − z0). The latter generates a displacement in the ith direction given by
where H(⋅) is the Heaviside function and c (that can be equal either to \(c_{P} = \sqrt {\lambda +2\mu /\rho }\) or \(c_{S}=\sqrt {\mu /\rho }\)) is the wave velocity, see [55]. By taking the derivative of (10) with respect to time and evaluating the result at z = z0 we can express f(t) as \(f(t) = 2 \rho c \frac {\partial \bar {u}_{i}}{\partial t}\). Finally, we introduce one of the most important seismic input for seismic wave propagation that is the so called double-couple source force. A point double-couple or moment-tensor source localized in the computational domain Ω is often adopted to simulate small local or near-regional earthquakes. Its mathematical representation is based on the seismic moment tensor m(x,t), defined in [1] as
where nF and sF denote the fault normal and the rake vector along the fault, respectively. M0(x,t) describes the time history of the moment release at x and V is the force elementary volume. The equivalent body force distribution is finally obtained through the relation f(x,t) = −∇⋅m(x,t), see [50].
3 Discrete Setting for PolyDG Methods
In this section we define the notation related to the subdivision of the computational domain Ω by means of polytopic meshes. We introduce a polytopic mesh \(\mathcal {T}_{h}\) made of general polygons (in 2d) or polyhedra (in 3d). We denote such polytopic elements by κ, define by |κ| their measure and by hκ their diameter, and set \(h = \max \limits _{\kappa \in \mathcal {T}_{h}} h_{\kappa }\). We let a polynomial degree pκ ≥ 1 be associated with each element \(\kappa \in \mathcal {T}_{h}\) and we denote by \(p_{h}:\mathcal {T}_{h}\to \mathbb {N}^{\ast }=\{n\in \mathbb {N}~|~ n\ge 1\}\) the piecewise constant function such that (ph)|κ = pκ. The discrete space is introduced as follows: \(\boldsymbol {V}_{h}=[\mathcal {P}_{p_{h}}(\mathcal {T}_{h})]^{d}\), where \(\mathcal {P}_{p_{h}}(\mathcal {T}_{h})\) is the space of piecewise polynomials in Ω of total degree less than or equal to pκ in any \(\kappa \in \mathcal {T}_{h}\).
In order to deal with polygonal and polyhedral elements, we define an interface of \(\mathcal {T}_{h}\) as the intersection of the (d − 1)-dimensional faces of any two neighboring elements of \(\mathcal {T}_{h}\). If d = 2, an interface/face is a line segment and the set of all interfaces/faces is denoted by \(\mathcal {F}_{h}\). When d = 3, an interface can be a general polygon that we assume could be further decomposed into a set of planar triangles collected in the set \(\mathcal {F}_{h}\). We decompose the faces of \(\mathcal {T}_{h}\) into the union of internal (i) and boundary (b) faces, respectively, i.e.: \(\mathcal {F}_{h}=\mathcal {F}_{h}^{i}\cup \mathcal {F}^{b}_{h}\). Moreover we further split the boundary faces as \(\mathcal {F}^{b}_{h} = \mathcal {F}^{D}_{h} \cup \mathcal {F}^{N}_{h} \cup \mathcal {F}^{A}_{h}\), meaning that on \(\mathcal {F}^{D}_{h}\) (resp. \(\mathcal {F}^{N}_{h}\) and \(\mathcal {F}^{A}_{h}\)) Dirichlet (resp. Neumann and absorbing) boundary conditions are applied.
Following [37], we next introduce the main assumption on \(\mathcal {T}_{h}\).
Definition 3.1
A mesh \(\mathcal {T}_{h}\) is said to be polytopic-regular if for any \( \kappa \in \mathcal {T}_{h}\), there exists a set of non-overlapping d-dimensional simplices contained in κ, denoted by \(\{S_{\kappa }^{F}\}_{F\subset {\partial \kappa }}\), such that for any F ⊂ ∂κ, the following condition holds:
Assumption 3.1
The sequence of meshes \(\{\mathcal {T}_{h}\}_{h}\) is assumed to be uniformly polytopic regular in the sense of Definition 3.1.
We remark that this assumption does not impose any restriction on either the number of faces per element nor their measure relative to the diameter of the element they belong to. Under Assumption 3.1, the following trace-inverse inequality holds:
see [37, Section 3.2] for the detailed proof and a complete discussion on inverse estimates. In order to avoid technicalities, we also make the following hp-local bounded variation property assumption.
Assumption 3.2
For any pair of neighboring elements \(\kappa ^{\pm }\in \mathcal {T}_{h}\), it holds \(h_{\kappa ^{+}}\lesssim h_{\kappa ^{-}}\lesssim h_{\kappa ^{+}}\) and \(\ p_{\kappa ^{+}}\lesssim p_{\kappa ^{-}}\lesssim p_{\kappa ^{+}}\).
Next, following [21], for sufficiently piecewise smooth scalar-, vector- and tensor-valued fields ψ, v and τ, respectively, we define the averages and jumps on each interior face \(F\in \mathcal {F}_{h}^{i}\) shared by the elements \(\kappa ^{\pm }\in \mathcal {T}_{h}\) as follows:
where ⊗ is the tensor product in \(\mathbb {R}^{3}\), ⋅± denotes the trace on F taken within the interior of κ±, and n± is the outward unit normal vector to ∂κ±. Accordingly, on boundary faces \(F\in \mathcal {F}_{h}^{b}\), we set 〚ψ〛 = ψn, {ψ} = ψ, 〚v〛 = v ⊗n, 〚v〛n = v ⋅n, {v} = v, {τ} = τ.
Finally, we introduced some important concepts employed for the convergence analysis of PolydG methods presented in the sequel, namely, the mesh covering \(\mathcal {T}_{\sharp }\) and the Stein extension operator \(\widetilde {\mathcal {E}}\). Indeed, the latter are used to extend standard hp-interpolation estimates on simplices to polytopal elements. We refer the reader to [16, 33, 36, 37] for all the details.
A covering \(\mathcal {T}_{\sharp }=\{\mathcal {K}_{\kappa }\}\) related to the polytopic mesh \(\mathcal {T}_{h}\) is a set of shape regular d-dimensional simplices \(\mathcal {K}_{\kappa }\) such that for each \(\kappa \in \mathcal {T}_{h}\) there exists a \(\mathcal {K}_{\kappa } \in \mathcal {T}_{\sharp }\) such that \(\kappa \subset \mathcal {K}_{\kappa }\). We suppose that there exits a covering \(\mathcal {T}_{\sharp }\) of \(\mathcal {T}_{h}\) and a positive constant CΩ, independent of the mesh parameters, such that
and \(h_{\mathcal {K}_{\kappa }} \lesssim h_{\kappa }\) for each pair \(\kappa \in \mathcal {T}_{\kappa }\) and \(\mathcal {K}_{\kappa } \in \mathcal {T}_{\sharp }\) with \(\kappa \subset \mathcal {K}_{\kappa }\). This latter assumption assures that, when the computational mesh \(\mathcal {T}_{h}\) is refined, the amount of overlap present in the covering \(\mathcal {T}_{\sharp }\) remains bounded.
For an open bounded domain \({\varSigma } \subset \mathbb {R}^{d}\) and a polytopic mesh \(\mathcal {T}_{h}\) over Σ satisfying Assumption 3.1, we can introduce the Stein extension operator \(\widetilde {\mathcal {E}}:H^{m}(\kappa )\rightarrow H^{m}(\mathbb {R}^{d})\) [84], for any \(\kappa \in \mathcal {T}_{h}\) and \(m\in \mathbb {N}^{\ast }\), such that \(\tilde {\mathcal {E}}v|_{\kappa }=v\) and \(\|\tilde {\mathcal {E}}v\|_{m,\mathbb {R}^{d}}\lesssim \|v\|_{m,\kappa }\). The corresponding vector-valued version mapping Hm(κ) onto \(\boldsymbol H^{m}(\mathbb {R}^{d})\) acts component-wise and is denoted in the same way. In what follows, for any \(\kappa \in \mathcal {T}_{h}\), we will denote by \(\mathcal {K}_{\kappa }\) the simplex belonging to \(\mathcal {T}_{\sharp }\) such that \(\kappa \subset \mathcal {K}_{\kappa }\).
3.1 Time Integration
We introduce here the time integration scheme used for the numerical simulations shown in the following sections. First, we anticipate that, fixing a suitable basis for the discrete space, all the semi-discrete PolydG formulations that we will introduce in the following can be written in the general abstract form:
where the precise definition of the unknown Xh, the right-hand side Sh, and the matrices Mh, Dh, and Ah will be given in the forthcoming sections. Assuming that Mh is invertible, we have
Then, we discretize the interval [0,T] by introducing a timestep Δt > 0, such that \(\forall \ k\in \mathbb {N}\), tk+ 1 − tk = Δt and define \({X_{h}^{k}}=X_{h}(t^{k})\) and \({Z^{k}_{h}}=\dot {X}_{h}(t^{k})\). Finally, to integrate in time (11) we apply the Newmark− β scheme defined by introducing a Taylor expansion for Xh and \(Z_{h}=\dot {X_{h}}\), respectively:
being \({\mathscr{L}}^{k}_{h}={\mathscr{L}}_{h}(t^{k}, {X^{k}_{h}}, {Z^{k}_{h}})\) and the Newmark parameters βN and γN satisfy the constraints 0 ≤ γN ≤ 1, 0 ≤ 2βN ≤ 1. The typical choices are γN = 1/2 and βN = 1/4, for which the scheme is unconditionally stable and second order accurate. We also remark that, when \({\mathscr{L}}_{h} = {\mathscr{L}}_{h}(t^{k}, {X^{k}_{h}})\), βN = 0, and γN = 1/2, the Newmark scheme (13) reduces to the leap-frog scheme which is explicit and second order accurate. We next address in detail the PolydG semi-discrete approximation of the problems we are considering.
Remark 1
We point out that, for long time integration, the Newmark− β scheme with γN = 1/2 is not well suited, as the discrete solution may be affected by oscillations. For long time integration, it is preferable to use βN ≥ (γN + 1/2)2/4 for a suitable γN > 1/2, see e.g., [73].
4 Elastic Wave Propagation in Heterogeneous Media
Hereafter, for the sake of presentation, we will consider the linear visco elastodyamics model, i.e. (4) and (3). We suppose ∂Ω = ΓD ∪ΓN and we consider homogeneous Dirichlet and Neumann boundary conditions on ΓD and ΓN, respectively. The system of equations can be recast as
The case with non homogenous Neumann conditions is treated in [17], while absorbing conditions are considered in [72]. Finally, we refer to [3, 79] for a detailed analysis of viscoelastic attenuation models. We suppose the mass density ρ and the Lamé parameters λ and μ to be strictly positive bounded functions of the space variable x, i.e. \(\rho ,\lambda ,\mu \in L^{\infty }({\varOmega })\). We also suppose the forcing term f to be regular enough, i.e., f ∈ L2((0,T];L2(Ω)) and that the initial conditions \((\boldsymbol {u}_{0}, \boldsymbol {u}_{1}) \in \boldsymbol {H}^{1}_{0,{\varGamma }_{D}}({\varOmega }) \times \boldsymbol {L}^{2}({\varOmega })\). The weak formulation of problem (14) reads as follows: for all t ∈ (0,T] find \(\boldsymbol u = \boldsymbol u(t)\in {\boldsymbol H}^{1}_{0,{\varGamma }_{D}}({\varOmega })\) such that
where for any \(\boldsymbol {u},\boldsymbol {v} \in \boldsymbol {H}^{1}_{0,{\varGamma }_{D}}({\varOmega })\) we have set
Problem (15) is well-posed and its unique solution \(\boldsymbol u \in C((0,T]; \boldsymbol {H}^{1}_{0,{\varGamma }_{D}}({\varOmega })) \cap C^{1}((0,T]; \boldsymbol {L}^{2}({\varOmega }) )\), see [74, Theorem 8-3.1].
4.1 Semi-discrete Formulation
Using the notation introduced in Section 3, we define the PolyDG semi-discretization of problem (15): for all t ∈ (0,T], find uh = uh(t) ∈Vh such that
for any vh ∈Vh, supplemented with the initial conditions \((\boldsymbol {u}_{h}(0),\partial _{t} {\boldsymbol u}_{h}(0))=(\boldsymbol {u}_{h}^{0}, \boldsymbol {u}_{h}^{1})\), where \(\boldsymbol {u}_{h}^{0}, \boldsymbol {u}_{h}^{1} \in \boldsymbol {V}_{h}\) are suitable approximations of u0 and u1, respectively. Here, we also assume the tensor \(\mathbb {D}\) and the density ρ to be element-wise constant over \(\mathcal {T}_{h}\). The bilinear form \(\mathcal {A}_{h}^{e}: \boldsymbol {V}_{h} \times \boldsymbol {V}_{h} \rightarrow \mathbb {R}\) is defined as
for all u,v ∈Vh. Here, we adopt the compact notation \((\cdot ,\cdot )_{\mathcal {T}_{h}} = {\sum }_{T\in \mathcal {T}_{h}} (\cdot ,\cdot )_{T}\) and \((\cdot ,\cdot )_{\mathcal {F}_{h}^{i} \cup \mathcal {F}_{h}^{D}}= {\sum }_{F\in \mathcal {F}_{h}^{i} \cup \mathcal {F}_{h}^{D}} (\cdot ,\cdot )_{F}\). The penalization function \(\eta :\mathcal {F}_{h}\rightarrow \mathbb {R}^{+}\) in (18) is defined face-wise as
where \(\overline {\mathbb {D}}_{\kappa }=|(\mathbb {D}|_{\kappa })^{1/2}|^{2}_{2}\) for any \(\kappa \in \mathcal {T}_{h}\) (here |⋅|2 is the operator norm induced by the l2-norm on \({\mathbb R}^{n}\), where n denotes the dimension of the space of symmetric second-order tensors, i.e., n = 3 if d = 2, n = 6 if d = 3), and σ0 is a (large enough) positive parameter at our disposal.
By fixing a basis for Vh and denoting by Uh the vector of the expansion coefficients in the chosen basis of the unknown uh, the semi-discrete formulation (17) can be written equivalently as:
where Mν denote the mass matrix scaled by the element-wise constant coefficient ν, and Ae is the stiffness matrix corresponding to the bilinear form \(\mathcal {A}^{e}(\cdot ,\cdot )\). Note that Fh is the vector representations of the linear functional (f,vh)Ω. We supplement (20) with initial conditions Uh(0) = U0 and \(\dot {\mathrm {U}}_{h}(0) = \text {U}_{1}\). Formulation (20) can be recast in the form (11)–(12) by setting Xh = Uh, Mh = Mρ, Dh = M2ρζ, \(\boldsymbol {A}_{h}= \boldsymbol A^{e} + \boldsymbol M_{\rho \zeta ^{2}}\) and Sh = Fh, cf. Section 3.1.
4.2 Stability and Convergence Results
In this section we recall the stability and convergence results for the semidiscrete PolyDG formulation (17). We refer the reader to [11] and to [10] for all the details. The results are obtained in the following energy norm
where
with \(\|\cdot \|_{\mathcal {T}_{h}}^{2} = (\cdot ,\cdot )_{\mathcal {T}_{h}}\) and \(\|\cdot \|_{\mathcal {F}_{h}^{i} \cup \mathcal {F}_{h}^{D}}^{2} = (\cdot ,\cdot )_{\mathcal {F}_{h}^{i} \cup \mathcal {F}_{h}^{D}}\).
Proposition 4.1
Let f ∈ L2((0,T];L2(Ω)). Let uh ∈ C1((0,T];Vh) be the approximate solution of (17) obtained with the stability constant σ0 defined in (19) chosen sufficiently large. Then,
where \(\|\boldsymbol u_{h}(0)\|^{2}_{\mathrm {E}} = \|\rho ^{\frac 12} {\boldsymbol u}_{1,h}\|^{2}_{{\varOmega }} + \|\rho ^{\frac 12}\zeta {\boldsymbol u}_{0,h} \|^{2}_{{\varOmega }} + \|\boldsymbol u_{0,h}\|_{\text {DG},e}^{2}\), being u0,h,u1,h ∈Vh suitable approximation of the initial conditions u0 and u1, respectively.
The proof of the previous stability estimate can be found for instance in [10, 11]. From (22) it is possible to conclude that the PolyDG approximation is dissipative. Indeed, when f = 0 (no external forces) the energy of the system at rest \(\|\boldsymbol {u_{h}^{0}}\|_{\mathrm {E}}\) is not conserved through time.
Concerning the convergence results of the PolyDG scheme we report in the following the main result. We refer the reader to [11] for the details and for the proof of the following theorem.
Theorem 4.1
Let Assumption 3.1 and Assumption 3.2 be satisfied and assume that the exact solution u of (15) is sufficiently regular. For any time t ∈ [0,T], let uh ∈Vh be the PolyDG solution of problem (17) obtained with a penalty parameter σ0 appearing in (19) sufficiently large. Then, for any time t ∈ (0,T] the following bound holds
where
with \(s_{\kappa } = \min \limits (p_{\kappa } +1, m_{\kappa })\) for all \(\kappa \in \mathcal {T}_{h}\). The hidden constant depends on the material parameters and the shape-regularity of the covering \(\mathcal {T}_{\sharp }\), but is independent of hκ, pκ.
4.3 Verification Test
We solve the wave propagation problem (14) in Ω = (0,1)2, choosing λ = μ = ρ = ζ = 1 and assuming that the exact solution u is given by
Dirichlet boundary conditions and initial conditions are set accordingly. We set the final time T = 1 and chose a time step Δt = 10− 4 of the leap-frog scheme, cf. (13). The penalty parameter σ0 appearing in (19) has been set equal to 10. We compute the discretization error by varying the polynomial degree pκ = p, for any \(\kappa \in \mathcal {T}_{h}\), and the number of polygonal elements Nel.
In Fig. 3 (left), we report the computed energy error ∥u −uh∥E at final time T as a function of the mesh size h. We retrieve the algebraic convergence proved in (23) for a polynomial degree p = 2,3,4. Next, we report the computed L2-error \(\|e_{\boldsymbol u}\|_{\boldsymbol L^{2}({\varOmega })} = \|\boldsymbol u-\boldsymbol u_{h}\|_{\boldsymbol L^{2}({\varOmega })}\) at time T obtained on a shape-regular polygonal grid (cf. Fig. 2) versus the polynomial degree p, which varies from 1 to 5, in semilogarithmic scale. We fix the number of polygonal elements as Nel = 160. In this case we observe an exponential converge in p, as shown in Fig. 3 (right).
Test case of Section 4.3. Example of computational domain having 100 polygonal elements
Test case of Section 4.3. Computed energy error as a function of the mesh size h for polynomial degree p = 2,3,4. The computed rate of convergence is also reported in the last row, cf. (23) (left). Computed L2-error as a function of the polynomial degree p in a semilogarithmic scale by fixing the number of polygonal elements as Nel = 160 (right)
5 Poro-elastic Media
In this section, we consider a poro-elastic material occupying a polyhedral domain Ωp ⊂Ω modeled by (6) and (7). We refer the reader to [15, Section 2] and [49, Chapter 5] for the derivation and analysis of the dynamic poro-elasticity problem described hereafter. The low-frequency Biot’s system [26] can be written as
where the density ρw is given by ρw = aϕ− 1ρf with tortuosity a > 1, η represents the dynamic viscosity of the fluid, k is the absolute permeability, and m denotes the Biot modulus. As in the previous section, we assume that the model coefficients \(\rho _{f}, \rho _{w}, \eta k^{-1}, m \in L^{\infty }({\varOmega }_{p})\) are strictly positive scalar fields and that the source term f, g and the initial conditions (w0,w1) are regular vector fields, namely \(\boldsymbol f,\boldsymbol g\in L^{2}((0,T];\boldsymbol L^{2}({\varOmega }_{p}))\) and \((\boldsymbol {w}_{0}, \boldsymbol {w}_{1})\in \boldsymbol {H}_{0,{\varGamma }_{pD}}(\text {div},{\varOmega }_{p})\times \boldsymbol L^{2}({\varOmega }_{p})\). The third and fourth equations in (24) correspond to the dynamic Darcy’s law and the conservation of fluid mass, respectively. For the sake of simplicity, in (24) we have also assumed that the clamped region ΓpD ⊂ ∂Ωp is impermeable and a null pore pressure condition is prescribed on the Neumann boundary ΓpN = ∂Ωp ∖ΓpD, cf. Fig. 4. We remark that more general boundary conditions can be treated up to minor modifications.
In what follows, we focus on the two-displacement formulation of the low frequency poro-elasticity problem [65], that is obtained by inserting the expression of the total stress \(\widetilde {\boldsymbol \sigma }\) and the pore pressure p in the other equations in (24). The corresponding weak formulation reads: for all t ∈ (0,T] find \((\boldsymbol u (t), \boldsymbol w (t)) \in {\boldsymbol H}^{1}_{0,{\varGamma }_{pD}}({\varOmega }_{p})\times {\boldsymbol H}_{0,{\varGamma }_{pD}}(\text {div},{\varOmega }_{p})\) such that
with \(\mathcal {A}^{e}:{\boldsymbol H}^{1}_{0,{\varGamma }_{pD}}({\varOmega }_{p})\times {\boldsymbol H}^{1}_{0,{\varGamma }_{pD}}({\varOmega }_{p})\to \mathbb {R}\) defined as the restriction to Ωp of the function in (16) and the bilinear forms \({\mathscr{M}}^{p}, \mathcal {A}^{p}\) defined as
for all \((\boldsymbol u, \boldsymbol w), (\boldsymbol v, \boldsymbol z) \in {\boldsymbol H}^{1}_{0,{\varGamma }_{pD}}({\varOmega }_{p})\times {\boldsymbol H}_{0,{\varGamma }_{pD}}(\text {div},{\varOmega }_{p})\). The well-posedness of the low-frequency poro-elasticity problem (25) has been established in [49, Section 5.2] in the framework of semigroup theory.
5.1 Semi-discrete Formulation
Proceeding as in Section 4.1, we derive the semi-discrete PolydG approximation of problem (25). We introduce a polytopic mesh \(\mathcal {T}_{h}^{p}\) of Ωp satisfying Assumptions 3.1 and 3.2 and denote by \(\mathcal {F}_{h}^{p}\) the set of faces of \(\mathcal {T}_{h}^{p}\). Here, we consider the same polynomial space for both the discrete solid displacement uh and filtration displacement wh, i.e. \(\boldsymbol u_{h},\boldsymbol w_{h}\in \boldsymbol {V_{h}^{p}}=(\mathcal {P}_{p_{h}}(\mathcal {T}_{h}^{p}))^{d}\), and we assume that all the model coefficients are piecewise constant over \(\mathcal {T}_{h}^{p}\). The PolydG semi-discrete problem consists in finding, for all t ∈ (0,T], the solution \((\boldsymbol u_{h} (t), \boldsymbol w_{h} (t)) \in \boldsymbol {V}_{h}^{p}\times \boldsymbol {V}_{h}^{p}\) such that
where \(\mathcal {A}_{h}^{e}:{\boldsymbol V}_{h}^{p}\times {\boldsymbol V}_{h}^{p}\to \mathbb {R}\) is defined as in (18) and the bilinear form \(\mathcal {A}_{h}^{p}\) defined such that
for all \(\boldsymbol w, \boldsymbol z \in {\boldsymbol V}_{h}^{p}\) and the penalization function \(\gamma \in L^{\infty }(\mathcal {F}_{h}^{p})\) is given by
where m0 is a positive user-dependent parameter. We remark that, owing to the H(div)-regularity of the filtration displacement w solving (25), the penalization term in (28) acts only on the normal component of the jumps. Problem (27) is completed with suitable initial conditions \((\boldsymbol {u}_{h}(0),\boldsymbol {w}_{h}(0),\partial _{t} {\boldsymbol u}_{h}(0), \partial _{t} {\boldsymbol w}_{h}(0))=(\boldsymbol {u}_{h}^{0}, \boldsymbol {w}_{h}^{0}, \boldsymbol {u}_{h}^{1}, \boldsymbol {w}_{h}^{1})\in {\boldsymbol V}_{h}^{p}\times {\boldsymbol V}_{h}^{p}\times {\boldsymbol V}_{h}^{p}\times {\boldsymbol V}_{h}^{p}\).
We conclude this section by observing that the algebraic representation of the semi-discrete formulation (27) is given by
with \([U_{h},W_{h},\dot {U}_{h},\dot {W}_{h}](0)=[U_{0},W_{0},U_{1},W_{1}]\) and [Fh,Gh]T corresponding to the vector representation of the right-hand side of (27). Recalling the notation introduced in Section 3.1 and setting Xh = [Uh,Wh]T, Sh = [Fh,Gh]T, and
(30) can be rewritten in the form (11).
5.2 Stability and Convergence Results
The aim of this section is to establish an a priori estimate for the solution of problem (27). First, we define for all \(\boldsymbol u, \boldsymbol w\in C^{1}([0,T];\boldsymbol {V}_{h}^{p})\) the energy function
with \(\rho _{u} = \frac {\rho _{s}(1-\phi )}2\), the norm \(\|\cdot \|_{\text {DG},e}: {\boldsymbol {V}_{h}^{p}}\to \mathbb {R}^{+}\) defined as in (21) and
One can easily check that \(\max \limits _{0\le t\le T}\| (\cdot ,\cdot )(t) \|^{2}_{\mathcal {E}}\) defines a norm on \(C^{1}([0,T];\boldsymbol {V}_{h}^{p}\times \boldsymbol {V}_{h}^{p})\), cf. [15, Remark 3.2]. We are now ready to derive the stability estimate for the PolydG semi-discretization.
Proposition 5.1
Let \(\boldsymbol f,\boldsymbol g\in L^{2}((0,T];\boldsymbol {L}^{2}({\varOmega }_{p}))\) and let \(\boldsymbol u_{h},\boldsymbol w_{h}\in C^{1}((0,T];\boldsymbol {V}_{h}^{p})\) be the solutions of (27) obtained with sufficiently large penalization parameters σ0 and m0. Let additionally assume that \(\rho _{u}^{-1}, k \eta ^{-1}\in L^{\infty }({\varOmega }_{p})\). Then, it holds
with
Proof
First, we observe that the bilinear form \({\mathscr{M}}^{p}\) is positive definite. Indeed, owing to the definition of the density functions ρ, ρu, and ρw and since \(\widetilde {a}=a-1>0\), for all (v,z)≠(0,0) one has
Furthermore, if the stability parameters σ0 and m0 are chosen sufficiently large, the bilinear forms \(\mathcal {A}^{e}_{h}\) and \(\mathcal {A}^{p}_{h}\) are coercive (see [15, Lemma A.3]), i.e., for all \(\boldsymbol v_{h}, \boldsymbol z_{h}\in {\boldsymbol V_{h}^{p}}\) it holds
Then, taking (vh,zh) = (∂tuh,∂twh) in (27) and integrating in time between 0 and t ≤ T, it is inferred that
with \(\widetilde {\mathcal {E}}_{0}={\mathscr{M}}^{p}(({\boldsymbol u_{h}^{1}}, {\boldsymbol w_{h}^{1}}), ({\boldsymbol u_{h}^{1}}, {\boldsymbol w_{h}^{1}}))+\mathcal {A}^{e}_{h}({\boldsymbol u_{h}^{0}}, {\boldsymbol u_{h}^{0}}) + \mathcal {A}^{p}_{h}(\beta {\boldsymbol u_{h}^{0}}+{\boldsymbol w_{h}^{0}}, \beta {\boldsymbol u_{h}^{0}}+{\boldsymbol w_{h}^{0}})\). Now, using (33) and (34) to infer a lower bound for the left-hand side of the previous identity and summing \(\|(\eta /k)^{\frac 12}{\boldsymbol w_{h}^{0}}\|_{{\varOmega }_{p}}^{2}\) to both sides of the resulting inequality, we obtain
where \(\mathcal {E}_{0} = \widetilde {\mathcal {E}}_{0} + \|(\eta /k)^{\frac 12}{\boldsymbol w_{h}^{0}}\|_{{\varOmega }_{p}}^{2}\) corresponds to the quantity defined in (32). Therefore, to conclude it only remains to bound the right-hand side of (35). To do so, we apply the Cauchy–Schwarz and Young inequalities to infer
and
Inserting the previous bounds into (35) and taking the maximum over t ∈ [0,T], yields the assertion. □
Remark 2
We observe that, proceeding as in [28, Lemma 7], it is possible to obtain a stability estimate for problem (27) requiring \(\mu ^{-1}\in L^{\infty }({\varOmega }_{p})\) together with \(\boldsymbol f\in H^{1}((0,T],\boldsymbol L^{2}({\varOmega }_{p}))\) instead of \(\rho _{u}^{-1}\in L^{\infty }({\varOmega }_{p})\). The key step is based on estimating the term \({{\int \limits }_{0}^{t}} (\boldsymbol f, \partial _{t} \boldsymbol u_{h})_{{\varOmega }_{p}}\) by using partial integration and the discrete Korn’s first inequality [29, Lemma 1].
For the sake of conciseness, we decide not to present here the convergence analysis for the PolydG formulation of the poro-elastic problem (27). However, an error estimate can be readily deduced from (46) below, in the case in which the exact solution on the acoustic part of the domain is null.
5.3 Verification Test
We consider problem (24) in Ωp = (− 1,0) × (0,1) and choose as exact solution
As before, Dirichlet boundary conditions and initial conditions are set accordingly. The model problem is solved on a sequence of polygonal meshes as the one shown in Fig. 5 (left), with physical parameters shown in Fig. 5 (right). The final time T has been set equal to 0.25, considering a timestep of Δt = 10− 4 for the Newmark-β scheme, γN = 1/2 and βN = 1/4, cf. (13). The penalty parameters σ0 and m0 appearing in definitions (19) and (29), respectively, have been chosen equal to 10.
Poro-elastic test case of Section 5.3. Polygonal mesh, with Nel = 100 polygons (left). Physical parameters (right)
In Fig. 6 (left) we report the computed energy error \(\|(\boldsymbol u-\boldsymbol u_{h}, \boldsymbol w-\boldsymbol w_{h}) \|_{\mathbb {E}}\), cf. (46), as a function of the mesh size h for a polynomial degree p = 2,3,4. In this case we retrieve the rate of convergence \(\mathcal {O}(h^{p})\) as proved in (46). In Fig. 6 (right) we plot the computed L2-errors for the elastic u and filtration w displacements as a function of the polynomial degree p in a semilog-scale. We fix the number of polygonal elements as Nel = 100. We observe an exponential rate of convergence since the solution (36) is analytic.
Test case of Section 5.3. Computed energy error as a function of the mesh size h for polynomial degree p = 2,3,4. The rate of convergence is also reported in the last row, cf. (46) (left). Computed L2-errors \(\|e_{\boldsymbol u}\|_{\boldsymbol L^{2}({\varOmega }_{p})} = \|\boldsymbol u-\boldsymbol u_{h}\|_{\boldsymbol L^{2}({\varOmega }_{p})}\) and \(\|e_{\boldsymbol w}\|_{\boldsymbol L^{2}({\varOmega }_{p})} = \|\boldsymbol w-\boldsymbol w_{h}\|_{\boldsymbol L^{2}({\varOmega }_{p})}\) as a function of the polynomial degree p in a semilogarithmic scale for Nel = 100 polygonal elements (right)
6 Poro-elastic-acoustic Media
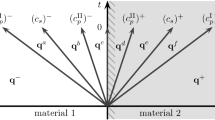
In this section, we present the PolydG discretization of the poro-elasto-acoustic interface problem. We refer the reader to [15] for the rigorous mathematical analysis of the model problem and the detailed derivation of the proposed method. In what follows, we assume that Ω is decomposed into two disjoint, polygonal/polyhedral subdomains: Ω = Ωp ∪Ωa, cf. Fig. 7. The two subdomains share part of their boundary, resulting in the interface ΓI = ∂Ωp ∩ ∂Ωa. We suppose that the interface ΓI is Lipschitz and has strictly positive measure. We set ∂Ωp = ΓpD ∪ΓpN ∪ΓI and ∂Ωa = ΓaD ∪ΓaN ∪ΓI, where the surface measures of ΓpD, ΓaD, and ΓI are assumed to be strictly positive. The outer unit normal vectors to ∂Ωp and ∂Ωa are denoted by np and na, respectively, so that np = −na on ΓI.
The subdomain Ωp represents a poro-elasto medium whose dynamical behavior is described by Biot’s equation (24). In the fluid domain Ωa, we consider an acoustic wave with constant velocity c > 0 and mass density ρa > 0 such that \(\rho _{a}, c^{-2}\in L^{\infty }({\varOmega }_{a})\). For a given source term \(h\in L^{2}((0,T]; L^{2}({\varOmega }_{a}))\), the acoustic potential φ satisfies
with \((\varphi _{0}, \varphi _{1})\in H^{1}_{0,{\varGamma }_{aD}}({\varOmega }_{a}) \times L^{2}({\varOmega }_{a})\). To close the coupled poro-elasto-acoustic problem, some interface conditions on ΓI are needed. Here, we consider physically consistent transmission conditions (see, e.g., [57] and [42]) expressing the continuity of normal stresses, continuity of pressure, and conservation of mass:
The parameter τ : ΓI → [0,1] denotes the hydraulic permeability at the interface and models different pores configurations, cf. Fig. 7. In the open pores region \(\tau ^{-1}(1)\subset {\varGamma }_{I}\) the second equation in (38) reduces to p = ρa∂tφ, while in the sealed pores subset τ− 1(0) we have ∂tw ⋅np = 0, implying that τ− 1(0) is impermeable. Finally, the imperfect pores region τ− 1((0,1)) models an intermediate state between open and sealed pores. For later use, we split the interface into two disjoint (possibly non-connected) subsets \({\varGamma }_{I} = {{\varGamma }_{I}^{s}}{\cup {\varGamma }_{I}^{o}}\), with
We remark that the first and second conditions in (38) play the role of a Neumann and a Robin-like conditions for system (24), respectively. Similarly, the third equation in (38) acts as a Neumann condition for problem (37). The existence and uniqueness of a strong solution to the poro-elasto-acoustic problem coupling (24), (37) and (38) is proved in [15, Appendix A].
In order to derive the weak formulation of the coupled problem, we introduce the function \(\zeta _{\tau }:{{\varGamma }_{I}^{o}}\to \mathbb {R}^{+}\), defined by ζτ = τ− 1(1 − τ), and the weighted space
equipped with the norm
The weak form of the problem obtained by coupling equations (24), (37) and (38) reads as: for any t ∈ (0,T], find \((\boldsymbol {u},\boldsymbol {w},\varphi )(t) \in \boldsymbol H^{1}_{0,{\varGamma }_{pD}}({\varOmega }_{p}) \times \boldsymbol {W}_{\tau } \times H^{1}_{0,{\varGamma }_{aD}}({\varOmega }_{a})\) s.t.
for all \((\boldsymbol {v},\boldsymbol {z},\psi ) \in \boldsymbol H^{1}_{0,{\varGamma }_{pD}}({\varOmega }_{p}) \times \boldsymbol {W}_{\tau } \times H^{1}_{0,{\varGamma }_{aD}}({\varOmega }_{a})\), where we have set
with \({\mathscr{M}}^{p},\mathcal {A}^{e},\mathcal {A}^{p}\) defined as in (26), (16) and (28), respectively. In (40), the bilinear form \(\mathcal {A}^{a}\) is defined such that \(\mathcal {A}^{a}(\varphi ,\psi )=(\rho _{a}\nabla \varphi ,\nabla \psi )_{{\varOmega }_{a}}\) for all \(\varphi ,\psi \in H^{1}_{0,{\varGamma }_{aD}}({\varOmega }_{a})\) and \(\langle \cdot ,\cdot \rangle _{{\varGamma }_{I}}\) denotes the \(H^{\frac 12}({\varGamma }_{I})\)-\(H^{-\frac 12}({\varGamma }_{I})\) duality product.
6.1 Semi-discrete Formulation
We decompose the polytopic regular mesh \(\mathcal {T}_{h}\) as \(\mathcal {T}_{h}=\mathcal {T}^{p}_{h}\cup \mathcal {T}^{a}_{h}\), where \(\mathcal {T}_{h}^{a}\) and \(\mathcal {T}_{h}^{p}\) are aligned with Ωa and Ωp, respectively. In a similar way, we decompose \(\mathcal {F}_{h}\) as \(\mathcal {F}_{h}=\mathcal {F}_{h}^{I} \cup \mathcal {F}_{h}^{p} \cup \mathcal {F}_{h}^{a}\), where \(\mathcal {F}_{h}^{I}=\{F\in \mathcal {F}_{h}:F\subset \partial \kappa ^{p}\cap \partial \kappa ^{a},\kappa ^{p}\in \mathcal {T}_{h}^{p},\kappa ^{a}\in \mathcal {T}_{h}^{a}\}\), and \(\mathcal {F}_{h}^{p}\) and \(\mathcal {F}_{h}^{a}\) denote the faces of \(\mathcal {T}_{h}^{p}\) and \(\mathcal {T}_{h}^{a}\), respectively, not laying on ΓI.
Remark 3
We point out that the computational grids \(\mathcal {T}^{p}_{h}\) and \(\mathcal {T}^{a}_{h}\) do not have to be conforming at the interface ΓI and can be generated independently one from the other.
The discrete spaces are selected as follows: given element-wise constant polynomial degrees \(p_{h}:\mathcal {T}_{h}^{p}\to \mathbb {N}^{\ast }\) and \(r_{h}:\mathcal {T}_{h}^{a}\to \mathbb {N}^{\ast }\), we let \(\boldsymbol {V}_{h}^{p}=[\mathcal {P}_{p_{h}}(\mathcal {T}_{h}^{p})]^{d}\) and \({V_{h}^{a}}=\mathcal {P}_{r_{h}}(\mathcal {T}_{h}^{a})\). Finally, we also assume that the coefficients ρa and c are piecewise constant over \(\mathcal {T}_{h}^{a}\) and τ is piecewise constant over \(\mathcal {F}_{h}^{I}\). Under this assumption, we can decompose the set of mesh faces belonging to ΓI as \(\mathcal {F}_{h}^{I} = \mathcal {F}_{h}^{Is}\cup \mathcal {F}_{h}^{Io}\), with \(\mathcal {F}_{h}^{Is}=\{F\in \mathcal {F}_{h}^{I}~|~ F{\subset {\varGamma }_{I}^{s}}\}\) and \(\mathcal {F}_{h}^{Io}=\mathcal {F}_{h}^{I}\setminus \mathcal {F}_{h}^{Is}\).
The semi-discrete PolydG formulation of problem (39) consists in finding, for all t ∈ (0,T], the discrete solution \((\boldsymbol {u}_{h},\boldsymbol {w}_{h},\varphi _{h})(t)\in \boldsymbol {V}_{h}^{p}\times \boldsymbol {V}_{h}^{p}\times {V_{h}^{a}}\) such that
for all discrete functions \((\boldsymbol {v}_{h},\boldsymbol {z}_{h},\psi _{h})\in \boldsymbol {V}_{h}^{p}\times \boldsymbol {V}_{h}^{p}\times {V_{h}^{a}}\). As initial conditions we take the L2-orthogonal projections onto \((\boldsymbol {V}_{h}^{p}\times \boldsymbol {V}_{h}^{p}\times {V_{h}^{a}})^{2}\) of the initial data (u0,w0,φ0,u1,w1,φ1). For all \(\boldsymbol {u},\boldsymbol {v},\boldsymbol {w},\boldsymbol {z}\in \boldsymbol {V}_{h}^{p}\) and \(\varphi ,\psi \in {V_{h}^{a}}\), the bilinear forms \(\mathcal {A}_{h}\) and \(\mathcal {C}_{h}\) appearing in (41) are given by
with \(\mathcal {A}_{h}^{e}:{\boldsymbol V}_{h}^{p}\times {\boldsymbol V}_{h}^{p}\to \mathbb {R}\) defined as in (18) and
Notice that the bilinear form \(\widetilde {\mathcal {A}}_{h}^{p}\) is different from \(\mathcal {A}_{h}^{p}\) defined in (28). Indeed, the definition of \(\widetilde {\mathcal {A}}_{h}^{p}\) in (42) also takes into account the essential condition z ⋅np = 0 on \({{\varGamma }_{I}^{s}}\) embedded in the definition of the functional space Wτ. The stabilization function \(\chi \in L^{\infty }(\mathcal {F}_{h}^{a})\) is defined such that
with ρ0 > 0 being a user-dependent parameter.
Denoting by (Uh, Wh, Φh) the vector of the coefficients of (uh,wh,φh) in the chosen basis for \({\boldsymbol V_{h}^{p}}\times {\boldsymbol V_{h}^{p}} \times {V_{h}^{a}}\), the algebraic form of problem (41) reads:
with initial conditions (Uh,Wh,Φh)(0) = (U0,W0,Φ0) and \((\dot {U}_{h},\dot {W}_{h},\dot {\Phi }_{h})(0)=(U_{1},W_{1},{\Phi }_{1})\). With the notation introduced in Section 3.1, problem (44) can be rewritten in the form of (12) by setting Xh = [Uh,Wh,Φh]T, Sh = [Fh,Gh,Hh]T, and
6.2 Stability and Convergence Results
In this section, we present the main stability and convergence results proved in [15]. First, we introduce the energy norm defined such that, for all \((\boldsymbol u, \boldsymbol w,\varphi )\in C^{1}([0,T];\boldsymbol {V}_{h}^{p}\times \boldsymbol {V}_{h}^{p}\times {V_{h}^{a}})\),
with \(\|\cdot \|_{\mathcal {E}}\) defined in (31) and \(\|\cdot \|_{\text {DG},a}:{V_{h}^{a}}\to \mathbb {R}^{+}\) given by
The stability of the semi-discrete PolydG problem (41) is a consequence of Proposition 6.1 below, which also implies that the formulation is dissipative. Indeed, in the case of null external source terms, it follows from estimate (45) that \(\|(\boldsymbol u_{h},\boldsymbol w_{h},\varphi _{h})(t)\|_{\mathbb {E}} \lesssim \|(\boldsymbol u_{h},\boldsymbol w_{h},\varphi _{h})(0)\|_{\mathbb {E}}\) for any t > 0. The proof of the following result is based on taking \((\boldsymbol {v}_{h},\boldsymbol {z}_{h},\psi _{h})=(\partial _{t}{\boldsymbol {u}}_{h},\partial _{t}{\boldsymbol {w}}_{h},\partial _{t}{\varphi }_{h}) \in \boldsymbol {V}_{h}^{p}\times \boldsymbol {V}_{h}^{p}\times {V_{h}^{a}}\) in (41), using the skew-symmetry of the coupling terms, and then reasoning as in Proposition 5.1 (see [15, Theorem 3.4] for the details).
Proposition 6.1
For sufficiently large penalty parameters σ0, m0, ρ0 and for any t ∈ (0,T], the solution \((\boldsymbol u_{h},\boldsymbol w_{h},\varphi _{h})(t)\in \boldsymbol {V}_{h}^{p}\times \boldsymbol {V}_{h}^{p}\times {V_{h}^{a}}\) of (41) satisfies
with hidden constant depending on time t and on the material properties, but independent of the interface parameter τ.
In what follows, we report the main result concerning the error analysis of the PolydG discretization (41). To infer the error estimate of Theorem 6.1 below, an additional assumption on the interface permeability τ is required.
Assumption 6.1
For each \(F\in \mathcal {F}_{h}^{Io}\) and \(\kappa \in \mathcal {T}_{h}^{p}\) such that \(F{\subset \partial \kappa \cap {\varGamma }_{I}^{o}}\), it holds \((\zeta _{\tau })_{|F}=(\frac {1-\tau }\tau )_{|F} \lesssim \frac {p_{p,\kappa }^{2}}{h_{\kappa }}\), with hidden constant independent of τ.
We remark that the previous assumption is used only for establishing the error estimate below but, according to our observation, it is not needed in practical applications. We refer the reader to [15, Theorem 4.3] for the detailed proof of the following result.
Theorem 6.1
Let Assumptions 3.1, 3.2, and 6.1 be satisfied and assume that the solution (u,w,φ) of the weak formulation (25) is sufficiently regular. For any time t ∈ [0,T], let \((\boldsymbol u_{h},\boldsymbol w_{h},\varphi _{h})(t)\in \boldsymbol {V}_{h}^{p}\times \boldsymbol {V}_{h}^{p}\times {V_{h}^{a}}\) be the PolydG solution of problem (41) obtained with sufficiently large penalization parameters σ0,m0 and ρ0. Then, for any time t ∈ (0,T], the discretization error E(t) = (u −uh,w −wh,φ − φh)(t) satisfies
where
with \(s_{\kappa } = \min \limits (p_{\kappa } +1, m_{\kappa })\) and \(q_{\kappa } = \min \limits (r_{\kappa } +1, l_{\kappa })\) for all \(\kappa \in \mathcal {T}_{h}\). The hidden constant depends on time t, the material properties, and the shape-regularity of the covering \(\mathcal {T}_{\sharp }\), but is independent of the discretization parameters and of τ.
6.3 Verification Test
As a verification test case, we study the poro-elasto-acoustic problem coupling (24) and (37) with the interface conditions (38) in the domain Ω = Ωp ∪Ωa = (− 1,1) × (0,1). We consider a sequence of polygonal meshes as the one shown in Fig. 8, the physical parameters listed in Fig. 5 (right) and c = ρa = 1. As exact solution we consider (36) in Ωp and
in Ωa in order to have a null pressure in the whole poro-elastic domain. Dirichlet and initial conditions are set accordingly. We remark that with this choice the interface coupling conditions are null on ΓI. For the following test cases we consider τ = 1 (open pores) at the interface, however similar results can be obtained with τ ∈ [0,1), cf. [15]. We fix the T = 0.25 and consider a time step Δt = 10− 4 for the Newmark-β scheme, γN = 1/2 and βN = 1/4, cf. (13). Penalty parameters σ0 and m0 in Ωp as well as ρ0 ∈Ωa are set equal to 10, cf. (19), (29) and (43), respectively.
Test case of Section 6.3. Polygonal mesh with Nel = 100 elements
Finally, in Fig. 9 (left) we report the computed energy errors as a function of the the mesh-size h, for the p = 2,3,4. Consistently with (46) the errors decays proportionally to hp. In Fig. 9 (right) we plot in a semilog-scale the computed L2-norms of the error fixing a computational mesh of Nel = 100 polygons and varying the polynomial degree p = 1,2,…,5. An exponential decay of the error is clearly attained.
Test case of Section 6.3. Computed energy error as a function of the mesh size h for polynomial degree p = 2,3,4. The rate of convergence is reported in the last row, cf. (46) (left). Computed L2-errors \(\|e_{\boldsymbol u}\|_{\boldsymbol L^{2}({\varOmega }_{p})} = \|\boldsymbol u-\boldsymbol u_{h}\|_{\boldsymbol L^{2}({\varOmega }_{p})}\), \(\|e_{\boldsymbol w}\|_{\boldsymbol L^{2}({\varOmega }_{p})} = \|\boldsymbol w-\boldsymbol w_{h}\|_{\boldsymbol L^{2}({\varOmega }_{p})}\) and \(\|e_{\varphi }\|_{L^{2}({\varOmega }_{a})} = \|\varphi -\varphi _{h}\|_{ L^{2}({\varOmega }_{a})}\) as a function of the polynomial degree p in a semilogarithmic scale with fixed the number of polygonal elements as Nel = 100 (right)
7 Examples of Physical Interest
7.1 Two Layered Media
In this section we consider a wave propagation problem in heterogeneous media taken from [68]. The aim of this test is to show how different assumptions on the model can determine and change the behavior of the wave propagation.
The domain of interest is Ω = (0,4.8)2 km2 and consists of two layers as depicted in Fig. 10. In the first case (a) the layers are perfectly elastic, cf. Table 1, while in the second case (b) the layers are assumed to be poro-elastic, cf. Table 2. A point-wise source f, cf. (8), acting in the y − direction is located in the upper part of the domain at point x = (2.4,2.7) km. The time evolution of the latter is given by a Ricker-wavelet (9) with amplitude A0 = 1 m, time-shift t0 = 0.3 s and peak-frequency fp = 5 Hz. For both models (a) and (b) we use a polygonal mesh with characteristic size h = 102 and a polynomial degree p = 3. We set homogeneous Dirichlet conditions on the boundary and use null initial conditions. To integrate in time model (a) we chose the leap-frog scheme while for model (b) the Newmark-β scheme with parameters βN and γN as in the previous section. We fix the final time T = 1 s and chose Δt = 10− 3 s.
Test case of Section 7.1. Computational domain: the location of the point-source force is superimposed in red
In Fig. 11 we report selected snapshots of the computed magnitude of the velocity field |∂tuh(t)| for models (a) and (b). As expected, the propagation of the wave in the elastic domain is regular and refraction phenomena are not very evident (due to a low contrast between the wave speeds). On the contrary, when porous media are accounted for, the refraction effects are more pronounced. This is in agreement with the findings in [68].
Test case of Section 7.1. Computed velocity field |∂tuh(t)| at the time instants t = 0.3 s (left), t = 0.6 s (center) and t = 1 s (right) for elastic model (a) (top) and poro-elastic model (b) (bottom)
7.2 Wave Propagation in Layered Poro-elastic-acoustic Media
As a first test case for this section, we consider a model with an acoustic layer on top of a homogeneous poro-elastic layer. The computational domain is the same as the one reported in Fig. 10. The properties of the porous medium are summarized in Table 3, while for the acoustic medium we choose ρa = 1020 [kg/m3] and c = 1500 [m/s]. Boundary and initial conditions have been set equal to zero both for the poro-elastic and the acoustic domain. Forcing terms are null in Ωp, while in Ωa we consider a vertical point source of the form (8) applied in x0 = (2400,2920) m, having a Ricker-wavelet time variation (9) with \(A_{0} = 10^{8}~[\text {Hz~m}^{3}]\), fp = 5 [Hz] and t0 = 0.5 s. We place one receiver at x1 = (2800,2940) m in the acoustic domain and a second receiver at x2 = (2450,2320) m in the poro-elastic domain. For the numerical discretization we use a polygonal mesh with characteristic size h = 102, as in the previous test case, and a polynomial degree p = 4. Time integration is performed by employing the Newmark-β scheme with parameters βN and γN as in the previous example. We fix the final time T = 2 s and chose Δt = 10− 2 s. The numerical results are compared with a reference solution obtained through the Cagniard-de Hoop method implemented in the open source software https://gitlab.inria.fr/jdiaz/gar6more2d, [46]. Figure 12 shows a very good agreement between the two different solutions, in particular as concerns the phase of the waves. The wave peaks seem to be slightly underestimated by the PolydG discretization, but in general, the comparison turns out to be satisfactory.
As a final test cases we consider the domain reproduced in Fig. 13 where an acoustic layer is in contact with a heterogeneous poro-elastic body.
Test case of Section 7.2. Computational domain. Location of the acoustic sources are also superimposed. A zoom of the non-conforming polygonal mesh is shown on the right
For the acoustic domain we set \(\rho _{a}=1500~[\text {kg/m}^{3}]\) and c = 1000 [m/s]. Physical parameters for the poro-elastic domain are chosen as in Table 2 where, for this case, the property of the former “Lower Layer” are assigned to the first poro-elastic subdomain, while those of the former “Upper Layer” to the second poro-elastic subdomain, cf. Fig. 13. In this numerical example we chose the dynamic viscosity η equal to 0.001. Boundary and initial conditions have been set equal to zero both for the poro-elastic and the acoustic domain. Forcing terms are null in Ωp, while in Ωa we consider a force of the form h = r(x,y)q(t), where q is a Ricker wavelet of the form (9) with \(A_{0} = 1~[\text {Hz~m}^{3}]\), \(\beta _{p} = 39.4784~[\text {Hz}^{2}]\) and t0 = 0.75 s. The function r(x,y) is defined as r(x,y) = 1, if \((x,y) \in \bigcup _{i=1}^{4} B({\boldsymbol x}_{i},R)\), while r(x,y) = 0, otherwise, where B(xi,R) is the circle centered in xi and with radius R. Here, we set x1 = (13097,8868) m, x2 = (16673,8868) m, x3 = (27079,8868) m, x4 = (29324,8868) m and R = 100 m. Notice that, the support of the function r(x,y) has been reported in Fig. 13, superimposed with a sample of the computational mesh employed.
Simulations have been carried out by considering: a non-conforming mesh consisting in N = 11270 polygons, subdivided into Na = 4208 and Np = 7062 polygons for the acoustic and poro-elastic domain, respectively; a Newmark scheme with time step Δt = 10− 2 s and γN = 1/2 and βN = 1/4 in a time interval [0,4] s; a polynomial degree pκ = rκ = p = 3. In Fig. 14, we show the computed pressure ph considering the interface permeability τ = 1. The latter value models an open pores condition at the interface, cf. (38). We remark that ph = ρa∂tφh in the acoustic domain while ph = −m(β∇⋅uh + ∇⋅wh) in the poro-elastic one. As one can see, the pressure wave correctly propagates from the acoustic domain to the poro-elastic one: the continuity at the interface boundary can be appreciated. Finally, we note how the second porous layer (sound absorbing material) produces a damping of the pressure field.
Test case of Section 7.2. Computed pressure ph in the poro-elastic-acoustic domain at four time instants (from up to down t = 1, 2, 3, 3.8s), with Δt = 10− 2 s
8 Conclusions
In this work we have presented a review of the development of PolyDG methods for multiphysics wave propagation phenomena in elastic, poro-elastic and poro-elasto-acoustic media.
After having recalled the theoretical background of the analysis of PolyDG methods we analysed the well-posedness and stability of different numerical formulations and proved hp-version a priori error estimates for the semi-discrete scheme. Time integration of the latter is obtained based on employing the leap-frog or Newmark methods. Numerical experiments have been designed not only to verify the theoretical error bounds but also to demonstrate the flexibility in the process of mesh design offered by polytopic elements. In this respect, numerical tests of physical interest have been also discussed.
To conclude, PolyDG methods allow a robust and flexible numerical discretization that can be successfully applied to wave propagation problems. Future developments in this direction include the study of multi-physics problems such as fluid-structure (with poro-elastic or thermo-elastic structure) interaction problems (we refer, e.g., to [9, 88] for preliminary results) as well as the exploitation of algorithms to design agglomeration-based multigrid methods and preconditioners for the efficient iterative solution of the (linear) system of equations stemming from PolyDG discretizations (see [18,19,20, 30, 31] for seminal results).
References
Aki, K., Richards, P. G.: Quantitative Seismology vol. 1. Sausalito CA: University Science Books, United States (2002)
Ambartsumyan, I., Khattatov, E., Yotov, I., Zunino, P.: A Lagrange multiplier method for a Stokes–Biot fluid–poroelastic structure interaction model. Numer. Math. 140, 513–553 (2018)
Antonietti, P. F., Ferroni, A., Mazzieri, I., Paolucci, R., Quarteroni, A., Smerzini, C., Stupazzini, M.: Numerical modeling of seismic waves by discontinuous spectral element methods. ESAIM Proc. Surveys 61, 1–37 (2018)
Antonietti, P. F., Brezzi, F., Marini, L. D.: Bubble stabilization of discontinuous Galerkin methods. Comput. Methods Appl. Mech. Eng. 198, 1651–1659 (2009)
Antonietti, P. F., Giani, S., Houston, P.: hp-version composite Discontinuous Galerkin methods for elliptic problems on complicated domains. SIAM J. Sci. Comput. 35, 1417–1439 (2013)
Antonietti, P. F., Facciolà, C., Russo, A., Verani, M.: Discontinuous Galerkin approximation of flows in fractured porous media on polytopic grids. SIAM J. Sci. Comput. 41, 109–138 (2019)
Antonietti, P. F., Facciolà, C., Verani, M.: Unified analysis of discontinuous Galerkin approximations of flows in fractured porous media on polygonal and polyhedral grids. Math. Eng. 2, 340–385 (2020). https://doi.org/10.3934/mine.2020017
Antonietti, P. F., Facciolà, C., Verani, M.: Polytopic discontinuous Galerkin methods for the numerical modelling of flow in porous media with networks of intersecting fractures. Computers & Mathematics with Applications (2021)
Antonietti, P. F., Verani, M., Vergara, C., Zonca, S.: Numerical solution of fluid-structure interaction problems by means of a high order Discontinuous Galerkin method on polygonal grids. Finite Elem. Anal. Des. 159, 1–14 (2019)
Antonietti, P. F., Facciolà, C., Houston, P., Mazzieri, I., Pennesi, G., Verani, M.: High-order discontinuous Galerkin methods on polyhedral grids for geophysical applications: Seismic wave propagation and fractured reservoir simulations. In: Di Pietro, D.A., Formaggia, L., Masson, R. (eds.) Polyhedral Methods in Geosciences, pp. 159–225. Springer, Cham (2021)
Antonietti, P. F., Mazzieri, I.: High-order Discontinuous Galerkin methods for the elastodynamics equation on polygonal and polyhedral meshes. Comput. Methods Appl. Mech. Eng. 342, 414–437 (2018)
Antonietti, P. F., Mazzieri, I., Muhr, M., Nikolić, V., Wohlmuth, B.: A high-order discontinuous Galerkin method for nonlinear sound waves. J. Comput. Phys. 415, 109484 (2020)
Antonietti, P. F., Bonaldi, F., Mazzieri, I.: A high-order discontinuous Galerkin approach to the elasto-acoustic problem. Comput. Methods Appl. Mech. Eng. 358, 112634 (2020)
Antonietti, P. F., Bonaldi, F., Mazzieri, I.: Simulation of three-dimensional elastoacoustic wave propagation based on a Discontinuous Galerkin Spectral Element Method. Int. J. Numer. Methods Eng. 121, 2206–2226 (2020)
Antonietti, P. F., Botti, M., Mazzieri, I., Nati Poltri, S.: A high-order discontinuous Galerkin method for the poro-elasto-acoustic problem on polygonal and polyhedral grids. SIAM J. Sci. Comput. 44, 1–28 (2022)
Antonietti, P.F., Cangiani, A., Collis, J., Dong, Z., Georgoulis, E.H., Giani, S., Houston, P.: Review of Discontinuous Galerkin finite element methods for partial differential equations on complicated domains. In: Barrenechea, G.R., et al. (eds.) Building Bridges: Connections and Challenges in Modern Approaches to Numerical Partial Differential Equations. Lecture Notes in Computational Science and Engineering, vol. 114, pp. 281–310. Springer, Cham (2016)
Antonietti, P. F., Ayuso de Dios, B., Mazzieri, I., Quarteroni, A.: Stability analysis of discontinuous Galerkin approximations to the elastodynamics problem. J. Sci. Comput. 68, 143–170 (2016)
Antonietti, P. F., Houston, P., Hu, X., Sarti, M., Verani, M.: Multigrid algorithms for hp-version interior penalty discontinuous Galerkin methods on polygonal and polyhedral meshes. Calcolo 54, 1169–1198 (2017)
Antonietti, P. F., Pennesi, G.: V-cycle multigrid algorithms for discontinuous Galerkin methods on non-nested polytopic meshes. J. Sci. Comput. 78, 625–652 (2019)
Antonietti, P. F., Houston, P., Pennesi, G., Süli, E.: An agglomeration-based massively parallel non-overlapping additive Schwarz preconditioner for high-order discontinuous Galerkin methods on polytopic grids. Math. Comput. 89, 2047–2083 (2020)
Arnold, D.N., Brezzi, F., Cockburn, B., Marini, L.D.: Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39, 1749–1779 (2002)
Bassi, F., Botti, L., Colombo, A., Di Pietro, D. A., Tesini, P.: On the flexibility of agglomeration based physical space discontinuous Galerkin discretizations. J. Comput. Phys. 231, 45–65 (2012)
Bécache, E., Givoli, D., Hagstrom, T.: High-order absorbing boundary conditions for anisotropic and convective wave equations. J. Comput. Phys. 229, 1099–1129 (2010)
Bermúdez, A., Rodríguez, R., Santamarina, D.: Finite element approximation of a displacement formulation for time-domain elastoacoustic vibrations. J. Comput. Appl. Math. 152, 17–34 (2003)
Bielak, J., Ghattas, O., Kim, E. -J.: Parallel octree-based finite element method for large-scale earthquake ground motion simulation. Comput. Model. Eng. Sci. 10, 99–112 (2005)
Biot, M. A.: Theory of propagation of elastic waves in a fluid-saturated porous solid. i. Low-frequency range. J. Acoust. Soc. Am. 28, 168–178 (1956)
Biot, M. A.: General theory of three-dimensional consolidation. J. Appl. Phys. 12, 155–164 (1941)
Boffi, D., Botti, M., Di Pietro, D. A.: A nonconforming high-order method for the Biot problem on general meshes. SIAM J. Sci. Comput. 38, 1508–1537 (2016)
Botti, M., Di Pietro, D. A., Guglielmana, A.: A low-order nonconforming method for linear elasticity on general meshes. Comput. Methods Appl. Mech. Eng. 354, 96–118 (2019)
Botti, L., Colombo, A., Bassi, F.: h-multigrid agglomeration based solution strategies for discontinuous Galerkin discretizations of incompressible flow problems. J. Comput. Phys. 347, 382–415 (2017)
Botti, L., Colombo, A., Crivellini, A., Franciolini, M.: {h–p–hp}-multilevel discontinuous Galerkin solution strategies for elliptic operators. Int. J. Comput. Fluid Dyn. 33, 362–370 (2019)
Breuer, A., Heinecke, A., Cui, Y.: EDGE: Extreme scale fused seismic simulations with the discontinuous Galerkin method. In: Kunkel, J.M., et al. (eds.) High Performance Computing, pp. 41–60. Springer, Cham (2017)
Cangiani, A., Georgoulis, E. H., Houston, P.: hp-version discontinuous Galerkin methods on polygonal and polyhedral meshes. Math. Models Methods Appl. Sci. 24, 2009–2041 (2014)
Cangiani, A., Dong, Z., Georgoulis, E. H., Houston, P.: hp-version discontinuous Galerkin methods for advection-diffusion-reaction problems on polytopic meshes. ESAIM Math. Model. Numer. Anal. 50, 699–725 (2016)
Cangiani, A., Dong, P., Georgoulis, E.H.: hp-Version discontinuous Galerkin methods on essentially arbitrarily-shaped elements. Math. Comput. 91, 1–35 (2022)
Cangiani, A., Dong, Z., Georgoulis, E.H.: hp-version space-time discontinuous Galerkin methods for parabolic problems on prismatic meshes. SIAM J. Sci. Comput. 39, 1251–1279 (2017)
Cangiani, A., Dong, Z., Georgoulis, E. H., Houston, P.: Hp-Version Discontinuous Galerkin Methods on Polytopic Meshes. SpringerBriefs in Mathematics. Springer, Switzerland (2017)
Carcione, J. M.: Wave Fields in Real Media, 3rd edn. Handbook of Geophysical Exploration, vol. 38. Elsevier Science, Oxford (2014)
Castagnede, B., Aknine, A., Melon, M., Depollier, C.: Ultrasonic characterization of the anisotropic behavior of air-saturated porous materials. Ultrasonics 36, 323–341 (1998)
Chaljub, E., Maufroy, E., Moczo, P., Kristek, J., Hollender, F., Bard, P. -Y., Priolo, E., Klin, P., de Martin, F., Zhang, Z., Zhang, W., Chen, X.: 3-D numerical simulations of earthquake ground motion in sedimentary basins: testing accuracy through stringent models. Geophys. J. Int. 201, 90–111 (2015)
Chiavassa, G., Lombard, B.: Wave propagation across acoustic/Biot’s media: A finite-difference method. Commun. Comput. Phys. 13, 985–1012 (2013)
Chiavassa, G., Lombard, B.: Time domain numerical modeling of wave propagation in 2d heterogeneous porous media. J. Comput. Phys. 230, 5288–5309 (2011)
Congreve, S., Houston, P.: Two-grid hp-DGFEMs on agglomerated coarse meshes. PAMM 19, 201900175 (2019)
De Basabe, J. D., Sen, M. K., Wheeler, M. F.: The interior penalty discontinuous Galerkin method for elastic wave propagation: grid dispersion. Geophys. J. Int. 175, 83–93 (2008)
de la Puente, J., Dumbser, M., Käser, M., Igel, H.: Discontinuous Galerkin methods for wave propagation in poroelastic media. Geophysics 73, 77–97 (2008)
Diaz, J., Ezziani, A.: Analytical solution for waves propagation in hetero- geneous acoustic/porous media part i: the 2d case. Commun. Comput. Phys. 7, 171–194 (2010)
Dumbser, M., Käser, M., Toro, E. F.: An arbitrary high-order Discontinuous Galerkin method for elastic waves on unstructured meshes-V. Local time stepping and p-adaptivity. Geophys. J. Int. 171, 695–717 (2007)
Duru, K., Rannabauer, L., Gabriel, A. -A., Kreiss, G., Bader, M.: A stable discontinuous Galerkin method for the perfectly matched layer for elastodynamics in first order form. Numer. Math. 146, 729–782 (2020)
Ezziani, A.: Modélisation Mathématique et numérique de la propagation d’ondes dans les milieux viscoélastiques et poroélastiques. Theses, ENSTA ParisTech. https://pastel.archives-ouvertes.fr/tel-00009179 (2005)
Faccioli, E., Maggio, F., Paolucci, R.: Quarteroni, A.: 2D and 3D elastic wave propagation by a pseudo-spectral domain decomposition method. J. Seismol. 1, 237–251 (1997)
Ferroni, A., Antonietti, P. F., Mazzieri, I., Quarteroni, A.: Dispersion- dissipation analysis of 3-D continuous and discontinuous spectral element methods for the elastodynamics equation. Geophys. J. Int. 211, 1554–1574 (2017)
Flemisch, B., Kaltenbacher, M., Wohlmuth, B.: Elasto-acoustic and acoustic-acoustic coupling on non-matching grids. Int. J. Numer. Methods Eng. 67, 1791–1810 (2006)
Flemisch, B., Kaltenbacher, M., Triebenbacher, S., Wohlmuth, B.: The equivalence of standard and mixed finite element methods in applications to elasto-acoustic interaction. SIAM J. Sci. Comput. 32, 1980–2006 (2010)
Galvez, P., Ampuero, J. -P., Dalguer, L. A., Somala, S. N., Nissen-Meyer, T.: Dynamic earthquake rupture modelled with an unstructured 3-D spectral element method applied to the 2011 M9 Tohoku earthquake. Geophys. J. Int. 198, 1222–1240 (2014)
Graff, K. F.: Wave Motion in Elastic Solids. Courier Corporation, United States (1975)
Grote, M. J., Schneebeli, A., Schötzau, D.: Discontinuous Galerkin finite element method for the wave equation. SIAM J. Numer. Anal. 44, 2408–2431 (2006)
Gurevich, B., Schoenberg, M.: Interface conditions for Biot’s equations of poroelasticity. J. Acoust. Soc. Am. 105, 2585–2589 (1999)
Haire, T. J., Langton, C. M.: Biot theory: a review of its application to ultrasound propagation through cancellous bone. Bone 24, 291–295 (1999)
Karamanou, M., Shaw, S., Warby, M. K., Whiteman, J. R.: Models, algorithms and error estimation for computational viscoelasticity. Comput. Methods Appl. Mech. Eng. 194, 245–265 (2005). https://doi.org/10.1016/j.cma.2004.05.013
Komatitsch, D., Liu, Q., Tromp, J., Süss, P., Stidham, C., Shaw, J. H.: Simulations of ground motion in the Los Angeles basin based upon the spectral-element method. Bull. Seismol. Soc. Am. 94, 187–206 (2004)
Komatitsch, D., Tromp, J.: Spectral-element simulations of global seismic wave propagation-I. Validation. Geophys. J. Int. 149, 390–412 (2002)
Kosloff, R., Kosloff, D.: Absorbing boundaries for wave propagation problems. J. Comput. Phys. 63, 363–376 (1986)
Krishnan, B., Divyadev, M., Raja, S., Venkataramana, K.: Structural and vibroacoustic analysis of aircraft fuselage section with passive noise reducing materials: a material performance study. In: Proceedings of the 4th International Engineering Symposium (2015)
Lombard, B., Piraux, J.: Numerical treatment of two-dimensional interfaces for acoustic and elastic waves. J. Comput. Phys. 195, 90–116 (2004)
Matuszyk, P. J., Demkowicz, L. F.: Solution of coupled poroelastic/acoustic/elastic wave propagation problems using automatic hp-adaptivity. Comput. Methods Appl. Mech. Eng. 281, 54–80 (2014)
McCallen, D., Petersson, A., Rodgers, A., Pitarka, A., Miah, M., Petrone, F., Sjogreen, B., Abrahamson, N., Tang, H.: EQSIM—A multidisciplinary framework for fault-to-structure earthquake simulations on exascale computers part i: Computational models and workflow. Earthq. Spectra 37, 707–735 (2021)
Moczo, P., Kristek, J., Gális, M.: The Finite-Difference Modelling of Earthquake Motions: Waves and Ruptures. Cambridge University Press, United Kingdom (2014)
Morency, C., Tromp, J.: Spectral-element simulations of wave propagation in porous media. Geophys. J. Int. 175, 301–345 (2008)
Morozov, I. B.: Geometrical attenuation, frequency dependence of q, and the absorption band problem. Geophys. J. Int. 175, 239–252 (2008)
Pelties, C., Puente, J., Ampuero, J. -P., Brietzke, G. B., Käser, M.: Three-dimensional dynamic rupture simulation with a high-order discontinuous Galerkin method on unstructured tetrahedral meshes. J. Geophys. Res Solid Earth 117, B02309 (2012)
Pitarka, A., Akinci, A., De Gori, P., Buttinelli, M.: Deterministic 3D ground-motion simulations (0–5 Hz) and surface topography effects of the 30 October 2016 Mw 6.5 Norcia, Italy, Earthquake. Bull. Seismol. Soc. Am. 112, 262–286 (2022)
Quarteroni, A., Tagliani, A., Zampieri, E.: Generalized Galerkin approximations of elastic waves with absorbing boundary conditions. Comput. Methods Appl. Mech. Eng. 163, 323–341 (1998)
Quarteroni, A., Valli, A.: Numerical Approximation of Partial Differential Equations. Springer Series in Computational Mathematics, vol. 23. Springer Berlin, Heidelberg (1994)
Raviart, P. -A., Thomas, J. -M.: Introduction à L’Analyse Numérique Des Équations Aux Dérivées Partielles. Masson, France (1983)
Ricker, N.: The form and laws of propagation of seismic wavelets. Geophysics 18, 10–40 (1953)
Rivière, B., Wheeler, M. F.: Discontinuous finite element methods for acoustic and elastic wave problems. Contemp. Math. 329, 271–282 (2003)
Rivière, B. M., Shaw, S., Whiteman, J. R.: Discontinuous Galerkin finite element methods for dynamic linear solid viscoelasticity problems. Numer. Methods Partial Differ. Equ. 23, 1149–1166 (2007). https://doi.org/10.1002/num.20215
Rivière, B., Shaw, S., Wheeler, M. F., Whiteman, J. R.: Discontinuous Galerkin finite element methods for linear elasticity and quasistatic linear viscoelasticity. Numer. Math. 95, 347–376 (2003). https://doi.org/10.1007/s002110200394
Rivière, B., Shaw, S., Whiteman, J. R.: Discontinuous Galerkin finite element methods for dynamic linear solid viscoelasticity problems. Numer. Methods Partial Differ. Equ. 23, 1149–1166 (2007)
Rockafellar, R. T.: Lagrange multipliers and optimality. SIAM review 35, 183–238 (1993)
Shaw, S.: An a priori error estimate for a temporally discontinuous Galerkin space–time finite element method for linear elasto- and visco-dynamics. Comput. Methods Appl. Mech. Eng. 351, 1–19 (2019). 10.1016/j.cma.2019.03.025
Sidler, R., Carcione, J. M., Holliger, K.: Simulation of surface waves in porous media. Geophys. J. Int. 183, 820–832 (2010)
Smeulders, D. M. J.: On Wave Propagation in Saturated and Partially Saturated Porous Media. PhD thesis, Citeseer (1992)
Stein, E. M.: Singular Integrals and Differentiability Properties of Functions, vol. 2. Princeton University Press, United States (1970)
Stupazzini, M., Paolucci, R., Igel, H.: Near-fault earthquake ground-motion simulation in the Grenoble valley by a high-performance spectral element code. Bull. Seismol. Soc. Am. 99, 286–301 (2009)
Tavelli, M., Dumbser, M.: Arbitrary high order accurate space-time discontinuous Galerkin finite element schemes on staggered unstructured meshes for linear elasticity. J. Comput. Phys. 366, 386–414 (2018)
Triebenbacher, S., Kaltenbacher, M., Wohlmuth, B., Flemisch, B.: Applications of the mortar finite element method in vibroacoustics and flow induced noise computations. Acta Acust. united Acust. 96, 536–553 (2010)
Zonca, S., Antonietti, P.F., Vergara, C.: A polygonal discontinuous Galerkin formulation for contact mechanics in fluid-structure interaction problems. Commun. Computat. Phys. 30, 1–33 (2021)
Funding
Open access funding provided by Politecnico di Milano within the CRUI-CARE Agreement. This work has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 896616 (project PDGeoFF: Polyhedral Discretisation Methods for Geomechanical Simulation of Faults and Fractures in Poroelastic Media). The authors are members of the INdAM Research Group GNCS and this work is partially funded by INdAM-GNCS. Paola F. Antonietti has been partially funded by the research projects PRIN n. 201744KLJL and PRIN n. 20204LN5N5 funded by MIUR.
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. The first draft of the manuscript was written by Ilario Mazzieri and Michele Botti. All authors commented on previous versions of the manuscript and approved the final one.
Corresponding author
Ethics declarations
Conflict of Interests
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Availability of data and material
The datasets generated during the current study are available from Ilario Mazzieri upon reasonable request.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Dedicated to Professor Alfio Quarteroni on the occasion of his 70th birthday.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Antonietti, P.F., Botti, M. & Mazzieri, I. On Mathematical and Numerical Modelling of Multiphysics Wave Propagation with Polytopal Discontinuous Galerkin Methods: a Review. Vietnam J. Math. 50, 997–1028 (2022). https://doi.org/10.1007/s10013-022-00566-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10013-022-00566-3
Keywords
- Poroelasticity
- Acoustics
- Discontinuous Galerkin method
- Polygonal and polyhedral meshes
- Stability and convergence analysis