Computational modeling of fluorescence loss in photobleaching

Abstract

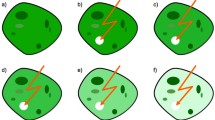
Fluorescence loss in photobleaching (FLIP) is a modern microscopy method for visualization of transport processes in living cells. Although FLIP is widespread, an automated reliable analysis of image data is still lacking. This paper presents a framework for modeling and simulation of FLIP sequences as reaction–diffusion systems on segmented cell images. The cell geometry is extracted from microscopy images using the Chan–Vese active contours algorithm (IEEE Trans Image Process 10(2):266–277, 2001). The PDE model is subsequently solved by the automated Finite Element software package FEniCS (Logg et al. in Automated solution of differential equations by the finite element method. Springer, Heidelberg, 2012). The flexibility of FEniCS allows for spatially resolved reaction diffusion coefficients in two (or more) spatial dimensions.

Appendices

Appendix 1: Shape gradients

The Chan–Vese energy (2) consists of two parts: Minimizing the length of the curve has some regularizing effect $E_{\mathrm {reg}}(\varGamma ) = \int _\varGamma \; \mathrm {d} \sigma$. Without loss of generality, we may assume parametrization with respect to arc-length

$$\begin{aligned} \varGamma = {\gamma }(\sigma ) : [0, l] \rightarrow {\mathbb R}^2 \end{aligned}$$

such that $|\gamma '|=1$ and $l = \int _\varGamma \; \mathrm {d} \sigma = \int _0^l |\gamma '(\sigma )|^2 \; \mathrm {d} \sigma$. Let $\omega$ be another closed, $C^1$-curve $\omega : [0,l] \rightarrow {\mathbb R}^2$ such that $\omega (0)=\omega (l)$ and $\omega '(0)=\omega '(l)$. Consider an $\epsilon$-variation of the curve $\varGamma$ given by $\gamma _\epsilon = \gamma + \epsilon \omega$. The variation of $E_{reg} = \int _0^l |\gamma '(\sigma )|^2 \; \mathrm {d} \sigma$ is defined as

$$\begin{aligned} \left. \delta E_{\mathrm {reg}} (\gamma , \omega ) = \frac{\mathrm {d}}{\mathrm {d}\epsilon }E_{\mathrm {reg}} (\gamma _\epsilon ) \right| _{\epsilon =0} \end{aligned}$$

By differentiation we find

$$\begin{aligned} \delta E_{\mathrm {reg}} (\gamma , \omega )&\left. = \frac{\mathrm {d}}{\mathrm {d}\epsilon }\int _0^l |\gamma '(\sigma )+\epsilon \omega '(\sigma )|^2 \; \mathrm {d} \sigma \right| _{\epsilon =0}\\&= \left. 2 \int _0^l (\gamma '(\sigma )+\epsilon \omega '(\sigma )) \omega '(\sigma ) \; \mathrm {d} \sigma \right| _{\epsilon =0} \\&= 2 \int _0^l \gamma '(\sigma ) \omega '(\sigma ) \; \mathrm {d} \sigma . \end{aligned}$$

By partial integration, using periodicity of $\gamma '$ and $\omega$

$$\begin{aligned} \delta E_{\mathrm {reg}} (\gamma , \omega ) = -2 \int _0^l \gamma ''(\sigma ) \omega (\sigma ) \; \mathrm {d} \sigma . \end{aligned}$$

By definition, the $L^2$-shape gradient of $E_{\mathrm {reg}}$ is

$$\begin{aligned} \nabla _\varGamma E_{\mathrm {reg}}(\gamma ) = -2 \gamma ''. \end{aligned}$$

In arc-length parametrization $\gamma '' = - \kappa \cdot \mathbf {n}$, where $\mathbf {n}$ is the outward unit normal. Finally

$$\begin{aligned} \nabla _\varGamma E_{\mathrm {reg}}(\gamma ) = 2 \kappa \mathbf {n}. \end{aligned}$$

(23)

The fitting energy is

$$\begin{aligned} E_{\mathrm {fit}}(\gamma ) = \int _{{\mathrm {int}}\varGamma } (I(\mathbf {x})-c_-)^2 \; \mathrm {d} \mathbf {x}+ \int _{{\mathrm {ext}}\varGamma } (I(\mathbf {x})-c_+)^2 \; \mathrm {d} \mathbf {x}. \end{aligned}$$

The integral over the exterior segment equals the integral over the entire image without the interior part

$$\begin{aligned} E_{\mathrm {fit}}(\gamma ) =&\int _{{\mathrm {int}}\varGamma } (I(\mathbf {x})-c_-)^2 - (I(\mathbf {x})-c_+)^2 \; \mathrm {d} \mathbf {x}\\&+ \int _{{\mathrm {int}}\varGamma \cup {\mathrm {ext}}\varGamma } (I(\mathbf {x})-c_+)^2 \; \mathrm {d} \mathbf {x}. \end{aligned}$$

The last integral does not depend on the curve $\varGamma$ and the first one is subject of the next Lemma.

Lemma 1

Let $\gamma$ and $\omega$ be closed $C^1$-curves. Let $V : {\mathbb R}^2 \rightarrow {\mathbb R}$ be integrable. The variation of

$$\begin{aligned} E(\gamma ) = \int _{{\mathrm {int}}\gamma } V(\mathbf {x}) \; \mathrm {d} \mathbf {x}\end{aligned}$$

is

$$\begin{aligned} \delta E(\gamma , \omega ) = \int _0^l V(\gamma (\sigma )) \mathbf {n}(\sigma ) \cdot \omega (\sigma ) \; \mathrm {d} \sigma . \end{aligned}$$

The proof below shows that for Lemma 1 to hold true, arc-length parametrization is not necessary but convenient. Otherwise the unit normal n is to be replaced by the non-unit outward normal. As a result we have that the $L^2$-shape gradient is given by

$$\begin{aligned} \nabla _\varGamma E(\gamma ) = V(\gamma ) \mathbf {n}. \end{aligned}$$

(24)

Proof of Lemma 1

Let $P(x_1,x_2)=0$ and $Q(x_1,x_2)=\int _{0}^{x_1} V(\xi ,x_2) \; {\mathrm {d}} \xi$.

$$\begin{aligned} E(\gamma ) = \int _{{\mathrm {int}}\gamma } V(\mathbf {x}) \; \mathrm {d} \mathbf {x}= \int _{{\mathrm {int}}\gamma } \frac{\partial Q}{\partial x_1} - \frac{\partial P}{\partial x_2} \; {\mathrm {d}} x_1 \; {\mathrm {d}} x_2 . \end{aligned}$$

By Green’s formula

$$\begin{aligned} E(\gamma ) = \int _\gamma Q \; {\mathrm {d}} x_2. \end{aligned}$$

In the last curve integral $\mathbf {x}=\gamma$, ${\mathrm {d}} x_2 = \gamma _2' \; \mathrm {d} \sigma$ and thus

$$\begin{aligned} E(\gamma ) = \int _0^l Q(\gamma (\sigma )) \gamma _2'(\sigma ) \; \mathrm {d} \sigma . \end{aligned}$$

Consider the $\epsilon$-variation $\gamma _\epsilon = \gamma + \epsilon \omega$ and find

$$\begin{aligned} \delta E(\gamma ,\omega )&= \left. \frac{\mathrm {d}}{\mathrm {d}\epsilon }E(\gamma _\epsilon ) \right| _{\epsilon =0} \\&= \left. \frac{\mathrm {d}}{\mathrm {d}\epsilon }\int _0^l Q(\gamma _\epsilon ) (\gamma _\epsilon ')_2 \; \mathrm {d} \sigma \right| _{\epsilon =0} \\&= \left. \int _0^l \nabla Q(\gamma _\epsilon ) \cdot \omega (\gamma _\epsilon ')_2 + Q(\gamma _\epsilon ) \omega _2' \; \mathrm {d} \sigma \right| _{\epsilon =0}\\&= \int _0^l \nabla Q(\gamma ) \cdot \omega \gamma _2' + Q(\gamma ) \omega _2' \; \mathrm {d} \sigma . \end{aligned}$$

By partial integration and periodicity

$$\begin{aligned} \delta E(\gamma ,\omega )&= \int _0^l \nabla Q(\gamma ) \cdot \omega \gamma _2' - \frac{{\mathrm {d}}}{\mathrm {d} \sigma } \left( Q(\gamma )\right) \omega _2 \; \mathrm {d} \sigma \\&= \int _0^l \nabla Q(\gamma ) \cdot \omega \gamma _2' - \nabla Q(\gamma ) \cdot \gamma ' \omega _2 \; \mathrm {d} \sigma \nonumber \\&= \int _0^l \frac{\partial Q}{\partial x_1} \mathbf {n}\omega \; \mathrm {d} \sigma \\&= \int _0^l V(\gamma ) \mathbf {n}\omega \; \mathrm {d} \sigma . \end{aligned}$$

Here the (unit) normal is given by $\mathbf {n}= (\gamma _2', -\gamma _1')^T$ and our proof is complete. $\square$

The shape gradient of the Chan–Vese energy (3) follows from (23) and (24) where $V(\mathbf {x}) = (I(\mathbf {x})-c_-)^2 - (I(\mathbf {x})-c_+)^2$.

Appendix 2: Stability analysis

For simplicity of presentation we consider a reaction–diffusion system of type (9), but in one spatial variable and with diffusion coefficients scaled to unity

$$\begin{aligned} \begin{array}{rcccl} u_t &{}=&{} u_{xx} &{}+&{} k^- v - k^+ u, \\ v_t &{}=&{} v_{xx} &{}+&{} k^+ u - k^- v , \quad x \in (0,1) , \quad t > 0. \end{array} \end{aligned}$$

(25)

For illustration we consider homogenous Dirichlet and Neumann conditions for u and v, respectively

$$\begin{aligned} u(t,0)&= u(t,1) = 0 , \\ v_x(t,0)&= v_x(t,1) = 0. \end{aligned}$$

The interested reader can easily replace the Dirichlet condition by a Neumann condition as in (11). Initial data is given as in (12). The analysis uses elements by E. Bohl [4] which originally go back to R.S. Varga [26], L. Collatz [8] and E. Bohl [5]. We have chosen to present this concept, because it generalizes to two dimensions and applies to non-linear reaction diffusion problems.

The bilinear form

$$\begin{aligned} \int _\varOmega \varDelta u \phi \; \mathrm {d} x= - \int _\varOmega \nabla u \cdot \nabla \phi \; \mathrm {d} x\end{aligned}$$

acting on a finite dimensional approximation $u(x) = \sum _j u_j \phi _j(x)$ with piecewise linear elements $\phi _j(x_i) = \delta _{ij}$ is expressed as matrix–vector product

$$\begin{aligned} - \int _\varOmega \nabla u \cdot \nabla \phi _j \; \mathrm {d} x= \left( \mathbf {A}_h \mathbf {u}\right) _j . \end{aligned}$$

The vector $\mathbf {u}$ holds approximations on inner grid points $\mathbf {u}= (u_i)$, $u_i = u(x_i)$, $x_i=ih$, $i=1,2,\ldots , m$, and $(m+1)h=1$. The matrix is given by

$$\begin{aligned} \mathbf {A}_h = \left( a_{ij}\right) , \quad a_{ij} = -\int _\varOmega \nabla \phi _i \cdot \nabla \phi _j \; \mathrm {d} x. \end{aligned}$$

Due to the piecewise constant gradients $\nabla \phi _j$, the matrix becomes a well-known (finite difference) approximation to the second derivative. With homogenous Dirichlet conditions the linear operator reads

$$\begin{aligned} -u_{xx} \approx \mathbf {A}_h \mathbf {u}= \frac{1}{h^2} \left( \begin{array}{cccc} 2 &{} -1 &{} &{} \\ -1 &{} \quad \ddots &{} \quad \ddots &{} \\ &{} \quad \ddots &{} \quad \ddots &{} \quad -1 \\ &{} \quad &{} \quad -1 &{} \quad 2 \end{array}\right) \mathbf {u}. \end{aligned}$$

In the case of homogenous Neumann conditions $v_0=v_1$ and $v_m=v_{m+1}$, the second derivative on inner grid points is approximated by

$$\begin{aligned} -v_{xx} \approx \mathbf {B}_h \mathbf {v}= \frac{1}{h^2} \left( \begin{array}{ccccc} 1 &{} -1 &{} &{} &{}\\ -1 &{} \quad 2 &{} \quad -1 &{} \quad &{}\\ &{} \quad \ddots &{} \quad \ddots &{} \quad \ddots &{} \\ &{} \quad &{} \quad -1 &{} \quad 2 &{} \quad -1 \\ &{} \quad &{} \quad &{} \quad -1 &{} \quad 1 \end{array}\right) \mathbf {v}. \end{aligned}$$

Semi-implicit time stepping results in a linearly coupled, discrete system

$$\begin{aligned}{}[(1+\varDelta {t}k^+)\mathbf {Id}+ \varDelta {t}\mathbf {A}_h] \mathbf {u}^{n+1}= & {} \mathbf {u}^n + \varDelta {t}k^- \mathbf {v}^n , \nonumber \\ {[}(1+\varDelta {t}k^-)\mathbf {Id}+ \varDelta {t}\mathbf {B}_h] \mathbf {v}^{n+1}= & {} \mathbf {v}^n + \varDelta {t}k^+ \mathbf {u}^n . \end{aligned}$$

(26)

Naturally, step sizes are positive $\varDelta {t}$, $h > 0$ and reaction rates are non-negative $k^\pm \ge 0$. Again, $u_i^n$ is thought as approximation to $u(t_n,x_i)$. In fact one can prove that the numerical approximation converges to the solution of the PDE system.

The key argument relies on the fact that the finite difference operators $\mathbf {Id}+ \varDelta {t}\mathbf {A}_h$ as well as $\mathbf {Id}+ \varDelta {t}\mathbf {B}_h$ are inverse-monotone with bounded inverse. While $\mathbf {A}_h$ inherits its inverse-monotonicity from the negative Laplacian, $\mathbf {B}_h$ is obviously singular.

Lemma 2

With non-negative parameters $\varDelta {t}\ge 0$, $h>0$ and reaction rates $k^\pm \ge 0$ both system matrices $(1+\varDelta {t}k^+)\mathbf {Id}+ \varDelta {t}\mathbf {A}_h$ and $(1+\varDelta {t}k^-)\mathbf {Id}+ \varDelta {t}\mathbf {B}_h$ are regular with non-negative and uniformly bounded inverse.

An obvious consequence is:

Corollary 1

With non-negative initial data $u^0 \ge 0$ and $v^0 \ge 0$ and reaction rates $k^\pm \ge 0$, approximations computed by (26) remain non-negative for all discrete time levels $n \varDelta {t}\ge 0$.

The proof of Lemma 2 is based on inverse-monotone Z-matrices. A Z-matrix is characterized by its non-positive off-diagonal elements:

$$\begin{aligned} \mathbf {Z}= (z_{ij}) , \quad z_{ij} \le 0 , \quad i \ne j . \end{aligned}$$

A matrix $\mathbf {A}$ is called inverse-monotone if it is invertible with elementwise non-negative inverse $\mathbf {A}^{-1} \ge 0$. In this case $\mathbf {A}\mathbf {e}\ge 0$ implies $\mathbf {e}\ge 0$; i.e. solving the system preserves positivity. An inverse-monotone Z-matrix is called M-matrix.

Any strictly positive vector $\mathbf {p}>0$ defines a weighted max-norm

$$\begin{aligned} \Vert \mathbf {x}\Vert _p = \max _i \{|x_i|/p_i\}. \end{aligned}$$

The corresponding operator norm for a monotone (i.e. elementwise positive) matrix is $\Vert \mathbf {A}\Vert _p = \Vert \mathbf {A}\mathbf {p}\Vert _p$.

The following M-criterion can be found in E. Bohl [4], Chapter I, Theorem 5.1:

Lemma 3

A Z-matrix $\mathbf {A}$ is M-matrix if and only if $\mathbf {A}$ is semi-positive. That is, there exists $\mathbf {e}>0$ with $\mathbf {A}\mathbf {e}> 0$.

Obviously, adding a non-negative diagonal matrix to a M-matrix preserves the M-property. With these preparations, we are ready to prove the main stability result.

Proof of Lemma 2

Let $\delta = (1,\ldots ,1)^T$. Note that $\mathbf {A}_h\delta = (1,0,\ldots ,0,1)/h^2$ and $B_h\delta = 0$. Obviously $\mathbf {B}_h$ is singular. Both $\mathbf {Id}+\varDelta {t}\mathbf {A}_h$ and $\mathbf {Id}+\varDelta {t}\mathbf {B}_h$ are Z-matrices. Both are semi-positive

$$\begin{aligned} (\mathbf {Id}+\varDelta {t}\mathbf {A}_h)\delta \ge (\mathbf {Id}+\varDelta {t}\mathbf {B}_h)\delta \ge \delta > 0 . \end{aligned}$$

By Lemma 3 $\mathbf {Id}+\varDelta {t}\mathbf {A}_h$ and $\mathbf {Id}+\varDelta {t}\mathbf {B}_h$ are M-matrices. We may add any positive diagonal matrix $\varDelta {t}k \mathbf {Id}$ and the M-property is preserved. Thus both system matrices are M-matrices, even with non-constant, non-negative reaction rates $k^\pm$. It remains to show the uniform bound for the inverse. We have that

$$\begin{aligned} \left[ (1+\varDelta {t}k^+)\mathbf {Id}+\varDelta {t}\mathbf {A}_h\right] \delta \ge \delta , \\ \left[ (1+\varDelta {t}k^-)\mathbf {Id}+\varDelta {t}\mathbf {B}_h\right] \delta \ge \delta . \end{aligned}$$

Multiplying by the non-negative inverse, taking norms the desired bound follows

$$\begin{aligned} \begin{array}{rcl} \Vert \left[ (1+\varDelta {t}k^+)\mathbf {Id}+\varDelta {t}\mathbf {A}_h\right] ^{-1}\Vert _\delta &{}\le &{} 1 , \\ \Vert \left[ (1+\varDelta {t}k^-)\mathbf {Id}+\varDelta {t}\mathbf {B}_h\right] ^{-1}\Vert _\delta &{}\le &{} 1 \end{array} \end{aligned}$$

(27)

and the proof is complete. $\square$

Note that $\Vert \cdot \Vert _\delta$ is the well-known max-norm. Via the eigensystem of $\mathbf {A}_h$ one can also show that $\mathbf {A}_h$ itself is a M-matrix.

The uniform bound of the inverse system matrix implies stability of the numerical method: By linearity, errors are governed by the system (26) itself. Uniform boundedness (27) implies stability in the sense that errors at later time depend continuously on initial errors. Convergence towards a smooth solution of the reaction–diffusion system (25) follows from the discrete Gronwall lemma.