Getting started with uncertainty evaluation using the Monte Carlo method in R

Abstract

The evaluation of measurement uncertainty is often perceived by laboratory staff as complex and quite distant from daily practice. Nevertheless, standards such as ISO/IEC 17025, ISO 15189 and ISO 17034 that specify requirements for laboratories to enable them to demonstrate they operate competently, and are able to generate valid results, require that measurement uncertainty is evaluated and reported. In response to this need, a European project entitled “Advancing measurement uncertainty—comprehensive examples for key international standards” started in July 2018 that aims at developing examples that contribute to a better understanding of what is required and aid in implementing such evaluations in calibration, testing and research. The principle applied in the project is “learning by example”. Past experience with guidance documents such as EA 4/02 and the Eurachem/CITAC guide on measurement uncertainty has shown that for practitioners it is often easier to rework and adapt an existing example than to try to develop something from scratch. This introductory paper describes how the Monte Carlo method of GUM (Guide to the expression of Uncertainty in Measurement) Supplement 1 can be implemented in R, an environment for mathematical and statistical computing. An implementation of the law of propagation of uncertainty is also presented in the same environment, taking advantage of the possibility of evaluating the partial derivatives numerically, so that these do not need to be derived by analytic differentiation. The implementations are shown for the computation of the molar mass of phenol from standard atomic masses and the well-known mass calibration example from EA 4/02.

Introduction

One of the complicating factors in the evaluation and propagation of measurement uncertainty is the competence in mathematics and statistics required to perform the calculations. Nevertheless, standards such as ISO/IEC 17025 [1], ISO 15189 [2] and ISO 17034 [3] that specify requirements for laboratories to enable them to demonstrate they operate competently, and are able to generate valid results, require that measurement uncertainty is evaluated and reported. The well-known law of propagation of uncertainty (LPU) from the Guide to the expression of uncertainty in measurement (GUM) [4] requires the calculation of the partial derivatives of the measurement model with respect to each of the input variables.

In this primer, we (re)introduce the Monte Carlo method of GUM Supplement 1 (GUM-S1) [5], which takes the same measurement model and the probability density functions assigned to the input variables as the LPU to obtain (an approximation to) the output probability density function. We show, based on some well-known examples illustrating the evaluation of measurement uncertainty, how this method can be implemented for a single measurand and how key summary outputs, such as the estimate (measured value), the associated standard uncertainty, the expanded uncertainty and a coverage interval for a specified coverage probability, can be obtained.

The Monte Carlo method of GUM-S1 [5] is a versatile method for propagating measurement uncertainty using a measurement model. It takes the measurement model, i.e. the relationship between the output quantity and the input quantities, and random samples of the probability density functions of the input quantities to generate a corresponding random sample of the probability density function of the output quantity.

The use of probability density functions is well covered in the GUM [4] and further elaborated in GUM-S1 [5]. In this primer, the emphasis is on setting up an uncertainty evaluation using the Monte Carlo method for a measurement model with one output quantity (a “univariate” measurement model). GUM Supplement 2 (GUM-S2) [6] provides an extension of the Monte Carlo method to measurement models with two or more output quantities (“multivariate” measurement models) as well as giving a generalisation of the LPU to the multivariate case.

The vast majority of the uncertainty evaluations in calibration and testing laboratories are performed using the LPU [4]. This mechanism takes the estimates (values) of the input quantities and the associated standard uncertainties to obtain an estimate for the output quantity and the associated standard uncertainty. The measurement model is used to compute (1) the value of the output quantity and (2) the sensitivity coefficients, i.e. the first partial derivatives of the output quantity with respect to each of the input quantities (evaluated at the estimates of the input quantities). The second part of the calculation involving the partial derivatives is perceived as being cumbersome and requires skills that are often beyond the capabilities of laboratory staff and researchers. The computation of the sensitivity coefficients can also be performed numerically [7, 8]. One of the advantages of the Monte Carlo method is that sensitivity coefficients are not required. All that is needed is a measurement model, which can be in the form of an algorithm, and a specification of the probability distributions for the input quantities. These probability distributions (normal, rectangular, etc.) are typically already specified in uncertainty budgets when the LPU is used.

In this tutorial, we show how the Monte Carlo method of GUM-S1 can be implemented in R [9]. This environment is open-source software and specifically developed for statistical and scientific computing. Most of the calculations in laboratories, science and elsewhere are still performed using mainstream spreadsheet software. An example of using the Monte Carlo method of GUM-S1 with MS Excel is given in the Eurachem/CITAC Guide on measurement uncertainty [10]. It is anticipated that this tutorial will also be useful for those readers who would like to get started using other software tools or other languages.

Monte Carlo method

The heart of the Monte Carlo method of GUM-S1 can be summarised as follows [5]. Given a measurement model of the form

$$\begin{aligned} Y = f(X_1, \ldots ,X_N) \end{aligned}$$

and probability density functions assigned to each of the input quantities $X_1, \ldots ,X_N$, generate M sets of input quantities $X_{1,r}, \ldots ,X_{N,r}$ ($r = 1, \ldots , M$) and use the measurement model to compute the corresponding value for $Y_r$. M, the number of sets of input quantities should be chosen to be sufficiently large so that a representative sample of the probability density function of the output quantity Y is obtained. The approach here applies to independent input quantities and a scalar output quantity Y. For its extension to dependent input quantities, see GUM-S1 [5], and a multivariate output quantity, see GUM-S2 [6].

GUM-S1 [5, clause 6.4] describes the selection of appropriate probability density functions for the input quantities, thereby supplementing the guidance given in the GUM [4, clause 4.3]. GUM-S1 also provides guidance on the generation of pseudo-random numbers. Pseudo-random numbers rather than random numbers are generated by contemporary software since the latter are almost impossible to obtain. However, comprehensive statistical tests indicate that the pseudo-random numbers generated cannot be distinguished in behaviour from truly random numbers.

Considerable confidence has been gained by the authors over many years concerning the performance of the Monte Carlo method of uncertainty evaluation from a practical viewpoint. For measurement models that are linear in the input quantities, for which the law of propagation of uncertainty produces exact results, agreement with results from the Monte Carlo method to the numerical accuracy expected has always been obtained. Thus, weight is added to the above point: there is evidence that the effects of working with pseudo-random numbers and truly random numbers are identical.

If needed, the performance of a random number generator can be verified [11, 12]. For the purpose of this tutorial, it is assumed that the built-in random number generator in R is fit for purpose.

A refinement of the Monte Carlo method concerns selecting the number of trials automatically so as to achieve a degree of assurance in the numerical accuracy of the results obtained. An adaptive Monte Carlo procedure for this purpose involves carrying out an increasing number of Monte Carlo trials until the various results of interest have stabilised in a statistical sense. Details are provided in [5, clause 7.9] and since then an improved method in [13].

In many software environments, random number generators for most common probability density functions are already available; if not, they can be readily developed using random numbers from a rectangular distribution [5, annex C]. (The rectangular distribution is also known as the uniform distribution.) Should even a random number generator for the rectangular distribution not be available in the software environment, then the one described in GUM-S1 can be implemented as a basis for generating random numbers. The default random number generator in R is the Mersenne Twister [14], which is also implemented in many other programming environments, including MATLAB and MicroSoft Excel (since version 2010, see [15]). Based on this random number generator, there are generators available for a number of probability distributions [9].

The output of applying the Monte Carlo method is an array (vector) $Y_1, \ldots ,Y_M$ characterising the probability density function of the output quantity. This sample is, however, not in the form in which a measurement result is typically communicated. From the output $Y_1, \ldots ,Y_M$, the following can be computed:

• the measured value, usually taken as the arithmetic mean of Y₁, … , Y_M

• the standard uncertainty, usually computed as the standard deviation of Y₁, … , Y_M

• a coverage interval containing the value of the output quantity with a stated probability, obtained as outlined below;

• the expanded uncertainty;

• the coverage factor.

The last two items apply when the coverage interval can be reasonably approximated by a symmetric probability density function. Care should be taken in cases of asymmetric output probability density functions in which the mean of $Y_1, \ldots , Y_M$ might result in an unreliable estimator of the measurand, behaving worse than other estimators (such as the mode or the median) and even worse than the simple estimate obtained from $y = f(x_1, \ldots , x_n)$ provided by the measured model f directly applied to the input estimates $x_1, \ldots , x_n$.

The most general way of representing a coverage interval is by specifying its upper and lower limits. This representation is always appropriate whether the output distribution is symmetric or not. In many instances, however, the output probability density function is (approximately) symmetric, and then, the expanded uncertainty can be computed as the half-width of the coverage interval. The coverage factor can be computed from the expanded uncertainty U(y) and the standard uncertainty u(y), i.e. $k = U(y)/u(y)$. The symmetry of the output probability density function can be verified by examining a histogram of $Y_1, \ldots ,Y_M$, or obtaining a kernel density plot [16, 17], a smooth approximation to the probability density function.

Software environment

R is an open-source language and environment for statistical computing and graphics. It is a GNU project, similar to the S language and environment, which was developed at Bell Laboratories (formerly AT&T, now Lucent Technologies) by John Chambers and colleagues. R can be considered as a different implementation of S [9]. It is available for Windows, MacOS and a variety of UNIX platforms (including FreeBSD and Linux) [9].

Users of Windows, MacOS and a number of Linux distributions may also wish to download and install RStudio [18], which provides an integrated development environment, in which code can be written, the values of variables can be monitored, and separate windows for the console and graphics output are available. The R code provided in this primer has been developed in RStudio (version 1.2.1335, build 1379 (f1ac3452)).

Generating random numbers

In R, it is straightforward to generate a sample of random numbers from most common probability density functions. For example, the following code generates a sample of a normal distribution with mean $\mu = {10.0}$ and standard deviation $\sigma = {0.2}$ and a sample size $M = {10{,}000}$:

The function to be called to generate an array (vector) of random numbers having a normal distribution with mean mu and standard deviation sigma is called rnorm. The line set.seed(2926) is useful for debugging purposes, as it ensures that the random number generator starts at the same point every time. Any other value for the seed would also ensure the exact reproduction of the series of numbers obtained from the random number generator. If that is not required, the line can be omitted. In this tutorial, the seed is set, so that the reader can exactly reproduce the output. The output is collected in a variable named X1. It is an array with 10,000 elements.

The following code snippet shows the mean and standard deviation of the 10,000 generated numbers, using R’s built in functions mean and sd, respectively.

Using R’s functions plot and hist, a histogram of variable X1 can be plotted (Fig. 1). The code to generate Fig. is as follows:

where hist calculates the histogram from the array X1 and plot generates the figure. The plotted histogram resembles that of a normal distribution. The larger is the number of samples drawn from the random number generator, the closer the resemblance to the normal distribution will be.

Fig. 1

Histogram of $M =$10,000 samples of the random variable X1 having a normal distribution with mean 10.0 and standard deviation 0.2

From the first code fragment in this section, it is readily seen that R has a function for generating random numbers with a normal distribution. It also has functions for generating random numbers with a rectangular distribution (runif), the t distribution (rt), exponential distribution (rexp) and gamma distribution (rgamma). There exist a package (extension) called “trapezoid” [19] implementing among others the trapezoidal distribution, a package called “mvtnorm” [20] implementing the multivariate normal distribution (useful when some of the input quantities are dependent [5]) and a package called “triangle” [21] implementing the triangular distribution. So, apart from the curvilinear trapezoidal distribution and the arc sine distribution, random numbers for all probability density functions mentioned in GUM-S1 [5, table 1] are available in R.

The arc sine distribution can be implemented as follows in R. According to GUM-S1 [5, clause 6.4.6.1], a U-shaped random variable X on the interval [a, b] can be obtained through

$$\begin{aligned} X = \dfrac{a+b}{2} + \dfrac{b-a}{2} \sin \Phi , \end{aligned}$$

where $\Phi$ is a random variable with a rectangular distribution on $[0, 2\pi ]$. In R, a function rarcsin that provides such a random variable, and a call to that function, can be coded as follows:

The argument n determines the number of random numbers returned; a and b denote the lower and upper limits, respectively, of the interval over which the arcsine distribution has a nonzero density. If $n > 1$, the function returns an array; if $n = 1$, it returns a single number. This behaviour mimics the behaviour of the other functions implemented in R to generate random numbers.

The last line in the code snippet creates an array X2 of M elements ($M = {10{,}000}$ in this instance) of a random variable having an arcsine distribution over the interval $[-1,1]$. A histogram (obtained through the R function hist) is shown in Fig. 2.

Fig. 2

Histogram of the random variable X2 containing $M =$ 10,000 samples having an arcsine distribution between $-1$ and 1

Implementation of the Monte Carlo method

Molar mass of phenol

In this example, the molar mass of phenol (molecular formula C₆H₅OH) is computed. The example shows how an output quantity with an uncertainty is obtained from input quantities with uncertainty. There is no experiment involved. The example is pivotal for many calculations involving reference data, such as atomic weights, molar masses and enthalpies of formation.

The molar mass is computed from the standard atomic masses and the coefficients appearing in the molecular formula, which for the elements involved are 6 for carbon, 6 (5+1) for hydrogen and 1 for oxygen. The current relative atomic masses are used as published by IUPAC (International Union of Pure and Applied Chemistry) [22]. The relative atomic masses that apply to “normal materials” are called standard atomic weights [22, 23]. Their interpretation is described in an IUPAC technical report [24]. From this interpretation, it follows that the standard atomic masses are modelled using the rectangular distribution.

The molecular weight of phenol (chemical formula C₆H₅OH) is computed as

$${{M}}_{{\text{r}}} ({\text{C}}_{6} {\text{H}}_{5} {\text{OH}}) = 6A_{{\text{r}}} ({\text{C}}) + 6A_{{\text{r}}} ({\text{H}}) + A_{{\text{r}}} ({\text{O}})$$

The Monte Carlo method is implemented in R using $M = {100{,}000}$ trials. The R code that performs the evaluation reads as

The first line declares a variable M that holds the number of trials to be carried out by the Monte Carlo method. Then, for each of the elements, M samples are drawn using the rectangular distribution (using R’s function runif) and the lower and upper limits provided by the standard atomic weights of IUPAC [22]. These arrays have, respectively, the names C, H and O for the atomic masses of carbon, hydrogen and oxygen. The molar mass is then computed in the line defining MW. R is very efficient with vectors (arrays) and matrices (tables) [25]. The value of the molar mass (MW.val) is computed by taking the average of MW, the standard uncertainty by taking the standard deviation of MW and the expanded uncertainty by taking the half-width of the ${95}{\%}$ coverage interval. The latter is obtained by calculating the 0.025 and 0.975 quantiles (which provides a probabilistically-symmetric coverage interval) [5, clause 7.7]. In the last line, the coverage factor is computed as the ratio of the expanded uncertainty and the standard uncertainty.

The code to plot the output probability density function of the molar mass (MW) and to superimpose a normal distribution with the same mean and standard deviation is given as follows:

Fig. 3

Output probability density function of the molar mass of phenol and, superimposed, a normal distribution with the same mean and standard deviation

The first two lines compute the relevant part of the normal distribution around the mean ± 4 standard deviations. The subsequent lines plot the output probability density function and the normal distribution, respectively.

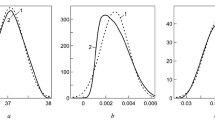
The graph is shown in Fig. 3. It is obvious that the normal distribution is not an appropriate approximation of the probability density function of the output quantity, which is close in appearance to a rectangular distribution and much narrower than the normal distribution. The molar mass is ${94.1108}\;\hbox {g}\hbox {mol}^{-1}$ with standard uncertainty ${0.0035}\;\hbox {g}\hbox {mol}^{-1}$. The expanded uncertainty is ${0.0059}\;\hbox {g}\hbox {mol}^{-1}$. The coverage factor is 1.67, which is much closer to the ${95}{\%}$ coverage factor of 1.69 for a rectangular distribution than that for a normal distribution (1.96).

Mass example from EA 4/02

In this section, the mass calibration example of EA 4/02 [26] is revisited. The evaluation using the Monte Carlo method rests on the same assumptions for the input quantities as in that example. In this example, we show how the Monte Carlo method can be implemented for any explicit measurement model with a single output quantity. The measurement model is coded in the form of a function, which promotes writing tidy code. It also allows iterative calculations to be readily implemented when the measurement model is defined implicitly [6]. This example describes the calibration of a 10 $\hbox {kg}$ weight by comparison with a standard 10 $\hbox {kg}$ weight. The weighings are performed using the substitution method. This method is implemented in such a way that three mutually independent observations for the mass difference between the two weights are obtained.

The measurement model is given by [26, S2]:

$$\begin{aligned} m_\mathrm {X} = m_\mathrm {S} + \updelta m_\mathrm {D} + \updelta m + \updelta m_\mathrm {C} + \updelta B, \end{aligned}$$

(1)

where the symbols have the following meaning:

$m_\mathrm {X}$:

   conventional mass of the weight being calibrated,

$m_\mathrm {S}$:

   conventional mass of the standard,

$\updelta m_\mathrm {D}$:

   drift of the value of the standard since its last calibration,

$\updelta m$:

   observed difference in mass between the unknown mass and the standard,

$\updelta m_\mathrm {C}$:

   correction for eccentricity and magnetic effects,

$\updelta B$:

   correction for air buoyancy.

For using the Monte Carlo method, probability density functions are assigned to each of the five input quantities [5]. These probability density functions are described in the original example [26].

The conventional mass of the standard $m_\mathrm {S}$ is modelled using the normal distribution with mean 10,000.005 $\hbox {g}$ and standard deviation 0.0225 $\hbox {g}$. The standard deviation (standard uncertainty) is calculated from the expanded uncertainty and the coverage factor provided on the calibration certificate. This interpretation is also described in GUM-S1 [5, 6.4.7]. The drift of the mass of the standard weight $\updelta m_\mathrm {D}$ is modelled using a rectangular distribution, centred at 0.000 $\hbox {g}$ and with a half-width of 0.015 $\hbox {g}$. The corrections for eccentricity and magnetic effects and that for air buoyancy are both modelled using a rectangular distribution with midpoint 0.000 $\hbox {g}$ and half-width 0.010 $\hbox {g}$.

The mass difference $\updelta m$ between the two weights computed from the indications of the balance is calculated as the mean of $n = 3$ independent observations. EA 4/02 explains that the associated standard uncertainty is computed from a pooled standard deviation 0.025 $\hbox {g}$, obtained from a previous mass comparison, divided by $\sqrt{n}$.

In the implementation of the Monte Carlo method, the three observations are simulated using normal distributions with means of the observed values (i.e. 0.010 $\hbox {g}$, 0.030 $\hbox {g}$ and 0.020 $\hbox {g}$, respectively) and a standard deviation of 0.025 $\hbox {g}$ for each. The mass difference is formed by calculating the arithmetic average of the three simulated observations.

The measurement model [Eq. (1)] can be coded in R as follows:

where m.std denotes the conventional mass of the standard weight, dm.d the drift correction of the conventional mass of the standard weight, diff the mass difference obtained from the substitution weighing, dm.c the correction due to eccentricity and magnetic effects and dm.B the correction due to air buoyancy. The function is called mass.x and returns the value of the output quantity $m_\mathrm {X}$.

Most programming languages implement a “for” loop, which enables executing a block of code a defined number of times. Anyone familiar with this “for” loop in computer programming would now use this kind of loop to code the recipe given in GUM-S1 clause 7.2.2 [5]. An implementation of the Monte Carlo method with a fixed value for the number of samples M would then read as follows:

On the first line, the probability level of the coverage interval (prob) is defined to be 0.95. In accordance with the guidance in clause 7.2.2 of GUM-S1 [5], M is calculated using the built-in function ceiling which returns the smallest integer not less than its argument. With prob = 0.95, the net effect of calling ceiling is that the floating point number is converted to an integer, as the result of 1/(1-prob) of 20; hence, the minimum number of Monte Carlo trials is $M = {10{,}000} \times {20} = {200{,}000}$. Then, an array (vector) m.x is declared that will hold the values calculated for the mass of the weight being calibrated. The vector m.data is a temporary storage for simulating the mass differences between the standard weight and the weight being calibrated. In the for loop, at each iteration a sample is drawn of the input quantities $m_\mathrm {S}$ (m.std), $\updelta m_\mathrm {D}$ (dm.d), $\updelta m_\mathrm {C}$ (dm.c) and $\updelta B$ (dm.B). The mass difference from comparing the two weights (m.diff) is simulated by drawing from a normal distribution with different means, but the same standard deviations, the three readings and taking the average. The measured value of the output quantity $m_\mathrm {X}$ (m.x) is finally obtained by calling the measurement model with as arguments the input quantities.

Running the above code provides the following output for the mean, standard deviation (standard uncertainty) and the coverage interval of $m_\mathrm {X}$:

where the argument probs holds the probabilities corresponding to the lower and upper ends of the probabilistically symmetric 95$\%$ coverage interval.

This way of coding an implementation of the Monte Carlo method would work in a large number of computer languages, including Python, MATLAB, Fortran, C, C++ and Pascal. While the above code in R does what is intended, the same task can be performed with greater effectiveness in R, exploiting the fact that R is very efficient in working with vectors and matrices [25]. Computational efficiency is especially important with more complex models and larger numbers of Monte Carlo trials, as it can greatly reduce the required computing time. The following code implements the same simulation, using vectors and matrices where possible:

Now the variables m.std, dm.d, dm.c and dm.B are vectors holding all M values for the input quantities. The data from comparing the weights are summarised in a matrix called m.data of M rows and 3 columns. The matrix is constructed by adding the means (0.01, 0.03 and 0.02) to the simulated data which have been generated using the normal distribution with mean 0 and standard deviation 0.025. The mass differences are computed by calculating the row means and storing these in m.diff using the R function apply. Note also that the measurement model can be called with vectors rather than scalars as arguments (last line of the code); in this case also, m.x is a vector of length M.

The second code runs in less than half the time of the first implementation. For this simple example, the difference is a matter of a few seconds, but for more complex models the difference in speed will be of more practical significance. Especially the steps that are repeated often should be carefully thought about. Another issue is memory use. The second implementation consumes appreciably more memory (for it holds all generated values for the input quantities) than the first (which only holds the last value for each of the input quantities).

The second code provides the following output for the mean, standard deviation (standard uncertainty) and the coverage interval of $m_\mathrm {X}$:

Fig. 4

Probability density function of the output quantity m.x and superimposed a normal distribution with the same mean and standard deviation

The output probability density function is shown in Fig. 4. Its form closely resembles that of a normal distribution with mean 10,000.025 $\hbox {g}$ and standard deviation 0.029 $\hbox {g}$. The following code computes the expanded uncertainty by taking the half-width of the 95$\%$ coverage interval and the coverage factor by dividing the expanded uncertainty by the standard uncertainty:

The expanded uncertainty is 0.057 $\hbox {g}$, and the coverage factor is 1.96. This coverage factor is that of a 95$\%$ coverage interval of the normal distribution. The coverage factor differs from that used in EA 4/02, which uses $k = 2$ for obtaining (at least) 95$\%$ coverage probability. The close agreement is readily explained, as the dominating uncertainty contributions are modelled using the normal distribution, and the sum of two normal distributions is also normally distributed (see also the measurement model, Eq. (1)). That the output quantity has an (approximately) normal distribution is reflected in the coverage factor obtained from the Monte Carlo method.

Now all results are obtained that commonly appear on a calibration certificate (as well as in many test reports), as described in ISO/IEC 17025 [1]:

• the measured value (= value of the output quantity);

• the expanded uncertainty;

• the coverage factor.

In this case, one might also be willing to state that the output probability density function is a normal distribution, whereas in this case such a statement can reasonably be made, in most cases the output probability density function cannot directly be approximated by a well-known analytic probability density function. Comparison of the three results listed above with those from the GUM would imply that for comparable data the GUM would be fit for purpose in a subsequent uncertainty evaluation. In a measurement model with $m_\mathrm {X}$ as one of the input quantities, the above information suffices to apply the GUM [4].

Law of propagation of uncertainty

The law of propagation of uncertainty (LPU) is the most widely used mechanism for propagating uncertainty. Whereas with the Monte Carlo method the lack of computing and programming skills can form a bottleneck, with the LPU it is often the calculation of the sensitivity coefficients, i.e. the partial derivatives of the output quantity with respect to the input quantities, that provides a difficulty. Most guidance documents, such as the GUM [4], GUM-S2 [6] and EA 4/02 [26] direct their readers to analytic differentiation of the measurement model to obtain the expressions for calculating the sensitivity coefficients. While this guidance is fully appropriate, it is not always practicable, for many people have lost their skills in differentiation. The fact that there are tables with derivatives of common functions (such as [27, 28]) is barely mentioned in such documents. Numerical approximation of the sensitivity coefficients [7, 8, 10, 29] is a very good alternative, provided that it is done properly. In this section, we show how to use numerical differentiation and the law of propagation of uncertainty to perform the uncertainty evaluation of the mass example of EA 4/02  [26].

The R package numDeriv provides the function grad (from gradient) that returns from a function a generally good approximation, using Richardson extrapolation [30], of the partial derivatives of the input variables. The function returns a vector holding the values of these partial derivatives. The function passed to grad should have only one argument, namely a vector holding all input variables. Hence, the measurement model needs to be reformulated as follows:

where x denotes the vector with input variables. For clarity and convenience, in the function body of mass2.x the same symbols have been used as in mass.x shown previously. The convenience extends to easier debugging the code as necessary. The penultimate line calculates the result of the function as the sum of the five input variables, just as in the case of the Monte Carlo method.

The uncertainty evaluation itself can be coded as follows:

The first line loads the package numDeriv (which needs to be installed in RStudio). The next two lines define the values of the input quantities. The vector sens on the fourth line holds the sensitivity coefficients returned by calling grad. The subsequent three lines calculate the standard uncertainties associated with the five input quantities. The penultimate line calculates the estimate of the output quantity m.x and the last line its associated standard uncertainty m.x.unc. Again, this last line shows the flexibility of R working with vectors.

The mass of the calibrated weight is 10,000.025 $\hbox {g}$ with standard uncertainty 0.029 $\hbox {g}$. Using a coverage factor $k = 2$, the expanded uncertainty becomes 0.059 $\hbox {g}$. These results reproduce those in example S.2 of EA 4/02 to the number of decimal digits given.

The values of the sensitivity coefficients are

and are identical to those given in EA 4/02 [26]. The code is also valid for measurement models with non-trivial sensitivity coefficients [8].

The approach described also works with correlated input variables. In that case, the calculation of the standard uncertainty associated with $m_\mathrm {X}$ is performed as follows:

The first two lines form the covariance matrix, diagonal in this case, associated with the five input quantities. (These are only needed to create the covariance matrix; if there were correlations between the five input variables, the code for creating it would have to be adapted accordingly.) The actual implementation of the LPU for correlated input variables is given in the last two lines of the previous code. By vector/matrix multiplication (see also the law of propagation of uncertainty in GUM-S2 [6]), a covariance matrix of dimension $1 \times 1$ associated with the output quantity is returned (tmp). The last line takes the square root of the only element in this matrix (holding the variance of $m_\mathrm {X}$) to obtain the standard uncertainty associated with $m_\mathrm {X}$. This standard uncertainty is 0.029 $\hbox {g}$.

Interfacing with Word, Excel and LaTeX

This article has been developed with R Sweave using the knitr package [31, 32]. R Sweave is implemented in RStudio [18] and enables LaTeX  to be combined with R (and other systems). Upon compilation, the PDF (portable document format) reflects the output after executing the R code, compiling the resulting LaTeX  file. It has the great advantage that the consistency between data, code and output is preserved [33].

Data collected in mainstream spreadsheet software can be processed in R, for instance, using the openxlsx package [34] which provides functions for reading and writing entire Excel workbooks. It supports the xlsx-format and also allows R to create new workbooks, fill these and write these.

Producing output in Microsoft Word or HTML format is possible using R markdown [35] and also available in RStudio [18]. The syntax resembles that of Word, with the possibility of including tables, graphs and calculations involving R. Formulæ  can be incorporated using a syntax that is similar to that in Word and LaTeX  and upon compilation to Word, results in editable formulæ, compatible with the equation editor of MS Word 2007 and later (using the docx file format).

Discussion and conclusions

In this tutorial, we have shown how straightforwardly the Monte Carlo method for propagating distributions can be implemented in software. True, it requires some programming skills, but the code provided can serve as a template for more complex applications. Two versions have been given, one working with most programming languages and a second optimised for R.

The framework shown for the mass example can readily be extended to nonlinear measurement models and models with multiple output quantities. The flexibility also extends to skewed probability density function for the output quantity. In this case, the Monte Carlo method may (correctly) provide a different estimate from just using the measurement model and the estimates of the input quantities. Also, a different 95$\%$ coverage interval (see GUM-S2 [6]) may be preferred to the probabilistically symmetric one as used in the examples (which both have an (approximately) symmetric output probability density function for the measurand).

We also have shown how the law of propagation of uncertainty can be used without the need for deriving the analytic expressions for the sensitivity coefficients (the partial derivatives of the output quantity with respect to the input quantity). Code, again in the form of a template, has been provided that after adaptation works with any univariate measurement model and also for the case of correlated input quantities.