Hyperbolic and pseudo-hyperbolic equations in the theory of vibration

Abstract

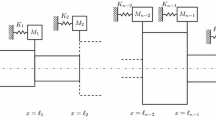
Longitudinal vibration of bars is usually considered in mathematical physics in terms of a classical model described by the wave equation under the assumption that the bar is thin and relatively long. More general theories have been formulated taking into consideration the effect of the lateral motion of a relatively thick bar (beam). The mathematical formulation of these models includes higher-order derivatives in the equation of motion. Rayleigh derived the simplest generalization of the classical model in 1894, by including the effects of lateral motion and neglecting the shear stress. Bishop obtained the next generalization of the theory in 1952. The Rayleigh–Bishop model is described by a fourth-order partial differential equation not containing the fourth-order time derivative. He took into account the effects of shear stress. Both Rayleigh’s and Bishop’s theories consider lateral displacement being proportional to the longitudinal strain. The Bishop model was generalized by Mindlin and Herrmann. They considered the lateral displacement proportional to an independent function of time and longitudinal coordinate. This result is formulated as a system of two differential equations of second order, which could be replaced by a single equation of fourth order resolved with respect to the highest order time derivative. To obtain a more general class of equations, the longitudinal and lateral displacements are expressed in the form of a power series expansion in the lateral coordinate. In this paper, all of the above-mentioned equations are considered in the framework of a general theory of hyperbolic equations, with the aim of classifying the equations into general groups. The solvability of the corresponding problems is also discussed.