Analytical expressions for the electrostatically actuated curled beam problem

Abstract

This works presents analytical expressions of the electrostatically actuated initially deformed cantilever beam problem. The formulation is based on the continuous Euler–Bernoulli beam model combined with a single-mode Galerkin approximation. We derive simple analytical expressions for two commonly observed deformed beams configurations: the curled and tilted configurations. The derived analytical formulas are validated by comparing their results to experimental data and numerical results of a multi-mode reduced order model. The derived expressions do not involve any complicated integrals or complex terms and can be conveniently used by designers for quick, yet accurate, estimations. The formulas are found to yield accurate results for most commonly encountered microbeams of initial tip deflections of few microns. For largely deformed beams, we found that these formulas yield less accurate results due to the limitations of the single-mode approximation. In such cases, multi-mode reduced order models are shown to yield accurate results.

Appendix

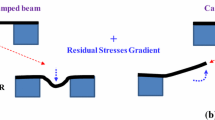
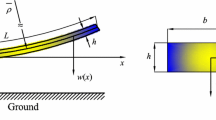
An initially deformed cantilever beam can be viewed as a stress-free structure that is brought to the deformed position through a moment M _o due to the stress gradient $\varGamma$ across its various layers (Senturia 2001; Fang and Wickert 1996; Younis 2011) (Fig. 5). Hence, its deflection can be described by

$$EI\frac{{d^{4} \hat{w}}}{{d\hat{x}^{4} }} = 0$$

(28)

The cantilever beam can have generally non-ideal (flexible) support (Fang and Wickert 1996; Younis 2011; Alkharabsheh and Younis 2013). Hence, generally, a rotational spring of constant k _r can be assumed at its anchor. The boundary conditions of the cantilever in this case are hinged with a rotational spring at $\hat{x}$ = 0 and shear-free with an applied constant moment at $\hat{x}$ = l, that is

$$EI\frac{{d^{2} \hat{w}(0)}}{{d\hat{x}^{2} }} = k_{r} \frac{{d\hat{w}(0)}}{{d\hat{x}}}; \, \hat{w}(0) = 0$$

(29)

$$EI\frac{{d^{3} \hat{w}(l)}}{{d\hat{x}^{3} }} = 0; \, EI\frac{{d^{2} \hat{w}(l)}}{{d\hat{x}^{2} }} = M_{0}$$

(30)

Integrating Eq. (28) four times successively with respect to $\hat{x}$ yields an algebraic equation with four constant coefficients, which can be written as

$$\hat{w} = c_{1} \hat{x}^{3} + c_{2} \hat{x}^{2} + c_{3} \hat{x} + c_{4}$$

(31)

where c ₁-c ₄ are the constants of integrations. Using Eqs. (29) and (30) in Eq. (31) gives

$$c_{1} = 0; \, c_{2} = \frac{{M_{0} }}{2EI}; \, c_{3} = \frac{{M_{0} }}{{k_{r} }}; \, c_{4} = 0$$

(32)

Substituting Eq. (32) into Eq. (31) yields the analytical expression of the beam profile.

$$\hat{w} = \frac{{M_{0} }}{2EI}\hat{x}^{2} + \frac{{M_{0} }}{{k_{r} }}\hat{x}$$

(33)

For perfectly clamped cantilever $k_{r} = \infty$, and recalling $M_{0} = I\varGamma$, yields the dimensional curling profile.

$$\hat{w} = \tilde{g}(x) = \frac{\varGamma }{2E}\hat{x}^{2}$$

(34)

Normalizing Eq. (34) using Eq. (3) yields the nondimensional beam profile of Eq. (13).

For a rigid beam, $E$ = ∞, which, yields the dimensional tilting profile.

$$\hat{w} = \frac{{M_{0} }}{{k_{r} }}\hat{x}$$

(35)

Here again we replace the typically unknown parameters $M_{0} /k_{r}$ with measured slope from the beam profile, $W_{0}^{tip} /l$; thus yielding the dimensional tilting profile of the beam.

$$\hat{w} = \frac{{M_{0} }}{{k_{r} }}\hat{x} = \frac{{W_{0}^{tip} }}{l}\hat{x}$$

(36)

Normalizing Eq. (36) using Eq. (3) yields the nondimensional beam profile of Eq. (24).